Energy and Power Engineering, 2013, 5, 756-762
doi:10.4236/epe.2013.54B146 Published Online July 2013 (http://www.scirp.org/journal/epe)
Analysis of Distribution Generation Influences on the Vol-
tage Limit Violation Probability of Distribution Line
Lu Zhang, Wei Tang, Muke Bai, Pengwei Cong
College of Information and Electrical Engineering, China Agriculture University, Beijing, China
Received April, 2013
ABSTRACT
Considering the time-sequence characteristic and randomness of load and natural resources, this paper studies on the
distributed generation (DG) impacts on voltage limit violation probability of distribution lines. The time-sequence
characteristic and randomness of load, wind and photovoltaic (PV) generation are analyzed; the indices and risk levels
of voltage limit violation probab ility of node and distribution line are proposed. By using probabilistic lo ad flow based
on semi-invariant method, the impact degrees of voltage limit violation are calculated with different distributed power
penetration levels, different seasons, different time periods, different allocation ratio between the wind power and PV
power. Voltage limit violation laws of distribution line, which are concluded by IEEE33 bus system simulation, are
very helpful to guide the voltage regulation of distribution line including distributed generation.
Keywords: Distribution Generation; Distribution Line; Voltage Limit Violation Probability; Ti me-sequence
Characteristic; Randomness
1. Introduction
Renewable energy is paid more attention and application
for its cleanness and environment protection in recent
years, so the research of distributed generation (DG) has
become focus. Effect of DG on voltage of distribution
line becomes serious with the increasing DG penetration
levels. As a result, the analysis o f voltage limits v iolation ,
which caused by DG, has important significance for en-
suring economic and safe oper ation of power grid.
There have been some researches on impact of voltage
limit violation of DG connected to power grid. Effect of
DG connected to transmission grid is analyzed by sensi-
tivity analysis method [1]. A probabilistic assessment
method was proposed [2], which adapt to different wind
speed levels in transmission grid. Reference [3] analyzed
impact of DG on voltage profiles using triangular load
model. Impact of photovoltaic (PV) power on voltage
was analyzed [4, 5]. Summarizing the literature [3-5],
only maximum output of DG and peak load was consid-
ered and the indices were calculated by certain method.
But in fact, load and output of DG fluctuate with seasons
significantly; daily load has large difference between peak
and valley, which also has strong uncertainty. Therefore,
the previous works are considered inadequately.
This paper comprehensively considers randomness
and time-sequence characteristic of load and DG. The
organization is as follows: Time-sequence characteristic
and randomness of load and DG is introduced in Section
2. Indices of distribution line voltage limit violation
probability and calculation method are proposed in Sec-
tion 3. Analysis of distribution line voltage limit viola-
tion is presented in Section 4, followed by conclusions in
Section 5.
2. Time-Sequence Characteristic and
Randomness of Load and DG
2.1. Time-Sequence Characteristic and
Randomness of Load
Load fluctuates in timing. The variation of load is dif-
ferent in four seasons a year. The differences of load are
great in different periods a day in same season, but there
are significant regularities. The period of peak happens
nearly at the same time every day and so does the period
of valley. Time-sequence characteristic of load in typical
day of different season s is shown in Figure 1.
On the other hand, load has randomness because of the
error of load forecasting and the causal factors, which
cause the load curve is not exactly the same as typical
day.
Load curves could be divided according to change law
of load time-sequence characteristics a day, and 24 hours
a day are segmented as shown in Table 1. Normal dis-
tribution mean value and standard deviation could be
obtained by statistical calculations of historical load data.

L. ZHANG ET AL. 757
Figure 1. Time-sequence characteristic of load.
Table 1. Load time-interval.
periods Early in morning Morning Noon Afternoon
Time (6-8] (8-11] (11-14] (14-17]
Periods Evening Night Late at night
Time (17-19] (19-23] (23-6]
2.2. Time-Sequence Characteristic and
Randomness of Wind Generation
Wind turbine generator (WTG) power, which changes
with wind speed, has apparent randomness. Affected by
natural conditions, wind speed has a very strong uncer-
tainty. Waybill distribution is generally used as the sta-
tistical description of the wind speed. The relationship of
WTG power an d wind speed can b e shown as a curve of
output characteristic.
WTG power also has time-sequence characteristic.
There is a big difference of wind speed between different
seasons [6]. In different periods a day, speed changes
also have a statistical characteristic. Wind speed timing
characteristic curve of different seasons could be ob-
tained by meteorological data, as shown in Figure 2.
2.3. Time-Sequence Characteristic and
Randomness of PV Generation
PV generator output has a direct relationship with the
solar intensity. Sunlight radiation intensity depends on
solar altitude and attenuation by clouds. The solar alti-
tude changing with time can be expressed by a certain
function. So PV generator output has time-sequence
characteristic [7], as shown in Figure 3, which has little
difference between different seasons. On the other hand,
PV generator output is random because of the random
attenuati on by clou ds.
Figure 2. Time-sequence characteristic of WTG power.
Figure 3. Time-sequence characteristic of PV.
It can be concluded from above that:
1) All of load, WTG and PV power have time-sequence
characteristic and randomness.
2) The mo men t of max i mum lo ad is n ot the same wi th
maximum WTG and PV power output, and the indices
calculated based on a certain value or certain levels of
load and DG output have large differences with that in
actual situation, so the results are not accurate.
3) Both load and DG output have randomness, certain
indices can’t fully reflect the po tential risk in power grid.
Therefore, it is importan t to calculate the voltage limit
violation prob ability in different p eriods of the day com-
prehensively considering time-sequence characteristic
and randomness of the load and DG in order to really
reflect the situation of voltage in power grid.
3. Indices of Distribution Line Voltage Limit
Violation Probability
3.1. Voltage Limit Violation Probability Indices
of Node and Distribution Line
According to China national standards, the allowable
deviation of node voltage in 10 kV distribution lines is

L. ZHANG ET AL.
758
the ± 7% of rated voltage, so when the node voltage is
higher than 1.07 pu or lower than 0.93 pu, voltage vio-
lates limits. Voltage upper or lower limit violation prob-
ability means the possibility of node voltage higher than
1.07 pu or belo w 0. 93 pu.
Distribution line voltage limit violation probability is
integrated statistics of node voltage. Assume that N
nodes voltage limit violation probability is (
t
k
Pk

, where t is period. The distribution line voltage
limit violation probability in a period can be expressed
as:
1,2... )N
1
1(1
N
t
k
k
P


)
t
P
)
t
P
)
t
P
(1)
Distribution line voltage upper limit violation prob-
ability is calculated by:
1
1(1
N
t
up iup
i
P

 
 (2)
where is the ith node in the distribution line volt-
age upper limit violation probability in t period. Line
voltage lower limit violation prob ability is calculated by:
t
iup
P
1
1(1
N
t
down idown
i
P

 
 (3)
where is the ith node in the distribution line vol-
tage lower limit violation probab ility in t period.
t
idown
P
If voltage of any node is over limit, the distribution
line is in risk state. According to the severity level, the
state is divided into no risk, mild risk, medium risk and
risk of severe, as shown in Table 2.
3.2. Calculation Method of Distribution Line
Voltage Limit Violation Probability Based
on Probabilistic Power Flow
Considering the randomness of the load and DG, this
paper uses probabilistic power flow to obtain probability
value of voltage limit violatio n. Probabilistic power flow
combined semi-invariant and Gram-Charlier expanding
is used in order to avoid the large amount calculation of
Monte Carlo method. The algorithm laniaries equations
of bus injected power and line flow by Taylor series ex-
panding at normal operation point:
00 00
00 00
()( ).....
()( )....
SSfXXfXJX
ZZgXXgXGX
 

 
 (4)
where 0, 0
S
X
and 0
Z
are expectation of bus injec-
tion power, state variable and line flow, respectively;
,
S
X
 and
Z
 are their random disturbance.
Assuming that loads of nodes random change is mutu-
ally independent, winds speed and sunlight intensity are
mutually independent, wind speed obeys distribution of
Waybill and sunlight intensity obeys beta distribution in
each period. Algebraic operations of semi-invariant take
the place of convolution calculation, and then all older
semi-invariant of unknown quantity are ob tained. Finally
the probability density function of state variables is cal-
culated by Gram-Charlier series expansion method.
Detailed procedures are as follows:
1) Enter the basic data of the power grid, including
grid structure and the basic parameters of the load and
DG.
2) Obtain the load and power curve of typical day in
different seasons by meteorological data or historical
data; calculate the time-sequence characteristic parame-
ters of load and DG in different periods and different
seasons.
3) Calculate nodes voltage limit violation probability
in different periods and different seasons by using prob-
abilistic flow based on semi-invariant.
4) Calculate voltage limit violation probability of dis-
tribution line by nodes’ in different periods and seasons.
5) Evaluate the risk level.
4. Analysis of Distribution Line Voltage
Limit Violation Probability
IEEE33 bus distribution system is used as example in
this paper. In 14, 23, 29 nodes join WTG and PV, as
shown in Figure 4, and related data are shown in Table
3, Table 4.
The penetration level can be changed by accessing
different numbers of DG. Load obeys the normal distri-
bution with 3% variance, the bu s 0 voltage taken 1.02pu,
and the line maximum load is 7430kW.
4.1. Effect of Load Rate and DG Penetration
According to load rate of 20%, 50%, 80%, this paper
divides distribution line into three types: light load, nor-
mal load and high load. Voltage upper and lower limit
violation probability of distribution lines is calculated in
different penetration levels, and the results are shown in
Figure 5 - Figure 7, Table 5 - Table 7.
Table 5 and Figure 5 show that: the voltage of light
load line without DG isn’t over limit. After joining DG,
with the increase of the penetration, voltage begins to
exceed upper limit, which mainly appears near DG and
Table 2. Risk levels of voltage limit violation probability.
limit violation probability(%) Risk level
(0-0.1] No risk
(0.1-20] Mild risk
(20-50] Medium risk
More than 50 Risk of severe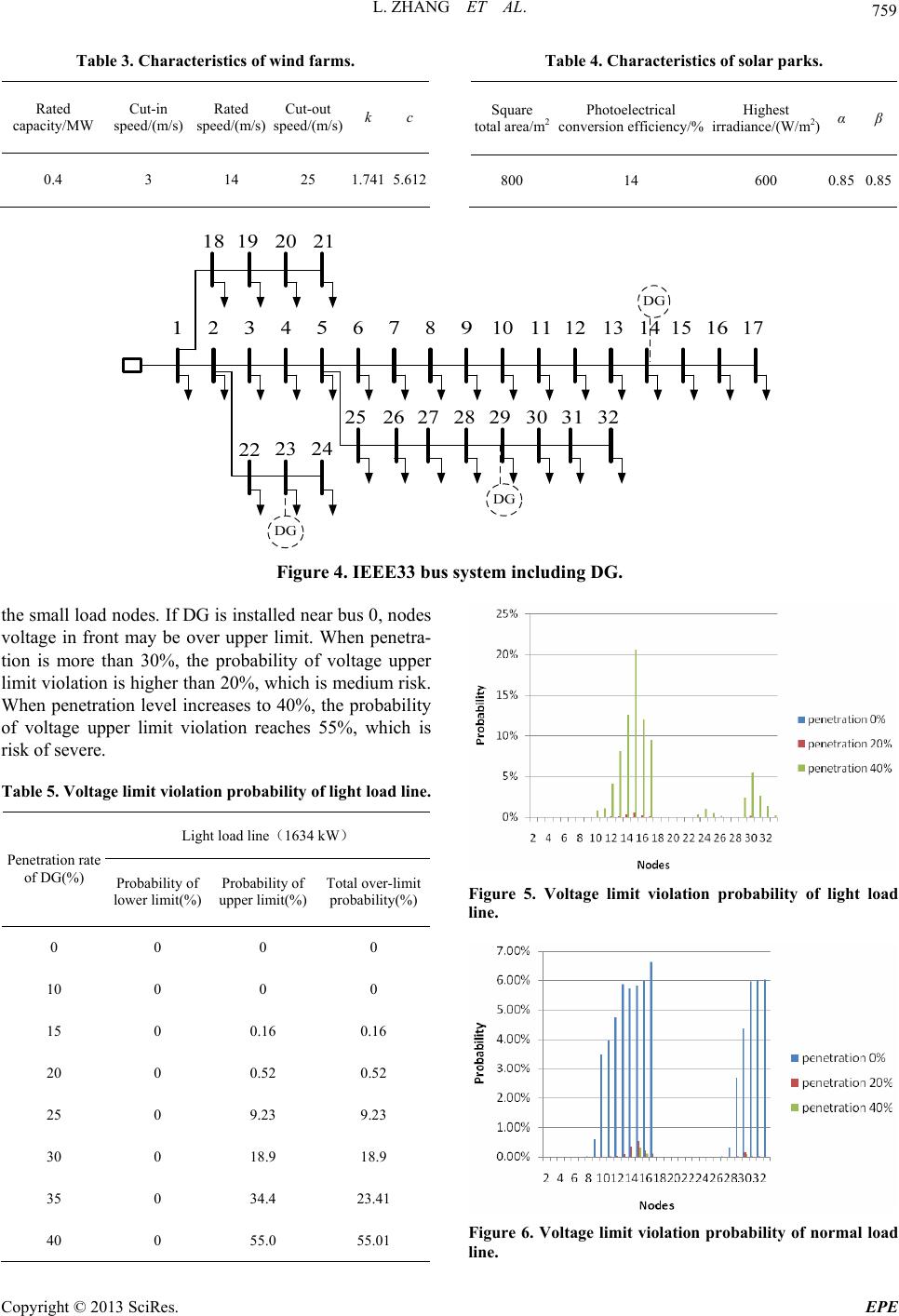

L. ZHANG ET AL.
759
Table 3. Characteristics of wind farms. Table 4. Characteristics of solar parks.
Rated
capacity/MW Cut-in speed/(m/s) Rated speed/(m/s) Cut-out speed/(m/s) k c
0.4 3 14 25 1.7415.612
Square
total area/m2Photoelectrical conversion efficiency/% Highest irradiance/(W/m2)α β
800 14 600 0.850.85
Figure 4. IEEE33 bus system including DG.
the small load nodes. If DG is installed near bus 0, nodes
voltage in front may be over upper limit. When penetra-
tion is more than 30%, the probability of voltage upper
limit violation is higher than 20%, which is medium risk.
When penetration level increases to 40%, the probability
of voltage upper limit violation reaches 55%, which is
risk of severe.
Table 5. Voltage limit violation probability of light load line.
Light load line（1634 kW）
Penetration rate
of DG(%) Probability of
lower limit(%) Probability of upper limit(%) Total over-limit probability(%)
0 0 0 0
10 0 0 0
15 0 0.16 0.16
20 0 0.52 0.52
25 0 9.23 9.23
30 0 18.9 18.9
35 0 34.4 23.41
40 0 55.0 55.01
Figure 5. Voltage limit violation probability of light load
line.
Figure 6. Voltage limit violation probability of normal load
line.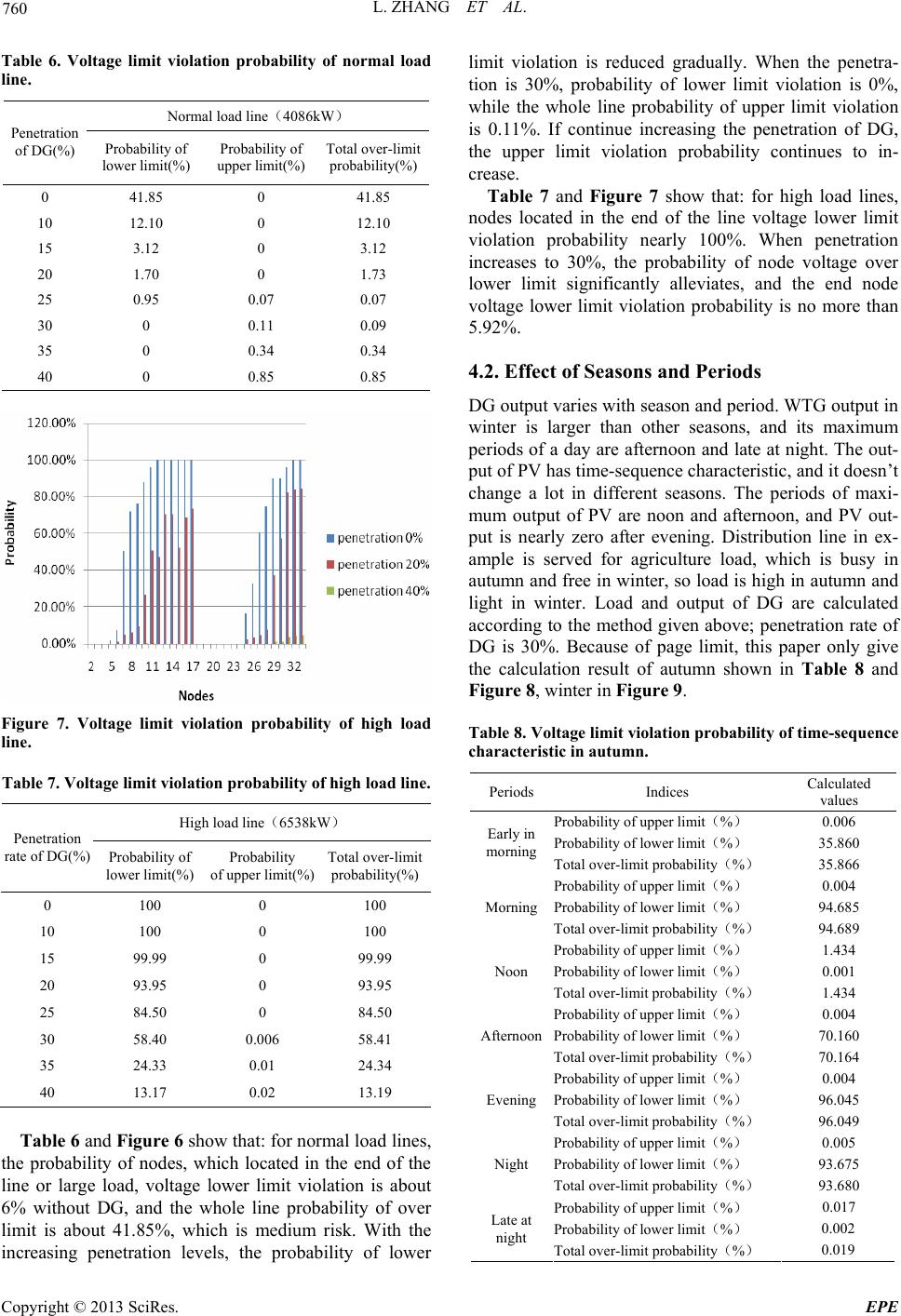

L. ZHANG ET AL.
760
Table 6. Voltage limit violation probability of normal load
line.
Normal load line（4086kW）
Penetration
of DG(%) Probability of
lower limit(%) Probability of upper limit(%) Total over-limit probability(%)
0 41.85 0 41.85
10 12.10 0 12.10
15 3.12 0 3.12
20 1.70 0 1.73
25 0.95 0.07 0.07
30 0 0.11 0.09
35 0 0.34 0.34
40 0 0.85 0.85
Figure 7. Voltage limit violation probability of high load
line.
Table 7. Voltage limit violation probability of high load line.
High load line（6538kW）
Penetration
rate of DG(%) Probability of
lower limit(%) Probability of upper limit(%) Total over-limit probability(%)
0 100 0 100
10 100 0 100
15 99.99 0 99.99
20 93.95 0 93.95
25 84.50 0 84.50
30 58.40 0.006 58.41
35 24.33 0.01 24.34
40 13.17 0.02 13.19
Table 6 and Figure 6 show that: for normal load lines,
the probability of nodes, which located in the end of the
line or large load, voltage lower limit violation is about
6% without DG, and the whole line probability of over
limit is about 41.85%, which is medium risk. With the
increasing penetration levels, the probability of lower
limit violation is reduced gradually. When the penetra-
tion is 30%, probability of lower limit violation is 0%,
while the whole line probability of upper limit violation
is 0.11%. If continue increasing the penetration of DG,
the upper limit violation probability continues to in-
crease.
Table 7 and Figure 7 show that: for high load lines,
nodes located in the end of the line voltage lower limit
violation probability nearly 100%. When penetration
increases to 30%, the probability of node voltage over
lower limit significantly alleviates, and the end node
voltage lower limit violation probability is no more than
5.92%.
4.2. Effect of Seasons and Periods
DG output v aries with season an d period . WTG ou tput in
winter is larger than other seasons, and its maximum
periods of a day are afternoon and late at night. The out-
put of PV has time-sequence characteristic, and it doesn’t
change a lot in different seasons. The periods of maxi-
mum output of PV are noon and afternoon, and PV out-
put is nearly zero after evening. Distribution line in ex-
ample is served for agriculture load, which is busy in
autumn and free in winter, so load is high in autumn and
light in winter. Load and output of DG are calculated
according to the method given above; penetration rate of
DG is 30%. Because of page limit, this paper only give
the calculation result of autumn shown in Table 8 and
Figure 8, winter in Figure 9.
Table 8. Voltage limit violation probability of time-sequence
characteristic in autumn.
Periods Indices Calculated
values
Probability of upper limit（%） 0.006
Probability of lower limit（%） 35.860
Early in
morning Total over-limit probability（%） 35.866
Probability of upper limit（%） 0.004
Probability of lower limit（%） 94.685 Morning
Total over-limit probability（%） 94.689
Probability of upper limit（%） 1.434
Probability of lower limit（%） 0.001
Noon
Total over-limit probability（%） 1.434
Probability of upper limit（%） 0.004
Probability of lower limit（%） 70.160
Afternoon
Total over-limit probability（%） 70.164
Probability of upper limit（%） 0.004
Probability of lower limit（%） 96.045
Evening
Total over-limit probability（%） 96.049
Probability of upper limit（%） 0.005
Probability of lower limit（%） 93.675 Night
Total over-limit probability（%） 93.680
Probability of upper limit（%） 0.017
Probability of lower limit（%） 0.002
Late at
night Total over-limit probability（%） 0.019

L. ZHANG ET AL. 761
Figure 8. Risk levels of voltage over upper limit in different
seasons and time periods.
Figure 9. Risk levels of voltage over lower limit in different
seasons and time periods.
Table 8 shows that: in autumn, load is large but DG
output is low, so the voltage lower limit violation prob-
ability is generally higher than other seasons. In winter,
load is low but DG output is large, so the voltage upper
limit violation probability is generally higher than other
seasons. Output of PV is largest at noon during a day, but
load is small in lunch break, so the voltage of line is eas-
ily over upper limit. At noon in winter, the voltage upper
limit violation probability of the line is 53.275%, which
is risk of severe. In the Aftern oon in winter, bo th PV and
WTG output are large, as the load in winter is generally
low, so the probability of upper limit violatio n is 10.14 %,
which is mild risk. Load is generally small late at night,
but output of WTG is large, so voltage upper limit viola-
tion probability is 11.015%, which is mild risk. Load in
periods of morning, afternoon, evening and night is large,
so probability of over lower limit is high if DG output is
small.
Figure 8 shows that: noon is high-fr equency period of
over upper limit, especially in winter and summer. Fig-
ure 9 shows that: morning, evening and night are high-
frequency periods of over lower limit, especially in au-
tumn and summer. Although load in afternoon is large,
DG output is larger, so the level of risk is reduced.
4.3. Effect of Allocation Ratio between The Wind
Power and PV Power
Because of the different natural resources in different area,
allocation ratio between the wind power and PV power is
different. Affected by local nature resources, allocation
ratio between the wind power and PV power will chan ge
the probability of voltage limit violation if penetration is
fixed. Probabilities of voltage limit violation in different
allocation ratios between the wind power and PV power
results are shown in Table 9.
Table 9 shows that: the allocation ratio affects the
voltage limit violation probability and the degree of ef-
fect depends on local natural resources. In the area major
in WTG, because of the small load and the large output
of WTG late at night, the probability of voltage upper
limit violation is 38.66%, which is medium risk. In the
area major in PV, probability of voltage upper limit vio-
lation at noon is 70.99%. But PV output is almost 0 from
evening to late at night, from 17 to 19 o’clock, the prob-
ability of line voltage over lower limit is 40.67%, and
from 19 to 23 o’clock, the probability is 51.34%. In area
where allocation ratio is balanced, risk of severe period
won’t appear during the whole day.
5. Conclusions
This paper comprehensively considers time-sequence
characteristic and randomness of load and DG, and re-
searches the effect of DG on distribution line voltage
limit violation probability with different penetration lev-
els, different seasons, different periods, different alloca-
tion ratio of wind and light. The result is as follows:
1) For different load ratio distribution line, DG pene-
tration has large affect on probability of voltage limit
violation. For light load lines, adding DG improves the
overall distribution line voltage levels, and the risk level
increases with the increasing penetration rate. For high
load lines, nodes in th e end of th e line voltag e over lo wer
limited probabilit y is high, and with the increasing pene-
tration levels, the probability will be reduced, and the
risk level dropped. Penetration rate of 30% can effec-
tively alleviate the vo ltage-limit.
2) For different seasons and periods, probability of
nodes’ voltage limit violation is different. Transformer
tap of substation and vo ltage regulator in distribu tion line
should be adjusted based on the time-sequence charac-
teristic of load and DG according to different seasons and
periods.
3) For different areas, the natural resources are differ-
ent greatly, so it makes a great difference in voltage limit
violation probability. Proper allocation ratio between the
wind power and PV power could effectively alleviate the
risk levels.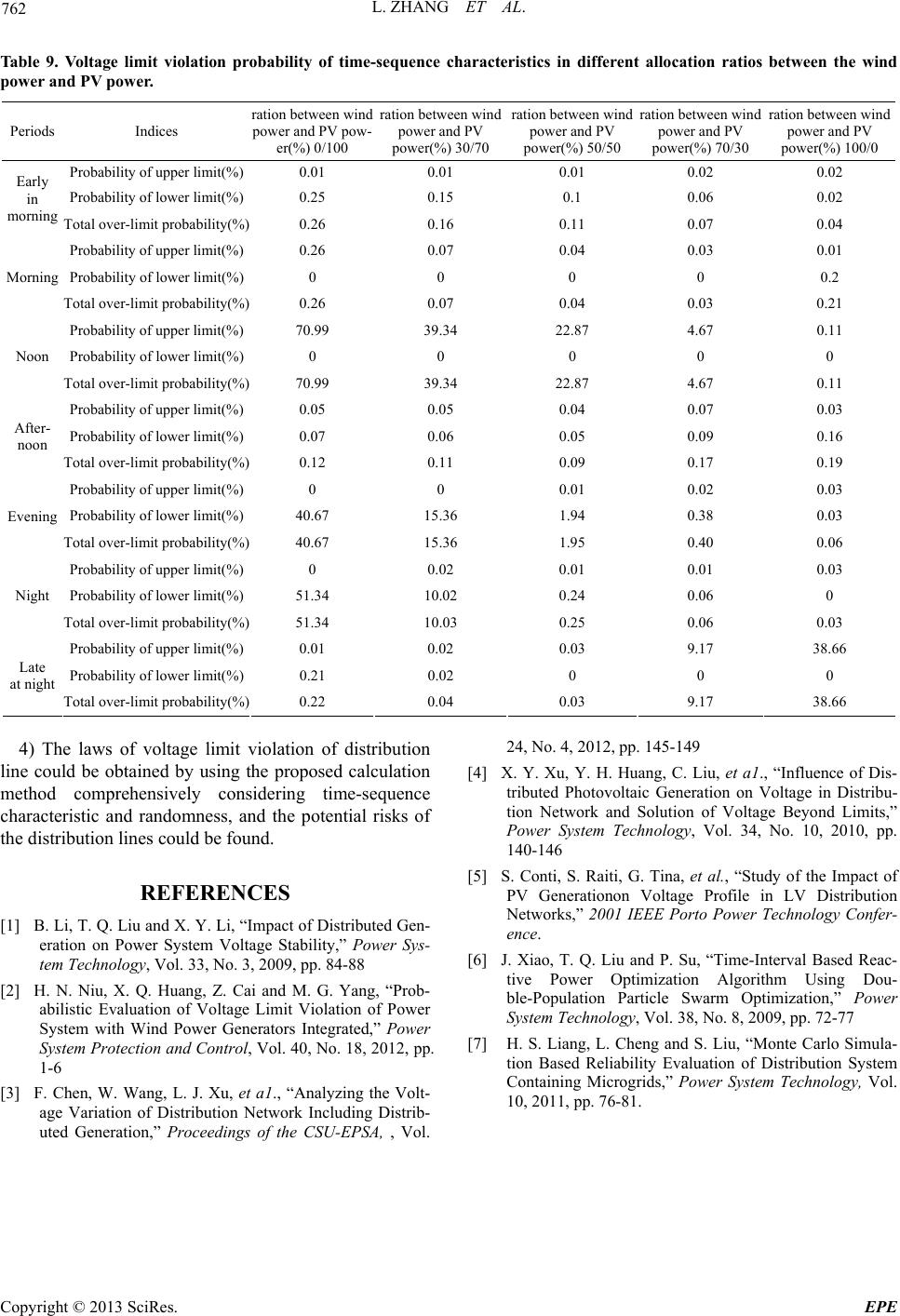

L. ZHANG ET AL.
762
Table 9. Voltage limit violation probability of time-sequence characteristics in different allocation ratios between the wind
power and PV power.
Periods Indices
ration between wind
power and PV pow-
er(%) 0/100
ration between wind
power and PV
power(%) 30/70
ration between wind
power and PV
power(%) 50/50
ration between wind
power and PV
power(%) 70/30
ration between wind
power and PV
power(%) 100/0
Probability of upper limit(%) 0.01 0.01 0.01 0.02 0.02
Probability of lower limit(%) 0.25 0.15 0.1 0.06 0.02
Early
in
morning Total over-limit probability(%) 0.26 0.16 0.11 0.07 0.04
Probability of upper limit(%) 0.26 0.07 0.04 0.03 0.01
Probability of lower limit(%) 0 0 0 0 0.2 Morning
Total over-limit probability(%) 0.26 0.07 0.04 0.03 0.21
Probability of upper limit(%) 70.99 39.34 22.87 4.67 0.11
Probability of lower limit(%) 0 0 0 0 0
Noon
Total over-limit probability(%) 70.99 39.34 22.87 4.67 0.11
Probability of upper limit(%) 0.05 0.05 0.04 0.07 0.03
Probability of lower limit(%) 0.07 0.06 0.05 0.09 0.16
After-
noon Total over-limit probability(%) 0.12 0.11 0.09 0.17 0.19
Probability of upper limit(%) 0 0 0.01 0.02 0.03
Probability of lower limit(%) 40.67 15.36 1.94 0.38 0.03 Evening
Total over-limit probability(%) 40.67 15.36 1.95 0.40 0.06
Probability of upper limit(%) 0 0.02 0.01 0.01 0.03
Probability of lower limit(%) 51.34 10.02 0.24 0.06 0 Night
Total over-limit probability(%) 51.34 10.03 0.25 0.06 0.03
Probability of upper limit(%) 0.01 0.02 0.03 9.17 38.66
Probability of lower limit(%) 0.21 0.02 0 0 0
Late
at night Total over-limit probability(%) 0.22 0.04 0.03 9.17 38.66
4) The laws of voltage limit violation of distribution
line could be obtained by using the proposed calculation
method comprehensively considering time-sequence
characteristic and randomness, and the potential risks of
the distribution lines could be found.
REFERENCES
[1] B. Li, T. Q. Liu and X. Y. Li, “Impact of Distributed Gen-
eration on Power System Voltage Stability,” Power Sys-
tem Technology, Vol. 33, No. 3, 2009, pp. 84-88
[2] H. N. Niu, X. Q. Huang, Z. Cai and M. G. Yang, “Prob-
abilistic Evaluation of Voltage Limit Violation of Power
System with Wind Power Generators Integrated,” Power
System Protection and Control, Vol. 40, No. 18, 2012, pp.
1-6
[3] F. Chen, W. Wang, L. J. Xu, et a1., “Analyzing the Volt-
age Variation of Distribution Network Including Distrib-
uted Generation,” Proceedings of the CSU-EPSA, , Vol.
24, No. 4, 2012, pp. 145-149
[4] X. Y. Xu, Y. H. Huang, C. Liu, et a1., “Influence of Dis-
tributed Photovoltaic Generation on Voltage in Distribu-
tion Network and Solution of Voltage Beyond Limits,”
Power System Technology, Vol. 34, No. 10, 2010, pp.
140-146
[5] S. Conti, S. Raiti, G. Tina, et al., “Study of the Impact of
PV Generationon Voltage Profile in LV Distribution
Networks,” 2001 IEEE Porto Power Technology Confer-
ence.
[6] J. Xiao, T. Q. Liu and P. Su, “Time-Interval Based Reac-
tive Power Optimization Algorithm Using Dou-
ble-Population Particle Swarm Optimization,” Power
System Technology, Vol. 38, No. 8, 2009, pp. 72-77
[7] H. S. Liang, L. Cheng and S. Liu, “Monte Carlo Simula-
tion Based Reliability Evaluation of Distribution System
Containing Microgrids,” Power System Technology, Vol.
10, 2011, pp. 76-81.