Energy and Power Engineering, 2013, 5, 751-755
doi:10.4236/epe.2013.54B145 Published Online July 2013 (http://www.scirp.org/journal/epe)
Localization of Voltage Regulators in Distribution
Systems by a Mixed Genetic –Tabu Sear ch Algorithm
M. C. Pimentel Filho1, M. F. Medeiros2
1UNP, LAUREATE, Natal, Brazil
2DCA, UFRN, Natal, Brazil
Received March, 2013
ABSTRACT
The optimal allocation of regulato rs banks in distribution systems is a me rely combinatorial prob lem in which the best
points of installation correspond to the best benefit, considering the admitted objective function, without violating and
operating limits. The obj ective function must be ch osen so that its value represents the operation state of the system. As
the problem possesses combinatorial nature, its complexity will increase expon entially with the number of po ssibilities.
Systems with large numbers of nodes and / or with the possibility of installin g more than one bank requ ire a large num-
ber of calculations to find the solution. An additional issue is the fact that the problem does not have a continuous na-
ture, presenting discontinuity points in the objective function, limiting the application of optimization methods based on
gradients. Based on the nature of the problem two optimization methods were used to solve the problem: Genetic Algo-
rithm (GA) and modified Tabu Search (TS). The GA function will scour the search space and find regions with local
minima that are candidates to be the solution. On the other hand the TS provides local search in the regions defined by
GA so that the overall optimum is achieved.
Keywords: Regulator Banks; Distribution Systems; Genetic Algorithms; Tabu Search
1. Introduction
The study for the determination of optimum points for
installing regulators banks is a quite new matter in tech-
nical literature. One of the earliest works was to [1]. Af-
ter this article, there was a deeper study of the subject
generating other works such as [2], [3] and [4]. Typically,
determination of optimal points for the installation of
regulators is based on experience and through simula-
tions of flow calculations for load testing a large number
of installation possibilities to find a convenient configu-
ration. Thus, an algorithm to determine the ideal points
of installing regulators, avoiding an exhaustive search,
could be an attractive tool.
The most elementary way to determine the optimum
point would be the test of all location possibilities, but
this would require a huge computational effort. For ex-
ample, for a system of 80 nodes 54.740 load flow calcu-
lations would be required to find the best location of in-
stallation of three regulators.
This way, an adequate optimization method to solve
the problem should be applied. For this purpose, an ob-
jective function must be initially defined, considering
operational constraints. The objective function must be
defined so that its optimum corresponds to maximal ben-
efit for the system operation, due to installation of the
banks. Operational limits must constrain the search re-
gion. The objective function proposed in this work was
idealized having an optimum corresponding to maintain
the voltage profile as close as possible to the rated sys-
tem voltage, as formalized in chapter 2.
Defined the objective function, the second step is to
design the optimization method to be applied to solve the
problem. Due to the discrete nature of the problem has,
with discontinuous objective function, gradient-based
methods are not the most suitable for solving the problem.
Another alternative is the use of methods based on a Me-
taheuristic as Genetic Algorithm (GA) like [5], Ant Col-
ony (AC), Simulated Annealing (SA), among others. The
advantage of using these methods is that they have the
capabilities to scour the search space efficiently by
avoiding the convergence to local minima. After testing
some methods, the experience led to the use of GA in
cooperation with a local search algorithm inspired by the
Tabu Search (TS). This way, by applying the GA, local
optimal points are found within the search space. Starting
with the points determined by the GA, TS modified per-
forms a local search in order to find a better solution than
that determined by GA, so that the process may be accel-
erated.

M. C. PIMENTEL Filho, M. F. MEDEIROS
752
2. Optimization Method
2.1. Objetive Function
The proposed objective function is defined by Equation
(01).
(01)
Submitted to:
(02)
Maximizing (01) corresponds to search for banks loca-
tions that result in all voltages (Vi) closest to the refer-
ence voltage (Vref). However some solution candidates
may present one or more voltag es below the mini mum. If
it happens, the solution will be discarded.
Figure 01 illustrates the behavior of the objective
function for variation of position of a regulators bank in a
distribution system. In this case, the regulators may be
installed at all nodes of the main feeder of the distribu-
tion system. On the abscissa axis are assigned the nodes
where the regulators bank was installed and the ordinates
are the values of objective function for each respective
installation node.
Note that the curve presents points of discontinuity in
derivatives, like nodes 05 and 07. Usually these points
are nodes of derivations, i.e., where laterals are con-
nected. When the regulator is position ed before them, the
corresponding lateral is covered b y its effect of rising (or
decreasing) voltages. However, when it is placed after
this node, the lateral is not contemplated. This is the rea-
son for a high increase in the value of the obj ective func-
tion near thi s node.
2.2. Genetic Algorithm (GA)
The GA sketch begins by defining the individual's con-
stitution and the rule of crossover between them. In the
case of this study each individual is defined by a set of
nodes, each node determining a regulators bank installa-
tion point . Figure 2 shows an example of an individual.
By the crossover, each child shall be composed by
parts of each parent. In the case of individuals formed by
3 nodes, two combinations are possible. Figure 3 shows
an example of two parents.
Figure 1. Behavior of objection function.
For the first possibility, the children generated by the
parents are shown in Figure 4.
In the second possibility, the children are according
Figure 5.
Defining criteria for each individual formation and
children generation rule, the GA is performed according
to the algorithm described below.
Algorithm:
1- Generate an initial population randomly;
2- Perform a load flow calculation for each individual
and determine the value of the objective function;
3- Order individuals according to their fitness;
4- Split the individuals into two groups, those with
higher fitness and lower;
5- Make the crossover between individuals of the first
set with the second;
6- Order parents and children according to their fit-
ness;
7- Generate mutant 2% of population;
8- Eliminate individuals with lower fitness, keeping
the number of individuals in the the original set;
9- Return to step 4 until the process is repeated for a
predetermined number;
10- List the best individuals.
2.3. Local Search
In radial distribution systems, each node presents few
31020
Figure 2. Example of individual.
31020

81540
Figure 3. Example of parents.
31540

81020
Figure 4. First possibility for crossover.
31040

81520
Figure 5. Second possibility for crossover.

M. C. PIMENTEL Filho, M. F. MEDEIROS 753
neighbors. They always are connected to merely one
previous nod e - in case it is a terminal node – or to a pre-
vious and to a subsequent – in case it is a passing node,
or to one anterior and more than one posterior node, if
this is a derivation node. However, most of the nodes in a
system are passing nodes, being connected just to two
nodes. This way, the search of the neighborhood of each
node doesn’t imply in a high number of combinations.
Unlike the GA, the Local Search characteristic does
not have to scour the search space efficiently. By other
side given a point of optimum location, the method is
able to examine their neighborhood looking for a solu-
tion of higher fitness. To apply the method, it is neces-
sary to define a starting point, i.e., any solution. From
this solution movements are defined looking for a more
attractive solution. As the number of neighbors of each
node is usually small, the computation al cost to test each
neighbor is not high. In this way, to find the optimal
should be followed the algorithm below.
Algorithm
Algorithm
1 - Set an initial solution (starting point);
2 - Take as starting node the first node of the individ-
ual;
3 - Move the position of the regulator to the neighbor-
ing node and execute a load flow calculation, by the
method shown in [6], for new configuration, calculating
the new fitness;
4 - Compare the new individual fitness of the with the
original, if higher, make the exchange the old for the new
one;
5 - Back to step 3 until the entire neighbor node is
tested;
6 - Back to step 3 until all nodes of the individual be
tested or no improvement on fitness of the individual is
verified;
7 - Show the best solution.
2.4. Complete Agorithm
The purpose of this paper is to show an algorithm to de-
fine the best installation point for regulators in distribu-
tion systems. The complete algorithm is described below,
consisting of a cooperation of two algorithms presented
previously.
Algorithm:
1- Read the system data;
2- Define, randomly, set of solution candidates;
3- Carry out a load flow calculation for each candidate
and calculate his fitness;
4- Order the individuals according to his fitness;
5- Split the individuals into two groups, those with
higher fitness and lower;
6- Make the crossover between individuals with the
first set with the second;
7- Order parents and children according to his fitness;
8- Generate mutants, randomly, in 2% of the popula-
tion;
9- Eliminate solutions that have voltage violations;
10- Eliminate individuals with lower fitness, keeping
the number of individuals of the original set;
11- Return to step 5 until the process is repeated for a
predetermined number;
12- list the best individu als;
13- Define the first individual of the set formed in step
12 and take as a starting point for the local search pro-
cess;
14- Move the position of the regulator to the neigh-
boring node and perform a load flow calculation for new
configuration, calculating the new fitness;
15- Compare the fitness of the new individual with the
original individual, if higher, make the exchange of the
old for the ne w n ode ;
16- Back to step 13 until every neighborhood of the
node is tested;
17- Back to step 13 until all nodes of the individual
being tested or no improvement on fitness of the indi-
vidual is verified;
18- Present the best solutions.
For implementation of the algorithm, one should ini-
tially define the quantities of individuals of each popula-
tion and the number of maximum generations. As high
each of them, greater the probability of finding the best
solution, but also greater will be the computational time,
and the process will be slower.
During the process, many generated individuals are
identical. To prevent repeated load flow calculations, the
result of each new calculation is stored in a memory.
This way, every time when it is necessary to carry out a
load flow calculation, the algorithm checks if it has been
done before. If so, it recovers the value of the objective
function of the memory, otherwise it carries out a new
calculation.
3. Results
In order to test the method simulations with two systems
were performed. The first one (system I), with 71 nodes,
and a loading of 4.0 MVA as described in [7], and the
second one is a local system of 88 nodes and 3.8 MVA
load (system II). As during the optimization process sev-
eral settings are tested, the results will present just the
best solutions. At all simulations each individual will
consist of 3 nodes. Although this configuration has been
chosen, the method can be applied to individuals with
more or fewer nodes. Before showing the results of ap-
plying the method, Table 1 shows the optimum location
of banks by regulators for systems I and II. In this case,
the optimum was determined by analyzing all possibili-
ties of allocation and selecting the best one. Table 3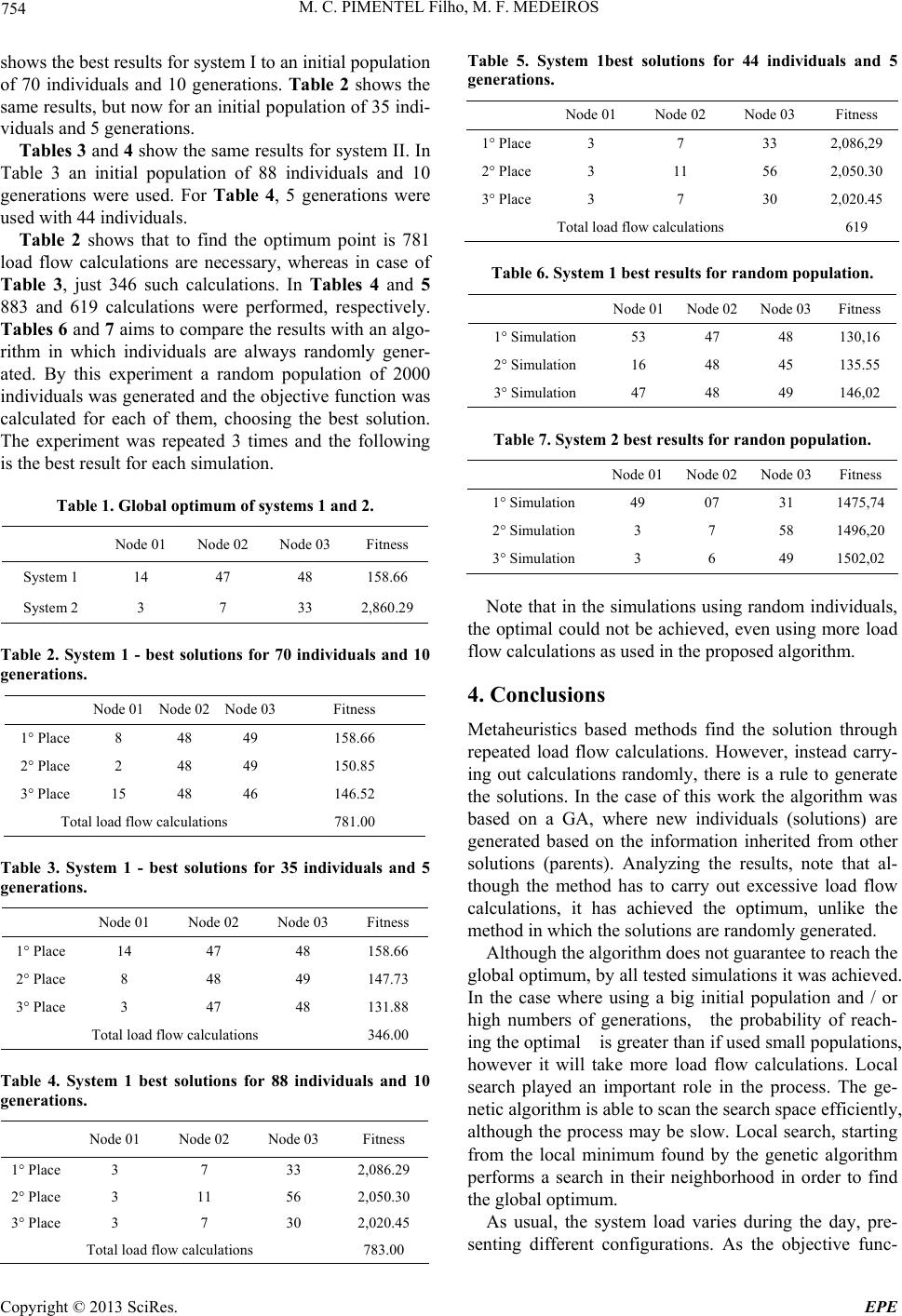

M. C. PIMENTEL Filho, M. F. MEDEIROS
754
shows the best results for system I to an initial popu lation
of 70 individuals and 10 generations. Table 2 shows the
same results, but now for an initial population of 35 indi-
viduals and 5 generations.
Tables 3 and 4 show the same results for system II. In
Table 3 an initial population of 88 individuals and 10
generations were used. For Table 4, 5 generations were
used with 44 individuals.
Table 2 shows that to find the optimum point is 781
load flow calculations are necessary, whereas in case of
Table 3, just 346 such calculations. In Tables 4 and 5
883 and 619 calculations were performed, respectively.
Tables 6 and 7 aims to compare the results with an algo-
rithm in which individuals are always randomly gener-
ated. By this experiment a random population of 2000
individuals was generated and the objective function was
calculated for each of them, choosing the best solution.
The experiment was repeated 3 times and the following
is the best result for each simulation.
Table 1. Global optimum of systems 1 and 2.
Node 01 Node 02 Node 03 Fitness
System 1 14 47 48 158.66
System 2 3 7 33 2,860.29
Table 2. System 1 - best solutions for 70 individuals and 10
generations.
Node 01 Node 02 Node 03 Fi tness
1° Place 8 48 49 158.66
2° Place 2 48 49 150.85
3° Place 15 48 46 146.52
Total load flow calcula tions 781.00
Table 3. System 1 - best solutions for 35 individuals and 5
generations.
Node 01 Node 02 Node 03 Fitness
1° Place 14 47 48 158.66
2° Place 8 48 49 147.73
3° Place 3 47 48 131.88
Total load flow calcula tions 346.00
Table 4. System 1 best solutions for 88 individuals and 10
generations.
Node 01 Node 02 Node 03 Fitness
1° Place 3 7 33 2,086.29
2° Place 3 11 56 2,050.30
3° Place 3 7 30 2,020.45
Total load flow calculations 783.00
Table 5. System 1best solutions for 44 individuals and 5
generations.
Node 01 Node 02 Node 03 Fitness
1° Place 3 7 33 2,086,29
2° Place 3 11 56 2,050.30
3° Place 3 7 30 2,020.45
Total load flow calculations 619
Table 6. System 1 best results for random population.
Node 01Node 02 Node 03Fi tness
1° Simulation 53 47 48 130,16
2° Simulation 16 48 45 135.55
3° Simulation 47 48 49 146,02
Table 7. System 2 best results for randon popu lation.
Node 01Node 02 Node 03Fitness
1° Simulation 49 07 31 1475,74
2° Simulation 3 7 58 1496, 20
3° Simulation 3 6 49 1502, 02
Note that in the simulations using random individuals,
the optimal could not be achieved, even using more load
flow calculations as used in the proposed algorithm.
4. Conclusions
Metaheuristics based methods find the solution through
repeated load flow calculations. However, instead carry-
ing out calculations randomly, there is a rule to generate
the solutions. In the case of this work the algorithm was
based on a GA, where new individuals (solutions) are
generated based on the information inherited from other
solutions (parents). Analyzing the results, note that al-
though the method has to carry out excessive load flow
calculations, it has achieved the optimum, unlike the
method in which the solutions are randomly generated.
Although the algorithm does not guarantee to reach the
global optimum, by all tested simulations it was achieved.
In the case where using a big initial population and / or
high numbers of generations, the probability of reach-
ing the optimal is greater than if used small populations,
however it will take more load flow calculations. Local
search played an important role in the process. The ge-
netic algorithm is able to scan the search space efficiently,
although the process may be slow. Local search, starting
from the local minimum found by the genetic algorithm
performs a search in their neighborhood in order to find
the global optimum.
As usual, the system load varies during the day, pre-
senting different configurations. As the objective func-

M. C. PIMENTEL Filho, M. F. MEDEIROS
755
tion depends only on the voltages of the nodes, the algo-
rithm was tested just for the worst case, i.e., the maxi-
mum load situation.
In case of this work the simulations were performed in
order to allocate just three regulators op timally. However,
the algorithm may be extended for a greater or smaller
number of regulators. For the case of allocating a small
number of regulators the process becomes less attractive,
since the solution with the test of all possibilities (ex-
haustive search) becomes feasible, in respect to neces-
sary computational time. In the case of system I, if all
possibilities were tested, performing 54,570 load flow
calculations would be necessary. Using the proposed
method for the same system, just 364 load flow calcula-
tions were performed, considering the best case. For the
system II an exhaustive search would require 109.736
load flow calculations, whereas the algorithm solved the
problem using merely 619 ones.
REFERENCES
[1] A. S. Safiagianni and G. J. Salis, “Optimum Voltage
Regulator Placement in a Radial Power Distribution
Network,” IEEE Transactions on Power Systems, [S.l.],
Vol. 15, No. 2, 2000, pp. 879-886.
[2] C. A. N. Pereira and C. A. Castro, “Optimal Placement of
Voltage Regulator in Distribution Systems,” IEEE Bu-
charest Power Tech Conference, Bucharest, Romania,
June 28th -July 2nd, 2009.
[3] S. A. Dolli and S. H. Jangamshetti, “Modeling and Opti-
mal Placement of Voltage Regulator for a Radial Sys-
tem,” Power, Signals, Controls and Computation (EP-
SCICON), 2012 International Conference
[4] Medeiros Jr., M. F. de, Pimentel Filho, M. C. , “Optimal
Placement of Various Voltage Regulators by Means of
Sensitivity Parameters from a Radial Load Flow,” IEEE
Eletric Power and Energy Conference, Winnipeg, Canada,
2011.
[5] Medeiros Jr., M. F. de, Pimentel Filho, M. C. . “A me-
metic Algorithm Based on Mixed Ant Colony
Optimization and Genetic Algorithm for Optimal Ca-
pacitor Placement” , Inteligent System Application to
Power Systems (ISAP), Crete, Greece, 2011.
[6] C. S. Cheng and D. Shirmohammad, “A Three Phase
Power Flow Method for Real-time Distribution System
Analysis,” IEEE Transactions on Power Apparatus and
System, Vol. 10, No. 2, 1998, pp. 671-679.
[7] M. E. Baran a nd F. F. Wu, “Optimal Sizing of Capacitors
Placed on a Radial Distribution System,” IEEE Trans. on
Power Delivery, Vol. 4, No. 1, 1989b, pp. 735-743.