Applied Mathematics, 2013, 4, 13-17
Published Online November 2013 (http://www.scirp.org/journal/am)
http://dx.doi.org/10.4236/am.2013.411A2003
Open Access AM
Hybrid Synchronization of a Chen Hyper-Chaotic System
with Two Simple Linear Feedback Controllers
Guomao Xu, Shihua Chen
School of Mathematics and Statistics, Wuhan University, Wuhan, China
Received August 14, 2013; revised September 14, 2013; accepted September 21, 2013
Copyright © 2013 Guomao Xu, Shihua Chen. This is an open access article distributed under the Creative Commons Attribution
License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
This paper brings attention on the hybrid synchronization of the Chen hyper-chaotic system by using some simple con-
trollers. We give the sufficient conditio ns for achieving the goal by using the Lyapu nov stability theory, and we verify
our conclusion by numerical simulations.
Keywords: Hybrid Synchronization; Chen Hyper-Chaotic System; Linear Feedback Control
1. Introduction
Since Li and Yoke first put up the concept of chaos [1] in
1975, chaos has attracted many researchers’ attention.
Recently, chaos synchronization has received much more
attention due to its broad application prospects in brain
disorder, secure communication, and information proc-
essing, etc. [2-4]. The original synchronization technique
is developed by Pecorra and Carrol in studying complete
synchronization [5]. Now the concept of synchronization
has been extended to a broader scope, such as anti-syn-
chronization, lag synchronization, phase synchronization,
etc. [6-9].
Although hybrid synchronization (both anti-synchroni-
zation and synchronization co-exist) has an important
application in information processing [10], only a few
researchers study about it. G. Li used a single variable to
control the hybrid synchronization of coupled Chen sys-
tem [11]. Zhang used a linear feedback control method
and an adaptive feedback control method to guarantee
the hybrid synchronization in general Lorenz system
[12].
It is believed that the chaotic systems with higher-di-
mensional attractor like hyper-chaotic systems have
much wider applications. In fact, the presence of more
than one positive Lyapunov exponents clearly improves
the security by generating more complex dynamics. Thus
hyper-chaos synchronization has become a new subject
of active research [13]. But there are few publications
studying about it. Sudheer used active controls to ac-
complish the hybrid synchronization of Lü hyper-cha-
otic system [13].
In this paper, we study the hybrid synchronization of a
Chen hyper-chaotic system by using a simple control
method. We design two linear feedback controllers so
that some parts of the system are synchronized and others
are anti-synchronized. We will find our method seems
simpler compared to Sudheer’s method [13].
2. Problem Formulation
We consider an autonomous chaotic system described by



x
fxt
 (1)
where n
x
R is a n-dimensional state vector of the
system, and :nn
f
RR defines a vector field in
n-dimensional space, it can be a linear or nonlinear func-
tion. If




f
xt is a nonlinear function, we can also
decompose it into a linear part and nonlinear part.
We often use the drive-response system method to
study the synchronization of chaotic system. Thus can be
described by

 
11
 
s
tfst
 (2)
and:





   
2212
,

s
tfstustst
 (3)
where






12
,us tst is a controller to be designed
which can be linear, linear or other form. (2) is called the
drive system and (3) is called the response system.
Definition 1. The chaotic syste m (2) and (3) a re called

G. M. XU, S. H. CHEN 14
to achieve hybrid synchronization, if the following situa-
tions are satisfied:
 
12
lim0,1,2,, ,
ii
t
s
tst im
  (4)
 
12
lim0,1,, .
ii
t
s
tst imn
  (5)
where 12ii
 
,
s
ts t are the component of the state vec-
tors. If only (4) is satisfied, then we call the two system
-achieve anti-synchronization. If only (5) is satisfied,
then we call the two system achieves synchronization.
3. Main Result
The differential equations of Chen hyper-chaotic system
[14] is described by :

x
ay xw
ydxxzcy
zxybz
wyzrw








(6)
where x, y, z, and w are state variables, and
are positive parameters. When , ,
,,,,abc dr
312c35ab

,
. , system (6) is chaotic, when
, , , . , sys-
tem (6) is hyper-chaotic, when , ,
7d35a0 0.085r
3b12c7d0.085
35a0.798 312c
r
b

,
. , system (6) is periodic.
7d0.7980.9r
In order to observe the hybrid synchronization behav-
ior of Chen hyper-chaotic system, assume that we have
two Chen hyper-chaotic systems where the drive system
with four state variables denoted by the subscript 1 and
the response system with identical equations denoted by
the subscript 2. Obviously, the initial condition on the
drive system is different from that of response system.
For the system (6), the drive and response systems are
defined below, respectively:

111
1111
11 1
111 1
1
1
x
ay xw
ydxxzcy
zxy bz
wyzrw

 






(7)
and

222
2222
222 2
222 2
2
2
x
ay xw
ydxxzcy
zxybz
wyzrw

 






(8)
where 1234 are four control functions to be de-
signed. In order to study the hybrid synchronization of
the two systems (7) and (8 ), we defined an error variab le
as
,,,uuuu
 
TT
1234121212 12
,,,,, ,eeeeexxyyzzww
Lemma 1. (Schur’s formula) Let P be a square matrix
partitioned as [15]
A
B
CD



.
If A is nonsingular, then:


detdet detPAP A,
where


1.PADCA B 

Then we will discuss the hybrid synchronization of a
Chen hyper-chaotic system below.
Based on the error vector e, we can derive the error
dynamical system:


12141
2122211
3322113
4422114
eaeeeu
edecexzxzu
ebexyxyu
ereyzyzu

2

 
 
 


 (9)
Obviously, from the v iewpoint of control theory, if the
error vector e converge to zero as time t goes to infinity,
i.e. asymptotical stability. As system (6) is hyper-chaotic,
thus y and z are all bounded. We suppose that N and M
are the upper bounds of the absolute values of y and z.
Then we can conclude that hybrid synchronization exists
between system (7) and (8).
Theorem 1. The hybrid synchronization existent in
system (7) and (8) if we choose 1, 212
0uuke

,
30u

, 42 uk
4
e

 as the control functions, where

2
12
4
ap dMb
k
apb N


c

2
k and satisfies and
2
kr


T1
det* *0CB AB


 where
20
2
N
ap
ANb








,22
02
ap dMp
BN




 




,
1
2
2
2
M
kc
CMkr









.
Proof: The control function

T
1234
,,,Uuuuu
1
21
3
42
0
0
u
uke
u
uk




1
2
e
(10)
. This leads to
Open Access AM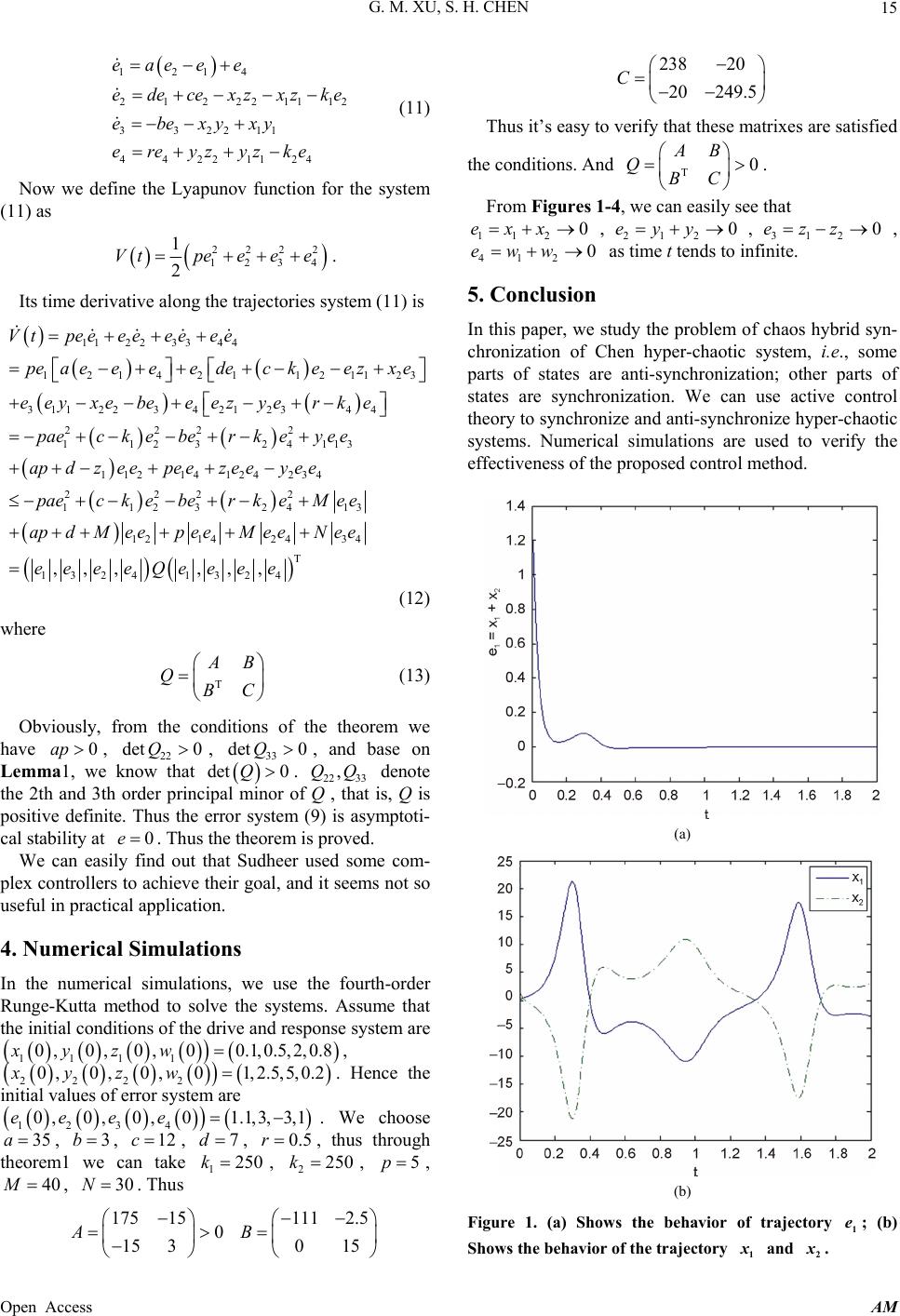

G. M. XU, S. H. CHEN 15

1214
21222111
332211
44221124
eaeee
edecexzxzke
ebexyxy
ereyzyzke


 
 



2
(11)
Now we define the Lyapunov function for the system
(11) as


2222
1234
1
2
Vt peeee.
Its time derivative along the trajectories system (11) is

 
 
 


1122 3344
121421 121123
3112234 212344
222 2
112324113
11214 124234
222
1123
Vtpee eeeeee
peae eeedecke ez xe
eeyxebe eezye rke
paeckeberkeyee
apdze epe ez eeyee
paeck eber



  

 










2
24 13
12 142434
T
1324 1324
,,, ,,,
ke Mee
apdMe epe eMeeNe e
eeeeQeeee

 

(12)
where
T
A
B
QBC




(13)
Obviously, from the conditions of the theorem we
have , 22 , , and base on
Lemma1, we know that
0ap det 0Q33
det 0Q


0Qdet . 2233 denote
the 2th and 3th order principal minor of Q , that is, Q is
positive definite. Thus the error system (9) is asymptoti-
cal stability at . Thus the theorem is proved.
,QQ
0e
We can easily find out that Sudheer used some com-
plex controllers to achieve their goal, and it seems not so
useful in practical application.
4. Numerical Simulations
In the numerical simulations, we use the fourth-order
Runge-Kutta method to solve the systems. Assume that
the initial conditions of the drive and response system are




1111
0 ,0 ,0 ,00.1,0.5,2,0.8xyzw
 

,


2222
0,0,0,01,2.5,5,0.2xyzw
  
. Hence the
initial values of error system are


1234
0, 0,0, 01.1,3,3,1eeee 
35a3b12c7d0.5r
1250k
. We choose
, , , , , thus through
theorem1 we can take

, ,
225k05p

,
, . Thus 40M30N
17515 0
15 3
A





111 2.5
015
B



238 20
20 249.5
C




Thus it’s easy to verify that these matrixes are satisfied
the conditions. And T0
AB
QBC





.
From Fi gu r e s 1-4, we can easily see that
1120exx

,2120eyy

,31 ,
20ezz
412
0eww

 as time t tends to infinite.
5. Conclusion
In this paper, we study the problem of chaos hybrid syn-
chronization of Chen hyper-chaotic system, i.e., some
parts of states are anti-synchronization; other parts of
states are synchronization. We can use active control
theory to synchronize and anti-synchronize hyper-chaotic
systems. Numerical simulations are used to verify the
effectiveness of the proposed control method.
(a)
(b)
Figure 1. (a) Shows the behavior of trajectory ; (b)
Shows the behavior of the trajectory and .
e1
x1x2
Open Access AM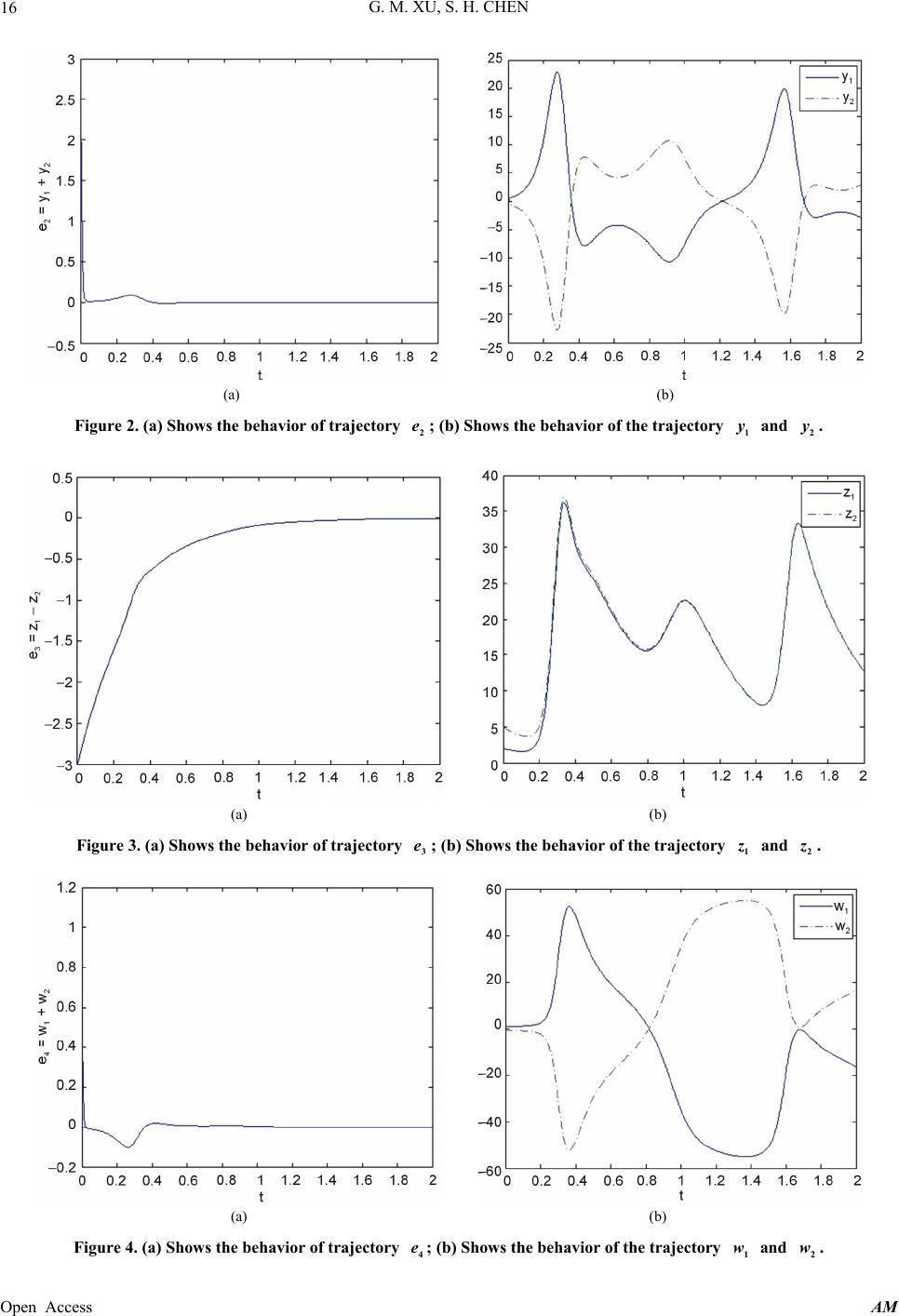

G. M. XU, S. H. CHEN
Open Access AM
16
(a) (b)
Figure 2. (a) Shows the behavior of trajectory ; (b) Shows the behavior of the trajectory e2
y
1 and
y
2.
(a) (b)
Figure 3. (a) Shows the behavior of trajectory ; (b) Shows the behavior of the trajectory and . e3z1z2
(a) (b)
Figure 4. (a) Shows the behavior of trajectory ; (b) Shows the behavior of the trajectory and .
4
e1 w2 w

G. M. XU, S. H. CHEN 17
6. Acknowledgements
e National Natural Scien
under Grant No. 6 127
[1] T. Y. Li and Je Implies Cha
The American, Vol. 82, No. 10.
[8] R. Mainieri and J. Rehacek, “Projective Synchronization
in Three-Dimensional Chaotic Systems,” Physical Review
This work is supported by th
Foundation (N NSF) of Chinace 3215.
REFERENCES
. A. Yorke, “Period Thre
Mathematical Monthlyos,”
1975, pp. 985-992. http://dx.doi.org/10.2307/2318254
[2] E. Rodriguez, N. George, J. P. Lachaux, J. Martinerie, B.
Renault and F. J. Varela, “Perception’s Shadow: Long-
Distance Synchronization of Human Brain Activity,” Na-
ture, Vol. 397, No. 6718, 1999, pp. 430-433.
[3] R. Y os hi da , M. T an a ka, S. Onod era, T. Yamaguchi an d E.
Kokufuta, “In-Phase Synchronization of Chemical and
Mechanical Oscillations in Self-Oscillating Gels,” The
Journal of Physical Chemistry A, Vol. 104, No. 32, 2000,
pp. 7549-7555. http://dx.doi.org/10.1021/jp0011600
[4] W. Singer, “Synchronization of Cortical Activity and Its
Putative Role in Information Processing and Learning,”
Annual Review of Physiology, Vol. 55, No. 1, 1993, pp.
349-374.
http://dx.doi.org/10.1146/annurev.ph.55.030193.002025
[5] L. M. Pec
otic Systems,” Physical Review Letters, Vol. 64, No. 8
ora and T. L. Carroll, “Synchronization in Cha-
,
1990, pp. 821-824.
http://dx.doi.org/10.1103/PhysRevLett.64.821
[6] S. Boccaletti, J. Kur
C. S. Zhou, “The Synchronization of Chaotic
ths, G. Osipov, D. L. Valladares and
Systems,”
Physics Reports, Vol. 366, No. 1, 2002, pp. 1-101.
http://dx.doi.org/10.1016/S0370-1573(02)00137-0
[7] M. G. Rosenblum, A. S. Pikovsky and J. Kurths, “P
Synchronization of Chaotic Oscillators,” Physical Rev
hase
iew
Letters, Vol. 76, No. 11, 1996, pp. 1804-1807.
http://dx.doi.org/10.1103/PhysRevLett.76.1804
Letters, Vol. 82, No. 15, 1999, pp. 3042-3045.
http://dx.doi.org/10.1103/PhysRevLett.82.3042
[9] C. M. Kim, S. Rim, W. H. Kye, J. W. Ryu and Y
“Anti-Synchronization of Chaotic Oscillators,”. J. Park, Physics
Letters A, Vol. 320, No. 1, 2003, pp. 39-46.
http://dx.doi.org/10.1016/j.physleta.2003.10.051
[10] Q. Xie, G. Chen and E. M. Bollt, “Hybrid Ch
Nization and Its Application in Information Processing,”
aos Synchro
Mathematical and Computer Modeling, Vol. 35, No. 1,
2002, pp. 145-163.
http://dx.doi.org/10.1016/S0895-7177(01)00157-1
[11] C. Li, Q. Chen and T
and Complete Synchronization in Coupled Chen S
. Huang, “Coexistence of Anti-Phase
ystem
via a Single Variable,” Chaos, Solitons & Fractals, Vol.
38, No. 2, 2008, pp. 461-464.
http://dx.doi.org/10.1016/j.chaos.2006.11.028
[12] Q. Zhang, J. Lü and S .Chen, “
and Complete Synchronization in the Generali
Coexistence of Anti-Phase
zed Lorenz
System,” Communications in Nonlinear Science and Nu-
merical Simulation, Vol. 15, No. 10, 2010, pp. 3067-
3072. http://dx.doi.org/10.1016/j.cnsns.2009.11.020
[13] K. S. Sudheer and M. Sabir, “Hybrid Synchronization of
Hyperchaotic Lu System,” Pramana, Vol. 73, No. 4,
2009, pp. 781-786.
http://dx.doi.org/10.1007/s12043-009-0145-1
[14] Y. Li, W. K. Tang a
via State Feedback Control,” International Jou
nd G. Chen, “Generating Hyperchaos
rnal of Bi-
r Science & Business Media, Inc., Boston, 2005.
furcation and Chaos, Vol. 15, No. 10, 2005, pp. 3367-
3375.
[15] F. Zhang, “The Schur Complement and Its Applications,”
Springe
http://dx.doi.org/10.1007/b105056
Open Access AM