Journal of Signal and Information Processing, 20 11 , 2, 37 - 43
doi:10.4236/jsip.2011.21006 Published Online February 2011 (http://www.SciRP.org/journal/jsip)
37
Performance Analysis on Output SINR of Robust
Two-Stage Beamforming
Tsui-Tsai Lin1, Fuh-Hsin Hwang2, Juinn-Horng Deng3
1Department of E l ectronic Eng i neering, Na t i o n al United Unive r s i ty, Miaoli, T aiw an; 2Department of Optoe lectronics and Communi-
cation Engineering, National Kaohsiung Normal University, Kaohsiung, Taiwan; 3Department of Communication Eng ineering, Yuan
Ze Unive r sity, Taoyuan, Tai wan.
Received October 30th, 2010; revised January 3rd, 2011; accepted January 4th, 2011
ABSTRACT
In this paper, we present a theoretical analysis of the output signal-to-interference-plus-noise ratio (SINR) for eigen-
space beamformers so as to investigate the performance degradation caused by large pointing errors. For the sake of
reducing such performance loss, a robust scheme, which consists of two cascaded signal processors, is proposed for
adaptive beamformers. In the first stage, an algorithm possessing time efficiency is developed to adjust the direc-
tion-of-arrival (DOA) estimate of the desired source. Based the achieved DOA estimate, the second stage provides an
eigenspace beamformer combined with the spatial derivative constraints (SDC) to further mitigate the cancellation of
the desired signal. Analysis and numerical results have been conducted to verify that the proposed scheme yields a bet-
ter robustness against pointing errors than the conventional approaches.
Keywords: Beamforming, Large Pointing Error, Output Signal-To-Interference-Plus-Noise Ratio (SINR), Eigenspace
Beamformer, Two-Stage
1. Introduction
It is well known that conventional adaptive beamfomers
are effective in suppressing strong interferers as long as
the error in the steering vector due to pointing inaccuracy
is small [1]. In the presence of steering vector errors,
these beamformers exhibit severe degradation in per-
formance in that the output signal-to-interference-plus-
noise ratio (SINR) drops dramatically. Remedies have
been proposed to lessen the effect of desired signal can-
cellation [2]. In particular, the linearly constrained mini-
mum variance (LCMV) beamformer uses the spatial de-
rivative constraints (SDC) to alleviate sensitivity to the
pointing errors by means of a flatter main-lobe response
[3,4]. Unfortunately, this in turn results in large sidelobes
and leads to a loss in array gain against noise. Further-
more, the decrement in the beamwidth as the input sig-
nal-to-noise ratio (SNR) increases makes it poor in inter-
ference suppression due to the directional mismatch [5].
In the extreme case of high input SNR, since the desired
signal may fall outside the main-lobe region, the SDC
beamformer would null out not only the interference but
also the desired signal. In [6], a robust scheme employs
the leaky elimination constraint and the interference null
constraint to preserve the desired signal and to keep nice
interference nulling simultaneously. This method needs
to identify the interference subspace for the sake of re-
storing the interference correlation matrix. However, in
the presence of weak interference, it is difficult to extract
the interference subspace from the received data. Chang
and Yeh [7] proposed the eigenspace beamformer, in which
the weight vector is constrained within the signal sub-
space of the received data correlation matrix. In spite of
success in dealing with a moderate pointing error, this
approach cannot completely remove the interference and
the residual interference impairs the system performance,
especially for the weak interference (low signal-to-inter-
ference ratio, SIR). To mitigate the effect of large point
errors, an iterative searching method [8] is considered for
constructing the correct constraint vector before beam-
forming. Its low convergence behavior because of a large
pointing error becomes crucial in practice. This approach,
at the worst, breaks down when the desired signal falls
outside the main-beam region in the case of high input
SNR and/or a large antenna array.
In this paper, the effect of pointing errors on the ei-
genspace beamformer is first investigated by using the
theoretical analysis. As a remedy, a robust two-stage

Performance Analysis on Output SINR of Robust Two-Stage Beamforming
38
scheme for adaptive beamformer is proposed [9]. The
design of this beamformer involves the following proce-
dure. First, an accuracy direction-of-arrival (DOA) esti-
mate is determined from a few angles-of-interest in ac-
cordance with the fact that the output power of the beam-
former decreases with the increment in the pointing error.
By exploiting the refined resultant, an eigenspace beam-
former incorporating with the SDC is used to further
mitigate the aggregate impacts due to the pointing errors .
A closed-form approximate SINR expression is given to
indicate the achievable performance improvement. Nu-
merical results then confirm the efficacy of the proposed
robust method and corroborate the predicted SINR re-
sults.
The remainder of the paper is organized as follows:
Section 2 reviews the array data model and presents the
SINR performance analysis of the eigenspace beam-
former. The proposed two-stage beamformer and its per-
formance analysis are provided in Section 3. Simulation
results and conclusion remarks are given in Sections 4
and 5, respectively.
The notations used in this paper follow the usually
conventional-bold capital letters denoting vectors and
matrices. I is an identity matrix with a proper dimen-
sion,

diag v is a diagonal matrix with its entries
formed by v,

T
 and

H
 are transpose and com-
plex conjugate transpose of


. Also,


Re

,


E

,
and  are used to denote real part, ensemble average,
and absolute operators, respectively.
2. Preliminary
The scenario considered herein involves a single desired
source and 1
K
 uncorrelated interfering sources, all
assumed to be narrowband with the same center fre-
quency. These sources are in the far field of a uniform
linear array consisting of
M
identical elements spaced
by half a wavelength. Adopting the complex envelope
notation, the array data obtained at a certain sampling
instant can be put in the 1
M
 vector form:
   
1
.
K
kk
k
nsn n 



xan (1)
The random scalars


k
s
n for 1, 2,,kK repre-
sent the signals with power2
k

. The 1
M
 vector


1sin
sin
1,, ,T
jM
j
ee M





 a is the array
steering vector, in which

is the physical angle meas-
ured with respect to the broadside of the array. Finally,
the vector

nn is additive white Gaussian noise with
power 2
n

I. Without loss of generality, suppose


1
s
n
is the desired signal.
The LCMV beamformer, which minimizes the array
output power subject to a unit constraint on the presumed
vector, is widely used to preserve the desired signal and
keep interference nulling simu ltaneou sly. Math ematically
speaking, the optimal weight can be obtaine d by [3]:

 
11
,
H
ss s



wRa aRa (2)
where


s

a is the steering vector associated with the
look direction
s

, and R is an
M
M received data
correlation m a tri x gi ven by
 

 
22
1
.
K
HH
kkkn
k
En n



 

Rxxaa I (3)
According to the orthogonality b etween the signal and
noise subspaces, the eigenspace technique can be used to
mitigate the effect of desired signal cancellation and its
corresponding weight vector is given by
 
11
,
H
sss
HH
sss ss





wEEw
EE RaaRa (4)
where the
M
K

matrix
s
E is formed by the
K
principal eigenvectors of R. Under proper conditions,
the eigenspace beamformer is found to achieve high
output SINR as long as the pointing error

1s

  is
negligible. Unfortunately, in the case of the large point-
ing error and/or high input SNR, its performance is lim-
ited mostly by the residual interference buried in the
beamformer output.
To gain further insights, we will describe the effect of
the residual interference caused by pointing inaccuracy.
For a manageable analysis, the scenario is simplified into
that involving a desired source with power 2
11


and
an interferer with power 2
2

only, i.e., 2K. Thus the
received data correlation matrix can be rewritten as




22
1122 2.
HH
n

  Ra aaaI (5)
In addition, for the ease of expression, the following
notations are defined:

kk

aa and H
kj kj

aa for
,1,2,kj s

. Note that kj

denotes the correlation be-
tween k
a and
j
a, and is close to zero for a well-sepa-
rated sources.
By using some algebraic manipulations, the received
data correlation matrix can be decomposed as
2
1111 12222 2
2
11112 222,
HHHHn
HH
n


 
 
 
R eeeeeeeeI
eeee I (6)
where



22
222
22212
11 212
1114 2;
1;1,1,2.
k
k
H
kkkk
k
 


  


 ea aee
(7)
Under the simplified scenario, the weight vector for
the eigenspace beamformer is given by

Performance Analysis on Output SINR of Robust Two-Stage Beamforming
39
112 2
12
22
12
112 2
12
22
12
,
HH
ss
s
nn
nn
gg

 

 




ea ea
wee
ee
(8)
where

12 21
1, 1,2.
H
kkss sk
gk   ea (9)
Note that we have omitted the normalized scalar since
it does not affect the analysis result. Using (8), the output
desired signal power d
P and the output interference-
plus-noise p ow e r in P are given by
11
2
112 2
11 12
22
12
2
11 12 22
22
12
2
22
112 211 12 22
2222
12 12
;
,
HH
ds s
HH
nn
nn
H
inssd
nn nn
P
gg
gg
PP
gg
gg

 
 
 
  
  








waaw
ae ae
wRw
(10)
in which we have used the facts that 1
Hkk


ae for
1, 2k. Taking the ratio of d P and in P with substitu-
tion of (10) yields the output SINR expression:
11 1222
22
12
22
112 211 1222
222 2
121 2
11
2
2
SINR
.
nn
nn n n
HH
ds s
oH
in ssd
P
PP
gg
gg gg
 
 
  
 

  
 



waaw
wRw
(11)
This result reveals that the output SINR is dependent
upon the look direction

1s
g
 , which decreases as the
pointing error increases.
Under the condition that the interference is far away
from the desired source, i.e, 121

, we have


2
122
2
11 22212
2
112 2221
1; ;
;1;
;1.
ss
gg








eaea (12)
Substituting (12) into (11), the output SINR can be
reduced to

2
2
12122
2222
1
22
2
22 2
12 12122
2222222
()()
222
1
SINR
11 1
ss
nn
o
ss ss
nnn n


 
 




 




2
12
2
22 2
121
222 2
2
2
2
1
22
12
1
2
21
21
22
12
1
11
1INR
SNR 1INR1 SNR
SNR ,
SNR ,INR1,
1&SNR 1
s
n
ss s
nn
n
si
isis i
is
ii
ssi
s


 
 


 


















aa


(13)
where 2
SNR 1
in

 and 22
2
INRin

  denote the
input SNR and interference-to-noise ratio (INR), respec-
tively. The results in (13) reveal several intrinsic features
of the eigenspace beamformer. First of all, as long as the
look direction is close to the DOA of the desired source
(1s

aa), the eigenspace beamformer performs like the
optimal quiescent beamformer, which can offer the
maximum output SINR equal to SNRi. The second one
is that the eigenspace beamformer can achieve a reliable
performance without severe desired signal cancellation
for INR 1
i. On the contrary, in presence of weak in-
terference, the beamformer fails to completely remove
the interference and the residual interference cannot be
negligible when compared with the output noise power,
leading to a substantial degradation in output SINR. Fi-
nally, in the case of high input SNR (SNR 1
i) and/or
large pointing errors (11
s

), the second term of the
denominator becomes large and cannot be negligible
when compared with the first term. This significantly
drops the performance of the eigenspace beamformer. To
make matters worse, the eigenspace beamformer reaches
a “saturation region”, in which the output SINR is inde-
pendent upon the input SNR.
3. Proposed Robust Two-Stage
Beamforming
As mentioned above, the eigenspace beamformer cannot
offer a reliable SINR performance as the error in DOA
estimate is large and/or the input SNR is high, especially
for weak interference. An alternative to enhancing ro-
bustness is to adjust the DOA estimate before beam-
forming. This prompts us to propose a two-stage scheme.
In the first stage, we determine an accuracy DOA esti-
mate based on the fact that the output power of the
LCMV beamformer decreases with the increment in the
pointing error. In the second stage, to mitigate desired
signal cancellation, we further leverage the spatial de-
rivative technique to incorporate the refined DOA esti-

Performance Analysis on Output SINR of Robust Two-Stage Beamforming
40
mate into the eigenspace beamformer.
3.1. Proposed Two-Stage Beamformer
According to (2), the output power of the LCMV beam-
former is given by
 
1
1, H
oss s
P 



 aRa (14)
which achieves a maximum output SINR when the
steering vector

s

a coincides with that of the desired
signal

1

a [8]. This suggests that an accuracy DOA
estimate can be chosen from the candidate angle set,

:2
ms
SmBN

  for ,1,,mNN N  in
accordance with maximizing the array output power:
 
 
1
1
1
ˆmax
min ,
m
m
H
smm
S
Hmm
S














aRa
aRa (15)
where B denotes the presumed angle region of inter-
esting. The choosing of N is a trade-off between accu-
racy in DOA estimate and computational load. A small
value of N leads to time-saving in searching ˆ
s

, but
poor performance in beamforming, and vice versa. Since
the major consideration in the first stage is to get rid of
desired signal cancellation due to a large pointing error, a
small value of N is preferred.
In order to further improve robustness against the error
in DOA estimation, an eigenspace beamformer is to in-
corporate a first-order SDC in the direction ˆ
s

. We have
the weight vector given by

1
11
11
11
1
1
1
ˆˆ ˆ
ˆˆ ˆ
ˆˆ
ˆ,
ˆˆ
HH
ss
HH
sssss
HH
sssss
H
Hss
s
ss
H
ss














wEERCCRCf
aDRDa EERa
aDRaEERDa
aDRa
EERID a
aDRDa
(16)
where

1, 0T f,

ˆ
ˆ
s
s

aa , and


ˆˆ
,
s
s
CaDa with


0,1,,1T diag MD. With the uses of 1
ˆs



and the Taylor’s series expansion [10], we have
11
ˆsj

aa Da, where


1ˆ
sinsin s

 




, such
that the weight vector in (16) reduces to



11
12 12
11
21ˆ
,sinsin
H
ss
HH
ss ss
os
jj  




 


 

wEER IDIDa
EE RaEERDa
wΓb
(17)
where 1H
ss 
ΓEE R, 21 bDa, and 11
H
oss

wEERa
denotes the optimal weight vector for the eigenspace
beamformer without pointing error. The second term in
(17) is due to the estimation error in the fir st stag e, which
is insignificant when compared with o w because of the
fact that 1

.
3.2. Algorithm Summary for the Proposed
Two-Stage Beamformer
The overall procedure of the proposed robust beam-
former can be summarized as below.
(1) Obtain the sample averaged version of the re-
ceived data correlation matrix ˆ R given by
 
1
ˆ,
s
NH
s
n
nnN

 Rxx (18)
where
s
N denotes the number of the data sam-
ples.
(2) Obtain the preliminary DOA estimate
s

for the
desired source [11].
(3) Compute the refined DOA estimate ˆ
s

according
to (15) with R replaced with ˆ R in (18).
(4) Compute the weight vecto r w according to (16).
3.3. Theoretical Analysis on the Output SINR
In this subsection, the analysis expression of the output
SINR associated with the proposed beamformer is pre-
sented. For a manageable analysis, we only consider a
two-source system again. Substituting (6) and (17) into
(11), along with some algebraic manipulations, the ex-
pansion of the output SINR for the proposed beamformer
is approximately expressed by





2
411 1
11 2
11 11 11
2
411 1
2
11 11
SINR11
SINR ,
1
HHH
H
oHHH
HHH
opt HH






 
aΓabΓbbΓa
aΓa
aΓaaΓaaΓa
aΓab ΓbbΓa
aΓaaΓa
(19)
where
22
11 122 2
22
12 11 22
11 122 2
11 22
12
SINR .
11
HH
Hnn
opt HHH
nn

 








ee ee
aΓaee ee
aΓa (20)
Note that SINRopt in (20) denotes the maximum out-
put SINR obtained by the optimal beamformer (without
pointing error). The result in (19) indicates that the pro-
posed beamformer performs like the optimal LCMV
beamformer with a slight degradation in output SINR,
which is proportional to 41  .
4. Computer Simulations
Computer simulations were conducted to ascertain the
performance of the proposed two-stage beamformer. The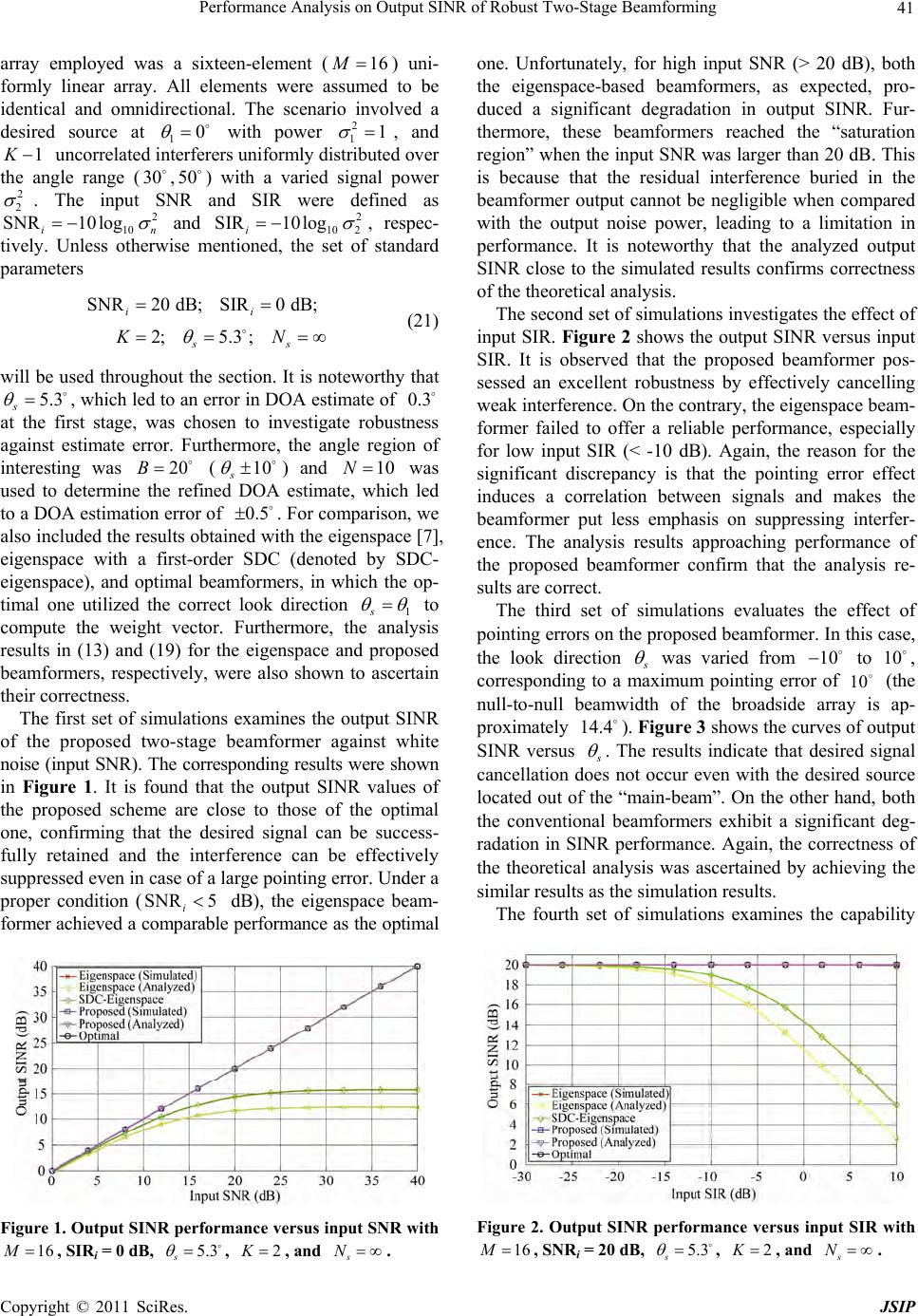

Performance Analysis on Output SINR of Robust Two-Stage Beamforming
41
array employed was a sixteen-element (16M) uni-
formly linear array. All elements were assumed to be
identical and omnidirectional. The scenario involved a
desired source at 10   with power 2
11


, and
1
K
 uncorrelated interferers uniformly distributed over
the angle range (30,50) with a varied signal power
2
2

. The input SNR and SIR were defined as
2
10
SNR 10log
in

 and 2
10 2
SIR 10log
i

 , respec-
tively. Unless otherwise mentioned, the set of standard
parameters
SNR20 dB;SIR0 dB;
2;5.3 ;
ii
ss
KN 

 
 (21)
will be used throughout the section. It is noteworthy that
5.3
s
 , which led to an error in DOA estimate of 0.3
at the first stage, was chosen to investigate robustness
against estimate error. Furthermore, the angle region of
interesting was 20B (10
s
 ) and 10N

was
used to determine the refined DOA estimate, which led
to a DOA estimation error of 0.5. For comparison, we
also included the results obtained with the eigenspace [7],
eigenspace with a first-order SDC (denoted by SDC-
eigenspace), and optimal beamformers, in which the op-
timal one utilized the correct look direction 1s



to
compute the weight vector. Furthermore, the analysis
results in (13) and (19) for the eigenspace and proposed
beamformers, respectively, were also shown to ascertain
their correctness.
The first set of simulations examines the output SINR
of the proposed two-stage beamformer against white
noise (input SNR). The corresponding results were shown
in Figure 1. It is found that the output SINR values of
the proposed scheme are close to those of the optimal
one, confirming that the desired signal can be success-
fully retained and the interference can be effectively
suppressed even in case of a large pointing error. Under a
proper condition ( SNR 5
i dB), the eigenspace beam-
former achieved a comparable performance as the optimal
Figure 1. Output SINR performanc e versus input SNR with
16M, SIRi = 0 dB, 5.3
s
 , 2
K
, and s N.
one. Unfortunately, for high input SNR (> 20 dB), both
the eigenspace-based beamformers, as expected, pro-
duced a significant degradation in output SINR. Fur-
thermore, these beamformers reached the “saturation
region” when the input SNR was larger than 20 dB. This
is because that the residual interference buried in the
beamformer output cannot be negligible when compared
with the output noise power, leading to a limitation in
performance. It is noteworthy that the analyzed output
SINR close to the simulated results confirms correctness
of the theoretical analysis.
The second set of simulations investigates the effect of
input SIR. Figure 2 shows the output SINR versus input
SIR. It is observed that the proposed beamformer pos-
sessed an excellent robustness by effectively cancelling
weak interference. On the contrary, the eigenspace beam-
former failed to offer a reliable performance, especially
for low input SIR (< -10 dB). Again, the reason for the
significant discrepancy is that the pointing error effect
induces a correlation between signals and makes the
beamformer put less emphasis on suppressing interfer-
ence. The analysis results approaching performance of
the proposed beamformer confirm that the analysis re-
sults are correct.
The third set of simulations evaluates the effect of
pointing errors on the proposed beamformer. In this case,
the look direction
s

was varied from 10 to 10,
corresponding to a maximum pointing error of 10 (the
null-to-null beamwidth of the broadside array is ap-
proximately 14.4). Figure 3 shows the curves of output
SINR versus
s

. The results indicate that desired signal
cancellation does not occur even with the desired source
located out of the “main-beam”. On the other hand, both
the conventional beamformers exhibit a significant deg-
radation in SINR performance. Again, the correctness of
the theoretical analysis was ascertained by achieving the
similar results as the simulation results.
The fourth set of simulations examines the capability
Figure 2. Output SINR performance versus input SIR with
16M

, SNRi = 20 dB, 5.3
s
 , 2K, and s
N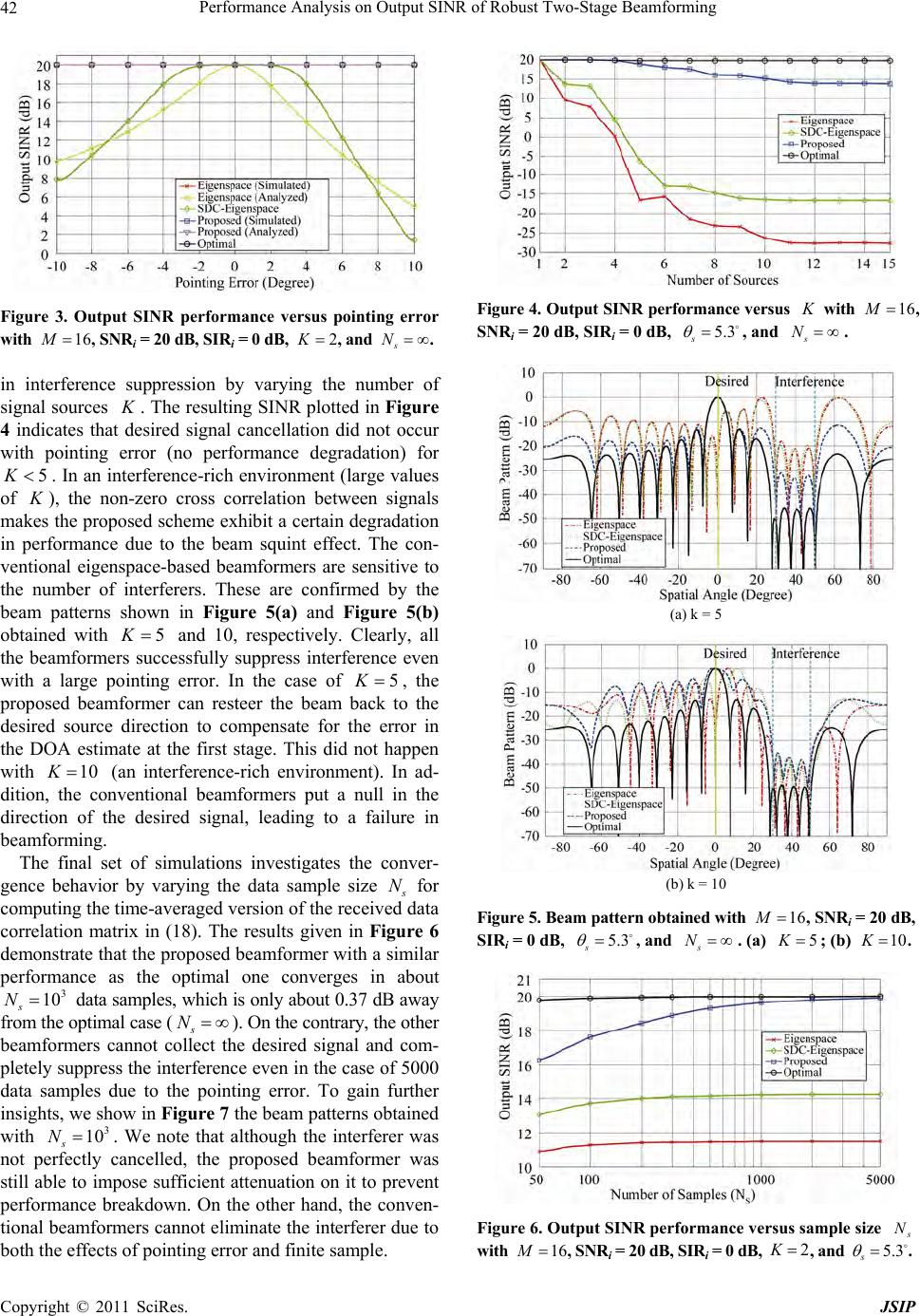

.

Performance Analysis on Output SINR of Robust Two-Stage Beamforming
42
Figure 3. Output SINR performance versus pointing error
with 16M, SNRi = 20 dB, SIRi = 0 dB, 2K, and s N

.
in interference suppression by varying the number of
signal sources
K
. The resulting SINR plotted in Figure
4 indicates that desired signal cancellation did not occur
with pointing error (no performance degradation) for
5K. In an interference-rich environment (large values
of
K
), the non-zero cross correlation between signals
makes the proposed scheme exhibit a certain degradation
in performance due to the beam squint effect. The con-
ventional eigenspace-based beamformers are sensitive to
the number of interferers. These are confirmed by the
beam patterns shown in Figure 5(a) and Figure 5(b)
obtained with 5K and 10, respectively. Clearly, all
the beamformers successfully suppress interference even
with a large pointing error. In the case of 5K

, the
proposed beamformer can resteer the beam back to the
desired source direction to compensate for the error in
the DOA estimate at the first stage. This did not happen
with 10K (an interference-rich environment). In ad-
dition, the conventional beamformers put a null in the
direction of the desired signal, leading to a failure in
beamforming.
The final set of simulations investigates the conver-
gence behavior by varying the data sample size
s
N for
computing the time-averaged version of the received data
correlation matrix in (18). The results given in Figure 6
demonstrate that the proposed beamformer with a similar
performance as the optimal one converges in about
3
10
s
N data samples, which is only about 0.37 dB away
from the optimal case (s N). On the contrary, the other
beamformers cannot collect the desired signal and com-
pletely suppress the interference even in the case of 5000
data samples due to the pointing error. To gain further
insights, we show in Figure 7 the beam patterns obtained
with 3 10
s
N. We note that although the interferer was
not perfectly cancelled, the proposed beamformer was
still able to impose sufficient attenuation on it to prevent
performance breakdown. On the other hand, the conven-
tional beamformers cannot eliminate the interferer due to
both the effects of pointing error and finite sample.
Figure 4. Output SINR performance versus
K
with 16M

,
SNRi = 20 dB, SIRi = 0 dB, 5.3
s
 , and s N.
(a) k = 5
(b) k = 10
Figure 5. Beam pattern obtained with 16M, SNRi = 20 dB,
SIRi = 0 dB, 5.3
s
 , and s N. (a) 5K; (b) 10K

.
Figure 6. Output SINR performance versus sample size
s
N
with 16M

, SNRi = 20 dB, SIRi = 0 dB, 2
K
, and 5.3
s

.

Performance Analysis on Output SINR of Robust Two-Stage Beamforming
43
Figure 7. Beam pattern obtained with 16M, SNRi = 20
dB, SIRi = 0 dB, 2
K
, 5.3
s
 , and 3 10
s
N.
5. Conclusions
In this paper, we have derived an output SINR closed-
form expression of the eigenspace beamformer in terms
of three important parameters including pointing errors,
input SNR, and SIR. According to these analytical results,
we find some intrinsic constraints imposed on the eigen-
space beamformer. These constraints inspire us to de-
velop a new beamforming scheme for combating large
pointing errors. Computer simulations are presented to
verify the derivation of the corresponding analysis. It is
shown that the proposed beamformer possesses a better
resistance to the pointing errors and excellent capability
of suppressing weak interference in comparison with the
conventional techniques, especially at a low input SIR.
6. Acknowledgement
This work was sponsored by the National Science Coun-
cil, R. O. C, under the Contract NSC 99-2221-E-239-
023.
REFERENCES
[1] R. A. Monzingo and T. W. Miller, Introduction to Adap-
tive Arrays, New York, NY: John Wiley & Sons, 1980.
[2] B. Widrow, K. M. Duvall, R. P. Gooch and W. C. New-
man, “Signal Cancellation Phenomena in Adaptive An-
tennas: Causes and Cures,” IEEE Trans. Antennas and
Propagat., Vol. 30, No. 5, pp. 469-478, May 1982.
[3] B. D. Van Veen and K. M. Buckly, “Beamforming: A
Versatile Approach to Spatial Filtering,” IEEE ASSP
Magazine, pp. 4-24, April 1988.
[4] M. H. Er, “Adaptive Antenna Array under Directional
and Spatial Derivative Constraints,” Proc. IEE, pt. H, Vol.
135, No. 6, pp. 414-419, 1998.
[5] K. C. Huang and C. C. Yeh, “Performance Analysis of
Derivative Constraint Adaptive Arrays with Pointing Er-
rors,” IEEE Trans. Antennas and Propagat., Vol. 40, No.
8, pp. 975-981, Aug. 1992.
[6] Y. Chu and W. Y. Horng, “A Robust Algorithm for Adap-
tive Interference Cancellation,” IEEE Trans. Antennas
and Propagat., Vol. 56, No. 7, pp. 2121-2124, July 2008.
[7] L. Chang and C. C. Yeh, “Effect of Pointing Errors on the
Performance of the Projection Beamformer,” IEEE Trans.
Antennas and Propagat., Vol. 41, No. 8, pp. 1045-1056,
Aug. 1993.
[8] M. H. Er and B. C. Ng, “A New Approach to Robust
Beamforming in the Presence of Steering Vector Errors,”
IEEE Trans. Signal Process., Vol. 42, No. 7, pp. 1826-
1829, July 1994.
[9] T. T. Lin, “A Two-Stage Beamformer with Enhanced
Resistance Against Larger Pointing Errors,” in Proc.
PIMRC 2009, Tokyo, Japan, pp. 983-987, Spet. 2009.
[10] G. H. Golub and C. F. Van Loan, Matrix Computations,
2nd ed., Baltimore, MD: Johns Hopkins University Press,
1989.
[11] J. C. Liberti, T. S. Rappaport, Smart Antennas for Third
Generation Mobile Communications, Artech House Pub-
lishers, 1998.