Energy and Power Engineering, 2013, 5, 708-712
doi:10.4236/epe.2013.54B137 Published Online July 2013 (http://www.scirp.org/journal/epe)
Research on Optimization for Units Start During Power
System Restoration
Jun Chen1, Wei -xing Zhao1, Hua-ying Su1, Jia-lin Bai1, Nian Liu2, Xiao-yan Qiu2, Qian Liao2
1Guizhou Power Grid Corporation of Dispatch Control Center, Guiyang, Guizhou, China
2School of Electrical Engineering and Information Sichuan University, Chengdu, China
Received March, 2013
ABSTRACT
Considering units starting and network constraints and the concept of optimization period, a optimization model which
is a typical multi-constraint knapsack problem is established to solve the selection optimization problem of units start-
ing in power system restoration period in this paper, and the objective of the model is to maximize the total power gen-
eration capability. A relative effectiveness assessment based on a improving data envelopment analysis is adopted to
select the initial units to be started, genetic algorithms are employed to solve the knapsack problem to determine the
most reasonable units be started at the current time. Finally, IEEE-39 bus system simulation result proves that the pro-
posed model is feasible and effective.
Keywords: Power system; Units start; data envelopment analysis; knapsack problem
1. Introduction
In recent years, although modern power system has im-
proved greatly in the running reliability, security, stabil-
ity and economic, but large-scale blackout in the world
still occur frequently, and the whole social activities and
people's lives are impacted seriously [1-4]. Large-scale
power system after the accident has usually affected
scope, and power failure time is long, which put forward
more severe challenges for the quick recovery of the ac-
cident of power system [5-7]. Therefore, how to make
the system restored after the blackout becomes one of the
important problems which each power grid have to faces.
The system recovery process is usually divided into three
stages, namely unit start-up, network reconfigurations
and load recovery. Unit’s recovery is the basis of the
whole power system for the control of recovery. The key
of unit’s recovery is how to optimize the unit start ac-
cording to the actual situation of the system during the
recovery process. So, how to reasonably select the start
units is the core issue of unit recovery.
The units start has been one of the important topics of
the research field of power system. Many scholars have
done a lot of research on the issue. The some of the con-
cepts of power system faults recovery and the matters
needing attention were concluded [8]. By using the ana-
lytical hierarchy process in the process of recovery unit
start sorting, the recovery units and various factors of
output were analyzed [9]. The genetic algorithm and the
expert system were combined to agile develop units re-
covery strategy [10]. The data envelopment analysis me-
thod is adopted to assess the effectiveness of the recovery
program technical verification; results included in the
assessment system, and use the actual input, output index
value to judge [11]. Therefore, considering units starting
constraints and network constraints which include the
unit start power constraint, maximum critical heat start
time constraint, the minimum critical start time constraint
and network constraints, a optimization model which is a
typical multi-constraint knapsack problem is established
to solve the selection optimization problem of units
starting in power system restoration period in this paper，
and the objective of the model is to maximize the total
power generation capability. A relative effectiveness
assessment based on a improving data envelopment
analysis is adopted to select the initial units to be started,
genetic algorithms is employed to solve the knapsack
problem to determine the most reasonable units be
started at the current time. Finally, IEEE-39 bus system
simulation result proves that the proposed model is feasi-
ble and effective.
2. Problem Fo mulation
2.1. Objective Function
*The project supported by GuiZhou Power Grid Corporation (12H-
0594), Technology Project of Science & Technology Department of Si-
chuan Province (No.2011GZ0036) The optimization goal to be maximize generation energy

J. CHEN ET AL. 709
which is provided by units in the optimization period in
this paper, so the objective function of the units start op-
timization model is defined as:
  
,
10
max
T
n
ii cri
i
Ut PtPdt




,
(1)
where:
n is the number of power plants; T is the optimization
period of the system unit recovery; Ui(t) is the state of the
i (i=1,…,n) unit（1 for start, 0 for outage；Pcr,i is the
required starting power of the i unit in startup process;
Pi(t) is the output function of the i unit, as shown in Fig-
ure 1.
2.2. Constraints
Unit constraint includes critical time constraints and
starting power constraint.
,
0
s
iCH
TTi
,
(2)
,
s
iCC
TTi

(3)
00, ,
1
()()( ())0
n
kk crkcri
k
PtC t PtPP


 (4)
where:
TCH,i is the maximum critical hot start time of i hot
start unit ; TCC,i is the minimum critical cold start time
of i cold start unit ; In the formula (4), P0(t0) is the initial
power of the system, Where the second term represents
the system power which provided by grid units; k is the
number of grid unit; Ck(t) is the state of the k grid unit ;
Pk(t) is the output function of the k grid unit; Pcr,k is the
required starting power of the k grid unit in startup proc-
ess.
Meanwhile, network constraints were considered in
this optimization model. The unit start network con-
straints can through the following indexes to show:
Power transmission path index (including power trans-
mission path charging reactive power and voltage switch-
ing frequency).
Load importance of index (considering the relative
importance of the units which is started near the load).
Hot start pressing index (mainly reflected in the cur-
rent time step, the unit is near its biggest critical heat
start time limit level).
3. Solving Method
3.1. The Solution Strategy of Optimization Mod-
el
The units start is a more complicated optimization prob-
lem; the direct solution has the certain difficulty. Using
model discrimination technique, the optimization time T
is divided into time step N, so the complicated continu-
ous time problem is disserted to be a simple optimization
problem of the unit start in the every step. If h is step
length, then each step for the start time and end time is
respectively h(kt-1) and hkt
（kt =1,…,N）, according to the
formula (1), the every step of objective function is
,
1(1)
max( )(( ))
t
T
n
ii cri
ihk
UtPtP dt


 (5)
From the above model, units start optimization prob-
lems with multiple constraints is a knapsack problem. In
this paper, the optimization problem was decomposed, a
part of constraint conditions which were smaller correla-
tion degree with objective function calculation were ex-
tracted in advance, and start unit were elected prelimi-
narily. The optimization problem was slack for the prob-
lem only considering starting power constraint conditions,
the unit can provide the biggest power generation. By
solving one-dimensional constraint knapsack problem,
the most reasonable current time start units were deter-
mined quantitatively.
3.2. Primary Election of Start unit
Data Envelopment Analysis (DEA) [12] is a method, on
which based relative efficiency concept as the foundation,
through the mathematical programming compare the
relative efficiency of each decision making unit, and to
make efficiency evaluation. The CCR model (in Charnes,
Cooper, Rhodes and three authors initials named) and its
equivalent linear programming model were commonly
used to solve the multi-objective decision making prob-
lem.
When the CCR model is used to evaluate and compare,
if multiple decision unit efficiency evaluation index Ek
are equal to 1, the decision making units cannot be given
comparison and ranking. An improved DEA model, that
is, super efficiency DEA model [13, 14] is fully applied
to compare and rank the decision making unit in this pa-
per.
Figure 1. Schema of generation unit output function.

J. CHEN ET AL.
710
In the units recovery model, according to start units
selection principle, each optional start units are launched
as decision unit, then combined with the improved DEA
model, the input and output index of the unit relative
efficiency evaluation are established. The index and its
calculation method as are shown in Table 1.
The calculation method of each index interpretation is
as follows.
Unit start power value is Pcr,i value.
Power transmission path index value is every km line
charging power Qcj multiply line length Lj product plus
weighted value of voltage conversion number ZT.
Load importance index is the reciprocal of each unit
near important load Lurg,i ratio all load LΣ,i .
Hot start pressing index is difference value of unit
TCH,I and the current time step over time hkt .
Unit power output index is the integral of the output of
generating unit in the optimization of time period.
4. Determining the most Reasonable Start
Unit by Solving Knapsack Problem
Units are primarily elected by the improved DEA, the
original optimization problem is slack for a one dimen-
sional constraint knapsack problem. In this problem, the
“backpack volume”, “efficiency indicators” and “volume
index” corresponding to the total power of the start units
which whole system is available for in the period, the
generation energy of units in the optimization period and
the starting power of the optional units, the model such
as type (6) and (7) show.
,
1(1)
max( )(( ))
t
T
n
ii cri
ihk
UtPtP dt


 (6)
00, ,
1
()()( ())0
n
kk crkcri
k
PtC t PtPP



(7)
Genetic algorithm is the most representative of the
evolutionary algorithm, which is the most basic intelli-
gent optimization algorithm; this method has the parallel
search, group optimization characteristics, widely used to
solve various completely non-deterministic polynomial
time problems. Because the quantity of units after pri-
mary selection is not big, the most reasonable units are
deter- mined by solving knapsack problem using genetic
algo- rithm.
5. Case Study
The IEEE-39 node system [15] is adopted to analyze this
problem, the system topology structure shown in Figure
2. And assume the initial conditions: the unit 30-1 as
black start unit, t0 =1.5 h, T =12 h, N =48. Each unit pa-
rameter is shown in Table 2.
Table 1. Input indices and output indices used in assess-
mentof units.
IndexDetails Calculation method
A Unit start power Pcr,i
B Power transmission path QcjLj + ZT
C Load importance LΣ,i /Lurg,i
D Hot start pressing TCH,I — hkt
E Unit power output ,
(1)
()( ())
t
T
ii cri
hk
UtPtP dt



Figure 2. Structure chart of IEEE- 39-bus power system.
Table 2. Parameters of the units of IEEE- 39-bus power
system.
Node UnitPcr/
MW
PM/
MW
Kp/
MW/h
Ts,i′
/h
TCC,i/
h
TCH,i/
h
3030-10 250 166.67 0 N/A N/A
31-118 378 150 0.7 3 N/A
31 31-215 300 120 0.5 N/A3
32-117.5350 130 0.67 N/A 3.5
32 32-215 300 120 0.5 N/A3
33-115 332 108 0.6 2.3 N/A
33 33-215 300 120 0.5 N/A2
34-116.5308 100 1.1 N/A 4.2
34 34-215 250 100 1.1 N/A3.5
35-117.5350 130 0.67 N/A 3.5
35-28 150 90 0.83 2 N/A 35
35-38 150 90 0.83 2 N/A
36-110 200 120 0.5 N/A2
36 36-218 350 130 0.67 N/A3.5
37-110 200 120 0.5 N/A2
37 37-217.5350 130 0.67 N/A 3.5
38-110 200 120 0.5 N/A2
38-210 200 120 0.5 N/A2 38
38-320 430 130 1.2 N/A3
39-122 500 200 1.2 N/A4
39 39-222 500 200 1.2 N/A4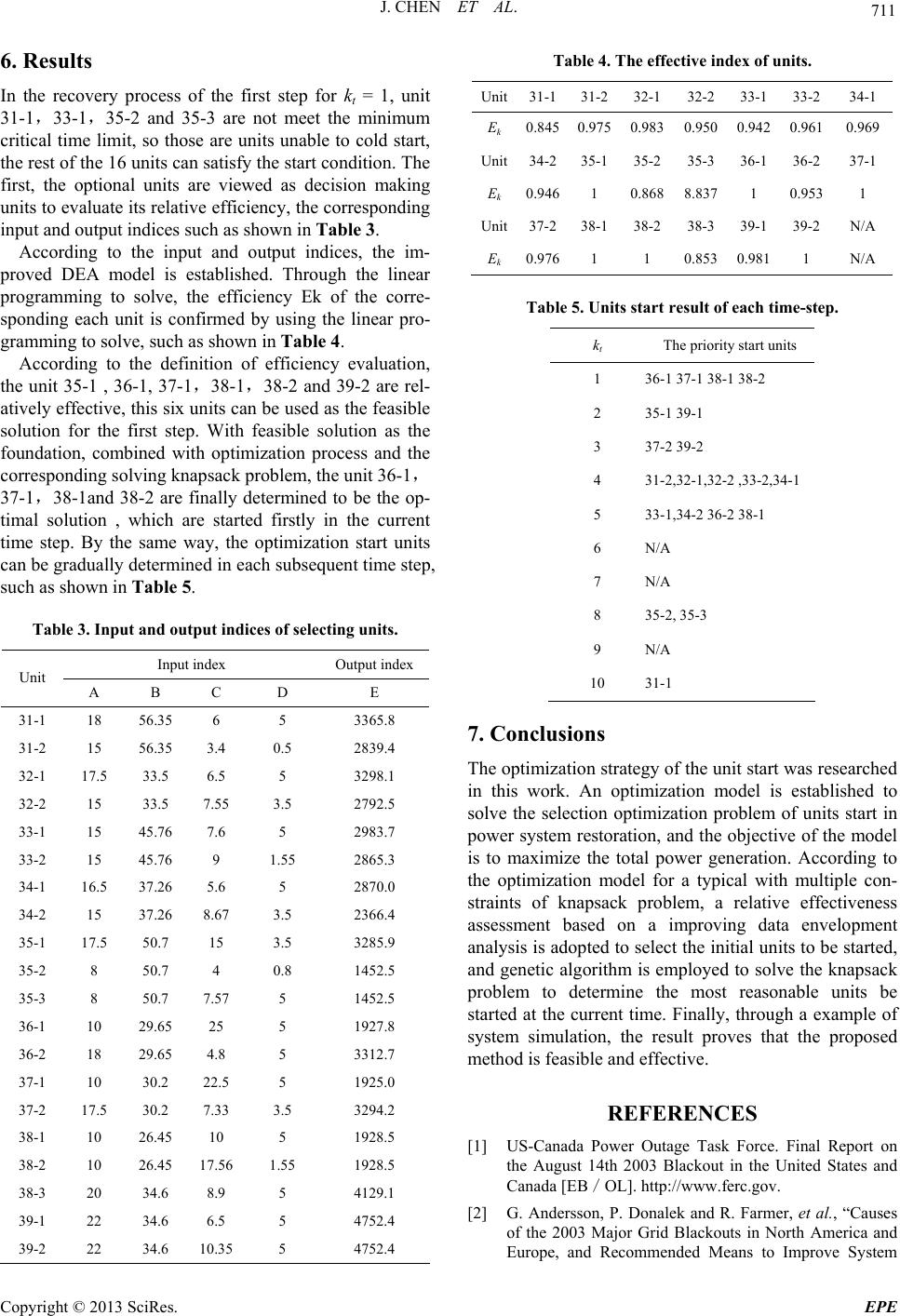

J. CHEN ET AL. 711
6. Results
In the recovery process of the first step for kt = 1, unit
31-1，33-1，35-2 and 35-3 are not meet the minimum
critical time limit, so those are units unable to cold start,
the rest of the 16 units can satisfy the start condition. The
first, the optional units are viewed as decision making
units to evaluate its relative efficiency, the corresponding
input and output indices such as shown in Table 3.
According to the input and output indices, the im-
proved DEA model is established. Through the linear
programming to solve, the efficiency Ek of the corre-
sponding each unit is confirmed by using the linear pro-
gramming to solve, such as shown in Table 4.
According to the definition of efficiency evaluation,
the unit 35-1 , 36-1, 37-1，38-1，38-2 and 39-2 are rel-
atively effective, this six units can be used as the feasible
solution for the first step. With feasible solution as the
foundation, combined with optimization process and the
corresponding solving knapsack problem, the unit 36-1，
37-1，38-1and 38-2 are finally determined to be the op-
timal solution , which are started firstly in the current
time step. By the same way, the optimization start units
can be gradually determined in each subsequent time step,
such as shown in Table 5.
Table 3. Input and output indices of selecting units.
Input index Output index
Unit
A B C D E
31-1 18 56.35 6 5 3365.8
31-2 15 56.35 3.4 0.5 2839.4
32-1 17.5 33.5 6.5 5 3298.1
32-2 15 33.5 7.55 3.5 2792.5
33-1 15 45.76 7.6 5 2983.7
33-2 15 45.76 9 1.55 2865.3
34-1 16.5 37.26 5.6 5 2870.0
34-2 15 37.26 8.67 3.5 2366.4
35-1 17.5 50.7 15 3.5 3285.9
35-2 8 50.7 4 0.8 1452.5
35-3 8 50.7 7.57 5 1452.5
36-1 10 29.65 25 5 1927.8
36-2 18 29.65 4.8 5 3312.7
37-1 10 30.2 22.5 5 1925.0
37-2 17.5 30.2 7.33 3.5 3294.2
38-1 10 26.45 10 5 1928.5
38-2 10 26.45 17.561.55 1928.5
38-3 20 34.6 8.9 5 4129.1
39-1 22 34.6 6.5 5 4752.4
39-2 22 34.6 10.355 4752.4
Table 4. The effective index of units.
Unit31-131-2 32-132-2 33-1 33-234-1
Ek 0.8450.9750.9830.950 0.942 0.9610.969
Unit34-235-1 35-235-3 36-1 36-237-1
Ek 0.9461 0.8688.837 1 0.9531
Unit37-238-1 38-238-3 39-1 39-2N/A
Ek 0.9761 1 0.853 0.981 1 N/A
Table 5. Units start result of each time-step.
kt The priority start units
1 36-1 37-1 38-1 38-2
2 35-1 39-1
3 37-2 39-2
4 31-2,32-1,32-2 ,33-2,34-1
5 33-1,34-2 36-2 38-1
6 N/A
7 N/A
8 35-2, 35-3
9 N/A
10 31-1
7. Conclusions
The optimization strategy of the unit start was researched
in this work. An optimization model is established to
solve the selection optimization problem of units start in
power system restoration, and the objective of the model
is to maximize the total power generation. According to
the optimization model for a typical with multiple con-
straints of knapsack problem, a relative effectiveness
assessment based on a improving data envelopment
analysis is adopted to select the initial units to be started,
and genetic algorithm is employed to solve the knapsack
problem to determine the most reasonable units be
started at the current time. Finally, through a example of
system simulation, the result proves that the proposed
method is feasible and effective.
REFERENCES
[1] US-Canada Power Outage Task Force. Final Report on
the August 14th 2003 Blackout in the United States and
Canada [EB／OL]. http://www.ferc.gov.
[2] G. Andersson, P. Donalek and R. Farmer, et al., “Causes
of the 2003 Major Grid Blackouts in North America and
Europe, and Recommended Means to Improve System

J. CHEN ET AL.
712
Dynamic Performance. IEEE Transactions on Power
Systems,” Vol. 20, No. 4, 2005, pp. 1922-1928.
doi:10.1109/TPWRS.2005.857942
[3] Y. V. Makarov, V. I. Reshetov, A. Stroev, et al., “Black-
out Prevention in the United States, Europe, and Russia,”
Proceedings of the IEEE, Vol. 93, No. 11, 2005, pp.
1942-1955.doi:10.1109/JPROC.2005.857486
[4] X. Y. Chen, Y. P. Chen, C. Y. Li, et al., “Constructing
Wide-area Security Defensive System in Bulk Power
Grid——A Pondering over the Large-scale Blackout in
the European Power Grid,” Automation of Electric Power
Systems, Vol. 31, No. 1, 2007, pp. 4-8.
[5] Cascade to Black [system blackouts]. IEEE Power and
Energy Magazine, Vol. 2, No. 3, 2004, pp. 54-57.
doi:10.1109/MPAE.2004.1293601
[6] S. H. Horowitz and A. G. Phadke, “Boosting Immunity to
Blackouts, “Power and Energy Magazine,” Vol. 1, No. 5,
2003, pp. 47-53. doi:10.1109/MPAE.2003.1231691
[7] Y. Kojima. S. Warashina, M. Kato and H. Watanabe,
“Application of Knowledge Engineering Techniques to
Electric Power System Restoration,” in Proc. 1988 IEEE
Artifkiul Intelligence Jar lndiis/riul Applicat ions. M'ork-
shop on, pp. 320 -325.
[8] J. Hu, Z. Z. Guo, Y. C. Liu and Q. Y. Guo, “Power Sys-
tem Restoration And Analysis Of Restoration Sequence
of Generating Sets,” Power System Technology, Vol. 28,
No. 18, 2004, pp. 1-4.
[9] Z. Z. Dong, J. L. Jiao, Q. H. Sun, “Arrangement of Prior-
ity Sequence of Thermal Unit Restoration on Analytical
Hierarchy Process Model,” Power System Technology,
Vol. 21, No. 6, 1997, pp. 48-51, 54.
[10] K. Salek, U. Spanel and G. Krost, “Flexible Support for
Operators in Restoring Bulk Power Systems,” CI-
GRE/IEEE PES International Symposium on Quality and
Security of Electric Power Delivery Systems, Montreal,
Canada, Oct. 2003, pp. 187-192.
[11] Y. Liu, X. P. Gu, D. Zhang, “Data Envelopment Analysis
Based Relative Effectiveness Assessment of Power Sys-
tem Black-start Plans,” Proceedings of the CSEE, Vol. 26,
No. 5, 2006, pp. 32-37, 94.
[12] Q. Liu, L. B. Shi, M. Zhou, G. Y. Li and Y. X. Ni, “Op-
timal Strategy for Units Start-up During Power System
Restoration,” Transactions of China Electrotechnical So-
ciety, Vol. 24, No. 3, 2009, pp. 164-170.
[13] Y. Chen, Ranking Efficient Units in DEA,” OMEGA,
Vol. 32, No. 6, 2004, pp. 213-219.
[14] X. Mei, P. T. Harker, “Note：Ranking DMUs with In-
feasible Super-efficiency DEA Models,” Management
Science, Vol. 48, No. 5, 2002, pp. 705-710.
doi:10.1287/mnsc.48.5.705.7805
[15] X. Gu and H. Zhong, “Optimisation of Network Recon-
figuration Based on a Two-layer Unit-restarting Frame-
work for Power System restoration,” IET Generation,
Transmission & Distribution, Vol. 6, No. 7, 2012, pp.
693-700. doi:10.1049/iet-gtd.2011.0591