Journal of Applied Mathematics and Physics, 2013, 1, 31-35
http://dx.doi.org/10.4236/jamp.2013.14006 Published Online October 2013 (http://www.scirp.org/journal/jamp)
An Algorithm of 0-1 Knapsack Problem
Based on Economic Model
Yingying Tian1, Jianhui Lv2, Liang Zheng3
1School of Information Science and Technology, Sun Yat-sen University, Guangzhou 510006, China
2College of Information Science and Engineering, Northeastern University, Shenyang 110819, China
3School of Information Science and Technology, Sun Yat-sen University, Guangzhou 510006, China
Received August 2013
ABSTRACT
In order to optimize the knapsack problem further, this paper proposes an innovative model based on dynamic expecta-
tion efficiency, and establishes a new optimization algorithm of 0-1 knapsack problem after analysis and research.
Through analyzing the study of 30 groups of 0-1 knapsack problem from discrete coefficient of the data, we can find
that dynamic expectation model can solve the following two types of knapsack problem. Compared to artificial glow-
worm swam algorithm, the convergen ce speed of this algorithm is ten times as fast as that of artificial glowworm swam
algorithm, and the storage space of this algorithm is one quarter that of artificial glowworm swam algorith m. To sum up,
it can be widely used in practical problems.
Keywords: 0-1 Knapsack; Economic Model; Optimization Algorithm; Storage Space
1. Introduction
In recent years, many experts and scholars have carried
on the thorough r esear ch. These ex isting method s include :
greedy algorithm, bound algorithm, backtracking algo-
rithm, dynamic programming algorithm, e-approximation
algorithm [1-4] and improved swarm algorithm, ant co-
lony algorithm, fireflies swarm algorithm [5-7]. These
algorithms are based on mathematical principles, since
different algorithm uses different mathematical model,
the complexity and the convergence speed of these algo-
rithms are different. Thus, it has great significance to
improve the convergence speed. Now 0-1 knapsack
problem can be described with more details as follows:
For 0-1 knapsack problem, the object is loaded into
backpack or not. The value determines whether the ob-
ject i is in the backpack or not. If
1
i
x=
, the object is in
the backpack, otherwise, it is not. There are the following
constraint equation and objective function through analy-
sis of 0-1 knap s a c k problem .
1
n
ii
i
wx M
=
≤
∑
(1)
1
max
n
ii
i
optpc x
=
=∑
(2)
Among them, M is deadweight of backpack,
i
w
is
weight of object, and i c is price of object. The ultimate
goal is to look for the solution vector
12
(, ,, )
n
X xxx=
which meets constraint Equation (1) and makes the ob-
jective function value reach its maximum.
2. Decision Algor ithm
2.1. Ideas Origin of Algorithm
In the general algorithm for solving the knapsack prob-
lem, these objects are arranged by their price-perfor-
mance ratio in descending order. If these objects of high-
er price-performance ratio are loaded into the backpack
in advance, the residual deadweight of backpack can
converge to 0 quickly and the value of objects loaded
into backpack can achieve maximum as far as possible,
which is the basic idea of greedy algorithm. Solution
achieved by greedy algorithm is optimal in local situation,
but not optimal in global situation. It suggests that when
the number of objects loaded into backpack in a certain
range—before the residual deadweight of backpack is
0—the solution is optimal in local backpack situation.
This pape r continues using greedy strategy.
Expectation efficiency [8] has a wide range of applica-
tions in commodity economy and stock exchange, it
means that when the event occurs normally, we can ex-
pect to get revenue efficiencies. In the process of expec-
tation, deadweight of backpack, the number of objects,
weight of individual object, price of individual object and
price-performance ratio of individual object all involve in
arithmetic. For the same 0-1 knapsack problem, if an y of
four factors remain unchanged and the other factor
changes, all these objects that will be loaded backpack

Y. Y. TIAN ET AL.
32
and the optimal solution basically change. An abstract
expectation model which is closely related into 5 factors
is given through the above analysis, as follows:
(,, ,,),,,,fM nwcrMnwcr∞
(3)
Those objects of higher p r ic e-performance ratio are
loaded into backpack in advance, the others do expecta-
tion efficiency operation according to the model (3).
These objects that have higher expectation efficiency
value are loaded backpack in advance, and the lower is
abandoned or delayed. The embodiment of model (3) is
the key link, it decides directly the quality of algorithm.
Algorithm ideas as follows:
(a) Greedy algorithm is very good and can attain the
optimal solution in solving the local problem. These first
n/2 objects are loaded into backpack in advance, if the
total weight of n/2 objects is beyond M, first n/4 objects
are selected to load into backpack in advance, according
to dichotomy like this way un til the total weight of n/2i (i
is the frequency of dichotomy) objects is no more than M.
And then, for these remaining objects, calculate the ex-
pectation efficiency.
(b) After using greedy strategy, the residual dead-
weight of backpack and the total value of objects loaded
into backpack need to focus on. The purpose of expecta-
tion is to ensure the residual deadweight of backpack can
converge to 0 quickly and the value of objects loaded
backpack reach the bigger as much as possible.
2.2. Establishment of Mathematical Model
It is necessary to balance the five key factors when
modifying this model. Referred to the theory of median
and average, we design a mathematical model and
show in Formula (4):
/2
11
1/2 1
/2
111
1/2 1
(,, ,,)
(( ))(1)
() (1)
i
ni
j jji
j jn
i
ni
ij jji
j jn
fM nwcr
optp iccxnic
r
rMwwxni w


−−
== + 



−
−−
== + 

=
−−− −+
−−− −+
∑∑
∑∑
(4)
Among them,
()optp i
is equal everywhere, so model
(4) is a static model. If model (4) is taken as a dynamic
expectation efficiency model,
()optp i
can’t be set equal
everywhere. After modifying model (4), a dynamic mod-
el is given in Formula (5):
/2
1 11
1/2 1
/2
111
1/2 1
(,, ,,)
() (1)
() (1)
i
ni
ij jji
j jn
i
ni
ij jji
j jn
fM nwcr
r Mwwxnic
r
rMwwxniw


− −−
== + 



−
−−
== + 

=
−−− −+
−−− −+
∑∑
∑∑
(5)
Some analyses are provided to illustrate model (5) in
next three respects.
(a) Ending condition of dynamic model. Generally,
when
/2
11
1/2 1
0
ni
j jj
j jn
M wwx


−−
== +


−− =
∑∑
the residual deadweight of backpack is 0, namely, it is
ending condition of dynamic.
(b) Ending condition of algorithm. For these existing
(,, ,,)
i
fM nwcr
, arrange them by their values in des-
cending order, and then to accumulate the price of the
corresponding object one by one, until the backpack fails
to hold on one more object.
(c) Special rule of algorithm. The average of value
according to greedy expectation is always greater than
the price of current object, in order to avoid the pheno-
menon, the algorithm has a rule: the symbol of absolute
value should be added to model (5) in case the expecta-
tion efficiency values of some objects are minus. These
objects, whose expectation efficiency values are minus
should be removed in advance. Namely, their corres-
ponding prices don’t accumulate any more.
2.3. Dispersion Coefficient
Given these individual data, they are
12
,,
n
yy y
, their
dispersion coefficient is shown in Formula (6).
2
1
()
ni
i
yy
n
vy
σ
=
−
=
∑
(6)
In this paper, we compute three kinds of dispersion
coefficient by Formula (6). Among them,
v
σ
is disper-
sion coefficient,
n
is the number of objects.
3. Description and Analysis of Algorithm
An optimization algorithm of 0-1 knapsack based on
dynamic expectation efficiency can be descripted as fol-
lows:
Step 1: Initially, the residual deadweight of backpack
is M and is 0.
Step 2: Arrange these objects by their price-perfor-
mance ratio in descending order.
Step 3: Modify the residual deadweight of backpack
and
optp
according to algorithm idea (a).
Step 4: Calculate
(,, ,,)
i
fM nwcr
of the correspond-
ing object, if the condition of model 5 (c) is satisfied,
0
i
x=
; otherwise, to step 5.
Step 5: If the condition of model 5 (a) is satisfied, to
step 6; otherwise, to step 4.
Step 6: If the condition of model 5 (b) is satisfied, to
step 7; otherwise, to continue loading the object which
has the hi g he r
(,, ,,)
i
fM nwcr
.

Y. Y. TIAN ET AL.
33
Step 7: Accumulate the price of the corresponding
object, and then modify the residual deadweight of
backpack and
optp
.
Step 8: End the algorithm.
The flowchart of DEE algorithm is shown in Figure 1.
4. Simulation Experiment
We present simulation experiments by writing C++ pro-
grams with VC6.0, and the experimental environment is
Windows7 of Intel Core2 Q8400 2.66GHZ CPU, 4.00GB
Memory. Two simulation experiments are given, one is
individual experiment of algorithm and analyzes optimal
solution by three kinds of dispersion coefficient, and the
other is comparison experiment with the artificial glow-
worm swarm optimization (GSO).
4.1. Individual Experiment
Given examples A and B, two kinds of dispersion coeffi-
cient are in the same level with example A, an d any kind
of dispersion coefficient is not in the same level with
example B. Among them, three kinds of dispersion coef-
ficient are the weight dispersion coefficient (WDC), the
price dispersion coefficient (PDC) and the price-perfor-
mance ratio dispersion coefficient (RDC).
A. n = 20, M = 550, w = {45, 2 7, 58, 25, 33, 4 2, 55, 62,
19, 72, 80 , 24 , 59, 35, 14, 66, 45, 83, 71, 40}, v = {93, 38,
90, 30, 56 , 43, 49, 77, 36 , 99, 120, 70, 48, 70, 38, 89 , 29,
94, 62, 80}. The values of three kinds of dispersion coef-
ficient are 0.4239, 0.3943 and 0.3955, it’ obvious that
Initialization
End
Arrange these objects by their price-
performance ratio in descending order
Algorithm
idea (a)
Calculate
f(i,M,n,w,c,r)
Formula
(5)(a) x(i)=0
Ending
condition of
model
Ending
condition of
algorithm
Calculate optp
Y
N
N
Y
N
Y
Figure 1. Process flow diagram based on DEE.
PDC and RDC are in the same level. The objective func-
tion values are equal before the 15th iteration in compar-
ison with dynamic expectation model and static expecta-
tion model. The objective function value remains un-
changed from the 15th iteration to the 20th iteration by
dynamic expectation model.
B. n = 50, M = 1500, w = {10, 25, 30, 68, 74, 55, 36,
120, 80, 95, 35, 45, 70, 85, 105, 48, 24, 15, 40, 50, 66, 58,
28, 11, 20, 18, 38, 42, 28, 22, 32, 49, 60, 8, 78, 44, 52, 23,
39, 19, 68, 99, 92, 77, 110, 69, 59, 43, 135, 136}, v = {20,
48, 54, 118, 125, 92, 69, 185, 120, 140, 50, 60, 88, 105,
128, 58, 29, 18, 46, 57 , 74, 65, 31, 12 , 21, 18, 36, 39, 26,
20, 29, 43, 51, 6, 59, 32, 34, 22, 10, 34, 40 , 28, 18, 16, 10,
7, 5, 13, 12}. The objective function values are equal
before the 49th iteration in comparison with dynamic
expectation model and static expectation model.
Two experiment results show in Figure 2.
4.2. Algorithm Proving
In order to do further research on the adaptive scope of
DEE algorithm, this paper gives 30 0-1 knaps ack prob-
lems [9]. Set the number of objects is 20, and the dead-
weight of backpack is in
[500,950]
. After executing
DEE algorithm, the experiment results show in Table 1
in the latter.
As can be seen from Table 1, the adaptive scope of
DEE algorithm is as follows: all the condition that any
two kinds of dispersion coefficient are in the same level;
the partial condition that all the three kinds of dispersion
coefficient are less than 1 and any two kinds of disper-
sion coefficient are not in the same level. However, the
condition that one kind of dispersion coefficient is great-
er than 1 and the other two kinds of dispersion coeffi-
cient are less than 1 and not in the same level is dead
zone of DEE algorithm.
4.3. Comparison Experiment with GSO
Algorithm
This part of experimental data is got by example 1 and 3
of reference [9]. The experiment results of comparison
on DEE algorithm and GSO algorithm at iteration num-
ber, the optimal solution and the spaces/the number of
fireflies are shown in Table 2.
Figure 2. Experiment diagram on example A and B.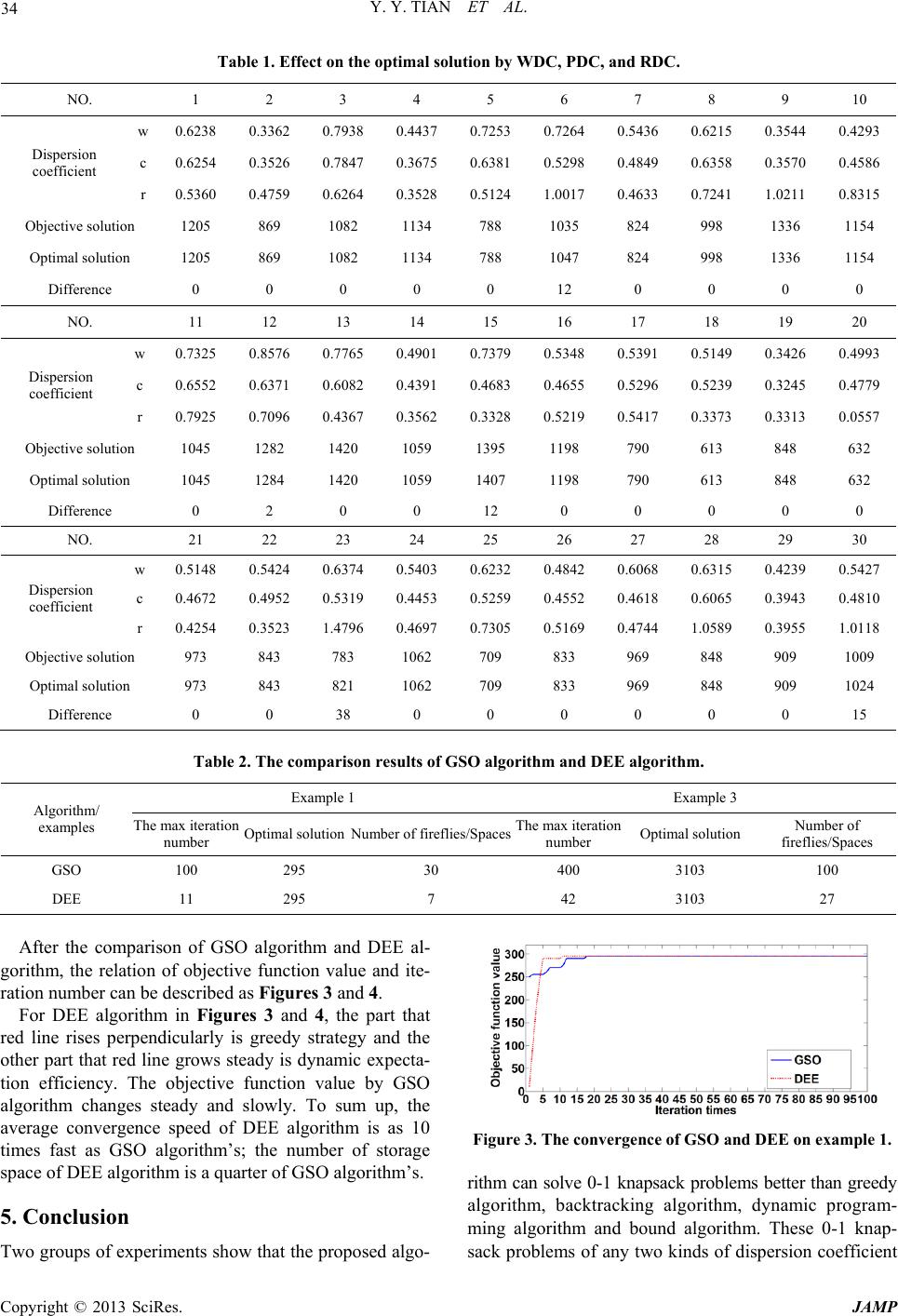

Y. Y. TIAN ET AL.
34
Table 1. Effect on the optimal solution by WDC, PDC, and RDC.
NO. 1 2 3 4 5 6 7 8 9 10
Dispersion
coefficient
w 0.6238 0.3362 0.7938 0.4437 0.7253 0.7264 0.5436 0.6215 0.3544 0.4293
c 0.6254 0.3526 0.7847 0.3675 0.6381 0.5298 0.4849 0.6358 0.3570 0.4586
r 0.5360 0.4759 0.6264 0.3528 0.5124 1.0017 0.4633 0.7241 1.0211 0.8315
Objective solution 1205 869 1082 1134 788 1035 824 998 1336 1154
Optimal solution 1205 869 1082 1134 788 1047 824 998 1336 1154
Difference 0 0 0 0 0 12 0 0 0 0
NO. 11 12 13 14 15 16 17 18 19 20
Dispersion
coefficient
w 0.7325 0.8576 0.7765 0.4901 0.7379 0.5348 0.5391 0.5149 0.3426 0.4993
c 0.6552 0.6371 0.6082 0.4391 0.4683 0.4655 0.5296 0.5239 0.3245 0.4779
r 0.7925 0.7096 0.4367 0.3562 0.3328 0.5219 0.5417 0.3373 0.3313 0.0557
Objective solution 1045 1282 1420 1059 1395 1198 790 613 848 632
Optimal solution 1045 1284 1420 1059 1407 1198 790 613 848 632
Difference 0 2 0 0 12 0 0 0 0 0
NO. 21 22 23 24 25 26 27 28 29 30
Dispersion
coefficient
w 0.5148 0.5424 0.6374 0.5403 0.6232 0.4842 0.6068 0.6315 0.4239 0.5427
c 0.4672 0.4952 0.5319 0.4453 0.5259 0.4552 0.4618 0.6065 0.3943 0.4810
r 0.4254 0.3523 1.4796 0.4697 0.7305 0.5169 0.4744 1.0589 0.3955 1.0118
Objective solution 973 843 783 1062 709 833 969 848 909 1009
Optimal solution 973 843 821 1062 709 833 969 848 909 1024
Difference 0 0 38 0 0 0 0 0 0 15
Table 2. The comparison results of GSO algorithm and DEE algorithm.
Algorithm/
examples
Example 1 Example 3
The max
iteration
number Optimal solution Number of fireflies/Spaces
The max iteration
number Optimal solution Number of
fireflies/Spaces
GSO 100 295 30 400 3103 100
DEE 11 295 7 42 3103 27
After the comparison of GSO algorithm and DEE al-
gorithm, the relation of objective function value and ite-
ration number can be described as F igures 3 and 4.
For DEE algorithm in Figures 3 and 4, the part that
red line rises perpendicularly is greedy strategy and the
other part that red line grows steady is dynamic expecta-
tion efficiency. The objective function value by GSO
algorithm changes steady and slowly. To sum up, the
average convergence speed of DEE algorithm is as 10
times fast as GSO algorithm’s; the number of storage
space of DEE algorithm is a quarter of GSO algorithm’s.
5. Conclusion
Two groups of experiments show that the proposed algo-
Figure 3. The convergence of GSO and DEE on example 1.
rithm can so lve 0-1 knapsack problems better than greedy
algorithm, backtracking algorithm, dynamic program-
ming algorithm and bound algorithm. These 0-1 knap-
sack problems of any two kinds of dispersion coefficient

Y. Y. TIAN ET AL.
35
Figure 4. The convergence of GSO and DEE on example 3.
were in the same level, and all the three kinds of disper-
sion coefficient were less than 1 and any two kinds of
dispersion coefficient were not in the same level. The
research on discrete coefficient of data, which is a new
idea this article explores, is the essence of this algorithm
for verification.
REFERENCES
[1] A. A. Razborov, “On Provably Disjoint NP-Pairs. Elec-
tronic Colloquium on Computational Complexity,” Tech-
nical Report TR, 1994, pp. 94-006.
[2] E. Maslov, “Speeding up Branch and Bound Algorithms
for Solving the Maximum Clique Problem,” Journal of
Global Optimization, 2013, pp. 1-12.
[3] H. Fouchal and Z. Habbas, “Distributed Backtracking
Algorithm Based on Tree Decomposition over Wireless
Sensor Networks,” Concurrency Computation Practice
and Experience, Vol. 25, No. 5, 2013, pp. 728-742.
http://dx.doi.org/10.1002/cpe.1804
[4] G. Lantoine, “A Hybrid Differential Dynamic Program-
ming Algorithm for Constrained Optimal Control Prob-
lems,” Journal of Optimization Theory and Applications,
Vol. 154, No. 2, 2012, pp. 418-423.
http://dx.doi.org/10.1007/s10957-012-0038-1
[5] F. Zhou, “A Particle Swarm Optimization Algorithm,”
Applied Mechanics and Materials, 2013, pp. 1369-1372.
[6] K.-S. Yoo, “A Modified Ant Colony Optimization Algo-
rithm for Dynamic Topology Optimization,” Computers
and Structures, Vol. 123, 2013, pp. 68-78.
http://dx.doi.org/10.1016/j.compstruc.2013.04.012
[7] Z. Y. Yan. “Exact Solutions of Nonlinear Dispersive K(m,
n) Model with Variable Coefficients,” Applied Mathe-
matics and Computation, Vol. 217, No. 22, 2011, pp.
9474-9479. http://dx.doi.org/10.1016/j.amc.2011.04.047
[8] J. H. Lv, “The Experiment Data on 0-1 Knapsack Prob-
lem.”
http://user.qzone.qq.com/1020052739/infocenter#!app=2
&via=QZ.HashRefresh&pos=add
[9] K. Cheng and L. Ma, “Artificial Glowworm Swarm Op-
timization Algorithm for 0-1 Knapsack Problem,” Appli-
cation Research of Computers, Vol. 30, No. 4, 2013, pp.
993-995.