 Journal of Applied Mathematics and Physics, 2013, 1, 18-24 http://dx.doi.org/10.4236/jamp.2013.14004 Published Online October 2013 (http://www.scirp.org/journal/jamp) Copyright © 2013 SciRes. JAMP Finite-Difference Solution of the Helmholtz Equation Based on Two Domain Decomposition Algorithms Wensheng Zhang1, Yunyin Dai2 1Institute of Computational Mathematics and Scientific/Engineering Computing, LSEC, Beijing, China 2Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, China Email: zws@lsec.cc.ac.cn, daiyy@lsec.cc.ac.cn Received July 2013 ABSTRACT In this paper, wave simulation with the finite difference method for the Helmholtz equation based on the domain de- composition method is investigated. The method solves the problem by iteratively solving subproblems defined on smaller subdomains. T wo domain decomposition algorithms both for nonoverlapping and overlapping methods are de- scribed. More numerical computations including the benchmark Marmousi model show the effectiveness of the pro- posed algorithms. This method can be expected to be used in the full-waveform inversion in the future. Keywords: Finite Difference; Domain Decomposition; Nonoverlapping; Overlapping; Helmholtz Equation; Preconditioner 1. Introduction The numerical solution of acoustic wave equation is an important problem. The Helmholtz equation is the ver- sion of acoustic wave equation in the frequency domain. It has applications in seismic wave propagation, imaging and inversion. In the geophysical frequency-domain in- version, one needs to do forward modeling which means solving the Helmholtz equation. During the inversion process, the synthetic model is continuously updated until a convergence is reached. Thus numerical methods for solving the Helmholtz equation have been under ac- tive research during the past few decades. The finite element method and the finite difference method have been used successfully for this problem. The discretiza- tion of the 2D Helmholtz for mid-frequency and high- frequency problems may lead to a large linear system because of the requirement of ten points per wavelength. This makes the problem even harder to solve. Direct me- thods easily suffer from inacceptable computational work. So many iterative methods for the Helmholtz equation have been developed, f or instance, see [1-6]. As the re- sulting system is non-Hermitian and indefinite, a good preconditioner is necessary for the iterative methods. Various preconditioners have been proposed [5-11], for example, a tensor product preconditioner [6], the incom- plete factorization preconditioner [7] and the Laplacian preconditioner [8,9]. We will use the shifted-Laplacian precondi tioner i n t hi s paper [9 ] . The domain decomposition method (DDM) is an ef- fective technique for solving large-scale problems [ 12- 22]. It splits the whole computational domain into several smaller subdomains and solves a sequence of similar subproblems on these subdomains. The number and size of subdomains can now be chosen so as to enable direct methods to solve the subproblems. Between adjacent subdomains the boundary conditions are adjusted itera- tively by transmission conditions. For the boundary of whole computational domain, absorbing boundary condi- tions (ABCs) are required. There exist several ABC me- thods, for instance, the paraxial approximation method [23] and the perfectly matched layer method [24]. In this paper, we use the former as our computational domain is a rectangular domain. In this paper, we focus on solving the Helmholtz with the finite difference method based on the nonoverlapping and overlapping DDM algorithms. More numerical computations demonstrate the correctness of the algo- rithms presented in this paper. The method will be used in the frequency -domain inversion in the future. 2. Theory 2.1. Finite Difference Scheme The 2-D acoustic wave equation can be written as 222 222 2 1(,) (,) uuu gxz vxz txz ∂∂∂ −−= ∂∂∂ , (1) with the absorbing bounda ry c ondition s , (2)  W. S. ZHANG, Y. Y. DAI Copyright © 2013 SciRes. JAMP where is the velocity of media and is the wavefield, is the source term. In the fre- quency domain (1) can be written as 222 22 (,) (,) uu k xzugxz xz ∂∂ −−− = ∂∂ , (3) where is the wave number and is the angular frequency. The boundary con- dition in the frequency domain is , (4) where is the outward normal of the boundary and is the imagine unit. We use the second-order difference scheme to discrete (3) and (4) and the result can be written as a linear system , , , (5) where is the total number of wavefield on the computational domain h Ω , and x and are the discretization number along and direc- tions respectively. The matrix is a complex matrix as the boundary condition contains complex number. Moreover, it is non-positive and non-Hermitian matrix. Usually we use the Krylov iterative methods to solve (5) as is a large-scale sparse matrix. The Bi-CGSTAB algorithm [25,26] is a good choice. The following is the Bi-CGSTAB algorithm for solving . Algorithm 1 [Bi-CGSTAB algorithm] Step 1. Give the matrix , vector and initial val- ue , the maximal iterative number and the to- lerance error tol ε , the preconditioned matrix , com- pute and set and ; Step 2. If and , turn to step 3; oth- erwise st op and out put ; Step 3. Compute , if or then stop; otherwise turn to step 4; Step 4. If then , otherwi s e c ompute , 11 111 () k kkkkk prp V βω −− −−− =+− ; (6) Step 5. Solve the system and compute , , ; (7) Step 6. Set , if then , otherwise stop and output ; Step 7. Solve the systems and , then compute , , (8) and set , let , turn to step 2. For the preconditioner matrix , we adopt the shifted- Laplace pre conditioned method [9] 22 2 22 (, ) SL Mk xy xy α ∂∂ =−−+ ∂∂ , (9) where and . A typical choice for is , named complex shifted-Laplace precondi- tioner. 2.2. Two Domain Decomposition Algorithms In this subsection we discuss how to s olve the problem (3) and (4) with DDM, including the nonoverlapping algo- rithm and overlapping algorithm. First of all, we consider the nonoverlapping problem. We divide the computa- tional domain into non-overlapped subdomains , . Denote be the value of at th iteration and on the mth subdomain . Obviously the division satisfies , , , . Given the iteration value , , solve the following system iteratively: 2,2, 2, 22 (,) nmnm nm ij ij uu kugx y xz ∂∂ −−−= ∂∂ , (10) , , (11) , 1, , 1, nmn r nmn r mr uu iku iku nn −− ∂∂ −=− − ∂∂ , (12) . The last Equation (12 ) is the interface equation. Using the standard five-point difference scheme, we obtain the following system , . (14) In the iterations, the is assumed to be known and is used in the interface equation. Thus we can give the following nonoverlapping DDM algorithm. Algorithm 2 [Nonoverlapping DDM algorithm] Step 1. Select initial value and set . Step 2. Obtain by solving the interface equation discretized from (12). Step 3. Solve the system (14). Step 4. Set , turn to step 2. In the following we consider the overlapping DDM. We still divide the computational domain into subdomains , : , (15 ) but now any two adjacent subdomains are overlapped, i.e., . (16 ) 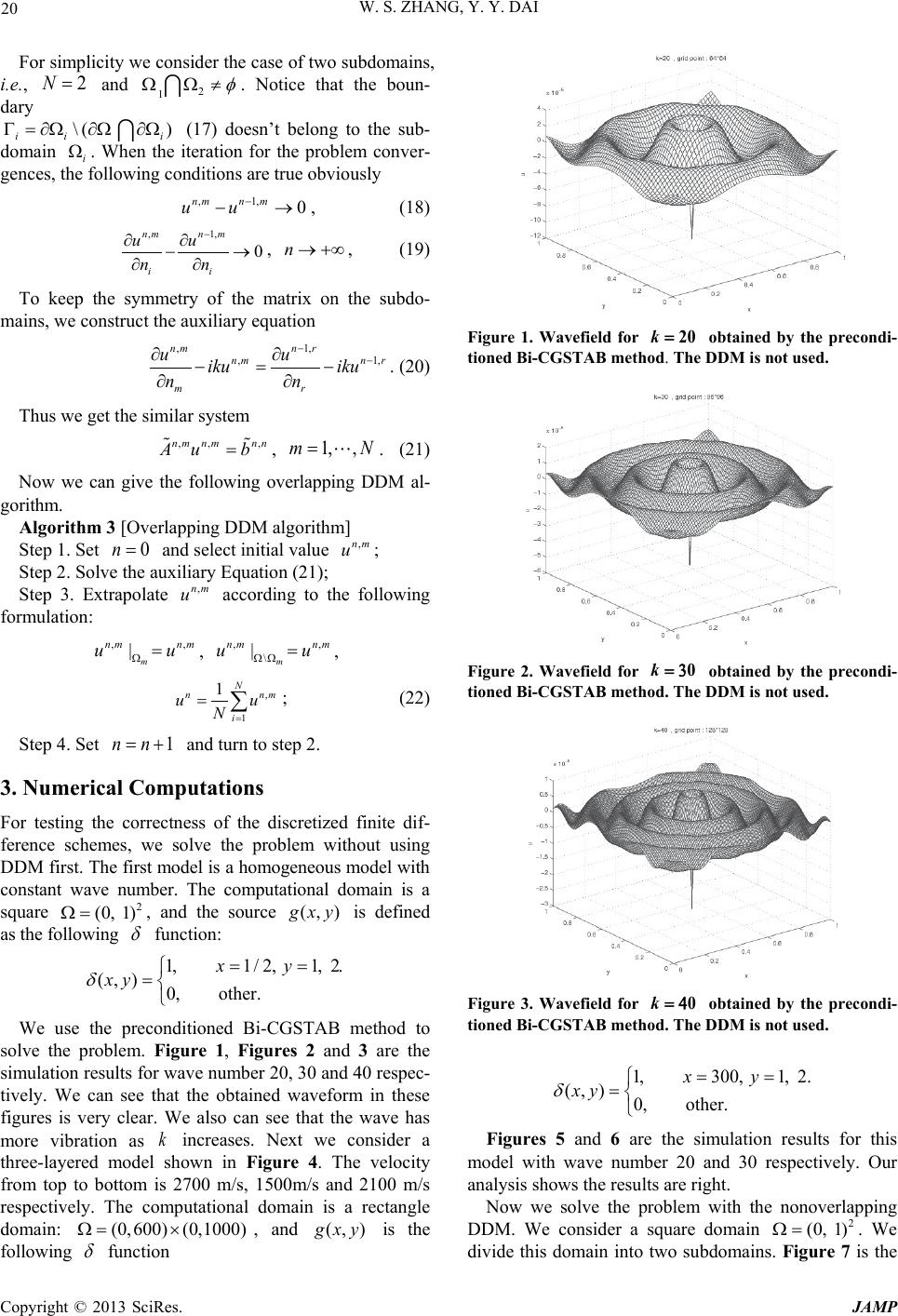 W. S. ZHANG, Y. Y. DAI Copyright © 2013 SciRes. JAMP For simplicity we consider the case of two subdomains, i.e., and . Notice that the boun- dary (17) doesn’t belong to the sub- domain . When the iteration for the problem conver- gences, the following conditions are true obviously , (18) , , (19) To keep the symmetry of the matrix on the subdo- mains, we construct the auxiliary equation , 1, , 1, nmn r nmn r mr uu iku iku nn −− ∂∂ −= − ∂∂ . (20) Thus we get the similar system , . (21) Now we can give the following overlapping DDM al- gorithm. Algorithm 3 [Overlapping DDM algorithm] Step 1. Set and select initial value ; Step 2. Solve the auxiliary Equation (21); Step 3. Extrapolate according to the following formulation: , , ; (22) Step 4. Set and turn to step 2. 3. Numerical Computations For testing the correctness of the discretized finite dif- ference schemes, we solve the problem without using DDM first. The first model is a homogeneous model with constant wave number. The computational domain is a square , and the source is defined as the following function: 1,1/2 , 1, 2. (, )0, other. xy xy δ = = = We use the preconditioned Bi-CGSTAB method to solve the problem. Figure 1, Figures 2 and 3 are the simulation results for wav e number 20, 30 and 40 resp ec- tively. We can see that the obtained waveform in these figures is very clear. We also can see that the wave has more vibration as increases. Next we consider a three-layered model shown in Figure 4. The velocity from top to bottom is 2700 m/s, 1500m/s and 2100 m/s respectively. The computational domain is a rectangle domain: , and is the following function Figure 1. Wavefield for obtained by the precondi- tioned Bi-CGSTAB method. The DDM is not used. Figure 2. Wavefield for obtained by the precondi- tioned Bi-CGSTAB method. The DDM is not used. Figure 3. Wavefield for obtained by the precondi- tioned Bi-CGSTAB m ethod. The DDM is not used. 1,300, 1, 2. (, )0, other. xy xy δ = = = Figures 5 and 6 are the simulation results for this model with wave number 20 and 30 respectively. Our analysis shows the results are right. Now we solve the problem with the nonoverlapping DDM. We consider a square domain . We divide this domain into two subdomains. Figure 7 is the 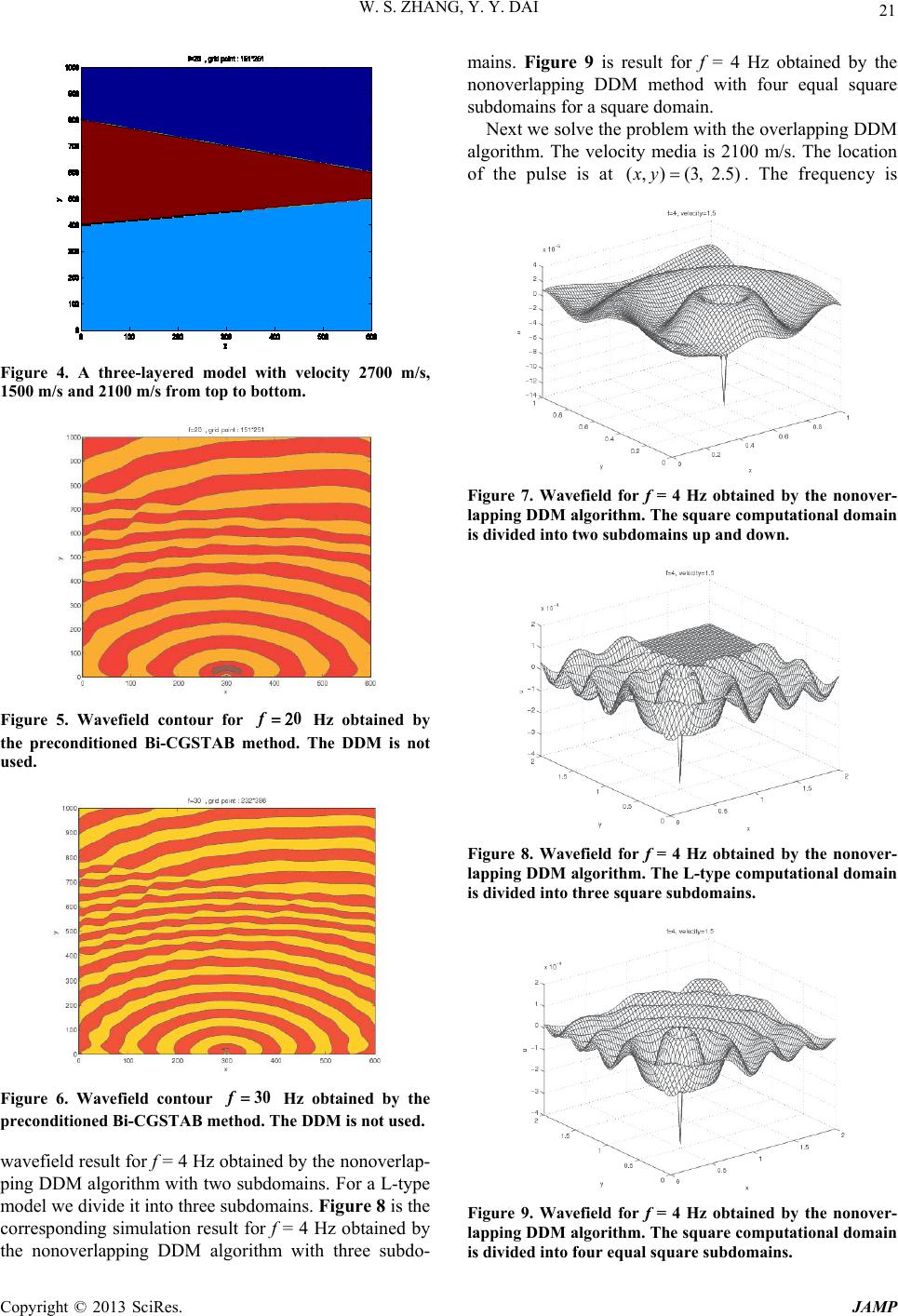 W. S. ZHANG, Y. Y. DAI Copyright © 2013 SciRes. JAMP Figure 4. A three-layered model with velocity 2700 m/s, 1500 m/s and 2100 m/s from top to bottom. Figure 5. Wavefield contour for Hz obtained by the preconditioned Bi-CGSTAB method. The DDM is not used. Figure 6. Wavefield contour Hz obtained by the preconditioned Bi-CGSTAB m ethod. The DDM i s not used. wavefield result for f = 4 Hz obtained by the nonoverlap- ping DDM algorithm with two subdomains. For a L-type model we divide it into three subdomains. Figure 8 is the corresponding simulation result for f = 4 Hz obtained by the nonoverlapping DDM algorithm with three subdo- mains. Figure 9 is result for f = 4 Hz obtained by the nonoverlapping DDM method with four equal square subdomains for a square domain. Next we solve the problem with the overlapping DDM algorithm. The velocity media is 2100 m/s. The location of the pulse is at . The frequency is Figure 7. Wavefield for f = 4 Hz obtained by the nonover- lapping DDM algorithm. The square computational domain is divided i nt o two subdomains up and down. Figure 8. Wavefield for f = 4 Hz obtained by the nonover- lapping DDM algorithm. The L-type computational domain is divided i nt o thr ee square subdomains. Figure 9. Wavefield for f = 4 Hz obtained by the nonover- lapping DDM algor ithm. The square computational domain is divided i nt o four equal square s ubdomains.  W. S. ZHANG, Y. Y. DAI Copyright © 2013 SciRes. JAMP f = 1 Hz. Figure 10 is the wavefield obtained by the overlapping DDM algorithm with two equal square sub- domains up and down. Figure 11 is the wavefield ob- tained by the overlapping DDM algorithm with three square subdomains for an L-type domain. Figure 12 is the Figure 10. Wavefield for f = 1 Hz obtained by the overlap- ping DDM algorithm. The computational domain is divided into two equal subdomains up and down. Figure 11. Wavefield for f = 1 Hz obtained by the overlap- ping DDM algorithm. The square computational domain is divided into t hree equal square subdomains. Figure 12. Wavefield for f = 1 Hz obtained by the overlap- ping DDM algorithm. The square computational domain is divided into f ou r equal subdomains. wavefield obtained by the overlapping DDM algorithm with four equal squ a re subdomains for a square domain. Finally we consider a typical inhomogeneous model named Marmousi model which is usually used to test the ability of seismic migration and inversion [27]. The ve- locity is shown in Figure 13. The velocity varies from 1500 m/s to 5500 m/s. We select a part of this model to simulate wave propagation. Figure 14 is the wavefield contour obtained by the preconditioned Bi-CGSTAB method for Hz and the DDM algorithm is not used. Figure 15 is the wavefield contour obtained by the non- overlapping DDM algorithm with two subdomains. Fig- ure 16 is the wavefield contour obtained by the overlap- ping DDM algorithm with two subdomains. Figure 17 is the similar result but for Hz. Comparing Fig- ures 15 and 16 with Figure 14, we know that they al- most the same which are just we expect. 4. Conclusion The acoustic wave equation in the frequency domain is solved by the finite difference method based on the do- main decomposition method. The discritizaiton of the Figure 13. Marmousi model. Figure 14. Wavefield contour for f = 5 Hz obtained by the preconditioned Bi-CGSTAB algorithm. The DDM algo- rithm is not use d.  W. S. ZHANG, Y. Y. DAI Copyright © 2013 SciRes. JAMP Figure 15. Wavefield contour for f = 5 Hz by Bi-CGSTAB preconditioned method. The nonoverlapping DDM algo- rithm with two subdomains is use d. Figure 16. Wavefield contour for f = 5 Hz obtained by Bi-CGSTAB preconditioned method. The overlapping DDM algorithm with two subdomains is used. Figure 17. Wavefield contour for f = 20 Hz obtained by Bi-CGSTAB preconditioned method. The overlapping DDM algorithm with two subdomains is used. problem leads to a sparse system which is solved by the complex shifted-Laplace preconditioned Bi-CGSTAB iteration method. Two DDM algorithms both for non- overlapping and overlapping method are given. Many numerical computational examples including the com- plex Marmousi model are implemented which show the correctness and effectiveness of the algorithms presented in this paper. This method can be used in the full-wave- form inversion. It can sometimes reduce the computa- tional complexity. 5. Acknowledgements This research is supported by the State Key project with grant number 2010CB73 1505 and the Foundation of N a- tional Center for Mathematics and Interdisciplinary Sciences, Chinese Academy of Sciences. The computa- tions are implemented in the State Key Laboratory of Scienti f i c an d Engineering Computing (LSEC). REFERENCES [1] A. Bayliss, C. I. Goldstein and E. Turkel, “The Numerical Solution of the Helmholtz Equation for Wave Propaga- tion Problems in Underwater Acoustics,” Computers and Mathematics with Applications, Vol. 11, No. 7-8, 1985, pp. 655-665. http://dx.doi.org/10.1016/0898-1221(85)90162-2 [2] R. E. Plexxis, “A Helmholtz Iterative Solver for 3D Seismic-Imaging Problems,” Geophysics, Vol. 72, No. 5, 2007, pp. SM185-SM197. http://dx.doi.org/10.1190/1.2738849 [3] A. Bayliss, C. I. Goldstein and E. Turkel, “An Iterative Method for the Helmholtz Equation,” Journal of Compu- tational Physics, Vol. 49, No. 3, 1983, pp.443-457. http://dx.doi.org/10.1016/0021-9991(83)90139-0 [4] C. W. Oosterlee and T. Washio, “Iterative Solution of the Helmholtz Equation by a Second Order Method,” SIAM Journal on Matrix Analysis and Applications, Vol. 21, No. 1, 1999, pp. 209-229. http://dx.doi.org/10.1137/S0895479897316588 [5] Y. A. Erlangga, “Advances in Iterative Methods and Pre- conditioners for the Helmholtz Equation,” Archives of Computational Methods in Engineering, Vol. 15, No. 1, 2008, pp. 37-66. http://dx.doi.org/10.1007/s11831-007-9013-7 [6] R.-E. Plessix a nd W. A. Mulder, “Separation of Variables as a Preconditioner for an Iterative Helmholtz Solver,” Applied Numerical Mathematics, Vol. 44, No. 3, 2003, pp. 385-400. http://dx.doi.org/10.1016/S0168-9274(02)00165-4 [7] M. M. M. Made, “Incomplete Factorization-Based Pre- conditionings for Solving the Helmholtz Equation,” In- ternational Journal for Numerical Methods in Engineer- ing, Vol. 50, No. 5, 2001, pp. 1077-1101. http://dx.doi.org/10.1002/1097-0207(20010220)50:5<107 7::AID-NME65>3.0.CO;2-P [8] N. Umetani, S. P. Maclachlan and C. W. Oosterlee, “A Multigrid-Based Shifted Laplacian Preconditioner for a Fourth-Order Helmholtz Discretization,” Numerical Li-  W. S. ZHANG, Y. Y. DAI Copyright © 2013 SciRes. JAMP near Algebra with Applications, Vol. 16, No. 8, 2009, pp. 603-626. http://dx.doi.org/10.1002/nla.634 [9] T. Airaksinen, E. Heikkola, A. Pennanen and J. Toivanen, “An Algebraic Multigrid Based Shifted-Laplacian Pre- conditioner for the Helmholtz Equation,” Journal of Computational Physics, Vol. 226, No. 1, 2007, pp. 1196- 1210. http://dx.doi.org/10.1016/j.jcp.2007.05.013 [10] Y. A. Erlangga, C. Vuik and C. W. Oosterlee, “On a Class of Preconditioners for Solving the Helmholtz Equa- tion,” Applied Numerical Mathematics, Vol. 50, No. 3-4, 2004, pp. 409-425. http://dx.doi.org/10.1016/j.apnum.2004.01.009 [11] Y. A. Erlangga, C. W. Oosterlee and C. Vuik, “A Novel Multigrid Based Preconditioner for Heterogeneous Helm- holtz Problems,” SIAM Journal on Scientific Computing, Vol. 27, No. 4, 2006, pp. 1471-1492. http://dx.doi.org/10.1137/040615195 [12] T. F. Chan and T. P. Mathew, “Domain Decomposition Algorithms,” Acta Numerica, Vol. 3, 1994, pp. 61-143. http://dx.doi.org/10.1017/S0962492900002427 [13] J. D. Benamou and B. Despres, “A Domain Decomposi- tion Method for the Helmholtz Equation and Relate d Op- timal Control Problems,” Journal of Computational Phys- ics, Vol. 136, No. 1, 1997, pp. 62-68. http://dx.doi.org/10.1006/jcph.1997.5742 [14] B. Smith, P. Bjorstad and W. Grop, “Domain Decompo- sition: Parallel Multilevel Methods for Elliptic Partial Differential Equations,” Cambridge University Press, Cambridge, 1996. [15] A. Quarteroni and A. Valli, “Domain Decomposition Methods for Partial Differential Equations,” Oxford Science Publications, Oxford, 1999. [16] A. Tosseli and O. Widlund, “Domain Decomposition Methods—Algorithms and Theory,” Springer, Berlin, 2005. [17] J. Xu, “Iterative Methods by Space Decomposition and Subspace Correction,” SIAM Review, Vol. 34, No. 4, 1992, pp. 581-613. http://dx.doi.org/10.1137/1034116 [18] J. Xu and J. Zou, “Some Nonoverlapping Domain De- composition Methods,” SIAM Review, Vol. 40, No. 4, 1998, pp. 857-914. http://dx.doi.org/10.1137/S0036144596306800 [19] S. Kim, “Doma in Decomposition Iterative Procedures for Solving Scalar Waves in the Frequency Domain,” Nume- rische Mathematik, Vol. 79, No. 2, 1998, pp. 231-259. http://dx.doi.org/10.1007/s002110050339 [20] S. Larsson, “A Domain Decomposition Method for the Helmholtz Equation in a Multilayer Domain,” SIAM Journal on Scientific Computing, Vol. 20, No. 5, 1999, pp. 1713-1731. http://dx.doi.org/10.1137/S1064827597325323 [21] F. Magoulès, F. X. Roux and S. Salmon, “Optimal Dis- crete Transmission Conditions for a Nonoverlapping Domain Decomposition Method for the Helmholtz Equa- tion,” SIAM Journal on Scientific Computing, Vol. 25, N o. 5, 2004, pp. 1497-1515. http://dx.doi.org/10.1137/S1064827502415351 [22] E. Heikkola, T. Rossi and J. Toivaned, “A Parallel Ficti- tious Domain Method for the Three-Dimensional Helm- holtz Equation,” SIAM Journal on Scientific Computing, Vol. 24, No. 5, 2003, pp. 1567-1588. http://dx.doi.org/10.1137/S1064827500370305 [23] R. Clayton and B. Engquist, “Absorbing Boundary Con- ditions for Acoustic and Elastic Wave Equations,” Bulle- tin of the Seismological Society of America, Vol. 67, No. 6, 1977, pp. 1529-1540. [24] J. P. Berenger, “A Perfectly Matched Layer for Absorb- ing of Electromagnetic Waves,” Journal of Computation- al Physics, Vol. 114, No. 2, 1994, pp. 185-200. http://dx.doi.org/10.1006/jcph.1994.1159 [25] H. A. van der Vorst, “Bi-CGSTAB: A Fast and Smoothly Converging Variant of Bi-CG for the Solution of Non- symmetric Linear Systems”, SIAM Journal on Scientific and Statistical Computing, Vol. 13, No. 2, 1992, pp. 631- 644. http://dx.doi.org/10.1137/0913035 [26] Y. Saad, “Iterative Methods for Sparse Linear Systems,” 2nd Edition, SIAM, Philadephia, PA, 2003. http://dx.doi.org/10.1137/1.9780898718003 [27] W. Zhang, “Imaging Methods and Computations Based on the Wave Equation,” Science Press, Beijing, 2009.
|