J
ournal o
f
A
pp
http://dx.doi.or
g
Copyright © 2
0
N
Propa
g
ABSTRA
C
A numerical-
“Earth-Atmo
s
dynamic equ
a
linearized Na
v
with respect t
o
of the reduce
d
Keywords: S
e
M
1. Introdu
c
In mathemati
c
elastic mediu
m
b
orders on v
a
fied on a fr
e
seismic wav
e
and the gene
r
waves in th
e
b
oundary are
i
In the last
investigations
tion between
mosphere. Pa
p
mic induction
Papers [2,3]
d
p
rocesses at
t
and an isoth
e
p
apers, prop
e
modified La
m
In the pres
e
algorithm to
s
seismic and
a
mogeneous “
A
the algorith
m
with a finite-
d
A similar
a
p
lied Mathemat
i
g
/10.4236/jamp
.
0
13 SciRes.
umeric
g
ation
i
T
h
Siber
i
C
T
analytical sol
u
s
phere” model
a
tions of elast
i
v
ie
r
-Stokes e
q
o
time, the fi
n
d
problem.
e
ismic Waves
;
M
etho
d
c
tion
c
al simulation
m
, it is typic
a
a
cuum, and b
o
e
e surface. S
p
e
s are assume
d
r
ation of aco
u
e
atmosphere
i
gnored.
decade, some
have shown
t
the waves i
n
p
er [1] descri
b
of an acousti
c
d
eal with theo
r
t
he boundary
b
e
rmal homog
e
e
rties of the
s
m
b waves are s
t
e
nt paper we c
o
s
imulate and
i
a
coustic-gravi
t
A
tmosphere-
E
m
is a combi
n
d
ifference met
h
a
pproach to so
i
cs and Ph
y
sics
,
.2013.14003 P
u
c
al Sim
u
i
n a He
t
with
W
B. G. Mik
h
h
e Institute of
C
i
an Branch of t
h
u
tion for seis
m
. Seismic wa
v
i
city theory.
P
q
uations with
t
n
ite integral F
o
;
Acous
t
ic-Gr
a
of seismic w
a
lly assumed t
h
o
undary cond
i
p
ecifically, at
d
to be abso
l
u
stic-gravity
w
and their in
t
theoretical a
n
t
hat there is a
s
n
the lithosph
b
es the effect
c
wave produc
r
etical investi
g
b
etween an e
l
e
neous atmos
p
s
urface Stone
l
t
udied.
o
nsider an eff
i
i
nvestigate th
e
t
y waves in
a
E
arth” model.
A
n
ation of inte
h
od.
lving the pro
b
,
2013, 1, 12-1
7
u
blished Online
O
u
lation
t
eroge
n
W
ind i
n
h
ailenko, A.
A
C
omputational
M
h
e RAS, pr. Ak
a
Email
Rece
m
ic and aco
u
v
e propagatio
n
P
ropagation o
f
t
he wind. The
o
urie
r
transfor
m
a
vity Waves;
N
ave fields in
a
h
at the mediu
m
i
tions are spe
c
the boundar
y
l
utely reflecte
w
aves by elas
t
t
eraction at t
h
n
d experimen
t
s
triking correl
ere and the
a
of acoustose
i
ed by a vib
r
at
o
g
ations of wa
v
l
astic half-spa
c
p
here. In the
s
l
ey-Scholte a
n
i
cient numeric
e
propagation
o
a
spatially inh
o
A
peculiarity
o
gral transfor
m
b
lem for a ver
t
7
O
ctobe
r
2013 (
h
of Aco
u
n
eous
E
n
the A
t
A
. Mikhailo
v
M
athematics and
a
d. Lavrentieva,
: mikh@sscc.r
u
ive
d
July 2013
u
stic-gravity
w
n
in an elastic
f
acoustic-gra
v
algorithm pr
o
m
along the s
p
N
avie
r
-Stokes
a
n
m
c
i-
r
y,
d,
t
ic
h
e
t
al
a-
a
t-
i
s-
o
r.
v
e
c
e
s
e
n
d
al
o
f
o
-
o
f
m
s
t
i-
cally i
n
coordi
n
dered i
n
is writ
t
terms
o
Cartesi
n
are ass
u
the me
d
coordi
n
The al
g
form
w
thod c
a
spectra
instead
that is
integra
l
trast to
the ini
t
which
t
of the
e
thod f
o
was fi
r
for pr
o
[9]. T
h
of this
guerre
Fourie
r
h
ttp://www.scir
p
u
stic-G
E
arth-
A
t
mosph
v
, G. V. Res
h
Mathematical
G
6, Novosibirsk
u
w
aves propag
a
half-space is
v
ity waves in
o
posed is base
d
p
atial coordin
a
Equations; L
a
n
homogeneou
s
n
ates with no
n
[4]. In the
p
t
en down as
o
f the velocit
y
n
system of c
u
med to be fu
n
d
ium is assu
m
n
ate. This pro
b
g
orithm is ba
s
w
ith respect t
o
a
n be conside
r
l method bas
e
of the freq
u
the degree
o
l
Laguerre tra
n
the Fourier tr
a
t
ial problem t
t
he parameter
e
quations and
o
r solving dy
n
r
st considered
o
blems of vis
c
h
e above-men
t
method and
transform ov
r
transform wi
t
p
.org/journal/ ja
m
ravity
W
A
tmosp
h
ere
h
etova
G
eophysics,
630090, Russia
a
tion is appli
e
described by
a
the atmosphe
d
on the integ
r
a
te with the fi
n
a
guerre Transf
o
s
model in a
wind in the
a
p
roblem state
m
a firs
t
-order
y
vector and
o
ordinates. T
h
n
ctions of onl
y
m
ed to be ho
m
b
lem statemen
t
s
ed on the in
t
o
the tempora
l
r
ed to be an a
n
e
d on the Fo
u
u
ency  , we
o
f the Lague
n
sform with r
e
a
nsform) mak
e
o solving a s
y
is present onl
y
has a recurre
n
n
amic proble
m
in papers [5,
6
c
oelasticity [7
t
ioned papers
the advantag
e
er the differ
e
t
h respect to ti
m
m
p )
W
aves
h
ere M
o
e
d to a heter
o
a
system of fi
r
re is describe
d
r
al Laguerre t
r
n
ite difference
o
rm; Finite Di
f
cylindrical s
y
a
tmos
p
here w
a
m
ent, the initi
a
hyperbolic s
y
stress tensor
h
e medium pa
r
y
two coordin
a
m
ogeneous in
t
t
is called a 2.
5
t
egral Laguer
r
l
coordinate.
T
n
alog to a we
l
u
rier transfor
m
have a para
m
rre polynomi
a
e
spect to time
e
s it
p
ossible
t
y
stem of equ
a
y
in the righ
t
-
h
n
ce relation.
T
m
s of elasticit
y
6
] and then d
e
,8] and poro
u
consider pec
u
e
s of the inte
e
nce methods
m
e.
JAMP
o
del
o
geneous
rst order
d
by the
r
ansform
solution
f
ference
y
stem of
a
s consi-
a
l system
y
stem in
in a 3D
r
ameters
a
tes, and
t
he third
5 D one.
r
e trans-
T
his
m
e-
l
l-known
m
, where,
m
eter p
a
ls. The
(in con-
t
o reduce
a
tions in
h
and side
T
his
m
e-
y
theory
e
veloped
u
s media
u
liarities
gral La-
and the

B. G. MIKHAILENKO ET AL.
13
2. Problem Statement
The system of equations for the propagation of acous-
tic-gravity waves in an inhomogeneous non-ionized iso-
thermal atmosphere in the Cartesian system of coordi-
nates (,,)
x
yz with the wind directed along the horizon-
tal axis x and vertical stratification along the axis z has
the following form:
0
1
x
xx
xz
uu v P
vu
tx xz 
 


 
, (1)
0
1
yy
x
uu P
v
tx y 
 

 
, (2)
00
1
zz
x
uu Pg
v
tx z


 

 , (3)
200
0xxzz
P PP
vc vuu
tx txzz
 

  
 

 

, (4)
0
0(, ,,)
y
x
z
x
z
u
uu
v
tx xyz
uFxyzt
z






 



 





(5)
Here
g
is the acceleration of gravity, 0()z

is the
reference atmosphere density, 0()cz is the sound speed,
()
x
vz is the wind velocity along the axis
x
,
(,,)
x
yz
uuuu is the velocity vector of displacement of
the air particles, P and

are the pressure and the
density perturbations, respectively, due to a wave propa-
gating from a source of mass 0
(, ,,)()()
F
xyztrr ft

 ,
where ()
f
t is a given time signal in the source. As-
sume that the axis z is directed upwards. Zero sub-
scripts for the medium physical parameters show their
values for the reference atmosphere. The atmospheric
pressure 0
P
and the density 0

for the reference at-
mosphere in a homogeneous gravitational field are:
0
0
P
g
z


, 01
( )exp(/)zzH


,
where H is the height of the isothermal homogeneous
atmosphere, and 1

is the density of the atmosphere at
the Earth’s surface, that is, at 0z.
The seismic waves propagation in an elastic medium is
described by the well-known system of first order equa-
tions of elasticity theory as the following relation be-
tween the displacement velocity vector components and
the stress vector components:
0
1()
iik
i
k
u
F
ft
tx




 , (6)
ikk i
ik
ik
uu div
txx

 




u. (7)
Here ij

is the Kronecker symbol, 123 (, , )
x
xx  and
12 3
(, , )
x
xx

are the elastic parameters of the medium,
012 3
(, , )
x
xx

is the density, 123 (, ,)uuuu is the dis-
placement velocity vector, and ij

are the stress vector
components. The equality 123
(, ,)
x
yz
x
yz FFFFeee
describes the distribution of a source located in space,
and ()
f
t is a given time signal in the source.
The combined system of equations for the propagation
of seismic and acoustic-gravity waves in the Cartesian
system of coordinates 123 (,,)(,,)
x
yzx xx can be writ-
ten down as
0103
1()
iiki x
ix zzx
k
uuv g
F
ftKve ue
txx x



 


 

,
(8)
0
1
ik
ikk i
ikik xz
ik
uu divK vgu
txx x



  
 
 
 
 
u
(9)
0
0xz
Kv divu
tx z







 


 


u. (10)
Here ij

is the Kronecker symbol, 0(,)
x
z

is the
density, (,)
x
z

and (,)
x
z

are the elastic parameters
of the medium, 123
(, , )uuuu


is the displacement ve-
locity vector, and ij

are the stress tensor components;
123
(, ,)
x
yz
x
yz FFF


F
eee describes the distribution
of a source located in space, and ()
f
t is a given time
signal in the source. The medium is assumed to be ho-
mogeneous along the axis
y
.
System (1)-(5) for the atmosphere is obtained from
system (8)-(10) at
1
атм
K

, 121323 0



 , 1122 33
P

  ,
2
00
c

 , 0


.
Set 0
атм
K

in system (9)-(10), and obtain the sys-
tem of Equations (6)-(7) for the propagation seismic
waves in an elastic medium.
In the problem in question, the atmosphere-elastic
half-space interface is assumed to be the plane
30zx

. In this case, the condition of contact of the
two media at 0z

is written as
0
00
00
,zz zz
zz z
zz
zz
uu gu
tt


 








,
000
xz yz
zz

 

. (11)
The problem is solved at the following zero initial da-
ta:
00 000,1, 2, 3.1, 2,3.
iij tt
tt
uPij 
 

(12)
All the functions of the wave field components are as-
sumed to be sufficiently smooth so that the transforma-

B. G. MIKHAILENKO ET AL.
14
tions presented below be valid.
3. Solution algorithm
At the first step, we use the finite cosine-sine Fourier
transform with respect to the spatial coordinate y, where
the medium is assumed to be homogeneous. For each
component of the system, we introduce the correspond-
ing cosine or sine transform:
0
cos( )
(,,,)(, ,,)()
sin( )
a
n
n
ky
x
zntxyztd y
ky




WW ,
0,1, 2,...,nN; (13)
with the corresponding inversion formula
1
12
(, ,,)(,0,,)(,,,)cos()
N
n
n
x
yztxztxnztk y




WW W
(14)
or
1
2
(, ,,)(,,,)sin()
N
n
n
x
yztxnzt ky


 WW , (15)
where n
n
ka

.
At rather a large distance a , consider a wave field
up to the time tT, where T is a minimum propaga-
tion time of a pressure wave to the boundary ra

. As a
result of this transformation, we obtain 1N indepen-
dent 2D unsteady problems.
At the second step, we apply to the thus obtained
1N independent problems the integral Laguerre
transform with respect to time
2
0
(,,)(,,,)( )( )( ),
0,1,2,...
pp
x
n zxn zthtlht dht
p






WW (16)
with the inversion formula
2
0
!
(,,,)()(,,)( )
()!
pp
p
p
x
nzthtxnzl ht
p







WW, (17)
where ()
p
lht

are the orthogonal Laguerre functions.
The Laguerre functions ()
p
lht

can be expressed in
terms of the classical standard Laguerre polynomials
()
p
Lht

(see paper [10]). Here we select an integer pa-
rameter 1

 to satisfy the initial data and introduce
the shift parameter h>0. Then we have the following
representation:
2
() ()exp(2)()
pp
lhththt Lht


 .
We take the finite cosine-sine Fourier transform with
respect to the coordinate x, similar to the previous trans-
form with respect to the coordinate y with the corres-
ponding inversion formulas:
1
1
(,, )(0,, )
π
2(,, )cos()
π
pi pi
M
pim
m
xnz nz
mnzk x



WW
W
(18)
or
1
2
(,, ,)(,, ,)sin()
π
M
iim
m
x
nz pmnzpkx

 WW , (19)
where m
m
kb

.
It should be noted that the medium in this direction is
inhomogeneous.
The finite difference approximation for the system of
linear algebraic equations with respect to z using the
staggered grid method was applied (see paper [11]) pro-
viding second order accuracy approximation. This
scheme is used for FD approximation within the compu-
tation domains in the atmosphere and in the elastic
half-space, the fitting conditions at the interface being
exactly satisfied. As a result of the above transformations,
we obtain 1N

systems of linear algebraic equations,
where N is the number of harmonics in the Fourier
transform with respect to the coordinate
y
.
The sought for solution vector W is represented as
follows:
01
( )((),( ),...,())T
K
ppp pWVVV,
[(0,...,; ),(0,...,; ),...
iixxi
mMzmMz   V
...(0,...,;),( 0,...,;)]T
iz i
PmMzu mMz.
Then for every n-th harmonic (0,...,nN) the sys-
tem of linear algebraic equations can be written down in
the vector form:
()()(1)
2
h
AE pp

WF . (20)
Note that only the right-hand side of the obtained sys-
tem of algebraic equations includes the parameter
p
(the degree of the Laguerre polynomials) and has a re-
current
p
dependence. The matrix A is thus inde-
pendent of
p
. A sequence of wave field components in
the solution vector V is chosen to minimize the number
of diagonals in the matrix A. The main diagonal of the
matrix has the components of this system multiplied by
the parameter h (the Laguerre transform parameter). By
changing the parameter h, the condition number of the
matrix can be considerably improved. Solving the system
of linear algebraic equations (20) determines spectral
values for all the wave field components (,,,)
i
mnzpW.
Then, using the inversion formulas for the Fourier trans-
form (14), (15), (18), (19), and the Laguerre transform
(17), we obtain a solution to the initial problem (8)-(12).
In the analytical Fourier and Laguerre transforms, when

B. G. MIKHAILENKO ET AL.
15
determining functions by their spectra, inversion formu-
las in the form of infinite sums are used. A necessary
condition in the numerical implementation is to deter-
mine the number of terms of the summable series to con-
struct a solution with a given accuracy. For instance, the
number of harmonics in the inversion formulas of the
Fourier transform (14), (15), (18), (19) depends on a mi-
nimal spatial wavelength in the medium and on the size
of the spatial calculation domain of the field given by the
finite limits of the integral transform. In addition, the
convergence rate of the summable series depends on
smoothness of functions of the wave field. The number
of the Laguerre harmonics for determining functions by
formula (17) depends on a signal given in the source
()
f
t, the parameter h, and the time interval of the
wave field. Papers [5-8] consider in detail how one can
determine the required number of harmonics and choose
an optimal value of the parameter h.
4. Numerical Results
Figures 1-3 show the results of numerical calculations of
a wave field as snapshots at a fixed time for the horizon-
tal component of the displacement velocity (, ,)
x
uxyz .
Figure 1 presents a snapshot of the wave field for
(, ,)
x
uxyz in the plane XZ at the time t=15 sec. This
model of the medium consists of a homogeneous elastic
layer and an atmospheric layer separated by a plane
boundary. The physical characteristics of the layers are
as follows:
 the atmosphere: sound speed 340
p
cm·sec–1. Den-
sity versus coordinate z was calculated by the formula
01
( )exp(/)zzH

 , where 3
11.22510



g·cm–3, 6700Hm;
 the elastic layer: pressure wave velocity 300
p
c

m·s e c–1, shear wave velocity 200
s
c m·sec–1, den-
sity 01.2

 g·cm–3.
A bounded domain, (,, )
x
yz=(15km,15km, 10 km),
was used for the calculations. A wave field from a point
source (a pressure center) located in the elastic medium
at a depth of ¼ of the length of a pressure wave with
coordinates 000
(,,)
x
yz=(6 km,7.5km,0.075 km) was
simulated. The figure shows the wave fields for the ho-
rizontal component
x
u of the displacement velocity in
the plane XZ at 07.5 kmyy : without wind (top),
with the wind speed in the atmosphere of 50 m·se c –1
(bottom). The elastic medium-atmosphere interface is
shown by the solid line. This figure demonstrates that in
the elastic medium, in addition to the spherical P-pressure
wave and the conic S-shear wave, there also propagates a
“non-ray” spherical wave S*, and then there follows a
surface Stoneley-Scholte wave. An acoustic-gravity
wave refracted at the Earth-atmosphere boundary propa-
gates in the atmosphere. At the boundary, this wave ge-
nerates the corresponding pressure and shear waves in
Figure 1. A snapshot at t = 15 sec for the velocity component
ux in the plane (XZ) without wind (top), with wind (bottom)
(wind speed 50 m·sec –1).
the elastic medium.
Figures 2 and 3 present snapshots of the wave field
when the seismic waves velocity in the elastic medium is
greater than the sound speed in the atmosphere. In this
model, the physical characteristics of the elastic medium
and the atmosphere are as follows:
 the atmosphere: sound speed 340
p
cm·sec–1. Den-
sity versus coordinate z was calculated by the formula
01
( )exp(/)zzH


, where 3
11.22510



g·cm–3, 6700H

m;
 the elastic layer: pressure wave velocity 800
p
c

m·s e c–1, shear wave velocity 500
s
c m·sec–1, den-
sity 01.5


g·cm–3.
A bounded domain(,,)(20 km, 16 km, 14 km)xyz,
was used for the calculations. A wave field from a point
source (the pressure center) located in the elastic medium
at a depth of ¼ of the length of a pressure wave with the
coordinates 000 (,,)(10 km,8 km,0.2 km)xyz

 was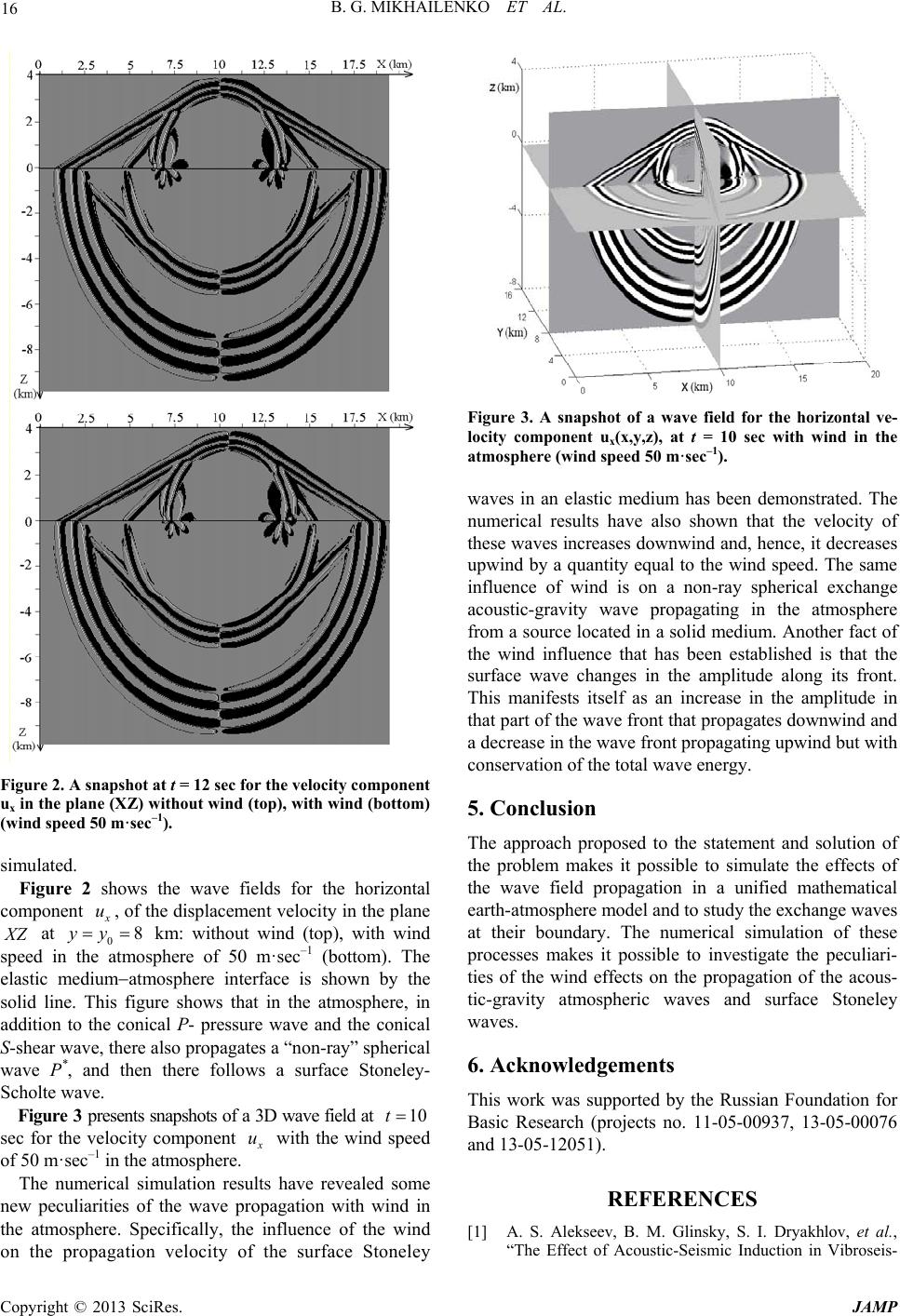

B. G. MIKHAILENKO ET AL.
16
Figure 2. A snapshot at t = 12 sec for the velocity component
ux in the plane (XZ) without wind (top), with wind (bottom)
(wind speed 50 m·sec–1).
simulated.
Figure 2 shows the wave fields for the horizontal
component
x
u, of the displacement velocity in the plane
XZ at 08yy
km: without wind (top), with wind
speed in the atmosphere of 50 m·sec–1 (bottom). The
elastic mediumatmosphere interface is shown by the
solid line. This figure shows that in the atmosphere, in
addition to the conical P- pressure wave and the conical
S-shear wave, there also propagates a “non-ray” spherical
wave P
*, and then there follows a surface Stoneley-
Scholte wave.
Figure 3 presents snapshots of a 3D wave field at 10t

sec for the velocity component
x
u with the wind speed
of 50 m·se c –1 in the atmosphere.
The numerical simulation results have revealed some
new peculiarities of the wave propagation with wind in
the atmosphere. Specifically, the influence of the wind
on the propagation velocity of the surface Stoneley
Figure 3. A snapshot of a wave field for the horizontal ve-
locity component ux(x,y,z), at t = 10 sec with wind in the
atmosphere (wind speed 50 m·sec–1).
waves in an elastic medium has been demonstrated. The
numerical results have also shown that the velocity of
these waves increases downwind and, hence, it decreases
upwind by a quantity equal to the wind speed. The same
influence of wind is on a non-ray spherical exchange
acoustic-gravity wave propagating in the atmosphere
from a source located in a solid medium. Another fact of
the wind influence that has been established is that the
surface wave changes in the amplitude along its front.
This manifests itself as an increase in the amplitude in
that part of the wave front that propagates downwind and
a decrease in the wave front propagating upwind but with
conservation of the total wave energy.
5. Conclusion
The approach proposed to the statement and solution of
the problem makes it possible to simulate the effects of
the wave field propagation in a unified mathematical
earth-atmosphere model and to study the exchange waves
at their boundary. The numerical simulation of these
processes makes it possible to investigate the peculiari-
ties of the wind effects on the propagation of the acous-
tic-gravity atmospheric waves and surface Stoneley
waves.
6. Acknowledgements
This work was supported by the Russian Foundation for
Basic Research (projects no. 11-05-00937, 13-05-00076
and 13-05-12051).
REFERENCES
[1] A. S. Alekseev, B. M. Glinsky, S. I. Dryakhlov, et al.,
“The Effect of Acoustic-Seismic Induction in Vibroseis-

B. G. MIKHAILENKO ET AL.
17
mic Sounding,” Dokl. RAN [in Russian], Vol. 346, No. 5,
1996, pp. 664-667.
[2] L. A. Gasilova and Yu. V. Petukhov, “On the Theory of
Surface Wave Propagation along Different Interfaces in
the Atmosphere,” Izv. RAN. Fizika Atmosfery i Okean [in
Russian], Vol. 35, No. 1, 1999. pp. 14-23.
[3] A. V. Razin, “Propagation of a Spherical Acoustic Delta
Wavelet along the Gas-Solid Interface,” Izv. RAN. Fizika
zemli [in Russian], No. 2, 1993, pp. 73-77.
[4] B. G. Mikhailenko and G. V. Reshetova, “Mathematical
Simulation of Propagation of Seismic and Acoustic-Gravity
Waves for an Inhomogeneous Earth-Atmosphere Model,”
Geologiya i geofizika [in Russian], Vol. 47, No. 5, 2006,
pp. 547-556.
[5] B. G. Mikhailenko, “Spectral Laguerre Method for the
Approximate Solution of Time Dependent Problems,”
Applied Mathematics Letters, Vol. 12, No. 4, 1999, pp.
105-110.
http://dx.doi.org/10.1016/S0893-9659(99)00043-9
[6] G. V. Konyukh, B. G. Mikhailenko and A. A. Mikhailov,
“Application of the Integral Laguerre Transforms for
Forward Seismic Modeling,” Journal of Computational
Acoustics, Vol. 9, No. 4, 2001, pp. 1523-1541.
[7] B. G. Mikhailenko, A. A. Mikhailov and G. V. Reshetova,
“Numerical Modeling of Transient Seismic Fields in
Viscoelastic Media Based on the Laguerre Spectral Me-
thod,” Journal Pure and Applied Geophysics, Vol. 160,
No. 7, 2003, pp. 1207-1224.
http://dx.doi.org/10.1007/s000240300002
[8] B. G. Mikhailenko, A. A. Mikhailov and G. V. Reshetova,
“Numerical Viscoelastic Modeling by the Spectral La-
guerre Method,” Geophysical Prospecting, Vol. 51, No. 1,
2003, pp. 37-48.
http://dx.doi.org/10.1046/j.1365-2478.2003.00352.x
[9] Kh. Kh. Imomnazarov and A. A. Mikhailov, “Use of the
Spectral Laguerre Method to Solve a Linear 2D Dynamic
Problem for Porous Media,” Sib. Zh. Industr. Matem [in
Russian], Vol. 11, No. 2, 2008, pp. 86-95.
[10] P. K. Suetin, “Classical Orthogonal Polynomials,” Nauka,
Moscow, 1974.
[11] J. Virieux, “P-SV Wave Propagation in Heterogeneous
Media: Velocity-Stress Finite-Difference Method,” Geo-
physics, Vol. 51, No. 4, 1986, pp. 889-901.