 Applied Mathematics, 2013, 4, 1537-1546 Published Online November 2013 (http://www.scirp.org/journal/am) http://dx.doi.org/10.4236/am.2013.411208 Open Access AM A Stochastic Optimal Contr ol Theory to Model Spontaneous Breathing Kyongyob Min Respiratory Division, Department of Internal Medicine, Itami City Hospital, Itami, Japan Email: in1007@poh.osaka-med.ac.jp Received September 1, 2013; revised October 1, 2013; accepted October 8, 2013 Copyright © 2013 Kyongyob Min. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT Respiratory variables, including tidal volume and respiratory rate, display significant variability. The probability density function (PDF) of respiratory variables has been shown to contain clinical information and can predict the risk for ex- acerbation in asthma. However, it is uncertain why this PDF plays a major role in predicting the dynamic conditions of the respiratory system. This paper introduces a stochastic optimal control model for noisy spontaneous breathing, and obtains a Shrödinger’s wave equation as the motion equation that can produce a PDF as a solution. Based on the lob- ules-bronchial tree model of the lung system, the tidal volume variable was expressed by a polar coordinate, by use of which the Shrödinger’s wave equation of inter-breath intervals (IBIs) was obtained. Through the wave equation of IBIs, the respiratory rhythm generator was characterized by the potential function including the PDF and the parameter con- cerning the topographical distribution of regional pulmonary ventilations. The stochastic model in this study was as- sumed to have a common variance parameter in the state variables, which would originate from the variability in meta- bolic energy at the cell level. As a conclusion, the PDF of IBIs would become a marker of neuroplasticity in the respi- ratory rhythm generator through Shrödinger’s wave equation for IBIs. Keywords: Biological Variability; Stochastic Processes; Optimal Stochastic Control Theory; Probability Density Function; Shrödinger’s Wave Equation 1. Introduction Classical physiology is grounded on the principle of ho- meostasis, in which regulatory mechanisms act to reduce variability and to maintain a steady state [1]. Cherniack et al. [2] applied a systems engineering approach to the control of respiration, describing a controller (brain stem respiratory pattern generator), sensors (chemo- and mech- anoreceptors), and a plant (airways, chest wall, muscles, and pulmonary tissue). With this model, fluctuations are often dismissed as “noise” of little or no significance. However, since many systems in nature, including respi- ration, operate away from an equilibrium point, the im- portance of taking fluctuations into account was well known from early models of the respiratory control mechanism. For example, measured interbreath intervals of a preterm baby at 39 and 61 weeks of postconcep- tional age have shown that the baby’s breathing pattern was highly irregular at 39 weeks, and that the fluctua- tions were significantly reduced by 61 weeks [2]. For constructing realistic models of control mechanisms with biological variability in spontaneous breathing, one is faced with the problem of finding suitable ways to characterize them. A characteristic feature of fluctuations is the impossibility of precisely predicting their future values, and thus some researchers have tried to use statis- tical concepts to model fluctuations. From this statistical viewpoint, Frey et al. and Suki have suggested three points on noisy biological variables: 1) the fluctuations obey their own probability distribution; 2) irregular fluc- tuations can carry information through the probability distribution; and 3) the probability distribution may be sensitive to physiological or pathological changes [3,4]. Thus, to define the physiological or pathological mean- ing of biological variability, it is important to show why the probability distribution of noisy breathing variables is sensitive to physiological or pathological changes. This paper introduces a stochastic optimal control the- ory to model spontaneous breathing. By implementing a stochastic process, the method reveals that the probabil- ity density function of noisy spontaneous breathing obeys a Shrödinger’s wave function, which was introduced for  K. MIN 1538 describing motions of a quantum particle. Based on the wave function for noisy breathing, this paper concludes that the probability density function of inter-breath in- tervals will be a marker of neuroplasticity in the central rhythm generator. 2. Differentiable Stochastic Processes [5] 2.1. Fluctuations as a Sequence of Random Variables A characteristic feature of fluctuations is the impossibil- ity of precisely predicting their values. A successful at- tempt is to model a disturbance as a sequence of random variables or a stochastic process. A stochastic process can be defined as a family of random variables 00 ,,1,Xttt t . It is possible to assume that the random variables t represent values on the real line or in an n-dimensional Euclidean space. A stochastic process is a function of two arguments ,Xt , where ω belongs to the sample space Ω. For fixed t, , t is a random variable and for fixed ω, ,X is a func- tion of time which is called a sample function or a tra- jectory. The trajectories can be regarded as elements of the sample function space Ω. For ordinary random vari- ables whose sample function spaces are Euclidean spaces, probability measures can be assigned by ordinary distri- bution functions and denoted by P. Let us assign a probability function to the multidimen- sional random variable for any k and arbitrary time with a distribution function F as follows, j t 12 12 112 2 ,,,;,,, ,,, kk kk Fttt PXt XtXt . (2.1.1) which satisfies the conditions of symmetry in all pairs , j t and consistency. The consistency condition is expressed by 12 12 12 12 ,,,;,,, lim ,,,;,,, k kk kk t Fttt tt t . (2.1.2) Thus, the mean value of a stochastic process m(t) is defined by use of the probability distribution density d, t as follows, d,mtFtEX t . (2.1.3) The symbol E[ ] denotes expectation, that is, integra- tion with respect to the measure P. The covariance of s and t are also given by cv,o ,Xs Xtr EXs msXt m t t s When both the mean value function m(t) and the co- variance r(s, t) exist, the stochastic process is said to be of second order. 2.2. A Wiener Process and a Markov Process Let us consider the stochastic process of second order ,1,2,3,, j tj k, and . When the set elements 123 k tt tt 11 211 ,, , kkkk Xt XtXt Xt XtXt Xt 2 , are mutually independent, the process is called a process with independent increments. If the variables are only uncorrelated, the process {X(t)} is called a process with uncorrelated or orthogonal increments. A Wiener process is one with orthogonal increments defined by the follow- ing conditions: 1) X(0) = 0, 2) X(t) is normal, 3) m(t) = 0 for all t > 0, and 4) the process has independent station- ary increments. Since a Wiener process has independent stationary increments and X(0) = 0, the variance of the process is 2 var X tt ct , and the covariance of the process is r(s, t) = c × (the minimal difference between t and s), where the parameter c is called the vari- ance parameter. A stochastic process t is called a Markov proc- ess if 12 ,,,k k PXtXt XtXt PXt Xt . (2.2.1) where k Xt denotes the conditional probability given k t. When the initial probability distribution 1 1 ,Xt 11 FtP and the transitional probabil- . (2.1.4) ity distribution ,,? tst s sPXt XsFt are given, the distribution function of the trajectory 12 ,,, k Xt Xt t is given by the Bayes’ rule as follows, 12 12 112211 11 ,,,;,,, ,,,, , kk kk kk Fttt ttFttF t . (2.2.2) (2.2.2) shows that a Markov process is defined by both the initial probability distribution and the transition prob- abilities. 2.3. Stochastic State Models State models, i.e., systems of first order difference or differential equations, are very convenient for the analy- sis of systems. An extension of this concept to stochastic state models requires that the probability distribution of the state variable x at future times should be uniquely determined by the actual value of the state. If X(t + 1) is a Open Access AM  K. MIN 1539 random variable which depends on the state variable x at the time t 1,, tXtbxtx t . (2.3.1) where ,bxt and , t are the conditional mean of X(t + 1) and a random variable given the state variable x at the time t. When the model (2.3.1) is a Markov process, the conditional distribution of , t given x is normal and the stochastic variable , t can always be nor- malized by its variance 2 through a Wiener process w(t) with unit variance parameter, , tw t . (2.3.2) 2.4. Stochastic Differential Equations of State Models Starting with the difference 2 , th Xtbxthoh . (2.4.1) where the term o(h2) denotes the omit terms of higher order than 2. One can easily obtain a stochastic differ- ence equation by adding a disturbance , t , 2 ,, , Xt hXt bxthxt hxtoh . (2.4.2) When the disturbance , t is a Markov process with independent increments, the conditional distribution of ,, th xt given x is normal. Hence ,, thxtwthwt . (2.4.3) where wt is a Wiener process with unit variance parameter. Thus, the stochastic state model is obtained for the stochastic process t 2 , Xt hXt bxthwt hwtoh . (2.4.4) Therefore, the expectation EXthXt and the variance var th X t are obtained as (2.4.5) and (2.4.6) respectively, 2 ,EXthXtbxth oh . (2.4.5) 2 22 22 varXt hXt Ewthwtoh hoh . (2.4.6) Then, let h go to zero in (2.4.4) and one obtains the following formal expression (2.4.7) dd,dd ttXtXtbxttwt .(2.4.7) function of ,bxt is called a forward drift function of the state x at e t. The stochastic differ the tim ential (2.4.7) is defined as the limit of (2.4.4). However, another expression is possible for dX(t) as follows, d tXtXth . (2.4.8) The difference dwtwthw *t is not de- ndent on th but on X(t), and the variance of pe * dwt is * va dt t r dw . Then, another stochastic erential equation is possible diff as follows, d * dd,d* tXtt Xtbxt t wt . (2.4.9 where ) *,bxt process is a backward drift function of t 3. A Stochastic Control Model of Noisy 3.1bles in Noisy Breathing es of tidal he sto- chastic given x at the time t. Breathing . State Varia Spontaneous breathing is described as a seri volumes or changes in respiratory rhythm. A series of tidal volumes is produced from the neural activity of the respiratory center in the brain. The neural activities of the respiratory center induce changes in the length of respi- ratory muscles, which are transformed into changes in the pleural pressure through the architectural properties of the ribcage. The changes in the pleural pressure are transformed to the alveolar pressure through the lung parenchyma. The alveolar pressure is transformed into airway pressure by the pulmonary lobule, and goes into the environment by producing airflows through the frac- tal bronchial tree (Figure 1). It is important to note in Figure 1 that there are two origins of fluctuations in this process: in the respiratory rhythm generator (the neural center of respiration) and in the fractal airway modulator (the phasic asynchronous contractions of airway smooth muscles in the lobular bronchioles) [6]. Then, based on that bronchial flow F(t) is composed of N-number of phasic lobular flow (q), a tidal volume VT is defined as following, 00 dd I I NN Tj jj IEII VFttqtqt qN d j . (3.3.1) where is inspiration priod, and j is 0 or 1 for the j-th lobular bronchiole. and are the mean value of j during inspirat and eration, respectively. On y state it is presumed that ion xpi stead IE and is less than 1 or sin , then T V i by the s expressed following, which is called a stochastic differential equation. The Open Access AM  K. MIN 1540 (a) (b) Figure 1. Components of respiratory system and produing of breathing motions. (a) Coystem: c mponents of respiratory s the ribcage consists of thoracic structures and the dia- phragm, the right lung parenchyma consists of many lob- ules, a sliced face of right upper lobe lobules with a single bronchiole, and a fractal bronchial tree integrates many lobules; (b) A series of tidal volumes is produced from the neural activity of the respiratory center in the brain. The neural activities of the respiratory center induce changes in the length of respiratory muscles, which are transformed into changes in the pleural pressure through architectural properties of the ribcage. The changes in the pleural pres- sure are transformed into alveolar pressure through the lung parenchyma, which is composed of a large number of lobules. The alveolar pressure is transformed into airway pressure by the pulmonary lobule, and goes into the envi- ronment by producing airflows through the fractal bron- chial tree, each branch of which has own bundle of smooth muscles. Bundles of airway smooth muscles dynamically change in length-tension to adapt with conditions of breath- ing. sin T VqN . (3.1.2) During a voluntary forced expir lobule exhales a flow simultaneously. T ex ation maneuver each hen, the forced piration volume in one second (FEV1.0) is defined by the following, 1 1.0 0 FEV d ttqN Thus, the state variable of noisy breathing x is VT nor- malized by FEV1.0 as the following, 1.0 sin FEV T V x . (3.1.3) The variable is the interbreath interval (IBI), and sin is the prtion of simultaneously relaxed lobular br cterized by a series of opor onchioles in the lung during a breath. 3.2. A Stochastic State Model The spontaneous breathing is chara respiratory variables T V. One will consider the series T V as a stochastic process t characterized by the following stochastation with the state variable x e variance 2 ic equ and th , ,ddd 0 dbxt twtt Xt ** ,d dd 0bxttwt t . (3.2.1) wt and * wt where are the forward Wiener proc- ess anackwner process with unit variance d the bard Wie parameter,spectivelye function, re. Th ,bxt or *,bxt is called the forward drift function or the backward drift function of state variable x at the givspect en t, reively as follows, d0 d0 l im lim dd tt tt dd , tXttXt bxt E E tt . (3.2.2a ) * d0 d0 dd ,limlim dd tt tt tXtXtt bxt EE tt (3.2.2b . ) t E where denotes the conditional expectation of stochastic ables at the given t. vari itions of the Stochastic State Model 3.3. Optimal Controlled Cond Optimal control deals with the problem of finding a con- trol that a certain optimality law for a given system such criterion is achieved. The optimality criterion includes a value of H similar to the total energy of a mechanical system. In the case of noisy breathing, a cost function H(t) should be of equilibrium at optimal controlled conditions as follows, 22 * ,, 1bxtb xt 22 2 d0 d tE Ux Ht t Open Access AM  K. MIN 1541 where U(x) is a potential function of the respiratory sys- tem. By use of the probability density function ρ(x, t), the stochastic optimal controlled conditions are expressed by the following, ,d 0 d2 22Ux xt x t . (3.3.1) 22 * ,, d1 bxtb xt 3.4. Einstein’s Diffusion Equation Consider a function f a continuous real valued function. The variable Xt is also a stochastic variable. Based on the of stochastic differentia definitionsls, two differentials for Xt are defined by use of the state variable x as follows, d d0 d lim d d lim t t t fXt Et 0 2 2 2 d dd ,d2 d t X t fx fx bxt xx ttfXt E d0 d0 2 2 * 2 d lim d lim d dd ,d2 d t t t t fXt Et XtfXtdt Et fx fx bxt xx Thus, the differential of EfXt by t is ex- pressed as follows, d0 d0 2 2 2 d d d lim EfXt tt d d limd dd ,d2 d t t EfXt t EfX t fXttfXt EE t fx fx Ebxt xx (3.4.1) t When the series of stochastic variables t have a probability density function , t of state variable x, the differential of EfX t by tpressed is also ex as follows, dd , dd , EfXtfxxt tt xt . (3.4.2) d d x x t fx Comparing (3.4.1) and (3.4.2), the following relation is necessary if the function f(x) is arbitrary, t.(3.4.3a) 22 2 ,dd ,, , d2 d xt bxt xtx tx x Starting from (3.3.1b), the following equation is also necessary, 22 * 2 ,dd ,, ,xt . d2 d xt bx t xt tx x (3.4.3b) By combining (3.4.3a) and (3.4.3b), two equations are obtained as follows, * ,d1,, d2 xt bxtbxt tx 0 . (3.4.4) 22 * 2 d1 d ,,, , d2 b xtbxtxtxt x . 2 dx (3.4.5) Here, let us introduce two functions, v(x, t) and u(x, t) as follows * 1 ,, 2 vxtbxtb xt , * 1 ,,, 2 uxtbxtbxt Then, the functional relationships of ,vxt, ,uxt , t can be established by the foo equa-llowig twn tions, ,d,, d xt vxt xt tx 0 . (3.4.6a) 22 2 dd ,, ,uxtxtxt . (3.4.6b) d2 d xx (3.4.6b) is equal to the diffusion equation of Einstein as follows 2d ,log 2d uxt xt x . , 4. ger’s Wave Equation as Optimal Controlled Conditions According to (3.3.1), the optimal condition of noisy breath- (3.4.7) Motion Equations for Noisy Breathing 4.1. Shrödin ing is defined using of functions ,vxt, ,uxtand , t as follows 22 d1 ,, d2 v xtu xt t ,d0U xxtx . (4.1.1) It is possible to transform (4.1.1) to the following Open Access AM  K. MIN 1542 equatio dix for details regarding the refer- ence [7]), n (see Appen dd ,, dd vx t vxtUx xx Accordin 22 2 ,dd ,,, d2 d vxt uxt uxtuxt tx x . g to Einstein’s diffusion equation of (3.3.7), the following equation is obtained, (4.1.2) 2 2 2 2 2 2 2 ,log, d 2d , d, 2d d xt t x ,, dd 2d , d, d, dd , 2d d, d, d,, 2d d uxt xt txt xt vxt xt x xxt t vxt x vxt xxt vxt vxtuxt x x . (4.1.3) The probability density function , t obeys the Fokker-Planck equation as follows, 2 2 2 , d,, d2 d d, t bxt xt tx x xt .(4.1.4) A set of transformations are applied to the functions ,xt and ,uxt as follows, v 2d ,, d vxt Sxt x ,l og, 2d uxtxt x , from), (4.1.3) and ( 2d Then (4.1.24.1.4) a set of partial differential equations are obtained as folws, lo 2 , d , Sxt t 2 22 2 2 , dd , 2d 2 t Ux x Sxt x xt . (4.1.5a) 2 22 2 ,d,d, d , dd d , t , txtSxtS xt txx x . (4.1.5b) xt Let us introduce a complex function as fol- lows, ,,exp, txtiSx t By use of , t formed t , the Equations (4.1.5a) and (4.1.5b) can be transo a single motion equation which equates to Shrödinger’s wave equation as follo cording to reference [7]), ws (ac- 2 4 2 2 ,d,, 2d xt xt iU tx . xxt (4.1.6 egiona entilations While noisy breathing is in the steady statof optimal co ditions ) 4.2. Distribution of Temporal and Rl Lung V e ntrolled con, the cost function would be equal to an optimal value of H. Thus, the wave function of noisy ventilations is defined by the following 42 dUx 2 2dxHx x . (4.2.1) When the state variable x is expressed by (3.1.3), the operator 2 2 d d is expressed by the following 2 2 22 2 d1 1 sin dsinx . (4.2.2) If the potential function U(x) is dependent on only the variable τ, (4.3.1) can be transformed to the Equation (4.2.3) after rewriting the wave function as xT Y , 2 1sin sinY . (4.2.3) Each side term of (4.2.3) contain different single ra 2 4 12 Tr rUH T 1Y pa- meter or , thus each side term of (4.2.3) should be a constant . An equation for is obtained from the right side term of (4.2.3) as follows, d 1d sin 0 sin dd YY . (4.2.4) When the transformation of cos is applied (4.2.4), the following equation is obtained, to 2 2 2 dd 12 d d Ys Ys ssY s s 0s . (4.2.5) e (4.2.5) is a Legendre equation, whose solutions are obtained as Legndre orthogonal polynomials only when 1kk 0,1, 2,3,k where as follows, Open Access AM 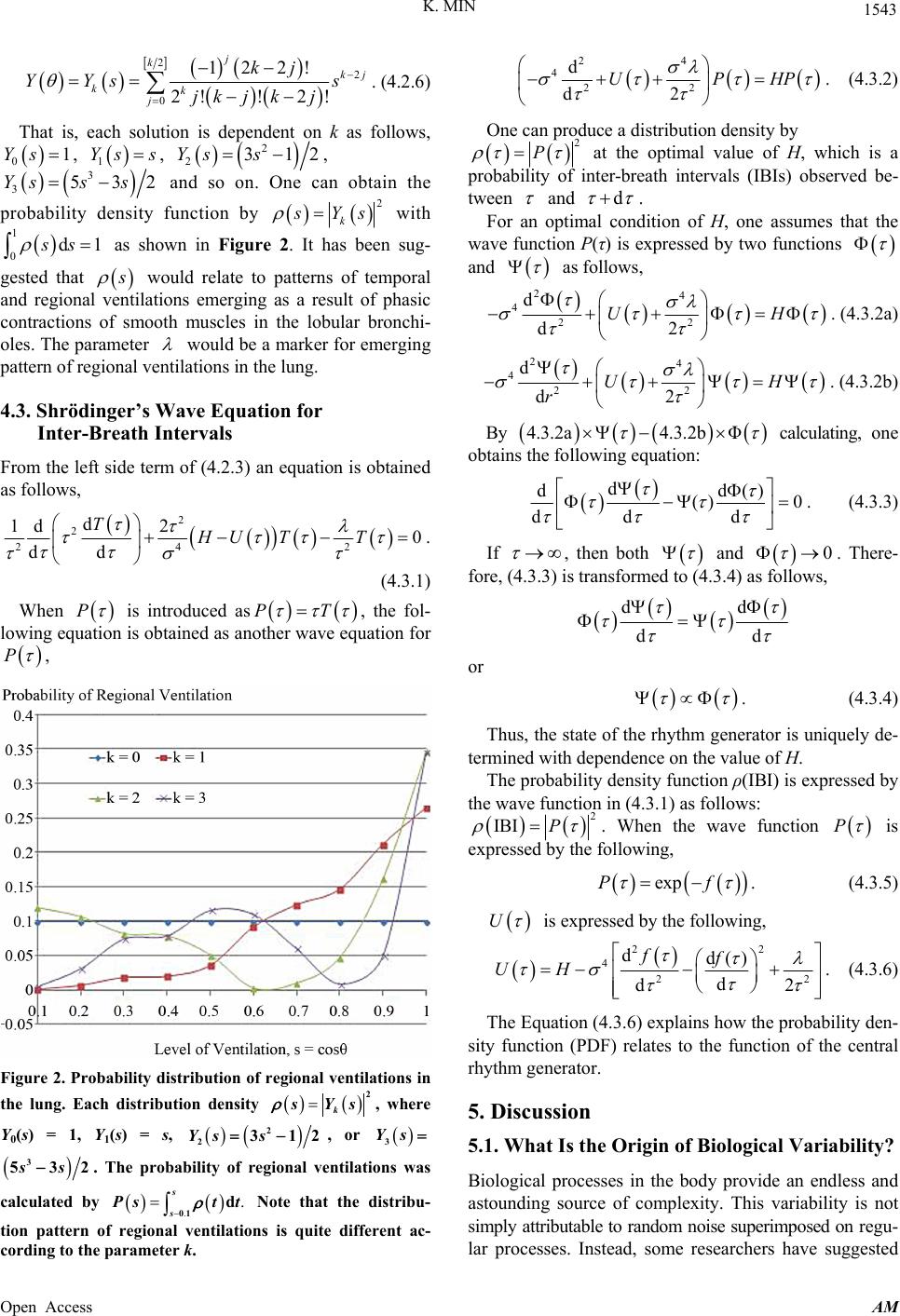 K. MIN 1543 212 2! j kkj 2 02!! 2! kj kk j YY s s jk jkj . (4.2.6) That is, each solution is dependent on k as follows, 1s, 1 Ys s, 0 Y 2 231Ys, 2s 3 3532Yss s and so on. One can obtain the probability density function by 2 k Ys with 1 0d1 s as shown in Figure 2. It has been ge sug- sted that would relate to patterns of temporal and regional ventilations emerging as a result of phasic of smoot the lobular brcontractions h muscles inonchi- oles. The parameter would be a marker for em pattern of regional ventilations in the lung. 4. Inter-Breath Intervals From the left side te erging 3. Shrödinger’s Wave Equation for rm of (4.2.3) an equation is obtained as follows, 2 20HU TT . 2d 1d T 24 2 dd (4.3.1) When P is introduced as PT , the fol- lowing equation is obtained as another wave equation for P , Figure 2. Probability distribution of regional ventilations in the lung. Each distribution density 2 k sYs , 24 4 22 d d2 UPH P . (4.3.2) One can produce a distribution density by 2 P probability of tween at the optimal value of H, which is a inter-breath intervals (IBIs) observed be- and d . For an optimal condition of H, one assumes that the wave function P(τ) is expressed by two functions and as follows, 24 4 22 d d2 UH . (4.3.2a) 24 4 22 d d2 UH r . (4.3.2b) By 4.3.2a4.3.2b Φ calculating, one obtains the following equation: d d0 d d() () dd (4.3.3 . ) If , t hen both and 0 . There- fore, (4.3.3) is 3.4) as follows, transformed to (4. dd dd or . Thus, the state of the rhythm generator is uniquely de- termined with dependence on the value of H. (4.3.4) The probability density function ρ(IBI) is expressed by the wave function in (4.3.1) as follows: 2 IBI P . When the wave function P is ssed bg, exprey the followin expPf . (4.3.5) U is expressed by the following, 2 2 4 22 dd() d d2 ff UH . (4.3.6) The Equation (4.3.6) explains how the probability den- sity function (PDF) relates to the function of the central rhythm generator. 5. iscuss bility? Biological processes in the body provide endless and astounding source of complexity. This variability is not ply attributable to random noise superimposed on regu- processes. Instead, some researchers have suggested where Y0(s) = 1, Y1(s) = s, 2 231Ys s Dion 5.1. What Is the Origin of Biological Varia 2 , or Ys 3 ss 3 532. The probability of regional ventilations wa calculated by s .. 01 d s s st regional ventilation an tNote that tion pattern ofs is quite di cording to the parameter k. the distribu- fferent ac-sim lar Open Access AM  K. MIN 1544 that hidden in the noise are tempo ma di l variables w in of biological variability. In thi epresented by a single value, ral structures which y be important markers of numerous acute and chronic seases [1]. Frey et al. and Suki have suggested that the probability distribution of noisy physiologica ould have biological information [3,4]. However, little work has been done in regard to the orig s study, fluctuations in respiratory state variables are assumed to be r 2 . and bolic fl com level Based on recent in vitro experim colleagues have proposed that e uell are essential ponents of biological variability [8]. If any biological variability originates from the variability of ene of the cell, it will be acceptable to hypothesize t the fluctuati ental studies, Suki nergetic and meta- ctuations at the level of the c rgy at the hat ons of physiological state variables are de- scribed by the single quantity of 2 . That is, a living cell would produce biological variability through mo- lecular fluctuations, and thisability could e universal constant biological vari be modeled by th2 , much like the the quantum I the medullary atory inger comopriobulbar neurons in the - te - function (PDF) of inter-bh intervals (IBIs). Planck constant in physics. 5.2. Temporal and Regional Distribution of Lobular Ventilations By using the lobule and fractal bronchial tree model (LBT model) [6], the state variable of spontaneous noisy breathing was expressed by the polar coordinate x, which is composed of two dimensional variables τ and θ. The biological variability of θ may be determined through the variability in the amplitude of tidal volume VT based on (3.1.3). The Legendre Equation (4.2.5) would describe the temporal and regional distribution of pulmonary ven- tilations, which Venegas et al. recently demonstrated as the images of positron emission tomography (PET) [9]. f biological variability originates at the level of the cell, the biological variability of perfusion in the lung is also expected to have the same motion equation as (4.2.5). In the case of pulmonary perfusion, it is necessary to define the state variable from the stroke volume (SV). If the biological variability in both VT and SV is measured simultaneously, one would be able to describe the venti- lation-perfusion matching in the lung according to (4.2.6). 5.3. Neuroplasticity of the Respiratory Rhythm Generator (RRG) Respiratory rhythm generation arises in neurons that initiate rhythmic inspiratory and expir activity. Several studies suggest that the pre-Bötz plex, a discrete group of pr ventrolateral medulla, plays a critical role in respiration rhythm generation, although this hypothesis is not with- out controversy [10]. Pattern-forming neurons include premotoneurons and motoneurons in the brain stem or spinal cord, where complex activation patterns arise from interactions between their intrinsic properties and synap- tic inputs. Pattern formation establishes the detailed spa- tio-temporal motor output of respiratory muscles, coor- dinating their activation to produce a breath with the ap- propriate characteristics. These coordinated, complex in ractions among groups of neurons in the brain produce an optimal breathing rhythm which is described by P(τ) in (4.3.6). Mitchell and Johnson have stated that a comprehensive conceptual framework of neuroplasticity in the respira- tory control system is lacking [10]. However, the Equa- tion (4.3.6) can provide a comprehensive framework for respiratory rhythm generation since this expression in- cludes an optimal total energy H of the respiratory sys- tem, the topographical distribution parameter λ of re gional ventilation in the lung, and the probability density reat Frey et al. [3] and Fadel et al. [11] demonstrated the fractal properties of PDFs of IBIs in preterm, term babies and a third of adults at rest. When there are fractal prop- erties in PDFs of IBIs as follows , according to (4.3.6) the potential U(τ) of the RRG is expressed by the following, 4 221 2 UH . (5.3.1) This potential of the RRG shows that development of the RRG in infants leads to a change in parameters α and λ, but no change in the structure of the potential function. If a change in the structure of the potential function sig- nals neuroplasticity, the developmental change of the RRG is not a neuroplastic process. 6. Conclusion ave equa- nd ano ned as a complex function including probability density functions of biological v both rhythm and amplitude of spontaneous noisy in Variability in spontaneous breathing is not simply attrib- utable to random noise superimposed on a regular respi- ratory process. Biological variability should originate from energetic fluctuations at the level of the cell, and thus it is acceptable to assume that biological variability is a universal constant amongst all physiological variables. Under this assumption, a stochastic state model for spon- taneous noisy breathing produced Shrödinger’s w tion as the motion equation. Based on the lobule and fractal bronchial tree model of the lung, two wave equa- tions were obtained from the Shrödinger’s equation: one for the respiratory rhythm generator ather for the modulator of airway smooth muscles in the lung. From these equations, the function of the respiratory rhythm generator was defi ariability in breath- g. The stochastic control model analysis in this study can thus provide a new tool applicable for the analysis of any noisy biological processes. Open Access AM  K. MIN Open Access AM 1545 icine, Vol. 163, No. 6, 2001, pp. 1289-1290. g/10.1164/ajrccm.163.6.ed1801a REFERENCES [1] A. L. Goldberger, “Heartbeats, Hormones, and Health: Is Variability the Spice of Life?” American Journal of Res- piratory and Critical Care Med http://dx.doi.or [2] N. S. Cherniack, G. S. Longobardo, O. R. Levine, R. Mellins and A. P. Fishman, “Periodic Breathing in Dogs,” Journal of Applied Physiology, Vol. 21, No. 6, 1966, pp. 1847-1854. [3] U. Frey, M. Silverman, A. L. Barabási and B. Suki, “Ir- regularities and Power Law Distributions in the Breathing Pattern in Preterm and Term Infants,” Journal of Applied Physiology, Vol. 85, No. 3, 1998, pp. 789-797. [4] B. Suki, “Fluctuations and Power Laws in Pulmonary Physiology,” American Journal of Respiratory and Criti- cal Care Medicine, Vol. 166, No. 2, 2002, pp. 133-137. http://dx.doi.org/10.1164/rccm.200202-152PP [5] K. J. Astroem, “Introduction to Stochastic Control The- ory,” Dover Books on Electrical Engineering, New York, 1970. [6] K. Min, K. Hosoi, Y. Kinoshita, S. Hara, H. Degami, T. Takada and T. Nakamura, “Use of Fractal Geometry to Propose a New Mechanism of Airway-Parenchymal In- terdependence,” Open Journal of Molecular and Inte- grated Physiology, Vol. 2, No. 1, 2012, pp. 14-20. http://dx.doi.org/10.4236/ojmip.2012.21003 [7] K. Yasue, “Quantum Mechanics and Optimal Stochastic Control Theory,” Kaimei-shya, Tokyo, 2007 (in Japanese). [8] B. Suki, N. Martinez, H. Parameswaran, A. Majumdar, R. Dellaca, C. Berry, J. J. Pillow and E. Bartolak-S uki, “Vari- Chaos, 2012, p. A2682. ability in the Respiratory System: Possible Origins And Implications,” B29, The Lung on the Border between Or- der and [9] J. G. Venegas, T. Winkler, G. Musch, M. F. Vidal Melo, D. Layfield, N. Tgavalekos, A. J. Fischman, R. J. Calla- han, G. Bellani and R. S. Harris, “Self-Organized Patchi- ness in Asthma as a Prelude to Catastrophic Shifts,” Na- ture, Vol. 434, No. 7034, 2005, pp. 777-782. http://dx.doi.org/10.1038/nature03490 [10] G. S. Mitchell and S. M. Johnson, “Invited Review: Neu- roplasticity in Respiratory Motor Control,” Journal of Applied Physiology, Vol. 94, No. 1, 2003, pp. 358-374. [11] P. J. Fadel, S. M. Barman, S. W. Phillips and G. L. Geb- ber, “Fractal Fluctuations in Human Respiration,” Journal of Applied Physiology, Vol. 97, No. 6, 2004, pp. 2056- 2064. http://dx.doi.org/10.1152/japplphysiol.00657.2004  K. MIN 1546 Appendix 22 d1 ,, ,d d2 v xtu xtUxxtx t 0 . (4.1.1) The first term of (4.1.1) is calculated as follows, 2 2 2 2 2 2 ,, ,, d1 11 ,,dd,, ,d d2 22 ,, 1d ,,,,,d, , 2d vxt xtvxtxt v xtxtxxv xtxtv xtx tttt vxtvxt vxt vxtxtvxtvxtxtxvxtvxt xtx tt x , ,d t (A.1) The second term of (4.1.1) is also transformed as follows, 2 2 2 22 22 2 ,, ,, d1 11 ,,dd,, ,d d2 22 d1d ,,d d d, d, dd d ,,,,, 2d 2dd , uxtxtuxtxt u xtxtxxu xtxtu xtx ttt tvxtxtx x xt vxt x u xtv xtxtxtu xt xxx xt t ,log,,, 2d 2 uxtxtxtux tx 2 22 2 2 2 1d ,,,,d 2d 1d d ,,, ,,,d d, d ,, ,,d d2 d 2 2 2d 2 d tuxtvxtxtx x uxtvxt xtuxtvxt xtx uxt uxtuxtvxtxtx xx xx (A.2) The third term of (4.1.1) is expressed by following, ,d dd ,dd,, d,, d dd xtU x UxxtxUxxUxvxt xtxvxtxtx ttxx d (A.3) By combining (A.1), (A.2) and (A.3), the criterion of optimal control is expressed by the following, 22 2 2 2 d1 ,, ,d d2 ,d,d, d,d ,, d2d d d v xtu xtUxxtx t vxtuxtuxtvxt Ux uxtvxtvxtxtx tx xx x ,,d0 (A.4) The Equation (4.1.2) is obtained as the necessity for the criterion of control (A.4) as follows, 2 2 2 ,d,d,d,d ,0 d d d v xtu xtu xtv xtUx vxt xx x , d2 ux t tx Open Access AM
|