 Applied Mathematics, 2013, 4, 1503-1511 Published Online November 2013 (http://www.scirp.org/journal/am) http://dx.doi.org/10.4236/am.2013.411203 Open Access AM The Sum and Difference of Two Constant Elasticity of Variance Stochastic Variables Chi-Fai Lo Department of Physics, Institute of Theoretical Physics, The Chinese University of Hong Kong, Hong Kong, China Email: cflo@phy.cuhk.edu.hk Received August 20, 2013; revised September 20, 2013; accepted September 27, 2013 Copyright © 2013 Chi-Fai Lo. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT We have applied the Lie-Trotter operator splitting method to model the d ynamics of both the sum and difference of two correlated constant elasticity of variance (CEV) stochastic variables. Within the Lie-Trotter splitting approximation, both the sum and difference are shown to follow a shifted CEV stochastic process, and approximate probability distri- butions are determined in closed form. Illustrative numerical examples are presented to demonstrate the validity and accuracy of these approximate distributions. These approximate probability distributions can be used to valuate two-asset options, e.g. spread options and basket options, where the CEV variables represent the forward prices of the underlying assets. Moreover, we believe that this new approach can be extended to study the algebraic sum of N CEV variables with potential applications in pricing multi-asset options. Keywords: Constant Elasticity of Variance Stochastic Variables; Probability Distribution Functions; Backward Kolmogorov Equation ; Lie-Trotter Splitting Approximation 1. Introduction Recently Lo [1] proposed a new simple approach to ta c k le the long-standing problem: “Given two correlated log- normal stochastic variables, what is the stochastic dy- namics of the sum or difference of the two variables?”; or equivalently, “What is the probability distribution of the sum or difference of two correlated lognormal stochastic variables?” The solution to this problem has wide appli- cations in many fields including financial modelling, act u- arial sciences, telecommunications, biosciences and phys- ics [2-15]. By means of the Lie-Trotter op erator splitting method [16], Lo showed that both the sum and difference of two correlated lognormal stochastic processes could be approximated by a shifted lognormal stochastic proc- ess, and approximate probability distributions were de- termined in closed form. Unlike previous studies which treat the sum and difference in a separate manner [2-5, 8,13,15,17-27], Lo’s method provides a new unified ap- proach to model the dynamics of both the sum and dif- ference of the two stochastic variables. In addition, in terms of the approximate solution s, Lo presented an ana- lytical series expansion of the exact solutions, which can allow us to improve the appro ximation systematically. In this communication we extend Lo’s approach to study the dynamics of both the sum and difference of two correlated constant elasticity of variance (CEV) stochas- tic processes. The CEV process was first proposed by Cox and Ross [28] as an alternative to the lognormal stochastic movements of stock prices in the Black- Scholes model. The CEV process, which is defined by the stochastic differential equation 2 ddfor0SSZ 2 (1) with dZ being a standard Weiner process, has been receiving much attention because it has the ability to give rise to a volatility skew and to explain th e volatility s mile [29-41]. In the limiting case 2 , the CEV model returns to the conventional Black-Scholes model, whilst it is reduced to the Orn stein-Uhlen beck mod el in the case of 0 . By the Lie-Trotter operator splitting method, we show that both the sum and difference of two corre- lated CEV processes can be modelled by a shifted CEV process. Approximate probability distributions of both the sum and difference are determined in closed form, and illustrative numerical examples are presented to demon- strate the validity and accuracy of these approximate dis- tributions.  C.-F. LO 1504 2. Lie-Trotter Operator Splitting Method We consider two CEV stochastic variables 1 and 2, which are described by the stochastic differential equa- tions: S S 2 dd , iii i SSZi 1,2 2 (2) for 0 . Here di denotes a standard Weiner process associated with , and the two Weiner proc- esses are correlated as 12 i S dd d Zt 1 . Without loss of generality, we also assume that 2 . The joint prob- ability distribution function , ,S t 1 2 ,,PSS t1020 0 of the two correlated CEV variables obeys the backward Kol- mogorov equation [42-45] ;S 121020 0 0 ˆ,,; ,,0LPSStSS t t (3) where 22 222 1101210 20 210 20 102 2 220 2 20 1 ˆ2 1, 2 LS SS SS S SS (4) subject to the bound ary condition 121020 0110220 ,,; ,,PSS tSSttSSSS . (5) This joint probability distribution function tells us how probable the two CEV variables assume the values and 2 at time 0, provided that their values at are given by 10 and 20 . Once is found, the probability distribution of the sum or dif- ference, namely 12 , of the two correlated CEV variables can be ob taine d by evaluati ng the integ ra l 1 S 0 t 0 ,t Stt S S SS 1 21020 ,,; ,PS StSS S 1020 0 1 21210 20012 00 ,; ,, dd, ,;,,. PStSS t SSPSStSS tSSS (6) Unfortunately, the joint probability distribution function is not available in closed form, except for the case of 0 . Hence, we must resort to numerical methods, e.g. the finite-difference method or Monte Carlo simulation. Nevertheless, the numerically exact solution does not provide any information about the stochastic dynamics of the sum or difference explicitly. It is observed that the probability distribution of the sum or difference of the two correlated CEV variables, i.e. 1020 0 ,; ,,PStSS t , also satisfies the same back- ward Kolmogorov equation given in Equation (3), but with a different boundary condition [43] 1020 01020 ,; ,,. StS S ttSSS (7) To solve for 1020 0 ,; ,, 000 0 ˆˆˆ,;,,0LLLPStSSt t 0 (8) where 2 2 2 00 0 112 00 2 20 22 00 1 ˆ121 22 1 SS S LSS S SS (9) 2 2 2 00 0 112 00 2 20 22 00 1 ˆ121 22 1 SS S LSS S SS (10) 2 22 00 00 01 200 ˆ22 SS SS LSS (11) 22 12 12 2. (12) The corresponding boundary condition now becomes 000 0 ,; , ,.PStSSttS S (13) Accordingly, the formal solution of Equation (8) is readily given by 000 00 0 ,; , , ˆˆˆ exp . PStSSt tt LL LSS (14) Since the exponential op erator 00 ˆˆˆ exp tt LLL is difficult to evaluate, we apply the Lie-Trotter operator splitting method1 to ap- *Suppose that one needs to exponentiate an operator which can be ˆ C split into two different parts, namely ˆ and ˆ . For simplicity, let us assume that ˆˆˆ CAB , where the exponential operator ˆ exp Cis difficult to evaluate but ˆ exp and ˆ exp are either solvable or easy to deal with. Under such circumstances the exponential operator ˆ exp C , with being a small parameter, can be approximated by the Lie-Trotter splitting formula (Trotter, 1959): 2 ˆˆˆ expexp exp.CABO This can be seen as the approximation to the solution at t of the equation ˆ ˆˆˆ dd Yt ABY by a composition of the exact solutions of the equations ˆ ˆˆ ddYtAY and ˆˆ ddYtBY StS S t , we first rewrite the backward Kolmogorov equation in terms of the new variables as 0102 SSS ˆ at time t . 0 Open Access AM  C.-F. LO 1505 proximate the operator by [16,46-49] 000 ˆˆˆ ˆ exp exp, LT OttLttLL (15) and obtain an approximation to the formal solution 000 ,; , , StSSt , namely 000 00 ,; , , ˆˆ exp LT LT PStSSt OSSttLSS 0 (16) where the relation 00 00 ˆˆ exp tt L LSSSS is util- ized. For 2 00 1SS , which is normally valid unless 10 and 20 are both close to zero, the operators S Sˆ L and can be approximately expressed as ˆ L 2 202 0 1 ˆ2 LS S (17) in terms of the two new variables: 22 12 00 2 SS S 0 (18) 2 00 0 22 12 .SS S (19) Here the parameters and are defined by 2 2 (20) 2 22 112 . 2 (21) Obviously, both and S S are CEV random vari- ables defined by the stochastic differential equations 2 dSSZ d, (22) and their closed-form probability distribution functions are given b y CEV 00 1212222 00 12 22 2 00 22 0 220 ,; , 24 22 2 exp 2 fStSt SS SS I tt tt SS tt (23) for 0, where denotes the modified Bessel function of order tt I . As a result, it can be inferred that within the Lie-Trotter splitting approximation both S and S are governed by a shifted CEV process. It should be noted that for the Lie-Trotter splitting ap- proximation to be valid, needs to be small. 20 tt 3. Illustrative Numerical Examples In Figure 1 we plot the approximate closed-form prob- ability distribution function of the sum of two un- correlated CEV variables ( i.e. S 0 ) given in Equation (23) for different values of the input parameters. We start with 10110S , 20 105S , 10.5 and 20.3 in Figure 1(a). Then, in order to examine the effect of 20, we decrease its value to in Figure 1(b) and to 65 in Figure 1(c). In Figures 1(d)-(f) we repeat the same investigation with a new set of values for 1 S 85 and 2 , namely 10.3 and 20.2 . Without loss of gener- ality, we set 01tt for simplicity. The (numerically) exact results which are obtained by numerical integra- tions are also included for comparison. It is clear that the proposed approximation can provide accurate estimates for the exact values. In order to have a clearer picture of the accuracy, we plot the corresponding errors of the estimation in Figure 2. We can easily see that major discrepancies appear around the peak of the probability distribution function and that the estimation deteriorates as the elasticity pa- rameter increases. It should be noted that the pro- posed approximation is exact in the special case of 0 , i.e. the Ornstein-Uhlenbeck model. We also observed that the errors increase with the ratio 00 SS and 2 (or equivalently, 1 and 2 ) as expected. Next, we apply the same sequence of analysis to the approximate closed-form probability distribution func- tion of the difference S given in Equation (23). Simi- lar observations about the accuracy of the proposed ap- proximation can be made for the difference S , too (see Figures 3 and 4). 4. Conclusion In this communication we have applied a new unified approach proposed by Lo (2012) to model the dynamics of both the sum and difference of two correlated CEV stochastic variables. By the Lie-Trotter operator splitting method, both the sum and difference are shown to follow a shifted CEV stochastic process, and approximate probability distributions are determined in closed form. Illustrative numerical examples are presented to demon- strate the validity and accuracy of these approximate distributions. These approx imate probability distributio ns can be used to valuate two-asset options, e.g. the spread options, where the CEV variables represent the forward prices of the underlying assets. Moreover, we believe that this new approach can be extended to study the Open Access AM  C.-F. LO Open Access AM 1506 (a) (b) (c) (d) (e) (f) Figure 1. Probability density vs. S1 + S2: the dotted lines denote the distributions of the approximate shifted CEV process, and the solid lines show the exact results. (a) S10 = 110, S20 = 105, σ1 = 0.5 and σ2 = 0.3; (b) S10 = 110, S20 = 85, σ1 = 0.5 and σ2 = 0.3; (c) S10 = 110, S20 = 65, σ1 = 0.5 and σ2 = 0.3; (d) S10 = 110, S20 = 105, σ1 = 0.3 and σ2 = 0.2; (e) S10 = 110, S20 = 85, σ1 = 0.3 and σ2 = 0.2; (f) S10 = 110, S20 = 65, σ1 = 0.3 and σ2 = 0.2. 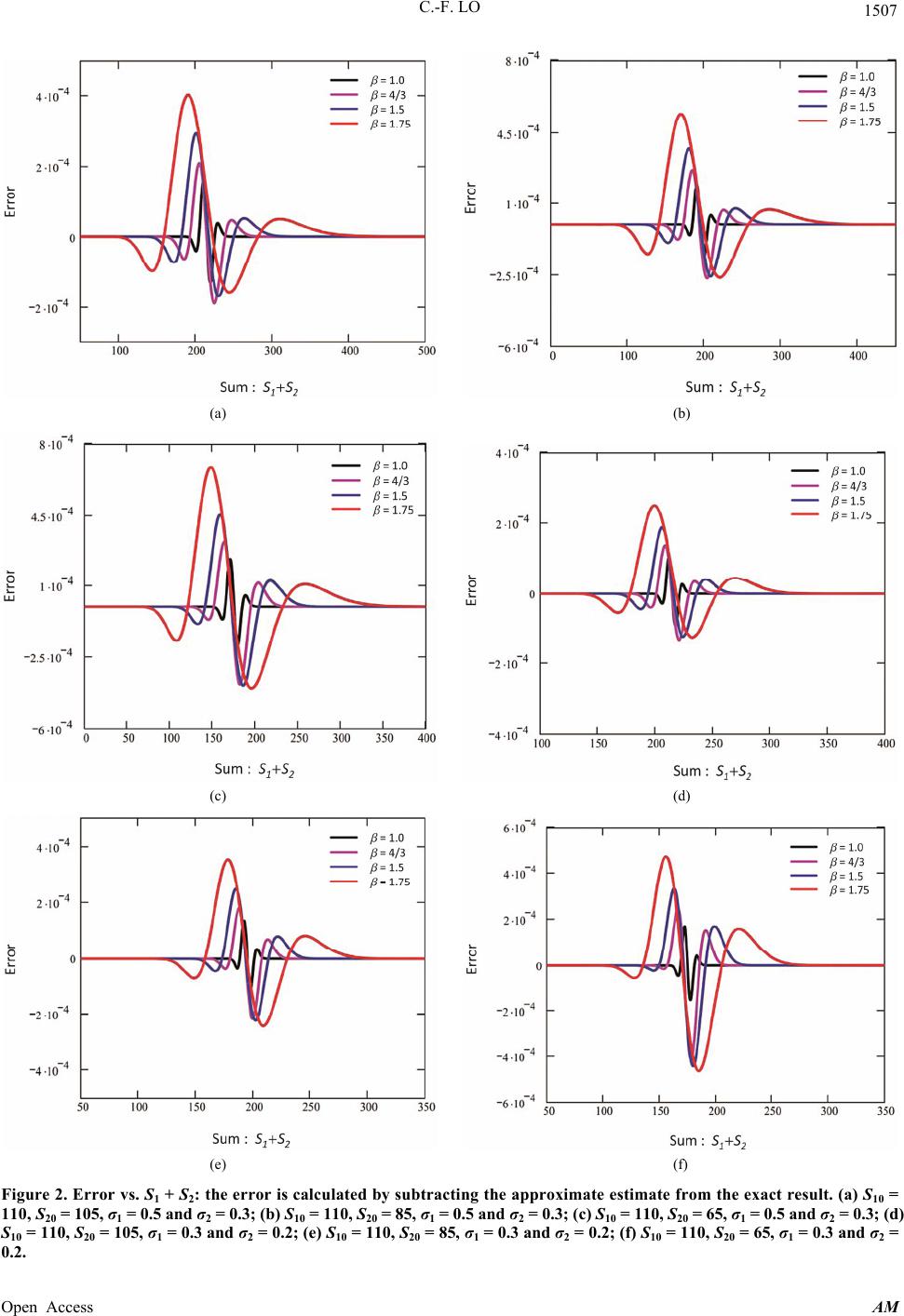 C.-F. LO 1507 (a) (b) (c) (d) (e) (f) Figure 2. Error vs. S1 + S2: the error is calculated by subtracting the approximate estimate from the exact result. (a) S10 = 110, S20 = 105, σ1 = 0.5 and σ2 = 0.3; (b) S10 = 110, S20 = 85, σ1 = 0.5 and σ2 = 0.3; (c) S10 = 110, S20 = 65, σ1 = 0.5 and σ2 = 0.3; (d) S10 = 110, S20 = 105, σ1 = 0.3 and σ2 = 0.2; (e) S10 = 110, S20 = 85, σ1 = 0.3 and σ2 = 0.2; (f) S10 = 110, S20 = 65, σ1 = 0.3 and σ2 = 0.2. Open Access AM 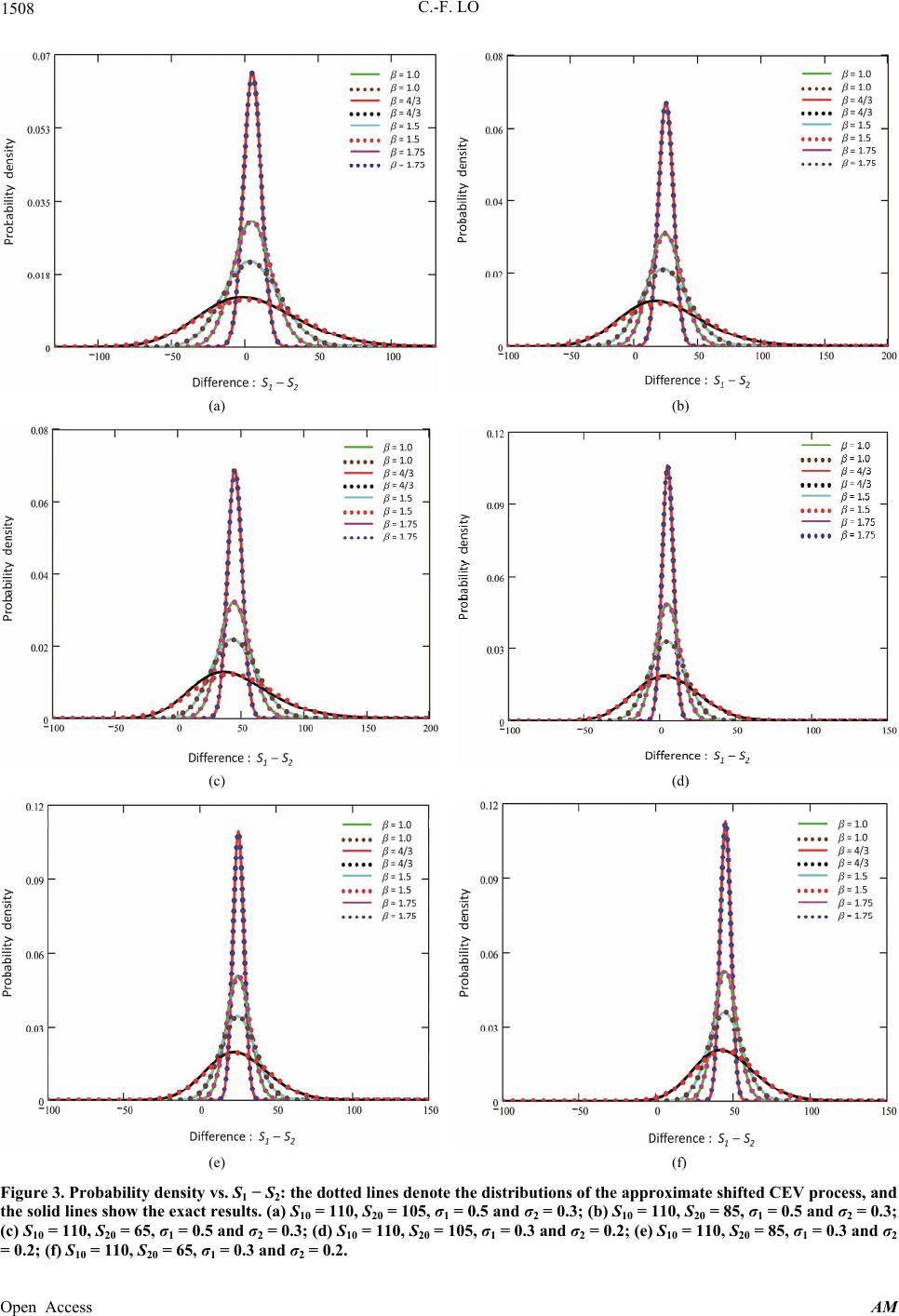 C.-F. LO 1508 (a) (b) (c) (d) (e) (f) Figure 3. Probability density vs. S1 − S2: the dotted lines denote the distributions of the approximate shifted CEV process, and the solid lines show the exact results. (a) S10 = 110, S20 = 105, σ1 = 0.5 and σ2 = 0.3; (b) S10 = 110, S20 = 85, σ1 = 0.5 and σ2 = 0.3; (c) S10 = 110, S20 = 65, σ1 = 0.5 and σ2 = 0.3; (d) S10 = 110, S20 = 105, σ1 = 0.3 and σ2 = 0.2; (e) S10 = 110, S20 = 85, σ1 = 0.3 and σ2 = 0.2; (f) S10 = 110, S20 = 65, σ1 = 0.3 and σ2 = 0.2. Open Access AM 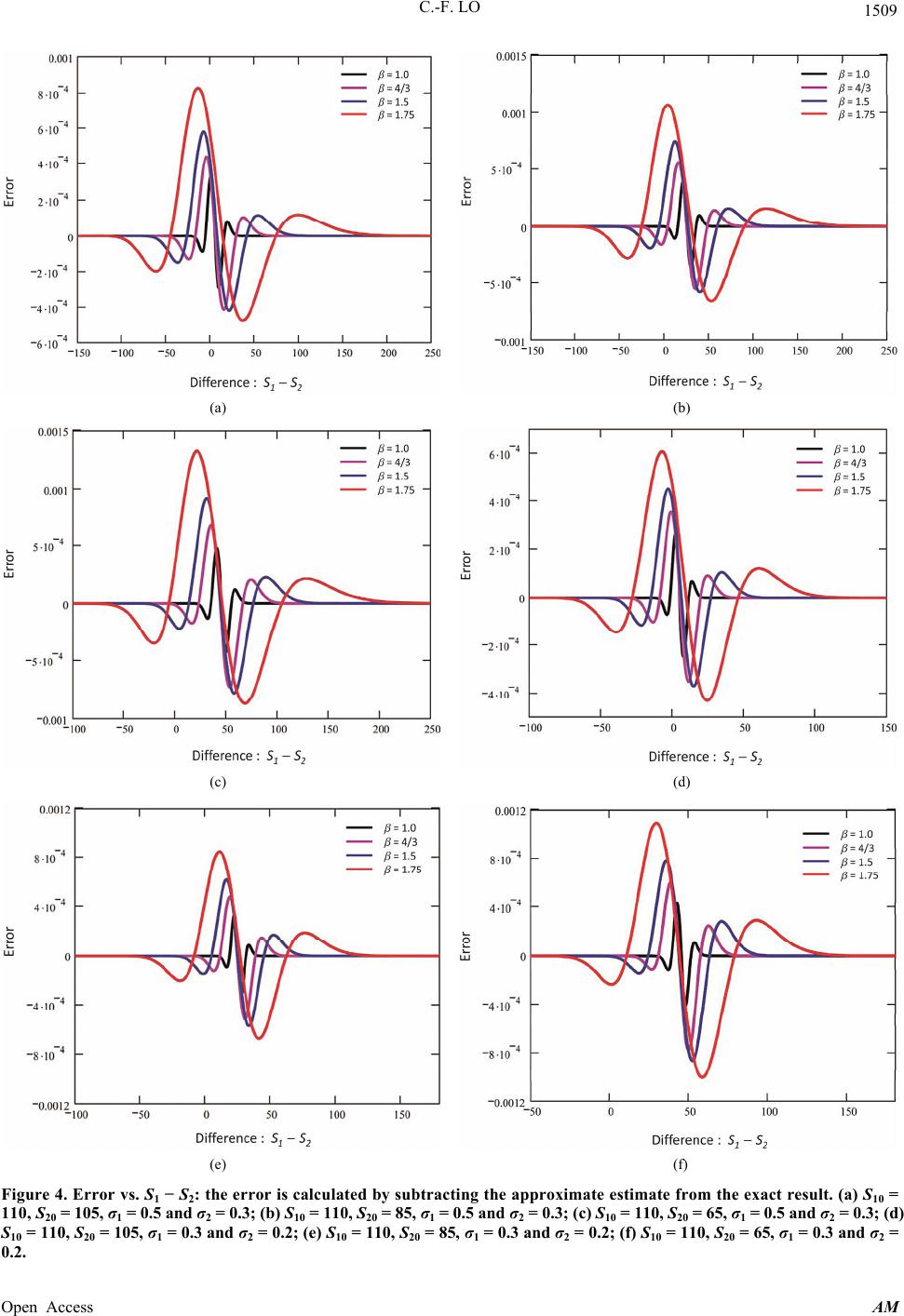 C.-F. LO 1509 (a) (b) (c) (d) (e) (f) Figure 4. Error vs. S1 − S2: the error is calculated by subtracting the approximate estimate from the exact result. (a) S10 = 110, S20 = 105, σ1 = 0.5 and σ2 = 0.3; (b) S10 = 110, S20 = 85, σ1 = 0.5 and σ2 = 0.3; (c) S10 = 110, S20 = 65, σ1 = 0.5 and σ2 = 0.3; (d) S10 = 110, S20 = 105, σ1 = 0.3 and σ2 = 0.2; (e) S10 = 110, S20 = 85, σ1 = 0.3 and σ2 = 0.2; (f) S10 = 110, S20 = 65, σ1 = 0.3 and σ2 = 0.2. Open Access AM  C.-F. LO Open Access AM 1510 algebraic sum of N CEV variables with potential applica- tions in pricing multi-asset options. REFERENCES [1] C. F. Lo, “The Sum and Difference of Two Lognormal Random Variables,” Journal of Applied Mathematics, Vol. 2012, 2012, Article ID: 838397. http://dx.doi.org/10.1155/2012/838397 [2] L. Fenton, “The Sum of Lognormal Probability Distribu- tions in Scatter Transmission Systems,” IRE Transactions on Communications Systems, Vol. 8, No. 1, 1960, pp. 57- 67. http://dx.doi.org/10.1109/TCOM.1960.1097606 [3] J. I. Naus, “The Distribution of the Logarithm of the Sum of Two Lognormal Variates,” Journal of the American Statistical Association, Vol. 64, No. 326, 1969, pp. 655- 659. http://dx.doi.org/10.1080/01621459.1969.10501004 [4] M. A. Hamdan, “The Logarithm of the Sum of Two Cor- related Lognormal Variates,” Journal of the American Statistical Association, Vol. 66, No. 333, 1971, pp. 105- 106. http://dx.doi.org/10.1080/01621459.1971.10482229 [5] C. L. Ho, “Calculating the Mean and Variance of Power Sums with Two Lognormal Components,” IEEE Trans- actions on Vehicular Technology, Vol. 44, No. 4, 1995, pp. 756-762. http://dx.doi.org/10.1109/25.467959 [6] M. A. Milevsky and S. E. Posner, “Asian Options, the Sum of Lognormals, and the Reciprocal Gamma Distri- bution,” Journal of Financial and Quantitative Analysis, Vol. 33, No. 3, 1998, pp. 409-422. http://dx.doi.org/10.2307/2331102 [7] J. Dhaene, M. Denuit, M. J. Goovaerts, R. Kaas and D. Vyncke, “The Concept of Comonotonicity in Actuarial Science and Finance: Applications,” Insurance: Mathe- matics and Economics, Vol. 31, No. 2, 2002, pp. 133-161. http://dx.doi.org/10.1016/S0167-6687(02)00135-X [8] R. Carmona and V. Durrleman, “Pricing and Hedging Spread Options,” SIAM Review, Vol. 45, No. 4, 2003, pp. 627-685. http://dx.doi.org/10.1137/S0036144503424798 [9] J. H. Graham, K. Shimizu, J. M. Emlen, D. C. Freeman and J. Merkel, “Growth Models and the Expected Distri- bution of Fluctuating Asymmetry,” Biological Journal of the Linnean Society, Vol. 80, No. 1, 2003, pp. 57-65. http://dx.doi.org/10.1046/j.1095-8312.2003.00220.x [10] M. Romeo, V. Da Costa and F. Bardon, “Broad Distribu- tion Effects in Sums of Lognormal Random Variables,” European Physical Journal B, Vol. 32, No. 4, 2003, pp. 513-525. http://dx.doi.org/10.1140/epjb/e2003-00131-6 [11] D. Dufresne, “The Log-Normal Approximation in Finan- cial and Other Computations,” Advances in Applied Prob- ability, Vol. 36, No. 3, 2004, pp. 747-773. http://dx.doi.org/10.1239/aap/1093962232 [12] S. Vanduffel, T. Hoedemakers and J. Dhaene, “Compar- ing Approximations for Risk Measures of Sums of Non- Independent Lognormal Random Variables,” North Ame- rican Actuarial Journal, Vol. 9, No. 4, 2005, pp. 71-82. [13] J. Wu, N. B. Mehta and J. Zhang, “Flexible Lognormal Sum Approximation Method,” Proceedings of IEEE Global Telecommunications Conference (GLOBECOM’05), Vol. 6, 2005, pp. 3413-3417. [14] A. Kukush and M. Pupashenko, “Bounds for a Sum of Random Variables under a Mixture of Normals,” Theory of Stochastic Processes, Vol. 13, No. 29, 2007, pp. 82-97. [15] X. Gao, H. Xu and D. Ye, “Asymptotic Behavior of Tail Density for Sum of Correlated Lognormal Variables,” In- ternational Journal of Mathematics and Mathematical Sciences, Vol. 2009, 2009, Article ID: 630857. [16] H. F. Trotter, “On the Product of Semi-Groups of Opera- tors,” Proceedings of the American Mathematical Society, Vol. 10, No. 4, 1959, pp. 545-551. http://dx.doi.org/10.1090/S0002-9939-1959-0108732-6 [17] N. C. Beaulieu and F. Rajwani, “Highly Accurate Simple Closed-Form Approximations to Lognormal Sum Distri- butions and Densities,” IEEE Communications Letters, Vol. 8, No. 12, 2004, pp. 709-711. http://dx.doi.org/10.1109/LCOMM.2004.837657 [18] C. L. J. Lam and T. Le-Ngoc, “Estimation of Typical Sum of Lognormal Random Variables Using Log-Shifted Gamma Approximation,” IEEE Communications Letters, Vol. 10, No. 4, 2006, pp. 234-235. http://dx.doi.org/10.1109/LCOMM.2006.1613731 [19] L. Zhao and J. Ding, “Least Squares Approximations to Lognormal Sum Distributions,” IEEE Transactions on Vehicular Technology, Vol. 56, No. 2, 2007, pp. 991-997. http://dx.doi.org/10.1109/TVT.2007.891467 [20] N. B. Mehta, J. Wu, A. F. Molisch and J. Zhang, “Ap- proximating a Sum of Random Variables with a Log- normal,” IEEE Transactions on Wireless Communica- tions, Vol. 6, No. 7, 2007, pp. 2690-2699. http://dx.doi.org/10.1109/TWC.2007.051000 [21] S. Borovkova, F. J. Permana and H. V. D. Weide, “A Closed Form Approach to the Valuation and Hedging of Basket and Spread Options,” The Journal of Derivatives, Vol. 14, No. 4, 2007, pp. 8-24. http://dx.doi.org/10.3905/jod.2007.686420 [22] D. Dufresne, “Sums of Lognormals,” Actuarial Research Conference Proceedings, Regina, 14-16 August 2008. [23] Q. T. Zhang and S. H. Song, “A Systematic Procedure for Accurately Approxi mating Lognormal- Sum Distri but i on s , ” IEEE Transactions on Vehicular Technology, Vol. 57, No. 1, 2008, pp. 663-666. http://dx.doi.org/10.1109/TVT.2007.905611 [24] T. R. Hurd and Z. Zhou, “A Fourier Transform Method for Spread Option Pricing,” SIAM Journal of Financial Mathematics, Vol. 1, No. 1, 2010, pp. 142-157. http://dx.doi.org/10.1137/090750421 [25] X. Li, V. D. Chakravarthy and Z. Wu, “A Low-Com- plexity Approximation to Lognormal Sum Distributions via Transformed Log Skew Normal Distribution,” IEEE Transactions on Vehicular Technology, Vol. 60, No. 8, 2011, pp. 4040-4045. http://dx.doi.org/10.1109/TVT.2011.2163652 [26] N. C. Beaulieu, “An Extended Limit Theorem for Corre- lated Lognormal Sums,” IEEE Transactions on Commu- nications, Vol. 60, No. 1, 2012, pp. 23-26. http://dx.doi.org/10.1109/TCOMM.2011.091911.110054 [27] J. J. Chang, S. N. Chen and T. P. Wu, “A Note to En-  C.-F. LO 1511 hance the BPW Model for the Pricing of Basket and Spread Options,” The Journal of Derivatives, Vol. 19, No. 3, 2012, pp. 77-82. http://dx.doi.org/10.3905/jod.2012.19.3.077 [28] J. C. Cox and S. A. Ross, “The Valuation of Options for Alternative Stochastic Processes,” Journal of Financial Economics, Vol. 3, No. 1-2, 1976, pp. 145-166. http://dx.doi.org/10.1016/0304-405X(76)90023-4 [29] J. C. Cox, “The Constant Elasticity of Variance Option Pricing Model,” Journal of Portfolio Management, Vol. 23, 1996, pp. 15-17. [30] C. F. Lo, P. H. Yuen and C. H. Hui, “Constant Elasticity of Variance Option Pricing Model with Time-Dependent Parameters,” International Journal of Theoretical and Applied Finance, Vol. 3, No. 4, 2000, pp. 661-674. http://dx.doi.org/10.1142/S0219024900000814 [31] D. Davydov and V. Linetsky, “The Valuation and Hedg- ing of Barrier and Lookback Option under the CEV Proc- ess,” Management Science, Vol. 47, 2001, pp. 949-965. http://dx.doi.org/10.1287/mnsc.47.7.949.9804 [32] J. Detemple and W. D. Tian, “The Valuation of American Options for a Class of Diffusion Processes,” Management Science, Vol. 48, No. 7, 2002, pp. 917-937. http://dx.doi.org/10.1287/mnsc.48.7.917.2815 [33] C. Jones, “The Dynamics of the Stochastic Volatility: Evidence from Underlying and Options Markets,” Jour- nal of Econometrics, Vol. 116, No. 1-2, 2003, pp. 181- 224. http://dx.doi.org/10.1016/S0304-4076(03)00107-6 [34] M. Widdicks, P. W. Duck, A. D. Andricopoulos and D. P. Newton, “The Black-Scholes Equation Revisited: Asymp- totic Expansions and Singular Perturbations,” Mathemati- cal Finance, Vol. 15, No. 2, 2005, pp. 373-391. http://dx.doi.org/10.1111/j.0960-1627.2005.00224.x [35] J. Xiao, H. Zhai and C. Qin, “The Constant Elasticity of Variance (CEV) Model and the Legendre Transform— Dual Solution for Annuity Contracts,” Insurance: Mathe- matics and Economics, Vol. 40, 2007, pp. 302-310. http://dx.doi.org/10.1016/j.insmatheco.2006.04.007 [36] Y. L. Hsu, T. I. Lin and C. F. Lee, “Constant Elasticity of Variance (CEV) Option Pricing Model: Integration and Detailed Derivation,” Mathematics and Computers in Si- mulation, Vol. 79, No. 1, 2008, pp. 60-71. http://dx.doi.org/10.1016/j.matcom.2007.09.012 [37] R. R. Chen, C. F. Lee and H. H. Lee, “Empirical Perfor- mance of the Constant Elasticity Variance Option Pricing Model,” Re view of Pacific Basin Financial Markets and Policies, Vol. 12, No. 2, 2009, pp. 1-41. http://dx.doi.org/10.1142/S0219091509001605 [38] J. Gao, “Optimal Portfolios for DC Pension Plans under a CEV Model,” Insurance: Mathematics and Economics, Vol. 44, No. 3, 2009, pp. 479-490. http://dx.doi.org/10.1016/j.insmatheco.2009.01.005 [39] M. Gu, Y. Yang, S. Li and J. Zhang, “Constant Elasticity of Variance Model for Proportional Reinsurance and In- vestment Strategies,” Insurance: Mathematics and Eco- nomics, Vol. 46, No. 3, 2010, pp. 9-18. [40] X. Lin and Y. Li, “Optimal Reinsurance and Investment for a Jump Diffusion Risk Process under the CEV Model,” North American Actuarial Journal, Vol. 15, No. 3, 2011, pp. 417-431. http://dx.doi.org/10.1080/10920277.2011.10597628 [41] H. Zhao and X. Rong, “Portfolio Selection Problem with Multiple Risky Assets under the Constant Elasticity of Variance Model,” Insurance: Mathematics and Econom- ics, Vol. 50, No. 1, 2012, pp. 179-190. http://dx.doi.org/10.1016/j.insmatheco.2011.10.013 [42] J. E. Ingersoll, “Theory of Financial Decision Making,” Rowman & Littlefield Publishers, Lanham, 1987. [43] D. R. Cox and H. D. Miller, “Theory of Stochastic Proc- esses,” Chapman & Hall/CRC, London, 2001. [44] J. Baz and G. Chacko, “Financial Derivatives: Pricing, Applications and Mathematics,” Cambridge University Press, Cambridge, 2009. [45] G. W. Gardiner, “Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences,” Springer, Berlin, 2004. [46] H. F. Trotter, “Approximation of Semi-Groups of Opera- tors,” Pacific Journal of Mathematic, Vol. 8, No. 4, 1958, pp. 887-919. http://dx.doi.org/10.2140/pjm.1958.8.887 [47] M. Suzuki, “Decomposition Formulas of Exponential Operators and Lie Exponentials with Some Applications to Quantum Mechanics and Statistical Physics,” Journal of Mathematical Physics, Vol. 26, No. 4, 1985, pp. 601- 612. http://dx.doi.org/10.1063/1.526596 [48] A. N. Drozdov and J. J. Brey, “Operator Expansions in Stochastic Dynamics,” Physical Review E, Vol. 57, No. 2, 1998, pp. 1284-1289. http://dx.doi.org/10.1103/PhysRevE.57.1284 [49] N. Hatano and M. Suzuki, “Finding Exponential Product Formulas of Higher Orders,” Lecture Notes in Physics, Vol. 679, 2005, pp. 37-68. Open Access AM
|