 International Journal of Medical Physics, Clinical Engineering and Radiation Oncology, 2013, 2, 147-160 Published Online November 2013 (http://www.scirp.org/journal/ijmpcero) http://dx.doi.org/10.4236/ijmpcero.2013.24020 Open Access IJMPCERO Creation of High Energy/Intensity Bremsstrahlung by a Multi-Target and Focusing of the Scattered Electrons by Small-Angle Backscatter at a Cone Wall and a Magnetic Field—Enhancement of the Outcome of Linear Accelerators in Radiotherapy W. Ulmer1,2 1Department of Radiotherapy, Klinikum München-Pasing, Göttingen, Germany 2MPI of Biophysical Chemistry, Göttingen, Germany Email: waldemar.ulmer@gmx.net Received September 21, 2013; revised October 20, 2013; accepted November 2, 2013 Copyright © 2013 W. Ulmer. This is an open access article distributed under the Creative Commons Attribution License, which per- mits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT The yield of bremsstrahlung (BS) from collisions of fast electrons (energy at least 6 MeV) with a Tungsten target can be significantly improved by exploitation of Tungsten wall scatter in a multi-layered target. A simplified version of a pre- viously developed principle is also able to focus on small angle scattered electrons by a Tungsten wall. It is necessary that the thickness of each Tungsten layer does not exceed 0.04 mm—a thickness of 0.03 mm is suitable for accelerators in medical physics. Further focusing of electrons results from suitable magnetic fields with field strength between 0.5 Tesla and 1.2 Tesla (if the cone with multi-layered targets is rather narrow). Linear accelerators in radiation therapy only need to be focused by wall scatter without further magnetic fields (a standard case: 31 plates with 0.03 mm thick- ness and 1 mm distance between the plates). We considered three cases with importance in medical physics: A very small cone with an additional magnetic field for focusing (the field diameter at 90 cm depth: 6 cm), a medium cone with an optional magnetic field (field diameter at 90 cm depth: 13 cm) and a broad cone without a magnetic field (the field diameter at 90 cm depth: 30 cm). All these cases can be positioned in a carousel. Measurements have been performed in the existing carousel positioned in the plane of the flattening filter and scatter foils for electrons. Keywords: Multitarget; Bremsstrahlung; Wall Scatter; Focusing by Magnetic Field 1. Introduction A principal problem in the creation of BS of linear ac- celerators used in radiotherapy is the lack of efficiency, since only a rather small part of the created BS is avail- able for applications. Even for a 40 × 40 cm2 field (dis- tance of 100 cm from the focus), the BS yield is small and most of it goes lost at the primary collimator and jaws. We have usually to deal in radiotherapeutic applications with much smaller field sizes than 40 × 40 cm2. Thus the effectivity in IMRT and stereotaxy are much smaller. A further source of BS loss is the flattening filter, which is used to homogenize transverse profiles. To circumvent some of the above disadvantages, a linear accelerator using multiple Beryllium targets has been suggested [1], with electron energies of the order of 80 - 100 MeV to yield a spectrum compared to a conventional machine with 4 - 6 MeV and a single Tungsten target. However, this concept has the disadvantage that electrons deceler- ated down to ca. 45 - 50 MeV have to be removed by a magnetic field, since they would produce low BS ener- gies in further Beryllium targets. In this communication, we present experimental re- sults of modified configurations of a multitarget system considered previously [2] consisting of very thin Tung- sten layers, with a thickness << 0.1 mm to create BS in a much more efficient way by the ordinarily used electron energies between 6 and 20 MeV. This way of BS crea- tion exploits two physical effects, which can be used to focus on scattered electrons, namely the wall scatter of high Z materials (Tungsten), a further option, and a suit-  W. ULMER Open Access IJMPCERO 148 able external magnetic field. 2. Material and Methods 2.1. Schematic Representation of BS by a Linear Accelerator The following Figure 1 shows the essential component modules of a linear accelerator. It starts with the imping- ing electron current on the BS target (Tungsten). The foregoing modules of the beamline such as klystron, modulator, acceleration tube, deflection of the electron current by a bending magnet are not of importance here. In the target two competition processes occur, namely BS creation and multiple scatter of electrons by simultaneous production of heat. This multiple scatter and heat production must be re- garded as the reason, that the BS creation does not show any preference direction. The beam line according to Figure 1 indicates that only that part of the BS can be used, which can pass through the opening of the primary collimator. The flattening filter immediately below the vacuum window affects the shape of the beam, which is further controlled by the jaws to obtain the desired field size. However, the flattening filter significantly attenu- ates the intensity of the photon beam, and due to the in- evitable Compton scattering, it also acts as a second source, which affects the shape of the profiles of larger field sizes (e.g. the penumbra). As a resume, we can conclude that the present linear accelerators do not provide a high efficiency, in particu- lar with regard to the novel irradiation techniques such as Stereotaxy, Rapid Arc, and IMRT, where very small field sizes are required and most of the produced BS goes lost by shielding of the accelerator head. Therefore the ques- tion arises, in which way we can significantly improve the yield of BS and reduce the required shielding mate- rial in the accelerator head. Figure 1. Schematic representation of a linear accelerator. 2.2. Qualitative Considerations with Regard to Focusing of Electron Scatter Figures 2 and 3 indicate that by restriction to a single Tungsten target there is no mean to prevent the scatter of electrons within the target material. The thickness of the target of standard linear accelera- tors amounts to ca. 1 mm Tungsten and immediately be- low 1 mm Copper in order to increase the removal of the produced heat from the target. The BS spectrum created in Copper is significantly lower than that of Tungsten; it is most widely absorbed in the flattening filter. Since the multiple scatter and heat production are responsible for the low efficiency and for a lot of necessary shielding of the accelerator head, we consider at first an alternative way to exploit BS by a multi-target. This consists of a configuration of very thin Tungsten layers. There thick- ness should not exceed 0.04 mm. We assumed previously a thickness of 0.01 mm for each plate we need 100 plates to reach an overall thickness of 1 mm with an effective Target (Tungsten, Copper) Bremsstrahlung (BS) Electron current: Gaussian profile Figure 2. Multiple scatter and creation of BS in the target. Figure 3. Small angle backscatter of electrons at a Tungsten wall (reflection) induces focusing of electrons. The backsca- tter is amplified by a cone configuration of the Tungsten wall.  W. ULMER Open Access IJMPCERO 149 depth of 10 cm [2]. This configuration requires a com- pletely new construction of the accelerator head. The present study is based on measurement data is based on measurement data with only a slight modification of the head, since the new target could have been tested by placing in a free position of the carousel. However, with regard to clinical accelerators it is possible to work with a smaller number of plates. Figure 3 qualitatively shows that a tilted wall makes the reflection angle small and therefore the backscatter can be increased. The left-hand side of this figure presents the consequence of this effect, namely a cone configuration of the wall, which embeds 31 Tungsten plates. The heat production in each plate is negligible and no additional removal of heat is needed. Thus we can verify that the configuration below makes the primary collimator itself to a cone target consisting of ca. 100 plates and the created BS shows the preference direction of a cone. This configuration implies two ad- vantages: The total depth of cone is assumed to amount to 100 mm, and the 100 plates with 1 mm distance be- tween the plates can be regarded as a continuum, i.e., a Tungsten density ρt of the multi-target part of the cone can be assumed. Therefore theoretical calculations can be simplified much. Otherwise, we have to perform com- plicated numerical step-by-step calculations (this is only possible with regard to Monte-Carlo calculations). The second advantage refers to the direction of the created BS. If the electron energy is much higher than 0.511 MeV (rest energy of the electrons), then the direction of the created BS approximately agrees with the direction of the impinging electrons. Thus BS with large angles cannot be completely avoided, but significantly reduced to a mi- nimum contribution. In a second order, there exists also a focusing effect of BS at the Tungsten wall due to the small-angle part of the Compton effect. According to Figure 4 we can exploit and, by that, amplify the focusing influence obtained by wall scatter, namely by an additional external magnetic field, which must have the property that a permanent gradient of the field component Br perpendicular to the propagation axis (z-axis) is present. Thus the complete configuration re- presents a similarity to features of an electron micro scope. Electromagnet/Ferromagnet Tungsten plate s Inner boundary of the cone: Tungsten wall z Figure 4. Schematic representation of a multi-layered target with an additional magnetic field for focusing. The influences of the additional magnetic field are the reduction of the reflection angle at the Tungsten wall and the corresponding decrease of the impinging angle of the inner electrons at each Tungsten plate. The additional magnetic field makes sense, if the cone is rather narrow, i.e. the opening angle is small and a very narrow radiation beam with extremely high intensity is required. However, the application of an additional magnetic field for focusing is optional, since many con- ceptual designs of medical accelerators can already be improved by a configuration without external magnetic field (Figure 3). It should be pointed out that in both Figures 3 and 4 we have used a qualitative presentation based on forestalled results of succeeding sections. The new conceptions of designing linear accelerators can be justified by the following synopsis: For electrons with energy >> mc2 (0.511 MeV) the di- rection of the created γ-quanta agrees with the actual di- rection of motion of electrons. This implies for electrons, which suffered large-angle scattering, that the created BS has unfortunately not the preference direction of the in- cident beam. There is additionally a non-negligible amount of energy loss of electrons and heat production as a con- sequence of multiple electron scatter. A multi-layer target is suitable to reduce multiple scat- ter significantly by exploiting focusing effects by the cone wall (high Z material, e.g. Tungsten) and optionally by a proper magnetic field. Thus we have to split the conventional Tungsten target (thickness: usually 1 mm) in, at least, 10 sub-targets whose thickness is of the order 0.1 mm and the distance between the layers should then amount to ca. 1 cm. However, a thickness of 0.012 mm (these layers can be purchased) and a distance of ca. 1 - 2 mm between each appears to be much more convenient. The geometrical configurations of the three cases un- der consideration are: Case 1 (magnetic field necessary) Diameter of the Tungsten plate at entrance: 3 mm, at the end of the cone with z = 3 cm: 5 mm; diameter of the circular field size at z = 90 cm: ca. 6 cm. Case 2 (magnetic field optionally possible) Diameter of the Tungsten plate at entrance: 3 mm, at the end of the cone with z = 3 cm: 7 mm; diameter of the circular field size at z = 90 cm: ca. 12 cm. Case 3 (magnetic field not required) Diameter of the Tungsten plate at entrance: 3 mm, at the end of the cone with z = 3 cm: 13 mm; diameter of the circular field size at z = 90 cm: ca. 30 cm. 2.3. Theoretical Calculations and Monte-Carlo Calculations with GEANT4 Monte-Carlo calculations including new boundary condi- tions (wall scatter by some proper materials, influence by magnetic fields) have been carried out by specific modi-  W. ULMER Open Access IJMPCERO 150 fications of the Monte-Carlo code GEANT4 [3], which have been described in detail in the previous study [2]. Therefore we intend to give here only a brief report on the underlying physical principles in order to provide a qualitative understanding. 2.3.1. Some Physical Toolkits General properties and requirements With respect to both calculation procedures (GEANT4 and analytical calculations) we have to use the relativistic energy-momentum relation: 224 2 Wmc cp (1) The relativistic energy E of a particle (without rest en- ergy) is given by: 222 1Emc mc vc (2) The relativistic energy-momentum relation in the pres- ence of a magnetic field (vector potential A) reads: 2 224 2 Wmcec cpA (3) Equation (3) represents a quantum-mechanical equa- tion, if the transition h i p is carried out. The geometrical configuration is shown in Figure 5. On the left-hand side: Small circle of the cone entrance (radius r0) for impinging electron beam. Right-hand side: Larger circle at the cone exit (radius rf). The inner circle symbolizes the area of the entrance. The angle θ shows the opening angle of the cone, which is usually small in those cases, where a strong magnetic field is required. This will be verified in the result section. The components of the magnetic induction B with div·B = 0 are given by: 222 xy z yzx zx y rxy BAzAy BAxAz BAyAx BBB (4) The field strength has to satisfy, at least, the following properties: 22 22 00 0 22 0 0 tan tan rff f Bzr BrzLBBrr rr zxy rrL (5) For the reason of symmetry the following condition r 0 r f Figure 5. Schematic representation of the geometrical pro- perties of the multilayer target. has to be valid: y BB (6) In the above equation Br(z) means the radial compo- nent as a function of z, r0 is the field radius at the en- trance of the beam (z = 0), and rf the related radius at the end (z = L). The possible devolution of some cases of interest is shown in Figure 6. However, the properties of this figure do not represent a rigid scheme, since it mainly depends on the design of the target, whether other lengths L of the cone (central axis) are required. We want also point out that the magnetic field does not disappear at z = L. This length has only to agree with the focusing part of the magnetic field, whereas a small area with a defocusing part cannot be avoided. It may serve to re- move those electrons with sufficiently low energy, where the production of BS is no longer desired. 2.3.2. Fermi-Eyges Theory, Multiple Scatter Theory of Molière and Inclusion of Magnetic Fields Fick’s law of diffusion plays a key role in a lot of physi- cal/chemical/physiological processes; it is also used for the description of scatter and absorption of electrons, protons or neutrons in a medium such as Tungsten and is referred to as Fermi-Eyges age equation [4]. A more ac- curate theory of scatter has been given by Molière [5]. 0 t D (7) with respect to Fick’s law D is the diffusion coefficient, ρ the particle (electron) density (concentration) and Δ the Laplace operator. In the case of the Fermi-Eyges theory, the particle density ρ has to be replaced by an energy- distribution E, which reads: 0 F t EDE (8) Since both equations formally agree, we now intro- duce the amplitude U in order to be independent of the actual meaning. The same fact is also valid with regard to the constant factor D, which may either be identified with a diffusion constant D or with a parameter DF in Fermi-Eyges theory. Equations (7) and (8) follow from the property that a gradient of the density is connected with a current:  W. ULMER Open Access IJMPCERO 151 0 0.2 0.4 0.6 0.8 1 1.2 00.511.522.53 BrinTesla distancezfromentrenceincm case1:narrowbeam case2:mediumbeam(optional) 3 cm 6 cm Ferromagnet + internal Solenoid cooling via air flow Ferromagnet + internal Solenoid (cooling via air flow) (a) Ferromagnet Solenoid (b) Figure 6. Increase of the radial component Br along the surface of the cone. M1 = case 1: B0 = 0.4 Tesla, Bf = 1.2 Tesla; case 2: B0 = 0.2 Tesla, Bf = 0.6 Tesla. (a) Schematic representation of the considered configuration; (b) Section of the magnet with rotational symmetry. jDU (9) In addition, a balance equation has also to hold: 0 t Udivj div jvU (10) The term v represents the scalar product of the 3D differential operator with a 3D velocity v. If the par- ticles have the charge q (for electrons: q = e) and a mag- netic field, described by the vector potential A, is present, then an additional momentum/velocity due to the mag- netic field (Lorentz force) has to be accounted for: 0 e pA c e vpmA cm divA A (11) The velocity v results from the division of the mo- mentum p by the particle mass M (= electron mass m) and c is the velocity of light. Now Equations (9) and (10) read: 0 t e jDAU Udivj mc (12) 0 t e UDUA U mc (12a) The last Equation (12a) can also be written in the form: div 0 t UDU vU (13) If we replace U by a probability distribution P, then Equation (13) turns out to be the Kolmogorov forward equation, and we regard v as an effect of a magnetic field. However, Equations (12) and (13) are not yet fully gauge invariant, since we have only modified the diffusion cur- rent j by the magnetic interaction. The magnetic effect is not yet included in the balance equation. In order to com- plete this condition. We have to write: 0 t ee UADAU mcD mc (14) 22 22 2 0 t e UDUA U mc eA Dmc U (14a) Besides gauge invariance a further reason for obtain- ing Equation (14) is the transition to the Schrödinger equation with magnetic field, since the simple Fick’s law of diffusion can be transformed to a Schrödinger equa- tion without external fields. Equation (14) provides a cor- respondence in the presence of an external magnetic field. It should be noted that the Kolmogorov forward equation is contained as in the special case of Equation (26) by setting A2 = 0. According to the Fermi-Eyges/diffusion theory we can always put: 22 2or 2 t DD (15) The parameter can replace the arbitrary time vari- able t, if scatter/diffusion only occurs in a short time in- terval. We consider the case, where the z-component B =  W. ULMER Open Access IJMPCERO 152 Bz = B0 of a constant magnetic field is responsible for the motion of electrons and pass to the general case thereaf- ter. Since the magnetic field strength B0 is given by rotBAxA, we can choose A as follows: 0 2222 0 2, 2 4 xy yx zy x AB AB BAxAyB ABxy (16) By that, Equation (14) becomes (U = E): 22222 2 0 1 4 . FF EtD EeBmcDxyE eB cmyxxyEE (17) Since in z-direction motion without magnetic interac- tion is allowed, the following separation of the above equation is possible: 2 1 , ,expexpexp. F ExyttikzkDt (18) This provides the following equation: 2222 0 2222 041 F FF yDyxxy DxyD t (19) The following parameters are given by: 00 eB mc (20) 1 (20a) It has to be pointed out that the Larmor frequency ω0 according to Equation (20) is identical with those ob- tained by a Schrödinger or Dirac equation with an exter- nal magnetic field. The basis solution (generating func- tion) from which we can construct all other solutions (see e.g. comparison with Schrödinger equation) is gi- ven by: 22 ,,exp2 exp yta xyt (21) 0 i (22) 222 00 42 F aDaiD (22a) The parameters a and λ' represent complex values; however, we can form a linear combination to get the real solution: Before we shall consider this property, we note that with respect to the z-coordinate a set of solu- tions of the diffusion equation are permitted [2]. They result from the Fourier transform of the specified z-de- pendent function: 2 2 01 2 1 ,expexpd 2F n n ztA kikzk D tk Akaak akak (23) Every power of k of the expansion of A(k) represents a solution, if the integral is carried out. We therefore de- note: 2 ,,exp4 nn F ztPztzDt (24) The polynomials Pn(z, t) have been previously defined by evaluation of the above integral (23): 0 0 2 0 1 ,expexpd2 2 k k ztikzDkt kk (25) The boundary parameter k0 is given by k0 = 1/z0. The evaluation of the integral (18) provides Equation (26): 2 12 ,exp4erferf F ztU tzDtss (26) The parameters of this equation are given by: 0 10 20 42 12 12 F FF FF Ut zDt zizDt Dt zizDt Dt (26a) With the help of Equation (26) we consider the solu- tion: 1 22 00 0 22 10 0 ,,,,exp cos 4 sin4F Exyzt ztt AxyDt xy Dt (27) The sine and cosine function appears by forming linear combinations of solutions of Equation (21), since a ac- cording to Equation (23) is an imaginary parameter and the theorem for complex exponential functions can be applied. It has to be mentioned that the cosine as well as the sine are solutions, and both may form linear combi- nations according to Equation (26). We should account for that the function in Equation (18) has not to be restricted to the simple sine and cosine, but we can also use the general solution manifold according to Equations (26) and (27). Before we shall study some properties of Equation (27), a comparison with the Schrödinger equa- tion is indicated. Before we shall study some properties of Equation (27), a comparison with the Schrödinger equation is in- dicated: 22it m (28) This equation assumes the character of an irreversible transport equation, if the substitution ti is carried out. By that, the diffusion constant is given in terms of the Planck’s constant: 2. F Dm However, the solution (27) is not the only possible one, and we are able to obtain a spectrum of solutions and their linear combinations. The complete solution spec- trum is given by the two different types.  W. ULMER Open Access IJMPCERO 153 Powers of even order: 222 222 22222 22 0 20 cos 4sin4 21,1,2,3 nmm nmnFnm nFn m n Dxy tBDxy t nn n (29) Powers of odd order: 21 2221 22 212 12121212121 0 21 0 cos 4sin4 210,0,1, 2,3 nmm nmnFn mnFn m n Dxy tBDxy t nnn (30) Please note that superpositions of different order and related eigen-frequencies are also possible solutions. Thus we can perform a linear combination of all solu- tions, e.g. a fast oscillating solution with a slow oscillat- ing solution can be combined to form beat oscillations. At first, we look at the connection between diffusion and the quantum mechanical Schrödinger equation with ex- ternal magnetic fields. The following aspects should be emphasized: The resonance conditions for ω0 are in both cases identical, this appears to be rather noteworthy. In a formal sense, we have only to substitute the real time t by an imaginary time it , and the reversibility of the Schrödinger equation goes lost. This behavior is also known from the path integral formulation according to Feynman et al. [6], which represents a further possible way to solve the complicated task of scatter and the role of magnetic fields by perturbation theory. With respect to the eigen-frequency 0 and its de- pendence on the related parameters e, m and B we are able to make the following statements: The z-part of the solution has also the character of an oscillator due to the complex argument yielding nodes (see e.g. the book of Abramowitz and Stegun 1970). Only for sufficient large time t a homogeneous charge distribution will be reached. The x-y-part does not allow broadening by diffusion. The behavior is compara- ble to that of a magnetic lense. Let us now consider an example of a magnetic bifurcation. Assume an oscillating propagation in the x-y plane with the highest frequency 0 given by the magnetic field strength B0. Thus a sud- den change of the magnetic field strength from +B0 to 00 0 BBB leads to a magnetic bifurcation, and, in particular, the antisymmetric sine functions change the sign, when the argument becomes negative. Such an ef- fect may be induced by an inhomogeneous magnetic field yielding changes of the field strength (amount and orientation). The symmetry is spontaneously broken. The same fact may also happen under a lot of similar external influences: The change of the homogeneity of the mag- netic field yields a change of the diffusion constant DF; a change of the energy distribution E may require the for- mation of complete different patterns and oscillation fre- quencies, etc. A principal result of the Bethe-Heitler theory is that the energy loss due to creation of BS is proportional to the actual electron energy. The differential equation for the radiation loss reads (in one dimension): 1 dd brert bre EzXE (31) A theory of the creation of “BS” can be formulated via propagator method [6]. The above mentioned phenome- nological description summarizes all these parameters resulting from the quantum theoretical treatment by the radiation length Xrl according to Equation (31). By iteration of Equation (31) we obtain a second order differential equation, and the extension to 3D can readily carried out, i.e. the Laplace operator Δ appears. This ex- tension has the advantage that the resulting equation can be added to further phenomenological equations con- taining the Laplace operator: 1 brert bre EXE (32) A further advantage results from the previous Figure 3: If the amount of Tungsten sublayers is high, and, by that, the distance between them is small (e.g. 1 mm in the cone target), it is possible to solve equation (32) under continuum conditions. The total Tungsten mass can be divided by the cone volume to obtain the medium density ρt. Step-by-step calculations (we do not report them here) showed that for 1 mm distances between the plates and identical overall mass a continuum approximation can be justified. In a phenomenological theory, we can summa- rize the complete problem by including both, energy loss by radiation loss (Bethe-Heitler theory) and energy dis- sipation (Fermi-Eyges theory): 22 2222 2 Fbrecolrlbrecolcol Et DEemcEeDmcEEEXEXE AA (33)  W. ULMER Open Access IJMPCERO 154 In Equation (33) the parameter Xrl is referred to as the radiation length, which is proportional to Z2, NA and AN, whereas Xcol refers to the energy absorption by the cone wall (collimator), which is proportional to Z, NA and AN. The nuclear charge is denoted by Z, the nuclear mass number by AN, and NA is the Avogadro number. The in- fluence of the magnetic field can be accounted by the following solution expansion: 2 22 2 0 2 21 2121 00 ,cos4 cos 4 Larmor frequency N nnF n n nnFn n ExyAD r BDr neBmcne BB (34) B' refers to as a correction of B0 by ΔB0, since the magnetic induction must not be constant in the volume under consideration. In principle, we have to account for N → ∞, which is impossible in numerical calculations. There are two possible procedures, which we have worked out: Solution of the scatter problem by a proper magnetic field acting between the subtargets and determination of the corresponding phase space for Monte-Carlo calcula- tions (GEANT4) with respect to collision interaction (Be- the-Bloch) and BS (Bethe-Heitler theory, see e.g. [6]). Complete solution of the above differential equation containing all 3 components using the tools given by deconvolution and inclusion of magnetic fields. In such a situation we have to put: Ebre = Ecol = E. The mathematical problem of scatter removal by de- convolution operators has been presented [7-9]; the ap- plication with inclusion of magnetic fields for scatter re- moval has been analyzed previously [2]. 2.3.3. M onte-Carlo C al c ulations w i th GEANT4 GEANT4 [3] represents an open system of a Monte- Carlo code. Significant features with regard to our prob- lem are creation of BS, multiple scatter according to Mo- lière, heat production (Bethe-Bloch equation), energy straggling (Gaussian-Landau-Vavilov), Compton scatter of γ-radiation, and the actual energy/momentum of the electron after interactions leading to energy loss and change of the momentum. More sophisticated applica- tions with regard to the focusing of a multi-layered Tung- sten target and back scatter of the cone walls (Tungsten, Tantalum, Lead) under boundary conditions require the explicit use of the differential cross-section formula q(θ) with the form-factor function F(θ). A further feature is the implementation of the magnetic field B (i.e. vector potential A) to account for the Lorentz force along the track of the electrons according to Equation (3). In order to obtain a reliable statistical foundation, each Monte- Carlo run has been performed with 500×106 histories. Figure 7 presents the back scatter properties (wall re- flectance) of 9 MeV electrons at a high Z wall (W, Ta, Pb); the corresponding properties of 6, 18 or 20 MeV are rather similar. Since the Figures 7 and 8 have methodical character, we should like to show them already in this section. In particular, Figure 7 has a fundamental meaning in this study, namely angle-dependence of the reflectance (back scatter) of fast electrons at wall consisting of high Z ma- terial (Tungsten, Tantalum, and Lead). Although Pb shows the high Z value, the density is much smaller than that of W or Ta, and therefore according to Figure 7 we prefer Tungsten as the wall material for focusing. In par- ticular, Figure 7 represents the essential properties used in Figure 3. Figure 8 shows the scatter behavior of fast electrons in air. In contrast to γ-radiation the scatter of electrons in air is not negligible. The initial condition in all 3 figures is an infinitesimally thin pencil ray of electrons. A conse- quence of these figures is that the multi-target has to be located in a vacuum in order to keep the lateral scatter Figure 7. Backscatter (reflection) of fast electrons in depen- dence of the impinging angle θ. Figure 8. Comparison of air scatter: 6 MeV and 20 MeV electrons.  W. ULMER Open Access IJMPCERO 155 of electrons as small as possible. We should also point out that cross-section formulas used in the theoretical part of the foregoing publication [2] would lead to a wrong behavior of reflection of elec- trons (e.g. for angles smaller than 20˚), if the form factor function F(θ) would have been omitted, since q(θ) would then be highly diverging. On the other side, it is our par- ticular interest to exploit small angle back scatter at the Tungsten wall. At this place it should also be mentioned that a smaller focusing effect in the multilayer cone is obtained by the Compton scatter of the γ-radiation, if the γ-quanta are scattered inside the cone. However, the fo- cusing of fast electrons is much more significant. Since the focusing via wall scatter works best with Tungsten, we do, in general, not present calculations with other material such as Tantalum or Lead. The only exception with a Ta/Pb combination of the cone wall is restricted to one case in order to verify the preference of a Tungsten wall. In all figures of the section results we have adjusted the impinging electron beam to real conditions: The ra- dial distribution at target surface is assumed to be a Gaussian with σ = 1 mm: 22 0exp 2Ir Ir (35) 2.3.4. Remarks to the Measuremen t Configuration The measurements have been carried out at a Varian Clinac, which has been subjected to demounting at the hospitals ‘Rhön-Klinikum’ in Frankfurt/München-Pasing, Germany. A free place in the carousel served as the source for positioning and testing the multi-target. The preparation of the Tungsten plates and wall with/without surrounding magnet has been handled in the machine shop Feuchter (Backnang, Germany) equipped with high technology facilities necessary for preparing of the mea- surements. The expenses have been paid by the author without any further support. 3. Results The succeeding Figure 9 serves as a reference standard for all other figures; this figure has been taken from the previous study [2] and serves as a comparison standard. The BS production according to Figure 1 (blue curve, standard target) is scored along the plane immediately below the Tungsten target. The height at the central axis (x = y = 0) is normalized to “1”, and the whole behavior of the intensity distribution shows all disadvantages of the conventional target, since it decreases slowly, and even at a radius of 7 cm a noteworthy intensity has been scored. Thus the domain with r > 1 cm results from mul- tiple electron scatter in the target with no benefit for any application and requires a lot of shielding material. The behavior in the domain r < 1 cm gives raise to study a multitarget cone with a radius of 1 cm at the end of the Figure 9. Comparison between standard target (Figure 1) and multi-layer target, electron energy E = 6 MeV. cone. The cone consists of 20 layers (distance 5 mm per layer), total depth: 10 cm, the thickness of the wall amounts to 0.02 mm Tantalum (inside) and 10 mm Lead (outside) in contrast to all other cases, where 2 mm Tung- sten have been used. It should be pointed out that the application of E = 18 MeV electron energy instead of E = 6 MeV leads to rather similar properties as shown in Figure 9. Therefore we do not report them. With regard to all forthcoming Figures we use standard conditions of the cone wall, which consists of 2 mm Tungsten (with and without ex- ternal magnetic field). It should be noted that in all re- sults we had to assume air between the plates, the cones were not positioned in vacuum. Now we want to turn the interest to the three cases ac- cording to Section 2. We should add that for comparison we have also considered the case, where the Tungsten wall has been replaced by Lucite. Figure 10 presents the difference in the energy spectrum between one single target (standard case) and the multi-target (case 1 with 1.2 T according to Figure 11). The shift to a higher en- ergy spectrum in the non-standard case is obvious. Fig- ures 11-13 show calculated results immediately below the exit of the photon beam at the cone end, where meas- urements were impossible. Figures 11-13 clearly show the role of wall reflec- tance of scattered electrons, if we consider Tungsten in- stead of Lucite, i.e. the focusing effect of Tungsten (high Z material) is significantly improved. Figures 14-16 present the situation at a distance of 90 cm from the end of the cone (calculations and measure- ments). The normalization of the fluence has been taken such that the maximum case according to Figure 14 is “1”, which is also valid with regard to the following Figures 17-19 related to measurement data. The rather small opening and the focusation by the magnetic fields can obviously compensate the (small) asymmetry of the incoming electron beam, which ap- pears to be a consequence of the measurement condi- tions. With regard to the larger field sizes the compa- rison between measurement and calculation appears to  W. ULMER Open Access IJMPCERO 156 Figure 10. Relative energy fluence spectrum of the BS of 6 MeV electrons: The standard target refers to the condition presented in [7], i.e. below the flattening filter. In contrast to this condition the multi-target spectrum is scored at the end of the cone. The flattening filter is superfluous. 0 10 20 30 40 50 60 70 ‐1.2 ‐0.8 ‐0.400.4 0.8 1.2 Fluence Radial distancerincm case1:Lucitewall case1:Tun g s ten wall case1:Tun g s ten wall+0.6T case1:Tun g s ten wall+1.2T Figure 11. Fluence distribution at the end plate of the cone. The cone diameter at this position amounts to 0.5 cm. 0 5 10 15 20 25 ‐2‐1.5 ‐1‐0.50 0.5 1 1.5 2 Fluence Radialdistancerincm case2:Lucitewall case2:Tungs te nwal l case2:Tungs te nwal l + 0.6T Figure 12. The diameter of the cone at the end plate now amounts to 0.7 cm, the case with the magnetic field strength 1.2 T has been omitted, since it is not necessary for in- creased field sizes. 0 1 2 3 4 5 6 ‐2‐1.5 ‐1‐0.500.511.52 Fluence Radialdistancerincm case3:Lucitewall case3:Tung st en wal l Figure 13. The diameter of the cone at the end plate now amounts to 1.3 cm (magnetic fields have been omitted). 0 0.25 0.5 0.75 1 ‐40 4 Re lati ve fluence Radial distancerincm Lucite Tung s ten0TTungs te n 0.6TTu n g s ten 1.2T Figure 14. Case 1 at z = 90 cm (diameter: 6 cm). 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 ‐9‐6‐30 3 6 9 Re lat i vefluence Radialdistancerincm Tun gs te n 0.6T Lucite Tun gs te n Figure 15. Case 2 at z = 90 cm (diameter: 12 cm). 0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02 ‐20 ‐15 ‐10 ‐5 05 101520 Re lativefluence Radialdistancerincm Lucite Tung s ten 0T Figure 16. Case 3 at z = 90 cm (diameter: 30 cm). Figure 17. Measurement data for the case 1 with 6 cm di- ameter. be more important (Figures 18 and 19). In particular, the last case shows best the asymmetry in measurements. However, in spit of this fact the agree- ment between theory noteworthy. 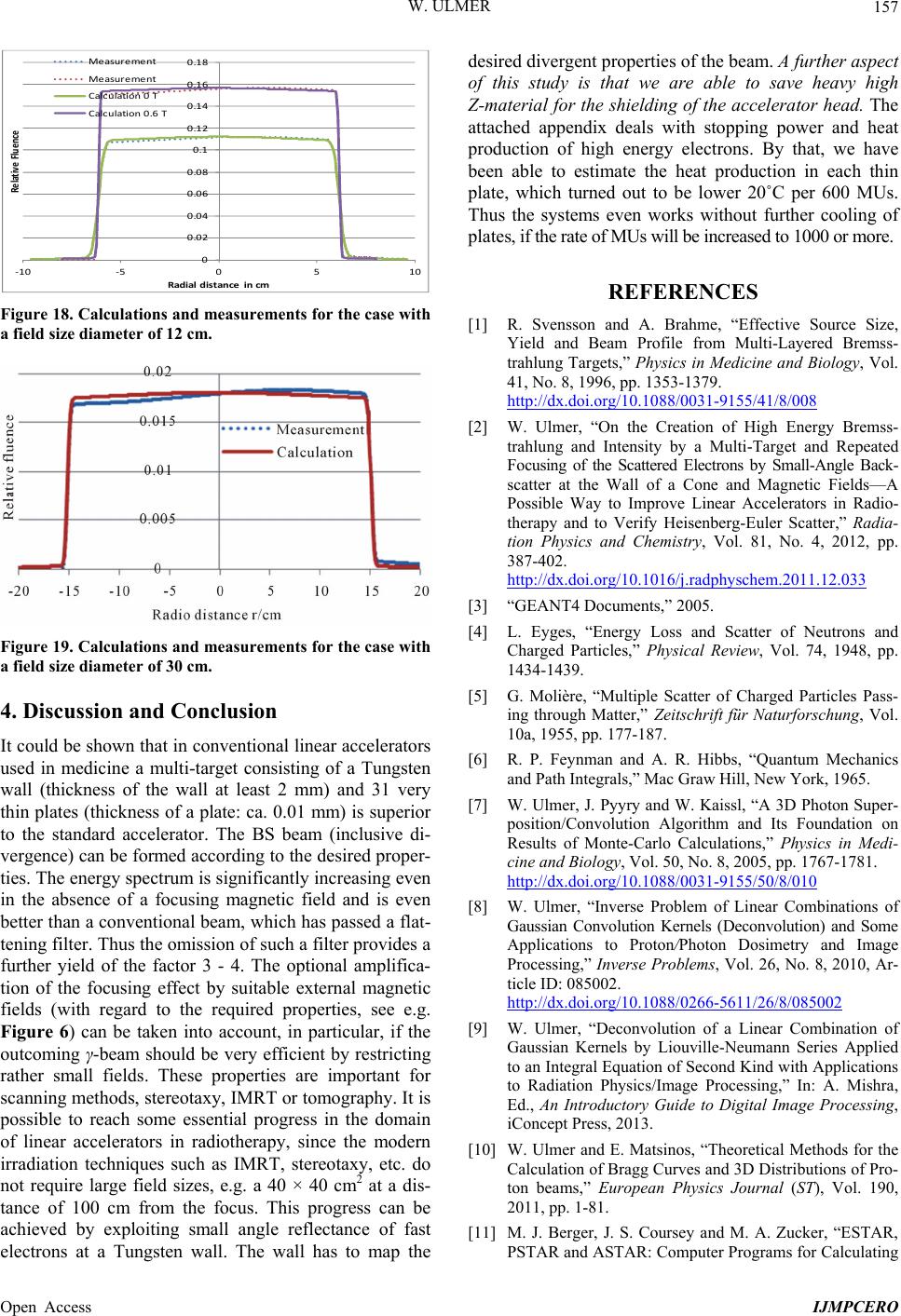 W. ULMER Open Access IJMPCERO 157 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 ‐10 ‐50 510 RelativeFluence Radial distanceincm Measurement Measurement Calculation0T Calculation0.6T Figure 18. Calculations and measurements for the case with a field size diameter of 12 cm. Figure 19. Calculations and measurements for the case with a field size diameter of 30 cm. 4. Discussion and Conclusion It could be shown that in conventional linear accelerators used in medicine a multi-target consisting of a Tungsten wall (thickness of the wall at least 2 mm) and 31 very thin plates (thickness of a plate: ca. 0.01 mm) is superior to the standard accelerator. The BS beam (inclusive di- vergence) can be formed according to the desired proper- ties. The energy spectrum is significantly increasing even in the absence of a focusing magnetic field and is even better than a conventional beam, which has passed a flat- tening filter. Thus the omission of such a filter provides a further yield of the factor 3 - 4. The optional amplifica- tion of the focusing effect by suitable external magnetic fields (with regard to the required properties, see e.g. Figure 6) can be taken into account, in particular, if the outcoming γ-beam should be very efficient by restricting rather small fields. These properties are important for scanning methods, stereotaxy, IMRT or tomography. It is possible to reach some essential progress in the domain of linear accelerators in radiotherapy, since the modern irradiation techniques such as IMRT, stereotaxy, etc. do not require large field sizes, e.g. a 40 × 40 cm2 at a dis- tance of 100 cm from the focus. This progress can be achieved by exploiting small angle reflectance of fast electrons at a Tungsten wall. The wall has to map the desired divergent properties of the beam. A further aspect of this study is that we are able to save heavy high Z-material for the shielding of the accelerator head. The attached appendix deals with stopping power and heat production of high energy electrons. By that, we have been able to estimate the heat production in each thin plate, which turned out to be lower 20˚C per 600 MUs. Thus the systems even works without further cooling of plates, if the rate of MUs will be increased to 1000 or more. REFERENCES [1] R. Svensson and A. Brahme, “Effective Source Size, Yield and Beam Profile from Multi-Layered Bremss- trahlung Targets,” Physics in Medicine and Biology, Vol. 41, No. 8, 1996, pp. 1353-1379. http://dx.doi.org/10.1088/0031-9155/41/8/008 [2] W. Ulmer, “On the Creation of High Energy Bremss- trahlung and Intensity by a Multi-Target and Repeated Focusing of the Scattered Electrons by Small-Angle Back- scatter at the Wall of a Cone and Magnetic Fields—A Possible Way to Improve Linear Accelerators in Radio- therapy and to Verify Heisenberg-Euler Scatter,” Radia- tion Physics and Chemistry, Vol. 81, No. 4, 2012, pp. 387-402. http://dx.doi.org/10.1016/j.radphyschem.2011.12.033 [3] “GEANT4 Documents,” 2005. [4] L. Eyges, “Energy Loss and Scatter of Neutrons and Charged Particles,” Physical Review, Vol. 74, 1948, pp. 1434-1439. [5] G. Molière, “Multiple Scatter of Charged Particles Pass- ing through Matter,” Zeitschrift für Naturforschung, Vol. 10a, 1955, pp. 177-187. [6] R. P. Feynman and A. R. Hibbs, “Quantum Mechanics and Path Integrals,” Mac Graw Hill, New York, 1965. [7] W. Ulmer, J. Pyyry and W. Kaissl, “A 3D Photon Super- position/Convolution Algorithm and Its Foundation on Results of Monte-Carlo Calculations,” Physics in Medi- cine and Biology, Vol. 50, No. 8, 2005, pp. 1767-1781. http://dx.doi.org/10.1088/0031-9155/50/8/010 [8] W. Ulmer, “Inverse Problem of Linear Combinations of Gaussian Convolution Kernels (Deconvolution) and Some Applications to Proton/Photon Dosimetry and Image Processing,” Inverse Problems, Vol. 26, No. 8, 2010, Ar- ticle ID: 085002. http://dx.doi.org/10.1088/0266-5611/26/8/085002 [9] W. Ulmer, “Deconvolution of a Linear Combination of Gaussian Kernels by Liouville-Neumann Series Applied to an Integral Equation of Second Kind with Applications to Radiation Physics/Image Processing,” In: A. Mishra, Ed., An Introductory Guide to Digital Image Processing, iConcept Press, 2013. [10] W. Ulmer and E. Matsinos, “Theoretical Methods for the Calculation of Bragg Curves and 3D Distributions of Pro- ton beams,” European Physics Journal (ST), Vol. 190, 2011, pp. 1-81. [11] M. J. Berger, J. S. Coursey and M. A. Zucker, “ESTAR, PSTAR and ASTAR: Computer Programs for Calculating  W. ULMER Open Access IJMPCERO 158 Stopping-Power and Range Tables for Electrons, Protons and -Particles (Version 1.2.2),” National Institute of Standards and Technology, Gaithersburg, 2000. [12] I. Kawrakow and D. O. Rogers, “The EGSnrc Code Sys- tem: Monte Carlo Simulation of Electron and Photon Transport,” NRCC Report PIRS-701 NRC Canada, 2000. 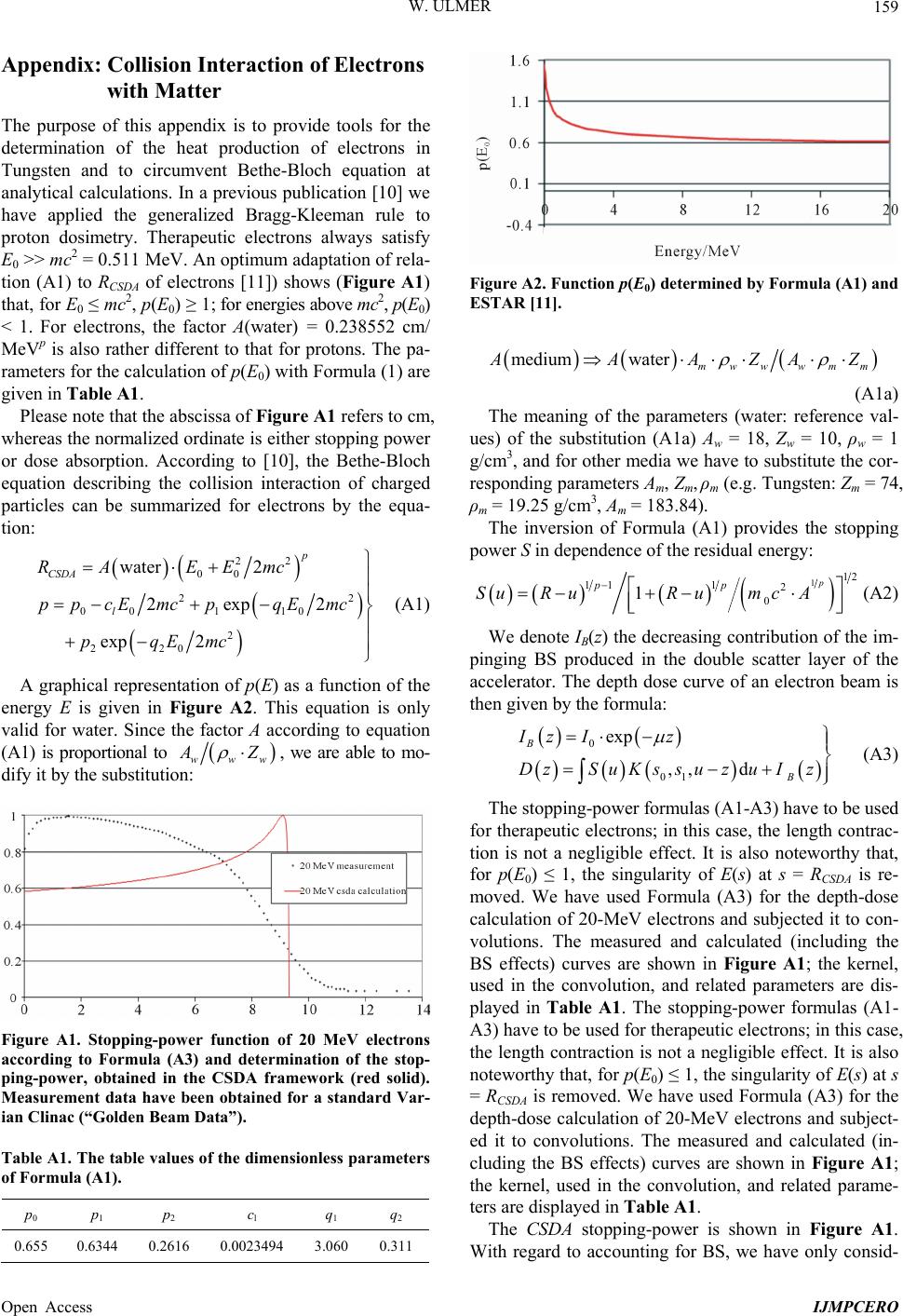 W. ULMER Open Access IJMPCERO 159 Appendix: Collision Interaction of Electrons with Matter The purpose of this appendix is to provide tools for the determination of the heat production of electrons in Tungsten and to circumvent Bethe-Bloch equation at analytical calculations. In a previous publication [10] we have applied the generalized Bragg-Kleeman rule to proton dosimetry. Therapeutic electrons always satisfy E0 >> mc2 = 0.511 MeV. An optimum adaptation of rela- tion (A1) to RCSDA of electrons [11]) shows (Figure A1) that, for E0 ≤ mc2, p(E0) ≥ 1; for energies above mc2, p(E0) < 1. For electrons, the factor A(water) = 0.238552 cm/ MeVp is also rather different to that for protons. The pa- rameters for the calculation of p(E0) with Formula (1) are given in Table A1. Please note that the abscissa of Figure A1 refers to cm, whereas the normalized ordinate is either stopping power or dose absorption. According to [10], the Bethe-Bloch equation describing the collision interaction of charged particles can be summarized for electrons by the equa- tion: 22 00 22 001 10 2 220 water 2 2exp2 exp 2 p CSDA l RA EEmc ppcE mc pqE mc pqEmc (A1) A graphical representation of p(E) as a function of the energy E is given in Figure A2. This equation is only valid for water. Since the factor A according to equation (A1) is proportional to www Z , we are able to mo- dify it by the substitution: Figure A1. Stopping-power function of 20 MeV electrons according to Formula (A3) and determination of the stop- ping-power, obtained in the CSDA framework (red solid). Measurement data have been obtained for a standard Var- ian Clinac (“Golden Beam Data”). Table A1. The table values of the dimensionless parameters of Formula (A1). p0 p1 p2 cl q1 q2 0.655 0.6344 0.2616 0.0023494 3.060 0.311 Figure A2. Function p(E0) determined by Formula (A1) and ESTAR [11]. mediumwater mww wmm AAZAZ (A1a) The meaning of the parameters (water: reference val- ues) of the substitution (A1a) Aw = 18, Zw = 10, ρw = 1 g/cm3, and for other media we have to substitute the cor- responding parameters Am, Zm, ρm (e.g. Tungsten: Zm = 74, ρm = 19.25 g/cm3, Am = 183.84). The inversion of Formula (A1) provides the stopping power S in dependence of the residual energy: 112 111 2 0 1p pp SuRuRumc A (A2) We denote IB(z) the decreasing contribution of the im- pinging BS produced in the double scatter layer of the accelerator. The depth dose curve of an electron beam is then given by the formula: 0 01 exp ,, d B B Iz Iz DzSuKssu zu Iz (A3) The stopping-power formulas (A1-A3) have to be used for therapeutic electrons; in this case, the length contrac- tion is not a negligible effect. It is also noteworthy that, for p(E0) ≤ 1, the singularity of E(s) at s = RCSDA is re- moved. We have used Formula (A3) for the depth-dose calculation of 20-MeV electrons and subjected it to con- volutions. The measured and calculated (including the BS effects) curves are shown in Figure A1; the kernel, used in the convolution, and related parameters are dis- played in Table A1. The stopping-power formulas (A1- A3) have to be used for therapeutic electrons; in this case, the length contraction is not a negligible effect. It is also noteworthy that, for p(E0) ≤ 1, the singularity of E(s) at s = RCSDA is removed. We have used Formula (A3) for the depth-dose calculation of 20-MeV electrons and subject- ed it to convolutions. The measured and calculated (in- cluding the BS effects) curves are shown in Figure A1; the kernel, used in the convolution, and related parame- ters are displayed in Table A1. The CSDA stopping-power is shown in Figure A1. With regard to accounting for BS, we have only consid-  W. ULMER Open Access IJMPCERO 160 ered the contribution resulting basically from the dou- ble-scatter foil. This contribution is determined by the software EGSnrc, see [12]. The low-energy BS (produc- ed by the electrons in water), its multiple scatter and ab- sorption can be easily explained by the energy-range/ straggling (this is basically relativistic and a single Gaus- sian is not sufficient). In order to include lateral scatter of the electron beam, we have to add a further scatter kernel in Equation (A3), which may based on the principles developed in Section 2.3.2. By using the methods work- ed out in a previous publication with regard to photon scatter [7], an efficient and fast superposition/convol- ution calculation model can readily be developed.
|