 Applied Mathematics, 2013, 4, 1495-1502 Published Online November 2013 (http://www.scirp.org/journal/am) http://dx.doi.org/10.4236/am.2013.411202 Open Access AM Pseudo-Spectral Method for Space Fractional Diffusion Equation Yiting Huang, Minling Zheng School of Science, Huzhou Teachers College, Huzhou, China Email: 272277349@qq.com, *mlzheng@aliyun.com Received July 7, 2013; revised August 7, 2013; accepted August 15, 2013 Copyright © 2013 Yiting Huang, Minling Zheng. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT This paper presents a numerical scheme for space fractional diffusion equations (SFDEs) based on pseudo-spectral method. In this approach, using the Guass-Lobatto nodes, the unknown function is approximated by orthogonal poly- nomials or interpolation polynomials. Then, by using pseudo-spectral method, the SFDE is reduced to a system of ordi- nary differential equations for time variable t. The high order Runge-Kutta scheme can be used to solve the system. So, a high order numerical scheme is derived. Numerical examples illustrate that the results obtained by this method agree well with the analytical solutions. Keywords: Riemann-Liouville Derivative; Pseudo-Spectral Method; Collocation Method; Fractional Diffusion Equation 1. Introduction Anormalous diffusion model, where a particle spreads at a rate inconsistent with the classical Brownian motion model, has been applied in many fields, such as in frac- tured and porous media, in chaotic or turbulent processes [1-6]. It is known that anomalous diffusion processes can be described by fractional partial differential equa- tions 2 1 12 ,, ,,0 1 uxtuxtfxt ttx (1.1) or ,,,,1 uxt uxtf xt tx 2 (1.2) where the fractional derivatives are defined as the Rie- mann-Liouville’s representation. The former is referred as time fractional diffusion equation and the latter as space fractional diffusion equation. The difference be- tween two cases can be shown using the interpolation of operator. It is well-known that the unknown ,uxt denotes the probability density function, which is the probability of finding the particle at position and at time . For time fractional diffusion Equation (1.1), it can be rewritten as (under suitable conditions) t 2 2 ,, ,,0 1 uxtuxtfxt tx (1.3) where depends only on . Hence, from the view point of mathematics, the Equation (1.3) can be thought as the interpolation of the equations in the case 0 and the case 1 . In a word, the particles described by the Equation (1.3) are diffused slowly in comparison with the classic situations, namely sub-diffusion. On the other hand, the fractional derivative of Equa- tion (1.2) can similarly be thought as the interpolation of operators and 22 . Note that ux de- scribes the free transport of particles and 2 ux 2 , the diffusion, due to the collisions of particles. So, in the model of space fractional diffusion the velocity of parti- cle is larger than one of ordinary diffusion, namely su- per-diffusion. Several methods have been developed for numerical solving the fractional diffusion equation. Langlands and Henry studied sub-diffusion equation based on L1 scheme [7]. The authors proposed an implicit difference scheme which is unconditional stable. Based on Grünwald-Let- nikov formula, an explicit difference scheme has been presented for sub-diffusion equation [8,9]. In contrast to sub-diffusion equation, numerical solu- *Corresponding author.  Y. T. HUANG, M. L. ZHENG 1496 tion of supper-diffusion equations have been studied and some methods are also developed. It is interesting to note that the explicit and implicit difference schemes based on Grünwald-Letnikov formula are all unconditional unsta- ble for super-diffusion Equation (1.2) and advection- diffusion equation [10,11]. However, the authors proved that a shifted Grünwald-Letnikov formula can produce stable difference scheme [10,11]. The finite difference method is the most classic method for fractional differential equation [12-16]. The recent works can see the references [17-19]. However, high order accuracy schemes are seldom derived by finite difference method. In general, extrapolation method is applied in order to obtain a high accuracy [10,16]. It is well-known that spectral methods are superior to finite different methods in many instances for partial differential equa- tions [20-24]. In the recent paper [25], the authors pre- sented a spectral method to calculate the fractional de- rivative and integral, and studied the numerical solution of differential equations by the spectral method. In this paper, we shall deal with the numerical solution of the one-dimensional variable coefficients space frac- tional diffusion equation ,,, ,,0,0, uxtdxu xtq xtxtLT tx (1.4) with the initial condition for ,0ux hx0 L and boundary conditions and 0, 0ut ,tgt ,t uL qx . Here, is variable coefficient and source term. dx Chebyshev spectral collocation method (often called pseudo-spectral) is used in this paper. By employing the Chebyshev polynomials and Gauss-Lobbato nodes, the unknown is approximated by using the orthogonal pro- jection and interpolation. So, the spatial fractional de- rivatives are easily computed and a system of ordinary differential equations in time can be derived. Then, high order Runge-Kutta method can be utilized and a high order accuracy scheme is obtained. In a comparison with the finite difference method, the Chebyshev spectral method used here shows remarkably superiority in terms of accuracy and the number of grid points required. The paper is arranged as follows. The Section 2 intro- duces some basic concepts of fractional derivative and Jacobi orthogonal polynomials and their properties. The third section presents the spectral method for calculating the Riemann-Liouville fractional derivative. The pseudo- spectral method and its implement are proposed in Sec- tion 4. In Section 5, several numerical examples are pro- vided. These numerical examples illustrate the high ac- curacy and efficiency of our method. Finally, we give the conclusion in Section 6. 2. Preliminary 2.1. Fractional Derivative The Riemann-Liouville fractional integral of order α(α > 0) for casual function x is defined by 11 12 00 0 1dd d n xx x nn fxxxfx x (2.1) where . is the Gamma function. Riemann-Liouville fractional integral is an analogue of the well-known Cauchy formula, which reduces the n-fold integration 11 12 00 0 dd d n xx x n nn xxx fx x into the Laplace convolution 0 Κd x n nn xxfx xsfs s where 1 1! n n x xn . For 0 0, xfx . It is easily obtained 1, 1 xx (2.2) for 0,1. The Riemann-Liouville representation of fractional derivative of order 0 for x is defined by 1 0 1d d d m mxm m Dfx Dfx sfs ma xs here 1mm . By the part integration formula, one can easily derive the following properties. Proposition 2.1. Let 1,mmmN , then 1 0 1 0 0 1 1d. k mk k xmm f Dfx x k xf m (2.3) Proposition 2.2. Let 1, 0, then 1 1 Dx x (2.4) 2.2. Jacobi Orthogonal Polynomials Given a weight function , the orthogonal polyno- mials sequence 0 j Px , with deg j j can be written into [26] 01 1, ,PxPxx 1 Open Access AM  Y. T. HUANG, M. L. ZHENG 1497 1111 ,1 nnnnn Px xPxPxn in which 1 ,,0 , nn n nn xP Pn PP , 1 1 11 ,,1 , nn n nn xP Pn PP here , denotes weighted inner product of a Hilbert space. For , the Jacobi polynomials is a orthogonal polynomials sequence 11,,1,1, ab xxxabx 1 , 0 ab nn Jx with ,, 01 ,,,,,, 11 11 1,2 , 22 ,1 ab ab ababababab ab nnnnnn JxJab xab Jx AxBJxCJxn (2.5) where ,212 21 1 ab n nab nab Annab 2 (2.6) 22 ,21 21 12 ab n ba nab Bnnab nab (2.7) ,2 112 ab n nanb nab Cnnabnab 2 (2.8) The following is some useful properties of Jacobi poly- nomials that will be used in present paper [26] (also refer to [25] and references therein). Proposition 2.3. 1) High order derivative for Jacobi polynomials ,,, , d,, d m ababa mbm nnmnm m xcJ xnmmN x (2.9) where , , 1 21 ab nm m nmab cnab . 2) Expression by the derivative of Jacobi polynomials ,,,,, 1 ,, 1 dd dd d,1 d abab abab ab nnnnn abab nn xJxJ xx Jxn x x (2.10) where , 1 , , , 0, 22 221 2 222 21 2122 ab ab n ab n ab n nanb n nabnabnab ab nab nab nab nabnab (2.11) By the previous Jacobi polynomials some special or- thogonal polynomials can be obtained. Legendre and Che- byshev polynomials are two important polynomials of the special cases of the Jacobi polynomials. For the case of 0, 1ab x , the corresponding polynomials is said to Legendre polynomials; and the case of 2 1 1, 21 ab x corresponds to Chebyshev polynomials. 3. Spectral Approximation to Fractional Derivative Let denote the set of polynomials of degree not exceeding N. It is clear that ,, , 01 ,,, ab abab NN spanJxJx Jx Denote the weighted inner product for weight function on interval 1, 1I ,d I uvux v xxx and the weighted Lebesgue space 2,LI fff with norm 1 2 2, L uuu . Define the orthogonal projection 2 : N LI H Then function 2 w uxL I can be approximated by the orthogonal projection ,, 0 ˆ Nab ab NN nn n uxuxuJx The expression coefficients is determined by , ˆab n u ,,,, ˆ,, ababab ab nnnn ww uuJ JJ. Therefore, the fractional derivative can be approximated by Dux ,,, ,,, 0 ˆ, Nab ababab Nnnnn n Duxudxd xDJx where Open Access AM  Y. T. HUANG, M. L. ZHENG 1498 1 , 1 1d d d mxm ab ab nn m DJ xxJ mx , Now, we consider the calculation of . Let ,,ab n dx 1 ,, , 1 1 ˆd, x ab ab nn dxx J Then, can be the computed by recurrence formula [25]. Clearly, ,, ˆab n dx ,, 0 1 ˆ, 1 ab x dx (3.1) 1 ,, 1 ,, 0 11 2 ˆ 221 ˆ 2 ab ab xx ab dx ab dx (3.2) By the three-term recurrence relation (2.5), ,1 ,, , 11 ,,,,,, 1 ˆd ˆˆ ab x ab ab n nn ab abab ab nn nn A dxx J Bd xCd x Note that 1, 1 1, 1 , 1 1d 1d 1d. xab n xab n xab n xJ xx J xJ In light of (2.10) and notice that ,1 11 !1 n ab n nb Jnb , one can obtain , 1 ,, 1 1 ,, ,, 1 , ,, ,,,,,, ,,, 11 1d 1d d dd d dd 11 11! 12 !1! ˆˆˆ xab n xab ab nn ab abab ab nn nn nb n bb nn ab abab abab ab nnnn nn xJ xJ JJ xnb bn nb nb nn dxdxd Thus, ,, 1 ˆab n dx can be derived ,,, ,, ,, 11 ,, ,, , ,, ,, ,,, ,, ˆˆ 1 ˆ 1 11 , 1 ababab ab ab nn n nn abab nn ab abab nn n ab n abab nn nab ab nn ab ab nn AC dx dx A xAB dx A Az x A (3.3) in which ,, , ,, 11! 12 1!1 1! ab ab nn ab ab nn nb znan nb nb nan nan and ,, ,, ab ab ab nnn , BC is defined as (2.6)-(2.8), ,ab n , ,ab n ,ab n as (2.11). Therefore, we obtain by (2.3) and (2.9) that , 1 ,, 0 1, 1 , 1, 0 ,,, , d1 d1 1 1d d () d 11 1 11! ˆ k ab mn kk ab n k m xmab n m nk ab mk nk k aba mb mm nmnm J x dx x k xJ m cnbx kbknk cd x (3.4) Remark 1. By the standard theory of orthogonal pro- jection, the spectral accuracy to approximate the frac- tional derivative Dux can be obtained (refer to the references [25,26]). 4. Collocation Method This section presents the Chebyshev collocation method (often called pseudo-spectral method) for solving the space fractional diffusion Equation (1.4). Firstly, we shall consider the Gauss-Lobatto nodes in order to obtain the collocation equation. Consider the Chebyshev polynomials n Tx of the first kind, which are the special case of Jacobi polynomi- als 2 211 , 22 2! ,0,1,2, 2! n nn n TxJxn n (4.1) for 11 . Chebyshev polynomials are the weighted orthogonal polynomials with weight function 2 1 1 wx . Open Access AM  Y. T. HUANG, M. L. ZHENG 1499 One can easily obtain the three-term recurrence for- mula 01 11 1, , 2, kkk TxTxx Tx xTxTxk 1,2, Denote 1NNN , here p, q is determined by satisfying . Then the roots of is named as the Chebyshev Gauss-Lobatto points (in this paper is also called Gauss-Lobatto points). Gauss-Lobatto points can be explicitly written as [26,27] 1 QxTxpT xqTx 10Q 0 Qx cos,0,1, 2,,. k k KN N Define the discrete inner product as 0 ,, N kk Nk ux vxuxvxk where k are the associated weights of Chebyshev Gauss-Lobatto integration 2for0, , ,1for1, ,1. kk k kN ckN cN By orthogonality it can easily be derived that 0 ,if N ik jkk k TxT xijN (4.2) Next, let us consider the following Gauss-Lobatto points cos,0,1, 2,,. 22 k LL k K N N (4.3) Assume that the approximate solution of the space fractional diffusion Equation (1.4) has separable forma- tion 0 2 ˆˆ ,, , N Nn n 1 uxtuxttT xxL for 0, . L Replacing in (1.4) by ,uxt , N uxt it results in the following equations on k 0 ,, 1, 2,,1 ,0,, Nkk Nkk NN N uxtdxuxt qxt tx kN uxtuxt gt ,, (4.4) with initial condition , where ,0 N ux hx12 . Set 2 ˆ1 k k x xL , then Equations (4.4) can be written into 0 ˆˆ 0 d ˆd ˆ,, k N nk n n N knkxxn k n Tx t t dxDTxtqxt for 1, 2,,1kN 0 . In addition, the boundary condi- tions for and can be expressed by 0 00 ˆˆ 0, NN nnN nn nn tT xtT xgt (4.6) Equations (4.5) and (4.6) is called the collocation equation for fractional diffusion Equation (1.4), and k defined by (4.3) is called the collocation points. The Equation (4.5) is a system of ordinary differential equations. The calculation of can be imple- mented by n DT x 21 20 21 ˆ 21 2 2 ,, 1d ˆ ˆd 2d 1d ˆˆ ˆd ˆ 22 d 2! ˆ 22! x nn x n n ab n DT xxT x LxT x n Ldx n here ˆ2,lLab 12 , therefore nk DT x can be conveniently calculated by making use of (3.4). Remark 2. 1) Equations (4.5) and (4.6) is also said to be the strong form of the collocation method. 2) In order to get high order schemes, high order Runge-kutta methods can be used to solve the system of ordinary differential Equation (4.5). Now, we employ the discrete inner product to deal with the initial condition. Notice that ,0 ,0 N ux hxxL , can be written into 0 2 ˆˆ ˆ 0, N nn n 1 TxhxxL Therefore, making use of (4.2) it gives , 0,1,2,, , kN k kk N hT kN TT 1. (4.7) In order to conveniently deal with the boundary condi- tions and initial condition, let us consider another form of the collocation method based on interpolation. Based on the Gauss-Lobatto nodes (4.3) above, the Lagrangian interpolation basis function k are given by ,0,1,, j k jk kj xx kN xx . Assume that the approximation be the in- terpolation , N uxt 0 , N Nj j uxttx j (4.5) Note that i xji , here δji denotes the Kronecker Open Access AM  Y. T. HUANG, M. L. ZHENG 1500 delta symbol. Then, the Equations (4.6) simply become 0,0 N tgt t , and the initial condition (4.7) is altered by 0,1,2,, jj hx jN 1, (4.8) Let T 12 1 (, ,, N ttt t . Equation (4.5) is correspondingly modified into tDMtNgtQt (4.9) where 11 2111 12221 2 112 11 1 N N NNN DX DXDx Dx DxDX M DxDXDX N 101 202 10 1NN dD x dD x N dD x 1 2 1N qt qt Qt qt and 121 diag,,, N Dddd , with for 11. ,,ddxqtqxt iii i In order to compute conveniently the coefficient ma- trix M, we expanse iN k into Taylor series 2 1 00 0. 2! NN kkk k xxx N Therefore, making use of Prop. 2.1 and Prop. 2.2 one can derive. 0 0, 1 m Njm j m Dx x m for 01 and 0. jN 5. Numerical Examples In this section, we consider the space fractional diffusion equations for different source terms and the values of utilizing the collocation method. Here, the fourth order Runge-Kutta method is used for all the examples with time step . The first example is a fractional equation with 1 0.05 t 1.5 and time variable belongs to 0, . The second example is associated to the prob- lem of time belonging to finite interval with 1.5 2 . For the first example, we use the second kind of colloca- tion method, namely based on the Lagrange interpolation, with 3N . The second example is solve by the Cheby- shev polynomials approximation with . 3N Example 1. Consider the following asymptotic prob- lem with 1.2 qxt 1.2 1.2 ,,,, ,0,10, uxtdxuxt x xt t with the initial condition 2 ,0, 0,1uxxx and boundary conditions 0, 0,0,1,e, t ut utt in which 2.2 1.8 2 dx x , and 2 ,1qxtx x e t ux . The exact solution (Ex-solution) is 2 ,e t t x 1t . The numerical solution (CM-solution) at time , us- ing the collocation method based on the Lagrange inter- polation, is shown in Figure 1. Example 2. Consider the following finite interval problem with 1.8 ,0 1.8 1.8 , ,,,,10, t u xtq xtxtT x tux d x with the initial condition 2 ,0, 0,1uxxx and boundary conditions Figure 1. The exact solution and collocation solution for asymptotic problem with α = 1.2 at time t = 1. Open Access AM 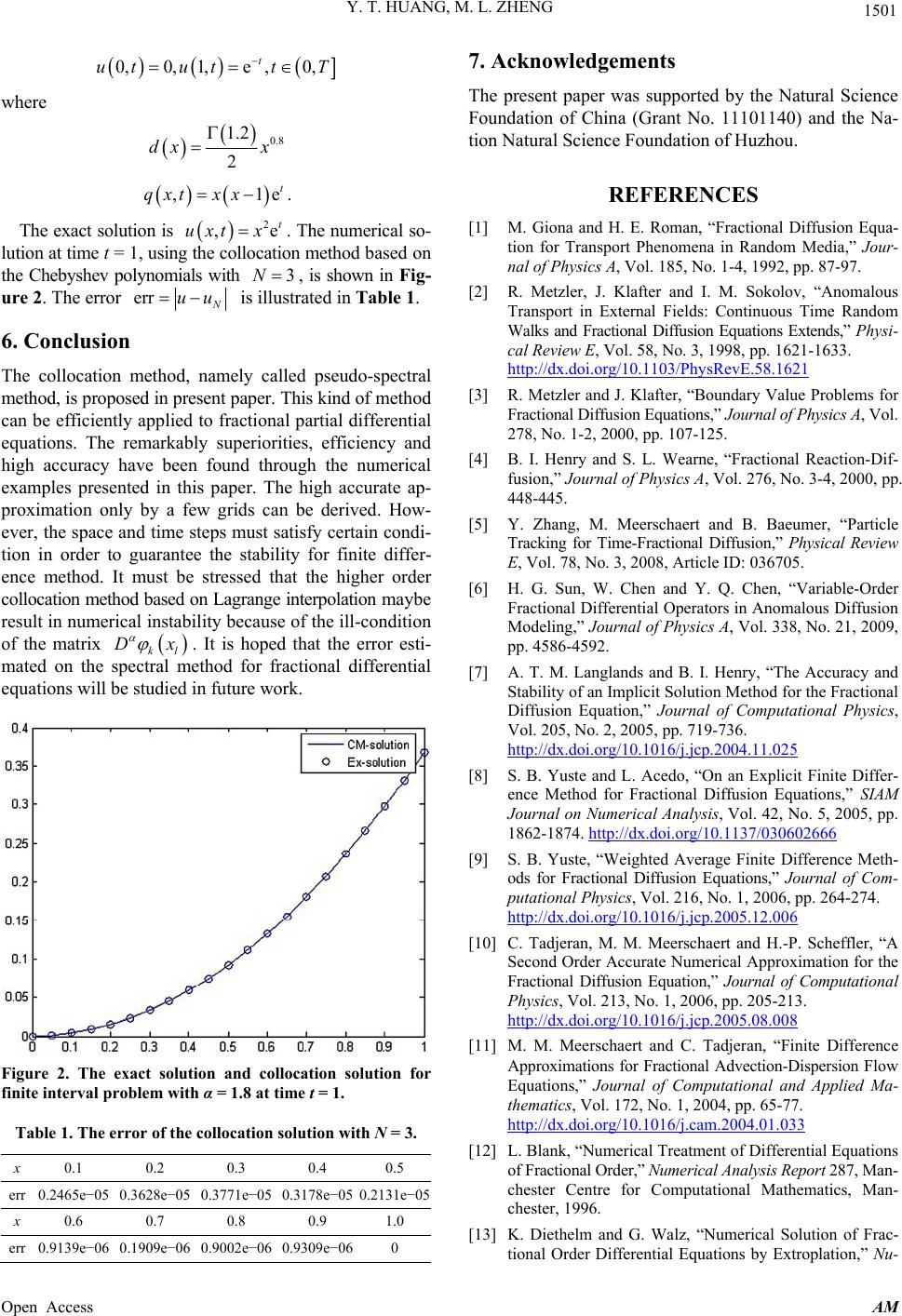 Y. T. HUANG, M. L. ZHENG 1501 0,0,1,e ,0, t ututt T where 0.8 1.2 2 dx x ,1 t qxt xx 2t e e . The exact solution is . The numerical so- lution at time t = 1, using the collocation method based on the Chebyshev polynomials with , is shown in Fig- ure 2. The error ,uxt x 3N err uu is illustrated in Table 1. 6. Conclusion The collocation method, namely called pseudo-spectral method, is proposed in present paper. This kind of method can be efficiently applied to fractional partial differential equations. The remarkably superiorities, efficiency and high accuracy have been found through the numerical examples presented in this paper. The high accurate ap- proximation only by a few grids can be derived. How- ever, the space and time steps must satisfy certain condi- tion in order to guarantee the stability for finite differ- ence method. It must be stressed that the higher order collocation method based on Lagrange interpolation maybe result in numerical instability because of the ill-condition of the matrix . It is hoped that the error esti- mated on the spectral method for fractional differential equations will be studied in future work. kl Dx Figure 2. The exact solution and collocation solution for finite interval problem with α = 1.8 at time t = 1. Table 1. The error of the collocation solution with N = 3. x 0.1 0.2 0.3 0.4 0.5 err 0.2465e−05 0.3628e−05 0.3771e−05 0.3178e−05 0.2131e−05 x 0.6 0.7 0.8 0.9 1.0 err 0.9139e−06 0.1909e−06 0.9002e−06 0.9309e−06 0 7. Acknowledgements The present paper was supported by the Natural Science Foundation of China (Grant No. 11101140) and the Na- tion Natural Science Foundation of Huzhou. REFERENCES [1] M. Giona and H. E. Roman, “Fractional Diffusion Equa- tion for Transport Phenomena in Random Media,” Jour- nal of Physics A, Vol. 185, No. 1-4, 1992, pp. 87-97. [2] R. Metzler, J. Klafter and I. M. Sokolov, “Anomalous Transport in External Fields: Continuous Time Random Walks and Fractional Diffusion Equations Extends,” Physi- cal Review E, Vol. 58, No. 3, 1998, pp. 1621-1633. http://dx.doi.org/10.1103/PhysRevE.58.1621 [3] R. Metzler and J. Klafter, “Boundary Value Problems for Fractional Diffusion Equations,” Journal of Physics A, Vol. 278, No. 1-2, 2000, pp. 107-125. [4] B. I. Henry and S. L. Wearne, “Fractional Reaction-Dif- fusion,” Journal of Physics A, Vol. 276, No. 3-4, 2000, pp. 448-445. [5] Y. Zhang, M. Meerschaert and B. Baeumer, “Particle Tracking for Time-Fractional Diffusion,” Physical Review E, Vol. 78, No. 3, 2008, Article ID: 036705. [6] H. G. Sun, W. Chen and Y. Q. Chen, “Variable-Order Fractional Differential Operators in Anomalous Diffusion Modeling,” Journal of Physics A, Vol. 338, No. 21, 2009, pp. 4586-4592. [7] A. T. M. Langlands and B. I. Henry, “The Accuracy and Stability of an Implicit Solution Method for the Fractional Diffusion Equation,” Journal of Computational Physics, Vol. 205, No. 2, 2005, pp. 719-736. http://dx.doi.org/10.1016/j.jcp.2004.11.025 [8] S. B. Yuste and L. Acedo, “On an Explicit Finite Differ- ence Method for Fractional Diffusion Equations,” SIAM Journal on Numerical Analysis, Vol. 42, No. 5, 2005, pp. 1862-1874. http://dx.doi.org/10.1137/030602666 [9] S. B. Yuste, “Weighted Average Finite Difference Meth- ods for Fractional Diffusion Equations,” Journal of Com- putational Physics, Vol. 216, No. 1, 2006, pp. 264-274. http://dx.doi.org/10.1016/j.jcp.2005.12.006 [10] C. Tadjeran, M. M. Meerschaert and H.-P. Scheffler, “A Second Order Accurate Numerical Approximation for the Fractional Diffusion Equation,” Journal of Computational Physics, Vol. 213, No. 1, 2006, pp. 205-213. http://dx.doi.org/10.1016/j.jcp.2005.08.008 [11] M. M. Meerschaert and C. Tadjeran, “Finite Difference Approximations for Fractional Advection-Dispersion Flow Equations,” Journal of Computational and Applied Ma- thematics, Vol. 172, No. 1, 2004, pp. 65-77. http://dx.doi.org/10.1016/j.cam.2004.01.033 [12] L. Blank, “Numerical Treatment of Differential Equations of Fractional Order,” Numerical Analysis Report 287, Man- chester Centre for Computational Mathematics, Man- chester, 1996. [13] K. Diethelm and G. Walz, “Numerical Solution of Frac- tional Order Differential Equations by Extroplation,” Nu- Open Access AM  Y. T. HUANG, M. L. ZHENG Open Access AM 1502 merical Algorithms, Vol. 16, 1997, pp. 231-253. http://dx.doi.org/10.1023/A:1019147432240 [14] K. Diethelm, “An Algorithm for the Numerical Solution of Differential Equations of Fractional Order,” Electronic Transactions on Numerical Analysis, Vol. 5, 1997, pp. 1-6. [15] N. Ford and A. Simpson, “The Numerical Solution of Fractional Differential Equations: Speed versus Accu- racy,” Numerical Analysis Report 385, Manchester Centre for Computational Mathematics, Manchester, 2001. [16] K. Diethelm, N. Ford and A. Freed, “A Predictor-Cor- rector Approach for the Numerical Solution of Fractional Differential Equations,” Nonlinear Dynamics, Vol. 29, No. 1-4, 2002, pp. 3-22. http://dx.doi.org/10.1023/A:1016592219341 [17] C.-M. Chen, F. Liu and K. Burrage, “Finite Difference Methods and a Fourier Analysis for the Fractional Reac- tion-Subdiffusion Equation,” Applied Mathematics and Computation, Vol. 198, No. 2, 2008, pp. 754-769. http://dx.doi.org/10.1016/j.amc.2007.09.020 [18] B. Baeumer, M. Kovacs and M. M. Meerschaert, “Nume- rical Solutions for Fractional Reaction-Diffusion Equa- tions,” Computers & Mathematics with Applications, Vol. 55, No. 10, 2008, pp. 2212-2226. http://dx.doi.org/10.1016/j.camwa.2007.11.012 [19] S. Shen, F. Liu and V. Anh, “Numerical Approximations and Solution Techniques for the Space-Time Riesz-Caputo Fractional Advection-Diffusion Equation,” Numerical Al- gorithms, Vol. 56, No. 3, 2011, pp. 383-403. http://dx.doi.org/10.1007/s11075-010-9393-x [20] C. Canuto, M. Y. Hussaini, A. Quarteroni and T. A. Zang, “Spectral Methods. Fundamentals in Single Domains,” Springer-Verlag, Berlin, 2006. [21] D. Funaro and D. Gottlieb, “A New Method of Imposing Boundary Conditions in Pseudospectral Approximations of Hyperbolic Equations,” Mathematical and Computer, Vol. 51, No. 184, 1988, pp. 599-613. http://dx.doi.org/10.1090/S0025-5718-1988-0958637-X [22] G.-Q. Chen, Q. Du and E. Tadmor, “Spectral Viscosity Approximations to Multidimensional Scalar Conservation Laws,” Mathematical and Computer, Vol. 61, No. 204, 1993, pp. 629-643. http://dx.doi.org/10.1090/S0025-5718-1993-1185240-3 [23] T. Y. Hou and R. Li, “Computing Nearly Singular Solu- tions Using Pseudo-Spectral Methods,” Journal of Com- putational Physics, Vol. 226, No. 1, 2007, pp. 379-397. http://dx.doi.org/10.1016/j.jcp.2007.04.014 [24] S. Esmaeili and M. Shamsi, “A Pseudo-Spectral Scheme for the Approximate Solution of a Family of Fractional Differential Equations,” Communications in Nonlinear Science & Numerical Simulation, Vol. 16, No. 9, 2011, pp. 3646-3654. http://dx.doi.org/10.1016/j.cnsns.2010.12.008 [25] C. Li, F. Zeng and F. Liu, “Spectral Approximations to the Fractional Integral and Derivative,” Fractional Cal- culus & Applied Analysis, Vol. 15, No. 3, 2012, pp. 383- 406. http://dx.doi.org/10.2478/s13540-012-0028-x [26] J. Shen and T. Tang, “Spectral and High-Order Methods with Applications,” Science Press, Beijing, 2007. [27] A. Quarteroni and A. Valli, “Numerical Approximation of Partial Differential Equations,” Springer-Verlag, Berlin, 1997.
|