Paper Menu >>
Journal Menu >>
 Journal of Signal and Information Processing, 20 11 , 2, 18 - 25 doi:10.4236/jsip.2011.21003 Published Online February 2011 (http://www.SciRP.org/journal/jsip) Copyright © 2011 SciRes. JSIP A Novel Approach to Blind I/Q Mismatch & Carrier Offset Compensation Sunita Panda1, S. P. Panigrahi2, D. D. Meena2, R. K. Mishra2, M. Sahu2, H. Sahu2, N. Panda2, M. Singh2 1ECE, KIT, Berhampur, India; 2Electrical Engineering, KIST, Bhubaneswar, India. Email: siba_panigrahy15@rediffmail.com Received December 10th, 2010; revised January 11th, 2011; accepted February 18th, 2011 ABSTRACT This paper proposes a novel approach for I/Q mismatch compensation. Simulation results proves the superior per- formance of the proposed technique. Keywords: Channel Equalization, I/Q Mismatch compensation 1. Introduction In order to increase the receiver flexibility while also emphasizing the receiver integrability and other imple- mentation related aspects, the design of radio receivers is no longer dominated by the traditional superheterodyne architecture. Instead, alternative receiver structures, like the direct conversion [1,2] and low-IF [1,3,4] architec- tures, are receiving more and more interest. The analog front-end of these types of receivers is partially based on complex or I/Q signal processing [5-7]. More specifically, the frequency translation from radio frequencies (RF) closer to base-band is carried out using I/Q downconver- sion. Since, in theory, the I/Q downconversion corre- sponds to a pure frequency translation, the fundamental image signal problem is basically avoided during the downconversion. In thismanner, the requirements for RF image rejection filtering are greatly relaxed in practice [1-4]. The assumption of infinite image signal rejection dur- ing the downconversion is strictly valid only if ampli- tudes and phases of the analog front-end I and Q branches are perfectly matched [7]. In practice, this is not the case. Some mismatch or imbalance will always exist due to imperfections of practical analog electronics. Am- plitude imbalances of 1% - 5% and phase imbalances of 1-5 represent feasible design Figures [1-4]. This corre- sponds to approximately 25-40 dB image signal attenua- tion. These levels of image attenuation are clearly insuf- ficient in low-IF-type receivers where the image band can carry a signal with much higher power level than the desired signal. Some digital signal processing (DSP)- based approaches to improve this image attenuation in IF receivers are presented, for example, in [7-10]. In di- rect-conversion receivers, the image signal is inherently a self-image (the desired signal itself at negative frequen- cies), and the analog front-end image attenuation might be sufficient with low-order modulations. However, with higher-order modulations, such as 16- or 64-QAM, the distortion due to self-image cannot be neglected and again some kind of compensation is needed [11-13]. This is also one of the topics of this pa- per. The idea in this paper is first to show that I/Q mis- match causes crosstalk between the I and Q components. Then this crosstalk or mixing of the I and Q is removed using blind signal separation (BSS) techniques [14-16]. Compared to the other available solutions in the literature [12,13], the proposed concept is especially attractive since no known training signals are needed. Also the ability to follow possible time dependencies in the mis- match parameters (due to, e.g., temperature changes) is another highly desirable feature. Another challenging practical problem in radio com- munications is carrier synchronization [6]. In practice, it is unlikely that the frequency and relative phase of the receiver local oscillators exactly match those of the re- ceived carrier. In case of linear modulations, a constant phase offset introduces a constant rotation to the received constellation, which needs to be compensated unless dif- ferential phase modulation is used. Even a bigger prob- lem is caused by errors or offsets in frequency that basi- cally results in time-varying rotation of the constellation.  A Novel Approach to Blind I/Q Mismatch & Carrier Offset Compensation Copyright © 2011 SciRes. JSIP 19 This is obviously unacceptable for most modulation types and needs to be efficiently compensated for. In this paper, the carrier offsets are shown to result in time- varying leakage between the I and Q, and carrier tracking is implemented with adaptive signal separation methods. Furthermore, when combined with the previous I/Q mis- match compensation, a single BSS stage can accomplish both tasks jointly in a blind manner. These kinds of ap- proaches have not been considered in the literature so far. In addition to the above front-end-related issues, the distortion due to transmission channel [6,15] is inevitable in any radio receiver and needs to be addressed with care. As will be shown, a general bandpass channel can be viewed to cause frequency-selective crosstalk between the transmitted I and Q data. Based on this, convolutive mixture (or FIR-MIMO) separation techniques working on the observed I and Q signals are applied to implement channel equalization. 2. Direct-Conversion Receiver 2.1. Background The fundamental tasks to be carried out in the front-end of any communications receiver include 1) amplification of the attenuated desired signal, 2) downconversion of the desired signal spectrum from around the RF carrier frequency closer to base-band, 3) attenuating the un- wanted spectral components appearing in the antenna signal, and 4) synchronizing the receiver local oscillators for downconversion and sampling with the received sig- nal. Key tasks of the baseband digital signal processing include channel estimation, equalization, and detection. In traditional receiver designs, these tasks are imple- mented more or less independently of each other, aiming at close-to-ideal operation in each signal processing stage. This has lead to the use of the superheterodyne receiver architecture [1,4] in order to meet the tight RF specifica- tions in terms of image band attenuation and nonlinear effects of the receiver front-end stages. In such receivers, the RF signal is first downconverted to a fixed interme- diate frequency (IF) where the receiver selectivity is im- plemented using a fixed IF filter. The down-conversion is usually done with a simple real mixer, and the spectral components on the image signal band need to be attenu- ated sufficiently by the RF stages before the mixer. Due to the high number of discrete components and high power consumption, the superheterodyne architecture is, however, not the most appropriate choice for highly in- tegrated implementations [1-4]. Furthermore, the use of fixed discrete components in the analog front-end limits the receiver flexibility. Thus, architectures with more simplified analog front-ends with less RF processing are generally needed. In addition, it has recently been demonstrated [7-9] that various non-idealities and distortion effects due to the simplifica- tion of the analog front-end can in general be compen- sated by advanced DSP techniques. This is also the cen- tral theme in this paper. 2.2. Direct-Conversion Architecture A simple way to reduce the number of components in the receiver and alleviate the problem of receiver complexity is to avoid the use of intermediate frequency and quad- rature down-convert the desired channel signal directly from RF to baseband. Complete elimination of the IF stage results in highly simplified structure, the so-called direct-conversion receiver, where most of the channel selectivity and amplification are implemented at base- band [1,2]. Firstly, since most of the signal processing tasks take place at low frequencies, the power consump- tion is minimized. On the other part, very low-noise op- eration is called for in all the remaining analog compo- nents since the amplificatio n provided by the RF stag e is only moderate. The direct-conversion receiver concept is depicted in Figure 1. Figure 1. The direct-conversion receiver architecture. The leading principle in this paper is to show that various receiver signal processing tasks can be carried out blindly by forcing the observed I and Q signals as independent as possible using blind signal separation.  Current Distortion Evaluation in Traction 4Q Constant Switching Frequency Converters Copyright © 2011 SciRes. JSIP 20 In the direct-conversion principle, since the IF is ef- fectively zero, the image signal is actually the desired signal itself (at negative center frequency). Ideally, with perfect analog processing, the image band is completely attenuated in general. However, practical analog imple- mentations of the needed I/Q signal processing have mismatches in the amplitude and phase responses of the I and Q branches, leading to finite atten uation of th e image band signal. In the direct-conversion case, the effect of imperfect (self-)image rejection is seen as a linear trans- formation of the original signal constellation [11-13]. As a result, the image attenuation requirements are not ex- tremely tight, especially if low-order modulations are used. In effect, the 25-40 dB image attenuation of a prac- tical analog front-end can be sufficient with low-orde modulations.Wi th higher-order spectrally efficient modu- lation methods, however, the distortion due to selfimage can establish an error floor and needs to be compensated. In practice, the use of zero IF introduces also some other problems. The major drawback in direct-conversion principle is the DC offset problem [1,2]. Due to zero IF, the local oscillator frequency is o n the same frequency as the desired chann el. Then, if the LO signal leaks into the mixer input port, it self-mixes down to baseband causing interfering signal components at zero frequency. These are called DC offsets and can be orders of magnitude larger than the desired channel signal. Besides the LO leakage, another contributor to the offset problems is 1/f noise of the active front-end components. For a better receiver performance, some compensation of the DC offsets is needed. Another analog RF-related problem is that higher linearity is required because in a direct-con- version receiver, second-order inter-modulation products may fall in the signal band (in superheterodynes, the weaker third-order intermodulation products usually set the linearity requirements). These problems have limited the use of direct-conversion principle in practical systems earlier, but nowadays this approach is widely utilized in mobile terminals. However, the introduction of higher- order modulations in future wireless communication sys- tems sets higher demands for the receiver performance, and the I/Q imbalance effects, for example, to be dis- cussed in Section 4 are likely to pose big challenges. 3. Blind Signal Separation Currently, more and more applications call for proper representation of multivariate data. An exten sion of prin- cipal component analysis (PCA) called independent component analysis (ICA) is one good example of such techniques [16]. The ICA and its signal processing ap- plication, blind signal separation [14,16], is applied in this paper to communications receiver signal processing. The purpose of this section is to introduce the basic con - cepts and notations after which the actual applications to I/Q mismatch and carrier offset compensation as well as to channel equalization are discussed and analyzed in Sections 4 and 5. Generally speaking, blind signal separation deals with the recovery of some interesting signals, called sources, based on observing their linear1 mixtures, and falls under the umbrella of multiple-input multiple-output (MIMO) signal processing [14-16]. The term blind is used here to emphasize the fact that no prior knowledge of the mixing process or the temporal structure of the underlying source signals is needed, but only the statistical properties are utilized. The leading principle in this context is the as- sumption of statistical independence of the original sources [14-16]. Thus in practice the recovery consists of forcing the separator output signals to be “as independent as possible,” according to the selected independence- measure. Commonly used approaches in this context are, for example, nonlinear decorrelation and minimization of mutual information. As is obvious, the relative order of the recovered sources or the individual amplitude/power levels cannot be blindly id entified. In addition to statistical independence, another key assumption is that only o ne of the sources (if any) can be Gaussian [14-17]. This is easy to understand since for Gaussian signals uncorrelatedness implies independence, making it impossible to distinguish any (remaining) or- thogonal/orthonormal transformation . Luckily most com- munications signals are, indeed, non-Gaussian. In the following, M and N denote the number of observed and original source signals, respectively. 3.1. Instantaneous MIMO Models Assuming the mixing process is instantaneous, the mth observation, say m x k is of the form m x k ,1 1,mmNN askas k, where, n x k denotes the nth source signal and ,1m arepresents the relative weight of the source n s k in the observation n x k. Stack- ing the observed and source signal samples at time-in- stant k into column vectors 1,T N s ksksk and x k 1,T N xkx k respectively, the system model can be simply written as: x kAsk (1) where the M × N matrix A describes the mixing process with , ,mn mn A a. In general, the matrix A is assumed unknown but nonsingular (full rank). This is a natural assumption and is fundamental for the identifiability of the model; see [14,16-18] for more details. Generally speaking, the separator processes a sequence of the ob- servation vectors and tries to “invert” the model in (1). In adaptive separation, the parameters of the separator are  A Novel Approach to Blind I/Q Mismatch & Carrier Offset Compensation Copyright © 2011 SciRes. JSIP 21 updated iteratively which also enables tracking the pos- sible time-variant features of the mixturemodel. The separator output at time k is commonly written as y kWkxkWkAskTksk (2) Where, Wk denotes the N × M separator matrix, Tk WkA is the total equivalent system matrix (N × N), and 1,T N yky kyk . For successful separation, T(k) should converge to a “quasi-identity” (permutation and scaling) matrix with only one nonzero element on each of its row and column. Various algorithms, with varying computational com- plexity and performance, to determine the separator co- efficients exist in the literature; see [14,16] for excellent reviews. One exciting feature of th e separation stage is the pos- sibility for uniform performance. This being the case, the separation performance is independent of the underlying mixture coefficients (i.e ., the matrix A, as long as it is full rank) and depends only on the source statistics. One such algorithm with this desirable property is the so-called equivariant adaptive separation via independence (EASI), proposed originally in [19], whose performance depends only on the certain nonlinear moments of the source sig- nals. The EASI algorithm consists formally of two sub- tasks; a whitening (second order decorrelation) part and a nonlinear decorrelation part where the selection of the used nonlinear function depends on the source statistics. The exact alg orithm descri ption can be found i n [19]. This algorithm is used also in this paper in Section 4. Notice, however, that this is done only to illustrate the principal operation of the proposed receiver concepts; thus any other adaptive separation approach could be tested and used as well in practice. 3.2. Convolutive MIMO Models A more general class of signal models is obtained if the assumption of instantaneous mixing is dropped. In other words, the mixing process can also containmemory and thus be frequency selective [14,16,20]. A direct exten- sion of the model in (1) results in l l x kAskl (3) Which represents a MIMO convolution of the sequences ,1, 1,sk sksk and 101 ,,,,AAA with each l A being size M × N. In other words, each observation n x k is a convolutive mixture of the original source signals. In this case, the identifiability condition related to the mixing process is generally for- mulated in terms of the corresponding system (MIMO) transfer function l l l A zAz ; the recovery of the original source contributions is feasible if this system transfer f unct ion has full r an k [14,16,20 ] . Practical recovery of the source signals consists of multichannel filtering of the observed vectors and can generally be written as: l l y kWkxkl (4) where, the N × M separator matrices l Wkare adapted to minimize the predetermined dependence measure be- tween the components of y(k). In terms of system trans- fer functions, the relation between the source signals and the separator output signals is of the form: ,,Tzk WzkAa (5) where, W(z, k) is the transfer function of the separator at time k. For successful source recovery, the total system T(z, k) should converge to a matrix with only one non- zero element in each row and column. As in case of instantaneous mixtures, also here a wide variety of different algorithms for separator adaptation exists in the literature, and some of them can be claimed to have the uniform separation performance [14,16,20]. One example is the natural gradient-based approach de- scribed in [20]. This algorithm is applied also in this pa- per in Section 5 to the channel equalization problem in terms of the I and Q signals. 4. Blind I/Q Mismatch & Carrier Offset Compensation In this section, the I/Q mismatch problem due to analog front-end nonidealities as well as the carrier synchrona- tion task are addressed in detail for direct-conversion receivers. The basic idea is to show that both of these practical problems can be viewed to create dependence between the observed I and Q signals. Then, a signal separation algorithm is applied to remove this depend- ence and thus to recover the original I and Q data.. 4.1. Signal Models and I/Q separation-based Compensation I/Qmismatch: For analysis purposes, the received RF signal, say rt, is written as: Re exp cos sin c IcQc rtztj t ztt ztt (6) where, IQ ztz tjzt denotes the corresponding ideal baseband equivalent of the desired channel to be recovered by the receiver front-end. Now, to model the amplitude and phase mismatches of the analog front-end, the (complex) LO signal of the I/Q down- converter is written as:  A Novel Approach to Blind I/Q Mismatch & Carrier Offset Compensation Copyright © 2011 SciRes. JSIP 22 12 cos sin exp exp LO cc cc xttjg t K jt Kjt (7) 12 1 exp1 exp , 22 g jgj KK (8) where, g and φ represent the relative amplitude and phase mismatches, respectively. The latter form of (7) indicates that two frequency translations take place due to mis- matches. Indeed, the down-conversion of r(t) combined with low-pass filtering results in: 12 * x tKztKzt (9) and the corresponding self-image rejection ratio is: 22 10 12 10log KK. To examine the mismatch effect from the I and Q sig- nal point of view, the model in (9) can be written as IQ x txtjxt , where, cos sin II QQI xt zt x tgztg zt (10) In other words, I/Q mismatch tends to create depend- ence between the I and Q signals. Assuming that the original I and Q signals are statistically independent, which holds, for example, for square QAM type of con- stellations, these original I and Q components can be recovered blindly using a signal separation algorithm. Carrier offsets: To see the explicit effect of carrier offsets more for- mally, the I/Q down-converter LO signal is now written as: cos sin exp LO cc c xtt jt jt (11) where, Δω and θ model the frequency and phase offsets, respectively, relative to th e received sign al in (6). Now, it is common to write the down-converted signal after low- pass filtering as: expxt ztjt (12) Interestingly, when written in terms of the I and Q sig- nals, the model in (12) can be expressed as: cos sin cos sin II Q QQ I x ttztjtzt x ttztjtzt (13) Thus, from the I/Q point of view, the carrier offsets correspond to time-varying mixing of the I and Q signals, and an adaptive signal separation algorithm can be used to track and remove this effect. A combined signal model incorporating both the I/Q mismatch and the carrier offset effects is given next. Us- ing analysis similar to those given above, it is relatively easy to show that observable signal after down-conver- sion and low-pass filtering appears as: 1 2 exp *exp xt Kztjt Kz tjt (14) Here it is naturally assumed that the frequency offset is smaller than the guard band between the adjacent fre- quency channels. Now, the complex signal in (14) corre- sponds to an I/Q signal pair of the form: cos sin cos sin IIQ QQ I x ttzttzt xt gtzt gt zt (15) Joint compensation using blind I/Q signal separa- tion: As given in (15), the observable I and Q signals in the presence of I/Q mismatch and carrier offsets appear as instantaneous and time-varying mixtures of the true I and Q signals. Switching to discrete-time notations I x k I x kTs , and so forth, we introduce 2 × 1 source and observation vectors ,T IQ s kzkzk and x k ,T IQ xkxk and write the model in (15) as x(k) = A(k)s(k), where, cos sin sin cos kk Ak gk gk (16) Notice that the frequency offset Δω refers here to the “normalized” frequency variable Δω = 2πΔf / fS. Now an adaptive signal separation algorithm, such as the EASI algorithm discussed in Section 3, can be used to blindly estimate the source signals zI (k) and zQ(k). It is interesting to note that the identifiability of the model in (16) is independent of the carrier offset levels and also practically independent of the mismatch values. This can be seen more formally by examining the deter- minant of A(k): det cosAk g (17) Thus, the system matrix A(k) is invertible given that 0g and /2 . The first requirement (0g ) simply states that the downconversion stage needs to produce two non-zero signals while the second one pre- vents the case where the two signals after down-conver- sion would be just scaled versions of each other. These are more than natural requirements for any I/Q front-end and are always fulfilled by any practical analog design. Thus this indicates that the proposed idea is robust in the face of dif- ferent imbalance and offset levels in terms of identifiability.  A Novel Approach to Blind I/Q Mismatch & Carrier Offset Compensation Copyright © 2011 SciRes. JSIP 23 There are some further practical issues related to the proposed compensation scheme. First of all, as discussed in Section 2, the direct-conversion architecture suffers from the well-known DC offset problem [1,2,4] due to self-mixing of the LO signal leaking into the mixer RF port. Most signal separation algorithms, in turn, assume zero-mean data, so the DC offset needs to be compen- sated prior to the separation stage. Another practical as- pect is related to the amount of frequency offsets toler- ated. On one hand, the frequency offset should be smaller than the guard band between adjacent frequency channels. If not, the receiver is not anymore really zero IF but closer to low IF and the nearby channel signal (or at least part of it located on the true image band) appears as in- terference on top of the desired signal after downconver- sion. On the other hand, the frequency offset determines the dynamics of the system matrix A(k) in (16), which is indeed the dynamics that the adaptive separation algo- rithm needs to follow. In other words, this dynamics should be within the tracking capability of the applied adaptive algorithm. Commonly, this poses some limita- tions to the used step-sizes such that a relatively large stepsize is needed. The used step-size, in turn, is usually directly related to the separator steady-state performance and cannot, of course, exceed its own algorithm-specific stability limit [14,16,19]. Thus we can conclude that even though the frequency offset level is irrelevant from the identifiability point of view, the tracking capability of the practical algorithms as well as the role of the image sig- nal limit the applicability of the proposed concept to mild frequency offset. In other words, coarse frequency syn- chronization should be implemented by other means prior to the separation stage. Notice also that due to the amplitude (sign) and ordering ambiguities mentioned in Section 3, it is possible that the recovered constellation still formally suffers from 1) a constant phase rotation of (integer multiple of) 90 and/or 2) complex conjugation. In practice, these issues can be easily resolved using a little side information in the actual data detection stage. It should be noted that any blind algorithm is subject to similar ambiguities in general. As mentioned above, these ambiguities can be reduced in a later stage of the receiver, for example, by using a minimal number of known symbols (pilot or training sym- bols specified in the signaling frame structure) or by us- ing differential coding/mapping between bits and sym- bols. In general, for modulations other than square QAM, the effects of possible dependence between the true I and Q should be explored individually. 5. Simulations Here some example results are given to illustrate the ef- ficiency of the proposed compensation idea. In the simu- lations, imbalance levels of 3% and 3 are used corre- sponding to an approximate of 30 dB image attenuation which should represent a typical practical case. Phase offset in the system is assumed to be 20 and the (remain- ing) frequency offset 0.0001 × 2π. Given, for example, a 10 MHz sampling frequency, this corresponds to 1 kHz absolute frequency offset. The data modulation is 16 QAM. The model also in- cludes additive white Gaussian noise (AWGN) with the signal-to-noise ratio (SNR) ranging from 0 dB to 20 dB. The EASI algorithm discussed in Section 3 is then used as an example algorithm in the separation stage with a step-size of 0.01 and a third-order (cubic) nonlinearity [19]. The time-varying mixture coefficients are illustrated in Figure 2a, followed below by an example realization of the separator coefficients in Figure 2b with SNR of 20 dB. Clearly, the separation algorithm is able to track the time- varying mixture coefficients successfully. The cor- responding symbol rate output samples without and with compensation are depicted in Figure 3. As is evident, the signal without compensation is useless due to I/Q mis- match and carrier offsets. The compensator output signal, however, is a good estimate of the transmitted symbol constellation. The most fundamental performance measure of any digital communication system is the bit or symbol error rate (BER/SER). This is assessed next for the proposed compensator as a function of additive noise SNR. The decisions are made symbol by symbol using the mini- mum distance detection principle. The obtained results are depicted in Figure 4 which also shows the SER with additive noise only for refere nce. The corresponding SER without any compensation is close to one, independ ently of the SNR, and is not shown for simplicity. As is evident, the proposed compensator can efficiently estimate the transmitted signal, bringing the error rate close to the AWGN bound. Especially in the raw SER levels of 10-1 to 10-2, which is the crucial operating range of any practical system before error- control decoding, the proposed receiver is really close (within 1 dB) to the noise limit. 6. Conclusions In this paper, blind I/Q signal separation-based ap- proaches for receiver signal processing were proposed. More specifically, the I/Q mismatches and carrier offsets as well as the linear distortion due to general band pass channels were shown to create crosstalk between the transmitted I and Q signals. Then compensation structures utilizing blind signal separation were used to compensate for these effects. Also some simulation results were given to illustrate the efficiency of the proposed techniques. Combining the 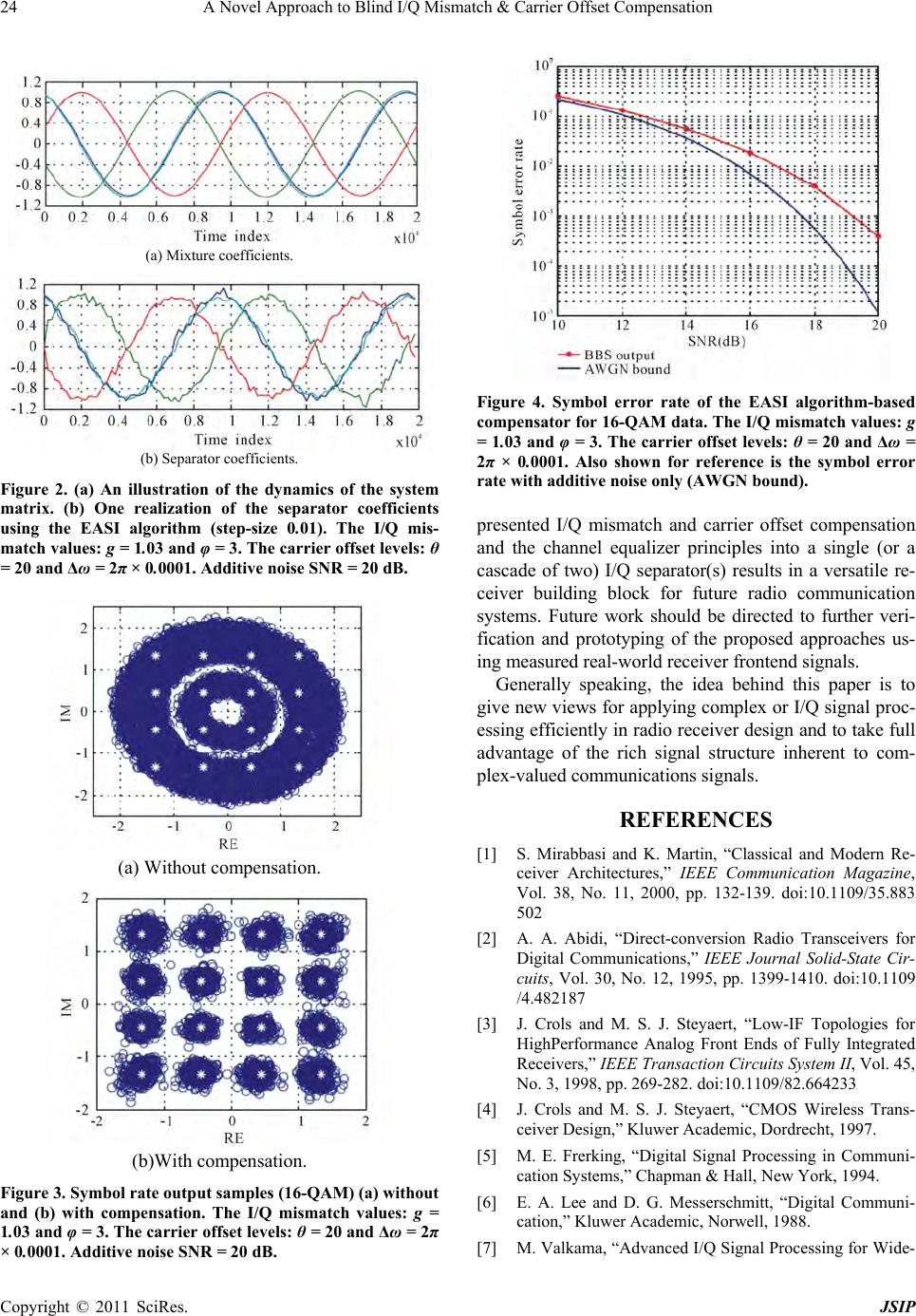 A Novel Approach to Blind I/Q Mismatch & Carrier Offset Compensation Copyright © 2011 SciRes. JSIP 24 (a) Mixture coefficients. (b) Separator coefficients. Figure 2. (a) An illustration of the dynamics of the system matrix. (b) One realization of the separator coefficients using the EASI algorithm (step-size 0.01). The I/Q mis- match values: g = 1.03 and φ = 3. The carrier offset levels: θ = 20 and Δω = 2π × 0.0001. Additive noise SNR = 20 dB. (a) Without compensation. (b)With compensation. Figure 3. Symbol rate output samples (16-QAM) (a) without and (b) with compensation. The I/Q mismatch values: g = 1.03 and φ = 3. The carrier offset levels: θ = 20 and Δω = 2π × 0.0001. Additive noise SNR = 20 dB. Figure 4. Symbol error rate of the EASI algorithm-based compensator for 16-QAM data. The I/Q mismatch values: g = 1.03 and φ = 3. The ca rrier offset levels: θ = 20 and Δω = 2π × 0.0001. Also shown for reference is the symbol error rate with additive noise only (AWGN bound). presented I/Q mismatch and carrier offset compensation and the channel equalizer principles into a single (or a cascade of two) I/Q separator(s) results in a versatile re- ceiver building block for future radio communication systems. Future work should be directed to further veri- fication and prototyping of the proposed approaches us- ing measured real-world receiver frontend signals. Generally speaking, the idea behind this paper is to give new views for applying complex or I/Q signal proc- essing efficiently in radio receiver design and to take full advantage of the rich signal structure inherent to com- plex-valued communications signals. REFERENCES [1] S. Mirabbasi and K. Martin, “Classical and Modern Re- ceiver Architectures,” IEEE Communication Magazine, Vol. 38, No. 11, 2000, pp. 132-139. doi:10.1109/35.883 502 [2] A. A. Abidi, “Direct-conversion Radio Transceivers for Digital Communications,” IEEE Journal Solid-State Cir- cuits, Vol. 30, No. 12, 1995, pp. 1399-1410. doi:10.1109 /4.482187 [3] J. Crols and M. S. J. Steyaert, “Low-IF Topologies for HighPerformance Analog Front Ends of Fully Integrated Receivers,” IEEE Transaction Circuits System II, Vol. 45, No. 3, 1998, pp. 269-282. doi:10.1109/82.664233 [4] J. Crols and M. S. J. Steyaert, “CMOS Wireless Trans- ceiver Design,” Kluwer Academic, Dordrecht, 1997. [5] M. E. Frerking, “Digital Signal Processing in Communi- cation Systems,” Chapman & Hall, New York, 1994. [6] E. A. Lee and D. G. Messerschmitt, “Digital Communi- cation,” Kluwer Academic, Norwell, 1988. [7] M. Valkama, “Advanced I/Q Signal Processing for Wide-  A Novel Approach to Blind I/Q Mismatch & Carrier Offset Compensation Copyright © 2011 SciRes. JSIP 25 band Receivers: Models and Algorithms,” Ph.D. Disser- tation, Tampere University of Technology, Tampere, 2001. [8] G. Fettweis, M. L¨ohning, D. Petrovic, M. Windisch, P. Zillmann and E. Zimmermann, “Dirty RF,” Proceeding on Wireless World Research Forum, Oslo, June 2004. pp. 133-148. [9] M. Valkama, J. Pirskanen and M. Renfors, “Signal Proc- essing Challenges for Applying Software Radio Princi- ples in Future Wireless Terminals: an Overview,” Inter- national Journal of Communication Systems, Vol. 15, 2002, pp. 741-769. doi:10.1002/dac.561 [10] J. P. F. Glas, “Digital I/Q Imbalance Compensation in a low-IF Receiver,” IEEE Proceeding on Global Telecom- munications Conference, Sydney, November 1998, Vol. 3, pp. 1461-1466. [11] ] M. Valkama and M. Renfors, “Digital I/Q Imbalance Compensation in Direct-Conversion Receivers,” Pro- ceeding on Workshop on Software Radios, Karlsruhe, March 2002, pp. 51-55. [12] I.-H. Sohn, E.-R. Jeong and Y. H. Lee, “Data-aided Ap- proach to I/Q Mismatch and DC-offset Compensation in Communication Receivers,” IEEE Communication Let- ters, Vol. 6, No. 12, 2002, pp. 547-549. doi:10.1109/ LCOMM. 2002.806451 [13] J. K. Cavers and M. W. Liao, “Adaptive Compensation for Imbalance and Offset Losses in Direct Conversion Transceivers,” IEEE Transaction on Vehicular Technol- ogy, Vol. 42, No. 4, 1993, pp. 581-588. doi:10.1109 /25.260752 [14] S. Haykin, “Unsupervised Adaptive Filtering, Vol. I: Blind Source Separation,” John Wiley & Sons, New York, 2000. [15] S. Haykin, “Unsupervised Adaptive Filtering, Vol. II: Blind Deconvolution,” JohnWiley & Sons, New York, 2000. [16] A. Hyv¨arinen, J. Karhunen and E. Oja, “Independent Component Analysis,” JohnWiley & Sons, New York, 2001. doi:10.1002/0471221317 [17] J. Eriksson and V. Koivunen, “Identifiability, Separabil- ity, and Uniqueness of Linear ICAmodels,” IEEE Signal Processing Letters, Vol. 11, No. 7, 2004, pp. 601-604. doi:10.1109/LSP.2004.830118 [18] J.-F. Cardoso, “Blind Signal Separation: Statistical Prin- ciples,” Proceeding of the IEEE, Vol. 86, No. 10, 1998, pp. 2009-2025. doi:10.1109/5.720250 [19] J.-F. Cardoso and B. H. Laheld, “Equivariant Adaptive Source Separation,” IEEE Transaction Signal Processing, Vol. 44, No. 12, 1996, pp. 3017-3030. doi:10.1109/78. 553476 [20] S. Amari, S. C. Douglas, A. Cichocki and H. H. Yang, “Multichannel Blind Deconvolution and Equalization us- ing the Natural Gradient,” 1st IEEE Proceeding on Work- shop on Signal Processing Advances in Wireless Com- munications, Paris, April 1997, pp. 101-104.. [21] S. C. Douglas and S. Haykin, “On the Relationship Be- tween Blind Deconvolution and Blind Source Separa- tion,” 31st Proceeding on Asilomar Conference on Sig- nals, Systems, and Computers (ASILOMAR ’97), Calif, November 1997, pp. 1591-1595. [22] S. Haykin, “Adaptive Filter Theory,” 3rd edition, Pren- tice-Hall, New Jersey, 1996. |

