 Engineering, 2013, 5, 226-232 http://dx.doi.org/10.4236/eng.2013.510B047 Published Online October 2013 (http://www.scirp.org/journal/eng) Copyright © 2013 SciRes. ENG Cell Segmentation and Tracking in Microfluidic Platform Lipan Ouyang1, Jiandong Wu2, Michael Zhang3, Francis Lin2, Simon Liao1 1Department of Applied Computer Science, University of Winnipeg, Winnipeg, Canada 2Department of Biosystems Engineering, University of Manitoba, Winnipeg, Canada 3Winnipeg Regional Health Authority, Winnipeg, Canada Email: ************ Received June 2013 ABSTRACT In this research, we have concentrated on trajectory extraction based on image segmentation and data association in order to provide an economic and complete solution for rapid microfluidic cell migration experiments. We applied re- gion scalable active contour model to segment the individual cells and then employed the ellipse fitting technique to process touching cells. Subsequently, we have also introduced a topology based technique to associate the cells between consecutive frames. This scheme achieves satisfactory segmentation and tracking results on the datasets acquired by our microfluidic platform. Keywords: Microfluidic Devic e; Image Segmentation; Data Association; Active Contour Model; Cell Tracking 1. Introduction Cell migration plays an important role in many biomedi- cal fields, such as drug test and disease diagnosis [1]. Traditionally, cell migration is observed under Boyden chamber or Tran swell assays and other cell migration assays. However, these conventional methods lack of chemical gradients control and capability for quantitative analysis and often require large amounts of reagents and cell samples. Compared with the abovementioned me- thods, the microfluidic devices provide a more satisfac- tory platform for quantitative cell migration due to its capability of configuring precise and stable chemical concentration gradients, lower cells and reagents con- sumption, and the potential for high-th roughput experi- ments [2-4]. High-throughput of images makes the manual obser- vation of cell migration a labor-requiring and time-con- suming process, and the accuracy of manual tracking highly depends on the experience and judgment of the individual researchers. Therefore, an effective automatic multiple objects tracking system is essential to conduct the quantitative analysis. Most cell tracking techniques are composed of two phases, detecting and segmenting cells frame by frame, and then associating the detected same cells over two or more consecutive frames. A large number of segmenta- tion methods have been introduced in the past decades, and many of them are still receiving intensive attention from medical image analysis community, such as water- shed [5,6], edge detector [7], split and merge [7-9], re- gion growth [10-12], and some clustering methods [13- 16]. In this research, we have employed the active contour model, which was first introduced by Kass et al. [17]. Given an initial contour, this method would evolve to- wards image features such as object boundaries, and the evolution will continue until the energy functional reaches the minimal. However, the original model is pa- rametric and would fail when topology changes happen [1]. To handle the topology changes, Caselles et al. pro- posed the geodesic active contours with th e flexibility of topology, which evolves the contours under a level-set framework [18]. With the level-set framework, the cell tracking group in Carnegie Mellon University has pro- posed several important improvements of active contour models to distinguish touching cells, though these me- thods require large computational time and memory load [19-23]. The objects association has been a focus o f research ers in some scientific fields such as radar system and video surveillance. Multiple Hypothesis Tracking (MHT) [24] and Joint Probabilistic Data Association Filter (JPDAF) [25] are two well-known examples of using Recursive Bayesian estimation, which is an effective method in objects association. While MHT needs the construction of exhaustive hypothesis set to select the optimal trajec- tory, even with the pruning techniques, this procedure requires substantial computation time and memory space [26]. In contrast, JPDAF is a simpler and suboptimal approach that demands only fixed computational re- sources per iteration [27]. Data association, in general,  L. P. OUYANG ET AL. Copyright © 2013 SciRes. ENG can be regarded as an optimal assignment problem and could be resolved by Hungarian algorithm [28]. We refer to [29] for a background study on data association tech- niques. 2. Device Fabrication and Cell Preparation We have employed the similar fabrica tion of microfluidic devices with the same standard soft-lithography protocol described in [30]. The pattern was designed in a comput- er and printed into a transparency film to make a mask. A silicon wafer was coated with a thin layer of photo resist using a spinner. The master was finished by patterning the design on the wafer through the mask by UV processing. Liquid PDMS was poured on the master and cured in an oven. The PDMS replica was then peeled off and bonded to a glass slide by plasma treating to make the microfluidic device. The device was then coated by fibronection for one hour and blocked by BAS for another hour before starting the cell experiment to help cell bonding and migration on the substrate in the microflui- dic channel. The neutrophils were isolated from human whole blood using the gradient density centrifugation method. The cells were cultured in an incubator before loading in the microfluidic device. A 10 nM IL-8 gradient was gen- erated in the microfluidic channel. The device was then put under the microscope and time-lapse image acquisi- tion and further analysis was done by the custom-devel- oped program. 3. Segmentation by Active Contour Model 3.1. Region-Based Active Contour Models For an image function I(x,y) in the image domain, the CV model proposed by Chan and Ves e [31] is: 2 12 11 () 2 22 () ( ,,)|()| |()|| | outside C inside C F C ccIxcdx I xcdxv C λ λ = − + −+ ∫ ∫ (1) where C is any possible curve, inside(C) and outside(C) are two regions inside and outside the contours, and c1 and c2 are the average image intensity of inside(C) and outside(C), respectively. The first two terms in Equation (1) are called as “global fitting energy”, which will have the minimum values if curve C is the real boundary of an object. Since the CV model is piecewise constant and do not contain any local information, therefore, the optimal constants c1 and c2 might be significantly different from the real image data if the intensities inside or outside the curve C are inhomogeneous. Considering such a situation happens commonly when an image is captured by time- lapse microscopy, the region-based active contour model is a more desirable adaptation in our research. In the re- gion-based active contour model, the global fitting ener- gy is replaced by a Region-Scalable Fitting energy (RSF ), which contains local intensity information . Assume Ω1 = outside(C) and Ω2 = inside(C), the RSF for each pixel is defined as: 2 12 1 2 (,( ),( ))() |()( )| i Fit xi i i Cf xfxKxy I yfxdy ελ Ω = = − − ∫ ∑ (2) where λ 1 and λ 2 are positive constants , and f1(x) and f2(x) are the approximate image intensities in Ω1 and Ω2. The intensities I(y) are taken into account in the fitting energy come from the region centered at pixel x, the size of which is under the control of the kernel function K. A Gaussian kernel was chosen in [32]. Propagating the energy ε Fit x on the entire image, it de- rives the following: 12 12 (,(),( )) (,(),( ))|| Fit x Cfxf x Cfxfxdxv C ε ε = + ∫ (3) The second term in Equation (3) is a penalty term to smooth the contour C. Since this model is parametric, it is necessary to translate the parametric active contour to a geometric active contour, which is more desirable to deal with topology changes [18,33]. By applying Heavi- side and Dir ac functions, numerical approximation of the evolution of the level set function can be written as: 2 1122 || () ()()() || div t vdive e εε φφ µφ φ φ δφδφλ λ φ ∂∇ = ∇− ∂∇ ∇ + −− ∇ (4) 2 ( )()|()( )|,1,2 ii exKyxIxfydy i σ =−− = ∫ (5) where f1 and f2 are () [(())()] (),1, 2 () (()) i i i KxMxIx fx i Kx Mx ε σ ε σ φ φ × = = × (6) For more details of the active contour model, we would refer to [32]. 3.2. Splitting Touching Cells by Ellipse Fitting In general, the segmentation of touching cells is a chal- lenging task [34,35]. When the traced cells enter into a blob, the boundaries of the contacting cells are blurred, and most segmentation algorithms would fail in finding the edges of cells in this situation. In our research, we first select a region larger than the blob where touching happens, then apply the ellipse fit- ting [36,37] to estimate the features of contacting cells. Figure 1(a) shows an example of two touching cells. It is  L. P. OUYANG ET AL. Copyright © 2013 SciRes. ENG (a) (b) (c) (d) (e) (f) Figure 1. (a) Contour of two touching cells; (b) Binary im- age of touching cells; (c) Result of ultimate erosion; (d) The set of candidate ellipses; (e) Best fitting ellipses of all the seeds; (f) Best fitting ellipses after overlapping deletion. obvious that the cells could be presented by two ellipses in this case. Therefore, splitting the cells is equivalent to estimate the parameters of the ellipses which best fit the real data. To apply the ellipse fitting, first, a set of seeds for the closed contours produced by the Region-Scalable Fitting based Active Control model are generated by ultimate erosion, which is a binar y operator in mathematical mor- phology. The ultimate erosion repeat eroding an object until the object disappears, while the residual points are considered as seeds. Figu re s 1(b) and (c) illustrate the beginning and result of an ultimate erosion process, re- spectively. For convenience, we denote the pixels on the contours as C(xc,yc), and the seeds as Si, where i = 1, 2, ..., N and N is the number of seeds. For each of seeds Si, we then sort C(xc,yc) into increasing order according to the distance from C(xc,yc) to Si. At the end of so rting proc ess, there would be N increasing order lists of C(xc,yc), de- noted as Ci sorted(xc,yc). First M elements are selected from Ci sorted(xc,yc) into a set Ci 1(xc,yc), and then incrementally append more elements into the set Ci k(xc,yc), where k means at the kth stage. In each stage, an ellipse is fitted to the pixel coordinates in set Ci k(xc,yc) by direct least squares fitting o f ellipse [38]. After processing all stages, a number of candidate ellipses, as shown in Figure 1(d), are produced and the best fitting ellipse will be selected from them. The obtained 4 best fitting ellipses of the seeds in Figure 1(c) are presented in Figure 1(e). To rank the fitness of the ellipses, we have adopted the fol- lowing measurement (( ,))(( ,)) (|(( ,))| |((,)) |) ii k cck ccobject i k ccobject i objectk cc VCx yaEllipseC x y bEllipse Cxy Ellipse Cxy ϕ ϕ ϕ =⋅ ∩− ⋅ ∩+ ∩ (7) where Ellipse(Ci k(xc,yc)) denotes the ellipse fitted by the point Ci k(xc,yc), ϕ object represents the touching objects, and a and b are the weights. Two essential features are taken into account in our criterion of fitn ess, the first term of Equation (7) rewards the ellipse belonging to the region of object, while and the second term penalizes the ellipse out of the region of object. The ellips e with the high est value of this criterion will be chosen as the best fitting from a list of candidate ellipses. By performing the selection process to all of N increasing order lists, we would obtain N best fitting el- lipses from N seeds. In the ultimate erosion process, since the number of seeds would likely be more than the touching cells, thus it is necessary to make a decision that which of the best fitting ellipses represents the true cell. As a solution, we have arranged the N best fitting ellipses in decrease order by the fitting criterion values, and eliminated all ellipses that have an overlap over 60% with the previously selected ellipse. The rest two ellipses representing the touching cells are shown in Figure 1(f). 4. Data Association Using Graph Theory An association process after successful cell segmenta- tions is to link the corresponding cells between two con- secutive frames. In our cell migration experiment, we have focused on investigating the slower moving cells which are bonded to the glass substrate. Since these un- adhered cells are not desirable and can be discarded, we employ a data association method based on graph theory [39], which is less costly in computational complexity and more suitable to address the adhered cells in our ex- periments. The migration speeds of cells are different in our ex- periments. The cells moving faster are regarded as active cells, while the ones with smaller displacement between two consecutive frames are classified as lazy type. Zhang et al. has presented a real -life example to explain th e idea of this approach [39]. For example, if the neighbors 1, 2, 3, 4, and 5 of A and B in Figure 2(a) are already identi- fied in Figure 2(b), then A, B and X, Y can be matched correctly according to the topology information of their identified n e ighbors. 4.1. Lazy Cells Recognition As the example shown in Figure 2, obtaining the identi- (a) (b) Figure 2. Example of objects association.  L. P. OUYANG ET AL. Copyright © 2013 SciRes. ENG fied neighbors is an essential procedure to discriminate the un-matched objects. Naturally, the objects moving slower are more likely to be recognized, therefor e a good association strategy is to identify these lazy type cells first. In the situation that cells almost remain their posi- tions and shapes, a nearest neighborhood search is an effective method in despite of its simple basis. Assume that N cells (Ti; i = 1, ..., N) have been tracked up to the last frame, and M cells (Ci; i = 1, ..., M) have been detected in the current frame. A cost function is introduced here to present the similarity between Ti and Ci: 22 2 2 22 1(),if 0,otherwise ij ijijii ij i ii dls dj G Cost GLd Sd αβ γ −×+ ×+×< = (8) where Gi is the maximum Euclidean distance that a cell i can move between two consecutive frames, Ldi and Sdi are the maximum differences of perimeters and areas for the possible matched cells between two consecutive frames, r es pectively. If the distance dij is greater than Gi, then Costij is set to zero and the correspondence will be ignored. For each of cells in the current frame, we select the track with the highest Cost value among the N tracks in the last frame and then assign the cell the same label with the track. Sin ce the assignment between a cell and a track is a one to one relationship , a process of optimizing is essential when more than one cell tend to be associated with the same track. Hungarian algorithm [28] is an ef- fective solution to obtain the optimal assignment in our case, and is applied in this study. In our experiments, most of cells nearly maintain th eir positions between two frames. Therefore, lower threshold Gi can significantly reduce the computational time since majority of cells are unnecessary to be considered. The marked lazy cells are presented in Figure 3. 4.2. Active Cells Associat ion by Graph Theory After having successfully tracked lazy cells, which can provide the essential topology information about the neighbors of the unmatched active cells, we now will focus on the unmatched cells pairs. The term of an un- matched cells pair represents an unmatched cell in the current frame and the one in previous frame. Two phases are correlated with the linking of two un- matched cells pairs in consecutive frames. Firstly, a search region is assigned to each of the unmatched cells pairs. If the neighbors in the search region of an un- matched cells pair are the same in the consecutive frames, the two unmatched cells pairs are claimed as associated. In other words, the unmatched cells pair should have the same number of neighbors that are similar in directional positions. The directional position (a) (b) Figure 3. (a) All marked cells in the previous frame; (b) Marked lazy cells in the current frame. is measured by calculating the difference of degree val- ues of each correlated neighborhood pair [39]: k1 ,( ),'() (( ),( )) k F RiFR j Diff AnglekAnglek θ ε + < (9) where Fk and Fk+1 denote the index of frames, R(i) and R'(j) compose an unmatched cells pair, k is the index of the correlated neighbors in the neighborhood group, and Angle indicates the degree value of neighbor in a space centered on the unmatched cells pair. Figure 4 illustrates an example of AngleFk ,R(i)(k) which is represented by D(k). Then, for the rest of unmatched cells, the neighbors of the unmatched cells pair with the same label are called as Share Source Neighborhoods (SSN). The likelihood of a cell pair is evaluat e d by [39]: (( ),'()) (( ),'())(( ),'()) dist SSN QRi Rj QRi R jQRi Rj= × (10) where (( ),'()) (( ),'())(( ),'()) [] dist DS QRiR j DistR iRjSize R iRj exp αβ δδ ×× =−− 1 ,( ),'() 1 ((),'()) (( ))(( )) kk SSN MF RikFRjk k QRi Rj Angle DAngle D exp nbr θ αβ δ + = − − = ∑ 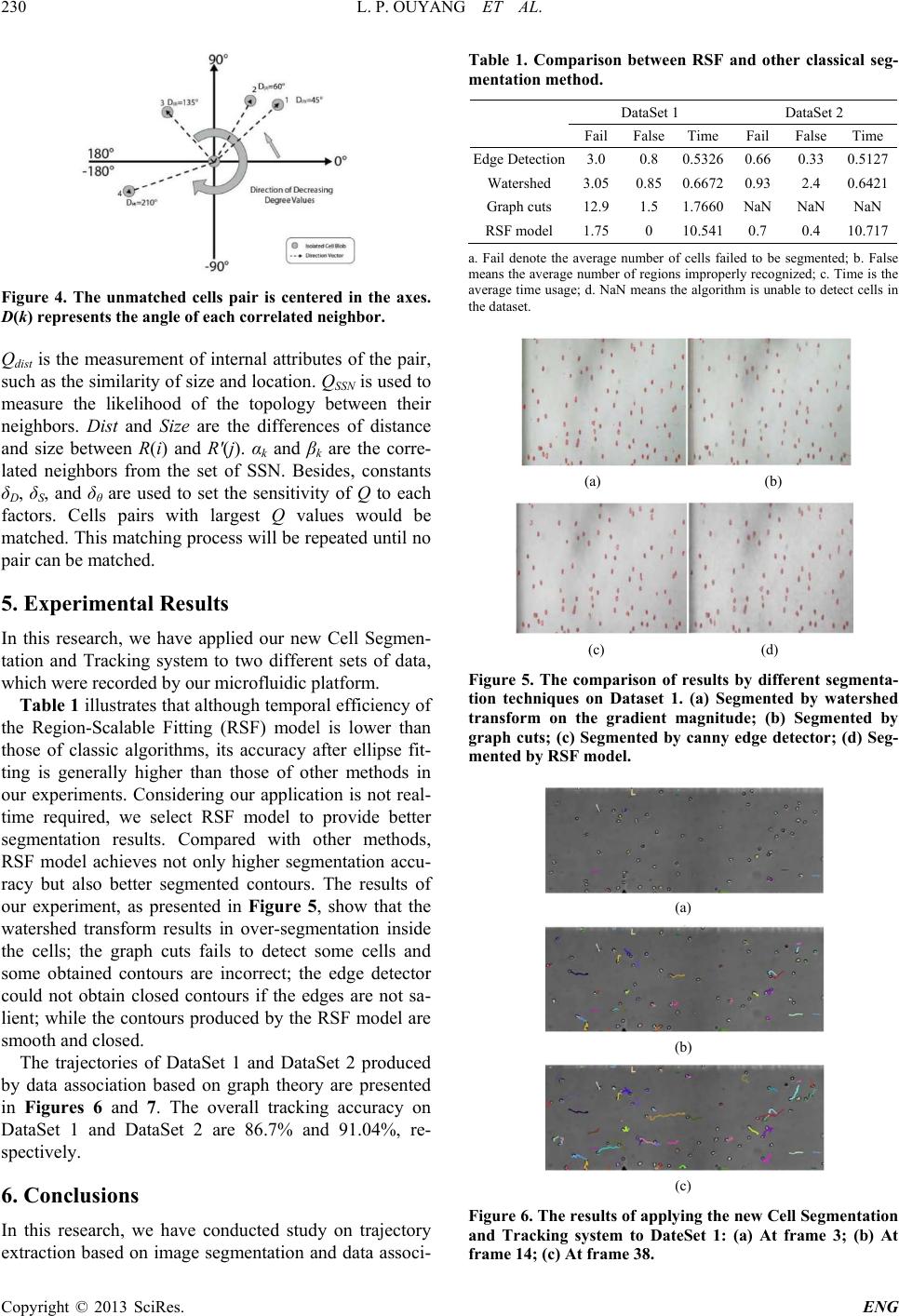 L. P. OUYANG ET AL. Copyright © 2013 SciRes. ENG Figure 4. The unmatched cells pair is centered in the axes. D(k) represents the angle of each correlated neighbor. Qdist is the measurement of internal attributes of the pair, such as the similarity of size and location. QSSN is used to measure the likelihood of the topology between their neighbors. Dist and Size are the differences of distance and size between R(i) and R'(j). αk and βk are the corre- lated neighbors from the set of SSN. Besides, constants δD, δS, and δθ are used to set the sensitivity of Q to each factors. Cells pairs with largest Q values would be matched. This matching process will b e repeated until no pair can be matched. 5. Experimental Results In this research, we have applied our new Cell Segmen- tation and Tracking system to two different sets of data, which were recor ded by our microflui dic platf o rm. Table 1 illu strates that although temporal efficiency of the Region-Scalable Fitting (RSF) model is lower than those of classic algorithms, its accuracy after ellipse fit- ting is generally higher than those of other methods in our experiments. Considering our application is not real- time required, we select RSF model to provide better segmentation results. Compared with other methods, RSF model achieves not only higher segmentation accu- racy but also better segmented contours. The results of our experiment, as presented in Figure 5, show that the watershed transform results in over-segmentation inside the cells; the graph cuts fails to detect some cells and some obtained contours are incorrect; the edge detector could not obtain closed contours if the edges are not sa- lient; while the contours produced by the RSF model are smooth and closed. The trajectories of DataSet 1 and DataSet 2 produced by data association based on graph theory are presented in Figures 6 and 7. The overall tracking accuracy on DataSet 1 and DataSet 2 are 86.7% and 91.04%, re- spectively. 6. Conclusions In this research, we have conducted study on trajectory extraction based on image segmentation and data associ- Table 1. Comparison between RSF and other classical seg- mentation method. DataSet 1 DataSet 2 Fail False Time Fail False Time Edge Detection 3.0 0.8 0.5326 0.66 0.33 0.5127 Watershed 3.05 0.85 0.6672 0.93 2.4 0.6421 Graph cuts 12.9 1.5 1.7660 NaN NaN NaN RSF model 1.75 0 10.541 0.7 0.4 10.717 a. Fail denote the average number of cells failed to be segmented; b. False means the av erage number of regions improperly recognized; c. Time is the average time usag e; d. NaN means the algorit hm is unable to det ect cells in the dataset. (a) (b) (c) (d) Figure 5. The comparison of results by different segmenta- tion techniques on Dataset 1. (a) Segmented by watershed transform on the gradient magnitude; (b) Segmented by graph cuts; (c) Segmented by canny edge detector; (d) Seg- mented by RSF m od el. (a) (b) (c) Figure 6. The results of applying the new Cell Segmentation and Tracking system to DateSet 1: (a) At frame 3; (b) At frame 14; (c) At frame 38.  L. P. OUYANG ET AL. Copyright © 2013 SciRes. ENG (a) (b) (c) Figure 7. The results of applying the new Cell Segmentation and Tracking system to DateSet 2: (a) At frame 2; (b) At frame 22; (c) At frame 45. ation in order to provide a solution for rapid microfluidic cell immigration experiments. We applied region scala- ble active contour model to segment the individual cells and the ellipse fitting technique to process touching cells. We have also introduced a topology based technique to associate the cells between consecutive frames. By applying our new Cell Segmentation and Tracking system to two different sets of data recorded by micro- fluidic device, we have came up with some encouraging outcome. The overall tracking accuracy on two sets of data is 86.7% and 91.04%, respectively. REFERENCES [1] C. Zimmer, E. Labruyere, V. Meas-Yedid, N. Guillen and J. C. Olivo-Marin, “Segmentation and Tracking of Mi- grating Cells in Videomicroscopy with Parametric Active Contours: A Tool for Cell-Based Drug Testing,” IEEE Transactions on Medical Imaging, Vol. 21, No. 10, 2002, pp. 1212-1221. http://dx.doi.org/10.1109/TMI.2002.806292 [2] S. Kim, H. J. Kim and N. L. Jeon, “Biological Applica- tions of Microfluidic Gradient Devices,” Integrative Bi- ology, Vol. 2, 2010, pp. 584-603. http://dx.doi.org/10.1039/c0ib00055h [3] F. Lin, “Chapter 15. A Microfluidics-Based Method for Chemoattractant Gradients,” Methods in Enzymology, Vol. 461, 2009, pp. 333-347. http://dx.doi.org/10.1016/S0076-6879(09)05415-9 [4] F. Li n and E. C. Butcher, “T Cell Chemotaxis in a Simple Microfluidic Device,” Lab on a Chip, Vol. 6, 2006, pp. 1462-1469. http://dx.doi.org/10.1039/b607071j [5] S. Beucher and C. Lantuejoul, “Use of Watersheds in Contour Detection,” International Workshop on Image Processing: Re al-Time Edge and Motion Detec- tion/Estimation, Rennes, 1979. [6] L. Vincent and P. Soille, “Watersheds in Digital Spaces: An Efficient Algorithm Based on Immersion Simulations,” IEEE Transactions on Pattern Analysis and Machine In- telligence, Vol. 13, No. 6, 1991, pp. 583-598. http://dx.doi.org/10.1109/34.87344 [7] R. C. Gonzalez and R. E. Woods, “Digital Image Processing,” 2nd Edition, Addison-Wesley Longman Publishing Co., Inc., Boston, 2001. [8] P. Bonnin, J. B. Talon, J C. Hayot and B. Zavidovique, “A New Edge Point/Region Cooperative Segmentation Deduced from a 3d Scene Reconstruction Application,” SPIE Applications of Digital at Image Processing XII, Vol. 1153, 1990, pp. 579-591. http://dx.doi.org/10.1117/12.962359 [9] P. C. Chen and T. Pavlidis, “Image Segmentation as an Estimation Problem,” Computer Graphics and Image Processing, Vol. 12, No. 2, 1980, pp. 153-172. http://dx.doi.org/10.1016/0146-664X(80)90009-X [10] A. Tremeau and N. Borel, “A Region Growing and Merging Algorithm to Color Segmentation,” Pattern Recognition, Vol. 30, No. 7, 1997, pp. 1191-1203. http://dx.doi.org/10.1016/S0031-3203(96)00147-1 [11] T. Sandor, D. Metcalf and Y.-J. Kim, “Segmentation of Brain ct Images Using the Concept of Region Growing,” International Journal of Bio-Medical Computing, Vol. 29, No. 2, 1991, pp. 133-147. http://dx.doi.org/10.1016/0020-7101(91)90004-X [12] R. Adams and L. Bischof, “Seeded Region Growing,” IEEE Transactions on Pattern Analysis and Machine In- telligence, Vol. 16, No. 6, 1994, pp. 641-647. [13] G. B. Coleman and H. C. Andrews, “Image Segmentation by Clustering,” Proceedings of the IEEE, Vol. 67, No. 5, 1979, pp. 773-785. http://dx.doi.org/10.1109/PROC.1979.11327 [14] D. Comaniciu and P. Meer, “Mean Shift Analysis and Applications,” The Proceedings of the Seventh IEEE In- ternational Conference on Computer Vision, Vol. 2, 1999, pp. 1197-1203. [15] D. Comaniciu and P. Meer, “Mean Shift: A Robust Ap- proach toward Feature Space Analysis,” IEEE Transac- tions on Pattern Analysis and Machine Intelligence, Vol. 24, No. 5, 2002, pp. 603-619. http://dx.doi.org/10.1109/34.1000236 [16] A. K. Jain, M. N. Murty and P. J. Flynn, “Data Clustering: A Review,” ACM Computing Surveys, Vol. 31, No. 3, 1999, pp. 264-323. http://dx.doi.org/10.1145/331499.331504 [17] M. Kass, A. Witkin and D. Terzopoulos, “Snakes: Active Contour Models,” International Journal of Computer Vi- sion, Vol. 1, No. 4, 1988, pp. 321-331.  L. P. OUYANG ET AL. Copyright © 2013 SciRes. ENG http://dx.doi.org/10.1007/BF00133570 [18] V. Caselles, R. Kimmel and G. Sapiro, “Geodesic Active Contours,” 1997. [19] T. Kanade and K. Li, “Tracking of Migrating and Proli- ferating Cells in Phase-Contrast Microscopy Imagery for Tissue Engineering,” In: Y. X. Liu, T. Z. Jiang and C. S. Zhang, Eds., Computer Vision for Biomedical Image Ap- plications, Volume 3765 of Lecture Notes in Computer Science, Springer, Berlin, Heidelberg, 2005, pp. 24-24. [20] S. K. Nath, K. Palaniappan and F. Bunyak, “Cell Seg- mentation Using Coupled Level Sets and Graph-Vertex Coloring,” Medical Image Computing and Comput- er-Assisted Intervention, Vol. 9, Pt. 1, 2006, pp. 101-108. [21] K. Li, E. D. Miller, M. Chen, T. Kanade, L. E. Weiss and P. G. Campbell, “Cell Population Tracking and Lineage Construction with Spatiotemporal Context,” Medical Im- age Analysis, Vol. 12, No. 5, 2008, pp. 546-566. http://dx.doi.org/10.1016/j.media.2008.06.001 [22] K. Li, E. D. Miller, L. E. Weiss, P. G. Campbell and T. Kanade, “Online Tracking of Migrating and proliferating Cells Imaged with Phase-Contrast Microscopy,” Confe- rence on Computer Vision and Pattern Recognition Workshop, 2006, pp. 65-65. [23] D. Padfield, J. Rittscher, N. Thomas and B. Roysam, “Spatio-Temporal Ce ll Cycle Pha se Analy sis Using Level Sets and Fast Marching Methods,” Medical Image Analy- sis, Vol. 13, No. 1, 2009, pp. 143-155. http://dx.doi.org/10.1016/j.media.2008.06.018 [24] D. B. Reid, “An Algorithm for Tracking Multiple Tar- gets,” IEEE Transactions on Automatic Control, Vol. 24, 1979, pp. 843-854. http://dx.doi.org/10.1109/TAC.1979.1102177 [25] T. Fortmann, Y. Bar-Shalom and M. Scheffe, “Mul- ti-Target Tracking Using Joint Probabilistic Data Associ- ation,” 19th IEEE Conference on Decision and Control, 1980, pp. 807-812. [26] Y. Bar-Shalom, “Multitarget-Multisensor Tracking: Ad- vanced Applications,” Artech House, Norwood, 1990, 391 Pages. [27] I. J. Cox, “A Review of Statistical Data Association Techniques for Motion Correspondence,” International Journal of Computer Vision, Vol. 10, 1993, pp. 53-66. http://dx.doi.org/10.1007/BF01440847 [28] H. W. Kuhn, “The Hungarian Method for the Assignment Problem,” Naval Research Logistic Quarterly, Vol. 2, 1955, pp. 83-97. http://dx.doi.org/10.1002/nav.3800020109 [29] Y. Bar-Shalom and T. E. Fortmann, “Tracking and Data Association, Volum e 179 of Mathematics in Science and Engineering,” Academic Press Professional, Inc., San Diego, 1987. [30] F. Lin a nd E. C. Butcher, “T Cell Chemotaxis in a Simple Microfluidic Device,” Lab on a Chip, Vol. 6, 2006, pp. 1462-1469. http://dx.doi.org/10.1039/b607071j [31] T. F. Chan and L. A. Vese, “Active Contours without Edges,” IEEE Transactions on Image Processing, Vol. 10, No. 2, 2001, pp. 266-277. http://dx.doi.org/10.1109/83.902291 [32] C. M. Li , C.-Y. Kao, J. C Gore and Z. H. Ding, “Minimi- zation of Region-Scalable Fitting Energy for Image Seg- mentation,” IEEE Transactions on Image Processing, Vol. 17, No. 10, 2008, pp. 1940-1949. http://dx.doi.org/10.1109/TIP.2008.2002304 [33] V. Caselles, F. Catté, T. Coll and F. Dibos, “A Geometric Model for Active Contours in Image Processing,” Nume- rische Mathematik, Vol. 66, No. 1, 1993, pp. 1-31. http://dx.doi.org/10.1007/BF01385685 [34] O. Al-Kofahi, R. J. Radke, R. K. Goderie, Q. Shen, S. Temple and B. Roysam, “Automated Cell Lineage Con- struction: A Rapid Method to Analyze Clonal Develop- ment Established with Murine Neural Progenitor Cells,” Cell Cycle, Vol. 5, No. 3, 2006, pp. 327-335. http://dx.doi.org/10.4161/cc.5.3.2426 [35] W. M. Yu, H. K. Lee, S. Hariharan, W. Y. Bu and S. Ahmed, “Level Set Segmentation of Cellular Images Based on Topological Dependence,” In Proceedings of the 4th International Symposium on Advances in Visual Computing, ISVC ’08, pages 540-551, Springer-Verlag, Berlin, 2008. [36] G. Zhang, D. S. Jaya s and N. D. G. White, “Separation of Touching Grain Kernels in an Image by Ellipse Fitting Algorithm,” Biosystems Engineering, Vol. 92, No. 2, 2005, pp. 135-142. http://dx.doi.org/10.1016/j.biosystemseng.2005.06.010 [37] J. Hukkanen, A. Hategan, E. Sabo and I. Tabus, “Seg- mentation of Cell Nuclei from Histological Images by El- lipse Fitting,” Proceedings of the European Signal Processing Conference, Aalborg, Denmark, 2010, pp. 1219-1223. [38] A. Fitzgibbon, M. Pilu and R. B. Fisher, “Direct Least Square Fitting of Ellipses,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 21, No. 5, 1999, pp. 476-480. http://dx.doi.org/10.1109/34.765658 [39] L. L. Zhang, H. K. Xiong, K. Zhang and X. B. Zhou, “Graph Theory Application in Cell Nuleus Segmentation, Tracking and Identification,” Proceedings of the 7th IEEE International Conference on Bioinformatics and Bioen- gineering, 2007, pp. 226-232.
|