Energy and Power Engineering, 2013, 5, 677-682
doi:10.4236/epe.2013.54B131 Published Online July 2013 (http://www.scirp.org/journal/epe)
A Critical Eigenvalues Tracing Method for the Small
Signal Stability Analysis of Power Systems
Shao-Hong Tsai1, Yuan-Kang Wu2, C h in g - Yi n Lee3
1Department of Electrical Engineering, Hwa Hsia Institute of Technology.
2Department of Electrical Engineering, National Chung Cheng University.
3Department of Electrical Engineering, Tungnan University.
Received February, 2013
ABSTRACT
The continuation power flow method combined with the Jacobi-Davidson method is presented to trace the critical ei-
genvalues for power system small signal stability analysis. The continuation power flow based on a predictor- corrector
technique is applied to evaluate a continuum of steady state power flow solutions as system parameters change; mean-
while, the critical eigenvalues are found by the Jacobi-Davidson method, and thereby the trajectories of the critical ei-
genvalues, Hopf bifurcation and saddle node bifurcation points can also be found by the proposed method. The numeri-
cal simulations are studied in the IEEE 30-bus test system.
Keywords: Critical Eigenvalue Trajectory; Continuation Power Flow; Hopf bifurcation; Saddle Node Bifurcation;
Small Signal Stability; Jacobi-Davidson Method
1. Introduction
The stability analyses of the rapid increase in complexity
of modern power systems require the development of
efficient and robust numerical methods. In terms of small
signal stability analysis, power systems are usually mod-
eled by systems of differential-algebraic equations with
large nonlinear dynamics. Simulation in frequency do-
main of the resulting dynamical systems heavily relies on
numerical methods for eigenvalue problems and systems
of linear equations. Direct application of conventional
methods (e.g., QR method) for power system eigenvalue
problems is computationally not feasible or inefficient.
Thus, many special intensive researches for the small
signal stability analysis of power systems have been
proposed in the last two decades, which devoted to eva-
luating a selected (critical) subset of eigenvalues associ-
ated with the complete system response.
In [1, 2], only the electromechanical modes; i.e. the
rotor angle ones, are considered to be the critical eigen-
values and computed by a frequency response approach
without formulating the system state matrix. A more
general modal model reduction method, Dominant Pole
Algorithm (DPA), has been proposed in [3] to compute
the dominant poles in any specified Single Input Single
Output (SISO) transfer function. The selective modal
analysis approach [4] uses a reduced order model to
compute the desired critical eigenvalues relevant to the
selected modes. The invariant subspace iteration methods
[5-15] are based on the use of the augmented system
state equations, exploiting the Jacobian matrix sparsity,
and most of them incorporate spectral transformations
such as the shift-invert transformation [5,6], the S-matrix
method [7] and the Cayley transformation [8,9] for the
identification of the set of dominant eigenvalues (i.e., the
largest modulus), which are the mapping of the critical
(i.e., rightmost) eigenvalues of the system state matrix.
Among them, the Jacobi-Davidson (JD) method [14, 15]
is a recently developed subspace iteration method. Based
on its characteristic on iterative construction of a partial
Schur form, the deflation technique, and the effective
restart, the JD method is suitable for the efficient com-
putation of a selected partial eigenvalues and is highly
effective in detecting the clustered eigenvalues.
All of the above mentioned critical eigenvalue solvers
are normally applied to calculate critical eigenvalues
under a given system operating scenario. As the system
equilibrium point often vary with respect to any control
and load variations, critical eigenvalues should also be
recalculated. In such case, the critical eigenvalue trace
methods are of interest to the researchers. In [16], an
integration based eigenvalue trajectory tracing method
was proposed to identify both oscillatory stability margin
and damping margin, and indexes were derived to iden-
tify Hopf bifurcation. A critical eigenvalue tracing me-
thod based on the continuation of the invariant subspace
algorithm combined with the projected Arnoldi method is

S.-H. TSAI ET AL.
678
proposed in [17].
In this paper, the continuation power flow combined
with the Jacobi-Davidson method is proposed to trace the
critical eigenvalues for power system small signal stabil-
ity analysis.
2. Small Signal Stability
The dynamic behavior of power systems can be de-
scribed by a set of nonlinear differential equations to-
gether with a set of algebraic equations (DAEs) [18]
(,, )
0(,,)
f
u
g
u




xxy
xy

(1)
where x is the vector of the state variables, y is the vector
of the algebraic variables, and u is the vector of system
parameters, e.g., the load level of the whole system. In
the case of small signal stability analysis, (1) is linearized
around a system operating point to yield the linearized
DAEs model
() ()
() ()
0
xy
total
xy
fu fu
x
xx
A
gu guyy
 
 


 


 


(2)
where Atotal is the total system Jacobian matrix,  denotes
an incremental change in steady state value. By elimi-
nating the algebraic variables y in (2), the equivalent
system state matrix can be formulated as
1
()()()()
xyyx
A
fufug ugu

 .
According to the Lyapunov's first method [19], the small
signal stability of the nonlinear system (1) in the neigh-
borhood of the operating point can be analyzed by in-
specting the eigenvalues of the linearized system (2); e.g.,
all of the eigenvalues of the system state matrix A should
have negative real parts to maintain the stability. Ac-
cordingly, eigenvalues close to the imaginary axis of the
complex plane are the critical eigenvalues of interest to
analyze the stability of power system oscillations.
Equation (3) describes that the critical eigenvalues and
corresponding eigenvectors construct a dominant invari-
ant subspace with respect to the entire eigenspace of the
system state matrix A.
() ()()()AuVuVuΛu (3)
where the column vectors in V(u) are the basis in the in-
variant subspace, and the eigenvalues of
 (u) are a frac-
tion of the corresponding eigenvalues in the full matrix
A(u). Additionally, when the operating point varies with
respect to the system parameters changes, the critical
eigenvalues and corresponding eigenvectors may also
change. A Hopf bifurcation arises when there is a com-
plex conjugate eigenpair cross the imaginary axis first. In
such case, the system becomes oscillatory unstable. At
the loadability limit, the traditional Newton- Raphson
method of obtaining load flow solution will break down.
In this case, the system Jacobian will become singular,
thus so-called saddle node bifurcation.
3. Critical Eigenvalues Tracing Method
The idea of proposed method is based on combing con-
tinuation power flow with the Jacobi-Davidson method
to identify and trace the critical eigenvalue trajectories.
The continuation power flow calculates a series of power
system steady state solutions with respect to a given
power injection variation scenario. During the continua-
tion power flow process, the Jacobi-Davidson method
with deflation technique is applied to effectively calcu-
late the critical eigenvalues, and thereby the critical ei-
genvalue trajectories, Hopf bifurcation (HB) and saddle
node bifurcation (SNB) points can also be found.
3.1. Continuation Power Flow
The concept of the continuation power flow [20] is based
on a predictor-corrector technique to evaluate a con-
tinuum of steady state power flow solutions starting at
some base load and leading to the steady state stability
limit (SNB) of the system. A salient feature of the con-
tinuation power flow is that it remains well-conditioned
around the SNB point. As a consequence, divergence due
to ill-conditioning is not encountered in the vicinity of
SNB point, even when single-precision computation is
used.
The continuation power flow based on a predictor-
corrector technique is described as follows, and is shown
in Figure 1.
 Predictor step: The function of the predictor is to
find an approximation point for the next solution. – Sup-
pose the continuation process is at the ith step with the
solution (, ,).
iii
x
yu The predictor tries to find an approxi-
mation point(, ,)
p
pp
x
yu for next solution )
1!1
(,,
iii
x
yu

,
and can be formulated as
Figure 1. Continuation power flow .

S.-H. TSAI ET AL. 679
pi
pi
pi
x
xx
yy
uu

 
 







y
u
(4)
where u is the loading parameter which will vary from
base case to the point of maximum loadability,  is the
step-size for the next prediction, and


































1
0
0
1
T
k
uyx
uyx
e
ggg
fff
u
y
x
where ek is a column vector of zeros with a single 1 at the
position of the unknown that is chosen to be the con-
tinuation parameter.
 Corrector step: Using the predicted value as the ini-
tial condition),, for the nonlinear iteration, the
augmented power flow equations (5)-(6) are then solved
by the Newton iterative method to achieve the solu-
tion ),,( 111 i
y.
(ppp uyx
i
u
i
x
1
0
xyu
xyu
T
k
x
fff f
ygggg
ue


 
  
 
 
  

  

(5)
1
1
1
ip
ip
ip
x
xx
yy
uu








y
u
(6)
3.2. Jacobi-Dav ids on M e t hod
The Jacobi-Davidson (JD) subspace iteration method [14]
is applicable to a selected eigenvalue and corresponding
eigenvector approximations of a general unsymmetric
matrix A, in which each iteration combines the
idea of Davidson’s and Jacobi’s methods. In this ap-
proach, a search subspace span{V} is generated onto
which the given eigenproblem, , is projected,
where V is a complex n matrix and its columns
constitute an orthonormal basis v1,v2,…,vj, j<<n. The
‘Davidson’ part, based on the Ritz-Galerkin condition:
nn

qλAq 
j
},...,,{
~
21vvvVuλj
AVu , is to select an approximate
eigenpair of A with the reduced system, which
can be represented as
jj
.0)
~
(**  uVVλAVV (7)
Then the projected eigenproblem (7) is solved and a
solution is selected. The Ritz pair is defined as
to form an approximate eigenpair of A, with
the residual vector
),
~
(uλ
)Vu
~
,
~
(qλ
qIλAr
~
)
~
( . The ‘Jacobi’ part
forms an orthogonal correction for the current eigenvec-
tor approximation q
~
, by the solution of qv
~
 in the
following correction equation







.)
~~
)(
~
)(
~~
(
0
~
**
*
rvqqIIλAqqI
vq (8)
Equation (8) defines an optimal expansion (orthogonal
basis) of the search subspace, span{V, v}; the search
subspace accumulates valuable information for the de-
sired eigenvector approximation for every iteration.
When the search subspace V reaches a certain maxi-
mum dimensionnj


max , the JD method adopts an im-
plicit restart strategy to reduce the dimension of the
search subspace from jmax to jmin (jmin ≤ j ≤ jmax) by dis-
carding the columns 1
min j
v through, and contin-
ues the next JD iteration with min . Here,
the JD algorithm is obviously easy to implement because
is already orthogonal, and the JD algo-
rithm is repeated until the norm of the residual ||r|| is
smaller than a given tolerance.
max
j
v
1(:,VU ): jV 
):1(:,min jVU
A JD-style method, called JDQR [15], is designed to
find a number of desired eigenpairs by constructing a
partial Schur form of A iteratively. A deflation technique
has been successfully incorporated into the JDQR me-
thod, which would avoid repeated computation of the
detected eigenvalues. The JDQR method is described as
follows.
Suppose that k-1 Schur pairs have been detected and
formed with the partial Schur form111 

kkkRQAQ ,
where 1k is a Q)1(


kn
(k
,(λ
matrix with orthonormal
columns, and 1k is a upper triangu-
lar matrix. The diagonal elements of Rk-1 are eigenvalues
of A, and the first column of Qk-1 is an eigenvector of A.
A suitable new Schur pair will be used to expand
and , so that
R)1()1 k
)q
1k
Q1k R








 λ
sR
qQqQAk
kk 0
1
11 (9)
where , which satisfies
qIλAQs k)(
*
1 









.0))()((
,0
*
11
*
11
*
1
qQQIIλAQQI
qQ
kkkk
k (10)
Thus, the new Schur pair is also an eigenpair
of the deflated matrix ,
and the deflated matrix
),( qλ
1
kQQ )()(
ˆ*
11
*
1 kkk QQIAIA
A
ˆ
)( I
has the same eigenvalues as
A except the detected eigenvalues that are transformed to
zero; the deflation part 11  effectively avoids
repeated computation of the detected eigenvalues. Then,
the search subspace span {V} is expanded by the or-
thogonal complement of v to V, where v is the solution of
the following deflated correction equation
*
kk QQ












,)
~~
(
))(
~
)()(
~~
(
and0
~
,0
*
*
11
*
11
*
**
1
rvqqI
QQIIλAQQIqqI
vqvQ
kkkk
k
(11)

S.-H. TSAI ET AL.
680
where and
.
qQQIIλAQQIr kkkk ~
))(
~
)(( *
11
*
11  
0
~
*
1qQk
3.3. Implementation of Algorithm
The flowchart of the solution algorithm is shown in Fig-
ure 2, and the step-by-step procedure is described as
follows:
a) Solve base case power flow solution: Perform a
specified base case Newton-Raphson power flow for
evaluating the initial conditions of state variables.
b) Find Jacobian matrix: Compute the linearized DAEs
model (2) by both the initial conditions and the power
flow solution.
c) Find critical eigenvalues: Compute the critical ei-
genvalues of the Jacobian matrix by the JD method with
a given sorting criterion, i.e. the rightmost eigenvalues or
the least damping ratio eigenvalues.
d) Identify Hopf bifurcation: Detect the real part of the
critical eigenvalues for Hop bifurcation, i.e. the complex
conjugate eigenvalue crosses through the imaginary axis
of the complex plane first.
e) Find the next equilibrium states: Perform the con-
tinuation power flow with a given control strategy (a
specified control variable and increment factor) for the
next operating equilibrium states.
Figure 2. Flowchart for critical eigenvalues tracing.
f) Identify stability limit: Check the SNB point by
monitoring the control variable variations. If the system
reaches to the SNB point, stop the algorithm; otherwise
go to step b).
4. Numerical Results
In this section, numerical examples were examined
through the IEEE-30 bus test system. The system has 6
machines and 59 state variables, and the dynamic model
is linearized around a base operation point with a total
load of 275.2 MW. Figure 3 shows the distribution of
the partial rightmost eigenvalues at the based load. The
software package MATLAB v7.1 is used to implement
the proposed method. In our work, the damping ratio and
the real part of the eigenvalues were used as the selection
criteria to trace the critical eigenvalues. The convergence
tolerance of the JD method is set to 10-8. The load in-
crease pattern is mainly performed on the PQ buses
starting at the base load and leading to the steady state
stability limit of the system.
4.1. Tracing of the Rightmost Eigenvalues
For this case, the critical eigenvalues with largest real
part are the desired eigenvalues. There are 6 rightmost
eigenvalues are traced by the proposed method as shown
in Figure 4. The Hopf bifurcation occurs on the 1.859
p.u. load level with respect to the base case, i.e., there is
an eigenpair passing through the imaginary axis of the
complex plane. When the system has a load level of
2.275 p.u., the system reaches to stability limit, i.e., the
SNB occur. In such case, the system operates at point
where the Jacobian matrix has a zero eigenvalue. When
system power demands go beyond the maximum power
limit, the power system is divergent and becomes un-
solvable. The continuation power flow remains well-
conditioned around the SNB point.
-10-9 -8 -7-6-5 -4-3 -2 -10
-20
-15
-10
-5
0
5
10
15
20
Real
Imag
Figure 3. Distribution of the partial rightmost eigenvalues
for the IEEE-30 bus test system.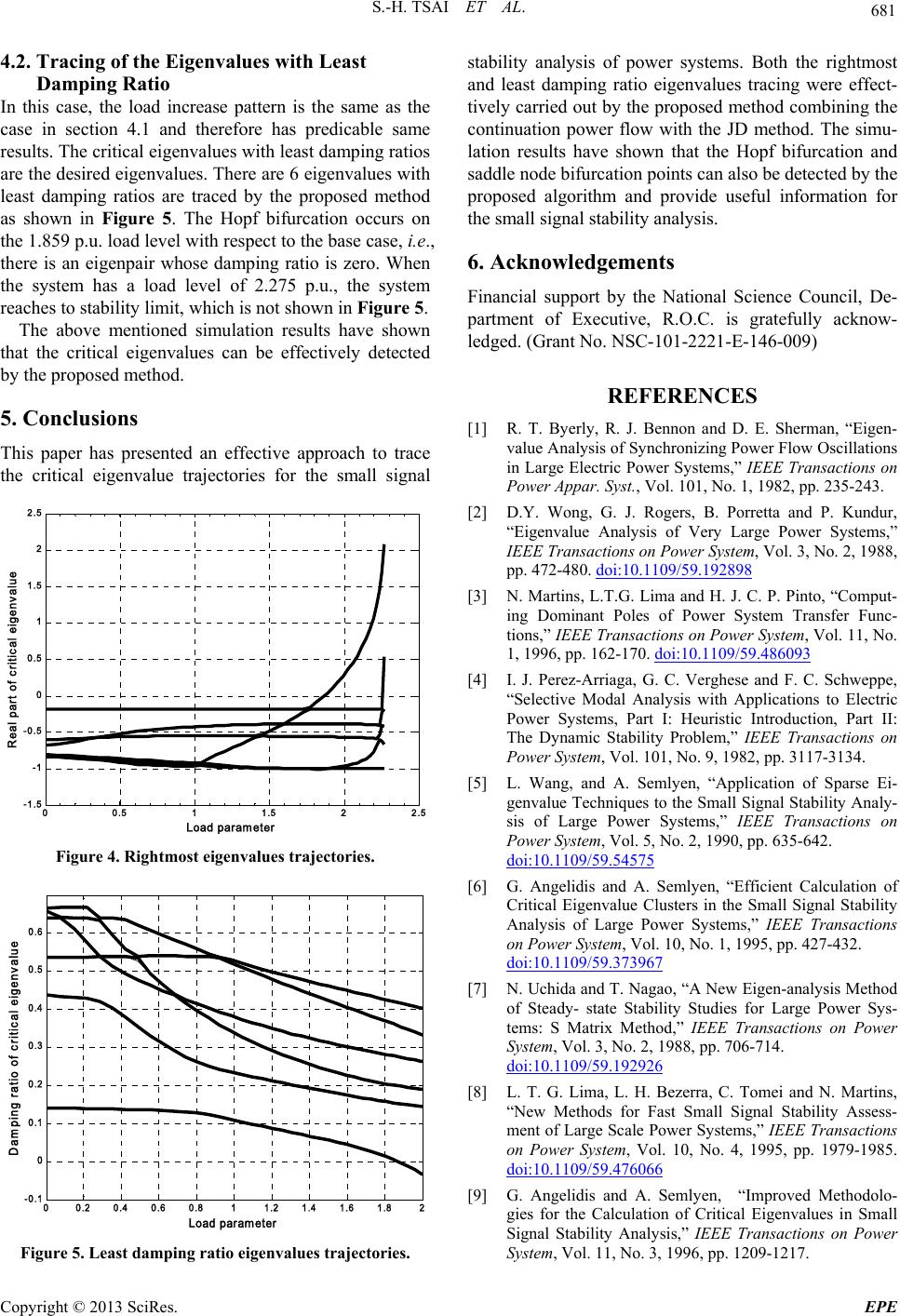

S.-H. TSAI ET AL. 681
4.2. Tracing of the Eigenvalues with Least
Damping Ratio
In this case, the load increase pattern is the same as the
case in section 4.1 and therefore has predicable same
results. The critical eigenvalues with least damping ratios
are the desired eigenvalues. There are 6 eigenvalues with
least damping ratios are traced by the proposed method
as shown in Figure 5. The Hopf bifurcation occurs on
the 1.859 p.u. load level with respect to the base case, i.e.,
there is an eigenpair whose damping ratio is zero. When
the system has a load level of 2.275 p.u., the system
reaches to stability limit, which is not shown in Figure 5.
The above mentioned simulation results have shown
that the critical eigenvalues can be effectively detected
by the proposed method.
5. Conclusions
This paper has presented an effective approach to trace
the critical eigenvalue trajectories for the small signal
00.5 11.5 22.5
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
Load parameter
Real part of critical eigenv alue
Figure 4. Rightmost eigenvalues trajectories.
00.2 0.4 0.6 0.811.2 1.4 1.6 1.82
-0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
Load parameter
D am ping ratio of c ritical eigenvalue
Figure 5. Least damping ratio eigenvalues trajectories.
stability analysis of power systems. Both the rightmost
and least damping ratio eigenvalues tracing were effect-
tively carried out by the proposed method combining the
continuation power flow with the JD method. The simu-
lation results have shown that the Hopf bifurcation and
saddle node bifurcation points can also be detected by the
proposed algorithm and provide useful information for
the small signal stability analysis.
6. Acknowledgements
Financial support by the National Science Council, De-
partment of Executive, R.O.C. is gratefully acknow-
ledged. (Grant No. NSC-101-2221-E-146-009)
REFERENCES
[1] R. T. Byerly, R. J. Bennon and D. E. Sherman, “Eigen-
value Analysis of Synchronizing Power Flow Oscillations
in Large Electric Power Systems,” IEEE Transactions on
Power Appar. Syst., Vol. 101, No. 1, 1982, pp. 235-243.
[2] D.Y. Wong, G. J. Rogers, B. Porretta and P. Kundur,
“Eigenvalue Analysis of Very Large Power Systems,”
IEEE Transactions on Power System, Vol. 3, No. 2, 1988,
pp. 472-480. doi:10.1109/59.192898
[3] N. Martins, L.T.G. Lima and H. J. C. P. Pinto, “Comput-
ing Dominant Poles of Power System Transfer Func-
tions,” IEEE Transactions on Power System, Vol. 11, No.
1, 1996, pp. 162-170. doi:10.1109/59.486093
[4] I. J. Perez-Arriaga, G. C. Verghese and F. C. Schweppe,
“Selective Modal Analysis with Applications to Electric
Power Systems, Part I: Heuristic Introduction, Part II:
The Dynamic Stability Problem,” IEEE Transactions on
Power System, Vol. 101, No. 9, 1982, pp. 3117-3134.
[5] L. Wang, and A. Semlyen, “Application of Sparse Ei-
genvalue Techniques to the Small Signal Stability Analy-
sis of Large Power Systems,” IEEE Transactions on
Power System, Vol. 5, No. 2, 1990, pp. 635-642.
doi:10.1109/59.54575
[6] G. Angelidis and A. Semlyen, “Efficient Calculation of
Critical Eigenvalue Clusters in the Small Signal Stability
Analysis of Large Power Systems,” IEEE Transactions
on Power System, Vol. 10, No. 1, 1995, pp. 427-432.
doi:10.1109/59.373967
[7] N. Uchida and T. Nagao, “A New Eigen-analysis Method
of Steady- state Stability Studies for Large Power Sys-
tems: S Matrix Method,” IEEE Transactions on Power
System, Vol. 3, No. 2, 1988, pp. 706-714.
doi:10.1109/59.192926
[8] L. T. G. Lima, L. H. Bezerra, C. Tomei and N. Martins,
“New Methods for Fast Small Signal Stability Assess-
ment of Large Scale Power Systems,” IEEE Transactions
on Power System, Vol. 10, No. 4, 1995, pp. 1979-1985.
doi:10.1109/59.476066
[9] G. Angelidis and A. Semlyen, “Improved Methodolo-
gies for the Calculation of Critical Eigenvalues in Small
Signal Stability Analysis,” IEEE Transactions on Power
System, Vol. 11, No. 3, 1996, pp. 1209-1217.

S.-H. TSAI ET AL.
682
doi:10.1109/59.535592
[10] P. Kundur, G. J. Rogers, D. Y. Wong, L. Wang and M. G.
Lauby, “A Comprehensive Computer Program Package
for Small Signal Stability Analysis of Power Systems,”
IEEE Transactions on Power System, Vol. 5, No. 4, 1990,
pp. 1076-1083. doi:10.1109/59.99355
[11] B. Lee, H. Song, S.-H. Kwon, D. Kim and K. Iba, “Cal-
culation of Rightmost Eigenvalues in Power Systems Us-
ing the Block Arnoldi Chebyshev Method (BACM),” IET
Gener. Transm. Distrib., Vol. 150, No. 1, 2003, pp. 23-27.
doi:10.1049/ip-gtd:20020718
[12] J. Rommes and N. Martins, “Efficient Computation of
Transfer Function Dominant Poles Using Subspace Ac-
celeration,” IEEE Transactions on Power System, Vol. 21,
No. 3, 2006, pp. 1218-1226.
doi:10.1109/TPWRS.2006.876671
[13] N. Martins, “The Dominant Pole Spectrum Eigensolver,”
IEEE Transactions on Power System, Vol. 12, No. 1,
1997, pp. 245-254. doi:10.1109/59.574945
[14] G. L. G. Sleijpen and H. A. Van Der Vorst, “A Jaco-
bi–Davidson Iteration Method for Linear Eigenvalue
Problems,” SIAM Journal on Matrix Analysis Applica-
tions, Vol. 17, No. 2, 1996, pp. 401-425.
doi:10.1137/S0895479894270427
[15] D. R. Fokkema, G. L. G. Sleijpen and H. A. Van Der
Vorst, “Jacobi-Davidson Style QR and QZ Algorithm for
the Reduction of Matrix Pencils,” SIAM Journal on Sci-
entific Computing, Vol. 20, No. 1, 1998, pp. 94-125.
doi:10.1137/S1064827596300073
[16] X. Y. Wen and V. Ajjarapu, “Application of a Novel
Eigenvalue Trajectory Tracing Method to Identify Both
Oscillatory Stability Margin and Damping Margin,” IEEE
Transactions on Power System, Vol. 21, No. 2, 2006, pp.
817-823. doi:10.1109/TPWRS.2006.873111
[17] D. Yang and V. Ajjarapu, “Critical Eigenvalues Tracing
for Power System Analysis Via Continuation of Invariant
Subspaces and Projected Arnoldi Mthod,” IEEE Transac-
tions on Power System, Vol. 22, No. 1, 2007, pp. 324-332.
doi:10.1109/TPWRS.2006.887966
[18] P. W. Sauer and M. A. Pai, “Power System Dynamics and
Stability,” Prentice-Hall, Inc., New Jersey, USA, 1998.
[19] A. Lyapunov, “The General Problem of the Stability of
Motion,” Taylor and Francis, London, 1892.
[20] V. Ajjarapu C. Christy, “The Continuation Power Flow:A
Tool for Steady State Voltage Stability Analysis,” IEEE
Transactions on Power System, Vol. 7, No. 1, 1992, pp.
416-423. doi:10.1109/59.141737