 Energy and Power Engineering, 2013, 5, 670-676 doi:10.4236/epe.2013.54B130 Published Online July 2013 (http://www.scirp.org/journal/epe) Optimal Static State Estimation Using hybrid Particle Swarm-Differential Evolution Based Optimization Sourav Mallick, S. P. Ghoshal, P. Acharjee, S. S. Thakur Department of Electrical Engineering, National Institute of Technology, Durgapur, India Email: sourav.nitdgp2009@gmail.com, spghoshalnitdgp@gmail.com, parimal.acharjee@ee.nitdgp.ac.in, sst_nit_ee@yahoo.co.in Received February, 2013 ABSTRACT In this paper, swarm optimization hybridized with differential evolution (PSO-DE) technique is proposed to solve static state estimation (SE) problem as a minimization problem. The proposed hybrid method is tested on IEEE 5-bus, 14-bus, 30-bus, 57-bus and 118-bus standard test systems along with 11-bus and 13-bus ill-conditioned test systems under dif- ferent simulated conditions and the results are compared with the same, obtained using standard weighted least square state estimation (WLS-SE) technique and general particle swarm optimization (GPSO) based technique. The perform- ance of the proposed optimization technique for SE, in terms of minimum value of the objective function and standard deviations of minimum values obtained in 100 runs, is found better as compared to the GPSO based technique. The sta- tistical error analysis also shows the superiority of the proposed PSO-DE based technique over the other two tech- niques. Keywords: Differential Evolution; Ill-conditioned System; Particle Swarm Optimization; State Estimation 1. Introduction An electric power system can be operated in efficient, economic and secure manner if the states are known for a known network topology and loading conditions [1]. The concept of state estimation (SE) was first introduced by Schweppe et al. [2] to find the best estimate of the states by minimizing or maximizing a selected criterion by us- ing redundant imperfect power system measurements. Thereafter, the volume of research works on SE has grown enormously and it has become a basic function in power system control centers (ECCs), specified by elec- tric utilities as a mandatory requirement and supplied by all major control centers as a standard software product. Although the SE has become a mature, field-proven workhorse, various aspects of SE like the solution algo- rithm [3-6], detection and identification of bad data [7-9], topological error detection [10-12], observability analysis [13,14] continue to be explored so as to enrich the SE software used in ECCs. Conventional SE methods as- sume that the objective function related to SE is differen- tiable and continuous. However, considering the nonlin- ear characteristics of the practical equipments, the objec- tive function is not always differentiable and continuous, and it is difficult to apply the conventional methods prac- tically. Therefore, a practical SE method considering the above-mentioned requirements has been eagerly awaited. Modern heuristic algorithms are considered as effective tools for nonlinear optimization problems. The algo- rithms do not require the objective function to be differ- entiable and continuous. Particle swarm optimization (PSO), one of the meta-heuristic algorithms, can be ap- plied to nonlinear and non-continuous optimization problems with ntinuous variables such as in SE. Based on the social behavior of birds’ flocking or fish schooling, particle swarm optimization (PSO) was de- veloped by Eberhart and Kennedy in 1995 [15]. PSO is biologically inspired computational stochastic search method which requires little memory. PSO has fast con- verging feature and better global searching ability at the beginning of the run [16]. But, it has local searching problem near the end of the run. It suffers from local optima at the end of execution of a program [17]. In or- der to overcome this local optima problem, many im- provisations are adopted by the researchers [16-19]. In 1995, in a pioneer paper, Storn and Prince proposed an algorithm [20] based on floating point encoded evolu- tionary technique for global optimization. This algorithm is termed as DE algorithm because in this algorithm, a special kind of differential operator is used to create new off-springs from parent chromosomes instead of classical crossover or mutation. Here, the target vector is mutated to find a trial vector using a difference vector which is obtained as a weighted difference between randomly selected vectors in the population. T. Hendtlass presented Copyright © 2013 SciRes. EPE  S. MALLICK ET AL. 671 a new population based algorithm as a hybrid of PSO and DE [21]. A few variants of this hybridization came later from various researchers [22,23] for different applica- tions. In this paper, to improve both global and local search- ing performance of PSO and to avoid suboptimal solu- tions, hybrid particle swarm-differential evolution opti- mization (PSO-DE) has been proposed to solve SE as an optimization problem. This also improves the error per- formance analysis based on statistical indices of SE. The proposed scheme of SE has been tested on different standard IEEE test systems and ill-conditioned systems under different simulated operating conditions and the results have been compared to those of standard Weighted Least Square (WLS) technique and general PSO (GPSO) based technique. 2. Problem Formulation 2.1. Weighted Least Square Estimation In SE, a power system with m-dimensional measurement vector z and n-dimensional state vector x may be mod- eled as, zhx (1) where is the m-dimensional vector of non-linear power flow equations and .h is the m-dimensional noise vector with the statistical properties, 0;E E. TR where E and superscript ‘T’ represent expectation operator and transposition of a matrix, respectively. ‘R’ is a diagonal matrix and is known as measurement error co-variance matrix. The WLS SE determines the esti- mated value of the state vector ˆ minimizing the per- formance index 1 .. T xzhxRzhx 1 (2) Minimization of (2) yields iterative solution as: 1 1TT HRHHR z k (3) where 1k xx and are known as the correction vector and mismatch vector, respec- tively; k being the index of iteration. k zzhx hx x is the Jacobian matrix. Using index notation, (2) can also be expressed as an optimization problem with the weighted sum of the squares of the residues as objective or fitness function . 2 1 m ii ii i xwzhx (4) In (4), weighting factor 2 1/ ii ii w , ii being the standard deviation of the meter error. 2.2. Particle Swarm Optimization with Differential Evolution GPSO is biologically inspired computational stochastic search method which requires little memory. GPSO ran- domly initializes the population (swarm) of individuals (particles) in the search space. Each particle in GPSO has a randomized velocity associated to it, which moves through the space of the problem [15,16]. The particle velocity is constantly adjusted according to the experi- ences of the particles and its companions. The velocity k v and position k h of particle index ‘j’ of kth popula- tion in the search space are adjusted by (5)-(7). maxmaxmin *max cy www wcy (5) ,1 ,, ,, , ,, *1*1* +2*2* k kk k jcy jcyjcy pbestj cy k cy j gbest cy wcrx vv x cr xx (6) ,1 ,,1 kkk cyj cyj cy xxv (7) where (6) represents the updated value of w with itera- tion cycle; ,, k bestj cy x represents pbest position at cyth iteration, i.e., the best position of the particle in the cur- rent iteration; ,, gbest cy denotes the global best position gbest, i.e., the best position of the particle in the popula- tion up to the present iteration and maxcy is the maxi- mum number of iteration cycles. After obtaining the suboptimal values of fitness function for total population set, differential evolution (DE) algorithm have been ap- plied to find the optimal solution. In DE, the initial pop- ulation is the population obtained from GPSO. The steps to incorporate DE algorithm with GPSO are shown be- low as x i Initialize population of particles (solutions).Set GPSO and DE parameters. ii Calculate fitness values and find gbest and pbest values. iii PSO is used to update velocities and positions of particles using (6) and (7). iv For the total population set, fitness values are cal- culated according to (4). These suboptimal fitness values are termed as . os GPSO Ct v The updated population set is used as the input of DE. The donor vector is calculated as, 12 1 , , 1* 2* HJK HJK kk donor jjjj cy k gbest jj xxFxx Fx x (8) where 1HJK and are indices generated within the population, to select the two random vectors within the population. 2HJK vi The fitness values are evaluated within the popula- tion using (4) and is termed as os onor Ct Copyright © 2013 SciRes. EPE  S. MALLICK ET AL. 672 vii Trial vectors Trial are formed by random cross- over of elements of donor vectors and target vectors de- pending on random number generated within ([0,1]), greater or less than a fixed probabilistic crossover ratio value (CRR = 0.3, in this case). If CRR is less than the random number, is assigned to ,Trialj x, onor j x; otherwise is assigned to ,Trialj x . viii The fitness function is evaluated for each jth trial vector using (4) and termed as. os Trial Ct ix In the Selection stage, either , onorj or ,Trialjis selected ( x x elect x os ) depending on the minimum value be- tween ono Ct r x Using the selected vectors , and . os Trial Ct Select xx and x bestgbest are updated. xi Check whether the maximum iteration cycle is reached, if yes, then x best is the optimal solution vector. Otherwise, go to step iii with the vectors as the input vectors of the GPSO. Select x 2.3. Bad Data Analysis For detection and identification of bad data, scheme proposed by N.G. Bretas et al. [9] has been adopted in this paper for its high efficiency. The idempotent matrix is formed as 1 PTT1 HRHHR z (9) The measurement residuals are expressed as ˆIM rzzzPzI PzS (10) Here, S(=IM P) is called the residual sensitivity matrix. M is the identity matrix with dimension equal to the length of Y. e is the complex noise vector. This S matrix is the operator that projects onto measure- ment Jacobean space (R(Y) ┴). Now for the ith measurement vector, that is, i m ii M with and i [0....1 ....0] i i T is the magnitude of the measurement i, the two components of measure- ments are found to be R( )R( ) P and (P) i YiiIMii iY MMMIM . Therefore, the innovative index (II) is calculated as R( ) R( ) i iY W W II MM iY (11) The largest element (Nth) in II is compared against a statistical threshold, , to decide on the exis- tence of bad data. The index value of the largest element gives the index of bad data of measurement. As the presence of bad data is detected and indentified, the measurements should be recovered from errors. The cor- rected normalized measurement error is computed using the following equation as suggested in [9]. 0.250 222 11 i m eII where is the measurement ith residual measurement. i In a power system, a sudden large change of load may occur. Therefore, it is very important to discriminate be- tween sudden large change of load and the presence of bad data in measurements. For this discrimination, an index, called asymmetry index (AI) [8], has been used. AI is defined as r 3 3, kk AI M (13) where 3,k is the third moment of the discrimination at time k and k t is the standard deviation of the distri- bution at . If AI is greater than a pre defined value (here k t max ), then measurements are with gross errors and if AI is less than max , large load change occurred is considered. 3. Simulation Details The simulation study has been carried over a period of 30 time samples by linearly varying the load at each bus from 70% to 120%. In addition, the system jitter is rep- resented by a normally distributed random fluctuation with a zero mean and a standard deviation of 2% of the trend component. As load variation is not possible for ill-conditioned systems, it is not done. The power factor is assumed to be constant, so that the reactive power fol- lowed the active counterpart. The change in total load has been distributed among the generators according to their participation factors. The true values of active and reactive powers are evaluated by successive load flows. For ill-conditioned systems, the method of Incremental power flow [24] has been used for obvious reasons. The simulated measurements are obtained by adding a nor- mally distributed error function with zero mean and a standard deviation of 2% of the true values. Also, simu- lated bad data of magnitude 15 for the active and reactive line flows at the 20th time step for the different test systems are as shown in Table 1. Flat voltage start has been used for both proposed schemes and the toler- ance value is set at 0.00001. The statistical threshold to find the existence of bad data is set at 3. For each optimization technique, the maximum cycles (maxcy) have been set to 500. The control parameters for the GPSO and the PSO-DE are as shown, respectively, in Table 2. These parameters are found to be the most suit- able to get the minimum value of fitness function used in the work. Table 1. Details of events simulation. Test System Time sample Bad data Measurements at IEEE 5-bus 20 P5,P2-3,Q2-3 IEEE 14-bus 20 Q10,P4-9,Q4-9 IEEE 30-bus 20 P15-18, P2-5,Q2-5 IEEE 57-bus 20 P12, Q12, P14-46,Q14-46 IEEE 118-bus 20 Q15, P89-92,Q89-92 ii r (12) Copyright © 2013 SciRes. EPE 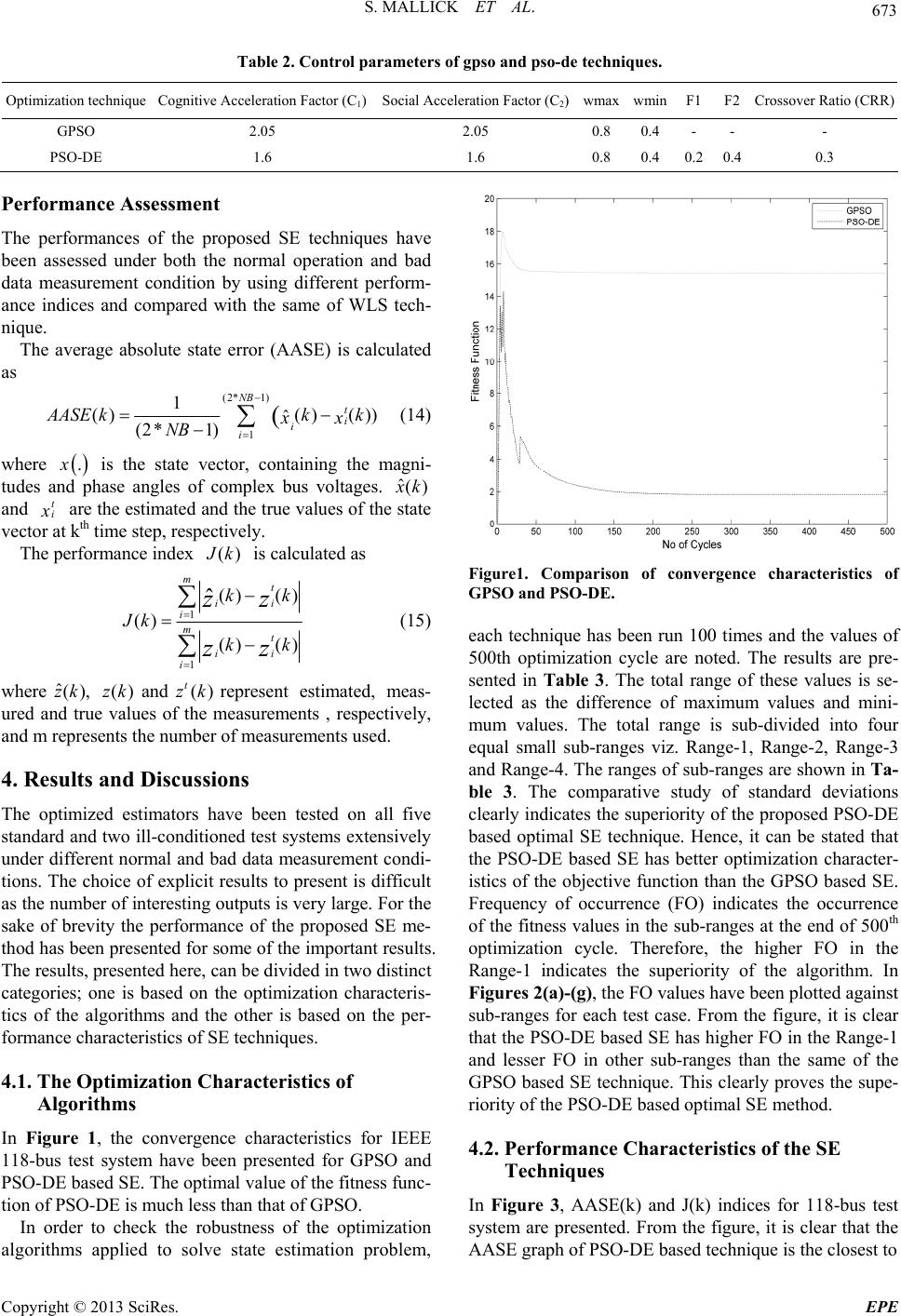 S. MALLICK ET AL. Copyright © 2013 SciRes. EPE 673 Table 2. Control parameters of gpso and pso-de tec hnique s. Optimization technique Cognitive Acceleration Factor (C1)Social Acceleration Factor (C2)wmaxwminF1 F2 Crossover Ratio (CRR) GPSO 2.05 2.05 0.8 0.4 - - - PSO-DE 1.6 1.6 0.8 0.4 0.2 0.4 0.3 Performance Assessment The performances of the proposed SE techniques have been assessed under both the normal operation and bad data measurement condition by using different perform- ance indices and compared with the same of WLS tech- nique. The average absolute state error (AASE) is calculated as (2* 1) 1 1 ()() ()) ˆ (2*1)( NB t i i i ASE kkk x x NB (14) where . is the state vector, containing the magni- tudes and phase angles of complex bus voltages. ˆ() k and t i are the estimated and the true values of the state vector at kth time step, respectively. The performance index () k is calculated as Figure1. Comparison of convergence characteristics of GPSO and PSO-DE. 1 1 () () () () () ˆ mt ii imt ii i kk Jk kk zz zz (15) each technique has been run 100 times and the values of 500th optimization cycle are noted. The results are pre- sented in Table 3. The total range of these values is se- lected as the difference of maximum values and mini- mum values. The total range is sub-divided into four equal small sub-ranges viz. Range-1, Range-2, Range-3 and Range-4. The ranges of sub-ranges are shown in Ta- ble 3. The comparative study of standard deviations clearly indicates the superiority of the proposed PSO-DE based optimal SE technique. Hence, it can be stated that the PSO-DE based SE has better optimization character- istics of the objective function than the GPSO based SE. Frequency of occurrence (FO) indicates the occurrence of the fitness values in the sub-ranges at the end of 500th optimization cycle. Therefore, the higher FO in the Range-1 indicates the superiority of the algorithm. In Figures 2(a)-(g), the FO values have been plotted against sub-ranges for each test case. From the figure, it is clear that the PSO-DE based SE has higher FO in the Range-1 and lesser FO in other sub-ranges than the same of the GPSO based SE technique. This clearly proves the supe- riority of the PSO-DE based optimal SE method. where and represent estimated, meas- ured and true values of the measurements , respectively, and m represents the number of measurements used. ˆ(),zk ()zk () t zk 4. Results and Discussions The optimized estimators have been tested on all five standard and two ill-conditioned test systems extensively under different normal and bad data measurement condi- tions. The choice of explicit results to present is difficult as the number of interesting outputs is very large. For the sake of brevity the performance of the proposed SE me- thod has been presented for some of the important results. The results, presented here, can be divided in two distinct categories; one is based on the optimization characteris- tics of the algorithms and the other is based on the per- formance characteristics of SE techniques. 4.1. The Optimization Characteristics of Algorithms In Figure 1, the convergence characteristics for IEEE 118-bus test system have been presented for GPSO and PSO-DE based SE. The optimal value of the fitness func- tion of PSO-DE is much less than that of GPSO. 4.2. Performance Characteristics of the SE Techniques In Figure 3, AASE(k) and J(k) indices for 118-bus test system are presented. From the figure, it is clear that the AASE graph of PSO-DE based technique is the closest to In order to check the robustness of the optimization algorithms applied to solve state estimation problem,  S. MALLICK ET AL. 674 Table 3. Description of ranges of minimum values of objective function and standard deviation of the minimum fitness func- tion values for different test systems for 100 runs of the algorithms. GPSO PSO-DE Test Bus system Minimum value of objective function Maximum value of objective function Range of sub-range values Standard deviation Minimum value of objective function Maximum value of objective function Range of sub-range values Standard deviation IEEE 5-Bus 0.3453 0.5630 0.0551 0.0417 0.0059 0.0350 0.0072 0.0046 IEEE 14-Bus 0.3745 0.8372 0.1541 0.1239 0.0099 0.0282 0.0045 0.0029 IEEE 30-Bus 0.4161 1.5096 0.2733 0.2295 0.0272 0.0414 0.0035 0.0031 IEEE 57-Bus 0.9642 3.1213 0.5392 0.3413 0.0842 0.2881 0.0509 0.0270 IEEE 118-Bus 15.4566 32.1037 4.1617 3.7259 1.8485 3.7460 0.4743 0.3110 11-Bus 5.9385 9.4668 0.8820 0.5958 0.3470 0.8692 0.1305 0.1127 13-Bus 0.1684 0.2427 0.0185 0.0114 0.0024 0.0035 0.0002 0.0002 Figure 2. Comparison of F.O. of the optimal values of objective function for 100th run of the algorithms the GPSO and the PSO-DE based SE. Copyright © 2013 SciRes. EPE 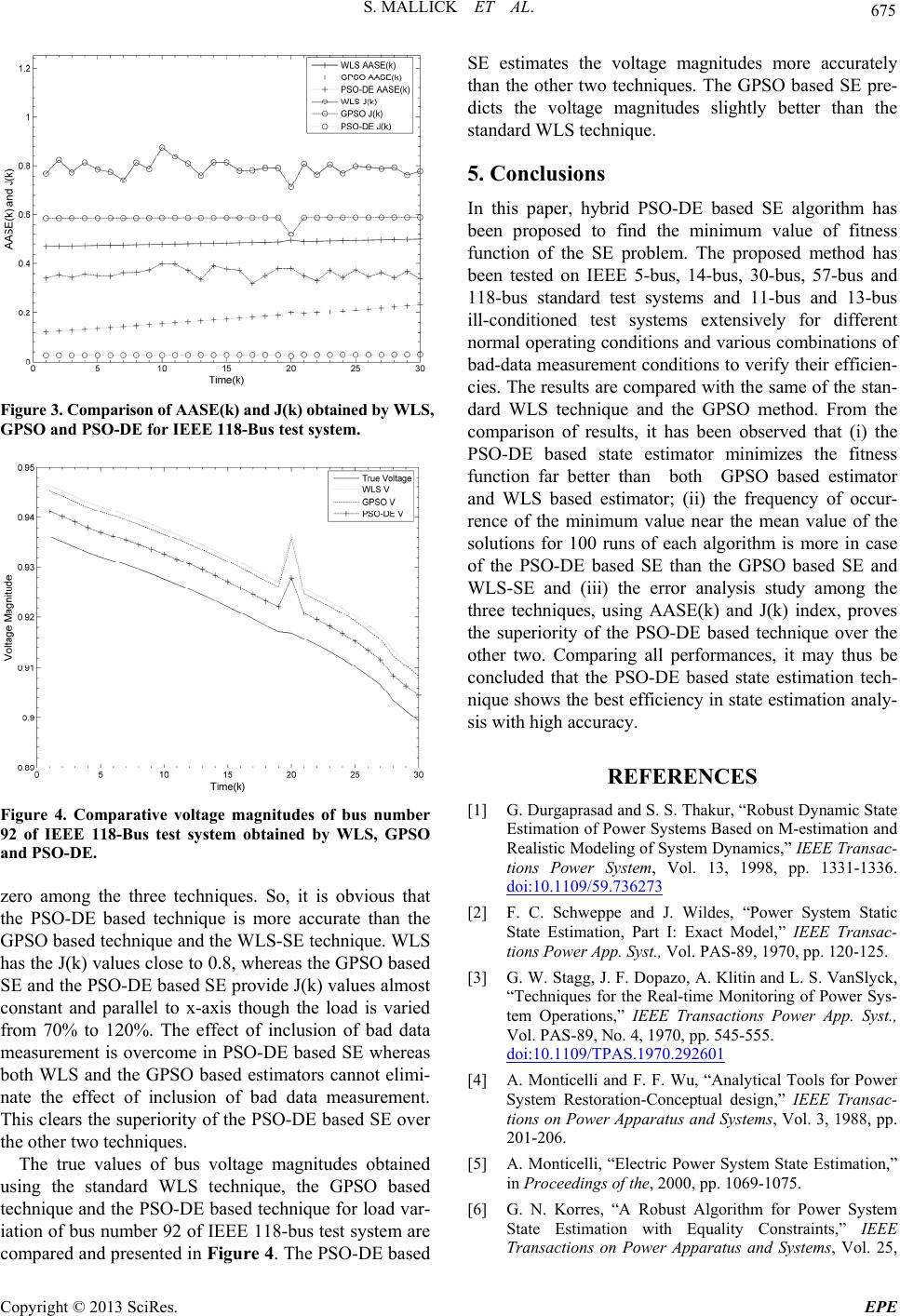 S. MALLICK ET AL. 675 Figure 3. Comparison of AASE(k) a n d J(k) obtained by WLS, GPSO and PSO-DE for IEEE 118-Bus test system. Figure 4. Comparative voltage magnitudes of bus number 92 of IEEE 118-Bus test system obtained by WLS, GPSO and PSO-DE. zero among the three techniques. So, it is obvious that the PSO-DE based technique is more accurate than the GPSO based technique and the WLS-SE technique. WLS has the J(k) values close to 0.8, whereas the GPSO based SE and the PSO-DE based SE provide J(k) values almost constant and parallel to x-axis though the load is varied from 70% to 120%. The effect of inclusion of bad data measurement is overcome in PSO-DE based SE whereas both WLS and the GPSO based estimators cannot elimi- nate the effect of inclusion of bad data measurement. This clears the superiority of the PSO-DE based SE over the other two techniques. The true values of bus voltage magnitudes obtained using the standard WLS technique, the GPSO based technique and the PSO-DE based technique for load var- iation of bus number 92 of IEEE 118-bus test system are compared and presented in Figure 4. The PSO-DE based SE estimates the voltage magnitudes more accurately than the other two techniques. The GPSO based SE pre- dicts the voltage magnitudes slightly better than the standard WLS technique. 5. Conclusions In this paper, hybrid PSO-DE based SE algorithm has been proposed to find the minimum value of fitness function of the SE problem. The proposed method has been tested on IEEE 5-bus, 14-bus, 30-bus, 57-bus and 118-bus standard test systems and 11-bus and 13-bus ill-conditioned test systems extensively for different normal operating conditions and various combinations of bad-data measurement conditions to verify their efficien- cies. The results are compared with the same of the stan- dard WLS technique and the GPSO method. From the comparison of results, it has been observed that (i) the PSO-DE based state estimator minimizes the fitness function far better than both GPSO based estimator and WLS based estimator; (ii) the frequency of occur- rence of the minimum value near the mean value of the solutions for 100 runs of each algorithm is more in case of the PSO-DE based SE than the GPSO based SE and WLS-SE and (iii) the error analysis study among the three techniques, using AASE(k) and J(k) index, proves the superiority of the PSO-DE based technique over the other two. Comparing all performances, it may thus be concluded that the PSO-DE based state estimation tech- nique shows the best efficiency in state estimation analy- sis with high accuracy. REFERENCES [1] G. Durgaprasad and S. S. Thakur, “Robust Dynamic State Estimation of Power Systems Based on M-estimation and Realistic Modeling of System Dynamics,” IEEE Transac- tions Power System, Vol. 13, 1998, pp. 1331-1336. doi:10.1109/59.736273 [2] F. C. Schweppe and J. Wildes, “Power System Static State Estimation, Part I: Exact Model,” IEEE Transac- tions Power App. Syst., Vol. PAS-89, 1970, pp. 120-125. [3] G. W. Stagg, J. F. Dopazo, A. Klitin and L. S. VanSlyck, “Techniques for the Real-time Monitoring of Power Sys- tem Operations,” IEEE Transactions Power App. Syst., Vol. PAS-89, No. 4, 1970, pp. 545-555. doi:10.1109/TPAS.1970.292601 [4] A. Monticelli and F. F. Wu, “Analytical Tools for Power System Restoration-Conceptual design,” IEEE Transac- tions on Power Apparatus and Systems, Vol. 3, 1988, pp. 201-206. [5] A. Monticelli, “Electric Power System State Estimation,” in Proceedings of the, 2000, pp. 1069-1075. [6] G. N. Korres, “A Robust Algorithm for Power System State Estimation with Equality Constraints,” IEEE Transactions on Power Apparatus and Systems, Vol. 25, Copyright © 2013 SciRes. EPE  S. MALLICK ET AL. 676 No. 3, 2010, pp. 1531-1541. doi:10.1109/TPWRS.2010.2041676 [7] A. Monticelli and A. Garcia, “Reliable Bad Data Proc- essing for Real-time State Estimation,” IEEE Transac- tions Power Apparatus and Systems, Vol. PAS-102, 1983, pp. 1126-1139. doi:10.1109/TPAS.1983.318053 [8] N. G. Bretas, “An Iterative Dynamic State Estimation and Bad Data Processing,” International Journal of Electrical Power and Energy Systems, Vol. 11, 2010, pp. 70-74. doi:10.1016/0142-0615(89)90010-0 [9] N. G. Bretas, A. S. Bretas and S. A. Piereti, “Innovation Concept for Measurement Gross Error Detection and Identification in Power System State Estimation,” The In- stitution of Engineering and Technology, Vol. 5, 2011, pp. 603-608. doi:10.1049/iet-gtd.2010.0459 [10] A. M. Sasson, S. T. Ehrmann, P. Lynch, and L. S. Van Slyck, “Automatic Power System Network Topology Determination,” IEEE Transactions Power Apparatus Systems, Vol. PAS-92, No. 2, 1973, pp. 610-618. doi:10.1109/TPAS.1973.293764 [11] K. A. Clements and A. S. Costa, “Topology Error Identi- fication Using Normalized Lagrange Multipliers,” IEEE Transactions Power Systems, Vol. 13, 1998, pp. 347-353. doi:10.1109/59.667350 [12] J. Chen and A. Abur, “Enhanced Topology Error Proc- essing Via Optimal Measurement Design,” IEEE Trans- actions Power Systems, Vol. 23, 2008, pp. 845-852. doi:10.1109/TPWRS.2008.926083 [13] A. Monticelli and F. F. Wu, “Observability Analysis for Orthogonal Transformation based State Estimation,” IEEE Transactions Power Systems, Vol. PWRS-1, 1986, pp. 201-206. doi:10.1109/TPWRS.1986.4334870 [14] G. N. Korres and P. J. Katsikas, “Reduced Model for Numerical Observability Analysis in Generalised State Estimation,” IET Gener.,Transm. And Distrib., vol. 152, pp. 99-108, 2005. doi:10.1049/ip-gtd:20041059 [15] R. C. Eberhart and J. Kennedy, “A New Optimizer Using Particle Swarm Theory,” in Symposium on Micro Ma- chine and Human Science. Japan: Nagoya, Piscataway, NJ, 1995, pp. 39-43. doi:10.1109/MHS.1995.494215 [16] R. C. Eberhart and Y. Shi, “Comparing Inertia Weights and Constriction Factors in Particle Swarm Optimiza- tion,” in Congress on Evolutionary Computation, La Jolla, CA , USA 2000, pp. 84-88. [17] P. Acharjee and S. K. Goswami, “Expert Algorithm Based on Adaptive Particle Swarm Optimization for Power Flow Analysis,” Expert Systems with Applications, Vol. 36, 2009, pp. 5151-5156. doi:10.1016/j.eswa.2008.06.027 [18] Y. Fukuyama and H. Yoshida, “A Particle Swarm Opti- mization for Reactive Power and Voltage Control in Elec- trical Power Systems,” in Proc. of 2001 Congress on Evo- lutionary Computation 2001, pp. 87-93. [19] M. A. Abido, “Optimal Design of Power-system Stabiliz- ers Using Particle Swarm Optimization,” IEEE Transac- tions on Energy Conversion, Vol. 17, 2002, pp. 406-413. doi:10.1109/TEC.2002.801992 [20] R. Storn and K. Price, "Differential Evolution a Simple and Effective Scheme for Global Optimization over Con- tinuous Spaces,” 1995. [21] T. Hendtlass, “A Combined Swarm Differential Algo- rithm for Optimization Problems,” in Proceedings of the fourteenth International conference on Industrial and Engineering Applications of Artificial Intelligence and Expert systems, 2001, pp. 11-18. [22] M. G. H. Omran, A. P. Engelbrecht and A. Salman, "Dif- feerential evolution based particle swarm optimization," in Proceedings of the IEEE Swarm Intelligence Sympo- sium, 2007, pp. 112-119. [23] B. Shaw, V. Mukherjee and S. P. Ghoshal, “Solution of Combined Economic and Emission Dispatch Problems Using Hybrid Craziness-based PSO with Differential Evolution,” Presented at the IEEE Symposium on Dif- ferential Evolution, 2011. [24] S. Mallick, D. V. Rajan, S. S. Thakur, P. Acharjee and S. P. Ghoshal, “Development of a New Algorithm for Power Flow Analysis,” International of Journal of Electtrical Power and Energy Sysems, Vol. 33, 2011, pp. 1479-1488. doi:10.1016/j.ijepes.2011.06.030 Copyright © 2013 SciRes. EPE
|