Energy and Power Engineering, 2013, 5, 667-669
doi:10.4236/epe.2013.54B129 Published Online July 2013 (http://www.scirp.org/journal/epe)
Research of Network Transient Performance
at Small Perturbations
T. A. Makhkamov, A. M. Mirzabaev
National Research University: Moscow Power Engineering Institute, Moscow, Russia,
Tashkent State Technical University, Tashkent, Uzbekistan
Received February, 2013
ABSTRACT
The advisability of the use of matrix methods of equations rearrangement for the investigated system which allows
writing a secular equation is considered in this article. This approach greatly simplifies the analysis of performance of
transient response in complicated multi-coupled electrical system at small perturbations.
Keywords: Stability; Process Control Performance Factors; Transient Response; Matrix Analysis; Coefficient Matrix;
Secular Equation
1. Introduction
The stability is necessary but an insufficient condition of
automatic control systems operability [1]. The control
system stability means only that there is a decaying of
the transient response in the system under the influence
of external control or perturbation action. Upon that, a
process decaying time, maximum deviation of controlla-
ble value and number of oscillations in the system are not
defined, however, these values are very important proc-
ess control performance factors.
Process control performance factors can be defined by
means of various methods. First of all, they comprise
transient response design by the set closed-loop transfer
functions, definition of performance factors by a disposi-
tion of zeroes and poles, integral performance criteria,
frequency-domain performance estimation and fre-
quency-domain methods of transient response design
[1-3].
2. Analysis
In case of electrical power system, the differential equa-
tion system describing processes in such system are lin-
ear (linearized) and look like in the matrix form [2]:
x
Ax
, (1)
where
11 121
21 222
12
.......
.......
.....................
........
n
n
nn nn
aa a
aa a
aa a
(2)
and х = [x1, x2, …, xn] – a column matrix comprising de-
viations of required parameters of electrical power sys-
tem condition.
The problems listed above become insuperable in cas-
es of the systems described by equations with high de-
grees, i.e. complicated or multi-coupled systems. A pri-
mal problem is deriving of a secular equation for the in-
vestigated system. In this connection it is expedient to
use matrix methods of rearrangement of the equations for
the investigated system, then to receive a coefficient ma-
trix for the differential equations A and further to set a
secular equation under known algorithms of its setting. It
is rather effective to apply Boher formulas [4] which
generate factors of a secular equation of the investigated
system. Let’s consider an algorithm of generation of se-
cular equation coefficients by a known matrix of coeffi-
cients of a matrix A.
Product of characteristic numbers of a square matrix A
is equal to a determinant of this matrix. Let’s notice that
in case of equality to zero of any characteristic number
the matrix A is singular [5, 7].
The sum of diagonal elements of a square matrix is
equal to the sum of its characteristic numbers. Consider-
ing importance of this property, the special title, namely,
a matrix trace is appropriated to the sum of diagonal
elements of such matrix. This property is used to form
coefficients of a secular equation for the investigated
system.
Having designated the trace Aк (of the matrix A multi-
plied k times by itself) by Tк it is possible to write the
useful recurrence formula expressing coefficients of a
secular equation in terms of various Tк, so: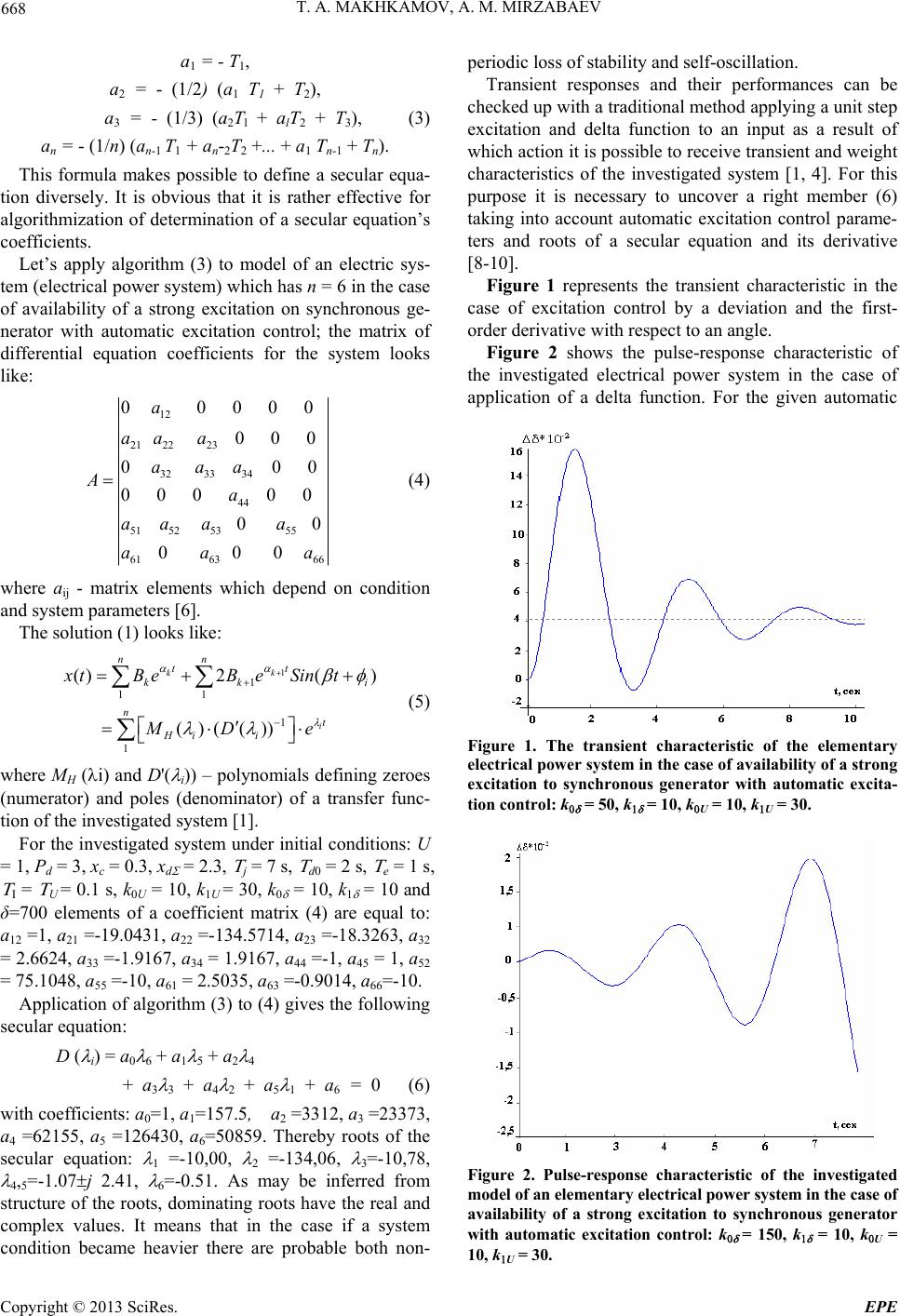

T. A. MAKHKAMOV, A. M. MIRZABAEV
668
a1 = - Т1,
а2 = - (1/2) (a1 T
1 + T2),
a3 = - (1/3) (a2Tl + a
lT2 + T 3), (3)
ап = - (1/n) (an-1 T1 + ап-2Т2 +... + а1 Tn-1 + Тn).
This formula makes possible to define a secular equa-
tion diversely. It is obvious that it is rather effective for
algorithmization of determination of a secular equation’s
coefficients.
Let’s apply algorithm (3) to model of an electric sys-
tem (electrical power system) which has n = 6 in the case
of availability of a strong excitation on synchronous ge-
nerator with automatic excitation control; the matrix of
differential equation coefficients for the system looks
like:
12
21 2223
3233 34
44
51 525355
61 6366
0 0000
000
0
000 00
00
000
a
aa a
aaa
Aa
aa aa
aa
00
a
i
(4)
where aij - matrix elements which depend on condition
and system parameters [6].
The solution (1) looks like:
1
1
11
1
1
()2( )
()(())
kk
i
nn
tt
kk
nt
Hi i
x tB eBeSint
MD e








 
 




(5)
where МН (i) and D'( 
i)) – polynomials defining zeroes
(numerator) and poles (denominator) of a transfer func-
tion of the investigated system [1].
For the investigated system under initial conditions: U
= 1, Рd = 3, xc = 0.3, xd

= 2.3, 
j = 7 s,

d0 = 2 s,

e = 1 s,

I =

U = 0.1 s, k0U = 10, k1U = 30, k0 
= 10, k1

= 10 and
δ=700 elements of a coefficient matrix (4) are equal to:
a12 =1, a21 =-19.0431, a22 =-134.5714, a23 =-18.3263, a32
= 2.6624, a33 =-1.9167, a34 = 1.9167, a44 =-1, a45 = 1, a52
= 75.1048, a55 =-10, a61 = 2.5035, a63 =-0.9014, a66=-10.
Application of algorithm (3) to (4) gives the following
secular equation:
D (

i) = a0

6 + a1

5 + a2

4
+ a
3

3 + a4

2 + a 5

1 + a 6 = 0 (6)
with coefficients: a0=1, a1=157.5, a2 =3312, a3 =23373,
a4 =62155, a5 =126430, a6=50859. Thereby roots of the
secular equation:

1 =-10,00,

2 =-134,06,

3=-10,78,

,5=-1.07j 2.41,

6=-0.51. As may be inferred from
structure of the roots, dominating roots have the real and
complex values. It means that in the case if a system
condition became heavier there are probable both non-
periodic loss of stability and self-oscillation.
Transient responses and their performances can be
checked up with a traditional method applying a unit step
excitation and delta function to an input as a result of
which action it is possible to receive transient and weight
characteristics of the investigated system [1, 4]. For this
purpose it is necessary to uncover a right member (6)
taking into account automatic excitation control parame-
ters and roots of a secular equation and its derivative
[8-10].
Figure 1 represents the transient characteristic in the
case of excitation control by a deviation and the first-
order derivative with respect to an angle.
Figure 2 shows the pulse-response characteristic of
the investigated electrical power system in the case of
application of a delta function. For the given automatic
Figure 1. The transient characteristic of the elementary
electric al power sy stem in the case of availability of a strong
excitation to synchronous generator with automatic excita-
tion control: k

= 50, k

= 10, kU = 10, kU = 30.
Figure 2. Pulse-response characteristic of the investigated
model of an elementary electrical p o wer syst em in the case of
availability of a strong excitation to synchronous generator
with automatic excitation control: k

= 150, k

= 10, kU =
10, kU = 30.

T. A. MAKHKAMOV, A. M. MIRZABAEV
669
ntrol parameters the system is self-oscillat-
3. Conclusions
ws, realization of the given techni
gement
of
REFERENCES
[1] N. N. IvaschenTheory and System
anical Processes in
excitation co
ing. The analysis shows that self-oscillation is removed if
to select (to optimize) amplification coefficients for the
first-order derivative with respect to an angle and gen-
erator voltage, provided that efficiency of the channel of
a derivative with respect to an angle is essentially higher,
than to the voltage channel.
As the analysis shoque [6] K. R. Allaev and A. M. Mirzabaev, “Matrix Methods of
Research of a Static Stability of Electric Systems,” Arti-
cle in the Issue of the Magazine.
for transient response research in case of complicated
electrical power system is most effective, as the secular
equation is formed on the basis of a coefficient matrix for
the investigated system, and the higher degree of the dif-
ferential equations, the more advantage as regards to
formalization and computing time consumption.
Thus, application of matrix methods for rearran
the equations for electrical power systems when re-
searching a static stability of system allows making ef-
fective algorithms and their rather simple software im-
plementation. The given technique can be applied to
control of electrical power system conditions in dis-
patching services.
ko, Automatic Control.
[10]
Elements. M: Mashinostroenie, 1973.
[2] V. A. Venikov. Transient Electromech
Electric Systems. М: Visshaya shkola, 1984.
[3] “Automation of Dispatching Control in Electric Power
Industry,” Under the editorship of Yu. N. Rudenko and V.
A. Semenov, M: Izdatelstvo, 2000.
[4] P. Derusso, R. Roy and C. Claws, “State Space in the
Control Theory,” Under the Editorship of M. V. Meerov,
Translated from the English, M: Nauka, 1970.
[5] F. R. Gantmakher, “Theory of matrices,” M: Fizmatlit,
2005.
[7] A. M. Lyapunov, “General Problem about Movement
Stability,” M - L. 1950. State Publishing House Tech. -
theor. lit.
[8] K. R. Allaev, “The Research of Static Stability of Electric
Systems by the Method of Liapunov Functions of Quad-
ric Form Т. Fan,” Proceedings of the Academy of Sci-
ences of the Republic of Uzbekistan, 1973, No.5, pp.
13-17.
[9] K. R. Allaev and A. M. Mirzabaev, “The Exploration of
Static Stability of Electric Energy Systems with Joint Ap-
plication of Lyapunov Function Method of Quadric Form
and Nodal Equations. In book: Stability and Reliability
Issues of Energy Systems. Under the editorship of L. А.
Koshev,” Institute of high temperatures of the USSR
academy of sciences, 1990, pp. 272-276.
K. R. Allaev and A. M. Mirzabaev, “To Application of
the Matrix Analysis for Research of a Static Stability of
Electric Systems,” Problems of Energy and Resource
Saving, 2009, No. 3-4, pp. 15-21.