Journal of Signal and Information Processing, 2011, 2, 11-17
doi:10.4236/jsip.2011.21002 Published Online February 2011 (http://www.SciRP.org/journal/jsip)
11
Evolutionary MPNN for Channel Equalization
Archana Sarangi1, Bijay Ketan Panigrahi2 & Siba Prasada Panigrahi3
1Department of AEI E, ITER, SOA Unive rsity, Bhubane swa r , I ndia ; 2Department of Electrical Engineering, IIT, Delhi, India ; 3 Depart-
ment of Electrical Engineering, KIST, Bhubaneswar, India
Received December 10th, 2010; revised January 11th, 2011; accepted February 18th, 2011
ABSTRACT
This paper proposes a novel equalizer, termed here as Evolutionary MPNN, where a complex modified probabilistic
Neura l Net wo rks (MPNN) acts as a filter for the detected signal pattern. The neurons were embedded with optimization
algorithms. We have considered two optimization algorithms, Bacteria Foraging Optimization (BFO) and Ant Colony
Optimization (ACO). The proposed structure has the ability to process complex signals also can perform for slowly
varying channels. Also, Simulation results prove the superior performance of the proposed equalizer over the existing
MPNN e qual i zers.
Keywords: Channel Equalization, Probabilist i c Neural Network, Bacteria Foraging, Ant Colony Optimization
1. Introduction
Channel equalization plays an important role in digital
communication systems. There are tremendous devel-
opments in equalize r structures since the advent of neural
networks in signal processing applications. Recent lite-
rature is healthy enough with newer applications of
neural networks [1-5] and in particular to independent
component analysis, noise cancellation and channel
equalization [6-16]. But all of these papers overlooked
two basic problems encountered. First is to train the
equalizer how to process complex signal. Second is to
get a adaptive nature of equalizer for slowly varying
channels. Authors in [17] have tried to address these two
problems, through a Modified Probabilistic Neural net-
work (MPNN), and were successful to process complex
signals and for a slowly varying signal. However, the
result was sub-optimal in nature, since the neurons were
not trained wit h an y o ptimization algorithms.
This paper takes the similar structure as that of [17].
But, novelty in this paper is to use the structure as a
neural filter for classifying detected signal pattern. Neu-
rons in network in [17] were embedded with stochastic
gradient, whereas in this paper, each of the neurons in
the structure is embedded with optimization algorithm
unlike that of in [17 ].
Recently, Particle Swarm Intelligence (PSO) [18],
Bacteria Foraging Optimization (BFO) [19-21] and Ant
colony Optimization (ACO) [22-26] have been used for
optimization purpose in different fields of research. This
paper uses BFO and ACO for optimization. Some suc-
cessful applications of these two techniques, i.e. BFO
and ACO can be fo und in [27-31]. Novelty in this paper
can be seen as, application of two known algorithms,
ACO and BFO, to the problem of channel equalization.
This underlines the improvement added by the optimiza-
tion algorithms. The proposed schemes outperform the
existing equalizers.
2. Problem Statement
Impulse response of channel & co-channel can be
represented as:
( )
1
,
0
0
i
pj
i ij
j
Hzazi n
−−
=
= ≤≤
∑
(1)
Here i pand
,ij
a
are length and tap weights of th
i
channel impulse response. We assume a binary commu-
nication system, which would make the analysis simple,
though it can be extended to any communication system
in general. The transmitted symbols
( )
i
xn
,
0in≤≤
for channel and co-channel are drawn from a set of in-
dependent, identically distributed (i.i.d) dataset compris-
ing of {± 1} and these are mutually independent. This
satisfies the cond ition
( )
0
i
Exn = 

(2)
()()() ()
1 212ij
Exn xnijnn δδ

=−−

(3)
where
[ ]
E⋅
represents the expectation operator and

Evolutionary MPNN for Channel Equalization
12
( )
10
00
n
nn δ
=

=≠

(4)
The channel output scalars can be represented as
( )( )( )( )
co
yndnd nn η =++
(5)
Here
( )
dn
desired received signal
( )
co
dn
is inter-
fering signal and
( )
n η
is noise component assumed to
be Gaussian with variance
( )
22
En
η
ησ

=

and uncor-
related with data. The desired and interfering signal can
be represented as
( )()
0
1
0, 0
0
p
j
j
dnax nj
−
=
= −
∑
(6)
( )()
1
,
10
i
p
n
coi ji
ij
dkaxn j
−
= =
= −
∑∑
(7)
The task of the equalizer is to estimate the trans mitted
sequence
( )
0ˆ
xnd
− based on channel observation vector
( )()()()
,1, ,1
T
ynynynyn m=− −+ 


, where
m
is
order of equalizer and
ˆ
d
is decision delay.
The cost function is t he MSE value of
( )
,, 1e pqn+
. So
( )
2
1,,1
2
Je pqn= +
(8)
The error generated at the output of equalizer should
be minimized to give an acceptable solution. The initial
condition for the equalizer model is derived from the
Decision Feedback Equalization (DFE) expressions. So,
determinatio n of the er ror at interio r po ints the cha nnel i s
essential. This paper assumes, input same as that of de-
sire d outp ut. Hence, the total error is the difference between
outp ut a nd i np ut of t he ne t wor k mod el . The co st fu nction
is the mean of the sum of squares of this error (MSE).
3. Proposed Equalizer
The proposed equalizer in this paper shown in Fi gure 1
and consists o f two basic compone nts, one MP NN filter
and one optimizer. The purpose of filter is to rece ive t he
distorted output from the channel and will form two
separate and independent patterns, one for
{ }
1+
and
next for
{ }
1+
. The p urpose of the optimizer is to optim-
ize the cost function of (8) and thereby minimizing the
error. The details of classifier and working algorithms
for the optimizer are discussed in following two sub-
sectio ns.
3.1. MPNN Filter
First part of the equalizer of this paper, the filter, shown
in Figure 2, is the same structure as that used in [17].
Authors in [17] used the structure for the purpose of
equalization without any evolutionary optimizing algo-
rithms. Authors in [17], embedded stochastic gradient to
neural nets. But, in this paper we have embedded opti-
mization algorithm to neural network. This optimization
algorithm is however, shown separately in the equalizer
structure and also discussed separately in following sub-
section.
The MPNN structure is based on Nadaraya-Watson
Regre ssion estimator [17] given by:
( )
( )( )
( )
( )( )
( )
2
1
2
1
exp 2
ˆexp 2
T n
k kk
k
T
n
kk
k
yxxxx
EYX xx xx
σ
σ
=
=
−− −
=−− −
∑
∑
(9)
Here,
x
is input sample. Each training input sample,
;1, 2,
k
xk n=, form a center in the input space. An
input vector to be evaluated
t
x
is weighted exponen-
tially acco r ding to its Euclidean distance from the centers.
The corresponding observed output from each center,
k
y
, is averaged to give the estimate
( )
ˆ
EYX
. T he val-
ue o f
σ
determines how t he network behaves.
In ge ner a l,
σ
governs the “closeness” between a point
of interest, say
t
x
, and the centers, ;1,2,
k
xk n=, in
the input space.
For a small
σ
value, only the corresponding observed
values,
:
k
yka=
, of the closest center, (:
k
xka
=)
appear significant, compare to the contribution fro m oth-
er centers, (: 1, ,
k
y knk a
= ≠). In this case, the net-
work does the nearest neighbor search. With a larger
σ
value, more of the observed outputs,
k
y
, are taken
into account, but with those corresponding to centers
close to
t
x
bei ng given mo r e we igh t.
Figure 1 . Proposed equalizer structure.
Ф
1
(x,c
1
,σ
1
)
Ф
j
(x,c
j
,σ
j
)
Ф
M
(x, c
M
,σ
M
)
Σ
Σ
Figure 2 . MPNN structure.

Evolutionary MPNN for Channel Equalization
13
This MPNN structure will be able to process complex
m-dimensional input vectors and complex outputs im-
plementing a mappi ng
:
N
fC C→
[17], if equation (9)
can be written as:
( )
( )( )
( )
( )( )
( )
2
1
2
1
exp 2
ˆexp 2
H
M
iiii
i
H
M
i ii
i
Zyxc xc
EYX Zxc xc
σ
σ
=
=
−− −
=−− −
∑
∑
(10)
where
( )
H
⋅denotes Hermitian operator (or conjugate
transpose). i Z, is the number of input training vector
associated with center
i
c
.
3.2. The Op t im iz e r
Second part of the equalizer proposed in this paper is an
optimizer. However, practically, one optimization algo-
rithm, which is discussed in this section, is embedded to
the neural network that is used as a filter. Embedding
neurons with optimization algorithms is achieved
through training the neurons for these algorithms like
that in [13,27]. We have taken two different optimization
algorithms, first one Bacteria foraging optimization and
next with Ant colony optimization. The algorithms are
discussed in following sections, and for clarity of the
readers, with different nomenclatures. This paper has not
tested the structure with any other optimization algo-
rithms and can be seen as one area for future work.
3.2.1. Bacteria Foraging Optimization
Natural selection tends to eliminate animals with poor
fora ging stra tegies a nd favor the pro pagation o f genes o f
those animals that have successful foraging strategies,
since they are more likely to enjoy reproductive success.
After a number of generations, poor foraging strategies
are either eliminated or shaped into good ones. This ac-
tivity of foraging led the researchers to use it as optimi-
zation process. T he E. coli bacteria that are present in our
intestines also undergo a foraging strategy. The control
system of thes e bacteria th at dictates h ow foraging should
proceed can be subdivided into four sections, namely,
chemo taxis, swarming, reproduction, and elimination and
dispersal. We will use following nomenclature for dif-
ferent parameters of BFO.
S
: Number of bacteria to be used for searching the
total region:
is
N
: Number of input sample
p
: Number of parameter to be optimized
s
N
: Swimming length after which tumbling of bacte-
ria will be underta ken in a chemota c tic loop
c
N
: Number of iterations to be undertaken in a che-
motactic loop. Always
re
N
: Maximum number of reproduction to be under-
taken
ed
N: Maximum number of elimination and dispersal
events to be imposed over the bacteria.
ed
P: Probability with which the elimination and dis-
persal will continue.
( )
Ci
: Run length uni t
For initialization, we must choose
,, , ,,
c s re
PSN N N
,
ed ed
NP
and the
( )
,1,2,Ci iS=
. In case of swarming,
we will also have to pick the parameters of the cel l-to-cell
attractant functions; here this paper uses the parameters
given above. Also, initial values for the
,1, 2,
i
iS θ =
must be chosen. Choosing these to be in areas where an
optimum value is likely to exist is a good choice. Alter-
natively, we may want to sim ply randomly distribute them
across the domain of the optimization problem. The al-
gorithm that models bacterial population chemo taxis,
swarming, reproduction, elimination, and dispersal is
given here (initiall y, 0jkl== =). For the algorithm,
note that updates to the i θ
automatically result in updates
to
P
. Clearly, we could have added a more sophisticated
termination test than simply specifying a maximum
number of iterations.
Eliminatio n -dispersal loop: 1ll= +
Reproduction loop: 1kk=+
Chemo taxis loop:
1jj= +
For
1, 2,iS=
take a chemo tactic step for bacte-
rium
i
as follo ws.
Compute
( )
,,,J i jkl
(i.e., add on the cell-to-cell at-
tractant effect to the nutrient concentration).
Let
( )
,,,
last
JJ i jkl=
to save this value since we may
find a better cost via a run.
Tumble: Generate a random vector
( )
P
iR∆∈
with
each element
( )
,1, 2,,
m
im p∆=
, a random number on
[–1, 1].
Move
()()( )( )()( )
1
1,, ,,
ii
t
jkljkl ciiii θθ + =+∆∆∆
This
results in a step of size
( )
ci
in the directio n of the tum-
ble for bacterium
i
.
Compute
( )
,1, ,J ijkl+
and then l et,
( )
()( )( )
( )
,1, ,
,1, ,1, ,.1,,
i
cc
J ijkl
Jij klJj klPj kl θ
+=
++ ++
Swim (note that we use an approximation since we de-
cide swimming behavior of each cell as if the bacteria
numbered
{ }
1, 2i
have moved and
{ }
1, 2ii s++
have not; this is much simpler to simulate than simulta-
neous decisions about swimming and tumbling by all
bacteria at the same time):
Let
0m=
(counter for swim length).
While
s
mN<
(if have not cl imbed down to o long)
Let
1mm= +
If
( )
,1, ,
last
J ijklJ+<
(if doing better),

Evolutionary MPNN for Channel Equalization
14
Let
( )
,1, ,
last
JJ ijkl=+
and let
()()()()( )()
1
1,, ,,
ii
t
jkljkl ciiii θθ + =+∆∆∆
and
use this
( )
1, ,
i
j kl θ +
to compute new
( )
,1, ,J ijkl+
as we did in above step.
Else, let
s
mN=
this is the end of the while statement.
Go to next bacterium
( )
1i+
if
iS≠
(i.e., go t o b) t o
process the next bacterium).
If c
jN
≤, go to step 3. In this case, continue chemo
taxis, since the life of the bacteria is not over.
Reproduction:
For the given k and l, and for each
1, 2,iS=
let
( )
1
1
,,,
c
N
i
health j
Jji jkl
+
=
=
∑
be the health of bacterium
i
(ameasure of how many nutrients it got over its lifetime
and how successful it was at avoiding noxious substances)
Sort bacteria and chemo tactic parameters
( )
ci
in order
of as cen ding c ost
health
J
(higher cost means lower health).
The r S bacteria with the highest health J values die
and the other r S bacteria with the best values split (and
the copies that are made are placed at the s ame location as
their parent).
If
re
KN≤
go to step 2. In this case, we have not
reach ed th e num ber of spe cifi ed reprodu cti on s teps , so w e
start the next generation in the c hemo tactic loop.
Eliminatio n -dispersal: for
1, 2,iS=
, with probabil-
ity ed
P
, elim inate and disperse each bacterium (this keeps
the number of bacteria in the population constant). For
doing this, if we eliminate a bacterium, simply disperse
one to a random location on the optimization domain.
If ed
IN
≤ then go to s t ep 1; otherwise end.
3.2.2. Ant Colony Optimization
Ant colony optimization (ACO) is a population-based
search technique working constructively to solve opti-
mization problems by using principle of pheromone in-
formation. This is an evolutionary approach where several
generations of artificial agents in a cooperative way
search for good solutions. These agents are initially ran-
domly generated on nodes, and stochastically move fro m
a start node to feasible neighbor nodes. While in the
process of finding feasible solutions, agents collect and
store information in p hero mo ne trails. Age nts can rele ase
pheromone online while building solutions. Also, the
pheromone will be evaporated in the search process to
avoid local convergen ce and to explore more search areas.
Then after, additional pheromone is deposited to update
pheromone trail offline so as to bias the search process in
favor of the currently optimal path. The pseudo code of
ant colony optimization is stated as [20]:
Procedure: Ant colony optimization (ACO)
Begin
While (ACO has not been stopped) do
Agents_generation_and_activity();
Pheromone_evaporation();
Daemon actions();
End;
End;
In th is A CO, a ge nts fi nd so l utio ns st art ing from a start
node an d moving t o feasibl e neig hbor nodes in the proces s
of Agents _generati on_and_activity. While in t he process,
information c ollected by agen ts is stored in t he so-called
pheromone trails. In this process, agents can release
pheromone along with building the solution (online
step-by-step) or while the solution is built (online de-
layed). An agent-decision rule, made up of the ph erom one
and heuristic information, governs agents_ search toward
neighbor nodes stochastically. The
th
k
ant at time
t
po-
sitioned on node
r
move to the next node
s
with the
rule governed by
( )
( )
{ }
0
arg maxk
ru ru
u allowedt
twhen qq
s
S otherwise
αβ
τη
=
 ≤

=


(15)
where
( )
ru
t τ
is the pheromone trail at time
t
, ru η is
the problem-specific heuristic information, a is a para-
meter representing the importance of pheromone infor-
mation,
β
is a parameter representing the im portance of
heuristic information,
q
is a random number uniformly
distributed in [0, 1], 0
q
is a pre-specified parameter
(
0
01q≤≤
), allowedk(t) is the set of feasible nodes cur-
rently not assigned by ant
k
at time
t
, and
S
is an
index of node selected from allowedk(t) according to the
probability distribution given by
( )
( )
( )
( )
( )
0
k
rs rsk
krs ru
rs u allowedt
tifsallowedt
t
Pt
otherwise
αβ
β
τη
τη
∈
∈


=



∑
(16)
Pheromone_evaporation is a process of decreasing the
intensities of pheromone trails over the course of time.
This process has been used to avoid locally convergence
and to explore more search space. Daemon actions may
or may not be used in ant colony optimization, and they
are often used to collect useful global information by
depositing additional pheromone. In the original algo-
rithm of [20], there is a scheduling process for the above
three processes. This is to provide freedom for conduct-
ing how these three processes should interact in ant co-
lony optimization and other approaches.
4. Simulation Results
To test the effectiveness of the propo sed equalizer, a real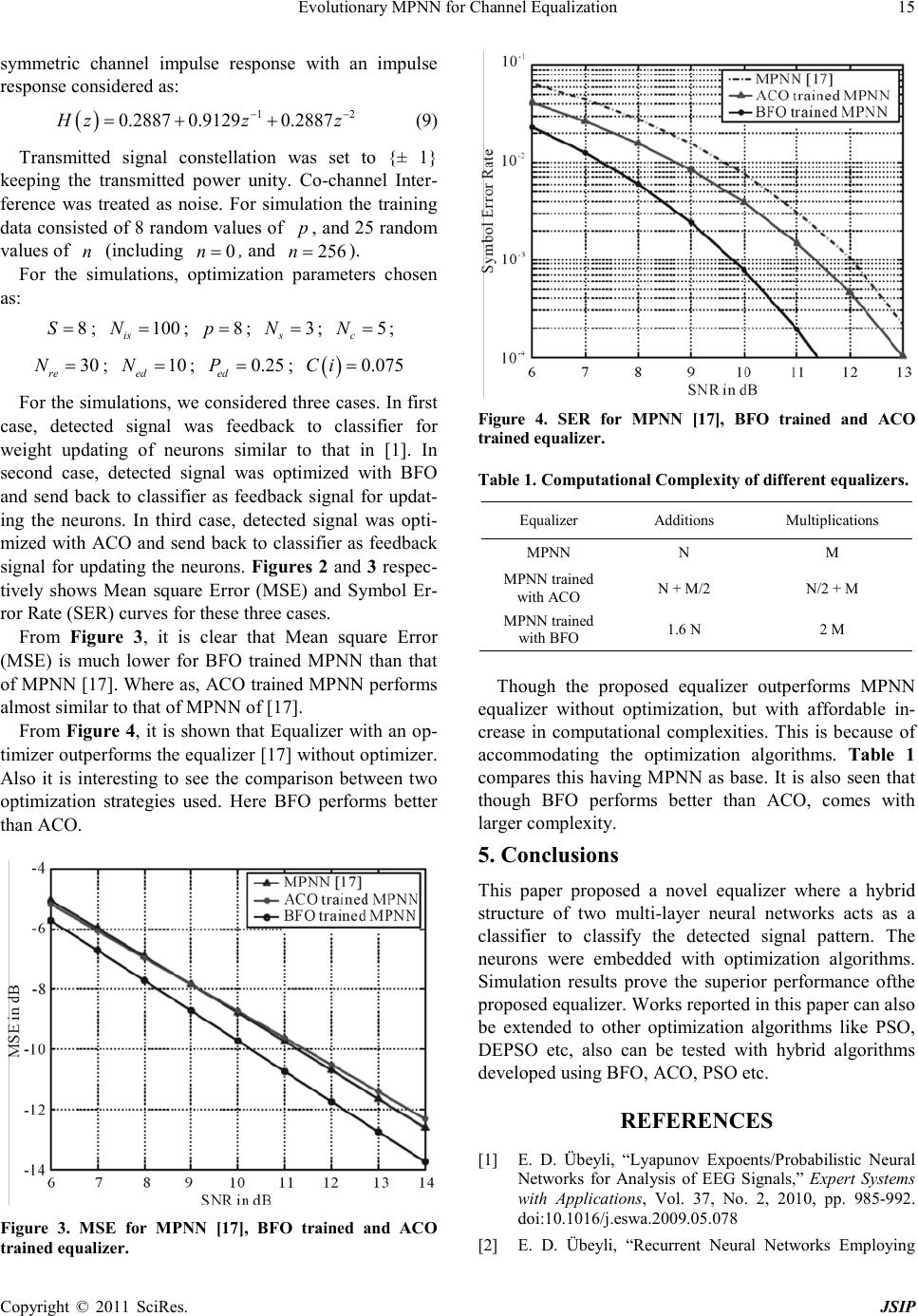

Evolutionary MPNN for Channel Equalization
15
symmetric channel impulse response with an impulse
response considered as:
( )
12
0.2887 0.91290.2887Hzz z
−−
=++
(9)
Transmitted signal constellation was set to {± 1}
keeping the transmitted power unity. Co-channel Inter-
ference was treated as noise. For simulation the training
data consisted of 8 random values of
p
, and 25 random
values of
n
(including
0n=
, and
256n=
).
For the simulations, optimization parameters chosen
as:
8S=
;
100
is
N=
;
8p=
; 3
s
N=; 5
c
N=;
30
re
N=
;
10
ed
N=
; 0.25
ed
P=;
( )
0.075Ci=
For the simulations, we considered three cases. In first
case, detected signal was feedback to classifier for
weight updating of neurons similar to that in [1]. In
second case, detected signal was optimized with BFO
and send back to classifier as feedback signal for updat-
ing the neurons. In third case, detected signal was opti-
mized with A CO and se nd bac k to classifier as feedback
signal for updating the neurons. Figur e s 2 and 3 respec-
tively shows Mean square Error (MSE) and Symbol Er-
ror Rate (SER) curves for these three cases.
From Figure 3, it is clear that Mean square Error
(MSE) is much lower for BFO trained MPNN than that
of MPNN [17]. Where as, ACO trained MPNN performs
almost similar to that of MPN N of [17].
From Figure 4, it is shown that Equalizer with an op-
timizer outperforms the equalizer [17] without optimizer.
Also it is interesting to see the comparison between two
optimization strategies used. Here BFO performs better
than ACO .
Figure 3. MSE for MPNN [17], BFO trained and ACO
trained equalizer.
Figure 4. SER for MPNN [17], BFO trained and ACO
trained equalizer.
Table 1. Computational Complexity of different eq uali zers.
Equalizer Additions Multiplications
MPNN N M
MPNN trained
with ACO N + M/2 N/2 + M
MPNN trained
with BFO 1.6 N 2 M
Though the proposed equalizer outperforms MPNN
equalizer without optimization, but with affordable in-
crease in computational complexities. This is because of
accommodating the optimization algorithms. Table 1
compares this having MPNN as base. It is also seen that
though BFO performs better than ACO, comes with
larger complexity.
5. Conclusions
This paper proposed a novel equalizer where a hybrid
structure of two multi-layer neural networks acts as a
classifier to classify the detected signal pattern. The
neurons were embedded with optimization algorithms.
Simulation results prove the superior performance ofthe
proposed equalizer. Works reported in this paper can also
be extended to other optimization algorithms like PSO,
DEPSO etc, also can be tested with hybrid algorithms
developed using BFO, ACO, PSO etc.
REFERENCES
[1] E. D. Übeyli, “Lyapunov Expoents/Probabilistic Neural
Networks for Analysis of EEG Signals,” Expert Systems
with Applications, Vol. 37, No. 2, 2010, pp. 985-992.
doi:10.1016/j.eswa.2009.05.078
[2] E. D. Übeyli, “Recurrent Neural Networks Employing

Evolutionary MPNN for Channel Equalization
16
Lyapunov Exponents for Analysis of ECG Signals,” Ex-
pert Systems with Applications, Vol. 37, No. 2, 2010, pp.
1192-1199. doi:10.1016/j.eswa.2009.06.022
[3] D.-T. Lin, et al., “Trajectory Production with Adaptive
Time-Delay Neural Network,” Neural Networks, Vol. 8,
No. 3, 1995, pp. 447-461. doi:10.1016/0893-6080(94)
00104-T
[4] L. Gao and S. X. Ren, “Combining Orthogonal Signal
Correction and Wavelet Pocket Transform with Radial
Basis Function Neural Networks for Multicomponent
Determination,” Chemometrics and Intelligent Laborato-
ry Systems, Vol. 100, No. 1, 2010, pp. 57-65. doi:10.
1016/j.chemolab.2009.11.001
[5] K.-L. Du, “Clustering: A Neural Network Approach,”
Neural Networks, Vol. 23, No. 1, 2010, pp. 89-107. doi:
10.1016/j.neunet.2009.08.007
[6] H. Q. Zhao, et al., “Adaptive Reduced Feedback FLNN
Filter for Active Control of Noise Processes,” Signal
Processing , Vol. 90, No. 3, 2010, pp. 834-847. doi: 10.
1016/j.sigpro.2009.09.001
[7] C. Potter, et al., “RNN Based MIMO Channel Predic-
tion,” Signal Processing, Vol . 90, No. 2, 2010, pp. 440-
450. doi:10.1016/j.sigpro.2009.07.013
[8] J. C. Patra, et al., “Nonlinear Channel Equalization for
Wireless Communication Systems Using Legendre Neur-
al Networks,” Signal Processing, Vol. 89, No. 11, 2009,
pp. 2251-2262. doi:10.1016/j.sigpro.2009.05.004
[9] S. P. Panigrahi, et al., “Hybrid ANN Reducing Training
Time Requirements and Decision Delay for Equalization
in Presence of Co-Channel Interferen ce,” Applied Soft
Computing, Vol. 8, No. 4, 2008, pp. 1536-1538. doi: 10.
1016/j.asoc.2007.12.001
[10] L. Zhang and X. D. Zhang, “MIMO Channel Estimation
and Equalization using Threelayer Neural Network with
Feedback,” Tsinghua Science & Technology, Vol. 12, No.
6, 2007, pp. 658-662. doi:10.1016/S1007-0214(07)70171
-2
[11] H. Q. Zhao and J. S. Zhang, “Functional Link Neural
NetWork Cascaded with Chevyshev Orthogonal Poly-
nomial for Nonlinear Channel Equalization,” Signal
Processing , Vol. 88, No. 8, 2008, pp. 1946-1957.
doi:10.1016/ j.sigpro.2008.01.029
[12] H. Q. Zhao and J. S. Zhang, “A Novel Nonlinear Adap-
tive Filter using a Pipelined Second-Order Volterra Re-
current Neural Network,” Neural Networks, Vol. 22, No.
10, 2009, pp. 1471-1483. doi:10.1016/j.neunet.2009.05.
010
[13] W.-D. Weng, et al., “A Channel Equalizer Using Re-
duced Decision Feedback Chebyshev Functional Link
Artificial Neural Networks,” Information Sciences, Vol.
177, No. 13, 2007, pp. 2642-2654. doi:10.1016/j.ins.2007.
01.006
[14] W. K. Wong and H. S. Lim, “A Robust and Effective
Fuzzy Adaptive Equalizer for Powerline Communication
Channels,” Neurocomputing, Vol. 71, No. 1-3, 2007, pp.
311-322. doi:10.1016/j.neucom.2006.12.018
[15] J. Lee and R. Sankar, “Theoretical Derivation of Mini-
mum Mean Square Error of RBF based Equalizer,” Sig-
nal Pro cessing, Vol. 87, No. 7, 2007, pp. 1613-1625. doi:
10.1016/j.sigpro.2007.01.008
[16] H. Q. Zhao and J. S. Zhang, “Nonlinear Dynamic System
Identification Using Pipelined Functional Link Artificial
Recurrent Neural Network ,” Neurocomputing, Vol. 72,
No. 13-15, 2009, pp. 3046-3054. doi:10.1016/j.neucom.
2009.04.001
[17] S. K. Padhy, et al., “No n -Linear Channel Equalization
using Adaptive MP NN,” Applied Soft Computing, Vol. 9,
No. 3, 2009, pp. 1016-1022. doi:10.1016/j.asoc.2009.02.
009
[18] M. A. Guzmán, et al., “A Novel Multiobjective Op timi-
zation Algorithm based on Bacterial Chemot axi s , ” Engi-
neering Applications of Artificial Intelligence, Vol. 23,
No. 3, 2010, pp. 292-301. doi:10.1016/j.engappai.2009.
09.010
[19] B. Majhi and G. Panda, “Development of Efficient Iden-
tification Scheme for Nonlinear Dynamic Systems using
Swarm Intelligence Techniques,” Expert Systems with
Applications, Vol. 37, No. 1, 2010, pp. 556-566. doi:10.
1016/j.eswa.2009.05.036
[20] D. P. Acharya, G. Panda and Y. V. S. Lakshmi, “Effects
of Finite Register Length on Fast ICA, Bacter ia Foragin g
Optimization Based ICA and Constrained Genetic Algo-
rithm based ICA Algorithm,” Digital Signal Processing,
Available Online, August 2009.
[21] B. K. Panigrahi and V. Ravikumar Pandi, “Congestion
Management Using Adaptive Bacterial Foraging Algo-
rithm,” Energy Conversion and Management, Vol. 50,
No. 5, 2009, pp. 1202-1209. doi:10.1016/j.enconman.
2009.01.029
[22] M. Korürek and A. Nizam, “Clustering MIT-BIH Arr-
hythmias with Ant Colony Optimization using Time Do-
main and PCA Compressed Wavelet Coefficients,” Digi-
tal Signal Processing, Available online 13 November
2009.
[23] M. H. Aghdam, et al., “Text F eature Selecti on Using Ant
Colony Optimization,” Expert Systems with Applications,
Vol. 36, No. 3, 2009, pp. 6843-6853. doi:10.1016/j.eswa.
2008.08.022
[24] S.-S. Weng and Y.-H. Liu, “Mining Time Series Dat a for
Segmentation by Using Ant Colony Optimization,” Eu-
ropean Journal of Operational Research, Vol. 173, No. 3,
2006, pp . 921-937. doi:10. 1016/j.ejor.2005.09.001
[25] J. Tian, et al., “Ant Colony Optimization for Image
Shrinkage,” Pattern Recognition Letters, Available on
line 7 January, 2010.
[26] W. Chen, N. Minh and J. Litva, “On Incorporating Finite
Impulse Response Neural Network with Finite Di fference
Time Domain Method for Simulating Electromagnetic
Problems,” Antennas and Propagation Society Interna-
tional Symposium, Vo l . 3, 1996, pp. 1678-1681.
[27] Y.-P. Liu, M.-G. Wu and J.-X. Qian, “Evolving Neural
Networks Using the Hybrid of Ant Colony Optimization
and BP Algorithms,” Lecture No tes in C omputer S cien ce,
Vol. 397 1, 2006.

Evolutionary MPNN for Channel Equalization
17
[28] D. H. Kim, A. Abraham, and J. H. Cho, “A Hybrid Ge-
netic Algorithm and Bacterial Foraging Approach for
Global Optimization,” Information Sciences, Vol. 177,
No. 18, 2007, pp. 3918-3937. doi: 10.1016/j.ins.2007.04.
002
[29] A. Biswas, S. Dasgupta, S. Das and A. Abraham, “Syn-
ergy of PSO and Bacterial Foraging Optimization — A
Comparative Study on Numerical Benchmarks,” Innova-
tions in Hybrid Intelligent Systems, Vol. 44, 2007, pp.
255-263. doi:10.1007/978-3-540-74972-1_34
[30] C. Grosan and A. Abraham, “Hybrid Evolutionary Algo-
rithms: Methodologies, Architectures, and Reviews,”
Hybrid Evolutionary Algorithms, Vol. 75, 2007, pp. 1-17.
doi:10.1007/978-3-540-73297-6_1
[31] H. Chen, Y. L. Zhu, K. Y. Hu, “Multi-Colony Bacteria
Foraging Optimization with Cell-to-Cell Communication
for RFID Network Planning,” Applied Soft Computing,
Vol. 10, No. 2, 2010, pp. 539-547. doi:10.1016/j.asoc.
2009.08.023