Energy and Power Engineering, 2013, 5, 488-492
doi:10.4236/epe.2013.54B094 Published Online July 2013 (http://www.scirp.org/journal/epe)
A Fuzzy Probability-based Markov Chain Model for
Electric Power Demand Forecasting of Beijing, China
Xiaonan Zhou1, Ye Tang1, Yulei Xie1, Yalou Li2, Hongliang Zh ang3
1Key Laboratory of Regional Energy System Optimization, Ministry of Education,
North China Electric Power University, Beijing, China
2China Electric Power Researc h I n s t itute, Beij i n g, China
3Electric Power Research Institute of Guangdong Grid Corporation, Guangzhou, China
Received December, 2012
ABSTRACT
In this study, a fuzzy probability-based Markov chain model is developed for forecasting regional long-term electric
power demand. The model can deal with the uncertainties in electric power system and reflect the vague and ambiguous
during the process of power load forecasting through allowing uncertainties expressed as fuzzy parameters and discrete
intervals. The developed model is applied to predict the electric power demand of Beijing from 2011 to 2019. Different
satisfaction degrees of fuzzy parameters are considered as different levels of detail of the statistic data. The results indi-
cate that the model can reflect the high uncertainty of long term power demand, which could support the programming
and management of power system. The fuzzy probability Markov chain model is helpful for regional electricity power
system managers in not only predicting a long term power load under uncertainty but also providing a basis for making
multi-scenarios power generation/development plans.
Keywords: Fuzzy Probability; Markov Chain Model; Power Load Prediction; Satisfaction Degree; Uncertainty
1. Introduction
Electric power is one of the most usual and important
energy in human life and economic development. With
the incensement of urbanization and the improvement of
people’s living standard, electric power demand in in-
dustries, commerce and people’s daily is on the increase
during a long period. Thus, the electric power industry
must take various actions (e.g. power expansion and
transmission expansion) to meet the user’s demand.
However, there are many uncertain and limited factors
that exist in many system parameters and their interrela-
tionships, including the influence of weather, nature en-
vironment, human activities and economic structural ad-
justment. All of those would lead to the uncertainty in
long term power load forecasting and the versatility of
electric power demand in future. Therefore, it is desired
to develop an effective method to forecast long-term
power load under considering the uncertainties of electric
power system.
Previously, a variety of forecasting models of electric
power load have been developed, such as grey Markov
model[1], artificial neutral model[2], recurrent support
vector machines with genetic algorithms (RSVMG)
model[3], hybrid ellipsoidal fuzzy systems (HEFST) [4]
and adaptive network based fuzzy inference system
(ANFIS) [5]. All of these models attempt to minimize the
forecasting error, but have less ability to reflect different
possible of power demand caused by uncertainty, espe-
cially the economic structural adjustment in developing
countries (e.g. China). The different possible of power
demand is more obvious after a long time (more than 5
years). Therefore, it is desired to develop a set which
include different possible of power demand in power
load forecasting.
In this study, the objective is to develop a fuzzy prob-
ability based Markov chain model to predict long term
regional electric power demand. The model is coupled
with fuzzy probability and discrete interval method to
Markov chain in order to deal with the vagueness and
uncertainty in system parameters and their interrelation-
ships. The model can reflect the different possible of
power demand and provide information to a long term
power system programming. The model is applied to the
case of Beijing. The power load of Beijing is forecasted
in different satisfaction degrees.
2. Fuzzy Probability Markov Chain Model
2.1. Markov Chain
A Markov chain is a sequence of random variables with

X. N. ZHOU ET AL. 489
Markov property, in other words, the present state only
dependents on the last state, and doesn’t depend on the
states before the last state. Let t
X
denotes a random
variable which representing th e state of a system at time t,
where If 1t
0, 1,2,...t
X
 only depends on the state
t
of
X
，and does not depend on the states befo t re
X
,
formally
11122
1+1
(|,,,
(|)
n
nnnn
PXx XxXxXx
PXxX x


 
 
)
nn
We can say t
X
with Markov property, and the series
t
X
is a Markov chain. If
1n+1n -1-1
(|)=(|
nnnnn
PXxX xPX xXx
 ) n
,
t
X
is a stationary Markov chain (or time-homogeneous
Markov chain). Let p
ij denotes the probability that the
system is in a state j at time 1t

given the system is in
state i at time t. If the system has a finite number of states,
1, 2
s
，, the stationary Markov chain can be defined by a
transfer probability matrix[6]:
11 121
21 222
12
s
s
s
ss
pp p
pp p
P
pp p








 
s
(1)
11
js
ij
j
p



 (2)
The transfer probability matrix of a stationary Markov
chain can be generated from the observations of the sys-
tem state in the past. Provided with the observations of
the system state012 ,,,
n
X
XX X,, at time ,
we can get the transfer probability matrix as follow[7]
0,..., 1tN
ij
ij i
N
PN  (3)
where ij is the number of observation pairs t N
X
and
1t
X
 with t
X
in state i and 1t
X

t
in state j; i is the
number of observation pairs N
X
and 1t
X
 with t
X
in
state i and 1t
X
 in any state.
2.2. Fuzzy Probability Markov Chain Model
Let t denotes the electric power load in period t, and
denotes the growth rate of power load in period t.
tcan be divided into three states 1, 2 and 3
DE
t
R
Rrrr

. The
power load in the period before the first programming
period is and its growth rate is in state
0
DE m r

The power load in period t:
01
(1 )
i
t
ti
DEDE R




(4)
Rt is composed of 3 states, so there are 3t probabilities
of the power load in period t:
011r 1,2,3;
h
hDEDE h

（） (5)
1,3 h211,2,3; 1,2,3;
t
tth
DDrt h

 (6)
1,3 h 121,2,3; 1,2,3;
t
tth
DDrt h


  (7)
1,3 h3 1,2,3; 1,2,3;
t
tth
DDrt h

  (8)
Transfer probability matrix:
11 1213
21 2223
31 3233
ppp
Pppp
ppp











(9)
ij
ij i
N
PN  (10)
where ij is the number of observation pairs t and
1t
NR
R

with t in state i and t in state j in historical
data; i is the number of state i occurs in historical
data except the last period.
R R
N
However, the probabilities gotten from historical data
are approximate value which can not reflect the real
transport probability. The actual transfer probabilities
distribute in the range around the statistics (It can be as-
sumed that the range is from 0.5 times to 1.5 times of the
statistic). Assume that the transfer probabilities are tri-
angular fuzzy numbers, the satisfaction degree is 1 when
the transport probability is the statistic value, and the
satisfaction degree is 0 when the transport probability is
one of the boundaries of the range.
When the satisfaction is higher than u , the
lower bo und: (0 1)u
=(1)(0.5
ij ijijij
PPu PP
 )
)
(11)
the upper bound:
+=(1)(1.5
ij ijijij
PPu PP (12)
The transfer probability matrix:
11 1213
21 2223
32 33
31
ppp
Ppp p
ppp
















(13)
T step transfer probability matrix:, the third row
of every t composed to a new matrix
=t
t
QP
Qtj
X
, tj
x
is the
probability of state j occurring in period t.
Ther e are 3t probabilities of the power load in period t,
let h Prt

denotes the probability of demand scenario h in
period t. It is obviously that when
1t
111 122 133
Pr; Pr; Pr;
mm
pp
 

m
p (14)
when , according to Bayes formula 2t
1,3 h2,1
PrPr 2,3; 1,2,3;
t
tthk
pt h

 (15)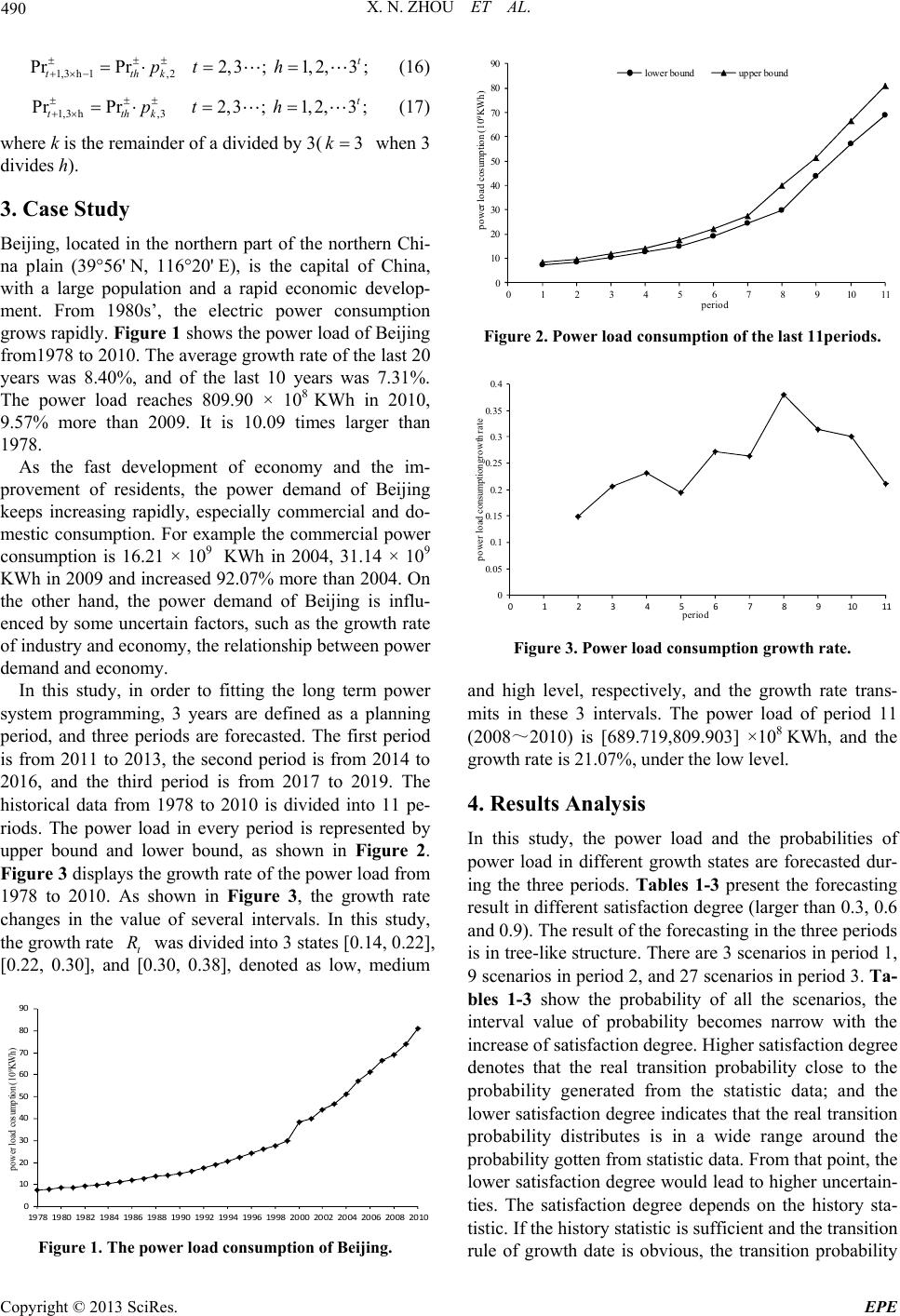

X. N. ZHOU ET AL.
490
1,3 h 1,2
PrPr 2,3; 1,2,3;
t
tthk
pt h


  (16)
1,3 h,3
PrPr 2,3; 1,2,3;
t
tthk
pt h

  (17)
where k is the remainder of a divided by 3( when 3
divides h). 3k
3. Case Study
Beijing, located in the northern part of the northern Chi-
na plain (39°56' N, 116°20' E), is the capital of China,
with a large population and a rapid economic develop-
ment. From 1980s’, the electric power consumption
grows rapidly. Figure 1 shows the power load of Beijing
from1978 to 2010. The average growth rate of the last 20
years was 8.40%, and of the last 10 years was 7.31%.
The power load reaches 809.90 × 108 KWh in 2010,
9.57% more than 2009. It is 10.09 times larger than
1978.
As the fast development of economy and the im-
provement of residents, the power demand of Beijing
keeps increasing rapidly, especially commercial and do-
mestic consumption. For example the commercial power
consumption is 16.21 × 109 KWh in 2004, 31.14 × 109
KWh in 2009 and increased 92.07% more than 2004. On
the other hand, the power demand of Beijing is influ-
enced by some uncertain factors, such as the growth rate
of industry and economy, the relationship between power
demand and economy.
In this study, in order to fitting the long term power
system programming, 3 years are defined as a planning
period, and three periods are forecasted. The first period
is from 2011 to 2013, the second period is from 2014 to
2016, and the third period is from 2017 to 2019. The
historical data from 1978 to 2010 is divided into 11 pe-
riods. The power load in every period is represented by
upper bound and lower bound, as shown in Figure 2.
Figure 3 displays the growth rate of the power load from
1978 to 2010. As shown in Figure 3, the growth rate
changes in the value of several intervals. In this study,
the growth rate t was divided into 3 states [0.14, 0.22],
[0.22, 0.30], and [0.30, 0.38], denoted as low, medium
R
0
10
20
30
40
50
60
70
80
90
19 7819 8019 8219 84198619 8819 9019 9219 9419 9619 9820 0020 0220 04200620 0820 10
powe r l oa d cosumption (109KWh)
Figure 1. The power load consumption of Beijing.
0
10
20
30
40
50
60
70
80
90
0123456789101
power load cosum pti on (109KWh)
period 1
low er boundupper bound
Figure 2. Power load consumption of the last 11periods.
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0123456789101
power load consumptio n growth rate
period 1
Figure 3. Power load consumption growth rate.
and high level, respectively, and the growth rate trans-
mits in these 3 intervals. The power load of period 11
(2008～2010) is [689.719,809.903] ×108 KWh, and the
growth rate is 21.07%, un der the low level .
4. Results Analysis
In this study, the power load and the probabilities of
power load in different growth states are forecasted dur-
ing the three periods. Tables 1-3 present the forecasting
result in different satisfaction degree (larger than 0.3, 0.6
and 0.9). The result of the forecasting in the three periods
is in tree-like structure. There are 3 scenarios in period 1,
9 scenarios in period 2, and 27 scenarios in period 3. Ta-
bles 1-3 show the probability of all the scenarios, the
interval value of probability becomes narrow with the
increase of satisfaction degree. Higher satisfaction degree
denotes that the real transition probability close to the
probability generated from the statistic data; and the
lower satisfaction degree indicates that the real transition
probability distributes is in a wide range around the
probability gotten from statistic data. From that point, the
lower satisfaction degree would lead to higher uncertain-
ties. The satisfaction degree depends on the history sta-
tistic. If the history statistic is sufficient and the transition
rule of growth date is obvious, the transition probability

X. N. ZHOU ET AL.
491
Table 1. The forecasting results of power load in period 1.
Probability in different satisfaction degree
Growth state Power load (108 KWh) 0.3 0.6 0.9
L [786.280,998.082] [0.217,0.450] [0.266,0.40] [0.317,0.350]
M [841.457,1052.874] [0.433,0.900] [0.33,0.800] [0.633,0.700]
H [896.635,1117.666] 0 0 0
Table 2. The forecasting results of power load in period 2.
Probability in different satisfaction degree
Growth state Power load (108 KWh) 0.3 0.6 0.9
L-L [896.359,1205.459] [0.0469,0.2024] [0.0711,0.1600] [0.1003,0.1225]
L-M [959.261,1284.506] [0.0939,0.4050] [0.1422,0.3200] [0.2005,0.2450]
L-H [1022.163,1363.553] 0 0 0
M-L [959.261,1284.506] [0.0939,0.4050] [0.1422,0.3200] [0.2005,0.2450]
M-M [1026.578,1368.736] [0.0939,0.4050] [0.1422,0.3200] [0.2005,0.2450]
M-H [1093.894,1452.966] [0.0939,0.4050] [0.1423,0.3201] [0.2006,0.2451]
H-L [1022.163,1363.553] 0 0 0
H-M [1093.894,1452.966] 0 0 0
H-H [1165.625,1542.379] 0 0 0
Table 3. The forecasting results of power load in period3.
Probability in different satisfaction degree
Growth state Power load
(108 KWh) 0.3 0.6 0.9
L-L-L [1021.849,1470.661] [0.0102,0.0911] [0.0189,0.0640] [0.0318,0.0429]
L-L-H [1093.558,1567.097] [0.0203,0.1822] [0.0379,0.1280] [0.0635,0.0857]
L-L-H [1165.266,1663.534] 0 0 0
L-M-L [1093.558,1567.097] [0.0203,0.1822] [0.0379,0.1280] [0.0635,0.0857]
L-M-M [1170.298,1669.858] [0.0203,0.1822] [0.0379,0.1280] [0.0635,0.0857]
L-M-H [1247.039,1772.618] [0.0203,0.1822] [0.0379,0.1280] [0.0635,0.0857]
L-H-L [1165.266,1663.534] 0 0 0
L-H-M [1247.039,1772.618] 0 0 0
L-H-H [1328.812,1881.702] 0 0 0
M-L-L [1093.558,1567.097] [0.0203,0.1822] [0.0379,0.1280] [0.0635,0.0857]
M-L-M [1170.298,1669.858] [0.0469，0.3645] [0.0759,0.2560] [0.1270,0.1715]
M-L-H [1247.039,1772.618] 0 0 0
M-M-L [1770.298,1669.858] [0.0203,0.1822 ] [0.0379,0.1280] [0.0635,0.0857]
M-M-M [1252.425,1779.357] [0.0203,0.1822] [0.0379,0.1280] [0.0635,0.0857]
M-M-H [1334.551,1888.856] [ 0.0234,0.2224] [0.0379,0.1280] [0.0635,0.0857]
M-H-L [1247.039,1772.618] [0.0234,0.2224] [0.0379,0.1280] [0.0635,0.0857]
M-H-M [1334.551,1888.856] 0 0 0
M-H-H [1422.062,2005.093] [0.0407,0.3646] [0.0759,0.2561] [0.1271,0.1715]
H-L-L [1165.266,1663.534] 0 0 0
H-L-M [1247.039,1772.618] 0 0 0
H-L-H [1328.812,1881.702] 0 0 0
H-M-L [1247.039,1772.618] 0 0 0
H-M-M [1328.812,1881.702] 0 0 0
H-M-H [1442.062,2005.093] 0 0 0
H-H-L [1328.812,1881.702] 0 0 0
H-H-M [1422.062,2005.093] 0 0 0
H-H-H [1515.312,2128.483] 0 0 0

X. N. ZHOU ET AL.
492
gotten from statistic data can reflect the actual transition
probability really, so high satisfaction degree should be
selected. In contrast, if the uncertainty of transition
probability is higher, low satisfaction degree should be
chosen.
From the above tables, the probabilities of several re-
sults are 0, and many forecasting power loads are with
the same value. If those scenarios with the probability
value of 0 are left out, the results obtained from the mod-
el could be simplified. In addition, the results with the
same power load value could be integrated by accumu-
late the probability of the equal power load. Therefore,
when the forecasting is for a very long term, the simpli-
fication would have advantage to make the results brief.
However, there is also a disadvantage of the simplifica-
tion. For example, the primary result is in tree structure,
and convenient for scenario analysis. The results would
become net structure when simplified, which is not con-
venient for decision making and analysis.
5. Conclusions
In this study, a fuzzy probability Markov chain is devel-
oped to forecast regional long term power load. The
model can deal with the uncertainties in long term power
load forecasting. The developed fuzzy probability Markov
chain is applied to long term power load forecasting of
Beijing. The forecasting result concludes all the power
load scenarios. The data of the result is in tree-like struc-
ture. The disadvantage of the method is that the amount
of data increases largely when deal with many periods.
The forecasting result can be simplified by integrate the
power loads with the same value. The simplification can
deal with the disadvantage in some extent. But the sim-
plification would make the data structure complex, which
is disadvantage to analysis and decision making. In con-
clusion, the fuzzy probability Markov chain model can
reflect the vague and ambiguous during the process of
power load forecasting through allowing uncertainties
expressed as fuzzy parameters and discrete intervals. The
forecasting result by the model is helpful for regional
electricity power system managers in not only predicting
a long term power load under uncertainty but also pro-
viding a basis for making multi-scenarios power genera-
tion/development plans.
REFERENCES
[1] Y. Cui, et al, “Application of Grey-Markov Prediction
Model on Long-Term Load Forecasting,” Modern Elec-
tric Power, Vol. 3, No. 28, 2011,pp. 38-47.
[2] C. C. Hsu and C. Y. Chen, “Regional Load Forecasting in
Taiwan-Applications of Artificial Neural Networks,” En-
ergy Conversion Management, Vol. 44, No. 12, 2003, pp.
1941-1949. doi:10.1016/S0196-8904(02)00225-X
[3] P. F. Pai and W. C. Hong, “Forecasting Regional Elec-
tricity Load Based on Recurrent Support Vector Ma-
chines with Genetic Algorithms,” Electric Power Systems
Research, Vol. 74, No. 3, 2005, pp. 417-425.
doi:10.1016/j.epsr.2005.01.006
[4] P. F. Pai, “Hybrid Ellipsoidal Fuzzy System in Forecast-
ing Regional Electricity Loads,” Energy Conversion
Management, 2006, Vol. 47, No. 15-16, pp. 2283-2289.
doi:10.1016/j.enconman.2005.11.017
[5] L.-C. Ying and M.-C. Pan, “Using Adaptive Network
Based Fuzzy Inference System to Forecast Regional Elec-
tric Loads,” Energy Conversion and Management, Vol.
49, 2008, pp. 205-211.
[6] N. Ye, “A Markov Chain Model of Temporal Behavior
for Anomaly Detection,” Workshop on Information As-
surance and Security, 2000.
[7] T. M. Mithchel, Machine Learning, Boston, Ma:
McGraw- Hill, 1997.