 American Journal of Computational Mathematics, 2013, 3, 52-55 doi:10.4236/ajcm.2013.33B009 Published Online September 2013 (http://www.scirp.org/journal/ajcm) Copyright © 2013 SciRes. AJCM The Planar Ramsey Numbers PR (K4-e, Kl)* Yongqi Sun1, Yali Wu1, Rui Zhang1, Yuansheng Yang2 1School of Computer and Information Technology, Beijing jiaotong University, Beijing, China 2Department of Computer Science, Dalian University of Technology, Dalian, China Email: yqsun@bjtu.edu.cn, yangys@dlut.edu.cn Received 2013 ABSTRACT The planar Ramsey number PR (H1, H2) is the smallest integer n such that any planar graph on n vertices contains a copy of H1 or its complement contains a copy of H2. It is known that the Ramsey number R(K4 − e, K6) = 21, and the planar Ramsey numbers PR(K4 − e, Kl) for l ≤ 5 are known. In this paper, we give the lower bounds on PR (K4 − e, Kl) and determine the exact value of PR (K4 − e, K6). Keywords: Planar Graph; Ramsey Number; Forbidden Subgr ap h 1. Introduction We consider only finite undirected graphs without loops or multiple edges. For a graph G with vertex set V(G) and edge set E(G), we denote the order and size of G by p(G) = |V(G)| and q(G) = |E(G)|, respectively. We refer to the regions defined by a plane graph as its fac es. A face is said to be incident with the vertices and edges in its boundary. The length of a face is the number of edges with which it is incident. If a face has length α, we say it is an α-face . For a plane graph G, let f denote the number of faces, and fα the number of α-faces. Let d(v) denote the degree of a vertex v ∈ V(G), δ(G) the minimum degree of G. The neighborhood and the closed neighborhood of a vertex v ∈ V(G) are denoted by N(v) = {u∈ V(G)|uv ∈ E(G)} and N[v] = N(v)∪{v}, respectively. Let G ∪ H denote a disjoint sum of G and H, and nG is a disjoint sum of n copies of G. G ___ denotes the complement of G. For W ⊆ V(G), let G〈W〉 denote the subgraph of G in- duced by W, and W\v the subset of W obtained by re- moving the vertex v. A graph G of order n will be called an (H1, H2; n)-graph if H1 ⊈ G and H2 ⊈ G ___ For the Ramsey number R(K4 − e, K6), McNamara proved that its exact value is 21 (cf. [4] ). In this paper, we prove that PR(K4 − e, K6)=17 and PR(K4 − e, Kl) ≥ 3l + ⌊(l − 1) / 4⌋−2. So, the values of PR (K4 − e, Kl) for l ≥ 7 are still open. 2. Preliminary Results Lemma 2.1. If G is a (K4 − e, Kl ; n)-P-gra ph, then δ(G) ≥ n − PR(K4 − e, Kl−1). Proof. Assume that δ(G) < n − PR(K4− e, Kl−1). Let v be a vertex of degree δ(G) and H = G〈V(G) − N[v]〉, then p(H) = n − δ(G) – 1 ≥ PR(K4 − e, Kl−1). Since K4 – e ⊈ H, we have Kl−1 ⊆ . If a (H1, H2; n)-graph is planar, we call it an (H1, H2; n)-P-graph. The planar Ramsey number PR(H1, H2) is the smallest integer n such that there is no (H1, H2; n)-P -graph. The definition of planar Ramsey number was firstly introduced by Walker [7]. Steinberg and Tovey [3] studied the case when both H1 and H2 are complete. For a connected graph H1 of order at least 5, Gorgol proved that PR (H1, Kl)=4l−3 [2]. Bielak and Gorgol [1] determined that PR (K4 − e, K3)= 7 and PR(K4 − e, K4) = 10. It was shown that PR(K4 − e, K5) = 14 and PR(K4 − e, K6 − e) = 16 [5, 6]. H ___ . The appropriate l−1 vertices of H together with v would yield a Kl in G ___ , a contradiction. So, δ(G) ≥ n − PR(K4 − e, Kl−1). Lemma 2.2 and 2.3 were proved in [5]. Lemma 2.2. If G is a planar graph such that K4 − e ⊈ G, then q(G) ≤ ⌊12(p(G) − 2) /5⌋. Lemma 2.3. If G is a (K4 – e, K4; 9)-P-graph, then 3K3 ⊆ G or G9-0 ⊆ G, where G9-0 is shown in Fig ure 2.1. By an argument similar to the one in the proof of paper [5], we can prove Lemma 2.4, Figure 2.1. The graphs G9-0. 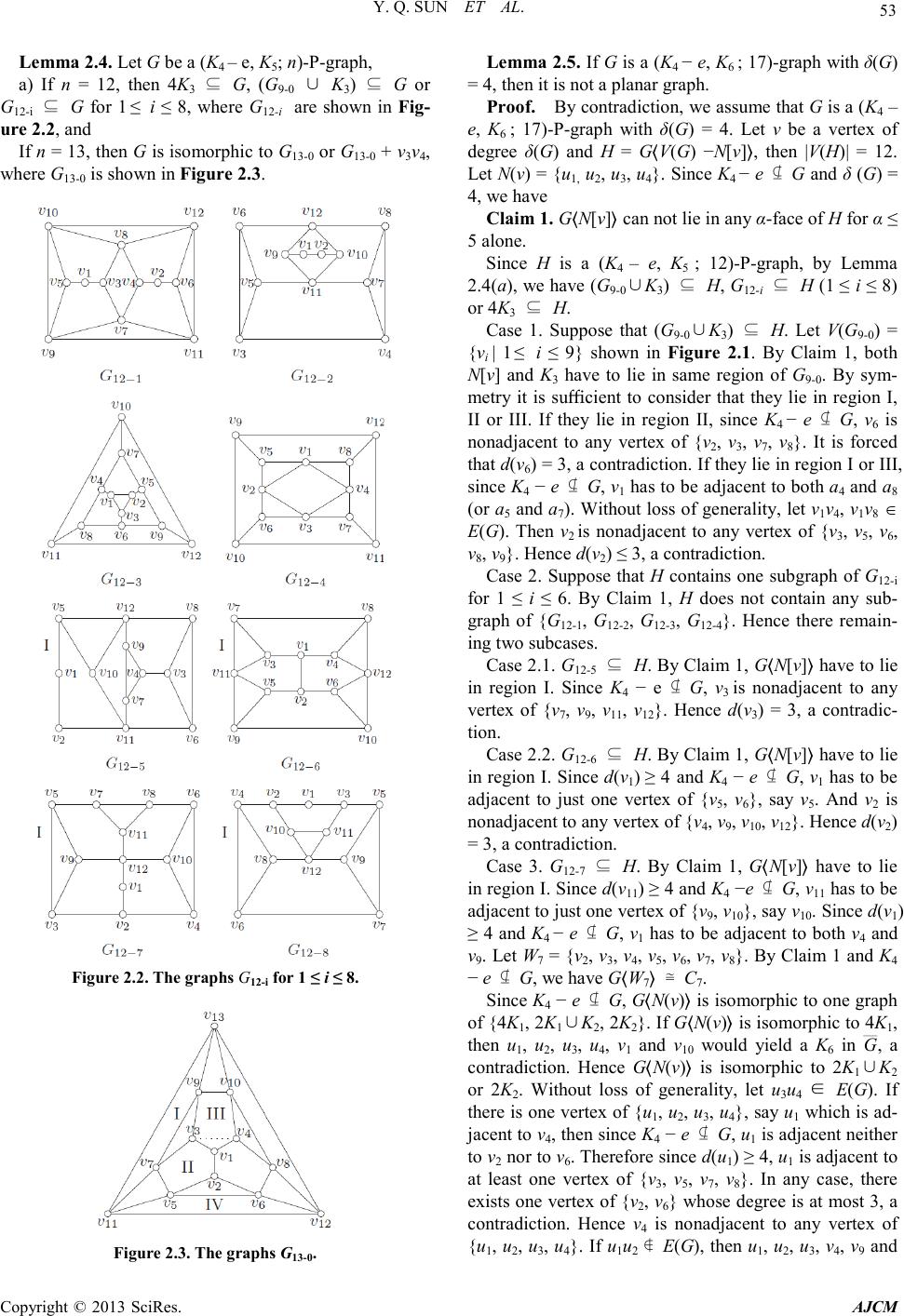 Y. Q. SUN ET AL. Copyright © 2013 S ciRes. AJCM Lemma 2.4. Let G be a (K4 – e, K5; n)-P-gra ph, a) If n = 12, then 4K3 ⊆ G, (G9-0 ∪ K3) ⊆ G or G12-i ⊆ G for 1 ≤ i ≤ 8, where G12-i are shown in Fig- ure 2.2, and If n = 13, then G is isomorphic to G13-0 or G13-0 + v3v4, where G13-0 is shown in Figur e 2.3. Figure 2.2. The graphs G12-i for 1 ≤ i ≤ 8. Figure 2.3. The graphs G13-0. Lemma 2.5. If G is a (K4 − e, K6 ; 17)-graph with δ(G) = 4, then it is not a planar gr ap h. Proof. By contradiction, we assume that G is a (K4 – e, K6 ; 17)-P-graph with δ(G) = 4. Let v be a vertex of degree δ(G) and H = G⟨V(G) −N[v]⟩, then |V(H)| = 12. Let N(v) = {u1, u2, u3, u4}. Since K4 − e ⊈ G and δ (G) = 4, we have Claim 1. G⟨N[v]⟩ can not lie in any α-face of H for α ≤ 5 alone. Since H is a (K4 – e, K5 ; 12)-P-graph, by Lemma 2.4(a), we have (G9-0∪K3) ⊆ H, G12-i ⊆ H (1 ≤ i ≤ 8) or 4K3 ⊆ H. Case 1. Suppose that (G9-0∪K3) ⊆ H. Let V(G9-0) = {vi | 1 ≤ i ≤ 9} shown in Figure 2.1. By Claim 1, both N[v] and K3 have to lie in same region of G9-0. By sym- metr y it is sufficient to consider that they lie in region I, II or III. If they lie in region II, since K4 − e ⊈ G, v6 is nonad j acent to any vertex of {v2, v3, v7, v8}. It is forced that d(v6) = 3, a contradiction. If they lie in region I or III, since K4 − e ⊈ G, v1 has to be adjacent to both a4 and a8 (or a5 and a7). Without loss of generality, let v1v4, v1v8 ∈ E(G). Then v2 is nonadjacent to any vertex of {v3, v5, v6, v8, v9}. Hence d(v2) ≤ 3, a contradiction. Case 2. Suppose that H contains one subgraph of G12-i for 1 ≤ i ≤ 6. By Claim 1, H does not contain any sub- graph of {G12-1, G12-2, G12-3, G12-4}. Hence there remain- ing two subcases. Case 2.1. G12-5 ⊆ H. By Claim 1, G⟨N[v]⟩ have to lie in region I. Since K4 − e ⊈ G, v3 is nonadjacent to any vertex of {v7, v9, v11, v12}. Hence d(v3) = 3, a contradic- tion. Case 2.2. G12-6 ⊆ H. By Claim 1, G⟨N[v]⟩ have to lie in region I. Since d(v1) ≥ 4 and K4 − e ⊈ G, v1 has to be adjacent to just one vertex of {v5, v6}, say v5. And v2 is nonadjacent to any vertex of {v4, v9, v10, v12}. Hence d(v2) = 3, a contradiction. Case 3. G12-7 ⊆ H. By Claim 1, G⟨N[v]⟩ have to lie in region I. Since d(v11) ≥ 4 and K4 −e ⊈ G, v11 has to be adjacent to just one vertex of {v9, v10}, say v10. Since d(v1) ≥ 4 and K4 − e ⊈ G, v1 has to be adjacent to both v4 and v9. Let W7 = {v2, v3, v4, v5, v6, v7, v8}. By Claim 1 and K4 − e ⊈ G, we have G⟨W7⟩ ≅ C7. Since K4 − e ⊈ G, G⟨N(v)⟩ is isomorphic to one graph of {4K1, 2K1∪K2, 2K2}. If G⟨N(v)⟩ is isomorphic to 4K1, then u1, u2, u3, u4, v1 and v10 would yield a K6 in G ___ , a contradiction. Hence G⟨N(v)⟩ is isomorphic to 2K1∪K2 or 2K2. Without loss of generality, let u3u4 ∈ E(G). If there is one vertex of {u1, u2, u3, u4}, say u1 which is ad- jacent to v4, then since K4 − e ⊈ G, u1 is adjacent neither to v2 nor to v6. Therefore since d(u1) ≥ 4, u1 is adjacent to at least one vertex of {v3, v5, v7, v8}. In any case, there exists one vertex of {v2, v6} whose degree is at most 3, a contradiction. Hence v4 is nonadjacent to any vertex of {u1, u2, u3, u4}. If u1u2 ∉ E(G), then u1, u2, u3, v4, v9 and  Y. Q. SUN ET AL. Copyright © 2013 S ciRes. AJCM v11 would yield a K6 in G ___ , a contradiction. So, we have u1u2 ∈ E(G), that is, G⟨N(v)⟩ ≅ 2K2. Since δ(G) = 4, there are at least 8 edges between the vertices of {u1, u2, u3, u4} and W7\v4. Since K4 − e ⊈G, each vertex of W7\v4 is adjacent to at most two vertices of {u1, u2, u3, u4}. Hence there are just two vertices of W7\v4 which are adjacent to two vertices of {u1, u2, u3, u4}. By symmetry there are three cases. Case 3.1. Suppose that there is one vertex of {v3, v8} which is adjacent to u1 and u3 (or u2 and u4). Without loss of generality, let v3u1, v3u3 ∈ E(G). Then since d(v5) ≥ 4 and K4 − e ⊈ G, v5 has to be adjacent to one vertex of {u2, u4}, say u2. Thus there is at least one vertex of {u1, u3, u4} whose degree is at most 3, a contradiction (see G17.1 in Fig ur e 2.4). Case 3.2. Suppose that there is one vertex of {v5, v7} which is adjacent to u1 and u3 (or u2 and u4). Without loss of generality, let v5u1, v5u3∈E(G). Then since d(v3) ≥ 4 and K4 − e ⊈ G, v3 has to be adjacent to one vertex of {u2, u4}, say u2. Thus there is at least one vertex of {u1, u3, u4} whose degree is at most 3, a contradiction(see G17.. 2 in Fig. 2.4) . Case 3.3. Suppose that both v2 and v6 are adjacent to two vertices of {u1, u2, u3, u4} respectively, say v2u1, v2u3∈ E(G), v6 is adjacent to one vertex of {u1, u2} and one vertex of {u3, u4}. Then since K4 − e ⊈G, there is at least one vertex of {u1, u2, u3, u4} whose degree is at most 3, a contradiction (see G17.3 in Fig ur e 2.4). Case 4. G12−8 ⊆ H. By Claim 1, G〈N[v]〉 have to lie in region I. Since d(v8) ≥ 4 and K4 − e ⊈ G, v8 has to be adjacent to v9. Since d(v10) ≥ 4 and K4 − e ⊈ G, v10 has to be adjacent to just one vertex of {v1, v4}. Similarly, v11 has to be adjacent to just one vertex of {v1, v5}. Since K4− e ⊈ G, v1 is adjacent to at most one vertex of {v10, v11}. By symmetry it is sufficient to consider that v4v10, v1v11∈ E(G) or v4v10, v5v11∈ E(G). If v4v10, v1v11∈ E(G), then the proof is same as Case 3 (see G17.4 in Fig ure 2.5 ). So it remains that v4v10, v5v11∈ E(G). By Claim 1, we have v4v5 ∉ E(G) and v1 is non- adjacent to any vertex of {v6, v7}. Since K4 − e ⊈ G, G〈N(v)〉 is isomorphic to one graph of {4K1, 2K1∪K2, 2K2}. If G〈N(v)〉 is isomorphic to 4K1, then u1, u2, u3, u4, v8 and v10 would yield a K6 in G ___ Case 4.1. Suppose that G〈N(v)〉 ≅ 2K1∪K2, say u3u4 ∈ E(G). If each vertex of {u1, u2, u3, u4} is adjacent neither to v4 nor to v5, then u1, u2, u3 (or u4), v4, v5 and v12 would yield a K6 in , a contr adic t io n . Hence G〈N(v)〉 is isomorphic to 2K1∪K2 or 2K2. G ___ , a contradiction. Hence there is at least one edge between vertex sets {u1, u2, u3, u4} and {v4, v5}. Assume that there is at least one edge between vertex sets {u1, u2} and {v4, v5}, say u1v4 ∈ E(G). Then since d(u1) ≥ 4 and K4 − e ⊈G, u1 has to be adjacent to one vertices of {v3, v5, v7}. In any case, there exists at least one vertex of {v1, v6} whose degree is at most 3, a contradiction. Hence there is no edge between vertex sets {u1, u2} and {v4, v5}. Then there is at least one edge between vertex sets {u3, u4} and {v4, v5}, say u3v4∈ E(G). If u4v5 ∉ E(G), then u1, u2, u4, v4, v5 and v12 would yield a K6 in G ___ , a contradiction too. Hence we have u4v5 ∈ E(G) (see G17.5 in Figur e 2.5). There also exists at least one vertex of {v1, v6, v7} whose degree is at most 3, a contradiction. Case 4.2. Suppose that G〈N(v)〉 ≅ 2K2, say u1u2, u3u4 ∈ E(G). Since d(v1) ≥ 4 and K4 –e ⊈G, v1 has to be adjacent to one vertex of {u1, u2} and one vertex of {u3, u4}, say v1u1, v1u3 ∈ E(G). Then since K4 − e ⊈G, v1 is adjacent neither to u2 nor to u4. If there is no edge between vertex sets {u2, u4} and {v4, v5}, then u2, u4, v4, Figure 2.4. The graphs G17.1−G17.3. Figure 2.5. The graphs G17.4−G17.6.  Y. Q. SUN ET AL. Copyright © 2013 S ciRes. AJCM v5, v1 and v12 would yield a K6 in G ___ , a contradiction. Hence there is at least one edge between vertex sets {u2, u4} and {v4, v5}, say u2v4 ∈ E(G). Then since d(u2) ≥ 4 and K4 − e ⊈G, u2 has to be adjacent to at least one vertex of {v3, v5, v7}(see G17.6 in Figure 2.5). In any case, we have d(v6) = 3, a contradiction. By an argument similar to the above proof, we can prove that 4K3 ⊈ H. However, the proof of 4K3 ⊈ H is more complicated than Case 3 or 4, and it is available from the authors. Hence the assumption does not hold. 3. The Main Resu lts Lemma 3.1. There is no (K4−e,K6;17)-P-graph. Proof. Assume that there is a (K4 − e, K6; 17)-P-graph G. Let v be a vertex of degree δ(G) and H = G(V(G)− N[v]). Since PR(K4 − e, K5) = 14, by Lemma 2.1, it follows δ(G) ≥ 3. By Lemma 2.2, q(G) ≤ ⌊12(17−2) /5⌋ = 36 implying δ(G) ≤ 4. By Lemma 2.5, we have δ(G) ≠ 4. It is forced that δ(G) = 3, thus p(H) = 13. Let N(v)={u1, u2, u3}. Since K4−e ⊈ G, we have |E(G(N(v)))| ≤ 1. Without loss of generality, let u1u2, u1u3 ∉ E(G). Since d(u1) ≥ 3 and K4 − e ⊈ G, N[v] can not lie in any triangle of H. By Lemma 2.4(b), H is isomorphic to G13-0 or G13-0+v3v4. If H ≅ G13-0, by symmetry it is sufficient to consider that N[v] lie in region I or II. If H ≅ G13-0 + v3v4, by symmetry it is sufficient to consider that N[v] lie in region I, II, III or IV (see Figure 2.3). If N[v] lie in region I, then u1,u2,v3,v5,v10 and v12 would yield a K6 in G ___ , a contradiction. If N[v] lie in region II, then u1, u2, v4, v6, v9 and v11 would yield a K6 in G ___ , a contradiction. If N[v] lie in region III or IV, then u1, u2, v2, v7, v8 and v13 would yield a K6 in G ___ Proof. Note that G13-0 shown in Figure 2.3 is a (K4 − e, K5; 13)-P-graph. Let G be a graph which is a union of ⌊(l−1)/4⌋ copies of G13-0 and (l−4×⌊(l−1)/4⌋−1) copies of a triangle, then K4 – e ⊈ G. Since K5 ⊈ , a contradiction too. Theorem 3.2. If l ≥ 3, then PR(K4−e, Kl) ≥ 3l+⌊(l−1)/4⌋−2. G ___ [1] H. Bielak and I. Gorgol, “On Planar Ramsey Number for a Small and a Complete Graph,” Manuscript, 1997. 13-0, G contains independent set of size at most l − 1. Hence G is a (K4 − e, Kl; n)-P-graph, where n=3l+⌊ (l−1)/4⌋−3. By Lemma 3.1 and Theorem 3.2, taking l = 6, we have Theorem 3.3. PR(K4 − e, K6) = 17. Furthermore, we have the following conjecture, Conjecture 3.4. If l ≥ 3, the n PR(K4−e, Kl) = 3l+⌊(l−1)/4⌋−2. By Bielak and Gorgol [1], Sun et al. [5]and Theorem 3.3, the conjecture is true for l ≤ 6. REFERENCES [2] I. Gorgol, “Planar Ramsey Numbers,” Discussiones Ma- thematicae Graph Theory, Vol. 25, No. 1-2, 2005, pp. 45-50. doi:10.7151/dmgt.1258 [3] R. Steinberg and C. A. Tovey, “Planar Ramsey Number,” Journal of Combinatorial Theory, Series B, Vol. 59, No. 2, 1993, pp. 288-296. doi:10.1006/jctb.1993.1070 [4] S. P. Radziszowski, “Small Ramsey Numbers,” Elec tronic Journal of Combinatorics,http://www.combin atorics .org/, #R13, 2011, p. 84. [5] Y. Q. Su n, Y. S. Yang, X. H. Lin and J. Qiao, “The Pla- nar Ramsey Number PR (K4 − e, K5),” Discrete Mathe- matics, Vol. 307, No. 1, 2007, pp. 137-142. doi:10.1016/j.disc.2006.05.034 [6] Y. Q. Sun, Y. S. Yang and Z. H. Wang, “The Planar Ramsey Number PR (K4 − e, Kk − e),” ARS Combinatoria, Vol. 88, 2008, pp. 3-20. [7] K. Walker, “The Analog of Ramsey Numbers for Planar Graphs,” Bulletin of the London Mathemat ical Society, Vol. 1, No. 2, 1969, pp. 187-190. doi:10.1112/blms/1.2.187
|