American Journal of Computational Mathematics, 2013, 3, 41-51
doi:10.4236/ajcm.2013.33B008 Published Online September 2013 (http://www.scirp.org/journal/ajcm)
1
Means of Choice for Interactive Management of Dynamic
Geometry Problems Based on Instrumented Behaviour
Philippe R. Richard1, Michel Gagnon2, Josep Maria Fortuny3, Nicolas Le duc2, Michèle Tes-
sier-Baillargeon1
1Département de didactique, Université de Montréal, Canada
2Département de génie informatique et génie logiciel, École Polytechnique de Montréal, Canada
3Departament de Didàctica de les Matemàtiques i de les Ciències Experimentals, Universitat Autònoma de Barcelona, Spain
Received 2013
ABSTRACT
Our paper presents a project that involves two research questions: does the choice of a related problem by the tutorial
system allow the problem solving process which is blocked for the student to be restarted? What information about
learning do related problems returned by the system provide us? We answer the first question according to the didactic
engineering, whose mode of validation is internal and based on the confrontation between an a priori analysis and an a
posteriori analysis that relies on data from experiments in schools. We consider the student as a subject whose adapta-
tion processes are conditioned by the problem and the possible interactions with the computer environment, and also by
his knowledge, usually implicit, of the institutional norms that condition his relationship with geometry. Choosing a set
of good problems within the system is therefore an essential element of the learning model. Since the source of a prob-
lem depends on the student’s actions with the computer tool, it is necessary to wait and see what are the related to prob-
lems that are returned to him before being able to identify patterns and assess the learning. With the simultaneity of
collecting and analysing interactions in each class, we answer the second question according to a grounded theory
analysis. By approaching the problems posed by the system and the designs in play at learning blockages, our analysis
links the characteristics of problems to the design components in order to theorize on the decisional, epistemological,
representational, didactic and instrumental aspects of the subject-milieu system in interaction.
Keywords: Didactics of Mathematics; Competencies; Geometric Thinking; Tutorial System; Related Problems;
Dynamic Geometry; Instrumented Behavior; Cognitive Interactions; Conceptions; Mathematical Work
Space; Means of Choice; Didactic Contract
1. Foreword
In the third year of secondary school, two students tried
to solve a problem of proof at the interface of an interac-
tive tutorial system. It was to compare the area of two
triangles in a parallelogram and to proof the assumption
made. After reading the statement and constructing or
moving the elements of the figure in the dynamic ge-
ometry module (Figure 1), the students quickly agree on
equal areas. They began to create a mathematical proof
on the tutorial system interface and were therefore de-
lighted to see that Prof. Turing, an artificial tutor agent,
indicated with a smiley that their first intuition was well
founded. Even though they were good students, they
sometimes got stuck in their mathematical proof. Happily,
with his messages, Prof. Turing was always successful in
reviving the solution process. Without replacing the
teacher, this tutor agent has 69,000 potential solutions “in
mind” and was quickly able to target the solution envis-
aged by the students, thereby providing personalized
support. Prof. Turing also knows how to recognize a
student’s persistent difficulty and can suggest that he get
help from his teacher. Furthermore, once he arrives, the
teacher sees what has happened from the messages re-
ceived but instead of insisting on their meaning in the
context of the problem he rather asks that a new problem
be solved. The students launched on paper without too
much difficulty then one said to his companion: “look,
I’ve got it... look, this is why it works!” And the solution
to the original problem is relaunched. The use of a re-
lated problem therefore is a means of choice for this di-
dactic system. Can they be made available to Prof. Tur-
ing?
2. Introduction
According to the theory of didactic situations, we know
that the only way to “do” mathematics is to try and solve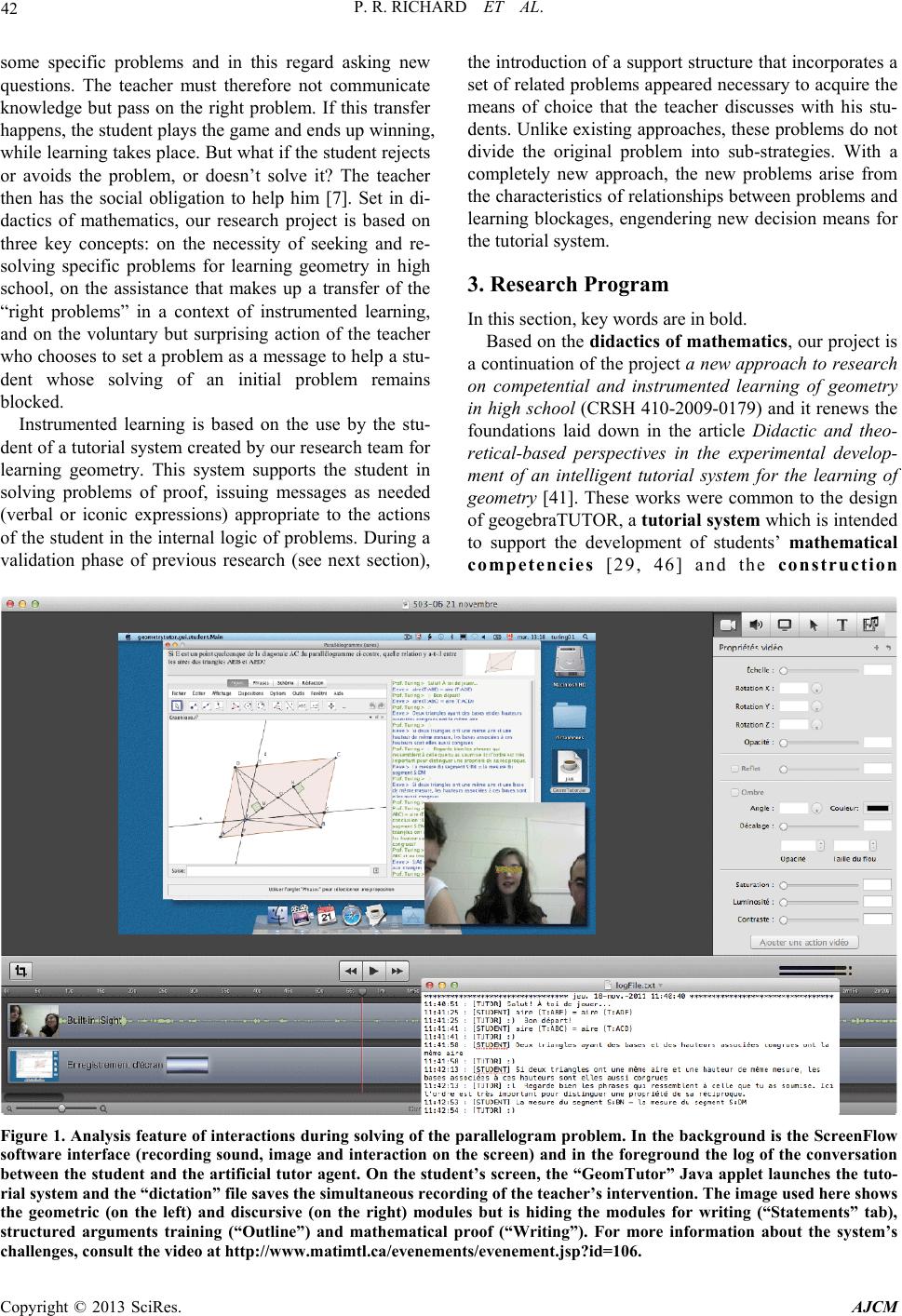

P. R. RICHARD ET AL.
42
some specific problems and in this regard asking new
questions. The teacher must therefore not communicate
knowledge but pass on the right problem. If this transfer
happens, the student plays the game and ends up winning,
while learning takes place. But what if the student rejects
or avoids the problem, or doesn’t solve it? The teacher
then has the social obligation to help him [7]. Set in di-
dactics of mathematics, our research project is based on
three key concepts: on the necessity of seeking and re-
solving specific problems for learning geometry in high
school, on the assistance that makes up a transfer of the
“right problems” in a context of instrumented learning,
and on the voluntary but surprising action of the teacher
who chooses to set a problem as a message to help a stu-
dent whose solving of an initial problem remains
blocked.
Instrumented learning is based on the use by the stu-
dent of a tutorial system created by our research team for
learning geometry. This system supports the student in
solving problems of proof, issuing messages as needed
(verbal or iconic expressions) appropriate to the actions
of the student in the internal logic of problems. During a
validation phase of previous research (see next section),
the introduction of a support structure that incorporates a
set of related problems appeared necessary to acquire the
means of choice that the teacher discusses with his stu-
dents. Unlike existing approaches, these problems do not
divide the original problem into sub-strategies. With a
completely new approach, the new problems arise from
the characteristics of relationships between problems and
learning blockages, engendering new decision means for
the tutorial system.
3. Research Program
In this section, key words are in bold.
Based on the didactics of mathematics, our project is
a continuation of the project a new approach to research
on competential and instrumented learning of geometry
in high school (CRSH 410-2009-0179) and it renews the
foundations laid down in the article Didactic and theo-
retical-based perspectives in the experimental develop-
ment of an intelligent tutorial system for the learning of
geometry [41]. These works were common to the design
of geogebraTUTOR, a tutorial system which is intended
to support the development of students’ mathematical
competencies [29, 46] and the construction
Figure 1. Analysis feature of interac tions during solving of the parallelogram problem. In the background is the ScreenFlow
software interface (recording sound, image and interaction on the screen) and in the foreground the log of the conversation
between the student and the artificial tutor agent. On the student’s screen, the “GeomTutor” Java applet launches the tuto-
rial system and the “dictation” file saves the simultaneous recording of the teacher’s intervention. The image used here shows
the geometric (on the left) and discursive (on the right) modules but is hiding the modules for writing (“Statements” tab),
structured arguments training (“Outline”) and mathematical proof (“Writing”). For more information about the system’s
challenges, consult the video at http://www.matimtl.ca/evenements/evenement.jsp?id=106.

P. R. RICHARD ET AL. 43
of geometric thinking [19, 22, 47]. It consists of two
subsystems, Turing1 (FQRSC 2005-AI-97435) and Geo-
Gebra (http://www.geogebra.org/), a dynamic geometry
software whose international influence is considerable in
teaching mathematics and which includes a three dimen-
sional geometry module in evolution [6]. By having to
account for teacher intervention [49, 50], we have en-
riched our research program with assessment tools de-
veloped within Intergeo (http://i2geo.net), a consortium
that manages a platform for sharing and assessment of
the quality of resources to which our secondary mathe-
matics teaching students have already contributed [51].
On the basis of these achievements, the current project
still aims to improve learning but it now innovates by the
original consideration of a structure of related problems
which meets these student learning blockages, with a
view to instrumented behaviour and whose reference
geometry allows adaptation to actual class didactic con-
tracts. Our reference to the decision-making theory of
Schoenfeld [48] sheds light on both the resources, goals
and orientations of the teacher intervention and the tuto-
rial action, and the notions of con cept ions [5] and
mathematical work space [21] pose an epistemological,
semiotic and instrumental view of cognitive interactions
that emerge from the student cognitive interaction with
the milieu. The notion of means of choice generalises
the teacher’s judgements and the decisions of the tutorial
system when it returns a related problem following a
learning blockage by the student, and that of a didactic
contract designates the most frequently implicit expecta-
tions that there are for the student and the teacher respec-
tively concerning mathematical knowledge.
4. Objectives
In seeking to better understand the means of choice for
interactive management of dynamic geometry problems
based on instrumented behaviour in high school, our re-
search project has the objectives in the Table 1.
The idea of means of choice, as a voluntary action to
consider one problem rather than another, transposes into
decision making means within the tutorial system. We
consider the instructional model (also known as instruc-
tional design) on two levels, that of didactics, the respon-
sibility of active educational members and those in train-
ing, and that of the technology of computer programming
and deployment, the responsibility of members with
technological training (see the section Research team,
latest results and student training). The achievement of
our research objectives will have a direct affect on
teacher training (Table 2).
5. Background
Well beyond the establishment of a simple online exer-
ciser or a learning guide in a deterministic MOOC struc-
ture [16], our research project is based on a computerised
environment for complex human learning which is in an
international dynamic geometry movement where com-
munity development and sharing of reference activities
are carried out among experts and teachers from different
traditions. The idea of a tutorial system that supports
students in problems of proofs is not new. Among first
generation achievements, we can mention the Geometry
Proofs Tutor [3], the Tigre-Mentoniezh project [32] and
Géométrix (http://geometrix.free.fr/ by Jacques Gressier).
All these systems are based on formal geometry models
that, despite an evident advantage of computer program-
ming, presuppose development in geometric thought
Table 1. The three general objectives.
Objective 1
Instructional
model
 Design, index, implement and test a structure
of related problems in a tutorial system
(geogebraTUTOR) which is based on the means
of usual choice for teacher intervention and the
instrumented behaviour of the student during
solving of fundamental problems involving proofs.
Objective 2
Interpretation
and theorizing
 Interpret and theorize on the decisional,
epistemological, representational, didactic and
instrumental aspects of the subject-milieu system
in interaction, with reference to the student’s
conceptions and the mathematical workspace.
Objective 3
Assessment
and control
 Assess the consistency of the subject-milieu
system in interaction, with reference to the
development of mathematical competencies,
construction of geometric thought and the
student’s learning in an instrumented perspective.
Table 2. The two training objectives.
Initial training
 Support, by trainees (university students), of a part
of the cognitive, heuristic, semiotic and metamathe-
matical means made available to students during
simulated situations, to develop their ability to iden-
tify with what the student knows and, reciprocally, to
test their teaching action.
Continuing
education
Development of disciplinary competencies in geome-
try, as professional successor, critiques and interprets
from its subjects or culture, in the exercise of his
functions.
 Richard, Cobo, Fortuny and Hohenwarter [40]
 Trgalová, Richard and Soury-Lavergne [52] 1 French acronym for TUtoRiel Intelligent en Géométrie and a nod to
the engineer and mathematician Alan Mathison Turing.

P. R. RICHARD ET AL.
44
by adherence to an axiomatic approach. Assisting student
learning blockages is therefore formal. The same applies
to second generation systems, although the interface,
communication with the user and processing of signifi-
cant actions are more developed. Among systems similar
to geogebraTUTOR [42] should be mentioned the Ad-
vanced Geometry Tutor [28], the Baghera project [23],
the Cabri-Euclide microworld [25] and the Geometry
Explanation Tutor [1]. There is also the Andes Physics
Tutor [54], for which some situations-problems are al-
ready premodeled in geometry.
Among the precursor achievements to our current sys-
tem are AgentGeom [10] and Turing [39]. Unlike the
systems which relate to formal axiomatic geometry,
AgentGeom and Turing were developed on cognitive
geometry models that lie between natural geometry and
the axiomatic natural geometry of Kuzniak [20]. This
allows full originality when considering situations-prob-
lems that bring together physical sciences to the process
of discovery in mathematics [12], as Clairaut [9] ap-
peared to desire in the Enlightenment by stating “this
presumed induction carries its demonstration with it” (p.
64), following the representation on paper of a “dy-
namic” geometric figure [43]. In addition, although cog-
nitive geometry is essential to considering reference ge-
ometry that is effectively practiced in the classroom, it
allows for constitution of a structure of related problems
that respond to informal learning blockages.
6. References Axes of the Conceptual
Framework
6.1. Epistemological Axis
In the process of mathematical discovery, the epistemo-
logical dialectic of proofs and refutations of [24] consid-
ers the criticisms that arise with counter-examples in
discussions between students and teacher. These criti-
cisms are likely to require an adjustment of the conjec-
ture, the proof or the counter-example itself, and also of
knowledge and the problem. Although they can be seen
as “breakpoints” [27] in solving a problem of proof, this
is because like Lakatos we believe that the steps of proof
are only summarised with formal or deductive ap-
proaches. In addition, we know that the supporting role
of these criticisms can be incorporated into the steps of
instrumented reasoning [18], while allowing the creation
of a geometric workspace in continuity with the devel-
opment of mathematical competencies inherited from
elementary school [11]. Our desire to bring together the
epistemology of mathematics into training programs, so
the student can perform his work in geometry, is an at-
tempt for subtle adaptation between an actual state of his
mathematical competencies and the intrinsic requirement
for performing geometry in class.
6.2. Semiotic Axis
When a study examines dynamic geometry and instru-
mented reasoning, questions on communications, proc-
essing of cognitive representations and objectivities of
virtual representations are essential. The Duval’s theory
of language functions [13] sets out the conditions for
learning based on the coordination of representation reg-
isters, of which the register of figures [14], and the func-
tional-structural approach of Richard and Sierpinska [44]
insists on the traditional semiotic means serving the qual-
ity of communications. When the student acts on a dy-
namic drawing, he is also acting on the system of repre-
sentation, possibly for the communication of inductive
reasoning [45]. This action can be the source of a learn-
ing blockage and, although the figural representations
convey reasoning [36, 37] or simulate movement [2],
they cannot generate it. In this context, a dynamic figure
is also a kind of problem.
6.3. Situational Axis
In Brousseau’s theory of didactical situations in mathe-
matics [7], the main intervention of the teacher (arrow 1,
Figure 2) occurs within a system which is itself in inter-
action, the student-milieu system (2), but with a didactic
milieu which brings a tutor agent to him the role of ar-
rows 1 and 2 is transposed with 6 and 7. According to
[26], Brousseau will consider the subject-milieu interac-
tion as the smallest unit of cognitive interactions. A state
of equilibrium for this interaction defines a state of
knowledge, the subject-milieu imbalance producing new
knowledge (search for a new equilibrium)”. However,
the theory of didactic situations characterises each item
of knowledge by situations that are specific to it, and the
knowledge model of Balacheff and Margolinas [5] lo-
cates conceptions in the subject-milieu interaction, while
first characterising a conception by the problems in
which it is involved. If it results in a strong conceptual
relationship between a moment of learning blockage and
a related problem, it is also because a learning blockage
is a breach of contract with what is expected in the con-
text of the root problem and that the appearance of a new
problem, in addition to relaunching the solving process,
is not a sophisticated response suggestion which at its
core considers the objective of the root problem.
6.4. Instrumental Axis
In Rabardel’s theory of instrumentation [34], the instru-
ment is the mode of action or thought constructed by the
subject when he uses a tool; the manner in which the
instrument is formed in the subject is the instrumental
genesis. According to [21], instrumental genesis consti-
tutes the geometric workspace and, when it is considered

P. R. RICHARD ET AL.
45
in the process of student-milieu interaction which creates
its own space, instrumental genesis operates both during
stages of discovery and validation [11]. Since the proc-
esses of instrumentation relate to the emergence and de-
velopment of patterns of use and instrumented action, the
progressive discovery of the tool’s intrinsic properties by
students, for whom the appearance of a related problem
following a learning blockage is accompanied by the
accommodation of their patterns and also changes in
meaning of the instrument, results in association of the
tool with new patterns [35]. The notions of conception
and instrument occupy dual places in modelling of the
subject-milieu [5].
6.5. Decisional Axis
The transposition of the teacher’s intervention in the
educational environment is necessarily accompanied by a
transposition of means of the choice. Although these
means can be interpreted in respect of a didactic contract,
the implicitly shared significance that it supposes com-
plicates understanding of the decisional process in all of
the fundamental relationships. According to [7], the di-
dactic contract is not really a true contract, since it is not
explicit or voluntary and because neither the conditions
for breach nor sanctions can be given in advance due to
their didactic nature, which depends significantly on a
knowledge of students that is as yet unknown. In
Schoenfeld’s decision making theory [48], if we know
enough about what someone’s resources, goals and ori-
entations are, teacher or student, we can even come to
understand, explain and model actions and decisions that
seem unusual or abnormal. In the Introduction paragraph,
the illustration of the sudden appearance of a new request
for solving problem, while it was the first solving proc-
essed that was blocked, may surprise the observer but
not the students, who are used to reacting to this type of
requirement from their teacher.
7. Methodology
7.1. General Direction
As with our previous projects, we take advantage of a
similar experimental effort to “verify a state or a change”
and “develop accordingly”. In fact, the illustration in the
Foreword comes from an experiment (see the link below
Figure 1 and [50] which allowed, firstly, verification of
the validity of a structure of messages from the tutor
agent when two classes of high school students resolved
problems of proof and, secondly, identification of the
means of choice of their teachers with the use of related
problems after indexation of conceptual, heuristic, semi-
otic and met mathematical criteria [42]. This requirement
invites us to consider together two paradigms on the
epistemological didactic level. On the conceptual side,
the learning models that we claim identify with the use of
our tutorial system based on the preceding axes. On the
methodological side, the approach implemented com-
bines the didactic engineering of Artigue [4] and the
grounded theory analysis of Glaser and Strauss [17].
Since the functional integration of a structure of related
problems in the instructional model is in line with our
project (see Acknowledgements), we can achieve objec-
tives 1 and 3 with a confirmatory model [53] of the hy-
pothesis-deduction type [4]. But the intervention of these
problems depends on the instrumented behaviour, and
since they generate a non-deterministic learning itinerary
(following related problems), the emergence of learning
models adapted to the use of an advanced tutorial system
commits us to achieving objective 2 using a compara-
tive-inductive type model [17].
Figure 2. Fundame ntal relationships in the rese arc h syste m. It is an adaptation of [7] on the r elationship of 1 to 4 between th e
teacher, the student and the milie u [41].
7.2. Description of Key Activities and Specific
Procedures
Here is a brief description of phases of the research in
relation to the objectives, for trimester Q.
Phase 1 (Q1-2) ↓ Conception of the instructional
model– preparation of objective 1 (1st part)
• From the 34 problems based on [33] and adaptation

P. R. RICHARD ET AL.
46
of these to the curriculum in effect in the regions of the
participating researchers, characterisation of problems
according to the identity of problems [38] and indexation
of them according to the above criteria.
• Implementation in geogebraTUTOR of a structure of
related problems and testing experts on the functioning
of the didactic milieu according to the learning model of
[41].
Phase 2 (Q3-4) ↓ 1
st experiment in the schools –
achievement of objective 1 (1st part)
To validate by cross-referencing primitive sources – or
“triangulation” [15]:
• Collection of student-milieu interactions and teacher
interventions in 3 classes of second cycle of high school
in three different regions when, in their normal courses,
students solve five problems of proof using the system
interface (qualitative data, [30]).
• Request to teachers to reconstruct their interventions
and compare the means of choice of the tutorial system
with the didactic contract of the course [31, 8] during 50
minute explanatory discussions [55].
In addition to the log files, there will be “ScreenFlow”
records (see Figure 1) for a sample of 24 volunteer stu-
dents (4 teams of 2 per class), as well as audio recordings
for the teachers of each class (intervention in class and
explanatory discussions), in accordance with the ethical
rules in force – ditto for entering and processing data in
all phases.
Phase 3 (Q5-6) ↓ Analysis and interpretation – prepara-
tion of objectives 2 and 3 (1st part)
• Analysis of times of learning blockage – or break-
points – according to the knowledge model of Balacheff
and Margolinas [5] by characterising conceptions C by a
defining set of problems (P) for which solving tools (R)
are provided based on representation systems (L) and a
control structure (Σ) which permits judgements and deci-
sions.
• Interpretation of times of learning blockage by join-
ing the student’s conceptions C = (P, R, L, Σ) with the
characteristics of the related problems in play (of the
system, phase 1; of teachers, phase 2).
Phase 4 (Q7-8) ↓ Cross-referencing, validation and
fine-tuning – preparation for objective 1 (2nd part) and
achievement of objective 2 (1st part)
• Pooling of the results of phase 3 between researchers
and identification of patterns.
• To improve the instructional model and better under-
stand the common or invariant characteristics of the sub-
ject-milieu system in interaction, expert validation of the
combination of phase 3.
• Optimisation of the articulation and continuity be-
tween the conception of the tutorial system and pursuit of
the conception during solving by the students (or “con-
ception in use”, [34]).
Phase 5 (Q9-10) ↓ 2
nd experiment in the schools –
preparation of objective 3 (2nd part) and achievement of
objective 1 (2nd part)
• Resumption of the procedures for phase 2, by this
time asking teachers to assess the solutions (without not-
ing them) with a view to assessing competencies [38].
Phase 6 (Q11-12) ↓ Modelling, synthesis, theorisation –
achievement of objectives 2 (2nd part) and 3
• Modelling of an ontology on the basis of didactic
contracts and instrumented behaviour.
• Summary of the non-deterministic learning itineraries
and underlying means of choice.
• Theorisation on the fundamental relationships of the
instrumented didactic situation (Figure 2).
8. Knowledge Mobilisation Plan
As a human sciences discipline, the teaching of mathe-
matics has a scientific side and a professional side, in-
cluding the initial and continuing training of teachers in
the field. When a project involves not only teaching
theories but also construction of computer environments
for human learning, questions arise in a very practical
way, which leads to seeking a functional modelling of
knowledge by making distinctions that are useful feed-
back for the teaching of mathematics as a whole. Our
plan for knowledge mobilisation, similar to that which is
grounded in our research program, aims to continue the
multidirectional exchange of knowledge between re-
searchers, teachers and other persons involved in the
world of teaching mathematics, in a collaborative spirit
of sharing which includes quality, integration and popu-
larisation. We can summarise the overall mobilisation
plan in terms of places2:
• Publication in journals for the quality of the research
(ESM, IJCML, ZDM, etc.), its integration (ADSC, REC,
PME, etc.) and its popularisation (AMQ, PME, UNO,
etc.);
• Organisation and participation in international sym-
posia on teaching mathematics (EMF, ETM, CERME,
etc.) as well as mathematics classroom technologies
(INTERGEO, CADGME, E-LEARN, etc.);
• Initial and continuing training sessions for teachers
(UDM, UAB, GRMS, etc.);
• Participation as appropriate in advisory bodies on
training or technology programs (UDM, CCPÉ, MATI,
etc.).
and of means, thanks to advanced technological skilled
of team members:
• Community and sharing development platform for
research quality (Turing, cK¢ wikibook, etc.), its integra-
tion (I2GÉO, NTLMP, etc.) and its popularisation
2We list acronyms and websites in the section References.

P. R. RICHARD ET AL. 47
(GIC-IGC, GeoGebraTube, etc.).
We are also planning to organise a workshop during
phase 3 in collaboration with other research groups, so
that researchers and teachers associated with a project
can share their experiences following the first experi-
mental phase. The formula proposed is a symposium,
like the one we organised most recently in Montreal
http://turing.scedu.umontreal.ca/etm/, in the collaborative
spirit typical of the Congress of European Research in
Mathematics Education http://www.cerme8.metu.edu.tr,
which balances quality (of seasoned researchers) and
integration (of young researchers).
9. Results Expected
In the Knowledge mobilisation plan section, we insisted
on the fact that the mutual contribution of didactics and
computers generates research advantages and impacts
within the university environment, with teachers and
other stakeholders in the educational world, through in-
teractions and increased access during the research itself.
By creating an “in use” tutorial system (within the
meaning of [34]), our research approach is empirically
based on the articulation and continuity between the in-
stitutional system design processes and the pursuit of the
design in problem solving by the student. Since it was
designed to produce a class of effects (support for learn-
ing through messages, problems and controls), imple-
mentation of the system, under the conditions provided
for each phase of the project (see Detailed description
section), allows updating of these effects following usage
noted during experimental phases. In other words, if the
cognitive outcome constitutes the design of the tutorial
system, it is the source of its own existence by an expert
anticipation of interactions of a of a changing stu-
dent-milieu system. Unlike existing tutorial systems (see
Background section), our choice of cognitive geometry is
a significant mark of originality since it lets us both adapt
the means of choice of the student’s instrumented be-
haviour and integrate the specifics of authentic didactic
contracts.
The idea of meeting a student’s learning blockage by
providing timely related problems to solve is an effective
solution to one of the major difficulties in teaching:
avoiding giving answers (discursive messages) at the
same time as the questions (root problems). In this sense,
our project theoretically answers the first didactic para-
dox of [7]: everything the teacher does to produce the
expected behaviours by students tends to reduce the stu-
dent’s uncertainty and thereby deprives him of the nec-
essary conditions for understanding and learning the in-
tended concept; if the teacher tells or signifies what he
wants from the student he can no longer get it other than
as performance of an instruction and not by the exercise
of his knowledge and judgement.
Apart from the institutional requirement for student
training, the dissemination of knowledge and the influ-
ence on the community of researchers in the field, the
integration of multidisciplinary doctoral research and the
effective collaboration of the school institution remains a
strategic advantage of the project, as is its influence on
teachers practise and training. Whether first to improve
students’ geometrical skills, including deductive (rea-
soning, arguing), visual (observing, exploring), figural
(modelling, conjecturing, defining) and operational (in-
strumentation, manipulation) skills, the potential for de-
velopment of the tutorial system then allows the teacher
to adapt a port of his pedagogical engineering according
to the division of his responsibilities with those of the
student. In initial training, these same arrangements
sharpen students’ abilities to simulate the effect of their
teaching activities and to identify student’s behaviour,
since the anticipation of solutions up to planning (and not
programming) learning itineraries adapted to the student.
The material benefits of our project are intended for
public use in schools.
10. Conclusions: Four Centres of Originality
Although the current project is a continuation of the
founding projects, it remains profoundly original in rela-
tion to it. We conclude by noting here four centres of
originality.
A first centre relates to the organisation of a structure
of related problems that responds to times of learning
blockage by the student. Although desirable, this type of
structure is unusual in math classes, since it is difficult to
put in place in a paper-pencil environment and even if
the use of related problems occasionally happens with
some teachers, the choice of the problem remains limited
by the environment. In addition, we know of no geome-
try tutorial system that integrates such organisation to
restart a block problem solving process.
A second centre affects the joint consideration of the
approaches to mathematical discovery and proof which,
in the same context as instrumented learning, links the
epistemology of mathematics with training programs.
Attached to a reference geometry based first on the
meaning of objects that it models and which makes as
such an approximation possible, geometry becomes a
means of learning and not longer its object, as is found
with tutorial systems which develop geometric thinking
by taking on an axiomatic approach.
A third centre relates to the functional modelling of
knowledge in our tutorial system. Most of the time, a
human learning computer environment is validated by
comparing the results of a pre-test and a post-test, while
requiring the user to comply with the system as it was
designed. This attitude undoubtedly leads fairly quickly

P. R. RICHARD ET AL.
48
to concrete accomplishments, but it is necessary for these
accomplishments to be effective learning aids. Although
our tutorial system aims for effectiveness of the tutorial
activity by first considering a modelling of human be-
haviour and designing a computer device which takes
this model account, it is due to the structure of related
problems is part of a learning model, distinct from the
model of assessing mathematical competencies in an
instrumented perspective.
A fourth centre looks at the non-deterministic charac-
ter of the system and considers a large number of solu-
tions. When a related problem is chosen, it is not so
much because we know exactly why the student was
blocked but because we suppose that the student knows
what is expected of him and in return the teacher or the
tutorial system knows the logic of the problem. The
question of correlation between related a problem and a
learning blockage is not deterministic since the system
does not indicate how to proceed. It follows the student
in his reasoning (by comparison with expert solutions
generally in the range of 50-100,000), regardless if it
belongs to a moment of discovery or proof and it invites
him to remain in the logic of the situation, simultane-
ously offering personalised assistance based on the in-
strumented behaviour of each student in a single class.
11. Acknowledgements
The development of the research is made possible by a
grant from the Conseil de recherches en sciences hu-
maines (CRSH 410-2009-0179, Gouvernement du Can-
ada) and a grant of the Secretaría de Estado de Investiga-
ción, Desarrollo e Innovación (EDU2011-23240, Go-
bierno de España).
REFERENCES
[1] V. Aleven, O. Popescu and K. R. Koedinger, “Towards
Tutorial Dialog to Support Self-explanation : Adding
natural Language Understanding to a Cognitive Tutor,
dans Artificial Intelligence in Education : AI-ED in the
Wired and Wireless Future (Éds. Moore, Redfield &
Johnson),” IOS Press, Amsterdam, 2002, pp. 246-255.
[2] C. Alsina and R. Nelsen, “Math Made Visual, Creating
Images for Understanding Mathematics”, Washington :
the Mathematical Association of America, 2006.
doi:10.5948/UPO9781614441007
[3] J. R. Anderson, C. F. Boyle and Yost, “The Geometry
Tutor”, The Journal of Mathematical Behavior, 1986, pp.
5-20.
[4] M. Artigue, “Ingénierie didactique, Recherches en didac-
tique des mathématiques 9.3”, 1990, pp. 281-308.
[5] N. Balacheff and C. Margolinas, “Modèle de connais-
sances pour le calcul de situations didactiques, dans Bal-
ises pour la didactique des mathématique”, (Éds. Mercier
& Margolinas), 2005, pp. 75-106. La pensée sauvage,
Grenoble.
[Overview of the model in line http://ckc.imag.fr/].
[6] M. Blossier and P. R. Richard, “Modélisation instru-
mentée et conceptions a priori dans un espace de travail
géométrique en évolution : un tour en géométrie dynami-
que tridimensionnelle”, Actes des journées mathé-
matiques 2011 de l’École Normale Supérieure de Lyon
(IFÉ 2011), Institut Français de l’Éducation , 2011, pp.
93-101.
[7] G. Brousseau, “Théorie des situations didactiques”, La
Pensée Sauvage, Grenoble, 1998.
[8] F. Caron and S. R. de Cotret, “Un regard didactique sur
l’évaluation en mathématiques : genèse d’une perspec-
tive” Actes du Colloque 2007 du Groupe de didactique
des mathématiques du Québec, 2007, pp. 123-134.
[9] A. C. Clairaut (2006), Éléments de géométrie, reproduc-
tion en fac-similé de l’édition de Paris chez David fils,
1741: Élémens de géométrie, Gabay, Paris.
[10] P. Cobo, J. M. Fortuny, E. Puertas and P. R. Richard,
Agentgeom : A multiagent system for pedagogical sup-
port in geometric proof problems, International Journal
of Computers for Mathematical Learning, Vol. 12, No. 1,
2007, pp. 57-79. doi:10.1007/s10758-007-9111-5
[11] S. Coutat and P. R. Richard, “Les figures dynamiques
dans un espace de travail mathématique pour
l’apprentissage des propriétés géométriques”, Annales de
didactique et de sciences cognitives, Vol. 16, 2011, pp.
97-126.
[12] J. J. Dahan, “La démarche de découverte expérimentale-
ment médiée par cabri-géomètre en mathématiques : un
essai de formalisation à partir de l’analyse de démarches
de résolutions de problèmes de boîtes noires”, Thèse de
Doctorat, Université Joseph Fourier Grenoble, 2005.
[13] R. Duval, “Sémiosis et pensée humaine : Registres sémi-
otiques et apprentissages intellectuels”, Peter Lang, Berne,
1995.
[14] R. Duval, “Les conditions cognitives de l’apprentissage
de la géométrie : développement de la visualisation, dif-
férenciation des raisonnements et coordination de leurs
fonctionnements”, Annales de didactique et sciences cog-
nitives, Vol. 10, 2005, pp. 5-53.
[15] M. A. Eisenhart, “The Ethnographic Research Tradition
and Mathematics Education Research”, Journal for Re-
search in Mathematics Education, Vol. 19, No. 2, 1988,
pp. 99-114. doi:10.2307/749405
[16] G. Gadanidis and P. R. Richard, “Report of the Working
Group in MOOCs and Online Mathematics Teaching and
Learning”, Actes de la rencontre 2013 du Groupe cana-
dien d'étude en didactique des mathématiques - Proceed-
ings of the 2013 Canadian mathematics education study
group conference, Brock University, 2013.
[17] B. G. Glaser and A. L. Strauss, “The discovery of
grounded theory : Strategies for qualitative research,” Al-
dine de Gruyter, Hawthorne, 1967.
[18] K. F. Hollebrands, A. M. Conner and R. C. Smith, “The
Nature of Arguments Provided by College Geometry
Students With Access to Technology While Solving

P. R. RICHARD ET AL. 49
Problems”, Journal for Research in Mathematics Educa-
tion, Vol. 41, No. 4, 2010, pp. 324-350.
[19] S. Johnston-Wilder and J. Mason, “Developing Thinking
in Geometry”, The Open University, 2005.
[20] A. Kuzniak, “Paradigmes et espaces de travail géométri-
ques. Éléments d’un cadre théorique pour l’enseignement
et la formation des enseignants en géométrie”, Revue ca-
nadienne de l’enseignement des sciences, des mathé-
matiques et des technologies, Vol. 6, No. 2, 2006, pp.
167-187.
[21] A. Kuzniak, “L’espace de travail mathématique et ses
genèses”, Annales de didactique et de sciences cognitives
Vol. 16, 2011, pp. 9-24.
[22] A. Kuzniak, P. R. Richard and A. Gagatsis, “CERME7
Working Group 4 : Geometry teaching and learning”,
Research in Mathematics Education, Vol. 14, No. 2, 2012,
pp. 191-192. doi:10.1080/14794802.2012.694285
[23] Laboratoire Leibniz, “Baghera assessment project : De-
signing an hybrid and emergent educational society”,
dans Rapport pour la commission européenne, Pro-
gramme IST, Les Cahiers du Laboratoire Leibniz nº 81
(Éd. Soury-Lavergne). Grenoble, 2003.
[24] I. Lakatos, Preuves et réfutations. Essai sur la logique de
la découverte mathématique. Hermann, Paris, 1984.
[25] V. Luengo, Some didactical and epistemological consid-
erations in the design of educational software : The
cabri-euclide example, International Journal of Com-
puters for Mathematical Learning, Vol. 10, No. 1, 2005,
pp. 1-29. doi.org/10.1007/s10758-005-4580-x
[26] C. Margolinas, Points de vue de l’élève et du professeur :
essai de développement de la théorie des situations didac-
tiques, Habilitation à diriger les recherches en sciences de
l’éducation, Université de Provence, version électronique
récupérée le 26 juillet 2010 à
http://tel.archivesouvertes.fr/docs/00/42/96/95/PDF/HDR
_Margolinas.pdf.
[27] J. Mason, Researching Your Own Practice : The Disci-
pline of Noticing. Londres et New York : Routledge,
2005.
[28] N. Matsuda and K. VanLehn, “Advanced geometry tutor :
An intelligent tutor that teaches proof-writing with con-
struction”, dans The 12th International Conference on
Artificial Intelligence in Education (Éds. Looi, McCalla,
Bredeweg & Breuker), 2005, pp. 443-450. IOS Press,
Amsterdam.
[29] MÉLS (2001, 2006 et 2007), Programme de formation de
l’école québécoise, éducation préscolaire, enseignement
primaire (2001), enseignement secondaire 1er cycle (2006)
et enseignement secondaire 2e cycle (2007). Publications
du Gouvernement du Québec.
[30] P. Paillé and A. Mucchielli, “L’analyse qualitative en
sciences humaines et sociales”, Paris : Armand Colin,
2008.
[31] M. J. Perrin-Glorian and Y. Reuter, “Les méthodes de
recherche en didactiques”, Villeneuve d’Ascq, France :
Presses Universitaires du Septentrion, 2006.
[32] D. Py, Aide à la démonstration en géométrie : le projet
Mentoniezh, Sciences et Techniques Educatives, Vol. 3,
No .2, 1996, pp. 227-256.
[33] D. Py, “Environnements interactifs d’apprentissage et
démonstration en géométrie”, Habilitation à diriger des
recherches, Université de Rennes, 2001.
[34] P. Rabardel, “Les hommes et les technologies : Approche
cognitive des instruments contemporains”, Armand Colin,
Paris, 1995.
[35] P. Rabardel and Pastré, “Modèles du sujet pour la con-
ception : dialectiques activités développement”, Tou-
louse : Octarès, 2005.
[36] P. R. Richard, “Raisonnement et stratégies de preuve dans
l’enseignement des mathématiques”, Peter Lang, Berne,
2004a.
[37] P. R. Richard, “L’inférence figurale : Un pas de raison-
nement discursivo-graphique”, Educational Studies in
Mathematics, Vol. 57, No. 2, 2004b, pp. 229-263.
doi:10.1023/B:EDUC.0000049272.75852.c4
[38] P. R. Richard (2010a et b), “La geometría dinámica como
herramienta para desarrollar competencias de modeli-
zación en el Bachillerato” (2010a), “La evaluación de
competencias matemáticas : una apuesta de aprendizaje
desde la elección de situaciones-problemas” (2010b),
dans Competencias matemáticas. Instrumentos para las
ciencias sociales y naturales (Éd. Chacón) 21-57 et 59-81.
Publicaciones del Ministerio de Educación, Gobierno de
España.
[39] P. R. Richard and J. M. Fortuny, “Amélioration des com-
pétences argumentatives à l’aide d’un système tutoriel en
classe de mathématique au secondaire”, Annales de di-
dactique et de sciences cognitives, Vol. 12, 2007, pp.
83-116.
[40] P. R. Richard, P. Cobo, J. M. Fortuny, M. Hohenwarter,
“Training teachers to manage problem-solving classes
with computer support”, Journal of Applied Computing,
Vol. 5, No. 1, 2009, pp. 38-50.
[41] P. R. Richard, J. M. Fortuny, M. Gagnon, N. Leduc, E.
Puertas and M. Tessier- Baillargeon, “Didactic and theo-
retical-based perspectives in the experimental develop-
ment of an intelligent tutorial system for the learning of
geometry, dans Interoperable interactive geometry for
Europe (Éds. Kortenkamp & Laborde)”, ZDM - The In-
ternational Journal on Mathematics Education, Vol. 43,
2011, pp. 425-439.
[42] P. R. Richard, J. M. Fortuny, M. Hohenwarter and M.
Gagnon, “geogebraTUTOR : une nouvelle approche pour
la recherche sur l’apprentissage compétentiel et instru-
menté de la géométrie à l’école secondaire”, Actes de la
World Conference on E-Learning in Corporate, Govern-
ment, Healthcare, and Higher Education, 2007.
[43] P. R. Richard, V. Meavilla and J. M. Fortuny, “Textos
clásicos y geometría dinámica : estudio de un aporte mu-
tuo para el aprendizaje de la geometría”, Revista En-
señanza de las Ciencias, Vol. 28, No. 1, 2010, pp.
95-111.
[44] P. R. Richard and A. Sierpinska, “Étude fonction-
nelle-structurelle de deux extraits de manuels anciens de

P. R. RICHARD ET AL.
50
géométrie”, In Lemoyne, G. et Sackur, C. (rédactrices in-
vitées) Le langage dans l’enseignement et l’apprentissage
des mathématiques, Revue des sciences de l’éducation,
Numéro thématique, Vol. 30, No. 2, 2004, pp. 379-409.
[45] P. R. Richard, S. Coutat and C. Laborde,
“L’apprentissage instrumenté de propriétés en géométrie :
propédeutique à l’acquisition d’une compétence de dé-
monstration”, Educational Studies in Mathematics (sous
presse), 2013.
[46] P. R. Richard, V. Freiman and D. H. Jarvis,
“L’enseignement des mathématiques au Québec”, Actes
de l’Espace mathématique francophone 2012, groupe
spécial Comparaison de l’enseignement des mathé-
matiques à travers les pays francophones : résultats, sens
et usages, Genève, 2013, pp. 7-30.
[47] P. R. Richard, E. Swoboda, M. Maschietto and J. Mithalal,
“Introduction to the Geometrical Thinking Working
Group”, Actes du Congress of European Research in
Mathematics Education (CERME8), 2013, pp. 1-7.
[48] A. H. Schoenfeld, “How We Think - A Theory of
Goal-Oriented Decision Making and its Educational Ap-
plications”, New York : Routledge, 2011.
[49] M. Tessier-Baillargeon, V. Leduc and P. R. Richard,
“Niveaux d’intervention enseignante pour le développe-
ment d’un système tutorial : une expérience didactique à
l’école secondaire avec le système géogébraTUTOR”,
Actes des journées mathématiques 2011 de l’École Nor-
male Supérieure de Lyon (IFÉ 2011), Institut Français de
l’Éducation, 2011, pp. 201-208.
[50] M. Tessier-Baillargeon, N. Leduc and P. R. Richard,
“Développement expérimental d’un système tutoriel in-
telligent pour le développement de compétences en
géométrie à l’école secondaire”. Dans Formation à la re-
cherche en didactique des mathématiques (Éds. Hitt &
Cortés), pp. 101-113. Québec : Loze-Dion.
[51] J. Trgalová and P. R. Richard, “Analyse de ressources
comme moyen de développement professionnel des en-
seignants”, Actes de l’Espace mathématique francophone
2012, groupe de travail Ressources et développement
professionnel des enseignants, 2012, pp. 12-23, Genève.
[52] J. Trgalová, P. R. Richard and S. Soury-Lavergne,
“Évaluation de la qualité des ressources de géométrie dy-
namique : un outil pour le développement de compétences
professionnelles des enseignants de mathématiques”,
Actes des journées mathématiques 2011 de l’École Nor-
male Supérieure de Lyon (IFÉ 2011), Institut Français de
l’Éducation, 2011, pp. 131-138, Lyon.
[53] J. M. Van der Maren, “Méthodes de recherche pour
l’éducation”, De Boeck Université, Bruxelles, 1996.
[54] K. Vanlehn, C. Lynch, K. Schulze, J. A. Shapiro, R.
Shelby, L. Taylor, et al., “The andes physics tutoring
system : Lessons learned”, Int. J. Artif. Intell. Ed., Vol. 15,
No. 3, 2005, pp. 147-204.
[55] P. Vermersch, L’entretien d’explicitation en formation
initiale et continue, ESF, Paris,1994.

P. R. RICHARD ET AL. 51
References to main websites
cK¢ wikibook http://ckc.imag.fr/index.php/Main_Page
GeoGebraTube http://www.geogebratube.org
GDM http://turing.scedu.umontreal.ca/gdm/
GIC-IGC http://www.geogebracanada.org/home
I2GÉO http://i2geo.net (access to activities for registrants)
Turing http://turing.scedu.umontreal.ca (access to Moodle for registrants)
Acronym reference
AC-GGB Associació Catalana de geogebra
ADSC Annales de didactique et de sciences cognitives
AMQ Bulletin of the Association mathématique du Québec
CADGME Computer Algebra and Dynamic Geometry Systems in Mathematics Education
CCPÉ Advisory Committee on the curriculum of the Quebec Ministry of Education
CERME Congress of European Research in Mathematics Education
CRSH Conseil de recherche en sciences humaines du Canada
E-LEARN World Conference on E-Learning in Corporate, Government, Healthcare & Higher Education
EMF Espace mathématique francophone Symposium
ESM Educational Studies in Mathematics – An International Journal
ETM Symposium Espace de travail mathématique
GRMS Group of leaders in high school mathematics
IJCML International Journal of Computers for Mathematical Learning
INTERGEO Interoperable Interactive Geometry Conference
MATI Roland-Giguère training and learning technologies House
NTLMP International Newsletter on the Teaching and Learning of Mathematical Proof
PME Publicaciones del Ministerio de Educación de España
REC Revista enseñanza de las ciencias – Investigación y experiencias didácticas
UAB Universitat Autònoma de Barcelona
UDM Université de Montréal
UNO Revista Uno – Didáctica de las matemáticas
ZDM Zentralblatt für Didaktik der Mathematik – The International Journal on Mathematics Education