Paper Menu >>
Journal Menu >>
 American Journal of Computational Mathematics, 2013, 3, 1-6 doi:10.4236/ajcm.2013.33B001 Published Online September 2013 (http://www.scirp.org/journal/ajcm) Hierarchical Linear Model of Monthly Rainfall with Regional and Seasonal Interaction Effects Yonghua Zhu1, Hongtao Lu1, Zilin Zhu2 1Mathematics and physics department of North China Electric Power University, Beijing, China 2Information Engineering Department of Huazhong University of Science and Technology, Wuhan, China Email: zhuyh59@163.com, 476502425@qq.com, 363036808@qq.com Received June, 2013 ABSTRACT According to the hierarchical characteristics of monthly rainfall in different regions, the paper takes the geographical factors and seasonal factors into the hierarchical linear model as the level effect. Through clustering methods we select two more representative regional meteorological data. We establish three-layer model by transforming the interactive structure date into nested structure data. According the model theory we perform the corresponding model calculations, optimization and analysis, accordingly to interpret the level effects, and residual test. The results show that most of the difference in Monthly Rainfall was respectively explained by Variables (Meteorological factors, seasonal effects, geo- graphic effects) in different levels. Keywords: Monthly Rainfall; Hierarchical Linear Model; Regional Effects; Interaction Effect Component 1. Questions and Data Description For the defects of the past rainfall’s regression, the lit- erature [1] propose the regression model which take the factors and other effects into consideration. From the characteristics of monthly rainfall, we establish a two- layer model with the seasonal effect, in the model longi- tudinal data is grouped by month. Then through a series of operations, such as correlation analysis, data preproc- essing, classification of seasonal effects, establishment of virtual indicators, gradually building models, the inter- pretation of fixed effects and random effects to complete the HLM2 model on monthly rainfall[1]. To dig the effect of monthly rainfall and various factors in different seasons and regions, we consider the data set: The meteorological data of Beijing, Tianjin and other 34 major cities in 1996-2009(monthly rainfall/(mm), av- erage temperature/(℃), sunshine hours/(h), average rela- tive humidity/(%), average air pressure/(100pa), herein- after referred to as rainfall, temperature, sunshine, hu- midity, pressure. To take Beijing and Nanjing for example, get the following figure. Figure 1 shows that, the monthly precipitation curve showed two features: the two regions’ data show a cer- tain cycle as a unit of year; overall, the Beijing’s rainfall is always greater than Nanjing’s. Therefore, in the study of the differences of rainfall, we not only should consider the impact factors and seasonal effects, but also need to consider the regional differences. Based on the previous two-layer model, we attempt to establish a three-layer model on the effects of a regional group and seasons. 2. Model and Analysis 2.1. Model Level 1 model: the regression between rainfall and tem- perature, sunshine, humidity, air pressure. Outcome va- riables Yij represents the rainfall of the month j of the year I (i=1,2,…14, j=1,2,…12), x1ij, x2ij, x3ij, respec- tively, for the temperature, sunshine, humidity of the month j of the year i. Figure 1. Beijing and Nanjing’s monthly rainfall map(red: Beijing; blue: Nanjing). Copyright © 2013 SciRes. AJCM  Y. H. ZHU ET AL. 2 Level 2 model: Create two new virtual season index CQ, X, to distinguish three kinds of seasonal effects (Winter, Spring, Summer). The combination of their values and other factors indicate the slope of the tem- perature, sunshine and humidity with rainfall in different seasons. Level 3 model: Establish geographical index to explain the intercept and slop Level 2 model (model about the relationship between season with the coefficient of Level 1). Comprehensive three-tier model, it express there is regression (intercept and slope) about different degrees of effect of various factors and seasonal precipitation in different regions. Basic data includes 31 cities, its geographical spread and the seasonal variations are large. If we want to estab- lish the index about geographical differences, which measure the monthly rainfall of 31 cities, and make three-tier regression. It would be difficult. If we want to establish virtual index, at least we should build five. But in the HLM2’s level 2, the maximum number of consid- ered geographical effects is five. Even have built a three-tier model, the fixed coefficients and random coef- ficient which need to test will be large (in Level 3, there will be 35 items including the intercept, slope, and ran- dom items), so effects analysis is not easy to make. If we take some quantitative methods (AHP, quantitative weight- ing, expert scoring method, etc) to establish a index which can unified measure geographical differences of 31 cities. It’s more difficult and difficult to estimate ac- curately the extent, because qualitative indicators are always randomness and fuzziness. Making scientific analysis and rigorous validation to its quantitative is an- other major issue [3]. The two effects which affect the rainfall are seasonal effect and geographical effects. But we find there are three seasonal effects in geography, and in a season there are also two geographical effects, two effects are interac- tion effect, rather than simply “students- class- school” nested structure. In this case Raudenbush (1993) devel- oped a method; Level 2 is the definition of “unit” effect which is classified by two interacted factors. Level 1 represents the link between variables under the influ- ence of the “unit”. This model has only two layers, known as Hierarchical Cross-classified Linear Model, HCM2 [2]. Taking rainfall for example, HCM model mainly research which independent variable the seasonal level and regional level have, and the characteristics of two- factor interactions between seasonal and regional levels. Here we attempt to establish a three-layer model to decompose the interaction structure of two-factor. We do hierarchical processing to the interactive structure as fol- lows. In the level 1 the data set formed by this method reach 48 groups (12 months * 4 cities) by the effect of six sea- sons; In level 2 model 6 units are influenced by two geo- graphical effects. The three-tier model is the same as the interaction effect model; each city’s monthly data is cor- responding to seasonal effects and regional effects. List 1. The virtual index of seasonal effects in Level 2. Month CQ X 12,1,2(winter) 0 0 3,4,5,9,10,11(spring) 1 0 6,7,8(summer) 0 1 List 2. Data’ two- factor interactions between seasonal and regional levels. Region Cities WinterSpring and Autumn Summer Beijing 1 2 12 3 4 5 9 10 11 6 7 8 North China Tianjin 1 2 12 3 4 5 9 10 11 6 7 8 Nanjing1 2 12 3 4 5 9 10 11 6 7 8 East China Hefei 1 2 12 3 4 5 9 10 11 6 7 8 List 3. Stratification of seasonal-geographical two-factor interacted structure. Region Season City monthly weather data North-Winter Beijing, Tianjin(12,1,2) North Spring Beijing, Tianjin (3,4,5,9,10,11) North China North-Summer Beijing, Tianjin (6,7,8) East-Winter Nanjing, Hefei(12,1,2) East-Spring Nanjing, Hefei (3,4,5,9,10,11) East China East-Summer Nanjing, Hefei (6,7,8) Copyright © 2013 SciRes. AJCM  Y. H. ZHU ET AL. 3 2.2. Zero Model Level 1 model: ijk0jk ijk Y=P+e Level 2 model: 00 00jkk jk PBr Level 3 model: 00000 00kk B=G+u 0jk is the average monthly rainfall in the region k and season j, ijk is the individual differences of monthly rainfall at the same region and season. 00k is the av- erage of all average seasonal rainfalls at region k, 0 PeB j k is the variational degree between different seasons at the same region. is the average rainfalls in all seasons at all regions, 00k represent the variational relative to he mean at different regions. Zero model parameter esti- mation results are listed below. r 000 Gu Based on the principle of variance decomposition de- scribed above we can obtain follows, the group differ- ences of monthly rainfall group differences account for 47.8%, The differences of monthly rainfall affected by seasonal effect account for 42.2%, regional impact ac- count for 10.0% of the total differences. That shows the 52.2% differences of monthly rainfall are related to the geographical and seasonal effects. This suggest us we should add more explanatory variables to the level 1 and level 2 to explain more variance of levels. 2.3. Random Effects Model Level 1 model: 12233ijk0jkjk 1ijkjkijkjkijkijk Y=P+Px +Px+Pxe Level 2 model: 00 0 1101 2202 330 0jkk jk j kkjk j kk jk k P=B r PBr PBr PB jk Level 3 model: 00000 00 10 100 20 200 30300 30 kk k k kk B=G u B=G B=G B=G u Compared to the zero model, the variance components of three-intercept of the random effects model were re- duced by 18%, 11%, 17%. Clearly, this variance is ex- plained by the various factors added to the level 1. 2.4. Optimalizing Full Model Model Overview:the total number of level 1 units is 672= 4 cities*12 months*14 years (in addition to missing values, the total is 660); the total number of level 2 units is 48=4 cities*12 months,belonging to 48 different “re- gions- season”; the total number of level 3 units 2=2 re- gions. Level 1 model: 12233ijk0jkjk 1ijkjkijkjkijkijk Y=P+Px +Px+Pxe Level 2 model: 00102 0 11211 22122 3313323 0jkk 0kjk 0kjk jkk jkjk jkkjk jk jkkjkjjk P=BBCQBX PBXr PBCQr PBCQBX List 4. Variance components’ estimation of levels. Random effects Standard error Variance components df Random item of Level1’s intercept 44.79** 2006.39 46 Random item of Level 1 47.65 2270.68 -- Random item of Level 3 21.84** 477.12 1 List 5. The results of random effects models. Random effects Standard deviation Variance df Level 1 Individual random effects 40.64 1651.81 -- Level 1 intercept 44.91** 2017.75 46 Temperature corresponds to the slop 7.24** 52.51 47 Level 2 Sunshine corresponds to the slop 0.32** 0.10 47 Level 2 intercept 19.91** 396.43 1 Level 3 The intercept of humidity corresponding to the slope 1.19** 1.42 1 Copyright © 2013 SciRes. AJCM  Y. H. ZHU ET AL. 4 Level 3 model: 00 001 01 010 02020 02 12 120 21 211 31310 311 32 320 kk k kk k kk kk k B=GD B=G B=G u B=G B=GD B=G GD B=G There are three parts affected by region in total: level 1’s intercept, sunshine slope in spring and autumn, Hu- midity slope in spring and autumn. In other words, the geographical differences are obvious in the overall mean. In the spring and autumn, the differences of the impact of humidity and sunshine to rainfall are significant [4]. In Figures 4-2 A stand for north, B stand for south, red stand for spring and autumn, blue stand for other seasons. Obviously, there is a positive correlation between rainfall and humidity. In southern spring and autumn (chart B), humidity causes greater impact on rainfall. In above figure, A stand for north, B stand for south, red stand for spring and autumn, blue stand for other seasons. There is a weak negative correlation between sunshine and rainfall in spring and autumn in two regions. The other seasons are messier and the relationship is un- known. The relationship can also be observed from the model and coefficients. There is a great negative correlation between sunshine and rainfall in autumn. Other seasons were not signifi- cant and the north and south regions’ differences were not significantly. Compared to the zero models, level 1 model’s random item variance changes little. [5]The random items of lev- el 2 and level 3 models are different, but we can obvi- ously find that the vast majority of random effects are ex- plained by different levels’ seasonal and geographical variables, and random item’s variance is very small. List 6. The results of fixed effects models. Fixed effects Coefficient Standard error df Intercept G001 45.55** 3.19 652 Winter and autumn G020 24.42** 2.84 652 Level 1 intercept Summer G030 112.08* 6.42 652 Temperature slope Summer G130 -10.42* 4.38 47 Sunshine slope Winter and autumn G221 -0.35* 0.15 47 Winter and autumn G320 1.08* 0.51 652 Winter and autumn G321 2.21* 1.01 652 Humidity slope Summer G330 4.81** 0.93 652 Figure 2. Scatter diagram about the relationship between humidity and rainfall in different regions. Figure 3. Scatter diagram about the relationship betw ee n sunshine and rainfall in different regions. Copyright © 2013 SciRes. AJCM 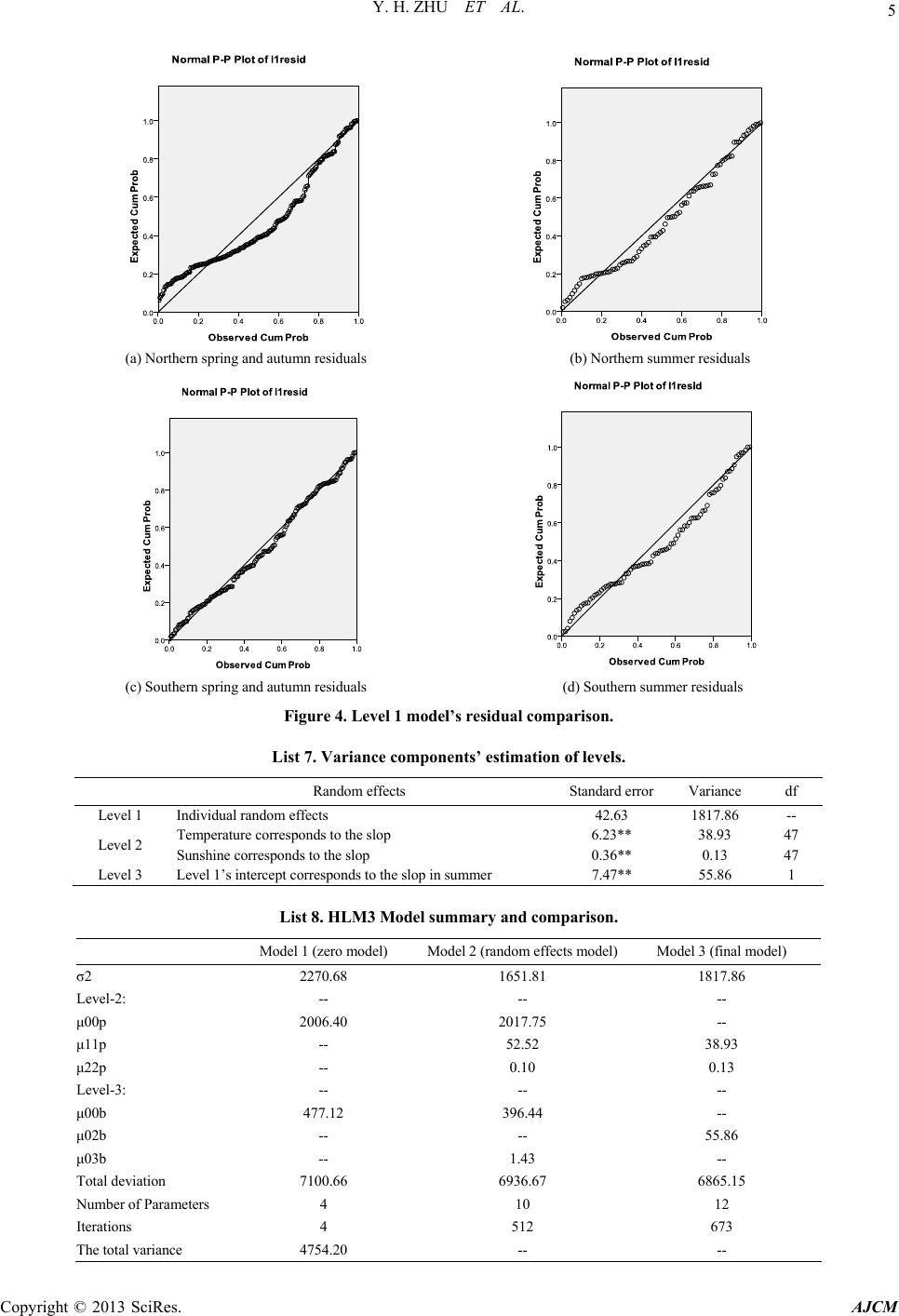 Y. H. ZHU ET AL. 5 (a) Northern spring and autumn residuals (b) Northern summer residuals (c) Southern spring and autumn residuals (d) Southern summer residuals Figure 4. Level 1 model’s residual comparison. List 7. Variance components’ estimation of levels. Random effects Standard error Variance df Level 1 Individual random effects 42.63 1817.86 -- Temperature corresponds to the slop 6.23** 38.93 47 Level 2 Sunshine corresponds to the slop 0.36** 0.13 47 Level 3 Level 1’s intercept corresponds to the slop in summer 7.47** 55.86 1 List 8. HLM3 Model summary and comparison. Model 1 (zero model) Model 2 (random effects model)Model 3 (final model) σ2 2270.68 1651.81 1817.86 Level-2: -- -- -- μ00p 2006.40 2017.75 -- μ11p -- 52.52 38.93 μ22p -- 0.10 0.13 Level-3: -- -- -- μ00b 477.12 396.44 -- μ02b -- -- 55.86 μ03b -- 1.43 -- Total deviation 7100.66 6936.67 6865.15 Number of Parameters 4 10 12 Iterations 4 512 673 The total variance 4754.20 -- -- Copyright © 2013 SciRes. AJCM  Y. H. ZHU ET AL. Copyright © 2013 SciRes. AJCM 6 3. Model Summary 3.1. Model Comparison Compared with the zero models, the random item’s vari- ance of level 1 changes little. The random items in level 2 and level 3 can’t be comparable. But we can obviously find that the vast majority of random effects are ex- plained by different levels’ seasonal and geographical variables, and random item’s variance is very small. Hi- erarchical interpretation of the effect of rainfall is sig- nificant, and seasonal and geographical explanatory va- riables play a good role in regression. 3.2. Residual Analysis From the above residual plots we can get two features: Overall, the residuals of the south are closer to the nor- mal distribution than those of the north, and spring sea- son is closer to the normal distribution than summer sea- son, because the southern seasonal effect and geographi- cal effect are more significant than the northern on the whole, and the summer’s effect is more significant than the winter and autumn’s. This result the differences of rainfall in the South in summer has been more fully ex- plained, assumption of the residuals closer to the normal- ity. Overall, HLM3 model’s size of the model residuals is similar to the HLM2 models, the summer’s residuals are bigger, but their relative offset is to a lesser extent. 4. HLM3 Model Conclusions In this paper, we mainly research the rainfall HLM3 model under the seasonal and geographical effects. Here is a brief summary of geographical effects. From the overall average level, the geographical dif- ferences of monthly rainfall are significant. Most of monthly rainfall’s differences between the groups can be explained by seasonal and geographical of variable levels. In spring and autumn the degree of humidity and sun- shine’s influence on the rainfall has significant differ- ences. Positive correlation with precipitation and humid- ity, sunshine is a negative correlation; In the summer there is a big negative correlation be- tween temperature and precipitation, but in the other seasons it’s not significant and the geographical differ- ences are obvious. From the data fit through the hierarchical model, al- though larger residuals in summer, its relative deviation is more minimum than the other seasons; the overall fit of the South is better than the North. 5. Summary After taking different regions of precipitation into com- parison, we take the effect of geographical factors as a higher level. Using cluster analysis, we select two re- gional more representative meteorological data. Translate structure of the interaction data into nested structure, and establish a corresponding three-level linear model (HL- M3). In accordance with model theory we do the corre- sponding model calculation, optimization and analysis and reach some major conclusions. The explanatory va- riables of various levels (the meteorological factors, sea- sonal effects, geographic effects) can well explained the differences in monthly rainfall. Hierarchical linear models have been widely used in social science fields. About the natural science problems we can make use of the professional knowledge and draw on some ideas and methods of appropriate social science to establish an appropriate model. With the development of a variety of technologies, in most cases the size of data will no longer be limited, a lot of data can be repeatedly observed and recorded, which cause the formation of the corresponding longitudinal data. Therefore, the hierar- chical linear model will be widely used. REFERENCES [1] Y. H. Zhu and G. X. Jiang, “Hierarchical Linear Model and Its Research on Hierarchical Characteristics of Rain- fall,” 2011 International Conference on Multimedia Technology (ICMT 2011), pp. 2146-2150. [2] S. W. Raudenbush, A. S. Bryk and Z. G. Guo, “Hierar- chical Linear Models: Application and Data Analysis Method,” Beijing: Social Sciences Academic Press, 2007, pp. 83-90. [3] J. C. Wang, H. Y. Xie and B. F. Jiang, “Application of Hierarchical Linear Model——Methods and Applica- tions,” Beijing: Higher Education Press, 2007, pp. 27-30. [4] L. Zhang, L. Lei and B. L. Guo, “Application of Hierar- chical Linear Model,” Beijing: Science and Education Press, 2003, pp. 28-40. [5] X. Zhang and J. Y. Wang, “The Study for the Sample Size Problem about Hierarchical Linear Models,” Statis- tics and Decision, Vol. 15, 2010, pp. 4-8. |

