Paper Menu >>
Journal Menu >>
 Engineering, 2 http://dx.doi.or g Copyright © 2 0 Id e ABSTRA C We investiga t network is es t dium signals r larity. Finally The method i s sitivity, speci f cates that our Keywords: R A 1. Introdu c Atrial fibrilla t menon in cli n tivities take p l heart rhythm. heart and m a will induce h i important to more serious. With the d complex net w analyze the d y the real worl d complex syst e lyzed by usin g In [9], the the two-dime n culated as th e diac arrhyth m racy of the d e spectively. B e thod needs to As we hav e electrical acti v will become w ity between t calculated to 013, 5, 22-26 g /10.4236/eng. 2 0 13 SciRes. e ntific a 1 Nati o 2 D C T t e the use of c t imated via th e r ecorded fro m , epicardium s s validated us i f icity and acc u approach ma y R ecurrence Co m A trial Fibrillati o c tion t ion (AF) is a n ic [1,2]. Dur i l ace in the he a AF deteriora t a y cause emb o i gh rates of m o detect AF a n d evelopment w or k [3-8] has y namical pro p d . Because th e em , the heart e g complex net w distribution e n n sional recon s e feature of el e m ia and the se n e tection were e cause of the be proposed. e known, for v ities, the si m w eake r , so fea t t wo recurren c identify AF. T 2 013.510B005 P a tion o f N Y a o nal Key Labor a D epartment of E Email: 11 2 c omplex netw o e joint recurre n m dogs into the s ignals are cl a i ng 1000 sam p u racy of the i d y lay a foundat i m plex Networ k o n a common arr h i ng AF, chaot a rt which resu l t es the functi o o lic events a n o rbidity and m n d prevent it of nonlinear become a po p p erties of com p e heart has b e e lectrical acti v w orks. n tropy of the p s tructed phase e ctrocardiogra m n sitivity, speci 86.0%, 96.0 % low sensitivi t complex net w m ilarity b etwee t ures represen t c e complex n e T his will be p P ublished Onlin e f Atrial N etwor k a juan Zhang a tory of ASIC a n E lectronic Engin e 2 10720090@fu Receive d o rk similarity n ce plot and H recurrence c o a ssified utilizi n p les including d entification a r i on for the pr e k ; Phase Spac e h ythmia phen o ic electrical a c l t in an irregul o n of the who n d stroke whi c m ortality. So it from becomi n dynamics, t h p ular method t p lex systems i e en proven to v ity can be an p oint density i space was c a m to detect c a ficity and acc u % and 92.7% r t y, a novel m w orks of chao t n two networ k t ing the simil a e tworks can b p roven with t h e October 2013 Fibrill a k Simi l 1,2 , Yuanyu a n d Syste m , Fud a eering, Fudan U dan.edu.cn, yy w d September 20 for the identi f H amming dist a o mplex netwo r n g the classifi c 500 atrial fibr i r e 98.2%, 98. 8 e diction of the e Reconstructi o - c- ar le c h is n g h e t o i n a a- i n a l- ar - u - e- e- t ic k s ar - b e h e experi m 2. Me 2.1. R e About series t h For ex a rithm t compl e series r posed t networ k p osed t the ti m the net w may be high d i curren c The networ k the rec o node a n the ph a recurre n plot. The structi o (http://www.sc i a tion U l arity a n Wang 1,2 a n University, S U niversity, Shan w ang@fudan.ed u 12 f ication of atr i a nce. Firstly, w r k. Then, we e c ation and re g i llation cases a 8 % and 98.5 % onset of atrial on; Classifica t m ent. thods e currence C how to cons t h ere have bee n a mple, Zhang t o transform p e x networ k w r epresented as t he visibility g r k based on “ v t o build the ne t m e series. Tho u w ork constru c e come difficul t i mensional sy s c e complex ne t r ecurrence n k s from a fra c o nstructed ph a n d the edge b a se space dis t n ce network recurrence pl o o n which can b rp.org/journal/ e sing C o S hanghai, China ghai, China u .cn i al fibrillation w e transform m e xtract feature s g ression tree w a nd 500 norm a % respectively. fibrillation. t ion and Regr e omplex Net w t ruct comple x n already som e and Small [ 3 p seudo period i w ith each cyc l a basic node. r aph to map f r v isibility”. Ya n t work from th u gh there are n c tion algorith m t to get necess a s tem. To rem e t work was pro p n etwor k [6-9 ] c tal time serie s a se space is r e etween two n o t ance. The ad j is interprete d o t starts from t b e described a s e ng) o mplex . The similari t m ulti-electrode s representing w ith extracted a l sinus ones. T This experi m e ssion Tree; w ork x networks fr o e approaches p 3 ] introduced i c time series l e of pseudo Lacasa et al. r actal time ser i n g and Yang e correlation m n o embedding m s mentioned a a ry informatio e dy this defec t p osed. ] constructs s . Each vector e presented by o des is deter m j acency matri x d from the re t he p hase spa c s below. Take ENG t y of the s epicar- its si m i- features. T he sen- m ent in d i- o m time p ropose d . an algo- into the periodic [4] pro- i es into a [5] pro- m atrix of steps in a bove, it n from a t , the re- complex point of a single m ined by x of the currence c e recon- a fractal 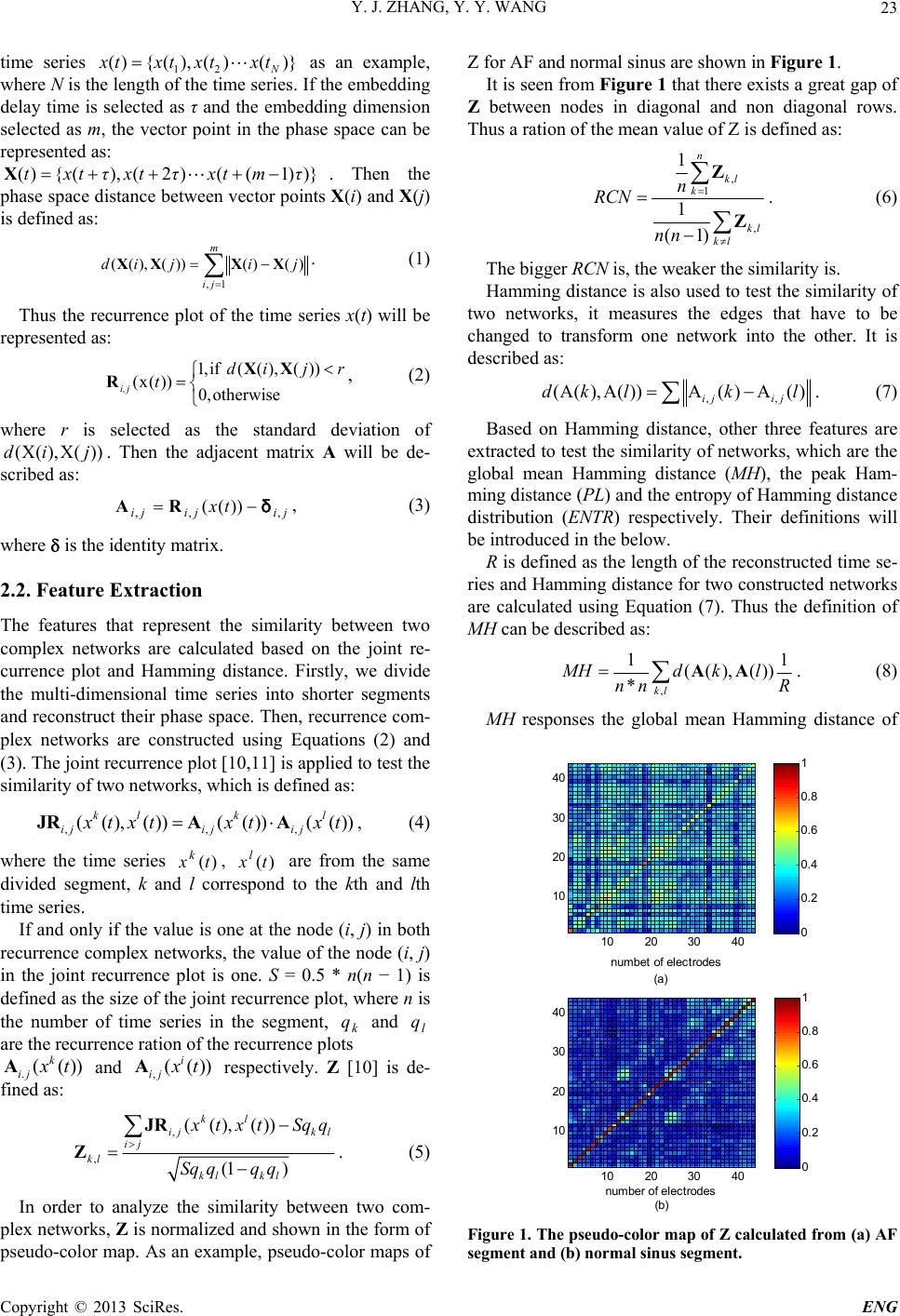 Y. J. ZHANG, Y. Y. WANG Copyright © 2013 SciRes. ENG 23 time series 12 (){ (),()()} N x txtxtxt as an example, where N is the length of the time series. If the embedding delay time is selected as τ and the embedding dimension selected as m, the vector point in the phase space can be represented as: (){ (),(2 )((1) )}txtτxt τxt mτ X. Then the phase space distance between vector points X(i) and X(j) is defined as: m ji jijid 1, )()())(),(( XXXX . (1) Thus the recurrence plot of the time series x(t) will be represented as: otherwise,0 ))(),((if,1 ))(x( rjid t ji, XX R, (2) where r is selected as the standard deviation of ))(X),(X( jid . Then the adjacent matrix A will be de- scribed as: jijiji tx ,,, ))(( δ RA , (3) where is the identity matrix. 2.2. Feature Extraction The features that represent the similarity between two complex networks are calculated based on the joint re- currence plot and Hamming distance. Firstly, we divide the multi-dimensional time series into shorter segments and reconstruct their phase space. Then, recurrence com- plex networks are constructed using Equations (2) and (3). The joint recurrence plot [10,11] is applied to test the similarity of two networks, which is defined as: ,,, ((),())(())( ()) klk l ijij ij x txtxt xtJRAA , (4) where the time series )(tx k, )(txl are from the same divided segment, k and l correspond to the kth and lth time series. If and only if the value is one at the node (i, j) in both recurrence complex networks, the value of the node (i, j) in the joint recurrence plot is one. S = 0.5 * n(n − 1) is defined as the size of the joint recurrence plot, where n is the number of time series in the segment, k q and l q are the recurrence ration of the recurrence plots .(()) k ij x tA and ,(()) i ij x tA respectively. Z [10] is de- fined as: , , ((),()) (1 ) kl ijk l ij kl kl kl x txtSqq Sq qq q JR Z. (5) In order to analyze the similarity between two com- plex networks, Z is normalized and shown in the form of pseudo-color map. As an example, pseudo-color maps of Z for AF and normal sinus are shown in Figure 1. It is seen from Figure 1 that there exists a great gap of Z between nodes in diagonal and non diagonal rows. Thus a ration of the mean value of Z is defined as: , 1 , 1 1 (1) n kl k kl kl n RCN nn Z Z. (6) The bigger RCN is, the weaker the similarity is. Hamming distance is also used to test the similarity of two networks, it measures the edges that have to be changed to transform one network into the other. It is described as: ,, (A(),A( ))A()A( ) ij ij dk lkl . (7) Based on Hamming distance, other three features are extracted to test the similarity of networks, which are the global mean Hamming distance (MH), the peak Ham- ming distance (PL) and the entropy of Hamming distance distribution (ENTR) respectively. Their definitions will be introduced in the below. R is defined as the length of the reconstructed time se- ries and Hamming distance for two constructed networks are calculated using Equation (7). Thus the definition of MH can be described as: , 11 ((),()) *kl MHd kl nn R AA . (8) MH responses the global mean Hamming distance of Figure 1. The pseudo-color map of Z calculated from (a) AF segment and (b) normal sinus segment. 10 203040 10 20 30 40 numb et of electrodes (a) 10 203040 10 20 30 40 numb er of el ectrodes (b) 0 0. 2 0. 4 0. 6 0. 8 1 0 0. 2 0. 4 0. 6 0. 8 1  Y. J. ZHANG, Y. Y. WANG Copyright © 2013 SciRes. ENG 24 each segment, while L represents the local mean Ham- ming distance for each network constructed from the same segment. The probability distribution of L is calcu- lated and rounded. It can be shown in bar plot. PL is de- fined as the distance which has the most probability: )(maxarg LpPL L , (9) where 11 ((),()) k k Ldkl nR AA and p(L) is the corre- sponding probability. For example, the distribution of L is shown in Figure 2. The feature that measures the similarity is the entropy of Hamming distance distribution (ENTR). It is defined as: *log( ( )) E NTRLp L . (10) 2.3. Classification and Regression Tree The CART [12] approach is used in our research for the identification of AF with extracted features. The CART classification model utilizes tree-like structures to assign samples based on the set of feature quantifiers. It divide samples in parent nodes into descendent child nodes based on the if-then rule. The rule is obtained by training the sample set. In the CART model, each parent node is optimally partitioned. The classification accuracy is measured by the decrease of the impurity [12] which is defined as: * (,)()( )() L LRR imsttim ttpim ttpim tt , (11) where pL denotes the proportion of cases in the left child node ttL to those in the parent node tt while pR denotes the proportion of cases in the right child node ttR to those Figure 2. The distribution of L of (a) normal sinus segment and (b) AF segment. in the parent node tt. im is the impurity function which is commonly selected as Gini diversity index criterion. The best split s* is selected to maximize ),( *ttsim and s* is obtained by solving * (,) argmaxΔ(, ) arg max((tt)()()) s sLLRR im sttim stt impim ttpimtt (12) 3. Experiments and Results The method is implanted in Mat lab R2011b and the platform is a computer workstation with a 3.07 GHz CPU and 32 G memory. The data are from dog experiments, in which the per- fusion of acetylcholine is used to induce AF in anesthe- tized open-chest dogs with the electrical stimulation of left atrium appendage. 128 unipolar electrodes are placed on the atrial epicardial surface and thus a recording of 128 channels is obtained. Signals are filtered between 3.5 - 600 Hz, and the sampling frequency is 2 kHz with 16-bit resolution. Due to that the anterior right atrium signals can well represent atrial activities, 44 recordings from the right atrium sur- face, marked from 1 to 44, are used to construct the re- currence complex networks. Signals are divided into short segments which are used as samples in the classifi- cation experiment. The classification and regression tree integrated with 10-fold cross-validation is used in our study. The classi- fication performance parameters used to measure the performance of methods are sensitivity (SE), specificity (SP) and accuracy (AC). They are defined as: TP SE TPFN , TN SP TN FP , TP TN AC TP FNTNFP , (13) where TP is the number of AF cases being correctly rec- ognized as AF, FN is the number of AF cases being wrongly recognized as normal sinus ones, TN is the number of normal sinus cases being truly recognized as normal sinus ones, and TP is the number of normal sinus cases being wrongly recognized as AF ones. 1000 samples are used in the classification experiment with 500 AF cases and 500 normal sinus ones and the network similarity parameters are calculated as classifi- cation features. The time interval of the segment may lead to the difference of the classification performance. Here we compare the classification results with various time intervals. Table 1 shows the classification perfor- mance with the interval of 100, 150, 200 and 250 ms respectively. The time interval is limited to 250 ms be- cause of the large computing amount. It is shown in Table 1 that the classification perfor- 050100 150 0 0.05 0.1 0.15 0.2 local hamming distance (a ) 050100 150 0 0.1 0.2 0.3 0.4 local hamming distance (b ) 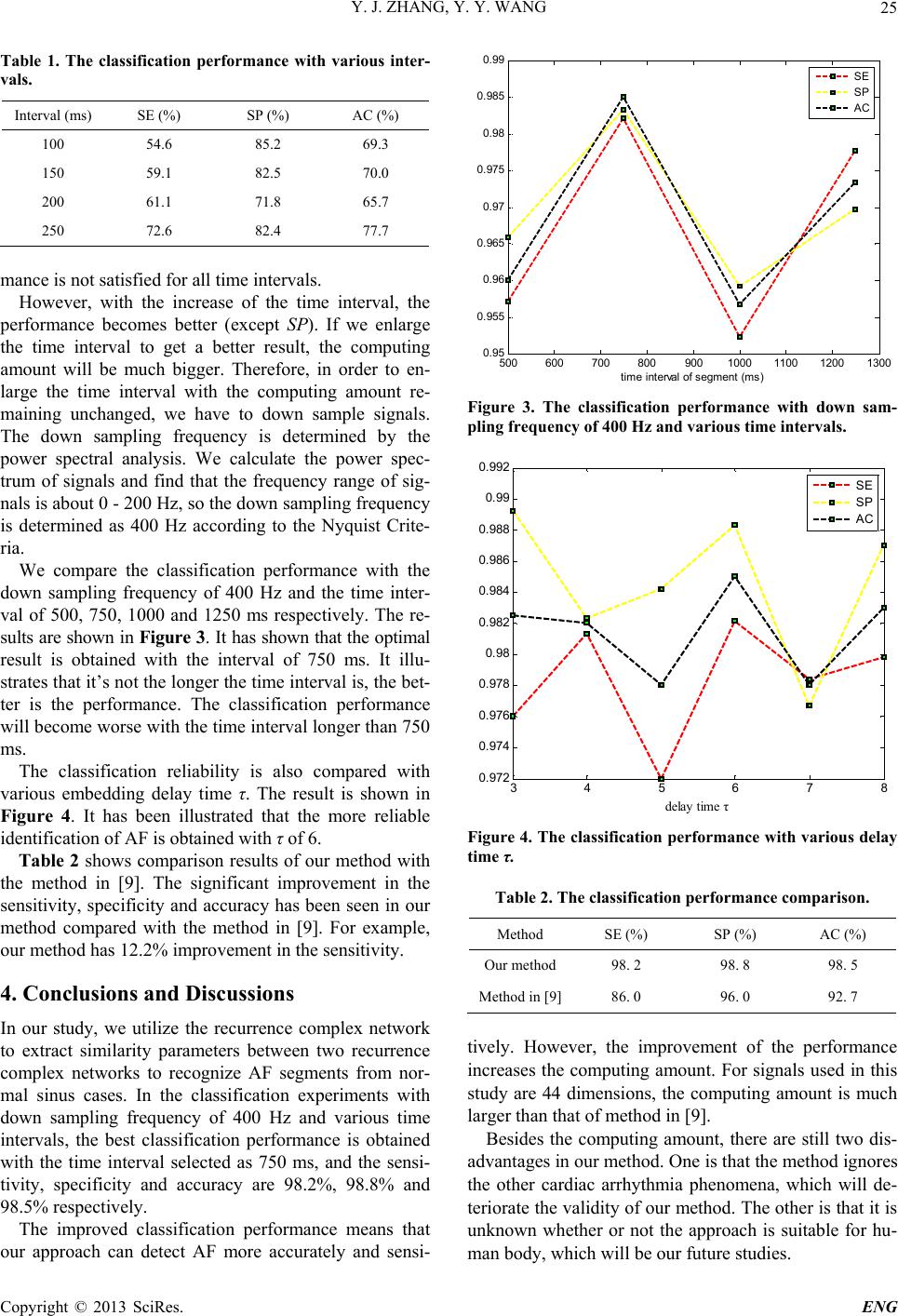 Y. J. ZHANG, Y. Y. WANG Copyright © 2013 SciRes. ENG 25 Table 1. The classification performance with various inter- vals. Interval (ms) SE (%) SP (%) AC (%) 100 54.6 85.2 69.3 150 59.1 82.5 70.0 200 61.1 71.8 65.7 250 72.6 82.4 77.7 mance is not satisfied for all time intervals. However, with the increase of the time interval, the performance becomes better (except SP). If we enlarge the time interval to get a better result, the computing amount will be much bigger. Therefore, in order to en- large the time interval with the computing amount re- maining unchanged, we have to down sample signals. The down sampling frequency is determined by the power spectral analysis. We calculate the power spec- trum of signals and find that the frequency range of sig- nals is about 0 - 200 Hz, so the down sampling frequency is determined as 400 Hz according to the Nyquist Crite- ria. We compare the classification performance with the down sampling frequency of 400 Hz and the time inter- val of 500, 750, 1000 and 1250 ms respectively. The re- sults are shown in Figure 3. It has shown that the optimal result is obtained with the interval of 750 ms. It illu- strates that it’s not the longer the time interval is, the bet- ter is the performance. The classification performance will become worse with the time interval longer than 750 ms. The classification reliability is also compared with various embedding delay time τ. The result is shown in Figure 4. It has been illustrated that the more reliable identification of AF is obtained with τ of 6. Table 2 shows comparison results of our method with the method in [9]. The significant improvement in the sensitivity, specificity and accuracy has been seen in our method compared with the method in [9]. For example, our method has 12.2% improvement in the sensitivity. 4. Conclusions and Discussions In our study, we utilize the recurrence complex network to extract similarity parameters between two recurrence complex networks to recognize AF segments from nor- mal sinus cases. In the classification experiments with down sampling frequency of 400 Hz and various time intervals, the best classification performance is obtained with the time interval selected as 750 ms, and the sensi- tivity, specificity and accuracy are 98.2%, 98.8% and 98.5% respectively. The improved classification performance means that our approach can detect AF more accurately and sensi- Figure 3. The classification performance with down sam- pling frequency of 400 Hz and various time intervals. Figure 4. The classification performance with various delay time τ. Table 2. The classification performance comparison. Method SE (%) SP (%) AC (%) Our method 98. 2 98. 8 98. 5 Method in [9]86. 0 96. 0 92. 7 tively. However, the improvement of the performance increases the computing amount. For signals used in this study are 44 dimensions, the computing amount is much larger than that of method in [9]. Besides the computing amount, there are still two dis- advantages in our method. One is that the method ignores the other cardiac arrhythmia phenomena, which will de- teriorate the validity of our method. The other is that it is unknown whether or not the approach is suitable for hu- man body, which will be our future studies. 500 600 700 800 9001000 1100 1200 1300 0.95 0. 955 0.96 0. 965 0.97 0. 975 0.98 0. 985 0.99 ti m e interval of segment (ms) SE SP AC 34 567 8 0. 972 0. 974 0. 976 0. 978 0. 98 0. 982 0. 984 0. 986 0. 988 0. 99 0. 992 delay time τ SE SP AC  Y. J. ZHANG, Y. Y. WANG Copyright © 2013 SciRes. ENG 26 5. Acknowledgements This work is supported by the National Natural Science Foundation of China (Grant No. 61271071 and No. 11228411), the National Key Technology R&D Program of China (No. 2012BAI13B02) and Specialized Research Fund for the Doctoral Program of Higher Education of China (No.20110071110017). REFERENCES [1] A. L. Waldo, “Mechanism of Atrial Fibrillation,” Journal of Cardiovascular Electrophysiology, Vol. 14, No. 12, 2003, pp. s267-s274. http://dx.doi.org/10.1046/j.1540-8167.2003.90401.x [2] S. Nattel, A. Shiroshita-Takeshita, B. Brundel and L. Rivard, “Mechanisms of Atrial Fibrillation: Lessons from Animal Models,” Progress in Cardiovascular Diseases, Vol. 48, No. 1, 2005, pp. 9-28. http://dx.doi.org/10.1016/j.pcad.2005.06.002 [3] J. Zhang and M. Small, “Complex Network from Pseu- doperiodic Time Series: Topology versus Dynamics,” Physical Review Letters, Vol. 96, No. 23, 2006, Article ID: 238701. http://dx.doi.org/10.1103/PhysRevLett.96.238701 [4] L. Lacasa, B. Luque, F. Ballesteros, J. Luque and J. C. Nuno, “From Time Series to Complex Networks: The Vi- sibility Graph,” PNAS, Vol. 105, No. 13, 2008, pp. 4972- 4975. http://dx.doi.org/10.1073/pnas.0709247105 [5] Y. Yang and H. Yang, “Complex Network-Based Time Series Analysis,” Physica A, Vol. 387, 2008, pp. 1381- 1386. http://dx.doi.org/10.1016/j.physa.2007.10.055 [6] Z. Gao and N. Jin, “Complex Network from Time Series Based on Phase Space Reconstruction,” Chaos, Vol. 19, No. 3, 2009, Article ID: 033137. http://dx.doi.org/10.1063/1.3227736 [7] N. Marwan , J. F. Donges, Y. Zou, R. V. Donner and J. Kurthsa, “Complex Network Approach for Recurrence Analysis of Time Series,” Physics Letters A, Vol. 373, No. 9, 2009, pp. 4246-4254. http://dx.doi.org/10.1016/j.physleta.2009.09.042 [8] L. Uldry, V. Jacquemet, N. Virag, L. Kappenberger and J. M. Vesin. “Estimating the Time Scale and Anatomical Location of Atrial Fibrillation Spontaneous Termination in a Biophysical Model,” Medical and Biological Engi- neering and Computing, Vol. 50, 2012, pp. 155-163. http://dx.doi.org/10.1007/s11517-011-0859-3 [9] R. Sun, Y. Wang, S. Yang and Z. Fang. “Detecting Car- diac Arrhythmias Based on Phase Space Analysis,” Jour- nal of Biomedical Engineering, Vol. 25, No. 4, 2008, pp. 934-937. [10] Y. Hirata and K. Aihara, “Identifying Hidden Common Causes from Bivariate Time Series: A Method Using Re- currence Plots,” Physical Review E, Vol. 81, 2010, Ar- ticle ID: 016203. http://dx.doi.org/10.1103/PhysRevE.81.016203 [11] N. Marwan, M. C. Romano, M. Thiel and J. Kurths, “Recurrence Plots for the Analysis of Complex Systems,” Physics Reports, Vol. 438, 2007, pp. 237-329. http://dx.doi.org/10.1016/j.physrep.2006.11.001 [12] H. Yanga, S. Bukkapatnamb, T. Leb and R. Komanduric, “Identification of Myocardial Infarction (MI) Using Spa- tio-Temporal Heart Dynamics,” Medical Engineering & Physics, Vol. 34, 2012, pp. 485-497. http://dx.doi.org/10.1016/j.medengphy.2011.08.009 |

