Energy and Power Engineering, 2013, 5, 435-441
doi:10.4236/epe.2013.54B084 Published Online July 2013 (http://www.scirp.org/journal/epe)
Wide-Area Delay-Dependent Adaptive Supervisory
Control of Multi-machine Power System Based on Improve
Free W eighting Matrix Approach*
Ziyong Zhang1, Zhijian Hu1, Yukai Liu1, Yang Gao2, He Wang1, Jianglei Suo1
1School of Electrical Engineering, Wuhan University, Wuhan, China.
2Jiangsu Suzhou Power Supply Company, STATE GRID Corporation of China, Suzhou, China
Received January, 2013
ABSTRACT
The paper demonstrates the possibility to enhance the damping of inter-area oscillations using Wide Area Measurement
(WAM) based adaptive supervisory controller (ASC) which considers the wide-area signal transmission delays. The
paper uses an LMI-based iterative nonlinear optimization algorithm to establish a method of designing state-feedback
controllers for power systems with a time-varying delay. This method is based on the delay-dependent stabilization
conditions obtained by the improved free weighting matrix (IFWM) approach. In the stabilization conditions, the upper
bound of feedback signal’s transmission delays is taken into consideration. Combining theories of state feedback con-
trol and state observer, the ASC is designed and time-delay output feedback robust controller is realized for power sys-
tem. The ASC uses the input information from Phase Measurement Units (PMUs) in the system and dispatches supple-
mentary control signals to the available local controllers. The design of the ASC is explained in detail and its perfor-
mance validated by time domain simulations on a New England test power system (NETPS).
Keywords: Adaptive Supervisory Controller (ASC); Delay-de pendent Dampi ng Co ntrol; Power Oscillation; IFWM;
LMI; Free Weighting Matrix Approa ch; Time-varying Delay; WAMS
1. Introduction
WITH the deregulation of power systems, many tie lines
between control areas are driven to operate near their
maximum capacity, especially those serving heavy load
centers. Stressed operating conditions can increase the
inter-area oscillation between different control areas and
can even break up the system. The incidents of system
outage resulting from these oscillations are of growing
concern.
Over the past few decades, attention has been focused
on designing controllers to dampen inter-area oscillations.
The traditional method of damping inter-area oscillations
is via the installation of power system stabilizers (PSS)
which provide control action through the excitation con-
trol of generators[1]. Local PSSs are usually tuned based
on several typical operating conditions of corresponding
generators. z An inappropriate coordination among the
local controllers may cause serious problems [2].
It has been suggested that centralized controllers using
wide-area signals rely on the PMUs technology[3].
PMUs are used to capture the power system’s dynamic
data (e.g., voltages, currents, angles and frequency.)
through synchronized measurements enabled by the GPS
satellites. It has been shown that by using the remote
signals the controller can enhance the damping of inter
area oscillations and improve the overall dynamic per-
formance of the power system[4]. A new PSS using two
signals, the first to dampen the local mode in the area and
the second, global signal, to dampen inter-area modes, is
propose d in [5].
Application of techniques for designing robust power
system damping controllers has been reported in the lite-
rature [6-9]. The solution to the control design problem
based on the method of Riccati equations usually pro-
duces a controller that suffers from pole-zero cancella-
tions between the system plant and the controller [10].
The application of the linear matrix inequality (LMI)
approach as an alternative for damping controller design
for PSS has been reported in [11,12]. A mixed -sensitivity
based LMI approach has been applied to inter-area
damping control design in [6,9]. In [9], FACTs are em-
ployed to damp inter-area oscillations. However, the cost
of FACTs devices is quite high so that it currently re-
*This work is supported by Special Scientific and Research Funds for Doc-
toral Speciality of Institution of Higher Learning(2011014111 0032) and
the
Fundamental Research Funds for the Central Universities(2012207020205).

Z. Y. ZHANG ET AL.
436
stricts their wide use in power systems.
In the controller design, signal transmission delays
should be considered [7,8]. The delays can typically be in
the range of 0.3 - 1.0 second[8]. As the delays are com-
parable to the time period of some of the critical in-
ter-area modes, it should be accounted for in the design
stage to ensure satisfactory control action.
In this paper, a wide-area adaptive supervisory con-
troller (ASC) for robust stabilization of multi-machine
power systems is proposed. Based on the IFWM ap-
proach and networked control system (NCS) theory [13-
16], the ASC is designed by delay-dependent stabiliza-
tion condition. In the stabilization conditions, the upper
bound of feedback signal’s transmission delays is taken
into consideration. The controller uses the input informa-
tion (e.g. frequency, active power) provided by conve-
niently located PMUs and dispatches control signals to
available local controllers. A particular feature of this
controller is that it operates in addition to existing con-
ventional PSSs and provides appropriate supplementary
control signals only if and when needed. The perfor-
mance and robustness of the controller are validated on a
4-generator 2-area test system.
2. Strategy of Adaptive Supervisory Control
A New England test power system (NETPS) is used as
the example to analysis strategy of adaptive supervisory
control. The model of the AVR with supplementary
WAM signals is shown in Figure 1. In this figure, VASCi
is the output signal of the ASC[17,18] which is added to
the AVR of each generator together with the output sig-
nal of four generators’ local PSS. The structure of the
ASC is shown in Figure 2.
3. Controller Design Considering Signals
Transmission Delay
3.1. Modeling of NCS-Based Power system with
Network-Induced Delay
Consider the following linear system:
()() ()x tAx tBu t= +

(1)
where
()
n
xt R∈
is the state vector;
()
m
ut R∈
is the
controlled input vector; and A and B are constant ma-
trices with appropriate dimensions.
For convenience, we make the following assumptions
[19].
Assumption 1 The NCS consists of a time-driven
sensor, an event-driven controller, and an event-driven
actuator, all of which are connected to a control network.
The calculated delay is viewed as part of the net-
work-induced delay between the controller and the actu-
ator.
Assumption 2 The controller always uses the most
recent data and discards old data. When old data arrive at
the controller, they are treated as packed loss.
Assumption 3 The actual input obtained in (1) with a
zero-order hold is piecewise constant function.
The control network itself induces transmission delays
and dropped data th at de grade the control performance of
the NCSs-based power system. Based on these three as-
sumptions, we can formulate a closed-loop power system
with a memoryless state-feedback controller:
{ }
**
()()()
( )(),,1,2,...,
k kk
x tAx tBu t
u tKxtti hk
ττ
= +


= −∈+=



(2)
where h is the sampling period;
1,2,3,...k=
are the
sequence numbers of the most recent data available to the
controller, which are assumed not to change until new
data arrive; k i is an integer denoting the sequence
number of the sampling times of the sensor
{ } { }
123
,,,...1, 2,3,...iii ⊆
; and k τ is the delay from the
instant
k
ih
, when a sensor node samples the sensor data
from the plant, to the instant when the actuator transfers
the data to the plant. Clearly,
[
)
[
)
11 10
,,
k kkkk
ihi ht ττ
∞
= ++
+ +=∞
.
From Assumption 2, 1
kk
ii
+> is always true. The
number of data packets lost or discarded is 11
kk
ii
+
−−
.
When
{ } { }
123
,,,...1, 2, 3,...iii =
, no packets are dropped.
If 11
kk
ii
+=+ , then 1
kk
h
ττ
+
+>
, which include
V
REF
E
F
+
V
ASCi
V
PSSi
-
+
+
Local PSS
1
1
R
sT+
1
A
A
K
sT+
Σ
ASC
△ ω
i
, △ Pi (i=1,3,5,8)
Adap tive supervisory controller
Globa l signals
GEN
i
△ ω
i
pss
K
1
w
w
sT
sT+
1
1
C
B
sT
sT
+
+
3
4
1
1
sT
sT
+
+
1
2
1
1
sT
sT
+
+
V
T
Figure 1. The de signed model of ith exciter using the WAMs
signals.
G1
G8
G3
G5
Area 1
Area 2
Adaptive
Supervi sory
c ontroller
△ ω
1
△ ω
3
△ ω
5
△ ω
8
V
ASC1
V
ASC3
V
ASC8
V
ASC5
Figure 2. The input and output signals of the adaptive su-
pervisory controller.
0k
ττ
= and
k
h τ <
as special cases. So, system (2)
represents an NCS-based power system and takes the

Z. Y. ZHANG ET AL.
437
effects of both a network-induced delay and dropped data
packets into account.
Below, we assume that () 0ut = before the first con-
trol signal reaches the plant, and that a constant
0 η >
exists that
11
(),1,2,...
kk k
i ihk τη
++
−+≤ = (3 )
Based on this inequality, we can rewrite NCS (2) as
[
)
0
11
()
0
()()( ),,,
1,2,...,
() ()(),
kkkkk
At t
xtAxt BKxiht ihih
k
xt xtet
η
ττ
ηφ
++
−+
= +∈++
=

=−=


(4)
where the initial condition function,
()t
φ , of the system
is continuously differentiable and vector-valued.
3.2. Delay-dependent Stability Analysis
This section first present a new stability criterion for
NCS (4), as s u ming the gain,
K
, is given.
Theorem 1. Consider NCS (4), given a scalar
0 η >
,
the system is asymptotically stable if there exist matrices
0, 0, 0,PQ Z>≥>
and 11 12
13
0
*
XX
XX

= ≥


, and any
appropriately dimensioned matrices 1
2
N
NN

=


and
12
T
TT
M MM

=

such that the following matrix in-
equalities hold:
11 121
22 2
*0,
**0
** *
T
TT
M AZ
M KBZ
Q
Z
φφ η
φη
φ
η

−

−

= <

−


−

(5)
1
0,
*
XN
Z

Ψ= ≥


(6)
2
0,
*
XM
Z

Ψ= ≥


(7)
where
111 111
121 2112
132 22222
,
,
.
TT
T
TT
PAAPQNNX
PBK NNMX
NNMM X
φη
φη
φη
=+++ ++
=−++ +
=−− +++
Proof. Choose the Lyapunov-Krasovskii functional
candidate to be:
0
( )()()()()
()(),
t
TT
tt
tT
t
VxxtPx txs Qx sds
xs Zx s dsd
η
ηθ
θ
−
−+
= +
+
∫
∫∫ 
(8 )
where
0, 0,PQ>≥
and
0Z>
are to be determined.
From the Newton-Leibnitz formula, the following
equations are true for any matrices
12
T
TT
N NN

=

and
12
T
TT
M MM

=
with appropriate dimensions:
0 2 ()()()(),
k
t
Tkih
tN xtxihxsds ς

= −−


∫ (9)
0 2 ()()()(),
k
ih
Tkt
tMxihxtxsds
η
ςη
−

=− −−


∫
(10)
where ()(),()T
TT
k
txtxih ς

=

. On the other hand, for
any matrix 1112
22
0,
*
XX
XX

= ≥


the following equation
holds:
0() ()() ()
() ()() ()() ()
k
k
tt
TT
tt
t ih
TT T
ih t
tXt dstXt ds
tX ttX tdstX tds
ηη
η
ςς ςς
ηςς ςςςς
−−
−
= −
=−−
∫∫
∫∫
(11)
In addition, the following equation is also true
() ()() ()()()
k
k
tt ih
T TT
tih t
xs Zx s dsxs Zx s dsxs Zx sds
ηη −−
− =−−
∫ ∫∫
 
(12)
Calculating the derivative of
()
t
Vx
along the solu-
tions of system (4) for
[ )
11
,
k kkk
tihih ττ
++
∈+ +
, adding
the right sides of (9)-(11) to it, and using (12) yield
()2()()()()()()
()()()()
2()()()()()()
()()()()()()
2
k
k
TTT
t
t
TT
t
TTT
t ih
TT T
ih t
T
VxxtPxtxtQxtx tQxt
xtZx txtZxtds
x tPxtx tQxtx tQxt
xtZx txs Zx s dsxs Zx s ds
η
η
ηη
η
ηη
η
ς
−
−
=+−− −
+−
=+−− −
+− −
+
∫
∫∫



 
1 1212
2 22
()()()()
2 ()()()()
() ()() ()()()
ˆ
()()(, )(, )
(,)(,)
k
k
k
k
k
k
t
kih
ih
Tkt
t ih
TT T
ih t
t
TT
ih
ih T
t
tN xtxihxsds
tM xihxtxsds
tX ttXtdstXtds
t ttstsds
ts tsds
η
η
η
ςη
ηςς ςςςς
ξφξξψξ
ξ ψξ
−
−
−

−−



+− −−


+− −
= −
−
∫
∫
∫∫
∫


,
∫
(13)
where
11 121
22 2
1
2
ˆ*,
**
( )(),(),(),
( ,)(),().
TT
TT
T
TTT
k
T
TT
A ZAA ZBKM
KBZBKM
Q
txtxih xt
tstx s
φη φη
φ φη
ξη
ξς

++ −

= +−


−



= −


=

Thus, if 0,1, 2,
ii
ψ ≥= and
ˆ
0 φ <, which is equiva-
lent to (5) by the Schur complement, then
()
t
Vx <

2
()xt ε −
for a sufficiently small
0 ε >
, which guaran-
tees that system (4) is asymptotically stable. This com-

Z. Y. ZHANG ET AL.
438
pletes the proof.
When
0M=
and
QI ε =
(where
0 ε >
is a suffi-
ciently small scalar), the following corollary readily fol-
lows from Theorem 1.
Corollary 1 Consider NCS (4), given a scalar
0 η >
,
the system is asymptotically stable if there exist matrices
0, 0,PZ>>
and
11 12
22
0
*
XX
XX

= ≥


, and any appro-
priately dimensioned matrix
1
2
N
NN

=

such that ma-
trix inequality (6) and the following one hold:
11 12
22
* 0,
**
T
TT
AZ
KBZ
Z
η
η
η

ΞΞ

Ξ= Ξ<


−


(14)
where
111 111
121 212
222 222
,
,
.
TT
T
T
PAAPNNX
PBK NNX
NN X
η
η
η
Ξ=++++
Ξ=−++
Ξ=− −+
3.3. Design of State F eedback Controller
Theorem 1 is extended to the design of a stabilization
controller with gain
K
for syste m (4).
Theorem 2. Consider NCS (4), for a given scalar
0 η >
, if there exist matrices
0,0, 0,LW R> ≥>
and
11 12
22
0,
*
YY
YY

= ≥


and any appropriately dimensioned
matrices
12 12
,
TT
TT TT
SSSTTT
 
= =
 
, and
V
such
that the following matrix inequalities hold:
11 121
22 2
*0,
** 0
***
T
TT
T LA
T VB
W
R
η
η
η

ΞΞ−

Ξ−

Ξ= <

−


−

(15)
110,
*
YS
LR L
−

Π= ≥


(1 6 )
21
0,
*
YT
LR L
−

Π= ≥


(1 7
where
111 111
121 2 112
22222 222
,
,
.
TT
T
TT
AL LAWSSY
BV SSTY
SS TTY
η
η
η
Ξ=+++ ++
Ξ=−+++
Ξ=− −+++
then the system is asymptotically stable, and 1 K VL− =
is a stabilizing controller gain.
Proof. Pre-and post-multiply
φ
in (5) by diag
{ }
1111
,,,PPPZ
−−−−
, and pre- and post-multiply
,1, 2,
ii
ψ = in (6) and (7) by di ag
{ }
111
,,PPP
−−−
. Then,
make the following changes to the variables:
{ }{ }
11
11 11
,,,
,,1, 2,
, ,,.
i iii
L PR ZVKL
SLN LTLMLi
WLQLYdiag PPXdiag PP
−−
−− −−
= = =
= ==
= =⋅⋅
These manipulations yield matrix inequalities (15)-
(17). This completes the proof.
Note that the conditions in Theorem 2 are no longer
LMI conditions due to the term
1
LR L
−
in (16) and (17).
Thus, that cannot use a convex optimization algorithm to
obtain an appropriate gain matrix,
K
, for the state-
feedback controller. This problem can be solved by using
the idea for solving a cone complementarity problem
[20].
Define a new variable, U, for which
1
LR LU
−
≥
; and
let
11
,,
PLHU
−−
==and
1
ZR
−
=
. Now, we convert the
nonconvex problem into the following LMI-based nonli-
near minimization problem:
Minimize
{ }
Tr LPUHRZ++
Subject to (15) and
0, 0,0,
** *
0,0,0.
** *
YS YTHP
UU Z
LI UIRI
P HZ

≥≥ ≥



≥ ≥≥



(18)
We use the ICCL algorithm to obtain
max
η
and
optimal
K for power systems because of its advantages.
Algorithm.
 Step1: Choose a sufficiently small initial
0 η >
,
such that there exists a feasible solution to (15) and (18).
Set a specified number of iterations N.
 Step2:Find a feasible set of values satisfying (15)
and (18),
0000 00
(,, ,,,,,,,,)PLWSTYZRU HV
.Set
0k=
 Step3: Solve the following LMI problem for the va-
riables
,, ,,,,,,, ,,PLWSTYZRUHV
and
K
:
Minimize
{ }
kkk kkk
TrLPLPUHUHRZRZ++ +++
Subject to (15) and (1 8).
Set
1111 1
,, ,,,
kkkk k
P PLLUUHHRR
++ +++
=====
and 1k
ZZ
+=.
 Step4: For the
K
obtained in step 3, if LMIs (15)
and (18) are feasible for the variables
,,,, ,PQZNM
and
X
, then set max
ηη
=, increase
η
, and return to
Step 2. If LMIs (5)-(7) are infeasible and without a spe-
cified number of iterations, then exit. Otherwise, set
1kk= +
and go to Step 3.
Figure 3 shows the flowchart of nonlinear iterative
optimization algorithm for the state feedback controller
design. This condition and nonlinear iterative optimiza-
tion algorithm, which has an improved stop condition,
are used to design a state-feedback networked controller.
But the operating state variables of wide-area power sys-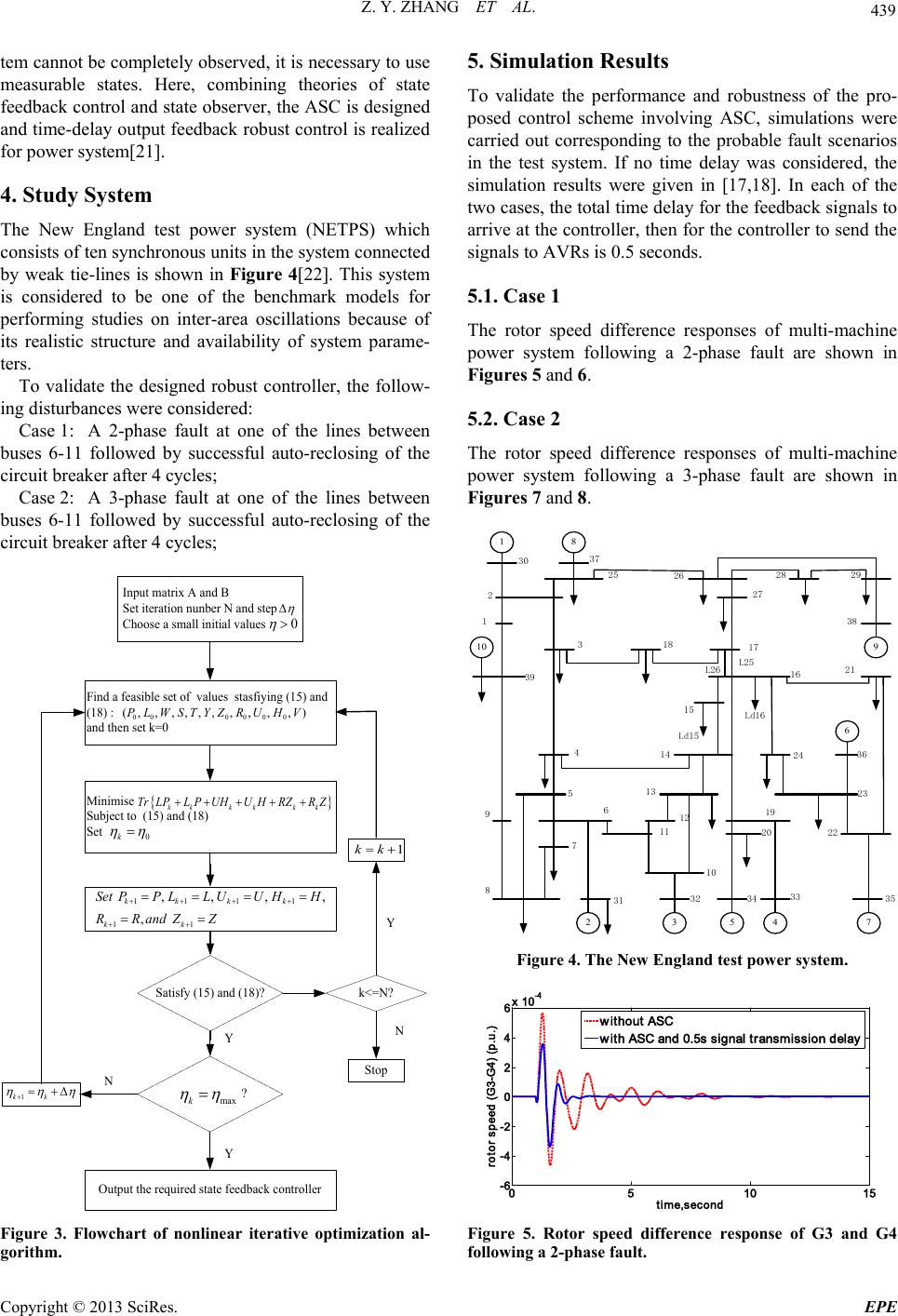

Z. Y. ZHANG ET AL.
439
tem cannot be completely observed, it is necessary to use
measurable states. Here, combining theories of state
feedback control and state observer, the ASC is designed
and time-delay ou tput feedback robust control is realized
for power system[21].
4. Study System
The New England test power system (NETPS) which
consists of ten synchronous units in the sys tem connected
by weak tie-lines is shown in Figure 4[22]. This system
is considered to be one of the benchmark models for
performing studies on inter-area oscillations because of
its realistic structure and availability of system parame-
ters.
To validate the designed robust controller, the follow-
ing disturbances were considered:
Case 1: A 2-phase fault at one of the lines between
buses 6-11 followed by successful auto-reclosing of the
circuit breaker after 4 cycles;
Case 2: A 3-phase fault at one of the lines between
buses 6-11 followed by successful auto-reclosing of the
circuit breaker after 4 cycles;
Y
N
{ }
kkk kkk
TrLPL PUHUHRZRZ++ +++
0 η >
0k
ηη =
0000 00
(,, ,,,,,,,,)PLWSTYZRU HV
η ∆
Minimise
Subject to (15) and (18)
Set
Find a feasible set of values stasfiying (15) and
(18) :
and then set k=0
Input matrix A and B
Set iteration nunber N and step
Choose a small initial values
1kk= +
1kk
ηη η
+
= +∆
Satisfy (15) and (18)?k<=N?
Stop
?
111 1
11
,, ,,
,
kkk k
kk
SetPPLLUUHH
RRandZZ
++ ++
++
= ===
= =
Output the required state feedback controller
maxk
ηη =
Y
Y
N
Figure 3. Flowchart of nonlinear iterative optimization al-
gorithm.
5. Simulation Results
To validate the performance and robustness of the pro-
posed control scheme involving ASC, simulations were
carried out corresponding to the probable fault scenarios
in the test system. If no time delay was considered, the
simulation results were given in [17,18]. In each of the
two cases, the total time delay for the feedback signals to
arri ve at th e controller, then for the controller to send th e
signals to AVRs is 0.5 seconds.
5.1. Case 1
The rotor speed difference responses of multi-machine
power system following a 2-phase fault are shown in
Figures 5 and 6.
5.2. Case 2
The rotor speed difference responses of multi-machine
power system following a 3-phase fault are shown in
Figures 7 and 8.
1
10 9
8
7
6
5 4 32
30 37
25 26 28 29
27
38
21
16
17
183
2
1
39
15
14 2436
23
22
35
4
5
96
11
12
13
19
20
7
8
10
31 3234 33
Ld15
L26
L25
Ld16
Figure 4. The New England test power system.
0510 15
-6
-4
-2
0
2
4
6x 10-4
time,seco nd
rotor speed (G3-G4) (p.u.)
without ASC
with ASC an d 0.5s signal tran smission delay
Figure 5. Rotor speed difference response of G3 and G4
following a 2-phase fault.

Z. Y. ZHANG ET AL.
440
05 10 15
-4
-3
-2
-1
0
1
2
3
4x 10
-4
tim e,second
rotor speed (G2-G3) (p.u.)
withou t ASC
with AS C and 0.5s signal tran smission delay
Figure 6. Rotor speed difference response of G2 and G3
following a 2-phase fault.
05 10 15
-1.5
-1
-0.5
0
0.5
1
1.5x 10-3
tim e,second
rotor speed (G3-G4) (p.u.)
withou t ASC
with ASC and 0. 5s signal transmission delay
Figure 7. Rotor speed difference response of G3 and G4
following a 3-phase fault.
05 10 15
-1.5
-1
-0.5
0
0.5
1
1.5x 10-3
time,second
rotor speed (G2-G3) (p.u.)
without ASC
with ASC and 0. 5s signal transmission delay
Figure 8. Rotor speed difference response of G2 and G3
following a 3-phase fault.
6. Conclusions
A wide-area adaptive supervisory controller (ASC) for
the robust stabilization of multi-machine power systems
accounting for the time delays of feedback signals from
remote locations is proposed. This paper first uses the
IFWM approach to establish an improved stability condi-
tion for NCSs-based power system that does not ignore
any terms in the derivative of the Lyapunov-Krasovskii
functional, but rather considers the relation ships among a
network -induced delay, its upper bound, and the differ-
ence between them. This condition and an ICCL algo-
rithm, which has an improved stop condition, are used to
design a state-feedback networked controller. Combining
theories of state feedback control and state observer, the
ASC is designed and time-delay output feedback robust
control is realized for power system. With the control of
the ASC, the system oscillations reduce considerably.
Additionally, the ASC ensures system stability even in
the case of cascading faults.
REFERENCES
[1] P. Kundur, Power system stability and control, New York:
McGraw-Hill, 1994.
[2] G. J. Rogers, “The Application of Power System Stabiliz-
ers to a Multi-Generator Plant,” IEEE Transacti Power
Systems, Vol. 15, No. 1,2000. doi:10.1109/59.852143
[3] B. Bhargava, “Synchronized Phasor Measurement System
Project at Southern California Edison Co.,” in Proc. IEEE
power Engineering Society Summer Meeting, 1999, pp.
16-22.
[4] H. Ni, G. T. Heydt and L. Mili, “Power System Stability
Agents Using Robust Wide Area Control,” IEEE Tran-
sacti Power Systems, Vol. 17, No. 4, 2002, pp.
1123-1131.doi:10.1109/TPWRS.2002.805016
[5] M. E. Aboul-Ela, A. A. Sallam, J. D. McCalley and A. A.
Fouad, “Damping Controller Design for Power System
Oscillation,”IEEE Transacti Power Systems, Vol. 11, No.
2, , 1996, pp. 76 7-773. doi:10.1109/59.496152
[6] M. Klein, L. Le, G. Rogers, S. Farrokpay and N. Balu,
“H∞ Damping Controller Design in Large Power Sys-
tem,” IEEE Transacti Power Systems, Vol. 10, No. 1,
1995, pp. 158-166. doi:10.1109/59.373938
[7] H. Wu, S. Tsakalis and G. T. Heydt, “Evaluation of Time
Delay Effects to Wide-area Power System Stabilizer De-
sign,” IEEE Transacti Power Systems, Vol. 19, No. 4,
2004, pp. 1935-1941. doi:10.1109/TPWRS.2004.836272
[8] B. Chaudhuri, R. Majumder and B. Pal, “Wide Area Mea-
surement Based Stabilizing Control of Power System
Considering Signal Transmission Del ay,” IEEE Transacti
Power Systems, Vol. 19, No. 4, 2004, pp.
1971-1979. doi:10.1109/TPWRS.2004.835669
[9] B. Chaudhuri, B. Pal, A. C. Zolotas, I. M. Jaimoukha and
T. C. Green, “Mixed-sensitivity approach to H∞ control
of power system oscillations employing multiple facts
devices,” IEEE Transacti P ower Systems, Vol. 18, No. 3,
2003, pp. 1149-1156. doi:10.1109/TPWRS.2003.811311
[10] S. Skogestad and I. Postlethwaite, Multivariable feedback
control, John Wiley and Sons, UK, 2001.
[11] P. Gahinet and P. Apkarian, “A Linear Matrix Inequality
Approach to H∞ Control,” International Journal of Ro-
bust and Non-linear Control, Vol. 4, No. 4, 1994, pp.
421-448. doi:10.1002/rnc.4590040403
[12] C. Scherer, P. Gahinet and M. Chilali, “Multi-Objective

Z. Y. ZHANG ET AL.
441
Output Feedback Control Via LMI Optimization,” IEEE
Transacti Automatic Control, Vol. 42, No. 7, 1997, pp.
896-911. doi:10.1109/9.599969
[13] Jianhua Z, Guolian H, Yunze W, et al., “Networked Con-
trol For Robotic Manipulators Via T-S Fuzzy Control
And Descriptor Representation,” 2006.
[14] Zhigang X, Chaoyang D, Lijie X, et al., Networked Con-
trol of Guided Weapon Using Time -delay Switched Sys-
tem with Compensatory Model[C]. 2009.
[15] G. C. Goodwin, H. Haimovich, D. E. Quevedo, et al., “A
Moving Horizon Approach to Networked Control System
Design, Automatic Control, IEEE Transactions on, Vol.
49, No. 9, 2004, pp. 1427-1445.
doi:10.1109/TAC.2004.834132
[16] G. P. Liu, Y. Q. Xia, D. Rees and W. S. Hu, “Design and
Stability Criteria of Networked Predictive Control Sys-
tems With Random Network Delay in the Feedback
Channel,” Systems, Man, and Cybernetics, Part C: Ap-
plications and Reviews, IEEE Transactions on, Vol. 37,
No. 2, 2007, pp. 173-184.
doi:10.1109/TSMCC.2006.886987
[17] Z. Hu and J. V. Milanović, “Damping of Inter-area Oscil-
lations by WAM Based Supplementary Controller,” in
Proc. IEEE PES GM 2007, 24-28 June 2007, Tampa,
Florida, USA.
[18] Z. Hu and J. V. Milanović, “The Effectiveness of WAM
Based Adaptive Supervisory Controller for Global Stabi-
lization of Power Systems,” in Proc. IEEE Power Tech
2007, 1-5, July 2007, Lausanne, Switzerl and.
[19] F.-L. Lian, J. K. Yook, D. M. Tilbury, et al., “Network
Architecture and Communication Modules for Guaran-
teeing Acceptable Control and Communication Perfor-
mance for Networked Multi-agent Sy st ems,” Industrial
Informatics, IEEE Transactions on, Vol. 2, No. 1, 2006,
pp. 12-24. doi:10.1109/TII.2005.857611
[20] L. El Ghaoui, F. Oustry and M. Aitrami, “A Cone Com-
plementarity Linearization Algorithm for Static Out-
put-Feedback and Related Problems,” Automatic Control,
IEEE Transactions on. Vol. 42, No. 8, 1997, pp.
1171-1176. doi:10.1109/9.618250
[21] F. Liu, R. Yokoy a ma, Y. Zhou, et al., SVC Robust Addi-
tional Damping Controller Design for Power System with
Considering Time-delay of Wide-area Signals. 2010.
[22] E. Vittal, M. O'Malley and A. Keane, “Rotor Angle Sta-
bility With High Penetrations of Wind Generation,”
Power Systems, IEEE Transactions on, Vol. 27, No. 1,
2012, pp. 353-362. doi:10.1109/TPWRS.2011.2161097