 Journal of Modern Physics, 2013, 4, 1213-1380 http://dx.doi.org/10.4236/jmp.2013.410165 Published Online October 2013 (http://www.scirp.org/journal/jmp) Copyright © 2013 SciRes. JMP Stochastic Quantum Space Theory on Particle Physics and Cosmology —A New Version of Unified Field Theory Zhi-Yuan Shen Email: zyshen@comcast.net Received May 14, 2013; revised June 14, 2013; accepted August 1, 2013 Copyright © 2013 Zhi-Yuan Shen. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT Stochastic Quantum Space (SQS) theory is a new version of unified field theory based on three fundamental postula- tions: Gaussian Probability Postulation, Prime Numbers Postulation, Vacuon Postulation. It build a framework with theoretical results agree with many experimental data well. Main conclusions of SQS theory are: 1) The 3-dimensional Space with face-centered lattice structure attached to Gaussian probability is stochastic in nature. 2) SQS theory is background independent at three levels. 3) Quarks with same flavor and different colors are different elementary parti- cles. There are 18 quarks in three generations based on 18 prime numbers. 4) There are only three generations of ele- mentary particles. 5) SQS theory elementary particles table listed 72 particles including 13 hypothetic bosons. Vacuon is the only elementary particle at the deeper level. 6) Photon has dispersion and special relativity is revised accordingly. 7) Graviton has zero spin. 8) Entangled particles are connected by physics link with limited distance and non-infinite superluminal speed. 9) All physical events are local, no “spooky action at a distance”. 10) Elementary particle is repre- sented by discrete trajectories on geometrical model with genus number from 0 to 3. 11) Characteristic points and re- lated triangles in elementary particle’s model provide its physics parameters. 12) Particles internal movements in a tra- jectory are deterministic and uncertainty only comes from jumping trajectories. 13) Fermion’s mass exceeds 2 /973.4 cGeVMMax must pair with anti-fermion serving as a boson state. 14) Fine structure constant is a running constant 2 )71/2( based on a mathematic running constant . 15) Converting rules based on Random Walk Theorem are introduced to deal with hierarchy problems. 16) Logistic recurrent process and grand number phenomena play impor- tant rules for converting factor in the transmission region between P L71 and Compton length. 17) Based on face-centered space structure, 36 symmetries )(rO , )(rC with P Lr 3 are identified as the intrinsic symmetries serving as the origin of all physics symmetries. 18) Heisenberg uncertainty principle is generalized with less uncertainty at sub-Planck scale. 19) There are close correlations between elementary particle theory and three finite sporadic Lie groups: M, B, Suz. 20) Cosmic structure and evolution are intrinsically correlated to elementary particles and prime numbers. 21) A part of dark matters is 2-dimensional membranes left over from cosmic inflation driven by e-boson as the inflaton. 22) After the big bang and before the current cosmic period, there are two cosmic periods with 3 1 1-dimensional space and 2-dimensional space. 23) A cyclic universe model is based on positive and negative prime numbers. 24) A multiverse includes 22 10~ member universes organized in two levels. 25) The limited anthropic prin- ciple is introduced. 26) A super-multiverse includes 44 10~ member multi-universes organized in two levels; Total number of universes in the super-multiverse is 66 10~ . 27) Based on Poincare theorem, SQS theory introduces the ab- solute black hole without any radiation. 28) A GUT including all four types of interactions occurs at 71 Planck lengths. 29) SQS theory primary basic equations are established based on Einstein equations for vacuum and redefined gauge tensors attached to Gaussian probability. SQS Theory provides 25 predictions for experimental verification. Keywords: Unified Field Theory; Space Structure; Elementary Particles; Gaussian Probability; Prime Numbers; Sporadic Groups; GUT; Dark Matter; Dark Energy; Cosmos Inflaton; Multiverse; Anthropic Principle; General Relativity; Primary Basic Equations  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1214 Section 1. Introduction This paper is the continuation and extension of the au- thor’s previous paper [1], which was published in Chi- nese. For people not familiar with Chinese language, a brief review of the previous paper is included in this paper. Stochastic Quantum Space (SQS) theory initially was intended to be a theory of space. It turns out as a unified field theory including particle physics and cosmology. In essence, SQS theory is a mathematic theory. Its re- sults are interpreted into physics quantities by using three basic physics constants, h, c, G or equivalently P L, P t, )(PP ME . In principle no other physics inputs are needed. SQS theory is based on three fundamental postulations, Gaussian Probability Postulation, Prime Numbers Postu- lation, Vacuon Postulation, which serve as the first prin- ciple of SQS theory. Based on three fundamental postulations, SQS theory builds a framework. Based on Einstein’s general relativity equations for vacuum and redefined gauge tensors attached to prob- ability, SQS theory established the basic equations in- cluding two parts. The microscopic part is the primary basic equations for elementary particles, interactions and things on upper levels. The macroscopic part as the av- eraged version includes two sets of basic equations, one set for gravity and the other set for electromagnetic force. SQS theory provides twenty five predictions for veri- fications. The basic ideas of SQS theory are summarized as the following: 1) Space is a continuum with grainy structure. It is stochastic in nature represented by Gaussian probability distribution functions at discrete points. Elementary par- ticles and interactions are different types of movement patterns of the space. 2) Cosmology and particle physics are intrinsically correlated with mathematics, in which prime numbers play the central role. 3) The correct way to unify general relativity theory with quantum theory is to introduce probabilities to Ein- stein’s original equations for vacuum. SQS theory laid down the foundations and built a framework. There are many open areas for physicists and mathematicians to explore and contribute. Section 2. Gaussian Probability Assignment According to Stochastic Quantum Space (SQS) theory, space is stochastic and continuous with grainy structure in Planck scale. The Planck length is: 35 31061625.1 2 c hG LP m, (2.1a) Based on P L, Planck time P t, Planck energy P E and Planck mass P M are defined as: s c hG c L tP P44 51039123.5 2 , (2.1b) J G hc L hc E P P10 5 1022905.1 2 , (2.1c) kg G hc cL h M P P7 10367498.1 2 . (2.1d) In which h, c and G are Planck constant, speed of light in vacuum and Newtonian constant of gravitation, respectively. Postulation 2.1A. Gaussian probability postulation. The relation between different points in space is stochas- tic in nature. Gaussian probability distribution function is assigned to each discrete point i x separated by Planck length. In 1-dimensional case, the Gaussian probability at point is: 2 2 2 2 1 ; i xx iexxp ; ,,0,,x; ,,2,1,0,1,2,, i x. (2.2) The distance between adjacent discrete points is nor- malized to 1 P L. Explanation: The Gaussian Probability Postulation serves as the first fundamental postulation of SQS theory. It represents the stochastic nature of space and also represents the quantum nature of space without sacrific- ing space as a continuum. The i xxp ; serves as the value at point from the Gaussian probability distribu- tion function centered at discrete point i x. Postulation 2.1 is for 1-dimensional case as the foundation for 3-dimensional case. The Standard Deviation (SD) of Gaussian prob- ability is selected to let the numerical factor in front of exponential term in (2.2) equal to 1: 014333989422804.0 2 1 . (2.3) The reason of selecting such specific value for will be explained later. Substituting (2.3) into (2.2) yields: 2 ;i xx iexxp ; ,,0,,x; ,,2,1,0,1,2,, i x. (2.4) Postulation 2.1B. In the 3-Dimensional Case, (2.2) is Extended as 2 222 2 3 2 3 2 1 ,,;,, kji zzyyxx kjiezyxzyxp ;  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1215 ,,0,,,, zyx ; ,,2,1,0,1,2,,,, kji zyx . (2.5) The values of are determined by the roots of the following equation: 01)2( 32/3 . (2.6) Equation (2.6) has three roots: 2 1 '0, 2 ' 3/2 1 i e , 2 ' 3/4 2 i e . (2.7) Substituting 2/1'0 into (2.5) yields: 222 ,,;,, kji zzyyxx kji ezyxzyxp ; ,,0,,,,zyx ; ,,2,1,0,1,2,,,, kji zyx . (2.8) In (2.8), only the real root of 2/1'0 is used. The meaning of all three roots will be discussed later. Definition 2.1: The Gaussian sphere centered at ),,( kji zyx is defined as its surface represented by the fol- lowing equation: 2222 )()()(Rzzyyxx kji . (2.9a) The radius of Gaussian sphere is defined as: 932743535533905.0 22 1R. (2.9b) Explanation: The 3-dimensional Gaussian probability distribution of (2.8) has spherical symmetry like a sphere with blurred boundary. The Gaussian sphere is defined with a definitive boundary. It plays an important role for the structure of space as shown in Section 22. For the 1-dimensional case, according to (2.4), the un- itarity of probability distribution function ),( i xxp with respect to continuous variable is satisfied for any dis- crete point i x: 1; 2 dxedxxxp xx ii . (2.10) In general, the unitarity of probability ),( i xxp with respect to discrete variable i x is not satisfied. Definition 2.2: S-Function. Define the summation of ),( i xxp with respect to i x as the xS-function: i i ix xx xiexxpxS 2 ; . (2.11) Theorem 2.1: S-function xS satisfies periodic con- dition: xSxS 1. (2.12) Proof: According to (2.11): )(1 2 22 )1(1 xSeeexS j j i i i i x xx x xx x xx . QED The values of xS in the region 10 x are listed in Table 2.1 and shown in Fig. 2.1. Table 2.1: The values of xS in region 10 x. In the region 1,0 , except two points at 25.0 x and 75.0 x, in general xS defined by (2.11) does not satisfy unitarity requirement, which has important impli- cations. 0.9 0. 92 0. 94 0. 96 0. 98 1 1. 02 1. 04 1. 06 1. 08 1.1 00.1 0.20.3 0.40.50.60.7 0.80.91 x S(x) Figure 2.1. xS curve in region 10 x. Theorem 2.2: xS satisfies the following symmet- rical condition: xSxS 1, 10 x. (2.13) Proof: According to (2.11): )(1 2 22 )1(1 xSeeexS j j i i i i x xx x xx x xx . QED Def inition 2.3: S -Function. Define the S - func- tion as: 1)( xSxS . (2.14) Numerical calculation found that xS satisfies the following approximately anti-symmetrical condition: xSxS 5.0 , 5.00 x. (2.15) The symmetry of xS with respect to 5.0 x in region 1,0 given by (2.13) is exact. The anti-symmetry of xS with respect to 25.0x in region 5.0,0 given by (2.15) is approximate with a deviation less than 5 10. The deviation is tiny, but its impact is signifi- cant. It plays a pivotal role for SQS theory, which will be shown later.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1216 Numerical calculation found that at the center 25.0 x of the region 5.0,0 : 152889999930253.025.0 S. (2.16) (2.16) indicates that, 25.0S has a deviation of 6 107~ from 1 required by the unitarity. Numerical calculation found a point c xin region [0, 0.5] satisfying unitarity: 1 c xS, (2.17) 5.0 0 0)(11)( c c x x dxxSdxxS , (2.18) 73026452499871562.0 c x. (2,19) On the x-axis, c xis located at the left side of 25.0x. It extends the region of 1xS and shrinks the region of 1xS . The special point c x has a pro- found effect on elementary particles and unifications of interactions, which will be given in later sections. Definition 2.4: Based on c x, three other special points a x,b x,d x are defined: 3726973550.250012845.0 cd xx . (2.20) 25.0 0 011 c a x x dxxSdxxS . 10 10882111819946879.5 a x. (2.21) 25.0 0 0 c b x x dxxSdxxS , -5 10918477191.18218617 b x. (2.22) The physics meaning of four special points, a x, b x, c x, d x, will be given later. In 3-dimensional case, according to (2.8), the unitarity of kjizyxzyxp ,,;,, with respect to continuous vari- ables x, y, z is satisfied for any discrete point kji zyx,, : .1 ,,;,, 2 2 2 222 )( )( )( dzedyedxe edzdydxzyxzyxdzpdydx k j i kji zz yy xx zzyyxx kji (2.23) In general, the unitarity of probability kji zyxzyxp ,,;,, with respect to discrete variables kji zyx ,, is not satis- fied. Definition 2.5: Define the summation of the probabil- ity kjizyxzyxp,,;,, with respect to kji zyx ,, as: ijk kji ijkxyz zzyyxx xyz kji ezyxzyxpzyxS 222 ,,;,,,, 3 . (2.24) Theorem 2.3: zyxS,, 3 can be factorized into three factors: ).()()( ,, 2 2 2 222 )( )( )( 3 zSySxSeee ezyxS k k j j i i ijk kji z zz y yy x xx xyz zzyyxx (2.25) Proof: The three-fold summation in (2.25) includes terms for all possible combinations of 2 )( i xx e , 2 )( j yy e , 2 )( k zz e . The three multiplications in (2.25) include the same terms. They are only different in processing, the results are the same. QED By its definition and (2.12), (2.25), zyxS,, 3 satisfies the following periodic conditions: zyxSzyxS,,,,1 33 , (2.26a) zyxSzyxS,,,1, 33 , (2.26b) zyxSzyxS ,,1,, 33 . (2.26c) Definition 2.6: Planck cube is defined as a cube with edge lengths 1 P L and with discrete point ),,( kji zyx at its center or its corner. The values of zyxS,, 3 at 125 points in a Planck cube with discrete points at its corner are calculated from (2.24) and listed in Table 2.2. Table 2.2. zyxS ,, 3 values at 125 points in a Planck cu- be (Truncated at 1000). Theorem 2.4: Probability Conservation Theorem. The average value of zyxS,, 3 over a Planck cube equals to unity: 1,,,, 3 1 0 1 0 1 0 3 zyxSdzdydxdvzyxS PlanckCube . (2.27) Proof: Substitute (2.24) into left side of (2.27): ijk kji ijk kji xyz zzyyxx xyz zzyyxx PlanckCube edzdydx edzdydx zyxSdzdydxdvzyxS 1 0 1 0 ])()()[( 1 0 ])()()[( 1 0 1 0 1 0 3 1 0 1 0 1 0 3 . ,,,, 222 222 (2.28) Change variables as:  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1217 ,'xxx i ,' yyy j zzz k'. (2.29) Substituting (2.29) into (2.28) and changing integra- tions’ upper and lower limits accordingly yield: .1''' ''' ,,,, 222 222 )'()'()'( 11 )'()'()'( 1 3 1 0 1 0 1 0 3 kji ijk i i j j kji k k zzyyxx xyz x x y y zzyyxx z z V edzdydx edzdydx zyxSdzdydxdvzyxS QED Probability Conservation Theorem is important. It proved that, even though in general zyxS ,, 3 does not satisfy unitarity requirement, but it does satisfy unitarity requirement in terms of average over a Planck cube. The conservation of probability means that, the event carriers of probability are moving around but they cannot be cre- ated or annihilated. Lemma 2.4.1: The average value of xS over re- gion [0,1] equals to unity: 1 0 1dxxS . (2.30) Proof: Substitute (2.11) into the left side of (2.30): i i i i x xx x xxedxedxxS 1 0 )( 1 0 1 0 2 2 . (2.31) Change variables as: xxx i'. (2.32) Substituting (2.32) into (2.31) and changing integra- tion’s upper and lower limits accordingly yield: 1' 22 ' 1 ' 1 0 dxedxedxxS x x x x x i i i . QED Lemma 2.4.2: Planck cube with volume 1 V (leng- th normalized to 1 P L) is divided into two parts 1 V and 2 V: 1 21 VVV , (2.33a) ,1 V Vdv , 1 1 V Vdv . 2 2 V Vdv (2.33b) Theorem 2.4 leads to the following equation: 12 ,,11,, 33 VV dvzyxSdvzyxS. (2.34) Proof: According to (2.27) and (2.33): 212112 21333 1),,(,,,, VVVVVV d dvVVVdvzyxSdvzyxSdvzyxS. Moving the terms on left and right sides yields (2.34). QED Section 3. Unitarity Unitarity is a basic requirement of probability. As shown in Section 2, the unitarity with respect to discrete vari- ables and continuous variables for Gaussian probability are contradictory. In this section, three schemes are pre- sented to solve the unitarity problem. Scheme-1. To Treat All Points in Space Equally For Scheme-1, Gaussian probabilities are not only as- signed to discrete points but to every point in the con- tinuous space. The summations in zyxS ,, 3 of (2.24) introduced in Section 2 become integrations: .1''' '''',',';,,,,;,,,, '')'( 3 2 2 zSySxSdzedyedxe dzdydxzyxzyxpzyxzyxpzyxS zzyyxx xyz kji ijk (3.1) The unitarity problem is solved. For Scheme-1, the discrete points are no longer special and all points in the space are on an equal footing. But Scheme-1 does not represent the space for SQS theory, instead, it represents the space for quantum mechanics. To introduce Scheme-1 is for comparison purpose. It indicates that, the uniform space does not have unitarity problem. The unitarity problem is caused by space grainy structure, which SQS theory must deal with. Let’s go back to the grainy space proposed by SQS theory. In Appendix 1, A Fourier transform is applied to probability xp of (2.4) to convert it into k-space. Ac- cording to (A1.2), the corresponding Gaussian probabil- ity function kP in k-space is: 4 2 2 1k ekP . (3.2) The standard deviation of kP is .2 k Mul- tiplying (A1.6) with yields: xpxk . (3.3) In (3.3), x and x pare 1-dimensional displacement and momentum difference, respectively. The on right side is two times greater than the minimum value 2/ from Heisenberg uncertainty principle. The increased uncertainty is due to the asymmetry of 2/1 and 2 k. The wave function corresponding to i xkP ; of (A1.1) is: i ikx k iieexkQkPxk 8 2 2 1 );()(; ; ,,0,, k; ,,2,1,0,1,2,, i x. (3.4) Notice that, the wave function (3.4) has following fea- tures: 1) The relation between i xkP ; and i xk; is con-  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1218 sistent with quantum mechanics: iii xkxkxkP;;; . (3.5) 2) Only discrete points i x appear in the phase func- tion i ikx e. 3). i xk; is not an eigenstate of k. The magni- tude )(kP of i xk; serves as distribution function for k. Before explore other schemes, a discussion for the es- sence of probability unitarity is necessary. Probability is associated with events. In Section 2, Table 2.2 data show that, in the vicinity of Planck cube’s center 5.0,5.0,5.0 zyx , the sum of probabilities 1,, 3zyxS. Because the set of events at these points are incomplete; some events are missing. These missing evens cause the sum of local probabilities less than one. In the vicinity of the Planck cube corners kji zyx ,, , 1,, 3zyxS , because the set of events over there includes some events belong to other places. These excessive evens cause the sum of local probabilities greater than one. In other words, events associated with their probabilities move around inside Planck cube causing the unitarity problem. To move these events back to where they belong will solve the discrete unitarity problem. But it distorts the Gaussian probability distribution and jeopardizes the unitarity with respect to continuous variables based on Gaussian prob- ability distribution. To solve the problem requires some new concept. Tra- ditionally, unitarity is local, which requires the sum of probability equals to unity at each point in space. 1,, 3zyxS is caused by events moving around. The foundation for local unitarity no longer exists. A gener- alized unitarity is proposed: 1) Recognize the fact that events associated with probabilities move around; 2) Follow the moving events for probability unitar- ity.According to Theorem 2.4, the Probability Conserva- tion Theorem, generalized unitarity is not contradictory to the traditional unitarity for the Planck cube as a whole entity. But it does change the rules inside the Planck cube. For the microscopic scales, as the events inside Planck cube are concerned, generalized unitarity is necessary. For the macroscopic scale including many Planck cubes, the local unitarity is still valid in the average sense. The following two schemes are based on generalized unitarity. Scheme-2. Unitarity via Probability Transportation on Complex Planes The complex planes are inherited from the 3-dimensional Gaussian probability. Consider a Planck cube centered at a discrete point )0,0,0( kji zyx as shown in Figure 3.1. According to (2.5), the 3-dimensional Gaussian probability is: 2 222 2 3 2 3 2 1 0,0,0;,, zyx ezyxp . (3.6) Normalize the three values of the standard deviations 0 ' ,1 ' , 2 ' of (2.7) as: 1'200 , 3/2 11 '2 i e , 3/2 22 '2 i e . (3.7) In which two of them 1 and 2 are complex num- bers. To keep the probabilities as real numbers related to 1 and 2 , it is necessary to extend the x-axis, y-axis, z-axis into three complex plans x -plane, y -plane, z - plane, respectively. Figure 3.1. The Planck cube with center at a discrete point )0,0,0( kji zyx. Definition 3.1: Define parameters to build three com- plex planes associated with x-axis , y-axis, z-axis: i exx 2,12,1 , (3.8a) i eyy 2,12,1 , (3.8b) i ezz 2,12,1 , (3.8c) 120 3 2 . (3.8d) In which ,, and ,, are real parameters. Explanation: In (3.8a), 2,1 represents two straight lines on complex x -plane intercepting to the real x-axis at with angles of 120 . Continuously  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1219 change the value of , 1 and 2 sweep across x-axis to construct the complex x -plane. Every point on the complex x -plane is the intersection of two straight lines defined by (3.8a). They -plane and z -plane associated with y-axis and z-axis are constructed in the same way. On the complex x -plane, three straight lines 1 , 2 and x-axis intercept at 0 x with 3-fold rotational symmetry as shown in Figure 3.2. The 3-fold rotational symmetry has its physics significance, which will be discussed later. Figure 3.2. Three straight lines with 3-fold rotational sym- metry on complex x -plane. Rule 3.1: In order to keep the values of i xxp ;, kji zyxzyxp , ,;,, and xS , zyxS ,, 3as real numbers, in the Gaussian probability exponential part, spatial va- riables y ,, in the numerator choice their path ac- cording to (3.8) matching the value in denominator to keep these values always equal to real numbers. Explanation: The validity of Rule 3.1 to i xxp;, kji zyxzyxp , ,;,, is obvious. Its validity for xS , zyxS ,, 3 needs explanation. According to the definition of xS : i i ix xx xiexxpxS2 ; . (2.11) All terms of i xi xxpxS ; except 0;xp have their “tail” in region ]5.0,5.0[ , which are equivalent to the “tails” of 0;xp in regions of ]5.0,[ and ],5.0[ : x x x x x x xx etoequivalente i i i 5.0 ,5.0 )0( 5.05.0 ;0 )( 2 2 . (3.9) xS in region [−0.5,0.5] can be viewed as a single probability distribution function 0;xp with “mul- ti-reflections” at the two boundaries of region [−0.5,0.5]. Figure 3.3 shows an example for the 0 i x term along with two adjacent terms 1 i x and 1 i x with their “tails” in region [−0.5,0.5]. In essence, probability trans- portation via complex plane for i xxp ; is also valid for xS . According to Theorem 2.3, )()()(,, 3xSySxSzyxS , the same argument is valid for zyxS,, 3 as well. Figure 3.3. Three adjacent Gaussian probability distribu- tion functions show the “tails”. For double check, let’s look it the other way, consider the i xxp; term in xS : 2 2 )( ; i xx iexxp . (3.10) In which i x is a real number and is a complex number. As long as the point corresponding to i xx is on the lines defined by (3.8a), i xxp; is a real number, and so is xS .. In the Planck cube centered at discrete point )0,0,0( kji zyx as shown in Fig. 3.1, a closed sur- face S is defined by 01,, 3zyxS , which divides Planck cube in two parts 1 V and 2 V. In the inner region 1 V, 01,, 1 3 V zyxS ; in the outer region 2 V, 01,, 2 3 V zyxS. By means of probability transportation, the excessive events associated with probabilities in the inner region 1 V transport to the outer region 2 V. Ac- cording to Theorem 2.4 and lemma 2.4.2, zyxS ,, 3 satisfies generalized unitarity. Since zSySxSzyxS 1113,, and xS , yS , zS have the same type of exponential expression, ex- ploring one, xS , is sufficient. (2.13) shows that, in region [0,1], xS is symmetry with respect to5.0 x, to explore xS in the half region [0,0.5] is sufficient. In region [0,0.5], (2.15) shows that 1)( xSxS is approximately anti-symmetry with respect to 25.0 x. In the meantime, let’s treat it as exactly anti-symmetry and consider the difference later. In Scheme-2, probabilities along with events transport back and forth to satisfy the discrete and continuous uni- tarity requirements alternatively. Fermions and bosons are essentially different particles with different properties. Their probability transporta- tions are different. It turns out that, bosons without mass  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1220 take the straight real path along the real axis; while Dirac type fermions take the zigzagging path on the complex plane. The following rules of probability transportation are for Dirac type fermions. Rule 3.2: The probability transportation rules for fer- mions are as follows. 1) Consider two points 25.00, 11 xx , 12 5.0xx )5.025.0( 2 x along the real x-axis, as shown in Fig. 3.4. The excessive probability 1 1xS at 1 x trans- ports along a set of complex lines 1 and 2 to 2 x where probability having deficient 1 2xS. The path length is: 12 2xxl . (3.11) The factor 2 in (3.11) comes from: 2120cos/1cos/1 . (3.12) The probability transportation makes 1 1 xS and 1 2xS to satisfy unitarity with respect to discrete va- riable i x. But it distorts the Gaussian probability with respect to continuous variable . Figure 3.4. Transporting paths with the same loop lengths and different routs on complex plane. 2) To reinstall the Gaussian probability distribution, it transports back from 2 x to 1 xalong another set of complex lines 1 and 2 via another path with the same path length 12 2xxl as shown in Fig. 3.4. The two paths form a closed loop with loop length: 12 42 xxlL . (3.13) The probability following its event goes back and forth between 1 x and 2 x around closed loops. 3) The path length of (3.11) and the loop length of (3.13) are valid for all zigzagging paths shown in Fig.3.4. The multi-path nature has its physics significance, which will be discussed in later sections The repetitive probability transportations along closed loops cause oscillating between two points 1 x and 2 x. In this way, the two types of local unitarity are satisfied alternatively, and the generalized unitarity is always sat- isfied. It provides a kinematic scenario for the oscillation. The dynamic mechanism and driving force of the oscilla- tion will be discussed in Scheme-3. As mentioned in Section 2, the anti-symmetry of xSxS 5.0 is only an approximation. In gen- eral, the unitarity by probability transportation is not ex- act. The tiny difference between 1 xS and 2 xS provides a slight chance for probability transportation path to go off loop. The off loop path goes to other places with different values of 1 x and 2 x corresponding to other particles, which provide the mechanism for interac- tions between particles and transformation of particles. This is the scenario of probability transportation on the complex x -plan associated with x-axis. The same is for the complex y -plane and -plane associated with y-axis and z-axis. For Scheme-2, the three real axes in 3-dimensional real space are extended to three complex planes with 6 independent variables instead of 3. The extended space with three complex planes is an abstract space. For SQS theory, the real space is 3-dimensional. The essence of complex plane is to add the phase angle to real spatial parameters. The physics meaning of the phase angle will be discussed later. Scheme 3. Unitarity in Curved 3-Dimensional Space According to general relativity, in 3-dimensional curved space, the distance between point ),,( zyxP and discrete point ),,( kjid zyxP is the geodesic length: kjiGdG zyxzyxLPPL ,,;,,; . (3.14) According to (A2.2) in Appendix 2, geodesic length dGppL ; is determined by following differential equa- tion: .,0 2 2 d cb a bc aPtoP ds dx ds dx ds xd (3.15) In which, ab g is the gauge tensor and a bc is Chris- toffel symbol of second type. Taking dG PPL ; 2 to re- place 222 )()()( kji zzyyxx in (2.24) yields: ijk kjidG xyz zyxPzyxPL ePS ),,();,,( 3 2 . (3.16) As mentioned previously, at point ),,( 1111 zyxP in 1 V shown in Fig. 3.1, there are excessive events associated with 01)( 1 13 V PS; at point ),,( 2222zyxP in 2 V, there  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1221 are deficient events associated with 01)( 2 23 V PS . For scheme-3, the probability transportation from 1 P to 2 P takes its geodesic path: ),,();,,(, 22221111212121 zyxPzyxPLPPL . (3.17) To adjust gauge tensor zyxgab,, along the path 2121 ,PPL in curved space, the unitarity of probability 01)(1 13V PS at 1 P and 01)( 2 23 V PS at 2 P are satis- fied. But the Gaussian probability is distorted. Then the gained probability at2 P transports back to1 P takes the geodesic path: ),,();,,(, 11112222121212 zyxPzyxPLPPL. (3.18) It goes back to1 P to reinstall Gaussian probability. The transportations via 2121 ,PPL and 1212 ,PPL fin- ish one cycle of oscillation. The process goes on and on. In this way, the local unitarity requirement with respect to discrete variables and continuous variables of Gaus- sian probability are satisfied alternatively, and the gener- alized unitarity is always satisfied. This is the scenario of probability oscillation in 3-dimesional curved space. Hypothesis 3.1: To adjust the gauge tensor zyxgab,, properly makes geodesic paths 2121 ,PPL such that 01)(1 13 V PS and 01)( 2 23 V PS are satis- fied. To adjust the gauge tensor zyxgab,, properly makes geodesic paths 1212 ,PPL such that the Gaussian probability is reinstalled. The adjusted zyxgab ,, de- termines the space curvature inside the Planck cube. Explanation: According to Hypothesis 3.1, the alter- native unitarity of Gaussian probability with respect to discrete variables and continuous variables is not only the driving force for probability oscillation, but also serves as the driving force to build the curved space in- side Planck cube. This is the expectation from SQS the- ory. Let’ go back to the 1-dimension case. Definition 3.2: S-equatio n. Define the S-equation along the x-axis as: 011)( 2 )( i i x xx exS . (3.19) Explanation: S-equation is the origin of a set of sec- ondary S-equations serving as the backbone of SQS the- ory. It plays a central role to determine particles parame- ters on their models, which will be discussed in later sec- tions. Theorem 3.1: Along the x-axis, the 1-dimensional un- itarity requires: 011)( 2 ))(( i i x xxx exS for all . (3.20) The only way to satisfy01)( xS for all is that )(x is a function of as a running constant. Proof: In Section 2, (2.17) show that, 1)73026452499871562.0()( SxSc. For allother points in region [1,0.5], 1 c xxS . In order to satisfy 01 xS for all x, something in the xS must be adjustable. There are only two constants e and in xS. In which e as a mathematical constant does not depend on geometry, while does. Therefore, the only way to satisfy unitarity of 1 xS for all x is that )(x is a function of as a run- ning constant. QED Explanation: For SQS theory, Theorem 3.1 plays a central role for the models and parameters of elementary particles, which will be demonstrated in later sections. In the 1-dimensional case, what does x mean? The answer is: x carrying information in curved 3-dimensional space around point , x indi- cates space having positive curvature corresponding to attraction force; x indicates space having nega- tive curvature corresponding to repulsive force. The real examples will be given later. In Table 3.1, the values of x calculated from (3.20) are listed along with the types of space curvatures and corresponding forces. Table 3.1. x as a function of calculated from (3.20) (i x truncated at 1000000 ). Notes: *The precision of values for 5 102.1 x is limited by 16- digit numerical calculation. The lower limits are listed. The attraction force is the ordinary gravitational force. The repulsive force means that, in the vicinity of discrete point gravity reverses its direction. This is one of predic- tions provided by SQS theory, which is important in many senses. For one, the repulsive force prevents form- ing singularity, which solves a serious problem for gen- eral relativity. For another, without repulsive force to balance the attraction force, space cannot be stable. The others will be given later. Theorem 3.2: At discrete points i xx , the unitarity equation of (3.20) requires: i x , for ,,2,1,0,1,2,, i x. (3.21)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1222 Proof: Consider the opposite. If i x is not infinity, When the summation index i x, i ii x xxx iexS 2 ))(( )( . Equation (3.20) cannot be satisfied. The opposite, i.e. i x must be true. QED Theorem 3.2 is a mathematic theorem with physics significance, which will be presented later. For Scheme-2, probability oscillation is to satisfy al- ternative unitarity, which does not provide the dynamic mechanism and the driving force. For scheme-3, the re- pulsive and attraction forces provide the dynamic me- chanism and the driving force for oscillation. At 1 xx where 1)( 1x , the repulsive force pushes the event associated with its probability towards 2 x. When it ar- rived 2 xx where 1)(2x , the attractive force pulls it back to 1 x. In this way, the oscillation continues. The dynamic scenario provides the mechanism of oscillation, which is originated from space curvature. As mentioned in Scheme-2, the approximation nature of anti-symmetry of (2.15) provides a slight chance for transportation off loop representing interactions, which is also valid for Scheme-3. For Scheme-3, the curvature patterns make the Planck scale grainy structure. As a summary, Table 3.2 shows a brief comparison of three schemes. Table 3.2. Summary of the features for three schemes. The three schemes are three manifestos of the vacuum state. Scheme-1 corresponds to the quantum mechanics vacuum state. Schemes-2 and Scheme-3 are SQS vacuum states at a level deeper than quantum mechanics. The probability oscillation in Scheme-2 is the same as in Scheme-3. It implies that Scheme-2 is equivalent to Scheme-3. Moreover, in Scheme-2, three complex planes have 6 independent real variables; in Scheme-3, the symmetrical 33 gauge matrix of ab g also has 6 in- dependent components. The correlation indicates that, the complex planes of Scheme-2 are closely linked to curved space of Scheme-3. It confirms that, the three complex planes associated with three real axes are some type of abstract expression of the curved 3-dimensional real space. For SQS theory, there is no additional dimen- sion or dimensions beyond the real 3-dimensional space in existence. In reference [2], Penrose demonstrated the correlation between Riemann surface and the topological mani- fold—torus. According to Penrose, 0 , 1 , 2 of (3.7) are three branch points of the complex function 2/13 )1( z on the Riemann surface: 1 0 z, 3 2 1 i ez ,3 4 2 2 i ez . (3.22) As shown in Figure 3.5(a), The Riemann surface for 2/13 )1( z has branch points of order 2 at 1, , 2 and another one at . Penrose showed that, for Rie- mann surface’s two sheets each with two glued slits, one from 1 to and the other from to 2 , these are two topological cylindrical surfaces glued correspond- ingly giving a torus as shown in Figure 3.5(b). On the torus surface, there are four tiny holes 1 h, h, h, 2 h representing 1, , , 2 on the Riemann surface, respectively. The four tiny holes on torus have important physics significance, which well be discussed in later sections. Figure 3.5. (a): Four branch points and two glued cuts on two sheets of Riemann surface; (b): Four tiny holes on torus surface. For SQS theory, the correspondence of Riemann sur- face and torus is very important. It plays a pivotal rule for constructing the topological models for quarks, lep- tons, and bosons with mass and much more, which will be discussed in later sections. Section 4. Random Walk Theorem and Converting Rules Random walk process is based on stochastic nature of space. It plays an important role for SQS theory. In this section, the Random Walk Theorem is proved and con- verting rules are introduced serving as the key to solve many hierarchy problems.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1223 Definition 4.1: Short Path and Long Path. In 3-dimensional space, there are two types of paths between two discrete points. The “short path” from point ),,( kji zyx to point ),,( '''kji zyx is defined as the straight distance between them. 2 ' 2 ' 2 'kkjjiizzyyxxL . (4.1a) The “long path” ˆ from point ),,( kji zyx to point ),,( ''' kji zyx is defined as step-by-step zigzagging path in lattice space with Planck length P L as step length Pi Ll. P N iiNLlL 1 ˆ, nmlN . (4.1b) The random walk from point ),,( kji zyx to point ),,( '''kjizyx takes l, m, n steps along , y , z directions, respectively. Theorem 4.1: Random Walk Theorem. Short path and long path L ˆ are correlated by the random walk formula: 2 ˆ ; or LL ˆ . (4.2) andL ˆ are normalized with respect to Planck lengt P L, both are numbers. Proof: According to (2.8), the probability from point ),,( kjizyx to point ),,('''kji zyx is: 2 2 ' 2 ' 2 ' ''',,;,, L zzyyxx kjikji eezyxzyxp kkjjii . (4.3) Take a random walk from kji zyx ,, to ''' ,,kjizyx with l, m, nsteps along , y, z directions, respectively. The probability of reaching the destination is: L lmn nml kjikji eeeeezyxzyxp ˆ 111 ''' 222 ,,;,, nmlL ˆ. (4.4) Combining (4.3) and (4.4) yields 2 ˆ . QED Obviously, Random Walk Theorem is based on Gaus- sian Probability Postulation introduced in Section 2. As a precondition, the standard deviation of 3-dimensional Gaussian probability must take the values to make the factor in front of exponential term equal to 1. Otherwise, Random Walk Theorem does not hold. It means that, the only parameter in the first fundamen- tal postulation of SQS theory is determined. Random Walk Theorem provides the foundation for conversions, which are governed by a set of converting rules. Physics quantities can be converted by applying these converting rules, which serve as the way to dealing with hierarchy problems. Definition 4.2: The converting factor for short path and long path is defined as: P LLN /. (4.5) Lemma 4.1: , L ˆ and are related as: P LNNLL 2 ˆ . (4.6) Proof: According to Theorem 4.1, the lengths and ˆ in (4.2) are normalized with respect to P L. Let P L appears in (4.2): PPPPPL L N L L L L L L L L 2 ˆ. (4.7) Multiplying P L to both sides of (4.7) yields: NLL ˆ. (4.8a) According to (4.5), substituting P NLL into (4.8a) yields: P LNL 2 ˆ. (4.8b) (4.8a) plus (4.8b) is (4.6). QED The basic unit of length in Theorem 4.1 and Lemma 4.1 as well as the step length of random walk is P L, which indicate the importance of Planck length. According to SQS theory, physics quantities at differ- ent scales have different values determined by converting factors, which are governed by converting rules origi- nated from Random Walk Theorem. Definition 4.3: The conversion factors for general purpose are defined as follows. 1) For bosons without mass: P LN / . (4.9) is the wavelength of the boson. 2) For particle s with mass: PC LN/ . (4.10) C is the Compton wavelength of the particle: c h C . (4.11) is the mass of that particle and c is the speed of light in vacuum. Conversion rules for general purpose are given as fol- lows. 1) For length: P LNNLL2 ˆ . (4.12) ˆ, L, and P L are long path, short path, and Planck length, respectively. 2) For time interval: P tNNtt 2 ˆ. (4.13) t ˆ, t, and P t are long path time interval, short path time interval, and Planck time, respectively. 3) For energy and mass: 2 // ˆNENEE P . (4.14) 2 // ˆNMNMM P . (4.15) E ˆ, , and P E are long path energy, short path energy,  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1224 and Planck scale energy, respectively. ˆ, , and P M are long path mass, short path mass, and Planck mass, respectively. Take the ratio of electrostatic force to gravitational force between two electrons as an example to show how converting rules work. According to Coulomb’s law, the electrostatic force between two electrons separated by a distance is: 2 0 2 4r e fE . (4.16) In which, e is the electrical charge of electron, 0 is permittivity of free space. According to Newton’s gravity law, the gravitational force between two electrons separated by a distance is: 2 2 M Gf e G. (4.17) In which, Gis Newtonian gravitational constant, e M is electron mass. According to (4.16) and (4.17), the ratio of electro- static force to gravitational force between two electrons is: 2 0 2 /4eG E GE GM e f f R (4.18) According to (4.15) and (2.1d): ePe NMM/, (4.15) G hc MP 2 , or 2 2 P M hc G . (2.1d) e N is the converting factor for electron. P M is Planck mass. Substituting (4.15) and (2.1d) into (4.18) yields: 2 2 2 0 2 22 0 2 /424 1 4e e P eG E GE N M M hc e GM e f f R (4.19) In (4.19), is the fine structure constant. At elec- tron mass scale: 05999084.137 1 2 )( 0 2 hc e Me . (4.20) In which, )51(035999084.137/1 is cited from 2010-PDG (p.126) according to references [3] and [4]. Electron converting factor is: 23 10501197.1 e P eM M N. (4.21) Substituting (4.20) and (4.21) into (4.19) yields: 42 /10164905.4 GE R. (4.22) GE R/ is one of many hierarchy problems in physics. By applying conversion rules not only solves the hierar- chy problem but also reveals its origin and mechanism. On the right side of (4.19), the first factor is electrically originated: 4 21084811744.1 4 . (4.23) The second factor 2 e N is mass originated: 46 2 23 2 210253593.210501197.1 e P eM M N. (4.24) According to Random Walk Theorem and Lemma 4.1, converting factor e N is equal to the ratio of long path over short path. Keep this in mind, the 46210~ e N factor can be explained naturally. For a pair of electron, the electrostatic force is inversely proportion to the square of the straight distance (short path) between them; while the gravitational force actually is inversely propor- tional to the square of the zigzagging long path rNr e ˆ between them. In terms of force mediators, photon takes the short path, while graviton takes the long path. Ac- cording to SQS theory, this is the mechanism of tremen- dous strength difference between electrostatic and gravi- tational forces, which is originated from random walk. It is the first time to show that Random Walk Theorem and the long path versus short path as well as the con- versing rules are real and useful. There are more exam- ples along this line in later sections. Once the mechanism is revealed, there are more in- sights to come. Rule 4.1: Electron’s converting factor )(lNe is a run- ning constant as a function of length scale l(in this case, l is the distance between two electrons) with different behaviors in two ranges. Range-I: For the length scale Ce l, : .)(,const LM M NlN P Ce e P ee for Ce l, . (4.25a) Range-II: For the length scale eCP lLl 71 min : PCee P Ce ee L ll M Ml NlN ,, )( for eCPlLl 71 min . (4.25b) In (4.25), Ce, is the Compton wavelength of electron, eCP lLl 71 min is the lower limit of l in Range-II, which will be given in Section 16. Explanation: The reason for .)(,constlNCee in Range-I is obvious. Otherwise, if)(,Cee lN is not a constant, then electron mass in macroscopic scale varies with distance, which is obviously not true. Range-II needs some explanation. According to Lemma 4.1, P LLN / , in this case Pe LlN /, (4.25b) is explained. Figure 4.1 shows the variation of )(lNe, the )(lNe versus l profile is made of two straight lines. In Range- I, )(lNe is a flat straight line with zero slop. In Range-II, )( lNe is a straight line with slop 1/1 P L. Two strai-  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1225 ght lines intersect at Ce l, . It shows a peculiar behav- ior of )(lNe. Most physics running constants vary as- ymptotically toward end. This one is different. The straight line with slop 1/1 P L on left suddenly stops at Ce l, and changes course to the flat straight line on right. At two straight lines’ intersecting point, the first derivative is not continuous. The mechanism of such peculiar behavior will be explained in Section 16. There is another factor)4/( 2 in GE R/, in which )( M is a running constant. The variation of )(M makes )( /lRGE different from lNe 2. It rounds the corner of )( /lR GE versus l curve at intersecting point show in Figure 4.1. The )( /lR GE for two electrons given by (4.19) is just an example. It can be extended to other charged particles. For instance, two protons separated by a distance , the ratio of electrostatic force to gravitational force is: 2 2 2 0 2 22 0 2 /4 )( 24 1 4prot prot prot prot prot GE N M N hc e GM e R ; protPprotMMN /. (4.26) In which, prot M, prot N, and )( prot M are mass, con- verting factor and fine structure constant at proton energy scale, respectively. Figure 4.1. )(lNe and )( /lRGE versus distance l curves. (Scales are not in proportion.) Substituting data into (4.26) and ignoring the differ- ence between )( prot M and )( e M of (4.20) yields the ratio for protons: 36 /10235343.1 prot GE R. (4.27) The conversion rules introduced in this section are subject to more verifications. Other applications of con- verting rules will be presented in later sections. Section 5. Apply to Quantum Mechanics and Special Relativity In this section, the converting rules introduced in Section 4 are applied to some examples in quantum mechanics and special relativity. According to Feynman path integrals theory [5], the state 22 ;tx at point 2 x and time 2 t is related to the initial state 11 ;tp at point 1 x and time 1 t as: 2 1 1122;1,2; x x dltxKtx , 12tt ; (5.1a) allpaths xx allpaths xx dttxxL h i txS h it t AeAeK 2121 2 1 ;, 1,2 . (5.1b) In which A is a constant, )(txS is action, txxL;, is Lagrangian, 1 x, 2 x, and )(tx are 3-dementional coordinates with simplified notations. The integral in (5.1a) and summation in (5.1b) include “all possible paths” from point 1 x to point 2 x. Assuming the particle is a photon with visible lights wavelength of m 7 10~ , it travels with speed c from 1 x to 2 x separated by distancemL 1. The photon traveling through mL 1 once takes time scLt9 103.3/ . The obvious question is: How does photon have time to travel so many times through “all possible paths” be- tween 1 x and 2 x? Theorem 4.1 and Lemma 4.1 pro- vide the answer. According to (4.9), the converting factor for photon with wavelength m 7 10~ is: 28 10~/ P LN . (4.9) According to (4.12), the photon’s long path wave- length is: lightyearsmN 52128 10~10~10~ ˆ . (5.2) The 28 10~N tremendous difference between long path wavelength ˆ and wave length is originated from the Random Walk Theorem. From SQS theory viewpoint, the “all possible paths” in (5.1) of Feynman path integrals theory are covered by photon’s long path wavelength m 2128 10~10~ ˆ . It is sufficient for the photon to cover through “all possible paths” via many billions of billions different routes from 1 x to 2 x. This is the explanation of Feynman path integrals theory for SQS theory. But there is a question. If the photon with wavelength m 7 10~ really travels through the long path m 2128 10~10~ ˆ , for a stationary observer, it only takes time interval of st 9 103.3 . The question is: What is photon speed seen by a stationary observer? If the stationary observer sees the long path, the speed is indeed superluminal. For example, photons with wave- length m 7 10~ , it travel along the long path with su-  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1226 perluminal speed: smsmcc L Ncv P /103/1031010~ 3682828 . (5.3) Question: Does the stationary observer sees the tre- mendous superluminal speed? According to SQS theory, the wave pattern of a particle such as photon is estab- lished step by step with step length P L during its zig- zagging long path journey. The short path is the folded version of the long path. For an ordinary photon, the folded long path is hidden in its wave pattern. The sta- tionary observer sees neither the hidden long path nor the superluminal speed. In case the photon’s long path shows up from hiding that is another story. It will be discussed later. The superluminal speed cNcv enhances the explanation of Feynman path integrals theory for SQS theory. The explanation for Feynman’s path can be used to explain other similar quantum phenomena such as the double-slot experiment for a single particle and quantum entanglements. Take the double slots experiment for a single photon as an example. Experiments have proved that, when the light source emits one phone at a time, the interference pattern still shows up. As mentioned previously, a photon with wavelength m 7 10~ has its long path wave- length m 212810~10~ ˆ and superluminal speed for vacuons (in Section 18, vacuon is defined as a geometri- cal point in space) to travel along the long path, which provide the condition to let the vacuons pass through two slits enormous times to form the interference pattern. Figure 5.1 shows the double-slit interference pattern for a single photon. Figure 5.1. The double-slit interference pattern for a single photon. The single photon’s long path builds the wave pattern step by step in the space between the plate with double- slit and the screen. The two waves come from two slits to form the interferential pattern on the screen just like the regular double-slit interference pattern. The single pho- ton strikes on the screen at a location according to prob- ability determined by the interference wave pattern’s magnitude square. When more photons strike on screen, the interference pattern gradually shows up. The long path provides the condition for a single photon’s wave pattern to interfere with itself. It is possible because of the long path’s extremely long length and vacuons’ su- perluminal speed, which allow the vacuons pass through two slits so many times. In this sense, a single photon does pass through two slits. According to the converting factor PPfLcLN // based on the Random Walk Theorem, as photon’s fre- quency f and energy increase, P fLcN / decreases. The difference between long path and short path de- creases accordingly. As a result, the wave pattern be- comes coarser and more random. In other words, the wave-particle duality is a changing scenario with energy, the particle nature is enhanced and the wave nature is diluted with increasing energy. The tremendous difference between short path and long path is related to special relativity. A stationary ob- server sees the photon having wavelength . The pho- ton travels along its short path with a speed v less than c and very close to c, according to Lorentz transfor- mation: 2 )/(1 ˆcv , 2 /1 1 ˆ cv . (5.4) From SQS theory perspective, and ˆ are pho- ton’s short path wavelength and long path wavelength originated from Random Walk Theorem. From special relativity perspective, versus ˆ is the result of Lo- rentz transformation. These two apparently different scenarios are two sides of the same coin. The key con- cept is to recognize photon traveling along its short path with a speed less than c and very close to c. It is a deviation from special relativity. Substituting / ˆ N into (5.4) yields: 22 1 1 /1 1 cv N. (5.5) and are the standard notations in special relativity. As shown by (5.5), converting factor is closely re- lated to and of special relativity. Substituting photons’ converting factor P LN/ from (4.9) into (5.5) yields: 2 /1 1 cv fL c LPP . (5.6) Solving (5.6) for photon’s speed as a function of frequencyfor wavelength yields:  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1227 2 /1)(cfLcfv P , (5.7a) 2 /1)( P Lcv . (5.7b) Photon’s speed varying with its frequency or wave- length means dispersion. (5.7) is the dispersion equation of photon. The speed of photon decreases with increas- ing frequency. The constant c is not the universal speed of photons, instead, it is the speed limit of photon with frequency approaching zero. This is a modification of special relativity proposed by SQS theory. According to the Gaussian Probability Postulation, space has periodic structure with Planck length P L as spatial period. It is well known that, wave traveling in periodic structure has (5.7) type dispersion. Look at it the other way: Dispersion is caused by the fact that photon interacts with space. For SQS theory, space is a physics substance. The dispersion effect of visible lights is extremely small. It is negligible in most cases. According to (5.7), the speed of a photon with wavelength m 7 10~ deviates from c in the order of 56 10~ . On the other hand, for - ray with extremely high energy, the disper- sion effect is detectable. It serves as a possible way for verification. On May 9th, 2009, NAS A’s Fermi Gamma-Ray Space Telescope recorded a -ray burst from source GRB- 090510 [6-8]. The observed data are given as follows. Low energy -ray Energy: JeVE 154 110602.1101 , Wavelength: m 10 11024.1 . High energy -ray Energy: JeVE910 210967.4101.3 , Wavelength m 17 210999.3 . Distance to -ray source: mlyLO259 10906.6103.7 . Observed time delay (after CBM trigger) for the high energy -ray: stO829.0 . According to (5.7b), the SQS theoretical value for time delay is: 2 1 2 2 2 2 2 1 2 2 2 1 21 21 12 2 /1/1 /1/1 11 PP PP PP TLL c L LL LL c L vv vv L vv Lt . (5.8) The approximation is due to1/,1/ 21 PP LL . Substituting observed data and O LL into (5.8) yields: .10881.1 2 20 2 1 2 2 1s LL c L tPPO T (5.9a) Substituting observed data and OPOOLLNLLL / ˆ into (5.8) yields: s LL c LL N L N c L tPP O PP O T047.0 2212 2 1 1 2 2 22 . (5.9b) O L ˆ is the long path of O L, P LN/ 11 and P LN / 22 are converting factors for 1 and 2 , respectively. The dispersion equation corresponding to (5.9b) according to some other theories is: cfLcLcfvPP/1/1 . (5.10) (5.7) and (5.10) can be expressed as one equation: n P n PcfLcLcfv /1/1 ; 1 n, 2 n. (5.11) In which, 1 n is for (5.10) and 2n is for (5.7). Superficially, the observed data seem to favor the re- sult of (5.9b) and 1 n for (5.11). Actually it is not true. After extensive analysis, the authors of [6-8] concluded: “… even our most conservative limit greatly reduces the parameter space for 1 n models. … makes such theo- ries highly implausible (models with 1n are not sig- nificantly constrained by our results).” The observation data from GRB090510 neither con- firm nor reject dispersion Equation (5.7). In fact, for the distance of lyLO9 103.7~ , to verify (5.7) directly re- quires the high energy -ray burst with energy level around eVE 20 210~, which is a very rare event. Quantum mechanics supports non-locality. For a pair of entangled photons separated by an extremely long distance, their quantum states keep coherent. Measure one photon’s polarization, the other one “instantane- ously” change its polarization accordingly. Einstein called it: “Spooky action at a distance.” SQS theory does not support non-locality. For a pair of entangled photons, SQS theory provides the following understanding and explanation. 1) There is a real physical link between entangled photons. They are linked by the long path. In case of en- tanglement, the long path shows up from hiding with energy extracting from entangled photons. 2) The transmission of information and interaction between two entangled photons does not occur instant- neously, instead, it takes time. Even though the time in- terval is extremely short, but it is not zero. For ordinary photons, the long path is folded to form photon’s wave pattern, the stationary observer only sees the short path with photon speed of c given by (5.7). For a pair of entangled photons, the long path shows up serving as the link. A stationary observer now sees the long path and superluminal speed. The speed of signal transmitting along the long path between two entangled photons is cc L NcNvv P ˆ. (5.12)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1228 For visible light with wavelength m 7 10~ , accord- ing to (5.12), cNcv 28 10~ ˆ. This is why territorial entanglement experimenters found that the interaction seems instantaneous. Actually it is not. The interaction between entangled photons is carried by a signal trans- mitting alone the long path with superluminal speed of (5.12). Recently, Salart et al report their testing results: the speed exceeds c 4 10 [9]. Indeed, it is superluminal. 3) In the entanglement system, two entangled photons and the link connecting them have the same wavelength to keep the system coherent. Entanglement provides a rare opportunity to peep at the long path. It is worthwhile to take a close look. According to (4.6) of Lemma 4.1 based on the Ran- dom Walk Theorem, the relations of photon wave- length , long path wavelength ˆ, converting factor and Planck length P L are: P NL , P LN/ , (5.13a) PP LLNN / ˆ22 . (5.13b) The relations given by (5.13) serve as the guideline to deal with photons entanglement. Postulation 5.1: For a pair of entangled photons, the entanglement process must satisfy energy conservation law and (5.13) relations. Under these conditions, a pair of entangled photons’ original wavelength 0 changes to 0 and the original long path wavelength 0 ˆ chan- ges to 0 ˆˆ according to the following formulas: link NL 2, (5.14a) link NLd 2/, /dNlink , (5.14b) P LN / , (5.14c) PP LLNN / ˆ22 . (5.14d) Explanation: The distance between two entangled photons is d. The link has two tracks, one track for one direction and the other for opposite direction. The total length of two tracks is dL 2. According to SQS theory, photon’s geometrical model is a closed loop with loop length of P L2. In the entanglement system, two entan- gled photons and the link connecting them share a com- mon loop. The link’s double-track structure is necessary to close the loop. P LN / is converting factor for photons with wavelength , /dNlink is the number of wavelengths in one track. Conservation of energy re- quires total energy for entanglement system kept con- stant: hc NN N hchc link link 222 0 , (5.15a) 1 /1 111 0link NN . (5.15b) In which, h is Planck constant. The term on (5.15a) left side is the energy of two photons with original wa- velength 0 . On (5.15a) right side, the first term is the energy of two photons with elongated wavelength 0 , the second term is the energy extracted from two photons to build the link. Substituting link N and from (5.14) into (5.15b) yields the formula to determine the elongated wavelength : d dLP ˆ 1 1 1 1 1 12 0 . (5.16) A 16-digit numerical calculation is used to solve (5.16) for as a function of d for mmm 3 0101 . The resultsare listed in Table 5.1. Table 5.1. Entangled photons wavelength )( d as a function of d for m 3 010 . The data listed in Table 5.1 show some interesting features. 1) Maximum entanglement distance: Solve (5.16) for d: P L d2 0 0 0 0 2 ˆ 2 . (5.17) It shows that, the distance d between two entangled photons increases with increasing wavelength . At the wavelength 0 2 , the distance d. It seems no limitation for d. But that is not the case. Because another requirement is involved: The link as an inte- grated part of entanglement system must have the same wavelength of two photons. Otherwise, there is no co- herency. In this case, 0 2 corresponds to 2/ 0 hfhf . A half (2/12/11 ) of each photon’s energy is extracted out to build the link. According to SQS theory, photon’s model is a closed loop with loop length of P L2, which corresponds to two wavelengths and two long path wavelengths inside the photon to build its wave pattern. The half energy extracted from two en- tangled photons is only sufficient to provide two wave- lengths and two long path wavelengths for the link. Un- der such circumstance, the only way to build the link with infinite length is to infinitively elongate the long  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1229 path wavelength as well as the wavelength in the link, which make them very different from two entangled photons’. It is prohibited by violating coherency re- quirement. So the entanglement distance ddoes have its limit. In fact, only one case satisfies both requirements: energy conservation and quantum coherency. The unique case is ˆ d. According to (5.16), ˆ d yields 000 2 3 ) 2 1 1(5.1 corresponding to 0 3 2hfhf . A third )3/13/21( of each photon’s energy is extracted out to build the link. The total energy is just right to make the original two wavelengths and two long path wavelengths in each photon becoming three wave- lengths and three long path wavelengths for the entan- gled system, in which two are kept for each photon itself and one extracted out to build one track with length ˆ d. In this way, both requirements are satisfied and self-consistent. Hence, there is a maximum distance max dbetween two photons to keep entangled, which is determined by (5.17) with 005.1 2 3 : 000 2 2 5.1 0 0 max ˆ 25.2 4 1 2 ˆ 2 3 ˆˆ 2 0 P L d. (5.18) When max dd , the link breaks down and two en- tangled photons are automatically de-coherent even without any external interference. The data for m 3 010 are listed in the bottom row of Table 5.1. 2) Energy balance: At the maximum distance max dd, 2 3 2 1 1/0 corresponds to 0 3 2hfhf. It indicates that, one third of each photon’s energy is extracted out to build the link. Because the double-track link extracts energy from tow photons, 003 2 ) 3 2 1(2 hfhf , the link has the same energy of each photon’s energy. The link acts like another photon with the some energy and the same wavelength of each entangled photon. In other words, at the maximum entanglement distance max dd, the entanglement system is seemingly made of three photons, in which two are entangled real photons and the third one makes the link to connect them. It serves as evidence that, the link is a physics substance with energy. At shorter distance max dd , the extracted energy gradually increases to build the link and to push the link for expansion. At distance beyond maximum distance, max dd , the entanglement system breaks automatically, because it lacks sufficient energy to main- tain the over expanded link. In this way, both require- ments are satisfied and everything is consistent. The key is to recognize the long path serving as the physics link for entanglement. 3) Entanglement red shift: The wavelength )(d increases with increasing distance d. The red shift is caused by the fact that, a portion of the entangled pho- tons energy is extracted out to build the physics link. It is the energy conservation law in action. According to (5.16), the red shift continuously increases with increas- ing distance. The maximum red shifted wavelength at max dd is. 00max5.1) 2 1 1( . (5.19) The entanglement red shift happens gradually. For a pair of photons separated by distance much shorter than the maximum distance, the tiny red shift is very difficult to detect. As listed in Table 5.1, for a pair of photons with wavelength m 3 10 at distance 6 10dm, the relative red shift is only 16 10~ . For entangled pho- tons with visible light wavelength m 7 10~ , the red shift is many orders of magnitude less than 16 10~ . This is why entanglement experiments with limited dis- tance haven’t found the red shift effect yet. But it is out there. Otherwise, the physics link energy has nowhere to come from. 4) De-coherent blue shift: When a pair of entangled photons is de-coherent, the outcomes depend on the de-coherence location. If the location is right at the mid- dle 2/d, the physics link is broken evenly and each photon gets back equal share of the link energy to resume original wavelength corresponding to a blue shift. Accord- ing to (5.16), the two de-coherent photon’s wavelength is shortened from to 0 causing the blue shift. d d dL dL P P ˆ 2 ˆ 1 2 1 2 2 0 . (5.20) At ˆ max dd , the blue shift is: 3 2 12 11 ˆ 0 d. (5.21) In terms of frequency, the blue shift is: 5.1 2 3 ˆ 0 ˆ 0 d d f f. (5.22) If the de-coherent location is at the close vicinity of one photon, this one does not gain energy to change its  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1230 wavelength and shows no blue shift. The other one gets all energy of the link and has the maximum de-coherent blue shift to the wavelength 0 ' shorter than the original wavelength 0 . According to energy balance of (5.15): dL hchchc NN N hchc P link link 2 01 22 ', or dL dL dL P P P 2 2 2 01 3 1 2 1 ' . For photon at distance d from de-coherent location, its wavelength is shortened to 0 ' : d d dL dL P P ˆ 3 ˆ 1 3 1 ' 2 2 0 . (5.23) For de-coherence at locations between 2/d and d, the blue shift for the far away one is between the two values given by (5.20) and (5.23). At the maximum en- tanglement distance ˆ max dd, according to (5.23), the maximum blue shift in terms of frequency is: 2 11 13 ' ' ˆ 0 max,0 d f f. (5.24) max,0 'f is the blue shifted frequency of the photon at the distance max dd from the de-coherence location. For de-coherence at locations between 2/d and d, the blue shift is between the two values given by (5.22) and (5.24). The de-coherent blue shift happens suddenly with a large frequency increase, which is relatively easy to detect, but the problem is the uncertainty of de-coherent timing. The above analyses show that, entangled photons are connected by a physics link, interactions and information between them are transmitted with superluminal speed ccLNcNvv P)/( ˆ . It is much faster than c but not infinite. From SQS the- ory standpoint, the physics link and the non-infinite su- perluminal speed serve as the foundation for locality. After all, Einstein was right: No spooky action at a dis- tance. Conclusion 5.1: Entanglement has limited distance. The distance between entangled particles cannot be infi- nitely long. Proof: Conclusion 5.1 is not based on Postulation 5.1. It is based on basic principle. Consider the opposite. If a pair of entangled particles is separated by infinite dis- tance, the physics link between them must have nonzero energy density, energy per unite length. Then the total energy of the link equals to infinity. That is impossible, the opposite must be true. QED Explanation: According to Conclusion 5.1, the max- imum entanglement distance max d given by (5.18) serves only as an upper limit. Whether a pair of entan- gled photons can be separated up to max dor not, it also depends on other factors. For entangled photons with very long wavelength, their quantum has very low energy. As the link stretched very long, the energy density be- comes lower than the vacuum quantum noise. The link could be broken causing de-coherence with distance shorter than the maximum distance max d. The other factor is external interferences causing do-coherence, which is well known and understood. According to SQS theory, photons travel along the short path with speed of c with dispersion given by (5.7); the signals between entangled photons transmit along the long path with superluminal speed NcNvv ˆ of (5.12). These are the conclusions derived from converting rules introduced in Section 4. The key concept is the long path, which is defined by (4.12) based the converting factor and originated from the Random Walk Theorem. If the existence of long path is confirmed, so are these conclusions as well as its foundation. If photon’s long-path is confirmed, the non-locality of quantum mechanics must be abandoned. Moreover, long path is based on converting rule. If it is confirmed mean- ing photon does have dispersion. Special relativity should been revised as well. The dispersion equation of (5.7) is not the final version. In Section 26, a generalized dispersion equations will be introduced, in which the Planck length in (5.7) is re- placed by longer characteristic lengths. It makes easier for experimental verifications. In this section, special relativity is revised. For most practical cases, the revision for photon’s speed in vac- uum is extremely small, but its impact are huge such as the introduction of superluminal speed ccLNcNvv P / ˆ . Is it inevitable? Let’s face the reality: Experiment [9] carried out by Salart et al proved that, the speed of signal transmitting between two entangled photons exceeds 10000c. It leaves us only two choices: One is to intro- duce non-infinite superluminal speed as we did in this section; the other is to accept “spooky action at a dis- tance”. Obviously, the second choice is much harder for physicists to swallow. Therefore, the superluminal speed is indeed inevitable. Besides, the superluminal speed introduced in this section is within special relativity framework. The key concept is that, the long path and the superluminal speed are hidden, they only show up in very special cases such as entanglement. The converting factor seemingly has two different meanings: One is from random walk; the other is from  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1231 Lorentz transformation. Actually, they are duality. Such duality is common in physics. One well known example is wave-particle duality. In the meantime, the mechanism of the random-walk versus Lorentz duality is not clear, which is a topic for further work; and so it the mecha- nism of the wave-particle duality. In fact, the long path concept digs into the mechanism of wave-particle duality down to a deeper level: The vacuons’ movement builds the wave-pattern step by step. Section 6: Electron. Define the DS-function as: 1 2 1 5.011 2 122 5.0 i i i i x xx x xx eexSxSxDS . (6.1) According to definition, xDS is symmetrical with respect to 25.0x in region 5.0,0 : xDSxDS 5.0 ; 5.00 x. (6.2) xDS satisfies the periodic condition: xDxDS 5.0 . (6.3) Fig. 6.1 shows xDS versus curve in region 25.0,0. The other part in region 5.0,25.0 is the mir- ror image of this part with respect to 25.0x. -8 -6 -4 -2 0 2 4 6 8 00.025 0.050.0750.10.125 0.150.1750.20.225 0.25 x DS(x)x10^6 Figure 6.1. xDS versus curve in region 25.0,0. Definition 6.1: Define the DS-equation as a member of the S-equation family: 01 2 122 5.0 i i i i x xx x xxeexDS (6.4) In region 5.0,0 , 0xDS has two roots: 125.0 1x, 375.0 2 x. According to (3.11), the path length of probability transportation from 1 x to 2 x via complex x -plane is: PPe LLxxl 5.0212 . (6.5) In (6.5), P L appears as the unit length hidden in (3.11). The reason for the factor 2 in (6.5) has been ex- plained mathematically in Section 3. Physically, accord- ing to the spinor theory proposed by Pauli, electron as Dirac type fermion has two components, which move in the zigzagging path called “zitterbewegung” phenome- non [10]. According to (3.13), the loop length corresponding to path length for 1 x and 2 x is: Pee LlL 2. (6.6) 0 xDS means that the probabilities compensation between excess and deficit is exact. The oscillation be- tween 125.0 1 x and 375.0 2x does not decay, which corresponds to a stable fermion. Electron is the only free standing stable elementary fermion, which nei- ther decays nor oscillates with other particles. It is the most probable candidate for this particle. Assuming the resonant condition for the lowest excita- tion in a closed loop with loop length e L is: cM h LCe ˆ . (6.7) In which, ˆ and C are the mass and Compton wavelength of the particle, respectively. Substituting (6.6) into (6.7) and solving for the mass of this particle yield: .10367498.1 ˆ7kg cL h M P (6.8) It is recognized that P MM ˆ is the Planck mass. According to 2010 PDG data, the mass of electron is: kgMe31 10)45(10938215.9 . (6.9) ˆ is 23 10~ time heavier than e M, which is one of the hierarchy problems in physics. It can be resolved by applying conversion rule. According to (4.10), the con- verting factor for electron is: cLM h L N PeP Ce e , . (6.10) The mass of (6.8) after conversion is: . / / ˆ e Pe P e M cLMh cLh N M M (6.11) The particle is identified as electron. Of cause, this is a trivial case, but it serves as the basic reference for non- trivial cases given later. The reason for miscalculating the mass with 23 10~ times discrepancy is mistakenly using Compton wave- length C in (6.7). In reality, the resonant condition in Planck scale closed loop should be: ,3,2,1; mmL P . (6.12) PCP LN / . (6.13)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1232 N is the converting factor for that particle. PP L is defined as the Planck wavelength. The number m in (6.12) is related to the spin of particle. For electron, 1 m corresponds to spin 2/h. In general, the spin of a parti- cle equals to 2/hm . Odd m corresponds to fermions, and even m corresponds to bosons. m is the first numeri- cal parameter introduced by SQS theory. Electron as a Dirac type fermion, its trajectory has two types of internal cyclic movements, one contributes to its spin and the other one does not. In (6.12), the loop with length P mL is the main loop celled loop-1 and the other loop is loop-2. The dual loop structure of electron corresponds to two components. The dual loop structure is not only for electron but also for other Dirac type fer- mions, which will be discussed in later sections. The basic parameters for electron are listed below. Mass: 231 /)13(510998910.010)45(10938215.9 cMeVkgMe (6.14) Compton wavelength: mcMh eeC 12 1042631022.2)/( . (6.15) Converting factor: 23 10501197.1/ ePe MMN . (6.16) Loop parameters: 125.0 1x, 375.0 2x, 5.0 e l, 1 e L. (6.17) At 125.0 1x, 375.0 2x, )(11)(21xSxS , the probability compensation is exact corresponding to elec- tron as a stable particle. At other locations, the probabil- ity compensation is not exact corresponding to unstable particles. Electron is unique. Its mass servers as basic unit used for calculating other fermion’s mass. The general for- mula to determine )( 12 xx for fermion with mass is: M M xx xx xx xx e e )(4 1 )(4 )(4 )(4 12 12 12 12 . (6.18) The reason for (6.18) is that, loop length )(4 12 xxL is inversely proportional to mass. According to (6.18), the values of 1 x and 2 x of the fermion with mass are: M M xx xe 8 25.0 2 25.0 12 1, (6.19a) 125.0xx . (6.19b) Along the x-axis, according to (2.19) and (2.20), the region between two special points c x and d x is: 3726973550.25001284 ,73026452499871562.0, dc xx (6.20) Inside region dc xx,, both 1 1xS and 1 2 xS , probability transportation for unitarity does not make sense. Rule 6.1: The special points c x sets a mass upper limit Max M for standalone fermions: 2 /97323432.4 25.0 125.0 cGeVM x Me c Max . (6.21) A fermion with mass heavier than Max M cannot stand alone. It must associate with an anti-fermion as compan- ion to form a boson state. Rule 6.2: A particle with 1 x and 2 x inside region dc xx, belong to gauge bosons with spin . Rule 6.3: The region cc xx',' belongs to scalar bo- sons with spin 0. Point c x' is defined as: 5 10552843726973.1 73026452499871562.025.025.0' ccxx . (6.22) The meaning and the effectiveness of these rules will be given in later sections. This section serves as the introduction of electron for SQS theory. It will be followed by later sections in much more details. Section 7: DS-Function on k-Plane as Particles Spectrum In Section 6, the)(xDS as a function of x is defined as: 1 2 122 5.0 i i i i x xx x xx eexDS . (6.1) Taking Fourier transformation to convert )(xDS into )(kDSk on complex k-plane yields: . 4 1 1 2 1 2 1 2 1 5.0 4 5.0 2 22 keee dxeeedxexDSkDS j kjiijk k ikx j xjxjikx k (7.1) Summation index i x in (6.1) is replaced by index j in (7.1) for simplicity. In (7.1), k is the wave-number on complex k-plane. Normalize k with respect to 2 as: 2/kk . (7.2) In terms of k, the )(kDSk function (7.1) becomes: . 4 15.022 2keeekDS j kjikjik k (7.3) kDSk and kDSk are the DS-functions on the complex k-plane and k-plane, respectively. Because and i x in (6.1) are normalized with respect to Planck length P L as numbers. In the Fourier transformation process, xk and kxi are also numbers, so k and k  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1233 are normalized with respect to P L/1 . Definition 7.1: The real part r k and imaginary part i k of k are related to particle’s complex mass as: e i e irM M i M M kikk . (7.4) and i Mare the real mass and the imaginary mass of the particle, respectively. e M is electron’s mass serving as the basic mass unit. Explanation: Definition 7.1 is based on the concept that, k-plane serves as the spectrum of particles. Ac- cording to (7.4), particle’s mass and its decay time t are: er MkM, (7.5a) i eC kc t . (7.5b) In which, e M and eC are the mass and Compton wavelength of electron, respectively. Formula (7.5a) is derived from real part of (7.4). Formula (7.5b) is derived from imaginary part of (7.4) as: cthc hf hc E h cM M M keCieCieCieC e i i . (7.6) i E andi f are imaginary part of energy and frequency of the particle, respectively. Numerical calculations of kDSk found the follow- ing results. 1) 01 kDSk, 1k is a root of 0kDSk. According to (7.5a) and (7.5b): e MM , t. (7.7) 0kDSk at 1k corresponds to electron as a fermion. 2) 0kDSk, 0k is a pole of kDSk. According to (7.5a) and (7.5b): 0M, t. (7.8) 0kDSk, 0k corresponds to photon as a boson. Rule 7.1: In general, the local minimum of kDSk corresponds to a fermion, while the local maximum of kDSk corresponds to a boson. At the local minimum or local maximum of kDSk, k with real value corres- ponds to a stable particle, k with complex value corre- sponds to an unstable particle. Explanation: Rule 7.1 is the generalization of 01 kDSk for electron as a fermion and 0kDSk for photon as a boson. Consider the factor 2 4 1k e in (7.3): iririr kkikkkik keeee 2)()( 222 2 4 1 4 1 4 1 (7.9) In (7.9), for 4 r k and rikk , 22 10 4 122 ir kk e , which drastically suppresses the magnitudes of local minimum and local maximum of kDSk and makes numerical calculation difficult. In (7.3), the -function k does not contribute except for 0 k. Let’s disregard the factor )4/( 2 k e and drop the k term to define the simplified version of kDSk as: j kjikji keekDS 5.022 . (7.10) In terms of the k value at local minimum or local maximum of kDSk, the error caused by simplifica- tion is evaluated in Appendix 3, which is negligible in most cases. The simplified kDSk of (7.10) is taken for technical reasons. It does not mean ignoring the importance of the factor )4/( 2 k e and the term k in the original kDSk of (7.3). In fact, the factor )4/( 2 k e serves as the suppression factor for the original kDSk of (7.3). The suppression factor plays an important role in Section 15 for unifications. In addition, as the suppression factor value decreases to extremely low level, the magnitudes of the local minimums and local maximums are sup- pressed too much and no longer distinguishable from the background noise. This scenario may relate to the early universe with extremely high temperatures. The term k in the original kDSk of (7.3) comes from the uni- tarity term “1” in xDS of (6.1). In Section 9, kDSk is extended based on the extension of the k term. Then the extended version is Fourier transformed back to the complex x -plane, a number of new things show up, which will be discussed in Section 9. kDSk serves as particles spectrum with fermions at local minimum and bosons at local maximum. Particle’s mass and decay time can be calculated from ir kikk according to (7.5). The summation index j in (7.10) must be truncated at integer n. The rules for truncation are: For odd n: 2/)1( 2/)1( )5.0(2 n nj kjikji keekDS , (7.11a) For even n: 2/ )12/( )5.0(2 n nj kjikji keekDS , or  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1234 12/ 2/ )5.0(2 n nj kjikji keekDS . (7.11b) The numerical parameter n assigned to particles is from the mass ratio: r e k M M n p. (7.12) For kDSk serving as spectrum, the number n for truncation in (7.12) must be integer, if the n-parameter in (7.12) is not an integer, multiplication is taken to convert it into an integer for the truncation in (7.11). In (7.12), n and p are the second and third numerical parameters introduced after the first one of m introduced in Section 6. For a particle, the set of three numerical parameters m, n, p plays important roles for particles models and parameters, which will be explained in later sections. As examples, (7.11) is used to calculate the parameters of muon and taon. The results of 16-digit numerical cal- culation are listed in Table 7.1. In which, the reason for taking the values of numerical parameters m, n, p will be given in later sections. Table 7.1. The calculated parameters of muon and taon. *The listed i k value corresponds to particle’s lifetime. **The relative dis- crepancy of mass is calculated with the medium value of 2010-PDG data. For the truncated kDSk of (7.11), the locations of local minimums and local maximums depend on the val- ue of n, which must be given beforehand. In other words, different n values give different mass values for different particles. Fortunately, the n value of a particle can be determined by other means. For instance, quarks’ n is selected from a set of prime numbers and it is tightly correlated to strong interactions. It can be determined within a narrow range and in many cases uniquely. The details will be given in later sections. Look at the spectrum from another perspective, kDSk actually provides a dynamic spectrum for all particles. As the value of n-parameter increases, the loca- tions of local maximums and minimums change accord- ingly corresponding to different particles. It is conceiv- able that, for the full range of n-parameter, kDSk ser- ves as the spectrum of all elementary particles. Whether it includes composite particles or not, which is an inter- esting open issue. Using 16-digit numerical calculations found that, for a given value of r ksuch as 30777692307692.206 r k for muon, there are a series of local minimums located at different values of i k. Table 7.2 shows muon twenty three i k values over a narrow range from 15 1068348.3 i k to 15 1068387.3 i k. there are 6 local minimums corresponding to 6 possible decay times. Table 7.3 shows )(kDSk profile as a function of i k over a broad range of i k alone 30777692307692.206 r k line. As shown in Table 7.3 muon i kvalues from 0 i k to 1 i kdivided into three regions. In Region-1 18 100 i k, average values of )(kDSk as base line keep constant. In Region-2 1418 1010 i k, )(kDSk base line is in the global minimum region. Region-2 is the effective region of muon’s decay activities. In which, 15 10683739.3 i k corresponds to muon’s mean life of s 6 10197034.2 . In Range-3 110 14 i k, )(kDSk base line increases monotonically. Table 7.2. Muon decay data in narrow range*. *The parameters m, n, p and r k are the same as those listed in Table 7.1.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1235 Table 7.3. )( kDSk over broad range for muon*. *The parameters m, n, p and r kare the same as those listed in Table 7.1. **2010-PDG listed muon’s mean life s 6 10000021.0197034.2 . Table 7.4 listed some samples of local minimums dis- tribution at 11 locations, which are used to estimate the average value of the separation between two adjacent local minimums. Table 7.4. Samples of local minimums of )(kDSk for muon at 30777692307692.206 r k*. *The parameters m, n, p and r kare the same as those listed in Table 7.1. A distinctive feature of these theoretical results is that, along a constkr straight line, )(kDSk has a series of local minimums corresponding to a series of possible decay times for a particle such as muon. Does it make sense? From the theoretical viewpoint, it does. According to the first fundamental postulation, SQS is a statistic theory in the first place. A series of )(kDSk local mi- nimums corresponding to a serious of possible decay times should be expected. On the practical side, muon’s mean life having a definitive value s 6 10197034.2 is for large numbers of muons as a group. For an indi- vidual muon, is the statistical average value of many possible decay times, it by no means must decay exactly at t. As shown in Table 7.4, the 121 local minimums are taken as samples from 18 101 i k to 12 101 i k with 21 10as variation step. It shows that, local mini- mums behavior randomly. The average separation be- tween two adjacent minimums is calculated from these samples as 20 20 20 10389.1 10641.1 10909.3 i k, which roughly kept constant over a broad region. These data is used to estimate the total number of local mini- mums in Region-2 between18 1, 101 i k and 14 2, 101 i k as: 5 1,2,10558.2 i ii k kk N. (7.13) Region-2 with decay time from st 7 100933.8 to st 3 100933.8 is the effective region of muon’s decay activity. There are 5 10558.2N local mini- mums in this region, each one corresponds to a possible decay time. The locations of local minimums determine the values of possible decay times. Besides Region-2, there are local minimums in Region-1 and in part of Re- gion-3, which will be discussed later. By counting all local minimums of )(kDSk, in prin- ciple, the theoretical mean life of muon can be calcu- lated by extensive number crunching. But it requires a tailor made program. In the meantime, let’s take a rough estimate. According to (7.5b), the separation tof two adja- cent possible decay times and corresponding decay time’s density (number of possible decays per unit time) N are: ck k ck t i ieC i eC 2 . (7.14a) ieC ik ck t N 2 1. (7.14b) In the i k domain, the local minimums have roughly even distribution as shown in Table 7.4. In the time do- main, because of the inverse relation 2 /1i kt of (7.14a), the local minimum of )(kDSk in the i k do- main corresponds to the temporal response as the local maximum in the time domain. As shown by (7.14a), the local maximums in time domain are unevenly distributed caused by the 2 i k factor in denominator of t.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1236 The effective Region-2 is divided into four sub-re- gions: Region-2a: 17181010i k with center at 18 105 i k; Region-2b: 1617 1010 i k with center at 17 105 i k; Region-2c: 1516 1010 i k with center at 16 105 i k; Region-2d: 1415 1010 i k with center at 15 105 i k. The values of i k, t, t, N and Nt at center of each sub-regions calculated according to (7.14) and Table 7.4 are listed in Table 7.5. Table 7.5. Parameters in the center of four sub-regions. The values at the center of each sub-region are treated as the average values for that sub-region. Take d ajjj NN/as the probability for muon decay in ),,,( dcbajj sub-region, muon’s mean life is roughly estimated as: s N tN td aj j j d aj j6 10838.1 . (7.15) The value of t is 83.7% of muon’s measured mean life s 6 10197034.2 , which is in the ballpark. Since only the activity in Region-2 is counted, the 16.3% discrepancy is understandable. The ballpark agreement shows that, the spectrum does contain the information of mean lifetime in the muon’s case and Region-2 is the effective region. The rough estimation is based on the assumption that, Region-2 is the effective region for muon’ decay activity. The effects of other two regions are not taken into ac- count, which need justification. The local minimums are not restricted in Region-2, they extended to Region-1 from 19 10~ i k to 23 10~ i k. According to (7.14b), the decay time density N is proportional to 2 i k, in Region-1, N value decreases rapidly as i k value decreasing. For instance, the N value at the boundary of Region-1 and Region-2, 18 10 i k, is roughly less than 7 10 of the N value at the center of Region-2 where muon’s mean life is close by. In other words, muon rarely decays in Region-1 with extremely low probability. Prediction 7.1: The probability of muon decay time longer than st3 100933.8 corresponding to 18 101 i kis less than 7 10 of the probability of muon decay at st 6 10197034.2 corresponding to 15 10684.3 i k. Explanation: According (7.14b), N is proportional to 2 i k. The ratio of decay probabilities at 18 101 i k and at 15 10684.3 i k is estimated as: 78 2 15 18 1010368.7 10684.3 101 . (7.16) For Region-1 with 18 101 i k, the ratio of decay possibilities is much less than 8 10368.7 , which can be estimated the same way. So the rough estimation of t disregarding Region-1 is justified. The local minimums are also extended in Region-3 with rapidly increasing density. However, it does not mean that muon decays more frequently in Region-3. In fact, muon decays rarely in Region-3, which needs ex- planation. )(kDSk serves as spectrum with fermion at local minimum. In the spectrum, the tendency for muon as a fermion to reach minimum value of )(kDSk actu- ally is in two senses, locally and globally. The former was considered, now it’s the time to consider the latter. In Region-1 and Region-2, as shown in Table 7.3, the base line of )(kDSk is almost flat with minor variations. The vast numbers of local minimums with different den- sities compete for the possible decay time. The base line of )(kDSk increases monotonically in Region-3 and the bottom values of local minimums increase with it. In most part of Region-3, the bottom values of local mini- mums are higher than the base line level in Region-1 and Region-2. The turning point is probably at the vicinity of 13 101 i kcorresponding to st 8 100933.8 . muons have very low probability for decay times shorter than st 8 100933.8 despite the fact that the values of N are many orders of magnitudes larger than those in Region-2. The abrupt drop of decay probability in Re- gion-3 is caused by the local minimums disqualified in the global sense, because their bottom values are higher than the base line in Region-1 and Region-2. So the rough estimation of t disregarding Region-3 for muon is also justified. Moreover, according to (7.14a), the time separation t is proportional to the inverse of 2 i k. In Region-3, as i k increases, t decreases rapidly. At certain point, the extremely crowded local maximums in time domain are overlapped and no longer distinguishable. Prediction 7.2: Muon has zero probability to decay at times shorter than st 13 min 102 . Explanation: The disappearance of local maximums in Region-3 happens at the point that, separation t becomes shorter than the width of the response in time domain for muon. At that point, individual response in time domain is no longer distinguishable. Muon’s decay is caused by weak interaction mediated by gauge bosons W or 0 with mean lifetime of s ZW 25 ,102 . The  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1237 muon’s decaying process must complete before its me- diators’ decay, which roughly determines the width of individual response in time domain. The criterion is ZW t, . According to (7.5b) and (7.14a), the min tfor muon is: s kckc t k tc ckc t i ZWeC i eC ieC eC i eC 13 , min 10075.2 (7.17) In which 20 10909.3 i k is the medium average value cited from Table 7.4. As another example, electron’s )(kDSk profile over broad range is sown in Table 7.6. The reason for taking such values of numerical parameters m, n, p for electron will be given in later sections. Table 7.6. )( kDSk over broad range for electron at 1 r k with m = 2, n = 1, p = 1. The distinctive features of electron’s )(kDSk profile over broad range are the disappearance of Region-2 and Region-1 becoming global minimum region with only one local minimum of 0)0( k DS at 0 i k corre- sponding to t. It is consistent with the fact that electron is stable. This is an important check point to verify that, the rough estimation of mean life based on the global minimum concept for muon is correct. It also increases the credibility of )( kDSk serving as particles spectrum with information of decay times and in some way related to mean life. But nuon and electron are just two examples, which are by no means sufficient to draw a conclusion. The real correlation between )( kDSk as spectrum and particle’s mean life is still an open issue. More works along this line are needed. As illustrated in this section, )(kDSk as a member of the S-equation family has rich physics meanings. In gen- eral, )(kDSk serving as particle mass spectrum is con- ditional. It subjects to a prior knowledge of numerical parameters. Even though, it does provide useful informa- tion. More importantly, )(kDSk serves as the base for an extended version, which reveals more physics signifi- cance. Details will be given in later sections. In this section, muon and taon are used as examples for )(kDSk serving as particles spectrum on the com- plex k-plane. More details of muon and taon will be giv- en in later sections. Section 8: Electron Torus Model and Trajectories As mentioned in Section 6, electron has two-loop struc- ture. Loop-1 is the primary loop with loop length1 L. Loop-2 perpendicular to loop-1 is the secondary loop with loop length2 L. Loop-2 center rotates around loop-1 circumference to forms a torus surface. According to SQS theory, all Dirac type fermions’ models are based on torus. Torus is a genus-1 topological manifold with one center hole and four tiny holes 1 h, h, h, 2 h corresponding to four branch points on Riemann surfaces described in Section 3. To begin with, torus as a topological manifold has neither definitive shape nor determined dimensions. The four tiny holes 1 h, h, h, 2 h without fixed loca- tion can move around on torus surface. To represent a particle such as electron, the torus model must have de- finitive shape and determined dimensions, and the loca- tion of four tiny holes must be fixed as well. To deter- mine these geometrical parameters, additional informa- tion is needed, which comes from SQS theory first prin- ciple. Fig. 8.1 shows the torus serving as electron model. There are three circles on x-y cross section shown in Fig. 8.1a. The two solid line circles represent the inner and outer edges of torus, and the dot-dashed line circle represents loop-1 and the trace of rotating loop-2 center. In Figure 8.1b, the right and left circles shown torus two cross sections are cut from line GO1 and line HO1on x-y plane, respectively. According to SQS theory, a set of three numerical pa- rameters, m, n, p is assigned to each fermion defined as: 1 2 L L m n, (8.1a) e M M n p (8.1b)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1238 In which, and e M are the mass of the fermion and electron, respectively. For electron, its original m, n, p parameters are se- lected as: 2m, 1n, 1p. (8.2) Substituting (8.2) into (8.1) yields: 2 1 1 2 L L, (8.3a) 1 1 e M M. (8.3b) The torus surface is divided into two halves as shown in Figure 8.1b. The outer half has positive curvature and the inner half has negative curvature. According to S- equation of (3.20), unitarity requires: 0112 )( N Nj xjx exS . (8.4) In (8.4), the original summation index i x is replaced by for simplicity. The lower and upper summation limits are truncated at for numerical calcula- tion. A sufficient large is selected for 1 xS to converge. As discussed in Section 6, the two points on real r x-axis of Figure 3.4 representing electron are: 125.0 1x, and 375.0 2x. (8.5) Substituting (8.5) into (8.4) and solving for )(x yields: 200378771029244.3)125.0( 1 x; (8.6a) 543918645924982.2)375.0( 2 x. (8.6b) )(1 x and )(2 x serve as the messengers to transfer information from S-equation to torus model. )(1 x corresponds to negative curvature on the inner half of torus; and )( 2 x corresponds to positive curvature on the outer half of torus. The distance between two loops’ centers is d, which is the radius of loop-1. For electron, loop-1 circumfer- ence equals to one Planck wavelength, 1 1 PP LL , which corresponds to 2/12/ 1 Ld . For conven- ience, let’s set 1d as the reference length for other lengths on the torus models, and consider its real value later. According to (8.3a) and 1 d, the radius of loop-2 for electron is determined as: 5.0 2 1 1 2 2 dd L L a. (8.7) The two dimensions of torus as electron model are de- termined as 1d, 5.0 2a. The next step is to fix the locations for four tiny holes 1 h, h, h, 2 h shown in Fig. 3.5b. Figure 8.1. Electron torus model: (a) x-y cross section; (b) Right is cross section along line GO1, left is cross section along line HO1. In fact, the electron torus model is shared with its an- ti-particle, the positron. For the four tiny holes 1 h, h, h, 2 h, two of them belong to electron and the other two belong to positron. The values of )(2 x and )( 1 x determine the locations of two characteristic points ,B for electron. 543918645924982.2)( 2 x of (8.6b) corre- sponds to the torus outer half with positive curvature like a sphere. On the GO1 cross section at the right of Fig 8.1b, the location of point 2 A at 22 ,ZzXx with origin at cross section center 2 O is determined by )( 2 x according to the following formulas: 0 )(2 cossin 22 2 2 2 2 2 2 xZ dttbta , 22 ab , (8.8a) 2 2 2 cos a X , (8.8b) 01 2 2 2 2 2 2 b Z a X, 22 ab. (8.8c) As shown in Fig. 8.1b, point 2 A and two loops’ cen- ters 1 O, 2 O form a triangle 212OOA. The three inner angles 2 , 2 , 2 of triangle 212 OOA are deter- mined by:  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1239 2 2 2 tan X Z , 22 180 , (8.9a) 2 2 2 tan Xd Z , (8.9b) 222 . (8.9c) On x-y plane shown by Fig. 8.1a, the location of point G at 33,YyXx with origin at 1 O is determined by angle 3 from )(2 x according to following for- mulas: 0 )(sin)( )( 232 32 xad ad , (8.10a) 2 2 2 3 2 3)( adYX . (8.10b) The three inner angles 3 , 3 ,3 of triangle 21OGO are determined by: dX Y 3 3 3 tan , 33 180 , (8.11a) 3 3 3 tan X Y , (8.11b) 333 . (8.11c) 44200373.87710292)(1 x of (8.6a) corresponds to the inner half of torus with negative curvature like a saddle surface with sinusoidal variation. The parameters of saddle surface are determined by )( 1 x according to following formulas: 0 2 2cos21 1 2 0 2 x dttAm, (8.12a) 12 cossin 2 0 2 1 2 1 dttbta A A m , 11 ab . (8.12b) m A and are the amplitudes of saddle sinusoidal variation on circles with radius 1 and radius 1 a, re- spectively. The locations of points 1 B and point D are determined by the following simultaneous equations: 0 22 1 2 RaAR, 22 1aadR , (8.13a) 01 2 2 1 2 2 2 b b a Aa , 11ab , 22 ab . (8.13b) Equation (8.13a) represents a circle with radius R centered at 1 O. The location of point D at 1 ),(ayARx with origin at 1 Ois determined. Equation (8.13b) represents the circle with radius 2 a centered at 2 'O on the HO1 cross section in Fig. 8.1b. The location of point 1 B at 12 ),(byAax with origin at 2 'O is determined. In the HO1 cross section in Fig. 8.1b, the three inner angles 1 , 1 , 1 of triangle 21 'DOB and angle 1 are determined by: Aa b 2 1 1 tan , (8.14a) b1 1 tan , (8.14b) 111 180 , (8.14c) R b 1 1 tan . (8.14d) On the x-y plane shown by Fig. 8.1a, The three inner angles 0 , 0 , 0 of triangle 2 'DEO and angle 0 are determined by: A a1 0 tan , 00 180 , (8.15a) Aa a 2 1 0 tan , (8.15b) 000 , (8.15c) R a 1 0 tan . (8.15d) According to the torus model and two characteristic points A, B determined by )( 1 x and )( 2 x from the S-equation, electron parameters calculated with the above formulas are listed in Table 8.1. Table 8.1. Parameters for electron torus model*. *All data are from 16-digit numerical calculations, only 8-digit after the decimal point is presented. **The reduced numerical parameters are the original numerical parameters divided by m. In Table 8.1, notice that: 24442009.24 32 , (8.16a) 45987086.28 23222 , (8.16b) 257547.55 10 , (8.16c) 88107155.29 01 . (8.16d)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1240 Let’s consider the meanings of (8.16a). 2 is the an- gle at the center of loop-2 between line GO2 and line 22AO as shown in Fig.8.1b, which serves as the initial phase angles of cyclic movements along loop-2. 3 is the angle at the center of loop-1 between the x-axis and line GO1on x-y cross section shown in Fig. 8.1a, which serves as the initial phase angles of cyclic movements along loop-1. 32 means that the two cyclic move- ments around loop-2 and loop-1 are synchronized in phase. (8.16b) indicates that the phase angles’ differences of 23 and 22 both equal to 45987086.28 2 , which is close to the Weinberg angle W . This is the first hint that, the characteristic points such as point and the triangle 212 OOA have something to do with par- ticle’s interaction parameters. (8.16c) and (8.16d) indi- cate that, the some types of synchronizations as (8.16a) and (8.16b) hold between angles 0 and 1 as well as between 1 and 0 in the inner half of torus shown by Fig. 8.1a and Fig. 8.1b on left side. These types of synchronizations are interpreted as the geometrical foundation of electron’s stability. It is the first conclusion drawn from electron’s torus model. The torus model represents electron, it must have all electron parameters expressed in geometrical terms. This is the job a model supposed to do. But the torus has only two geometrical parameters dand 2 a to determine its shape and size, which are by no means sufficient to rep- resent all parameters. )( 1 x and )(2 x come to help. They serve as the messengers to transfer information from S-equation to torus model to define the locations of characteristic points and the triangles associated with them. In this way, the torus model with defined charac- teristic points and triangles is capable to represent all parameters of electron. The details will be given later. For the standard model, particle is represented by a point. A point carries no information except its location and movement. That is why twenty some parameters are handpicked and put in for standard model. For SQS the- ory, parameters are derived from the first principle and represented by geometrical model. In which, two mes- sengers )( 1 x , )(2 x , the characteristic points and triangles play pivotal roles. The torus model provides a curved surface to support the trajectory of electron’s internal movement. Electron internal movement includes three types: (1) cyclic movement along loop-1; (2) cyclic movement along loop-2; (3) sinusoidal oscillation along trajectory. Fig. 8.2a and Fig. 8.2b show the projections of electron’s tra- jectory on x-y plane and x-z plane, respectively. On x-y plane shown in Fig. 8.2a, the top trajectory is for electron, and the bottom trajectory is for positron. Because these two trajectories are symmetrical, to explain the one for electron is sufficient to understand the other. Figure 8.2. Electron and positron trajectories on torus mo- del: (a) Projection on x-y plane; (b) Projection on x-z plane. The trajectory is a closed loop. It can start anywhere on the loop as long as it comes back to close the loop. Let’s look at trajectory starting at point A on torus out- er half bottom surface represented by the short dashed curve shown in Fig. 8.2(a). It passes through the torus outer edge and goes to the upper surface shown by solid curve. It passes the top center line getting into the inner half and reaches point B on torus inner half top surface to complete its first half journey. The second half journey starts from point . At the torus inner edge, it goes back to the bottom surface shown by dashed curve. It passes through the bottom center line and comes back to point A to complete a full cycle. The trajectory repeats its journey again and again. The x-z plane projection of the trajectory is shown in Fig. 8.2(b). The trajectory shown in Fig. 8.2 is a rough sketch. Its exact shape is determined by two geodesics on the torus surface. One from point A to point ; the other from point back to point A to close the trajectory loop. The characteristic points A and not only carry the  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1241 parameters information to define the triangles but also serve as the terminals for the two geodesics to form the trajectory. Notice that, in Figure 8.1 and Figure 8.2(a), the three points , 1 O, are not aligned. The difference be- tween two angles 0 and 3 is: 01312691.13942.2444200257547.55 30 .(8.17) is the angle deviated from 180 representing a perfect alignment of three points , 1 O, . It is impor- tant to point out that, and are not fixed points. Instead, they define two circles, circle-A and circle-B, with radius AO1 and BO1, respectively. The trajectory may start at a point on circle-A halfway through a point at circle-B and comes back to point A. The trajectory is legitimate as long as it kept the same angle of BAO1 : 98687309.166180 1 BAO. (8. 18) There are many trajectories on torus surface with the same angle BAO1 given by (8.18), all of them contain the same information carried by )(1 x and )( 2 x . These trajectories spread over torus entire surface. As shown in later sections, trajectories are discrete in nature and the number of trajectories is countable, which form a set of discrete trajectories on torus surface. At a given time, electron is represented by a trajectory. As time passing by, it jumps to other trajectories. The scenario is dynamic and stochastic. Physically, jumping trajectories on the same torus surface corresponds to emitting and absorbing a virtual photon by the electron. For the x-y projection shown in Figure 8.2a, the tra- jectory on the bottom for positron goes through two cha- racteristic points 'A and 'B with anti-clockwise direc- tion. As shown in Figure 8.2b, the x-z projections of two trajectories are coincided with opposite directions: an- ti-clockwise for electron and clockwise for positron. In essence, the S-equation determine the value of )( 1 x and )(2 x from 1 x and 2 x; )( 2 x and )( 1 x determine the location of characteristic points A and on torus model; Points , and two geodesics be- tween them define a trajectory on torus surface; Rotating points and defines circle-A and circle-B along with a set of discrete trajectories on torus model. The sinusoidal oscillation along trajectory path is rep- resented by a term in two ad hoc equations. Figure 8.3 shows two orthogonal differential vectors d and da 2 ': 2 2 2 2 2' ' 'a ad da d , (8.19a) cos'2 ad . (8.19b) The oscillation on trajectory is represented by a sinu- soidal term: sin'2 a, (8.20a) 1 2 22 2 L L M M m n n p m p e . (8.20b) Figure 8.3. Differential vectors on torus model. In which, and e Mare the mass of the particle and electron, respectively. For electron1// npMM e, 2/1// 12 mnLL and 1 , (8.20a) becomes: )sin(')sin('22 aa . (8.20c) As shown by (8.20), the sinusoidal oscillation term )sin(' 2 a is related to mass, it is called the “mass term”. Adding the mass term of (8.20c) to the numerator on right side of (8.19a) yields: 2 2 2 2 2 2' sin'' 'a aad da d , (8.21a) or daadd sin'' 2 2 2 2 . (8.21b) According to Figure 8.3 and (8.21b), the combined differential vector length is: daadaddadl 2 2 2 2 22 2 22 2sin'''' . (8.22) Take the integral of (8.22) from 0 to 2: 2 0 2 2 2 2 22 2 2 0 sin''' daadadlL . (8.23) According to (8.21b) and (8.19b), the differential an- gle along the -direction is: d ad aad d aad dcos' sin''sin'' 2 2 2 2 2 2 2 2 2 . (8.24) Take the integral of d from 0 to 2: 2 02 2 2 2 2 2 0cos' sin'' d ad aad d. (8.25) Definition 8.1: Define the Angle Tilt (AT) equation and the Phase Sync (PS) equation as:  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1242 1) AT-equation: 2 02 2 2 2 2 22 20 '2 sin''' 2 1 a d daada d; (8.26a) 2) PS-equation: 2 02 2 2 2 2 01 cos' sin'' 2 1d ad aad . (8.26b) In (8.26a), the factor 2 in the denominator of second term comes from Section 3: 2 )120cos( 1 )cos( 1 . (3.12) 120 is the separation angle of three lines on the complex plane shown in Figure 3.2. For 1d, solving the two equations of (8.26) for 2 'a yields: 222154918171173.0'2a. (8.27) AT and PS are two independent equations with one un- known 2 'a. Both equations are satisfied simultaneously with the same solution 222154918171173.0'2a. It indicates that they are self consistent and mean something. 22 'aa means that, the torus original circular cross section is distorted. To keep loop lengths ratio mnLL // 12 unchanged, the original cross section pa- rameters, 2 a and 22 ab must be changed accord- ingly, which makes the torus cross section elliptical. Definition 8.2: The Modification Factors (MF) of the f-modification are defined as: 2 2 ' a a fa, (8.28a) 2 2 ' b b fb. (8.28b) For electron, 5.0 2a, 5.0 2 b, 222154918171173.0'2a, and 2 'b is determined by: dttbtadttbta 2 0 22 2 22 2 2 0 22 2 22 2)(cos)(sin)(cos)'()(sin)'( , (8.29a) 197555081164600.0' 2b. (8.29b) Explanation: In essence, the f-modification is intro- duced to satisfy (8.26) and to keep loop-2 length2 L un- changed as shown by (8.29a). It is important to keep loop length ratio mnLL // 12 unchanged, because it is re- lated to interactions. According to Definition 8.2, the modification factors of electron are calculated as: 4443039836342346.0 ' 2 2 a a fa, (8.30a) 39510162329200.1 ' 2 2 b b fb. (8.30b) After the f-modification, the geometrical parameters are changed accordingly. The rules are to keep the initial phase angles unchanged as the originals: 22 ' , (8.31a) 33 ' , (8.31b) 11 ' , (8.31c) 00 ' . (8.31d) The other geometrical parameters of the modified to- rus model change accordingly. The rules are: (1) To keep the initial phase angles given by (8.31) unchanged; (2) The torus cross section becomes elliptical with 2 'a and 2 'b given by (8.27) and (8.29b), respectively. The rest is from geometry. The modified point 2 'A and triangle 212 'OOA re- lated angles are determined by: 222 180'180' , (8.32a) 2 2 2' ' 'tan Xd Z , 222''' , (8.32b) 2 2 2 2 2 2 2'tan'/1'/1 1 ' ba X , (8.32c) 222 'tan'' XZ . (8.32d) The modified point 'G and triangle 21 'OOG related angles are determined by: dX Y 3 3 3' ' 'tan , 33'180' , (8.33a) 33 ' , 333 ''' , (8.33b) 3 2 2 3'tan1 ' ' ad X, (8.33c) 333 'tan'' XY . (8.33d) The modified point 1 'B at 11',' ZyXx with origin at 2 'O and triangle 21 ''' ODB related angles are deter- mined by: 12 1 1'' ' 'tan Xa Z , (8.34a) 11 ' , 111''180' , (8.34b) 1 1 1' ' 'tan Xd Z , (8.34c) 1 2 2 2 2 2 1'tan'/1'/1 1 ' ba X , (8.34d) 111 'tan'' XZ . (8.34e) The modified point 'D at 00',' YyXx with ori- gin at 1 O and triangle 2 ''' OED related angles are de- termined by:  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1243 0 0 0' ' 'tanXd Y , (8.35a) 0 0 0' ' 'tan XR Y , 00 '180' , (8.35b) 000 ''' , (8.35c) 00 ' , (8.35d) 0 2 0'tan1 ' R X, (8.35e) 000 'tan'' XY . (8.35f) The modified data for electron are listed in Table 8.2. In which the effective parameters after f-modification are marked with the ‘ sign. Table 8.2. Modified parameters for electron torus model*. *All data are from 16-digit numerical calculations, only 8-digit after the decimal point is presented. **The reduced numerical parameters are the original numerical parameters divided by m. After modification, despite the change of 428.4794845''2 W from original 628.4598708 2 W, as shown in Table 8.2, three out of four synchronizations still hold with one slightly off: 24442009.24''32 , (8.36a) 47948454.28''''' 23222 , (8.36b) 257547.55'' 10 , (8.36c) 44799569.30'06432177.30' 0 0 1 . (8.36d) It indicates that electron stability is persistent and ro- bust. To understand the meaning of f-modification, in the AT-equation, let’s set the mass term 0sin'2 a to see its effect, (8.26a) and (8.28) become: 2 02 2 022 2 2 2 22 20 '2 1 1 '22'2 '' 2 1 aa d d d d a d dada d , 22 5.05.0' ada , 22 5.0' bb ; 1 baff. (8.37) 1 ba ff means no f-modification. It clearly shows that the effect of f-modification is caused by the added mass term of sin'2 a, which represents the mass ef- fect. In the standard model, particle acquires mass through symmetry broken. Likewise, in SQS theory, the mass term of sin'2 a breaks the 3-fold symmetry with 120 on the complex plane. This analogue plus the simultaneous satisfaction of two independent equations with the same solution 2 'a give some legitimacy to AT-equation and PS-equation despite their ad hoc nature. Let’s look at the geometrical meaning of the f-modi- fication. As shown in Section 3, the angle separates three lines on complex plane is: 120 3 2 . (3.8d) The f-modification causes the angle having a slight tilt from to ' : a f a ad 4443159836342346.0 )120cos( ' ' arctan180cos cos 'cos 2 2 2 2 (8.38a) 224600855504.119 ' ' arctan180' 2 2 2 2 a ad ,(8.38b) 785399144495.0' . (8.38c) is the tilting angle deviated from 120 . It indi- cates that, original 120 3-fold symmetry is slightly broken by tilting angle for electron having mass. After f-modification, AT-equation and PS -equation are satisfied simultaneously. It indicates that, the two cyclic movements of two loops and the sinusoidal oscillation along the trajectory are synchronized perfectly for elec- tron as a stable particle. Numerical calculations found that, AT-equation of (8.26a) has only one root 2 'a given by (8.27) with the a f value given by (8.30a). On the other hand, PS-equation of (8.26b) has a series of roots. Start from 4443039836342346.0 a f, varying its value with 16 10 steps calculate the values of )( a f as a function of a f: 2 02 2 2 2 2 1 cos' sin'' 2 1 )( d ad aad fa,  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1244 aa fafa 5.0'22 . (8.39) A sample of numerical calculated results are listed in Table 8.3. In Table 8.3, 0 0 means phase precisely synchronized, and 0 0 means off sync. The results of Table 8.3 are interpreted as that, electron’s torus model is dynamic and stochastic in nature. It changes its loop-2 tilting angle constantly corresponding to different a f, b f and 2 'a, 2 'b values representing different torus surfaces. Electron’s trajectory changes accordingly. The tilting angle changes discretely, so does the trajectory, which means that trajectories are quan- tized. At a given time, electron is represented by a tra- jectory on a torus surface. As time passing by, it jumps to other trajectories on another torus surface. It is a stochas- tic scenario of jumping trajectories on different torus surfaces. Physically, it corresponds to interactions such as emitting and absorbing a photon. As mentioned pre- viously, jumping trajectories on the same torus surface corresponds to emitting and absorbing a virtual photon by electron. Table 8.3. Some roots of equation (8.26b). *Note: )( a f and )4443039836342346.0( 00 a f . As shown in Table 8.3, PS-equation has 23 roots in re- gion 15 1050 a f corresponding root density of: 15 15 106.4 105 23 D. (8.40) The root density D roughly kept constant in the effec- tive region 1, a f. For orders of magnitude estimation, the total number of roots for PS-equation in region 1, a f is: 1315 1984.0 10544.7106.49836.01 DfN a. (8.41) As mentioned previously, there is a set of discrete tra- jectories on the same surface of a torus surface. Now on top of it, there is another set of discrete trajectories on 13 10544.7 N different torus surfaces caused by f-modifications. At a given time, the real trajectory is the one randomly chosen from these two sets of discrete tra- jectories. In other words, electron trajectories are dy- namic and stochastic in nature, which spread like clouds around the torus surfaces. The term “electron clouds” was used to describe electron’s behavior around a nu- cleon according to quantum mechanics wave function. Here the clouds appear in a deeper level, which should not be a surprise. As shown in Figure 3.4 of Section 3, the loop on the complex plane connecting 1 x and 2 x has many dif- ferent paths with the same loop length. That scenario is consistent with the different trajectories with the same length on different torus surfaces and different locations. It shows the consistency of the theory. In Table 8.3, the step ofa f variations and step of 2 'a and 2 'b variations are in the order of 16 10to 15 10 Planck length corresponding to 51 10 to 50 10 meters. The step of torus surface variations is extremely tiny. As the torus’ loop-2 tilts, the electron’s trajectory jumps from one torus surface to the other. In fact, this dynamic picture is expected from quantum theory. The three types of movement for electron described in this section all are deterministic in nature. Without trajectory jumping, the deterministic movements are contradictory to the uncer- tainty principle. Moreover, the Gaussian Probability Postulation of SQS theory is stochastic in the first place. The trajectory jumping is ultimately originated from the Gaussian probability assigned to discrete points in space. The 0 fluctuating data listed in Table 8.3 is an indication of the stochastic nature of SQS theory, even though the PS-equation of (8.26b) is not derived from the first principle. Figure 8.4 shows the right side of Figure 8.1b in de- tails. Points , ,2 O define a right triangle 2 AFO , which contains two additional right triangles: F and 2 FKO . The triangle 2 AFO is indentified as the Gla- show-Weinberg-Salam triangle, GWS-triangle for short. In the 1 c unit system, the sides of GWS-triangle are related to electroweak coupling parameters: eFK ,gAF ,' 2gFO,22 2'ggAO . (8.42) e, and , 'g are electric charge and two weak cou- pling constants, respectively. The following formulas are from geometry: 22 ' ' sin gg g g e W , (8.43a) ' cos g e W . (8.43b) Combining (8.43a) and (8.43b) yields: 22' cossin gg e WW . (8.44)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1245 Formula (8.44) is used extensively in later sections as the criterion to construct the model for other fermions. Figure 8.4. Glashow-Weinberg-Salam triangle. According to 16-digit numerical calculation, the original and effective Weinberg angles of electron are: Original: 64113828.4598708 o2 We , (8.45a) Effective: 3780828.4794845'2 WeM . (8.45b) One of SQS theory final goals is that, all parameters of an elementary particle should be derived from its model. To identify the GWS-triangle with Weinberg angle in the torus model is a step toward the final goal. Some other characteristic triangles will be introduced in later sec- tions. From Einstein’s unified field theory viewpoint, every- thing including all elementary particles and interactions are originated from geometry. For SQS theory, the model plays that role. Torus as a genus-1 topological manifold has one center hole, its shape and size are arbitrary to begin with. In order for the torus model to represent a particle with its parameters, additional steps must be taken. Take electron as an example. As the first step, the shape and dimensions of torus are determined by loop-2 to loop-1 length ratio of 2/1// 12 mnLL and dL 2 1. The second step is to fix the locations of cha- racteristic points and B on torus surface by utiliz- ing the curvature information carried by )( 2 x and )(1 x from the S-equation. In this way, the triangles such as the GWS-triangle are determined and the pa- rameters are determined as well. The process shows ma- thematics at work. The mathematics at work viewpoint will be enhanced further in later sections. Recall in Section 3, the four tiny holes 1 h, h, h, 2 hserved as four branch points 1, , , 2 on the Riemann surface. Moreover, the way Penrose built the torus is to glue a pair of slits on two sheets of Riemann surface together [2]. In fact, there are infinite sheets of Riemann surface corresponding to a general form of (3.22): 2 0 in ez , 2 3 2 1 ni ez , 2 3 4 2 2ni ez , 3,2,1,0n. (8.46) These sheets can be combined into pairs to build many genus-1 torus surfaces, which serve as the topological base of many torus surfaces with slightly different pa- rameters 2 'a and 2 'b derived from PS-equation as discussed earlier. After all, there are enormous numbers of torus surfaces provided by (8.46) for trajectory to jump on. This argument gives more credit to the ad hoc PS-equation. Moreover, the torus with four tiny holes shown in Fig. 8.5a is topologically equivalent to a pair of trousers with a large hole in their waistband shown in Figure 8.5b. The four tiny holes on torus with their edge extended out- wards form four tubes as the four ports. According to [11], if the loops around trousers shrink to points, the trousers with four ports degenerate to a Feynman dia- gram with one closed loop and four branch lines shown in Figure 8.5c. Feynman diagram is correlated to interac- tions. Therefore, the triangles such as GWS-triangle de- fined by characteristic points carry interactions informa- tion are natural. Figure 8.5(a). Torus with four tiny holes; (b) Four tiny holes’ edge extended into four tubes; (c) De generated into a Feynman diagram with one loop. In summary, electron’s torus model is built on three bases: 1) Loop lengths ratio 2/1// 12 mnLL and masses  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1246 ratio 1/1// npMM e are determined by a set of three numerical parameters, 2m, 1n, 1p. 2) The 3-dimensional Gaussian probability’s 0 , 1 , 2 plus are identified as four branch points on the Riemann surface, which are topologically equivalent to four tiny holes on torus. 3) The four tiny holes on torus correspond to charac- teristic points A, Band ' , ' . Their locations are fixed according to the information carried by )( 1 x and )( 2 x , which are the solutions of the 1-dimensional S-equation. In the three bases, No.2 and No.3 are originated from SQS theory first fundamental postulation, the Gaussian Probability Postulation. No.1 is a set of three numerical parameters. It is related to the second fundamental pos- tulation of SQS theory, which will be introduced in later section. These are the only things needed to build the model for a particle such as electron to carry all its pa- rameters. It shows the power and the simplicity of the first principle of SQS theory. The electron torus model introduced in this section serves as the basic building block. It is not the final ver- sion. The details will be given in Section 12. Section 9. Complex x -Plane and Fine Structure Constant kDSk of (7.1) is the Fourier transformation of xDS of (6.1): . 4 15.0 4 2 keeekDS j kjiijk k k (7.1) kDSk serves as particles spectrum. The local mini- mums of kDSk correspond to fermions and the local maximums of kDSk correspond to bosons. In this sec- tion, kDSk is extended as kEDSk. Then kEDSk is Fourier transformed back to the complex x -plane and compared with xDS to find some physics implica- tions. Definition 9.1: Define the kEDSk function as the extension of kDSk function ' 4 5.0 45.0'4'4 4 1 22 j k j kjiijk k kjkjkeeeekEDS (9.1) Explanation: In the kEDSk, the original term k in kDSk of (7.1) is extended by the second summation terms with two sets of -functions. The first term with 0' j in the second summation, )()'4( 0' kjkj is the original delta function )(k in kDSk, and all the other terms in the second summation are newly added delta functions. The extension adds a series of additional local maximums for kEDSk representing bosons. Look at (9.1) closely, the added -functions also affect fermions in (7.1). For instance, 2k (12/ kk ) in kDSk is a root of 0kDSk represents electron as a fermion. In kEDSk, the1'j, 2k term )0())5.0'(4( 2,1' kj jk causes 1'1' 12 j k j kkEDSkEDS . It represents a boson. Using Fourier transform to transfer kEDSk back to the complexx -plane: dkekEDSxEDS ikx kx . (9.2) Substituting (9.1) into (9.2) yields the xEDSx - func- tion on the complex x -plane: ' 5.0'45.0'4'4'45.0 2 2 22 2 1 )( j xjijxjij j xjxj xeeeeeexEDS . (9.3) In the xEDSx , the first summation is 1 xDS as expected; the second summation includes the unitarity term: 1 0' '4'4 2 j xjij ee . The other terms in the second summation correspond to bosons representing interactions, which are originated from delta functions added in kEDSk. Numerical calculations found that: In general on x -plane: )5.0( xEDSxEDS xx . (9.4a) On the real x-axis: xSxEDSx 1 . (9.4b) Errors of approximations are around 15 10and 5 10 for (9.4a) and (9.4b), respectively. Definition 9.2: Define the SS-function and SS- equa- tion on the complex x -plane as: j xjijxjij j xjxj m xjixjxjij j xjxj xx eeeeee eeeeee xEDSxEDSxSS , 2 1 2 1 5.0 5.05.045.045.0445.05.05.0 5.045.04445.0 2 2 22 2 2 22 (9.5a) 05.0 xEDSxEDSxSS xx . (9.5b) According to (9.4a) and (9.5a), 0xSS . The val- ues of xSS fluctuate around 1715 10~10 and oc- casionally equal to zero, 0xSS , which are the roots of 0 xSS . As shown in Section 6, 0xDS is a real equation on the real x-axis. It has a root at 125.0 1x on the  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1247 x-axis corresponding to electron. On the other hand, 0xSS is a complex equation and 125.0 1x is not its root. Instead, a root of 0xSS is found by nu- merical calculations at: W i exx 11' , (9.6a) 78213151240811255.0'1x, (9.6b) 1384598708641.28 W . (9.6c) 1384598708641.28 W is electron original Weinberg angle of (8.45a) before f-modification. 78213151240811255.0'1x is slightly less than 125.0 1x. According to (6.19a), 78213151240811255.0'1x correlates to the mass e M' slightly less than e M: )'25.0(8 1 ' 1 xM M e e . (9.7) As shown in Appendix-4, charged particle mass sub- jects to electromagnetic modification. According to (A4.5) and (9.7): 306879927026474.0 '25.08 1 1 ' 1 xM MM M M e EMe e e . (9.8) In which is “fine structure constant” of electron. Solving (9.8) for yields: 50359990834.137 '25.08 1 1 1 1 1 x . (9.9) According to references [3,4], 2010-PDG (p.126) pro- vides the experimental data: )51(035999084.137 1 . (9.10) The relative deviation of SQS theoretical value and 2010-PDG data medium value is 12 10013.4 . (9.11) xSS is also used for calculating the 1 values for electron quantum states with fractional charges. Ac- cording to (8.44) with assumption of constgg 22 ', the Weinberg angle FW , for particles with fractional charges are determined by: F WW FWFW cossin cossin ,, . (9.12) 3/1F, 3/2F, are for fractional charges, e/3, 2e/3, respectively. Formula (9.12) and 1384598708641.28 W are used to calculate the values of FW, . The definition of fine structure constant is: hc e 0 2 2 . (9.13) According to (9.13), is proportion to 2 e. For the electron states with fractional charges 3/e, 3/2e, (9.8) and (9.9) are changed accordingly as. 1 2 '25.08 1 1x F , (9.14) 1 1 21 '25.08 1 1 x F . (9.15) The SQS theoretical values of 1 , W and FW , for electron states with different charges from 16-digit numerical calculations are listed in Table 9.1. Table 9.1. , W , FW, for electron with different char- ges. *Note: is the relative deviation from 2010-PDG medium value of 035999084.137 1 . In fact, the electron fractional charge states did show up in the quantum Hall effect experiments. The effect on mass is originated from electro- magnetic interaction. It is consistent with the fact that xDS does not include interactions and xSS does. It also explains why 125.0 1x on the real x-axis does not require mass correction with and 78213151240811255.0'1 x with phase angle 1384598708641.28 W on the complex x -plane does. The values listed in Table 9.1 are not unique. In fact, 0xSS has a series of roots corresponding to a series of different values. The multi-value behavior re- flects the fact that is a running constant and the sto- chastic nature of SQS theory. The details will be dis- cussed in later sections. The xEDSx function introduced in this section is not only used to define xSS function but also has oth- er important applications, which will be given in Section 15. Section 10. Muon and Taon Torus Model and Parameters Muon and taon belong to the second and third genera- tions of lepton family. Their torus model is similar to electron torus model except that the x-z cross section is elliptical for the original version. Instead of one radius 2 a for the circular cross section of electron torus model, the elliptical cross section has two radii 2 a and 2 b. To  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1248 determine the parameter 2 b requires an additional equ- ation. The option taken in this section is to keep the original (before f-modification) Weinberg angle the same for all three charged leptons: WeOWO . (10.1a) WeO is the original Weinberg angle for electron, WO is the original Weinberg angle for muon or taon. According to (10.1a) and (8.45a), the original angle WeOWO 2 for muon and taon is determined: 1384598708641.28 2 WeOWO . (10.1b) The original numerical parameters m, n, p for muon and taon are selected as: Muon: 18m, 4 1 29n, 6048p; (10.2a) Taon: 42m, 120n, 417270p. (10.2b) The reasons for selecting such values of m, n, p will be given in later sections. The values of 1 x and 2 x for muon and taon are calculated according to (6.19): p n M M xe 8 25.0 8 25.0 1 , (10.3a) 12 5.0xx . (10.3b) In (10.3a), )8/()8/(pnMMe is according to npMM e// of (8.1b). Substitute the values of p and n given by (10.2) into (10.3) yields: Muon: 13095240.24939546 1x, 86904760.25060453 2x; (10.4a) Taon: 20526280.24996405 1x, 79473720.25003594 2x. (10.4b) Substituting 1 x,2 x of (10.4) into the S-equation (3.20) and solving for )( 1 x and )( 2 x yield: Muon: 424961436156775.3)( 1x , 40639671394911815.3)( 2x ; (10.5a) Taon: 268531416714823.3)( 1x , 14241414262265.3)( 2x . (10.5b) Most formulas of electron torus model to determine characteristic point , point B locations and other geometrical parameters in Section 8 are valid for muon and taon except some differences caused by the cross section change from circular to elliptical. The formula to calculate loop length ratio mnLL//12 is: m n L L d dttbta 1 2 2 0 2 2 2 2 2 )cos()sin( . (10.6) For the torus outer half, formulas (8.8b), (8.9a) through (8.9c), (8.10a) through (8.10b), (8.11a) through (8.11c) are also valid for muon and taon. The changes are (8.8a) and (8.8c), in which 22 ab is replaced by 22 ab . For the torus inner half, formulas (8.12a), (8.13a), (8.14a) through (8.14d), (8.15a) through (8.15d) are valid for muon and taon. The changes are: in (8.12b), 11 ab is replace by 11 ab; in (8.13b), 11 ab and 22ab are replaced by 11 ab and 22 ab . For the f-modification, (8.26a) and (8.26b) are for electron. For other fermions including muon and taon, they are generalized as: AT-equation: 2 02 2 2 2 2 22 20 '2 )sin(''' 2 1 a d daada d ; (10.7a) PS-equation: 2 02 2 2 2 2 01 cos' )sin('' 2 1d ad aad ; (10.7b) Mass term’s : e M M L L n p m n m p 1 2 22 2 . (10.7c) The cos in the denominator of PS-equation does not change, because it is originated from geometry rela- tion of (8.19b) and has nothing to do with mass. The rest of formulas for the f-modification, (8.28a), (8.28b), (8.29a), (8.31a) through (8.31d), (8.32a) through (8.32d), (8.33a) through (8.33d), (8.34a) through (8.34e), (8.35a) through (8.35f), angle tilt formulas (8.38a) through (8.38c) and (8.39) all are valid for muon and tuaon without change. The GWS-triangle and related formulas (8.40), (8.41) and (8.42) are also valid for muon and tuaon. Table 10.1 and 10.2 list the calculated parameters for muon and taon, respectively. In these tables, the parame- ters with the ‘mark are effective, i.e. after the f-modi- fication and the parameters without the mark are original, i.e. before the f-modification. The synchronization related angles in Table 10.1 are: 63018464.3'15808314.52' 32 , (10.8a) 91156239.18''''6163361.29' 23222 , (10.8b)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1249 38022705.34'40080232.9' 10 , (10.8c) 45108237.9'833.0215193' 01 . (10.8d) The synchronization of two loops cyclic movements for electron described in Section 8 no longer holds for muon. It indicates that, muon is not a stable particle. In fact, muon has a mean life of s 10)000021.0197034.2(6 (2010-PDG data). Table 10.1. The calculated parameters of muon torus mo- del*. Table 10.2. The calculated parameters of taon torus mo- del*. *All data are from 16-digit numerical calculations, only 8-digit after the decimal point is presented. **The reduced numerical parameters are the original numerical parameters divided by m. The synchronization related angles in Table 10.2 are: 02150092.1'89177471.51' 32 , (10.9a) 68251145.21''''18776233.29' 23222 , (10.9b) 86247726.24'3.27752516' 10 , (10.9c) 35382497.3'424.2338133' 01 . (10.9d) The synchronization of two loops cyclic movements for electron described in Section 8 no longer holds for taon. It indicates that, taon is not a stable particle. In fact, taon has a mean life of s 10)001.0906.2(13 (2010-PDG data). The parameters listed in Table 10.1 and Table 10.2 for muon and taon are calculated according to the formulas in Section 8 for electron with modifications introduced in this section, in which some of them are optional and subject to verification. If some of them are replaced by other options, related parameters should be changed ac- cordingly. The characteristic points, the trajectory, the circle-A, circle-B, the tilt angle breaking 180 3-fold symmetry, the jumping trajectories, the torus model with four tiny holes equivalent to trousers with a large hole in the waistband and 4 ports degenerated to Feynman dia- gram, these and related issues discussed in Section 8 for electron are also valid for muon and taon. The torus models for muon and taon introduced in this section serve as the basic building blocks, which are not the final version. The final version of models will be in- troduced in Section 12. Section 11. Quarks Model and Parameters Quarks torus model has elliptical x-z cross section. The formulas for muon and taon in Section 10 are valid for quarks with exception that formula (10.1) is replaced by following formulas for quarks with fractional charges. For up-type quarks: 0 3 2 cossin cossin ,2,2 WeOWeO uOuO , 2139796740885.16 ,2 uO ; (11.1a) For down-type quarks: 0 3 1 cossin cossin ,2,2 WeOWeO dOdO , 03841092834194.8 ,2 dO . (11.1b) In which, uO,2 and dO,2 are original values of the angle 221 OAO as shown in Figure 8.1 before the f-modification for up type and down type quarks, respec- tively. Formulas (11.1) is based on an assumption: constgg 22 ', which is optional. There is another difference. The top quark is different  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1250 from the other quarks. Because its mass exceeds the up- per limit set by (6.21), top quark’s model is spindle type torus with covered center hole as shown in Figure 11.1. The inner half of spindle shape torus also has positive curvature, which is consistent with top quark’s )(1 x. This difference makes top quark’s inner half two trian- gles with different definitions and different physics meanings. Figure 11.1. Spindle type torus model for top quarks. As shown in Figure 11.1, the location of points D and B are determined by )(1 x the same way as points G and A determined by )( 2 x. On x-y cross section: 0 )(sin10 0 xR R , daR 2, (11.2a) 0 22 0 2 0RYX. (11.2b) On HO1cross section: 0 )(2 cossin 11 2 2 2 2 1 1 xZ dttbta , 22 ab , (11.3a) 2 1 1 cos a X , (11.3b) 01 2 2 1 2 2 1 b Z a X, 22 ab . (11.3c) In Figure 11.1a, the triangle 21'ODO related angles are: 0 0 0 tan X Y , (11.4a) 0 0 0 tan Xd Y , (11.4b) 00 180 . (11.4c) 000 . (11.4d) In Figure 11.1b, the triangle 211 'OOB related angles are: 1 1 1 tan X Z , (11.5a) dX Z 1 1 1 tan , (11.5b) 11180 , (11.5c) 111 . (11.5d) The generalized AT- and PS-equations of (10.7) are applicable to all quarks except the top quark. The top quark’s model must have 1'2 da to qualify as the spindle type torus. The f-modification reduces 1 2 da to 15.0'2 da , that is not valid for spindle type torus. The effectiveness of f-modification for top quarks is lim- ited to the 1'2da part, which does not includes the root for the AT-equation. Before going further, one question must be answered: How many quarks are there? Postulation 11.1: Quarks with the same flavor and different colors are different elementary particles. There are eighteen quarks in three generations. Explanation: Elementary particles are distinguished from each other according to their different intrinsic pa- rameters. Quarks with the same flavor and different col- ors have at least two different intrinsic parameters: one is color and the other is mass. To recognize them as differ- ent elementary particles is inevitable and legitimate. According to Postulation 11.1, there are eighteen dif- ferent quarks instead of six, in which six flavors each has three colors as shown in Table 11.1. Postulation 11.1 has important impacts beyond quarks, which will be shown in later sections. Postulation 11.2: Prime Numbers Postulation. Pri- me numbers are intrinsically correlated to elementary particles’ parameters as well as cosmic space structure and cosmic evolution. Explanation: Prime Numbers Postulation serves as  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1251 the second fundamental postulation with importance next to the first fundamental postulation of Gaussian probabil- ity. It provides a principle. The details are given by cor- responding rules. Definition 11.1: A pair of two consecutive odd prime numbers with average value equal to even number is de- fined as an even pair. A pair of two consecutive odd prime numbers with average value equal to odd number is defined as an odd pair. The numerical m-parameters of 18 quarks are selected by the following rule. Rule 11.1: The eighteen least odd prime numbers in- cluding 1 are assigned as the m-parameters of eighteen quarks as shown in Table 11.1. The m-parameters of eighteen quarks are paired of up-type and down-type for each color. All nine pairs are even pairs. Table 11.1. 18 Prime numbers assigned to 18 quarks m- parameters*. *The m-parameters listed are their magnitude; the signs are defined by (11.6). Conclusion11.1: There are only three generations of quarks. Proof: As shown in Table 11.1, for the nine pairs of quarks in three generations, their m-parameters: 1 & 3, 5 & 7, 11 & 13, 17 & 19, 23 & 29, 31 & 37, 41 & 43, 47 & 53, 59 & 61 all are even pairs. The next prime numbers pair of 67 & 71 is not an even pair, which violates Rule 11.1. The fourth generation quarks are prohibited based on the Prime Numbers Postulation and the prime num- bers table. QED In fact, no quarks beyond three generations have found in experiments. The numerical parameters n and p of quarks are se- lected in the following rules. Rule 11.2: The quarks’ n-parameters are selected from prime numbers. The values of quarks n-parameter are closely related to strong interactions among them, which will be discussed in Section 13. Rule 11.3: For a quark, the p-parameter is determined by e MMnp // , in which, and e M are the mass of the quark and the mass of electron, respectively. The ratio mp /2 equals to an integer. The reasons for such rules will be explained later. Definition 11.2: The signs of numerical parameters m, n, p for fermions and anti-fermions with different hand- edness are defined as: Fermion with right handedness: 0m, 0n, 0p, (11.6a) Fermion with left handedness: 0 m, 0n, 0p, (11.6b) Anti-fermion with right handedness: 0m, 0 n, 0p, (11.6c) Anti-fermion with left handedness: 0 m, 0n, 0p. (11.6d) Explanation: According to definition 11.2, for all four cases, the ratios np / for mass are always positive as they should be. Loop ratios are different: 0/ mn for fermions and 0/ mn for anti-fermions, which serve as the mathematical distinction for fermions and an- ti-fermions. For all fermions, 0m represents right handedness, and 0 m represents left handedness. The verifications and applications of Definition 11.2 will be given later. The geometry parameters of quarks calculated by us- ing above formulas and rules are listed in Table 11.2. In which, for up, down, strange, charm, bottom quarks, the parameters with the ‘mark are effective, i.e. after the f-modification, and the parameters without the ‘ mark are original, i.e. before the f-modification. All parameters for top quarks listed in Table 11.2 are original. Table 11.2. Calculated parameters for 18 quarks*. 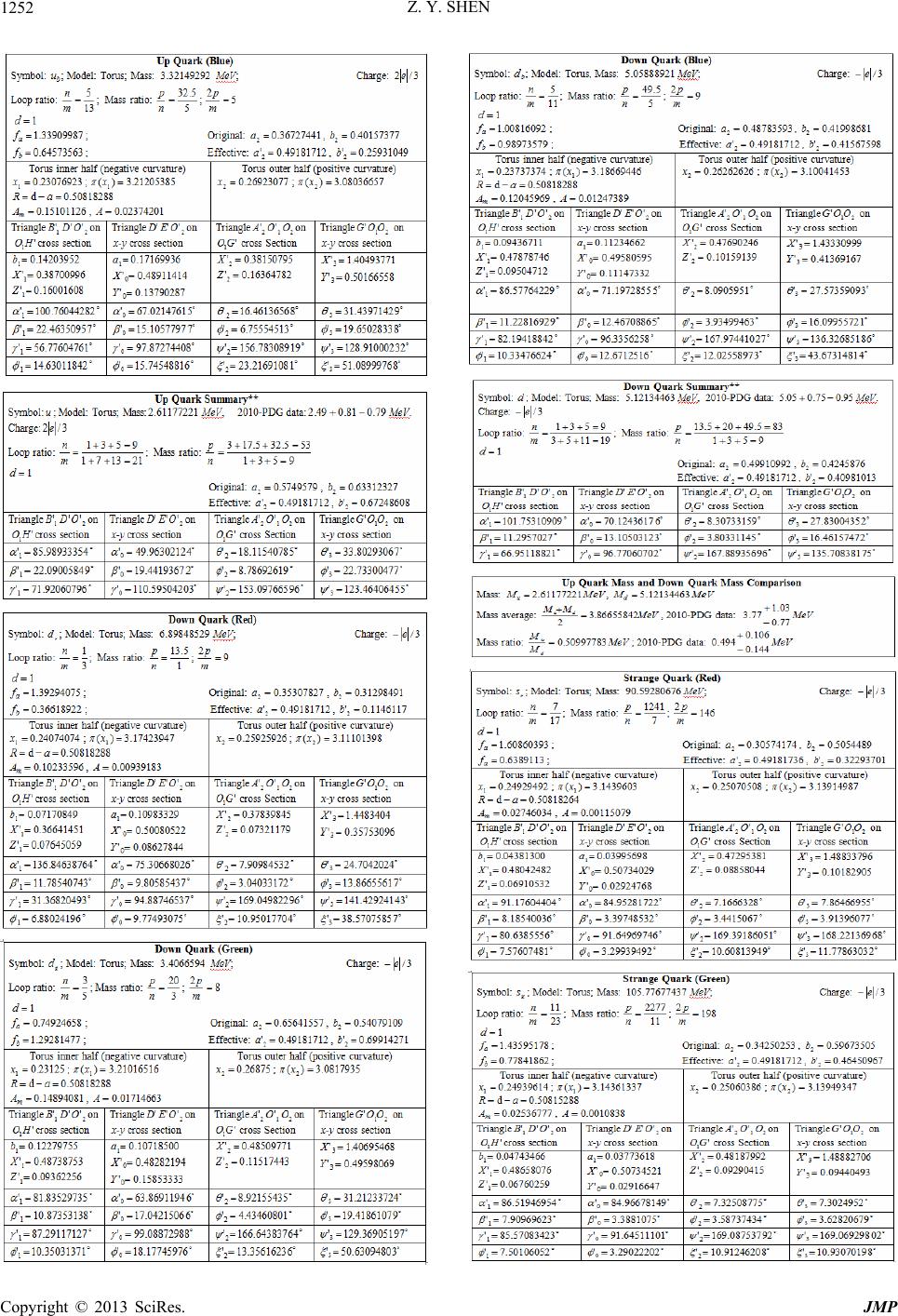 Z. Y. SHEN Copyright © 2013 SciRes. JMP 1252 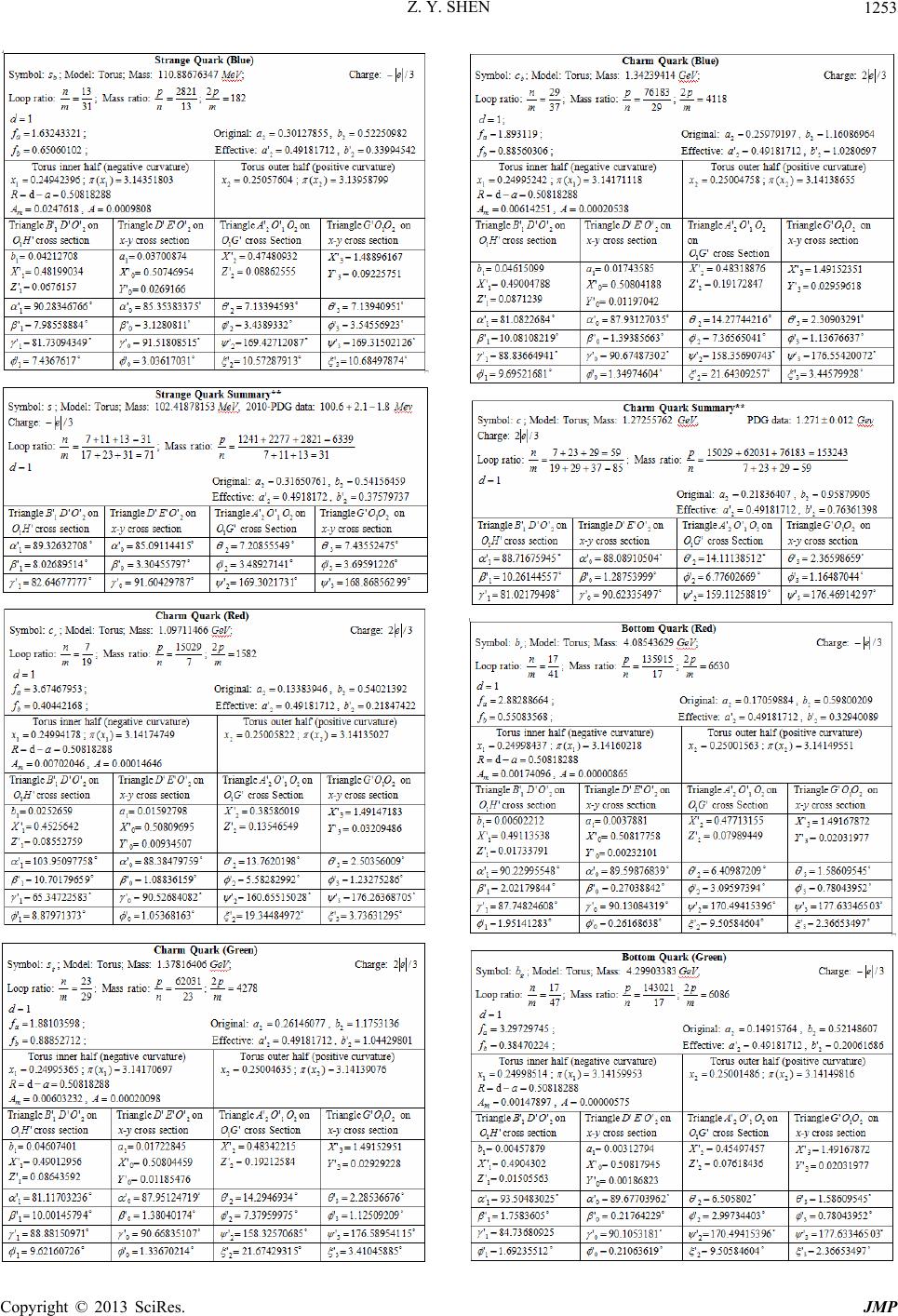 Z. Y. SHEN Copyright © 2013 SciRes. JMP 1253 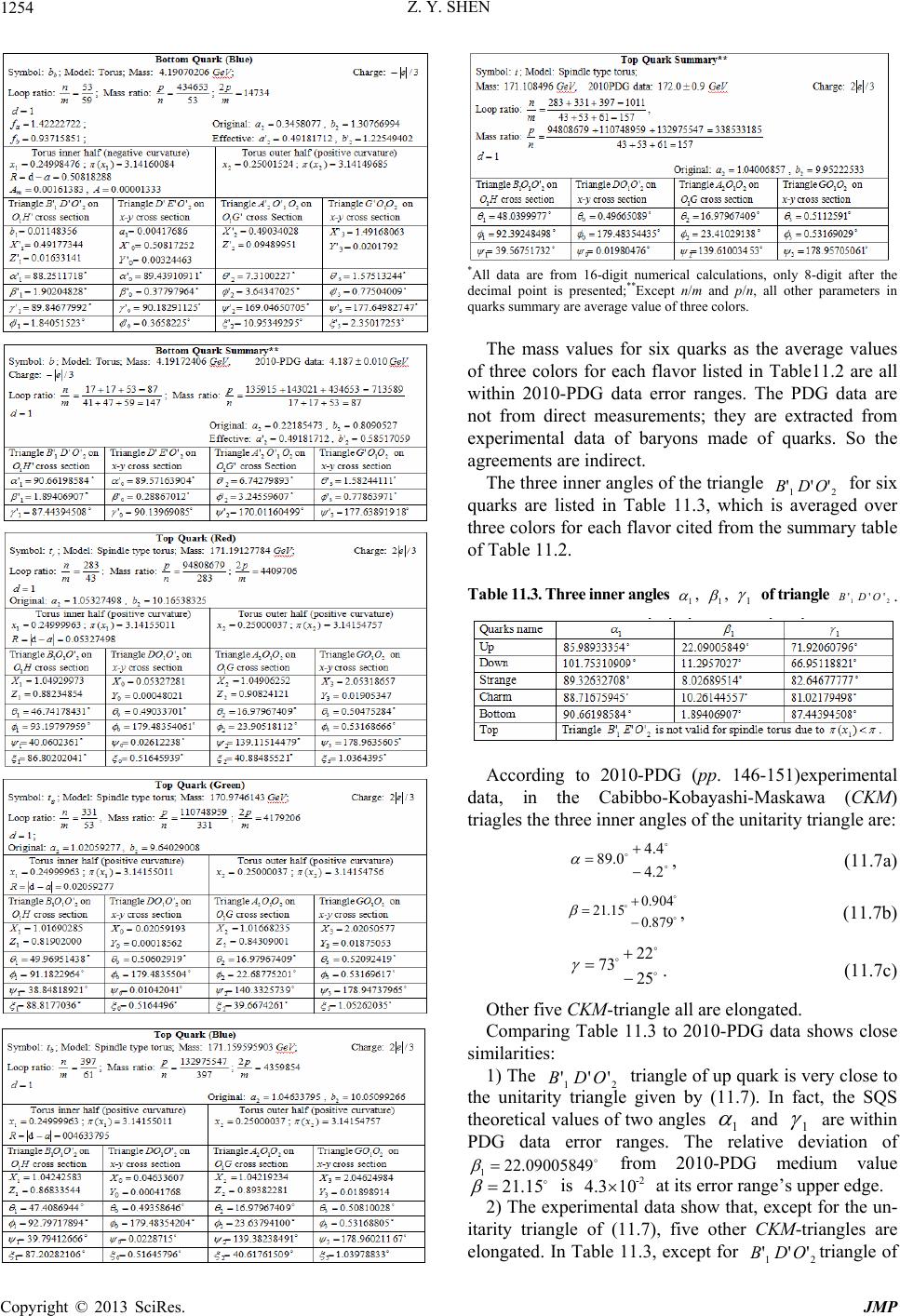 Z. Y. SHEN Copyright © 2013 SciRes. JMP 1254 *All data are from 16-digit numerical calculations, only 8-digit after the decimal point is presented;**Except n/m and p/n, all other parameters in quarks summary are average value of three colors. The mass values for six quarks as the average values of three colors for each flavor listed in Table11.2 are all within 2010-PDG data error ranges. The PDG data are not from direct measurements; they are extracted from experimental data of baryons made of quarks. So the agreements are indirect. The three inner angles of the triangle 21 ''' ODB for six quarks are listed in Table 11.3, which is averaged over three colors for each flavor cited from the summary table of Table 11.2. Table 11.3. Three inner angles 1 , 1 , 1 of triangle 21 ''' ODB. According to 2010-PDG (pp. 146-151)experimental data, in the Cabibbo-Kobayashi-Maskawa (CKM) triagles the three inner angles of the unitarity triangle are: 2.4 4.4 0.89 , (11.7a) 879.0 904.0 15.21 , (11.7b) 25 22 73 . (11.7c) Other five CKM-triangle all are elongated. Comparing Table 11.3 to 2010-PDG data shows close similarities: 1) The 21 ''' ODB triangle of up quark is very close to the unitarity triangle given by (11.7). In fact, the SQS theoretical values of two angles 1 and 1 are within PDG data error ranges. The relative deviation of 922.0900584 1 from 2010-PDG medium value 15.21 is -2 104.3 at its error range’s upper edge. 2) The experimental data show that, except for the un- itarity triangle of (11.7), five other CKM-triangles are elongated. In Table 11.3, except for 21 ''' ODB triangle of  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1255 the up quark, other four quarks’ 21 ''' ODB triangles are elongated and the one for top quark is not valid. 3) Required by unitarity of probability, the side be- tween angle and angle of CKM-triangle is nor- malized to unity. The side ''2DO of triangle 21''' ODB is normalized to unity for the other two sides represent- ing probabilities. According to SQS theory, there are fifteen 21 ''' ODB triangles comparing to five CKM-triangles for five fla- vored quarks except the top quark. This difference may provide an important clue for the question regarding CKM-triangle: Is the unitarity CKM-triangle really a tri- angle? This is a serious question. If the answer is no, the standard model must be revised. As shown by (11.7), two angles and have large error ranges, and the sum of three inner angles medium values equals to 15.183 instead of 180 . From SQS theory standpoint, the problem can be naturally resolved by recognized the fact that, there are eighteen quarks with different flavors as well as different colors. As a result, the unitarity CKM-triangle isn’t a single triangle, it is a set of three triangle corresponding to three different colored quarks r u, g u, b u. As listed in Table 11.2, three up quarks r u, g u, b u have 61137029.88 ,1 ur , 37440598.70 ,1 ug , 77604761.56 ,1 ub , respectively. The large error range of 252273 give by (11.7c) is the result of attempting to combine three different triangles into one. The same argument is applicable to angles and . So the large error ranges of CKM-triangle data have a reasonable explana- tion based on Postulation 11.1. There are other reasons to identify triangles 21 ''' ODB as the CKM-triangles. Quarks are represented by their torus models and characteristic points carry information from the S-equation to torus model. In principle, all pa- rameters including the CKM-triangles should be derived from the model. Moreover, if the angles are kept the same, the triangles are similar. As one side is normalized, the other two sides of the similar triangles also represent the same information. In this way, the converting prob- abilities among different quarks via weak interactions indicated by the other two sides of the CKM-triangle should be transferred to the 21 ''' ODB triangle as well. For all these reasons, the 21 ''' ODB triangles are identi- fied as the CKM-triangles. It is another step towards the final goal: All physics parameters of an elementary parti- cle are derived from its model. The generalized AT- and PS-formulas of (10.7) are used to calculate the angle tilt and phase sync data for fifteen quarks listed in Table 11.4. Three top quarks are excluded, because for them the f-modification is not fully applicable. The data for three charged leptons are listed for comparison. Table 11. 4. Phase sync data for 15 quarks and 3 charged leptons*. *1.The data are from 16-digit numerical calculations. Only three effective digits are listed. 2. The listed a f vary in -15 101 steps within range of -15 10100 . The features of these results are summarized as fol- lows: 1) Electron, three up quarks and three down quarks have perfect phase synch among two loops’ cyclic movements and the sinusoidal oscillation of the mass term indicated in Table 11.4 as “PS values at 0 AT ” equal to zero. Their angle tilt equation (10.7a) and phase sync equation (10.7b) are satisfied simultaneously. The perfect synchronization is interpreted as electron, up quarks and down quarks are stable fermions. In fact, these three types of particles are stable and serve as the building blocks of all atoms and molecules in the real world. 2) The other particles listed in Table 11.4 namely muon, taon, and strange, charm, bottom quarks are not perfectly synced indicated by their “PS values at 0 AT ” equal to nonzero values. According to the same reason, it can be interpreted as they are not stable particles. In fact, muon, taon, and all hadrons composited with strange, charm, bottom quarks are unstable and subject to decay. 3) All fifteen quarks and three charged leptons have fluctuation phase variations noted as the “PS value varia- tion” in Table 11.4. It means that all these particles have the trajectory jumping behavior similar to electron’s tra- jectory jumping behavior described in Section 8. Formulas of (8.38) are used to calculated the tilted an- gle deviated from 120 . The data along with 2 a, 2 'a and a f for three charged leptons and fifteen quarks are listed in Table 11.5. Three top quarks 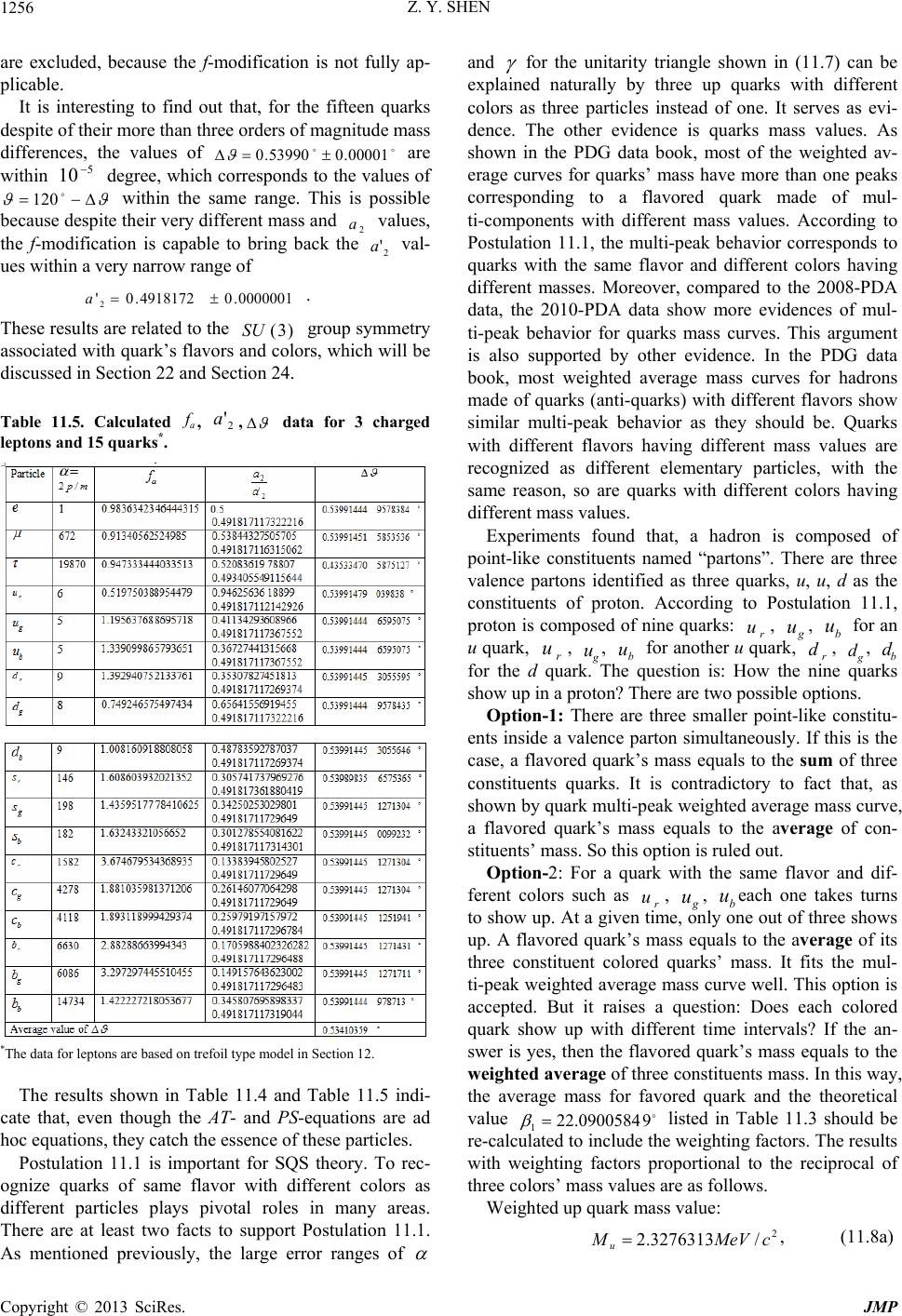 Z. Y. SHEN Copyright © 2013 SciRes. JMP 1256 are excluded, because the f-modification is not fully ap- plicable. It is interesting to find out that, for the fifteen quarks despite of their more than three orders of magnitude mass differences, the values of 00001.053990.0 are within 5 10 degree, which corresponds to the values of 120 within the same range. This is possible because despite their very different mass and 2 a values, the f-modification is capable to bring back the 2 'a val- ues within a very narrow range of 0000001.04918172.0'2a. These results are related to the )3(SU group symmetry associated with quark’s flavors and colors, which will be discussed in Section 22 and Section 24. Table 11.5. Calculated a f, 2 'a, data for 3 charged leptons and 15 quarks*. *The data for leptons are based on trefoil type model in Section 12. The results shown in Table 11.4 and Table 11.5 indi- cate that, even though the AT- and PS-equations are ad hoc equations, they catch the essence of these particles. Postulation 11.1 is important for SQS theory. To rec- ognize quarks of same flavor with different colors as different particles plays pivotal roles in many areas. There are at least two facts to support Postulation 11.1. As mentioned previously, the large error ranges of and for the unitarity triangle shown in (11.7) can be explained naturally by three up quarks with different colors as three particles instead of one. It serves as evi- dence. The other evidence is quarks mass values. As shown in the PDG data book, most of the weighted av- erage curves for quarks’ mass have more than one peaks corresponding to a flavored quark made of mul- ti-components with different mass values. According to Postulation 11.1, the multi-peak behavior corresponds to quarks with the same flavor and different colors having different masses. Moreover, compared to the 2008-PDA data, the 2010-PDA data show more evidences of mul- ti-peak behavior for quarks mass curves. This argument is also supported by other evidence. In the PDG data book, most weighted average mass curves for hadrons made of quarks (anti-quarks) with different flavors show similar multi-peak behavior as they should be. Quarks with different flavors having different mass values are recognized as different elementary particles, with the same reason, so are quarks with different colors having different mass values. Experiments found that, a hadron is composed of point-like constituents named “partons”. There are three valence partons identified as three quarks, u, u, d as the constituents of proton. According to Postulation 11.1, proton is composed of nine quarks: r u, g u, b u for an u quark, r u, g u, b u for another u quark, r d, g d, b d for the d quark. The question is: How the nine quarks show up in a proton? There are two possible options. Option-1: There are three smaller point-like constitu- ents inside a valence parton simultaneously. If this is the case, a flavored quark’s mass equals to the sum of three constituents quarks. It is contradictory to fact that, as shown by quark multi-peak weighted average mass curve, a flavored quark’s mass equals to the average of con- stituents’ mass. So this option is ruled out. Option-2: For a quark with the same flavor and dif- ferent colors such as r u, g u, b ueach one takes turns to show up. At a given time, only one out of three shows up. A flavored quark’s mass equals to the average of its three constituent colored quarks’ mass. It fits the mul- ti-peak weighted average mass curve well. This option is accepted. But it raises a question: Does each colored quark show up with different time intervals? If the an- swer is yes, then the flavored quark’s mass equals to the weighted average of three constituents mass. In this way, the average mass for favored quark and the theoretical value 922.0900584 1 listed in Table 11.3 should be re-calculated to include the weighting factors. The results with weighting factors proportional to the reciprocal of three colors’ mass values are as follows. Weighted up quark mass value: 2 /3276313.2 cMeVMu, (11.8a)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1257 Weighted up quark 1 value: 93059933.21 1 . (11.8b) Both results are within 2010PDG data error ranges. The importance of Postulation 11.2 and Rule 11.1 has been shown by Conclusion 11.1. In fact, Postulation 11.2 as the second fundamental Postulation of SQS theory has many important impacts far beyond quarks, which will be given in later sections. Section 12. Trefoil Type Model for Charged Leptons In this section, a broad view is taking to look at leptons. Based on Prime Numbers Postulation and intrinsic rela- tion between leptons and quarks, a new type of model with torus as building blocks is introduced for charged leptons. In Section 11, nine even pairs of prime numbers are assigned as the m-parameters for nine pairs of up type and down type quarks as listed in Table 11.1. Postulation 12.1: The original (before reduction) m-parameter of a lepton is an even number equal to the average value of the m-parameters of associated up type quark and down type quark. Explanation: In fact, this is the unstated reason in Section 8 and Section 10 to select 2, 18, and 42 for the original m-parameters of electron, muon and taon, re- spectively. 22/)31(2/)( drure mmm , (12.1a) 182/)1719(2/)( srcrmmm , (12.1b) 422/)4143(2/)( brtr mmm . (12.1c) According to Postulation 12.1, the results for six lep- tons are listed in Table 12.1. The m-parameters of eight- een quarks are also listed for reference. Table 12.1. The Leptons and quarks with assigned m-parameters*. *The m-parameters are their magnitude; signs are defined by (11.6). Conclusion 12.1: There are only three generations of quarks and leptons. The fourth generation is prohibited. Proof: In the “End” column of Table 12.1, the average of two m-parameters, 67 & 71, is an odd number: 692)7167( . According to Postulation 12.1, the fourth generation leptons are prohibited. According to Conclusion 11.1, the fourth generation quarks are pro- hibited. QED Conclusion 12.1 is the extension of Conclusion 11.1 based on the Prime Numbers Postulation and the intrinsic relation between quarks and leptons. On the experiment side, according to 2010-PDG data, the number of light neutrino types from direct measure- ment of invisible Z width is 05.092.2 . The number from ee colliders is 0082.09840.2 . Both results show no trace of fourth generation neutrino existence. These experimental data support Conclusion 12.1. Notice that, there are vacant cells marked with “?” in Table 12.1. The question is: Are there any undiscovered leptons? In the three generations, there are twelve lepton vacancies, in which six are e, , type, and the other six are e , , type. If these vacancies correspond to undiscovered leptons, the six e, , type would be charged leptons with mass ranging from a few 2 /cMeV to a few thousands 2 /cMeV . That is impossible, because charged particles in such mass range should be discov- ered already. The neutrinos e , , are intrinsi- cally associated with their companions leptons, e, , respectively. If there are no undiscovered charged lep- tons, so are no undiscovered neutrinos associated with them. To fill the vacancies with undiscovered leptons isn’t the only way. The other way is that, these vacancies serve as a hint for new structure of existing leptons. The first generation fermions are divided into four categories including two types of leptons e and e , and two flavors of quarks each with three colors, r u, g u, b u and r d, g d, b d. The second and third generations have the same structure. Should leptons also have colors? This is the initial thought inspired by the vacancies in Table 12.1. The basic idea is that, leptons’ new model has three branches. Each branch separately is a torus model. The three branches combine to form the new model. Leptons’ torus model has spin 2/. The new model made of three torus should also have spin 2/. There are two options to deal with the spin problem. Option-1. Let two branches have spin 2/, and one branches has spin 2/ . The sum of three branches spin is 2/)2/(2/2/ . But this option makes the new model lost three-fold circular symmetry. More seri- ously, the opposite spin in one branch abruptly reverses loop-1 movement direction, which violates the require- ment for smooth trajectory. It is not acceptable. Option-2. Let each branch has spin 6/. It can be done by selecting the reduced m-parameter 3/1 m for each branch. According to SQS theory, the lepton’s spin  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1258 equals to 2/m. For the new model as a whole entity, the reduced m-parameter add up to 13/13/13/1 m corresponding to the spin 2/. This option is accepted Next step is to find out how the three torus branches and three trajectories are combined. According to Pen- rose [12], there are two types of topological structures with three branches. The trefoil-knot-type shown in Fig- ure 12.1(a) is a single loop self-knotted to form a trefoil structure. It fits the job to combine three trajectories on three torus models into one trajectory on the trefoil type model. The Borromean-ring-type structure shown in Fig. 12.1(b) is irrelevant to leptons model, because its three loops do not combine into one. In Figure 12.2, the three loop-1 circles shown by dot-dashed lines touch each other tangentially from one circle to the other circle with continuous first order de- rivatives. In this way, loop-1 goes smoothly from one branch to the other. The total length of combined loop-1 equals precisely the sum of three branches’ loop-1 lengths representing 2/6/6/6/ h spin for electron as a whole entity. Figure 12.2 shows how the three branch trajectori- escombined into a trefoil trajectory. As mentioned in Section 8, on the electron torus surface, point-A and point-B in Fig.8.2 actually represent two circles, circle-A and circle-B. A trajectory may start at a point on circle-A and halfway through at a point on circle- B to keep the angle BAO1 : 98687309.166180 1 BAO. (8.18) This rule is originated from the S-equation and strictly related to)( 1 x , )( 2 x to determine curvatures of the torus model. To construct the trefoil trajectory, (8.18) is used to determine the location of point-B from the loca- tion of point –A for each branch. Figure 12.1. Three-branch patterns: (a) Trefoil-knot-type; (b) Borromean rings type. The other rules for the trefoil trajectory are: 1) The trefoil trajectory must go through points-A and point-B of three branches to satisfy the requirements of )(1 x and )( 2 x for each branch. 2) The trajectory is the geodesics between adjacent point-A and point-B on trefoil type model surface. 3) The three branches of trefoil trajectory have the same shape separated by 120 for the 3-fold circular symmetry. In Figure 12.2, the trajectory on top surface is shown by solid curve and on bottom surface is shown by dashed curve. Electron’s trajectory goes anti-clockwise through six characteristic points and back to close one cycle: rrgbbrggbr ABBABBABBA . (12.2) Indeed, the trajectory is a trefoil type closed loop with the correct topological structure and the 3-fold circular symmetry. The Weinberg angle 428.4794845' W is the same for all three branches as well as for electron as a whole entity. It needs explanation. As mentioned in Section 8, Weinberg angle is a phase shift between loop-1 and loop-2 periodic movements: -222 W. (12.3) For the trefoil trajectory, 2 W repeats three times at three locations, r A, g A, b A. The repetition means the same phase shift kept no change along trajectory at three locations. Therefore, the three angles should not be added up toW 3. Look at it the other way, the combined trajectory is the same one on the original genus-1 torus surface, which is reconfigured to fit the genus-3 manifold. The combined trajectory has one Weinberg angle 428.4794845''2 Wcorresponding to the charge of e for electron. Figure 12.2. The x-y plane cross section of electron trefoil type model and trefoil trajectory projec tion on x-y plane.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1259 The trajectory shown in Figure 12.2 is a samples se- lected from two sets of discrete possible trajectories. The jumping trajectories described in Section 8 for electron torus model are also valid for the trefoil type model. As long as the trajectories meet all rules, they are legitimate. In other words, the “electron clouds” is also a visualized description of electron behavior for the trefoil type model. The same is true for the trajectories on trefoil type mod- els of muon and taon. Introducing the trefoil type model solves the vacancies problem in Table 12.1. Table 12.2 shows the vacancies in Table 12.1 are filled with leptons’ branches. Table 12.2. The m-parameters of quarks and leptons with 3 branches*. *The m-parameters listed are their magnitude; their signs are defined by (11.6). **The number in parenthesis is the reduced m-parameter. For three generations of charged leptons, the formulas given by (12.1) of Postulation 12.1 are generalized for the original m-parameters (before reduction) of trefoil type model’s each branch and as a whole entity based on the original m-parameters of corresponding up type quark ji quptype m, ,and down type quark ji qdowntyp m, ,. For each branch: 23 1,,,, , jiji qdowntypquptype ji mm m, 3,2,1i,bgrj,,. (12.4a) For lepton as a whole entity: bgrj jii mm ,, ,, 3,2,1 i. (12.4b) The factor 3/1 in (12.4a) is introduced to make each branch with spin 6/. The index 3,2,1i is for three generations and the index bgrj ,, is for three branches. The rule to select the n-parameters for the trefoil type model is to make the loop ratio mn/ identical for all three branches. The formulas to determine the original n-parameters (before reduction) of trefoil type model each branch and as a whole entity are based on the m-parameters of (12.4) and the torus model original n-parameter torus n. For each branch: torus ri ji ji n m m n , , ,3 1, 3,2,1 i,bgrj ,,, (12.5a) For lepton as a whole entity: bgrj jii nn ,, ,, 3,2,1i. (12.5b) The rule to select the p-parameters for the trefoil type model is to make the mass ratio np/ identical for all three branches. The formulas to determine the original p-parameters of the trefoil model each branch and as a whole entity are based on the m-parameters of (12.4) and the torus model original p-parameter torus p. For each branch: torus ri ji jip m m p , , ,3 1, 3,2,1i,bgrj ,,, (12.6a) For lepton as a whole entity: bgrjjii pp ,, ,, 3,2,1 i. (12.6b) The original numerical parameters are reduced to make the m-parameter for the trefoil type model as a whole entity equals to 1 corresponding to spin 2/. The way of reduction is that, the original m, n, p are divided by the original m for each branch. In Table 12.3, the numerical parameters calculated according to formulas (12.4), (12.5), (12.6) are listed for each branch as well as for lepton as a whole entity for electron, muon and taon with trefoil type model. As shown in Table 12.3, all reduced numerical pa- rameters m, n, p are identical for three branches. It indi- cates that, the trefoil type model three branches are ma- thematically identical. After reduction, their differences in the original parameters no long show up. Table 12.3. Numerical parameters for three generations of charged leptons. The calculated parameters for electron, muon and taon with trefoil type model are listed in Table 12.4, Table 12.5 and Table 12.6, respectively. In which, the parame- ters with the ‘mark are effective, i.e. after f-modification and the parameters without the ‘mark are original, i.e. before f-modification. The generalized AT-equation and PS -equation of (10.7) are also valid for leptons’ trefoil model. As listed in Table 12.4, Table 12.5 and Table 12.6,  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1260 except the original numerical parameters differences, all reduced numerical parameters as well as other parame- ters for electron, muon and taon trefoil type model are the same of those for their torus model listed in Table 8.2, Table 10.1 and Table 10.2. The consistence is expected. The torus models and trajectories serve as the building blocks for trefoil type models and trajectories. The three torus models and three trajectories combine into one tre- foil type model and one trefoil trajectory. In the combi- nation process, the only thing changed is their dimen- sions shrunk to one third. Therefore, all angles as well as all normalized lengths are kept the same. There is an apparent problem. As listed in the tables, the values of np/ ratio for each branch are the same for the lepton as a whole entity. Since np / ratios equal to mass ratios: e MMnp // , the question is: Does the mass of each branch equal to the mass of the lepton? Of cause not, but it deserves an explanation. As shown by (10.7c) for the generalized AT-equation and PS-equation, the mass term is: e M M L L n p m n m p 1 2 2sin2sin 2 sinsin (10.7c) The mass term is oscillating along the entire trefoil trajectory. There is no way to define another mass term for each branch different from the one for the whole tre- foil model. The situation is similar to the Weinberg angle discussed earlier. The e MMnp// as mass ratio is not for each branch separately; it is for the lepton as a whole entity. It must emphasis that, lepton trefoil type model as a whole entity represents the lepton. The red, green, blue three branches are not separated particles. This is the ma- jor differences between leptons’ colors and quarks’ colors. Table 12.4. Parameters for electron with trefoil type model*. Table 12.5. Parameters of muon with trefoil type model*. Table 12.6. Parameters of taon with trefoil type model*. *All data are from 16-digit numerical calculations, only 8-digit after the decimal point is presented. **With different normalizations, the listed values of length parameters are the same for each branch and for taon as whole entity.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1261 For SQS theory, the trefoil type is the real model for leptons. Otherwise, the vacancies in Table 13.1 cannot be filled. However, the study for leptons’ torus model is not a waste effort. It serves as a rehearsal for the real show. Section 13. Gluons and Strong Interactions The strong interactions between quarks are mediated by eight gluons, which are gauge bosons with spin h and zero mass. In this section, the gluons and the strong in- teractions are treated in terms of mathematics. Definition 13.1: Eight gluons are made of eight pairs of quark and the same type anti-quark: rrddg 1, ggddg 2, gguug 3, bbddg 4, bbuug 5, rrssg 6, ggssg 7, bbssg 8; (13.1a) Or jji qqg; 8,7,6,5,4,3,2,1i; bgrbbggr sssududdj ,,,,,,,. (13.1b) According to Definition 13.1: ijjjijji gqqqqqqg ; 8,7,6,5,4,3,2,1i, bgrbbggr sssududdj ,,,,,,,. The anti-particle of gluon is itself: iigg , 8,7,6,5,4,3,2,1i. (13.2) Definition 13.2: The gluons numerical parameters are defined as follows: 1) The original m-parameter of gluon is defined as: q mm 2 . (13.3) q m is the m-parameter of gluon’s constituent quark. 2) The n parameter of gluon is defined as: 2 2 m n. (13.4) 3) The gluons handedness is defined as: For right handed gluons: 0m and 0n; (13.5a) For left handed gluons: 0m and 0n. (13.5b) 4) The gluon effective m-parameter as gauge boson with spin is defined as: 2)2( nmmEff . (13.6) 5) The p-parameter of gluon equals to zero for zero mass: 0p. (13.7) The numerical parameters of eight gluons are listed in Table 13.1. Table 13.1. The numerical paramete r s of eight gluons*. Explanation: The definitions of gluons numerical pa- rameters are based on their geometrical model. For con- venience, the following discussions are referring to glu- ons with right handedness. According to SQS theory, the model of a gluon as a boson without mass is a single loop with its m-parameter given by (13.3). As listed in Table 13.1, the original m-parameters for all eight gluons are 6m corresponding to spins of 32/ ms , which is contrsdictory to gluon as gauge boson with spin s. The problem can be solved by their model. As shown in Figure 13.1(a), the gluon loop’s two traces on opposite sides are merged into one and leave two small circles at two ends. Then the merged portion is twisted into 2/)2( mn turns akin to a spring shown in Figure 13.1(b). The loop unmerged portion is evenly divided into two small circles. Each circle’s circumferential length equals to PP L corresponding to spin 2/ with the same orientation. Two circles contribute the spin of 2/2/s for the gluon. This scenario is con- sistent with the number parameters listed in Table 13.1. The effective m-parameter of 2)1 2 (22 m mnmmEff corresponds to the spin of 2/ Eff ms . The n-para- meter equals to the number of turns shown in Figure 13.1(b). The p-parameters of gluons all equal to zero for zero mass. Figure 13.1. Gluon’s model.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1262 Rule 13.1: The strong interaction between two quarks (two anti-quarks, a quark and an anti-quark) 1 q and 2 q with parameters 11,nm and 22,nm is mediated by a link made of gluons with numerical parameters i m, i n satisfies the following equations: N iiimamm 1 21 , (13.8a) N iiinann 1 21 . (13.8b) N is the number of gluon types in the link; i a is the number of gluons of typei. Explanation: In (13.8), 1N means more than one types of gluons participating in the link; 1 i a means more than one gluons of type i participating in the link. Definition 13.3: The strong interactions between two quarks (two anti-quarks, a quark and an anti-quark) are classified into two categories. Regular type: All gluons in the link have the same handedness, i.e. all i mand all i n have the same sign. Weakened type: Some gluons in the link have differ- ent handedness, i.e. i mand i n having different signs. Explanation: In a link, all gluons share the same mo- mentum orientation. Gluons are bosons. The gluons with same handedness and same spin orientation have a ten- dency of condensation, which represents a strong attrac- tive force to enhance the link. The gluons with opposite handedness and opposite spin orientations weaken the link. Unless stated otherwise, strong interactions are refer- ring to the regular type. Theorem13.1: The regular type strong interaction between two members in a pair of quarks (anti-quarks, a quark and an anti-quark) with numerical parameters 11,nm and 22 ,nm satisfy: 1 2 1 2121 mmnn . (13.9) Proof: For the regular type strong interaction, accord- ing to Definition 13.3, (13.9) is subjected to the condition that, all gluons participated in the link have the same handedness. According to (13.4), and (13.8): 1 2 1 2 1 2 2 1 212121 mmammmanann ii iiii ii ;1 ii a. Formula (13.9) is proved for all gluons participated in the link with 0 i m and 0 i n or all gluons partici- pated in the link with 0 i m and 0 i n, which belong to the regular type. QED Lemma 13.1: A pair of quarks (anti-quarks, a quark and an anti-quark) with numerical parameters 11 ,nm and 22 ,nm violating (13.9) is prohibited to have the regular type strong interaction between two members in the pair. The strong interaction belongs to the weakened type. Proof: Lemma 13.1 is the reversed opposite of Theo- rem 13.1. QED According to Theorem 13.1 and Lemma 13.1, the strong interactions among quarks (anti-quarks, a quark and an anti-quark) have prohibitions meaning no regular type strong interactions between certain specific quarks (anti-quarks, a quark and an anti-quark). The selectivity of regular type strong interactions based on Theorem 13.1 and Lemma 13.1 plays an important rule for com- paring the theoretical results with experimental facts. The possible gluons links serving as mediators for the regular strong interaction among quarks (anti-quarks) are given in Table 13.2 and Figure 3.2. The form for nu- merical parameters used in Table 12.2 is: linkg N ii pairq linkg N ii pairq mamm nann 1121 1121 , N iii ga 1 ; (21 mm, 21 nn ). (13.10) In which, 11 ,nm and 22,nm are the m-parameter and n-parameter of two quarks (two anti-quarks or a quark and an anti-quark) involved; N is the number of gluon types in the link; i a is the number of gluons for type i; i m is the m-parameter of gluon type i; i n is the n-parameter of gluon type i. In the “Facts” row of Table 13.2, the “ / type” and “ / type” represent the two signs in numerator and denominator for the q-pair part in (13.10) take the same sign; the “ / type” and “ / type” represent the two signs in the nu- merator and denominator for the q-pair part in (13.10) take opposite signs. Table 13.2A. Gluons links between up quarks. Table 13.2B. Gluons links between dow n quarks.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1263 Table 13.2C. Gluons links between str a nge quar ks. Table 13.2D. Gluons links between charm quarks. Table 13.2E. Gluons links between bottom quarks. Table 13.2F. Gluons links between up and down quarks. Table 13.2G. Gluons links betwee n up and str a nge quarks. Table 13.2H. Gluons links between up and c har m quar ks. Table 13.2I. Gluons links between up and bottom quarks. Table 13.2J. Gluons links between down and strange quarks. Table 13.2K. Gluons links between down and charm quarks. Table 13.2L. Gluons links between down and bottom quarks.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1264 Table 13.2M. Gluons links between strange and charm quarks. Table 13.2N. Gluons links between strange and bottom quarks. Table 13.2O. Gluons links between charm and bottom quarks. Three top quarks r t, g t, b t are not listed in Table 13.2, because there is no regular type strong interaction among them and with other types of quarks. Figure 13.2. Regular type strong interactions among quarks. The multi-link of the same type between two quarks listed in Table 13.2 is represented by a single line. According to Table 13.2, Figure 13.2 shows the regu- lar strong interactions among quarks and anti-quarks. The solid line represents links between quark with quark or anti-quark with anti-quark (the “ / type” and “ / type”). The dashed line represents links between quark with anti-quark (the “ / type” and “ / type”). The dot-dashed lines represent the weakened links between top quark and top anti-quark, which will be discussed later. The strong interactions shown in Table 13.2 and Fig. 13.2 have following features: 1) In general, the hadrons consist of u, u, d, d, , , c, c, b, b can be constructed with the gluons links shown in Table 13.2 and Fig. 13.2 , which are agreed with known experimental facts as shown in the “Facts” row of Table 13.2. 2) For the three lighter quarks u, d, sshown in Fig. 13.2, there are only solid line links for quark with quark or anti-quark with anti-quark among different colors in the same flavor. It means that, the same flavor quarks are permitted to form baryons such as uuu , ddd and sss . But the quark and anti-quark with same flavor are prohibited to form standalone mesons such as uu , dd , ss . In fact, experiments confirmed these conclusions. 3) The neutral meson 2/)( 0dduu is special. Table 13.3 provides a possible explanation for the forma- tion of 0 . The gluons links consist of gluons with mixed “+” and “-” signs for uu and ddto form 2/)( 0dduu via weakened strong interaction. In fact, the weakened strong interaction may explain why 0 has a much shorter mean life s 17 104.8 comparing to , mean life s 8 106033.2 . Table 13.3A. Some gluons links between up quarks with weak- ened strong interaction. Table 13.3B. Some gluons links between down quarks with weakened s tron g inte raction.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1265 4) As shown in Fig. 13.2, for the two heavier quarks, c quarks have only dashed line links between different colors, and bquarks have only one solid line links be- tween different colors. It means that, the same flavor quarks and anti-quark are permitted to form mesons such as cc and bb ; and the same flavor quarks are prohib- ited to form baryons such as ccc or bbb. Experi- ments confirmed these conclusions. 5) There is no link from top quark or top anti-quark to any other quarks or anti-quarks, which means no strong interaction among them. It is confirmed by experiments. No hadrons made of top quark or top anti-quark with other type of quarks or anti-quarks have found. There is no regular link among three top quarks or three top an- ti-quarks either. As mentioned in Section 11, top quark and top anti-quark are produced in pairs. Table 13.4 pro- vides a possible explanation. In which, the links are weakened by the mixed “+” and “-” signs in gluons links. The result of such mixed links is a weakened strong in- teraction between t and t, which may contribute to tt pair’s very short lifetime of s 24 105.0 . In essence, Table 13.2 and Fig. 13.2 provide mathe- matical explanations for strong interactions among quarks, which agreed with known experimental results. The reason for such agreement is due to careful selection of then-parameters for quarks. According to definition 13.1 and Rule 13.1, there is still some room for alterna- tive selections of n-parameters for quarks. But in order to meet all known experimental facts of strong interac- tions among quarks and anti-quarks to forming hadrons, the room for selecting correct n-parameters is limited. Table 13.4. Weakened gluons links betw een top quarks and top anti-quarks. High energy experiments have shown quarks con- finement. When the gluons link between two quarks is broken, a quark and an anti-quark are created at the bro- ken ends. This phenomenon can be explained naturally by SQS theory. According to Definition 13.1, all gluons are made of quark and anti-quark pairs. The broken parts of gluons link are naturally a quark and an anti-quark. According to Definition 13.2, gluons have nonzero n-parameters corresponding to 0/ mn . Does 0/ mn mean gluons having loop-2? The answer is: No. The n-parameter assigned to gluon does not represent loop-2, instead, n is the number of turns of the “spring” made of the loop-1 merged portion as shown in Figure 13.1. However, there is a trick. When a gluon serve as the mediator of strong interactions, its n does act like regular n-parameter as shown in (13.8b). But gluon doing loop-2 job is not necessary mean itself having loop-2. Rule 13.2: The strong interaction between two gluons with parameters aa nm,and bb nm, by transmitting and receiving gluons with parameters i m,i n satisfies the following equations: M iiiba mamm 1 , 83,2,1,, iba , (13.11a) M iiiba nann 1 , 83,2,1,, iba . (13.11b) In (13.11), M is the number of gluon types in the link and i a is the number of gluons of type i. According to Rule 13.2, there are trivial cases with 2 , a mm 1, b mm 2 and a nn 1,b nn 2. Be- sides these trivial cases, there are other possibilities, which serve as the mediator for strong interaction be- tween gluons. Table 13.5 and Fig. 13.3 show some ex- amples of strong interactions between gluons. According to Rule 13.2 and as shown by Table 13.5 and Fig.13.3, the strong interactions among gluons have the following features. The existence of strong interactions among gluons means that strong interactions are nonlinear in nature as expected. In the second column from left, the strong interac- tions are regular type represented by all gluons in the link with the same “+” sign. In the third column from left, the strong interactions are weakened type represented by the gluons in the link with mixed “+” sign and “-” sign. The strong interaction mechanism introduced in this section is based on a link made of gluons sequence, which is a simplified concept. In reality, the scenario is more complicated. Inside a hadron, its valence quarks (valence anti-quarks) are surrounded by a network of gluons including many links. The strong interactions are dominated by the strongest link in the network. As shown in Table.13.2A, in certain cases such as gr uu , there is only one link for regular strong interac- tion. In other cases such as bguu and rb uu , each has two links for regular strong interaction in parallel. Besides, there are weakened links among r u, g u, b u listed in Table 13.3A not shown in Table 13.2A. Among three top quarks r t, g t, b t, there is no link for regular strong interaction. Under such circumstance, the next best option is to find the weakened link. So the overall scenarios are very rich and complicated, but the simpli- fied concept does catch the essence of strong interactions evidenced by its results agreed with experiments.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1266 Table 13.5. Some examples of strong interactions between gluons*. Figure 13.3. Some strong interactions among 8 gluons. The strong interaction mechanism introduced in this section by SQS theory has some similarities as well as differences with quantum chromodynamics (QCD) of the standard model. 1) Both theories have eight gluons serving as the me- diators for strong interactions. 2) Both theories explain the known experimental facts of strong interactions for hadrons. 3) Both theories indicate that strong interactions are nonlinear due to the fact that, there are strong interac- tions among gluons. 4) Both theories explain the confinement of quarks and anti-quarks. 5) According to QCD, gluons exhibit )3(SU symme- try. According to Definition 13.1, the eight gluons are made of eight quark and anti-quark pairs. They also ex- hibit )3(SU symmetries for flavors as well as colors like their constituent quarks. 6) According to QCD, the eight gluons are specifically assigned to a pair of quarks (anti-quarks) to transfer their colors. According to SQS theory, as described in this section, the eight gluons’ function is not specialized. To serve as mediator for a specific strong interaction, a combination of gluons is lined up to make the link. This difference between two theories can be explained by proper combinations of gluons. 7) According to QCD, gluons are represented by com- plex parameters. On the other hand, as presented in this section, the gluons are represented by real numerical pa- rameters. According to SQS theory, the phase of a com- plex number represents intrinsic time. Taking this factor into account, the difference is understandable.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1267 Theorem 13.2: For a hadron made of quarks (an- ti-quarks) and gluons, the gluons’ m-parameters cancel out and the gluons’ n-parameters also cancel out, which do not contribute to the hadron. In other words, only va- lence quarks (valence anti-quarks) m-parameters and n-parameters count for hadron as a composite particle. Proof: The strong interactions are mutual in nature. For a pair of quarks (a pair of anti-quarks, or a quark and an anti-quark), a q and b q, when a q sends a sequence of gluons with summed parameters ii mand ii n to b q, in return b q sends the same sequence of gluons with summed parameters ii m and ii n back to a q with the “-” sign representing opposite direction. As a result, the net changes of parameters for the hadron are: ii ii iimmm 0, ii ii iinnn 0. QED The argument is also applicable to strong interactions between gluons and gluons. Theorem 13.2 greatly simplifies the m-parameters and n-parameters of hadron as a composite particle. In es- sence, for hadron’s m-parameters and n-parameters, only its valence quarks (valence anti-quarks) count, gluons do not count. Theorem 13.2 plays important roles for com- posite particles, which will be presented in Section 19. The set of n-parameters for quarks used in Table 13.2 and Fig.13.2 is a specific selection cited from Table 11.2. It by no means the only selection. In fact, other selections are possible, which is worthwhile to explore further. In this section, a framework is built for strong interac- tions based on mathematics. More works are needed for detailed quantitative results. The basic idea of this section is to treat gluons and strong interactions in terms of mathematics and geometry. It is a step toward the final goal of SQS theory. Section 14. W Z Bosons and Weak Interactions In this section, SQS theory provides a framework for weak interactions based on mathematics. It includes a model for gauge bosons W and 0 along with other mediators associated with weak interactions. W and 0 particles are gauge bosons with mass heavier than 2 /973.4 cGeVM Max of (6.21). Their mod- el should have topological structure similar to the model of top quarks. But top quarks are fermions, and W and 0 are bosons. This problem can be solved by assuming two fermion states 1 Y and 2 Y as constituents. W and 0 are treated as two mixed states of 1 Y and 2 Y. Postulation 14.1: Two fermion states1 Y and 2 Y with spin 2/ and charges 2/e serve as the compo- nents of W and 0 . The mass of 1 Y and 2 Yexceeds max M, according to Rule 6.1, they must appear in pair serving as the con- stituents of W and 0 . In this way, the fractional charge does not show up. According to 2010-PDG data, W, 0 and top quark t have a mass relation: GeVM W023.0399.80 , (14.1a) GeVM Z0021.01876.91 0 , (14.1b) GeVM t9.0172 . (14.1c) GeVMGevMM tZW 9.01720251.05866.171 0 . (14.1d) The mass relation implies that, they are correlated. This is the first clue to determine the parameters of 1 Y and 2 Y. The second clue is W to 0 mass ratio correlated to Weinberg angle )( ZW M : 87667.0757.28cos)(cos88169.0 1876.91 399.80 0 ZW Z WM M M 757.28)( ZW M (14.2) and )12(23146.0)(si 2 ZW Mn are cited from 2010-PDS (p. 101). To combine (14.1d) and (14.2) yields an approximate mass relations for W,0 and top quark: W t ZM M cos1 , W W t WM M cos cos1 . (14.3) The third clue comes from an apparent symmetry in the Elementary Particles Table of Table 18.2 of Section 18, in which W,0 are located at right end and photon , graviton at left end. According to SQS theory, is correlated with electron and is correlated with up red quark. Accordingly, 0 and W should be corre- lated with taon and top blue quark. Keeping these clues in mind, the number parameters are selected for 1 Y and 2 Y as: For 1 Y: 53 1m, 371 1n, 33102475 1p, (14.4a) For 2 Y: 61 2m, 427 2 n, 38099075 2p. (14.4b) Formula (11.1b) is used to calculate YO,2 for 1 Y and 2 Ywith 3/1 replaced by 2/1 . The calculated parameters of 1 Y and 2 Y are listed in Table 14.1. 1 Y and 2 Yare not free standing particles, they serve as two branches of Wand 0 . According to Table 14.1, except the original numerical parameters m, n, p difference, all other parameters are the same for 1 Y and 2 Y, which is similar to the three branches of charged leptons trefoil model. 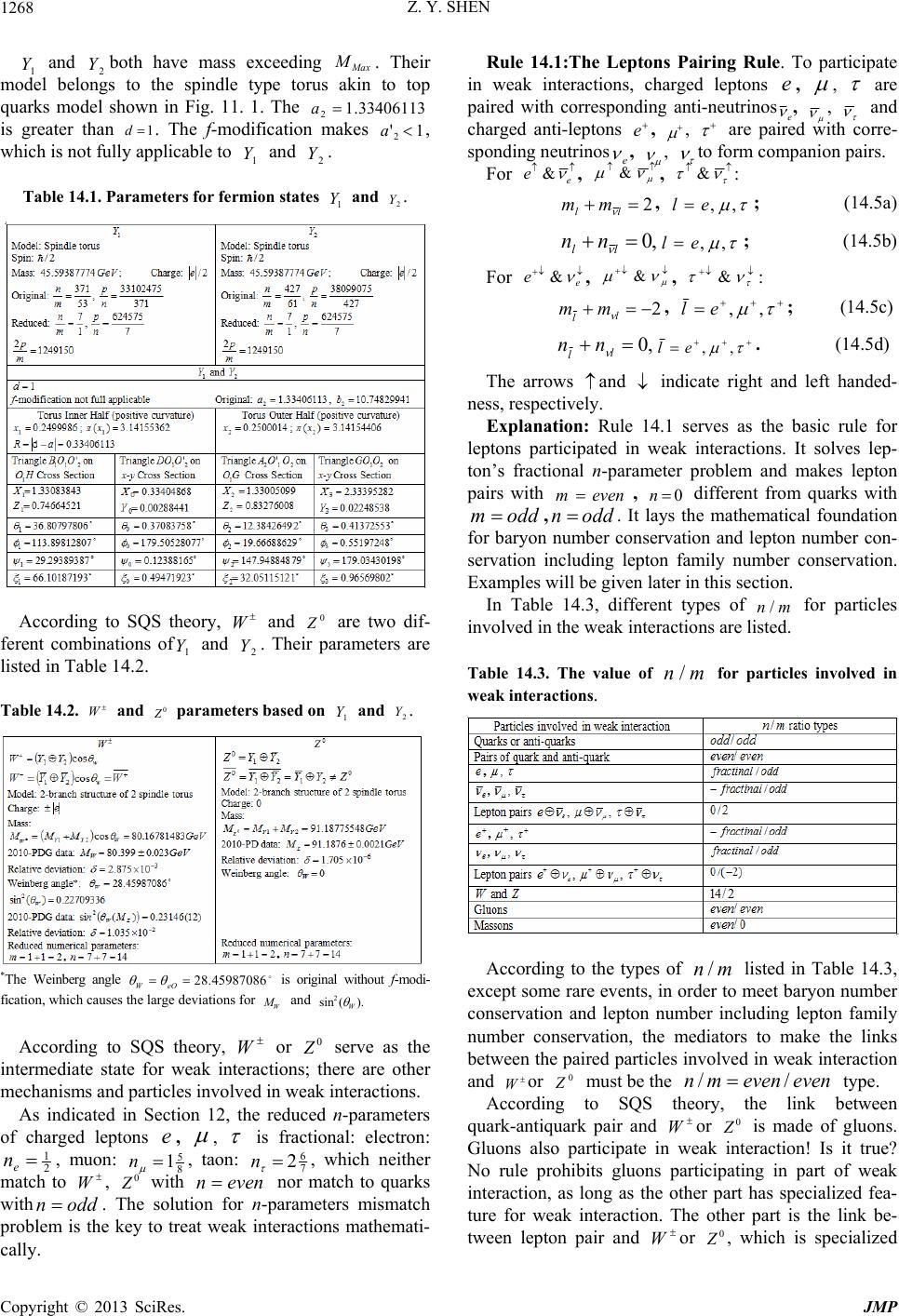 Z. Y. SHEN Copyright © 2013 SciRes. JMP 1268 1 Y and 2 Yboth have mass exceeding Max M. Their model belongs to the spindle type torus akin to top quarks model shown in Fig. 11. 1. The 33406113.1 2a is greater than 1d. The f-modification makes 1'2 a, which is not fully applicable to 1 Y and 2 Y. Table 14.1. Parameters for fermion states 1 Y and 2 Y. According to SQS theory, W and 0 are two dif- ferent combinations of1 Y and 2 Y. Their parameters are listed in Table 14.2. Table 14.2. W and 0 parameters based on 1 Y and 2 Y. *The Weinberg angle 45987086.28 eOW is original without f-modi- fication, which causes the large deviations for W M and ).(sin2W According to SQS theory, W or 0 serve as the intermediate state for weak interactions; there are other mechanisms and particles involved in weak interactions. As indicated in Section 12, the reduced n-parameters of charged leptons e, , is fractional: electron: 2 1 e n, muon: 8 5 1 n, taon: 7 6 2 n, which neither match to W, 0 with evenn nor match to quarks with oddn . The solution for n-parameters mismatch problem is the key to treat weak interactions mathemati- cally. Rule 14.1:The Leptons Pairing Rule. To participate in weak interactions, charged leptons e, , are paired with corresponding anti-neutrinose , , and charged anti-leptons e, , are paired with corre- sponding neutrinose , , to form companion pairs. For e e &, &, &: 2 ll mm , ,,el ; (14.5a) ,0 llnn ,,el ; (14.5b) For e e &, &, &: 2 l lmm , ,,el ; (14.5c) ,0 l lnn ,,el . (14.5d) The arrows and indicate right and left handed- ness, respectively. Explanation: Rule 14.1 serves as the basic rule for leptons participated in weak interactions. It solves lep- ton’s fractional n-parameter problem and makes lepton pairs with evenm , 0 n different from quarks with oddm ,oddn . It lays the mathematical foundation for baryon number conservation and lepton number con- servation including lepton family number conservation. Examples will be given later in this section. In Table 14.3, different types of mn / for particles involved in the weak interactions are listed. Table 14.3. The value of mn/ for particles involved in weak interactions. According to the types of mn / listed in Table 14.3, except some rare events, in order to meet baryon number conservation and lepton number including lepton family number conservation, the mediators to make the links between the paired particles involved in weak interaction and Wor 0 must be the evenevenmn // type. According to SQS theory, the link between quark-antiquark pair and Wor 0 is made of gluons. Gluons also participate in weak interaction! Is it true? No rule prohibits gluons participating in part of weak interaction, as long as the other part has specialized fea- ture for weak interaction. The other part is the link be- tween lepton pair and Wor 0 , which is specialized  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1269 for weak interactions. Notice that, in Table 14.3, the e e , , pairs and Wor 0 both have 2// evenmn. Since 022 and eveneveneven , the boson to make the link between e e , , and W or 0 must have 0m and evenn . Gluons are not qualified for the job. A new type of scalar bosons with 0m and evenn is introduced to do the job. Definition 14.1: Eight scalar bosons called massons labeled as i G (83,2,1i) are made of eight pairs of quark and the same type of anti-quark as: rrccG 1, ggccG 2, bbccG 3, rr bbG 4, gg bbG 5, bbbbG 6, rrttG 7, ggttG 8; (14.6a) jjiqqG , 83,2,1 i, grbgrbgr ttbbbcccj ,,,,,,,. (14.6b) Explanation: According to SQS theory, quarks have counterpart bosons. As shown in the Elementary Parti- cles Table of Table 18.2, r u has its counterpart ; b t has its counterpart ; r d, g d, g u, b d, b u, r s, g s, b s have their counterparts 1 g, 2 g, 3 g, 4 g, 5 g, 6 g, 7 g, 8 g, respectively. There are eight boson vacancies left in Table 18.2. To fill these vacancies, SQS theory introduces eight neutral scalar bosons with spin 0 as the building blocks to make the link between the lepton pairs e e , , or e e , , on one hand and W or 0 on the other for weak interac- tions. According to Definition 14.1: ijjjjjjiGqqqqqqG , 83,2,1i,grbgrbgr ttbbbcccj ,,,,,,,. The anti-particle of a masson is itself: ii GG, 83,2,1 i. (14.7) The parameters of eight massons are listed in Table 14.4. Table 14.4: The parameters of eight masson )82,1( iGi. The masson model is shown in Fig. 14.1. The twisted loop model is similar to gluon model with a difference: The loop is twisted in n turns without the small loops at two ends corresponding to masson with spin 0. As shown in Section 13, gluons are massless with spin h. Massons have mass with spin 0 as listed in Table 14.4. Gluon and masson both are bosons composed of a pair of quark and anti-quark. Why they are different in terms of mass and spin? The answer is the different ways to get their m-parameter and n-parameter from m-parameter and n-parameter of their constituent quark and anti-quark. The situation is similar to the massless photon with spin h and the “heave photon” as the inflaton having mass and spin 0. The details will be given in Section 24. Figure 14.1. Masson’s model. The distinguish features of massons are: (1) They are neutral scalar bosons with spin 0s; (2) Their numeri- cal parameters are 0// evenmn ; (3) They are pure mass stuff as the name implied. According to SQS theory, there are three types of bo- sons involved in weak interactions, namely W or 0 , gluons and massons. In which, W or 0 serves as the intermediate state; gluons and massons serve as the building blocks for two types of transitional links. Take muon decay as an example to demonstrate the weak interaction between leptons. 2010-PDG data show that, muon decay mode e e has branch- ing ratio %100/ i. As shown in Section 12 and Rule 14-1, the reduced m-, n-parameters of electron, muon and associated anti-neutrinos are: Electron e: 1 m, 2/1 n; (14.8a) Electron anti-neutrino e : 1 m, 2/1 n. (14.8b) Muon : 1 m, 8/51 n; (14.8c)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1270 Muon anti-neutrino : 1m, )8/51( n. (14.8d) In (14.8), the arrows in particle symbols indicate these particles with right-handedness. W serves as the intermediate state with reduced m-, n-parameters as: W gauge boson: 2m, 14n. (14.9) The “-” sign of n-parameter for W is due to the fact that W is the anti-particle of W. According SQS theory, e e decay mode includes two processes with two links: Process-1 with link-1: W ; Process-2 with link-2: e eW . In process-1, to replace is to represent the leptons pair of required by Rule 14.1. In presentation, serves as an input. In reality of muon’s decay, serves as an output. According to Feynman diagram, as input and as output are equivalent. Look it the other way, for process-1, W takes the as an input from a & pair out of vacuum to avoid violation of lepton number conservation and leaves the as decay prod- ucts. In this way, W boson status is justified and the lepton family number conservation law in process-1 and process-2 both are satisfied. The two processes are illustrated in Table 14.5 to show the makeup of two links. Table 14.5A. process-1 for muon decay mode e e . Table 14.5B. Process-2 for muon decay mode e e . As shown in Table 14.5A and B, the weak interaction in the muon decay mode e e has two links and both links are made of three massons 1 G, 5 G and 6 G. Take the free neutron decays to proton as an example to demonstrate the weak interaction involved baryons and leptons. According to 2010-PDG data, free neutron decay mode e epn has branching ratio %100/i. The mechanism of such decay is a down quark in the free neutron transforms into an up quark changing neutron to proton plus an electron and an elec- tron anti-neutrino: e eud . The decay mode also has two processes with two links and an intermedi- ate state. As shown in Section 11, the m-, n-parameters of three up anti-quarks and three down quarks are: r u: 1 m, 1 n; g u: 7m, 3n; b u: 13 m, 5 n. (14.10) r d: 3 m, 1 n; g d: 5m, 3n; b d: 11 m, 5 n. (14.11) In (14.10), bgr uuu ,, to replace bgr uuu,, has the same reason as to replace in the first example. The two processes are illustrated in Table 14.6 to show the makeup of two links. Table 14.6A. Process-1 for down quark decay mode e eud . Table 14.6B. Process-2 for down quark decay mode e eud . In this example, the process-1 is quark and anti-quark transforms to W mediated by gluons. The process-2 is W transforms to leptons mediated by massons. These two examples serve as the typical cases for the regular weak interactions. The examples show that Rule 14.1 serves the purpose well. Other cases can be treated by the same way. For the rarely occurred weak interactions, the violation of baryon number conservation and/or lepton number conservation will be treated differently. Definition 14.2: The weak interactions are classified into two types. Regular type: The weak interactions meet baryon number conservation and lepton number conservation in- cluding lepton family number conservation. Rare type: The weak interactions violate baryon num- ber conservation or lepton number conservation includ- ing lepton family number conservation. The weak interaction mechanism proposed by SQS theory has following features. 1) It is based on mathematics. SQS theory provides a mathematic framework for weak interactions. 2) In general, the rules introduced in this section meet the requirement of baryon number conservation. A single  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1271 quark or anti-quark cannot participate in regular weak interaction, because its oddoddmn // . To partici- pate in regular weak interaction, quark must pair with anti-quark to have combined parameters of evenevenmn // . 3) In general, the rules introduced in this section meet the requirement for lepton number conservation includ- ing lepton family number conservation. A single lepton or anti-lepton cannot participate in the regular weak in- teraction, because its oddfractionalmn// . To par- ticipate, the lepton is paired with its companion an- ti-neutrino to form a pair. The pair’s 2/0/ ppmn along with 2/14/ WW mn of W or 0 yield a combined 0/)/()(/ evenmmnnmn WpWpcombcomb , which naturally requires massons with 0//evenmn to serve as building blocks of the link between them. In this way, the lepton number and lepton family number are conserved, and the introduction of massons is justified. 4) For SQS theory, the conservation laws for baryon number and for lepton number including lepton family number are required by mathematics represented by Rule 14.1. 5) The rules introduced in this section are also appli- cable to some rare events. For instance, according to 2010-PDG data, the meson 0 has two rare decay channels: eeee with 5 10)16.034.3(/ i and ee with 8 10)33.046.6(/ i. For these two decay channels, there is no anti-neutrino involved, but lepton numbers including lepton family number are conserved. Because 0 is made of 2/)( 0dduu , the explanation for its quark and anti-quark part is similar to that of free neutron decay case. For the leptons part, the n/m ratio of e is 2/)2/1(/ mn, which is the same as e . The explanation for the leptons part is the same as two previous examples. But e is not e , Rule 14.1 is violated and the decay mode belongs to rare type. 6) It also provides possible mechanisms for the rare weak interaction events which violate lepton family number conservation. For instance, according to 2010- PDG data, 0 has three other very rare decay channels: channel-A, e 0 with 10 108.3/ i; chan- nel-B, e 0 with 9 104.3/ i; channel-C, ee 0 with 10 106.3/ i. Let’s take a look at channel-A. the m-parameters and n-parameters involved are: For : 1 m, 8 13 8 5 1 n, 1 8/13 m n; (14.12a) For e: 1 e m, 2/1 e n, 1 2/1 e e m n; (14.12b) For 0 : 2 0 Z m, 14 0 Z n; 2 14 0 0 Z Z m n. (14.12c) In this case, the problem is that, the n/m values of (14.12) do not match as the way e e did in Table 14.5B. To solve the problem, let’s multiply numerator and denominator of mn/ with 8 and 10 for and e, respectively. For : 8 13 8 8 ' ' m n m n, (14.13a) For e: 10 5 10 10 ' ' e e e em n m n, (14.13b) For e : 2 18 108 513 '' '' e e mm nn . (14.13c) The process-2 with link-2 can be carried out the same way as previous examples. For eZ 0: 0 4 22 1814 )''( )''( 0 0 eZ eZ mmm nnn . (14.14) The link of (14.14) can be made of 62 3GG with 003 118383 0 4 . (14.15) The same approach is applicable to channel-B and channel-C. Is multiplication of same number to numera- tor and denominator of mn/ legitimate? From math- ematic viewpoint, the answer is: Yes, of cause. If the reduction for the original mn/ is legitimate, so is the multiplication. From physics viewpoint, the multiplica- tion of an integer N to numerator and denominator of mn / means that, the cyclic movements in loop-1 and loop-2 both take N cycles instead of 1 cycle. For instance, in the case of (14.13), the process occurred at the mo- ment that, takes 8 cycles and e takes 10 cycles. The probability for such events occurred simultaneously determines the / ivalue for that decay channel, which explains the rarity of such decay channels. 7) The extremely rare “sphaleron” phenomenon [13] converts three baryons into three leptons which violate both baryon number conservation and lepton number conservation. Three baryons contain nine quarks. The combination has oddoddmn // , which serves as the mathematical origin for violating baryon number con- servation. Three leptons combination has  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1272 oddfractionmn //, which serves as the mathematical origin for violating lepton number conservation. The regular rules introduced in this section are not valid. But as long as multiplication can apply to mn/, the “sphaleron” phenomenon can be interpreted mathematically. In fact, almost any weak in- teraction rare event can be interpreted mathematically. The real difference is the probability of its occurrence. These features indicate that, the weak interaction rules have the capability and potential to explain weak interac- tions in terms of mathematics. But there are some ques- tions. 1) Is it possible that gluons and massons bypassing W and 0 directly link quark-antiquark pair to lepton pairs e e , or ? 2) Massons are scalar bosons. Are they qualified to serve as mediators for weak interactions? 3) Why gluons and massons are different? After all, both are quark anti-quark pairs and located in the same row in the Elementary Particles Table of Table 18.2. 4) 1 Y and 2 Y having mass around 2 /6.45 cGeV are originated from g t and b t having mass around 2 /1.171cGeV. There is a reversed mass gap between them. What’s to do with the mass gap? Question-1 and Question-2 are correlated. If massons must attach to W and 0 , it answers both questions. In fact, there are clues for massons attachment to W and 0 . If the )2(SU group symmetry associated with electroweak interaction is perfect, W and 0 have no mass. The )2(SU symmetry must be broken for W and 0 to gain mass. Massons may play a role to pro- vide mass for breaking the symmetry. Regarding Question-3, the spin and mass differences of gluon and masson are originated from their models as explained previously. The answer of Question-4: The reversed mass gap of is filled by massons some of them with negative sign. The negative sign for massons is permitted as shown in Table 14.5 and Table 14.6b. It shows that massons are in some way attached to W and 0 . Superficially, the introduction of eight massons seems to make theory complicated. In fact, it is just the opposite. The way SQS theory treated strong interaction and weak interaction is to reveal their mathematic nature in the simplest possible way. Gluons and massons both are made of quark and anti-quark pairs. This approach greatly simplified the theory. From SQS theory view- point, quarks and anti-quarks serve as the basic elements. Gluons and massons are composed with the basic ele- ments in different ways to serve their specific purposes. Moreover, the mathematic framework of weak and strong interactions are self-consistent without artificial additions. The whole approach shows simplicity and elegance. In Section 18, a new gauge boson will be introduced. It also plays some role for the weak interactions involved hadrons decay. In this section, a framework of weak interactions is in- troduced. It has the capability and potential to explain weak interactions including rear events based on mathe- matics. But it only provides a framework; some details need to be finalized. For instance, the different ways 1 Y and 2 Y are combined to make W and 0 with dif- ferent masses, which need more works to nail down the details. Section 15. Unified Interactions Traditionally Grand Unification Theory (GUT) is to uni- fy electromagnetic, weak, strong interactions, in which gravity is not included. For SQS theory, GUT means unification of all four interactions including gravity. The unification of interactions takes consecutive stages. Starts from electromagnetic interaction, weak interaction joints in, then strong interaction joints in, finally all in- teractions are unified with gravity. The GUT provided by SQS theory is based on mathematics. In xEDSx of (9.3), the second summation term not included in the original DS-function of (6.1) represents interactions mediated by bosons, which are originated from Fourier transformation of the added -function terms in kEDS k of (9.1). For convenience, xEDSx is divided into four summation terms labeled as A, B, C, D: ., , 2 1 , 2 1 ; 2 1 2 1 )5.0(4)5.0(444 )5.0()( 5.045.0444 )5.0( 22 2 2 2 2 22 j xjij j xjij j xj j xj j xjij j xjij j xj j xj x eeDeeC eBeA DCBAeeee eexEDS (15.1) Term-A and term-B represent fermions, while term-C and term-D represent bosons for interactions. According to their variables and )5.0( j versus and )5.0(x , term-C and term-D are related to term-A and term-B, respectively. If the term-A variable is in the )25.00( x range with )(x; then the term-B variable )5.0( x is in the 5.0)5.0(25.0 x range with )5.0( x. For the torus model, )(x and )5.0( x correspond to its inner half and outer half, respectively. It implies that, term-B and term-D corresponding to torus outer half are related to the GWS-triangle representing electroweak interaction. It is  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1273 natural to assume term-D related to electroweak interac- tion. With the same reason, term-A and term-C corre- sponding to torus inner half are related to the CKM-triangle representing hadrons decay. It is natural to assume term-C related to electroweak and strong interac- tions. Let’s take this argument as pre-assumption and verify it by its results later. In the )5(SU Grand Unified Theory [14,15], a sup- pression factor SF is introduced: 4 GUT proton M M SF . (15.2) 2 /)23(938272013.0 cGeVM proton is the proton mass; and 215 /10~ cGeVMGUT is the )5(SU GUT mass scale for the unification of three interactions except gravitation. In a previous paper [16], the author borrowed this concept and utilized (15.2) to calculate the mass scale ew M for the unification of elec- tromagnetic and weak interactions: 4ew proton ew SF M M. (15.3) In which, ew SF is the redefined suppression factor for electroweak unification derived from the dominate term of term-D in (15.1), in which is replaced by b x and is replaced by )( b x : 937019456.20 )( 10 )()5.0(4)5.0)((4 104234326.1 2 e eeeSF bbbb x orj xxjijx ew .(15.4) The term with 10 orj represents the dominate term, which has the maximum magnitude value in term-D. It dominates the suppression effect, because oth- er terms with 1j have much less value comparing to 10 orj term. In (15.4), the value of 5 108477191821861791.1 b x is defined by (2.22), the value of 37019456.20)( b x is cited from Table 3.1, in which only 8 digits after the decimal point are taken. Substituting (15.4) into (15.3) yields the mass of a scalar boson 1 U to unify electromagnetic and weak interactions: 2 49 4/75469.152 104234326.1 938272013.0 cGeV SF M M ew proton ew . (15.5) 2 /75469.152 cGeVM ew is within LHC capability, it can be verified experimentally. Corresponding energy GeVcMEewU 75469.152 2 1 of the scalar boson 1 U serves as the energy scale to unify electromagnetic and weak interactions. The suppression factor ews SF for electroweak-strong unification is derived from the term-C of (15.1). It is evaluated at 10 10882111819946879.5 a x of (2.21) and cited from Table 3.173631245.36)( a x with 8 digits after decimal point: 6473631245.364 )(4 1 )(4)(4 1052226012.1 2 eeeeSF aaaa x j xxjijx ews . (15.6) In (15.6), the 1j term is taken as the dominate term instead of the 0 j term, because 0 j term represents the summation of all probabilities equal to 1 required by unitarity. Using the value of ews SF giving by (15.6), the mass ews M of a scalar boson 2 U to unify electroweak and strong interactions is determined as: 215 16)( 4 /1044708.8 1011076508.1 938272013.0 cGeV e M SF M Ma x proton ews proton ews . (15.7) In standard model, the electroweak-strong unification is called the grand unification. In SQS theory, the grand unification is reserved for the one including gravity. Before dealing with the grand unification, let’s look at the principles suggested by SQS theory. 1) There are two types of forces (force is synonymous to interaction). The long range force including electro- magnetic force and gravitational force, both have unlim- ited effective range. The short range force including weak force and strong force has limited effective ranges. The first principle for grand unification is: All forces must be unified to a single force of the long range type. The reason is simple, long range includes short range, while short range does not include long range. According to the first principle, the weak force and strong force are not qualified as the final unified force. 2) Second principle: The force with selectivity is not qualified as the final grand unification force. Electro- magnetic force is only for charged particles. It is not qualified as the final unified force. Otherwise, the forces between electrically neutral particles are left out after the grand unification. 3) According to the first and second principles, the only force qualified as the final unified force is the grav- ity. The next question is: In the grand unification, which force is one finally unified with gravity? The answer comes from the Random Walk Theorem. In Section 4, the ratio of electrostatic force to gravity for a pair of electrons is 2 2 /4e G E GE N f f R . (4.19)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1274 In which, electron converting factor e N is interpreted as the ratio of long path to short path defined according to the Random Walk Theorem. It is natural to start with GE R/ to explore grand unification. According to SQS theory, grand unification happens at: 1/ /GEGEffR. (15.8) Substituting (15.8) into (4.19) yields: 2 e N. (15.9) In (15.9), the fine structure constant as a running constant varies with energy. The closest value available at such high energy level from 2010-PDG (p.126) is: 015.0916.127/1)( Z M . (15.10) )( Z M is the value of at 22 Z MQ around GeV91 . Substituting (15.10) as into (15.9) yields the con- verting factor at grand unification scale: 06279805.71 )( 2 Z GUT Planck GUT M M M N . (15.11) Corresponding length is the grand unification length scale: mLNLPGUTGUT 3335 10148552.11061625.106279805.71 . (15.12) The mass of the scalar boson 3 U for grand unifica- tion is: 2189 /1007948213.1109243515.1 2 )( 2 )( cGeVKg G hcM M M N M MZ Planck Z GUT Planck GUT . (15.13) For comparison, the suppression factor GUT SF and )( GUT x for grand unification are reversely calculated from GUT M as: 73 4 18 4 1070759593.5 1007948213.1 938272013.0 GUT p GUT M M SF , (15.14a) 58672847.41 4 )ln( )( GUT GUT SF x . (15.14b) Table 15.1 listed the calculated parameters for three types of unifications proposed by SQS theory. Table 15.1. The parameters for three types of unifications. *Note: 58672847.41)( GUT x and 73 107076.5 GUT SF are reversely calculated from GUT M . It is interesting to find out that, the mass ratio of GUT M to ews Mis very close to 1 )( Z M : 1 )(79353.127 Z ews GUT M M M . (15.15) The number 79353.127 is so close to the medium value of 916.127)( 1 Z M cited from 2010-PDG (P.126) data with a relative deviation of 4 10574.9 . Another way to check is to combine (15.13) and (5.15): 83433738.127 2 )( 3/2 1 ews Planck ZM M M . (15.16) The relative deviation is reduced to4 10384.6 . With such high accuracy, it is very unlikely that (15.15) and (15.16) are by coincidence. In other words, these correla- tions are real and mean something worthwhile to dig in. From theoretical perspective, (15.15) is an important finding, which has the following significances. 1) The parameters of grand unification and elec- troweak-strong unification are correlated with the fine structure constant)( M . )(M as a running constant, its reversed value varies from 035999084.137)( 1 e M to 916.127)( 1 Z M , a decrease of %655.6 for 5 10~ increase of energy scale. In the next 16 10 increase of energy scale to GeV 18 10 , the value of 1 )( M is only decreased 4 10384.6 . It shows a typical asymptotic behavior toward saturation: )()( GUTZ MMM . In other words, the majority of 4 10384.6 relative de- viation is not necessarily caused by error. 2) Combining (15.15) and (15.16) and replacing )( Z M with )( GUT M yields the correlation of three masses: Planck GUT GrandGUTews M M MMM 2 )( )( 2/3 . (15.17) Due to the asymptotic nature of fine structure constant, the replacement of )(Z M with )( GUT M in (15.17) only has a minor effect. 3) More importantly, the finding proves an important evidence for the consistency of two very different meth- ods used to deal with unifications for SQS theory. ews M is calculated according to the suppression factor from (15.6) and formula (15.7) as a borrowed formula, )( a x is originated from the S-equation. On the other hand, GUT Mis determined by the equality of static electrical force and gravity along with the converting factor GUT N originated from Random Walk Theorem. These two very different methods are consistent with a discrepancy less than 4 10384.6 . It gives the legitimacy for both meth- ods. After all, the borrowed formulas (15.3), (15.5) and (15.7) are legitimate; and the ways to determine suppres- sion factors by )( a x and )( b x are legitimate as well. It gives more credit to the theoretical results listed in Table 15.1. 4) It proves a way to convert proton mass proton M and  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1275 converting factor proton N to the Planck mass Planck M. Substituting ews M of (15.7) into (15.17) yields: Planck x GUTproton MeMM a)( 2/3 )( 2 1 , (15.18a) )( 2/3 )( 2 a x GUTproton Planck proton eMM M N . (15.18b) Proton is not an elementary particle. It composed of three quarks and many gluons. For such a complex sys- tem, its mass and converting factor can be derived from three mathematic constants, , e, a x and a running constant )( GUT M by (15.18). It is a surprise. This correlation is important in two senses. First, SQS theory is based on three physics constants, h, c, G and in principle no other physics inputs. The proton M in (15.3), (15.5), (15.7) is exceptional. With the help of (15.18a), proton M is replaced by Planck M, proton mass is no longer a physics input for SQS theory. Second, most formulas and equations in this paper can be traced directly or indirectly back to the first principle of SQS theory. (15.3), (15.5), (15.7) are exceptions, which are borrowed from other theory. With the help of (15.18), the problem is solved. For instance, ews M and ew M are expressed as: G hc MM M MMMGUTPlanck GUT GUTGUTews 2 )( 2 )( )( 2/3 2/3 . (15.19) G hc e M M e M M e M Mbababaxx GUT Planck xxGUT GUT xx GUT ew 2)( 2 )()( 4/)()( 2/3 4/)()( 2/3 4/)()( . (15.20) Only mathematic constants and basic physics con- stants appear in (15.19), (15.20). The value of converting factor GUT N given by (15.11) is twenty one orders of magnitudes less than electron converting factor: 23 10501197.1/ Pee LN . (6.16) The tremendous reduction of converting factor is the nature of random walk. As shown in Section 4, when the distance l of two electrons is equal or greater than its Compton wavelength eC , its converting factor is fixed at 23 10501197.1/ Pee LN , which is represented by a flat straight line on the )(lNe versus ldiagram shown in Fig. 4.1. This is the macroscopic scenario. When the distance of two electrons is reduce to eC l , the con- verting factor )(lNe starts to vary. According to Ran- dom Walk Theorem, the number of steps along the ran- dom walk path rw n is 2 strw nn . (15.21) st n is the number of steps along the straight line distance between two electrons. The ratio of random path length and straight line distance is: ststrwstrw nnnR / /. (15.22) strw R/ is linearly decreases with decreasing st n. In this region, )(lNe has a linear relation with l, which is represented by a straight line with 45 angle to the l-axis in )(lNe versus l diagram shown in Fig.4.1. The line stops at the grand unification length scale given by (15.12): mLNL PGUTGUT 33 1014855.1 . This process has its deeper meanings, which will be discussed in Section 16. As a summary of this section, let’s look at the process of unifications. 1) The electrical force and magnetic force are unified by Maxwell equations with no specific length scale. 2) At the length scale mLew 18 1011656.8 , weak force joints with electromagnetic force to unify as elec- troweak force. 3) At length scale mLews 31 1046778.1 , strong force joints with electroweak force to unify as elec- troweak-strong force. 4) Finally, at length scale mLGUT 33 1014855.1 , electroweak-strong force is unified with gravity, and all four forces become one. In the consecutive stages of the unifications process, the electromagnetic force, acting as the carrier, picks up other forces at different length scales and carries them to the final stage. At the final stage, all forces are united to gravity. This process follows the principles described at the beginning of this section. The electromagnetic force acting as the carrier has a deep reason. It is the force has direct connection with gravity via the random walk process. This is another example to show the importance of the Random Walk Theorem and its origin, the SQS theory Fundamental Postulation of Gaussian Probability. In some other source [17], fine structure constant at Z M has a value 020.0957.128)( 1 Z M different from PDG-2010 015.0916.127)( 1 Z M . The dis- crepancy indicates a different asymptotic path from 1 )( Z M towards 1 )( GUT M . It does not change the conclusion of the intrinsic link betweenews M and GUT M. In Section 23, the unification length scales ews L and GUT L serving as milestones play important roles in cos- mic history. In Section 24, a universal formula for the fine structure constant )(M will be given. Section 16. Logistic Equation and Grand Numbers In this section, an equation is discovered by 16-digit nu- merical calculation. It reveals the connections among logistic recurrence process, converting factor, Gaussian probability, random walk, S-equation and grand number  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1276 phenomena. It also provides important clues related to vacuum structure, cosmic history and finite sporadic Lei group. In Section 15, the converting factor of the scalar boson 3 U representing the grand unification is: 06279805.71)(2 1 ZGUT MN . (15.11) An equation is discovered by using 16-digit numerical calculation, which provides connection of the electron converting e N to other constants: 0106062632564145.4)(22141 )(2 1 e rx eMeN . (16.1) Equation (16.1) is not derived from the first principle. It is necessary to provide all information in details. On (16.1) right side, the number 14 106062632564145.4 is restricted by the resolution of 16-digit numerical cal- culation. It actually equals to zero. The values of two terms on left side of (16.1) are: 3825524601809.7322 1)( rx eeN , (16.2a) 3825524601809.73)(21 e M . (16.2b) It proves the right side of (16.1) actually equal to zero, which serves as one of evidences that equation (16.1) is not by coincidence. In (16.1), the following constants are cited from the medium value of 2010-PDG data, or derived from the S-equation. Electron converting factor: ePlancke MMN /, (16.3a) Planck mass: cL h M P Plank, (16.3b) Planck length: mLP35 1061625.1 , (16.3c) Electron mass from 2010-PGD data: kgMe31 1010938215.9 , (16.3d) Planck constant from 2010-PDG data: Jsh34 1062606896.6 , (16.3e) Speed of light in vacuum from 2010-PDG data: smc/1099792458.28 , (16.3f) From 2010-PDG data (p.126): 035999084.137)( 1 e M , (16.3g) From S-equation solution for electron: 200378771029244.3)125.0()(1 x. (16.3h) In Appendix 5, a brief introduction of logistic equation is presented. is a parameter of the logistic equation: )1( 1iii xrxx , 3,2,1,0i. (A5.3) Logistic equation represents a recurrence process with close connection to chaos theory. i x as a function of demonstrates different behaviors in different regions of r shown in Table 16.1. Table 16.1. The typical behaviors of i x in different ranges of values. In (16.1), the logistic parameter is: 3244445700363330.3 rrrc. (16.4) 5699457.3 c r, (16.5a) 5 1006330324.9 r. (16.5b) c r is the threshold of parameter . When c rr, the logistic recurrence process becomes chaotic. In the equation (16.1), as shown by (16.5), the differ- ence between parameter and c r is 5 1006330327.9 r. The relative deviation is: 5 10539.2/ c rr . (16.6) The value of just a litter bit more than the thresh- old of 5699457.3 c r. At that point and beyond, the logistic recurrent process becomes chaotic. It is important to point out that, 5 10539.2/ c rr does not all contribute to the error of (6.1). In fact, could be interpreted as the logistic recurrent process go- ing into chaotic region a coup of more steps. The error of (16.1) is less than 5 10536.2/ c rr. With such high accuracy, equation (16.1) cannot be by coincidence. We should take it seriously and dig in deeply. The second term on the left side of (16.1) is: 3825524601809.73)(2 1 e M . (16.2b) Obviously, (16.2b) is the electron version of (15.11) with the )(Z M replaced by )(e M at electron mass scale as it should be. Let’s look at the logistic equation (16.1) as a progres- sive process with as a variable. To show )(rNe as a function of . Rewrite (16.1) as: 0)(2)(2 1 )( 2 1 MerN rr e . (16.7) In (16.7), )( 1M is a running constant. The prob- lem is that )( 1M value varies with mass scale M. The experimental data of )( 1M are available only at a  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1277 couple of discrete points. 2010-PDG (p.126) data pro- vides: 035999084.137)( 1 e M . (16.3g) In Section 15, the value of )( 1Z M is cited from 2010-PDG (p.126) data as: 015.0916.127)( 1 Z M . (15.10) Fortunately, as shown in Section 15, above Z M mass scale the value of )( 1Z MM asymptotically ap- proaches saturation. Table 16.2 lists the related parame- ters as a function of . In which, )( 1e M is used at 2 cM e energy scale and )( 1Z M medium value is used for at and beyond 2 cM Z energy scale and its variation is ignored. Table 16.2. Parameters of electron logistic process. In Table 16.2, the logistic recurrent process belongs to the variable parameter type, in which parameter var- ies. It starts at 29898133.0r and stops at 57003633.3r. In the process, besides the three milestones, 1 , 2 , 3r, the other milestones correspond to elec- tro-weak, electroweak-strong and grand unifications are also listed. The term with 11 10874529.3)( ee NrN corresponds to electron intermediate state, the e-boson state, related to cosmic inflation will be explained in Sec- tion 23. Table 16.2 clearly demonstrates the dynamic nature of electron converting factor )(rN e. It provides a convinc- ing interpretation of )(rN e as a running constant. In essence, the variation of )(rN e is a random process originated from two correlated sources. One is the ran- dom walk process described in Section 4 and the other is the logistic recurrent process. In fact, i x and )1( i x of (A5.3) can be interpreted as binary probabilities. In some way, i x and )1( i x are related to the probabilities in the random walk. The details of the correlation are up to further exploration. With the help of logistic process, the peculiar behavior of )(lNe in Section 4 is understood now. Why )( ee lN is a running constant? Because its logistic process belongs to the varying parameter type. Why )( eCe lN does not show asymptotic behavior? Be- cause the logistic process abruptly stops at rrrc and becomes chaotic. This is the hidden scenario revealed in this section. Logistic recurrent process not only provides reasonable explanation for the peculiar behaviors of the converting factor )(lNe, but also links it to other constants such as c r and )(M . In Table 16.2, at the starting point of logistic process, 06279805.71)29898133.0( rNe. (16.8) It is the same as: 06279805.71 )( 2 Z GUT Planck GUT M M M N . (15.11) 06279805.71 GUT N is the converting factor for sca- lar boson 3 U representing grand unification, while 06279805.71)29898133.0( rNeis electron’s convert- ing factor at GUT scale. Why are these two numbers equal? The apparent reason is that they use the same )916.127/(1)( Z M . The deeper reason is that, at the GeVcM GUT 182 10~ energy scale, electron mass is in the same order of 3 U mass, which far exceeds Max M. Ac- cording to Rule 6.1, such heaver fermions must appear in pair; and a pair of fermions is a boson. It demonstrates the consistency of (15.11) from grand unification and (16.8) from logistic process of electron. Equation (16.1) is for electron. The corresponding taon version is: 01044441263880373.3)(22 131 )( 2 11 MeNrx . (16.9) The data in (16.9) are from the following sources: From 2010-PDG data: 19 1031732.4/ MMNPlanck , (16.10a) From 2010-PDG data: 015.0444.133)( 1 M, take 444.133)( 1 m. (16.10b) From S-equation: 268531416714823.3)526282499640520.0()( 1 x. (16.10c) The numerical solution of (16.9) for 1 ris: rrr c 1, (16.11a) 2 101734618773401.5 r, (16.11b) 2 11053.1/ rr . (16.11c) Comparing to the electron case, the value of rrrc 1 is increased. It means that for taon the logistic recurrent process goes further into the chaotic region before it stops. Consider electron macroscopic converting factor e N  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1278 and its square root e N in orders of magnitude: 11 1087.3~ e N, (16.12a) 23 105.1~ e N. (16.12b) e Nand e N are grand numbers representing typical hierarchy phenomena, which deal with the ratio of two quantities having many orders of magnitude difference. There are other phenomena related to great numbers. For example, the total number of stars in a galaxy is close to 11 10 ; the total number of galaxies in the visible universe is close to 11 10 . More examples will be given in later sections. Definition 16.1: The Rank-G grand number is defined as: G G N11 10~ . (16.13) A system consists of G G N11 10~ elements is defined as a rank-G grand system. A grand system subjects to the following conditions: 1) The elements in the system belong to the some type; 2) The interaction of elements in the system is weak; 3) The elements in the system behavior stochastically; 4) The interaction of elements is nonlinear in nature, and it provides a growth mechanism with negative feed- back. In fact, in (A5.3), i x represents growth and )1( i x represents negative feedback to suppress growth. Explanation: The grand number defined by (16.13) is based on decimal for convenience, which is not natural. The natural way to define it is: g G N37 2~ , (16.14a) 1137 10374.17213743895342 . (16.14b) The relations between and G are: GGg 259739876002444.0 )2ln(37 )10ln(11 , (16.15a) ggG 606660125554399.1 )10ln(11 )2ln(37 . (16.15b) For practical reasons, definition (16.13) is introduced and used throughout in the paper. Definition (16.14) serves as its natural origin. It is interesting to notice that, 2 and 37 both are prime numbers. According to Definition 16.1, galaxy is a 1 G grand system with 11 10~ stars and the visible universe is a 2G grand system with 22 10~ stars. The common feature of grand systems containing grand number of elements is related to the logistic recur- rence process. When the random process in the system reaches the critical point 5699457.3 c r, the system becomes chaotic and stops growing. It can only grow further by organizing a next higher level, such as the visible universe on top of galaxies. Since 23 105.1~ e N is close to a 2G grand number, a natural question is: What is the electron’s 1 G grand system with 11 1087.3~ e N? This is an important question, which will be discussed in Section 23. Notice that, 7106279805.71 GUT N deviates from a prime number 71 with a relative deviation of 4 10837.8 . It is not by coincidence. In fact, it provides a clue with important physics and mathematics signifi- cances, which will be discussed in later sections. The equation of (16.1) correlated ePlancke MMN / to other mathematic constants. It has important significance, which will be discussed in Section 21. The only thing left unexplained is the numerical factor 2 in Equation (16.1) and (16.9). It turns out that the factor 2 provides an important clue for the structure of space and much more. The details will be discussed in Section 22. In summary, Equation (16.1) is an important discovery. It reveals many important correlations including logistic recurrence process, converting factor, Gaussian probabil- ity, random walk, S-equation and grand number phe- nomena. Some of them are worthwhile to explore further. Section 17. Neutrinos Neutrinos are puzzling particles with peculiar behaviors. Despite extensive efforts in recent years tried to find out neutrinos’ properties, some of them are still not clearly known. In this section, only a framework is presented, in which many issues remain open. Let’s start with known facts. Fact-1: Neutrinos have tiny mass evidenced by oscil- lations among three different types. Fact-2: Neutrinos only have left-handedness and an- ti-neutrinos only have right-handedness. Fact-3: Neutrinos have no electrical charge or tiny remnant electrical charge. The main focus of this section begins with anti-neutrinos, because anti-neutrinos are the ones com- panioned with their changed leptons and play a pivotal role in most weak interactions. Rule 17.1: According to the Leptons Pairing Rule in Section 14, each charged lepton is paired with its com- panion anti-neutrino: e e &, &, & with com- bined numerical parameters evenm, 0 n; each charged anti-lepton is paired with its companion neutrino: e e & , & , & with combined numerical parameters evenm , 0n. The n-parameters mat- ching rules are: 0 l nnl , or l nn l , ,,el , ,, el ; (17.1a) 0 l nnl , or l nnl ,  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1279 ,,el, ,, el . (17.1b) Take electron anti-neutrino e as an example. As listed in Table 12.3, electron’s after reduction n-para- meter is 2/1 e n. According to (17.1a), the n-parameter of e is 2/1 e n , to make the match: 0)2/1(2/1 ee nn . (17.2) The e as an anti-fermion, according to Definition 11.2, its m-parameter must have opposite sign of its n-parameter: 0 eenm . (17.3) Because of 02/1 e n , e must have 0 e m corresponding to e right-handedness. The argument is also applicable to the other two types of anti-neutrinos, and . It shows that, anti-neutrinos unique hand- edness is hidden in Rule 17.1 and originated from ma- thematics. In reference [1] by the author, neutrinos were treated based on their companion leptons and the boson. The mass values of three types of anti-neutrinos were given as: 25 2 2 /102922.41 2ceV M M MM W e ee , (17.4a) 23 2 /108749.81 2ceV M MM MM W e ,(17.4b) 21 2 /104925.11 2ceV M MM MM W e .(17.4c) In (17.4), the mass values, e M, M, M, W M and the value of fine structure constant 035999084.137/1 are cited from 2010-PDG. e M , M, M are the mass values of three flavored anti-neutrinos e , , , respectively, which are in principle different from the eigenstate neutrinos 1 , 2 , 3 . The difference will be discussed later in this section. According to (17.4), the mass ratios of three anti-neutrinos to their companion charged leptons are: 11 2 /103996.81 2 W e e e ee M M M M R , (17.5a) 11 2 /103996.81 2 W e M M M M R , (17.5b) 11 2 /103996.81 2 W e M M M M R . (17.5c) The three ratios are identical, which indicate that three anti-neutrinos are closely related to their companion charged leptons as well as among themselves. To determine anti-neutrinos models and parameters, two issues must be dealt with. One is mass and the other is electrical charge, which are very different from their companion charged leptons. Let’s start from electron torus model and look for the ways to transfer it into the model of its companion an- ti-neutrino e . According to SQS theory, the mass e M of e is related to its model and numerical parameters in two ways. 1) According to (6.18) in Section 6, the distance be- tween 1 x and 2 x on x-axis for e is related to its mass e M and electron mass e M as: eeee RMMxx /12 /1/4 . (17.6) According to (17.5a) and (17.6): 9 /12109763.2)4/(1 ee Rxx . (17.7) It indicates that, 1 x and 2 x are separated by a vast distance alone x-axis. The values of )(1 x and )( 2 x are determined by 1 x and 2 x according to S-equation. 2) The numerical parameters m, n, p and the mass os- cillation term in AT-, PS-equations are related to the mass ratio.The mass ratio is defined as: 11 /103996.8 e e ee M M n p R , (17.8a) The mass oscillation term is: )/2(sin')/2(sin' /22 mnRampa ee . (17.8b) According to (17.8) and 1 e m , 2/1 ee nn , the way to reduce mass e M from e M is to reduce the value of the p-parameter: 1111 2 1 /101998.4103996.8 eeee Rnp . (17.9) The numerical parameters of and can be de- termine by the same way. The results are summarized as: Electron anti-neutrino e : 1 e m , 2/1 e n , 11 101998.4 e p ; (17.10a) Muon anti-neutrino : 1 m, )8/51( n,10 103649.1 p; (17.10b) Taon anti-neutrino : 1 m, )7/62( n, 10 103999.2 p.(17.10c) For the electrical charge difference, the key is to let the electrical charge to vanish for e and keep all related rules valid. As discussed in previous sections, particle’s electrical charge q is related to Weinberg angle W as WW q cossin . Let Weinberg angle 0 W or 0 W , the electrical charge follows 0q or 0 q. Based on these considerations, SQS theory provides two options for neutrinos model. The process starts from torus model and followed by trefoil model for easy to understand. Option-1: For Dirac type neutrinos In the electron’s torus model, move point and point ' to coincide with point G. As results, the torus  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1280 model and trajectory for e are shown in Figure 17.1. When point and ' coincide with point G, 0 2 , 180 2 , 0 2 , 0 2 , and 0 2 W, 0q. In the outer half of torus cross section, according to (8.8a), and ' coincided with point Gmake 0 2Z, 0 2 and 1 2 )cos()sin( 2 2 2 2 2 Z dttbta , (17.11a) )( 2 x. (17.11b) In the region 5.0,0 of x-axis, the S-equation of (2.11) has only one solution at 73026452499871562.0 c xx , )(c x. (17.12) According to )(xS function’s periodicity of (2.12) and symmetry of (2.13), (17.12) is extended to the entire x-axis as: )( Nx c, 3,2,1,0N; (17.13a) )1(Nxc, 3,2,1,0N. (17.13b) Figure 17.1. Torus model and trajectory for e according to Option-1. According to (17.7) and (17.13), there are two ways to determine 1 x and 2 x for e . Way-1: c xx 1,Nxx c 2; )()( 1c xx, )()(2Nxx c; (17.14a) Way-2: c xx 1, Nxx c 1 2; )()(1c xx , )1()( 2Nxx c. (17.14b) In both ways, )( 1 x and )( 2 x, which are required by probability matching. )(1 x means that, as point and point ' coincided with point G, point and 'B also coincide with point E as shown in Fig.17.1. The trajectory shown in Fig.17.1 is for e . The trajectory for e has the same projections as the trajec- tory for e with opposite direction along the switched solid line and dashed line on the x-y plane. The differ- ences of two ways are: For Way-1: NMMRxx eeee e)4/(4/ /12 integer, (17.15a) For Way-2: ceeee exNMMRxx 21)4/( /12 non-integer. (17.15b) Unfortunately, the accuracy of available data is not sufficient to choose which way to go. In the meantime, let’s take Way-1. In the above discussion, e serves as an example. The same principles are applicable to and based on the models of nuon and taon. Neutrinos e , , share the some models as anti-neutrinos e , , respectively with different trajectories’ directions. Theorem 17.1: The Dirac type neutrino only with left handedness and the anti-neutrino only with right hand- edness must have zero electrical charge: 0 qq . Proof: Let’s starts from the opposite. If 0 q and 0 q, then points and points ' are not exactly coincided with point G; point and point 'B are not exactly coincided with point E. In such case, there are four possible trajectories, in which two trajectories for with right and left handedness and two trajectories for with right and left handedness. This scenario vio- lates Fact-2, which must be not true. Then the opposite 0 qq must be true. QED The above discussions are based on torus model. The real model for e , , and e , , are tre- foil model with three branches. The way for three torus models combined into a trefoil type model is the same described in Section 12 for charged leptons. Figure 17.2 shows the trefoil type model and trajectory for e . The calculated parameters based on Option-1 trefoil type model are listed in Table 17.1, 17.2, 17.3 for e , , , respectively. The data are based on 0 q. The after f-modification parameters are marked with ‘ .  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1281 Figure 17.2. Trefoil type model and trajectory for e ac- cording to Option-1. The torus model and the trefoil type model provided by Option-1 are only valid for Dirac type neutrinos and anti-neutrinos with two components. There is a reason to introduce Option-2 to provide a Majorana type model with only one component, because eigenstate anti- neu- trinos belong to Majorana type as shown later in this sec- tion. Table 17.1. Parameters for electron anti-neutrino based on option-1. Table 17.2. Parameters for muon anti-neutrino based on option-1. Table 17.3. Parameters for taon anti-neutrino based on op- tion-1. Option-2: For Majorana type neutrinos Start from Option-1 torus model for e with 0 q. Let loop-2 center 2 O on right and center 2 'O on left move toward loop-1 center 1 O and coincides with 1 O. The torus surface becomes spherical surface for 1/22 ab or elliptical surface for 1/ 22 ab. In the new model, loop-2 is integrated into loop-1. It fits the one component Majorana type naturally. Spherical and ellip- tical surfaces belong to genus-0 topological manifold. The trajectory on torus surface is degenerated into a cir- cle on the spherical surface or elliptical surface with points G on its right and points E on its left as shown in Figure 17.3. The trajectory on trefoil type model is degenerated on sphere surface or elliptical surface as shown in Figure 17.4. The model is degenerated from genus-3 to genus-0  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1282 without branches but the degenerated trajectory still re- tains its 3-branch trefoil type with loop-2 integrated into loop-1. Figure 17.3. Torus model and trajectory degenerated to sphere for 1 according to Option-2. Figure 17.4. Trefoil type model and trajectory degenerated to sphere for 1 according to Option-2. In the process of weak interaction such as e epn , an anti-neutrino is created with a defini- tive flavor. The new born anti-neutrino flies with speed very close to the speed of light in vacuum. During it fly- ing journey, the anti-neutrino is oscillating among dif- ferent flavors. In other words, the flying anti-neutrino lost its flavor identity and becomes an oscillating system of eigenstate anti-neutrinos. When it is caught by a de- tector, the eigenstate anti-neutrino gets its flavor identity according to probability. The oscillating behaviors were found by experiments as the Fact-1, which serve as the evidence for anti-neutrinos having tiny mass. It is important to point out that, during their free flying journey, the oscillation is among the members of eigen- state version, and the members of flavored version only show up at their birth or been detected. As soon as they start to fly, the flavored version converts to the eigenstate version. Fine structure constant is a running constant de- pending on energy scales. In (17.4) and (17.5), the value is based on the 2010-PDG (p.126) data: 035999084.137/1)( e M . (17.16) Take (17.4c) for as an example, there are three different energy scales involved. If is treated as a running constant, (17.4c) probably should be rewritten as: 21 /105318.1)(1 2 )( 2 )(ceV m MM M MM M W e Z e (17.17) In (17.17), 2010-PDG (p.126) data medium values are used: 444.133/1)( M, (17.18a) 916.127/1)( Z M . (17.18b) The difference between (17.4c) and (17.17) is 2 106.2 . The mass data listed in Table 17.1, 17.2 and 17.3 did not take as a running constant into account, which may have up to 2 10~errors. According to 2010-PDG data, three charged leptons have a mass relation: 50649.3 M MMe. (17.19) According to (17.4) and (17.19), if ignore the effect of as a running constant, three anti-neutrinos have a similar mass relation: 50649.3 M MM e. (17.20) (17.20) indicates that, three types of neutrinos are closely correlated. The neutrino models and parameters proposed by SQS theory can be verified by checking on eigenstate neutri- nos mass values. 2010-PDG provides the experimental data for the differences of eigenstates mass squares: 2252 21 )/(10) 21.0 19.0 59.7(ceVM , (17.21a) 2232 32 )/(10)13.043.2(ceVM . (17.21b) Which are based on 2010PDG assumption: 2 31 2 32 ~MM . (17.21c) According to (17.4), the SQS theoretical values are: 22522 )/)(10876.7(ceVMM e , (17.22a) 22222 )/)(1022.2(ceVMM , (17.22b) 22222 )/)(10227.2( ceVMM e . (17.22c) The 22 e MM theoretical value of (17.22a) is close  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1283 to the experimental 2 21 M value of (17.21a). The other two are off by a factor of ~9 for mass square; for mass without square, they are off by a factor of ~3. The as- sumption 2 32 2 31 ~MM of (17.21c) also fits (17.22b) and (17.22c) well. But they are not fair comparisons. In principle, e M , M, M as flavored anti-neutrinos mass are different from eigenstates mass 1 M, 2 M, 3 M. Nevertheless, the 2010-PDG data provided some tenta- tive information. For instance, one possible interpretation of experimental data given by (17.21) is: e MM 1 ~, (17.23a) MM 2 ~, (17.23b) 3/ 3 ~ MM . (17.23c) Future experiments will check the interpretation. In this section, so far the focus is on anti-neutrinos. Now is the time to deal with neutrinos. Let’s do it by the logical way to start from facts and to treat according to rules. The facts are Fact-1, Fact-2 and Fact-3. The rules are Rule 17.1 and Rule 17.2. Rule 17.2: The right and left handedness defined by Definition 11.2 is universally valid for all fermions in- cluding two versions of neutrinos and anti-neutrinos. According to Fact-1 and Fact-2, there is a paradox. A chaser is chasing an anti-neutrino with a speed slightly faster than its speed. It is possible, because anti-neutrino has mass and its speed must be less than the speed of light in vacuum. The chaser behind it sees an an- ti-neutrino with right handedness. When the chaser gets ahead of it, he or she sees a neutrino with left handedness. This scenario is impossible. An anti-particle cannot turn into a particle by just looking at it in different ways. The “chaser’s paradox” must be eliminated. It serves as the key concept to introduce Hypothesis 17.1. Notice that, the chaser’s paradox is not applicable to flavored version neutrinos and anti-neutrinos, because they never fly. To avoid the paradox, the target is the flying eigenstate version. Hypothesis 17.1: After their birth, the flavored neu- trinos convert into corresponding eignstate neutrinos. The eigenstate neutrinos 1 , 2 ~ , 3 are Majorana type fermions with only one component and the anti-particles is the same as itself: ii , 3,2,1i. (17.24) After their detection, the eigenstate neutrinos convert into corresponding flavored neutinos. The flavored neu- trinos are Dirac type fermions with two components and have anti-particles: jj , ,,e . (17.25) Explanation: Hypothesis 17.1 suggests that, eigen- state neutrinos 1 ~ , 2 ~ , 3 are Majorana type. SQS theory is not the first one to do so. Similar ideas were proposed earlier. But there are differences. 1) Hypothesis 17.1 is based on mathematics. 2) Hypothesis 17.1 clearly points out that, flavored version neutrinos and anti-neutrinos are Dirac type. This is necessary to avoid contradiction with experimental facts. According to 2010-PDG data book, muon decay mode e e has %100/ i; taon decay modes e e has )%05.085.17(/ i and has )%05.036.17(/ i. Their charge conjugates and have corresponding decay modes. These facts clearly show that, the flavored version must have all fla- vored version neutrinos e , , and anti-neutrinos e , , Therefore, three flavored neutrinos must be Dirac type fermions and have corresponding an- ti-particles. Hypothesis 17.1 eliminates the chaser’s paradox. For the frying Majorana type eigenstate neutrino, when the chaser gets ahead of the neutrino, he or she merely sees the neutrino changed its right handedness to left handed- ness as it should be. Rule 17.3: The conversion between the flavored ver- sion e , e , , , , and the eigenstate ver- sion 1 , 2 , 3 are governed by converting probability matrixes: EF EF EFF P P P~ ~ ~ ,0 0, (17.26a) 1 ~ 1 ~ 1 ~ ,, ~0 0 EF EF EFFFFE P P PP. (17.26b) 3 ~ 2 ~ 1 ~ 3 ~ 2 ~ 1 ~ 3 ~ 2 ~ 1 ~ ~ ppp ppp ppp Peee EF , (17.27a) 3 ~ 2 ~ 1 ~ 3 ~ 2 ~ 1 ~ 3 ~ 2 ~ 1 ~ ~ ppp ppp ppp Peee EF . (17.27b) In the subscripts, and represent flavored ver- sion neutrinos and anti-neutrinos, respectively; repre- sents eigenatate version neutrinos; the and repre- sent right handedness and left handedness, respectively. Explanation: The distinctive feature of Rule 17.3 is that, in the converting process, the handedness does not change evidenced by the non-diagonal sub-matrixes all equal to zero as shown by (17.26a) and (17.26b). Ac- cording to Rule 17.3, the flavored anti-neutrinos only convert to the eigenstate neutrinos with right handedness, the flavored neutrinos only convert to the eigenstate neu- trinos with left handedness, and vice versa. According to (17.24), when flavored neutrinos convert to eigenstate neutrinos, the particle versus anti-particle distinction is  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1284 no longer valid. Nevertheless, the original distinction for flavored neutrinos and anti-neutrinos leave marks on their eigenstate version by different handedness. A new born flavored neutrino immediately converts to an eigen- state neutrino according to (17.26a), When caught by a detector it converts back to the flavored version accord- ing to (17.26b). The non-diagonal sub-matrixes equal to zero guarantee that, as the net result of two processes, the lepton numbersare conserved. According to Hypothesis 17.1, the flavored neutrinos include six members e , , , e , , and the eigenstate neutrinos include three members 1 , 2 , 3 . The flavored anti-neutrinos and neutrinos are differ- ent particles. Their model is Option-1 type. The eigen- state neutrinos have no counter-particles, their model is Option-2 type. These two models look very different. In essence, they are closely correlated by degeneration as described previously. Conclusion 17.1: Eigenstate neutrinos 1 , 2 , 3 have no electrical charge. Proof: Assuming 3,2,1, i i has charge q and i has charge q. According to Hypothesis 17.1, ii , then qq and 0 q. QED According to Conclusion 17.1, the eigenstate neutrinos have no electrical charge. According to Theorem 17.1, it seems that the flavored neutrinos and anti-neutrinos also have no electrical charge. Look at it closely, there is an uncertainty. Theorem 17.1 is based on geometry of Op- tion-1 model and Fact-2. The unique handedness stated in Fact-2 corresponds to particle’s spin orientation with respect to its momentum. But the flavored neutrinos and anti-neutrinos never fly. Only the eigenstate neutrinos fly and have persist momentum. Therefore, the unique han- dedness stated in Fact-2 cannot refer to the flavored ver- sion. Whither the flavored version neutrinos and an- ti-neutrinos have remnant electrical charge or not, it cannot be determined by Theorem 17.1 along. On the other hand, the eigenstate version neutrinos are without electrical charge for sure according to Conclusion 17.1. Based on conservation of electrical charge, should the flavored version neutrinos and anti-neutrinos also have no electrical charge? Consider all these facts and factors, SQS theory intends to favor no remnant electrical charge for the flavored version neutrinos and anti-neutrinos as well. On the experimental side, neutrino electrical charge data are not officially listed in 2010-PDG. Instead, it cites data from seven authors for the neutrinos charge upper limits ranging form e 4 103 to e 15 102 . Neu- trinos magnetic moment upper limit data from three au- thors are listed in 2010-PDG ranging from B 7 109.3 to B 10 1054.0 . These experimental data are not con- clusive. More experimental works are needed. In the visible universe, matters overwhelmingly do- minate antimatters. On the other hand, when the universe was born, the big bang should produce equal amount of matters and antimatters. Over the years, physicists were puzzled by the “missing antimatters” question: Where are these antimatters? Hypothesis 17.2 may provide the an- swer. Hypothesis 17.2: The eigenstate neutrinos 1 , 2 , 3 flying around in the universe provide a possible solu- tion for the “missing antimatters”. Explanation: Hypothesis 17.2 is based on two condi- tions: Condition-1: 2010-PDG data book stated that, the “baryon density of the universe” is )4(044.0b and “neutrino density of the universe” is 048.00009.0 . If further observations confirm )4(044.0048.0 b , it will serve as the foundation of Condition-2. Condition-2: If condition-1 is confirmed, then the question becomes: Are all these flying around eigenstate neutrinos with right handedness? Since the handedness of eigenstate neutrinos are not directly measurable, an indi- rect way is suggested to detect the cosmological origi- nated neutrinos and measure the converted flavored neu- trinos’ handedness. According to Rule 17.3, the handed- ness of eigenstate neutrinos can be determined. There are three possible outcomes: 1, All anti-neutrinos have right handedness, the “missing antimatters” are found; 2, More than 50% of anti-neutrinos have right handedness, part of the “missing antimatters” are found. 3, Less than 50% of anti-neutrinos have right handedness, Hypothesis is dis- proved. In this section, SQS theory provided a framework with the potential to explain neutrinos peculiar behaviors based on mathematics. Because of the complexity of the topic and limited available experimental data, some pa- rameters haven’t nailed down yet and many issues re- main open. Some of them will be discussed in later sec- tions. Section 18. Elementary Particles Table Elements periodic table not only is useful for under- standing chemical elements but also valuable for explor- ing what’s behind scene and for predicting new elements. Elementary particles table should do the same for physics at a deeper level. For comparison purpose, Table 18.1 shows the Stan- dard Model (SM) Elementary Particles Table. Table 18.1. Standard model elem e ntary particles table.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1285 In Table 18.1, there are 12 fermions and 12 bosons plus the higgs boson. The total number of elementary particles is 25 in which anti-particles are not included. After introduced almost all elementary fermions and bosons in previous sections, SQS theory is ready to in- troduce the Elementary Particles Table as Table 18.2. Table 18.2. SQS theory elementary particles table. Notes: 1. The particles marked with *are hypothetic particles. 2. Number in parenthesis is original m-parameter, number after parenthesis is effective m-parameter. Table 18.2 does not list the six flavored neutrinos e , , and anti-neutrinos e , , , instead the three eigenstate neutrinos 1 , 2 , 3 ~ are listed. It is an important issue. The eigenstate version 1 ~ , 2 , 3 and the flavored version e , , , e , , are equivalent. SQS theory Elementary Particles Table must choose one version to list not both versions. The question is: Which version should be chosen? As indicated in Sec- tion 17, the flavored version exist only in an extremely short time at their birth or been detected. On the other hand, the eigenstate version are flying in the universe all time, some of them since the big bang 13.7 billion years ago. Look at this way, the choice is obvious. In previous sections, close correlations were estab- lished between bosons and fermions. The 8 gluons are made of 8 pairs of quark-antiquark shown by (13.1). The 8 hypothetic massons are made of the other 8 pairs of quark-antiquark shown by (14.6). These 16 bosons fit into 16 cells in the boson row of Table 18.2. On the up- per left corner, the hypothetic graviton fits into the cell correlated to r u; on the upper right corner, the W boson fits into the cell correlated to b t. On the top row of Table 18.2, three scalar bosons 1 U,2 U,3 U fit into the cells correlated to three eigenstate neutrinos 1 , 2 , 3 , respectively. In the next row, photon and gauge boson fit into the two cells correlated to leptons e and , respectively. Another hypothetical neutral gauge boson 0 fits into the mid- dle cell correlated to lepton , which will be introduced later in this section. Comparing these two Tables, there are some similari- ties, but the differences are obvious. The major difference is the numbers of quarks. In the SM table, the number is 6. In the SQS table, the number is 18. The key is Postulation 11.1 based on Postulation 11.2 and Rule 11.1, which recognize quarks with the same flavor and different colors as different particles. It is a major step to open doors for new opportunities. It gives the hint that lepton has three branches to form the trefoil model. More im- portantly, it provided more cells for bosons. Other- wise, there is no room for 13 hypothetic bosons. In the SM table, graviton is not included, because SM theory does not include gravity. The SQS table in- cludes graviton g, because SQS theory aims at the grand unification for all four types of interactions, which should include graviton as the mediator of gravity. In addition to graviton, the SQS table includes twelve other hypothetic bosons, in which 1 U, 2 U, 3 U and )8,2,1(, iGi are scalar bosons, 0 is a gauge boson. These hypothetic bosons are not included in the SM table. SM theory includes the higgs boson. SQS theory does not need it for providing mass to particles. In the SM table, there is no clear correlation between fermions and bosons. In the SQS table, the correlation between fermions and bosons is clear, which is im- portant for predicting new particles. In SQS theory, elementary particles are categorized into three types: particle, antiparticle and neutral particle. The neutral particle p is defined as: . (18.1) According to (13.2), gluons are neutral particles. Ac- cording to (14.7), massons are neutral particles. Accord- ing to SQS theory, photon is ee and graviton is rr uug : eeeeeeee . (18.2) guuuuuugrrrrr . (18.3) 1 U, 2 U, 3 U are scalar bosons with mass and without charge, which also have no separate anti-particles: ii UU , 3,2,1 i. (18.4) Therefore, photons , gravitons and 1 U, 2 U, 3 U are neutral particles. There are three gauge bosons left: W,0 and the hypothetic 0 . According to PDG data, all properties of W and W are the same except charge. Even the de- cay modes and branching ratios totali / of W and W are charge conjugates. These experimental data clearly show that, W and W are a pair of particle and anti-particle. According to SQS theory, all neutral elementary bosons , , 1 g, 2 g, 3 g, 4 g, 5 g, 6 g,  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1286 7 g, 8 g, 1 G, 2 G, 3 G, 4 G, 5 G, 6 G, 7 G, 8 G, 1 U, 2 U, 3 U made of a pair of fermion and the same type anti- fermion have no separate anti-particles. 0 and 0 Xare different, because they are made of a pair of fermion and different type anti-fermion. According to Table 14.2 and (18.12), they have separate anti-particles: 21 0 2121 0YYZYYYYZ . (18.5) 21 0 2121 0ffffff XXXXXXXX (18.12b) In the SQS theory Elementary Particles Table, the three scalar bosons 1 U, 2 U, 3 U for unifications are the heaviest particle in each column of the table. The three eigenstate neutrinos 1 ~ , 2 , 3 correlated to 1 U, 2 U, 3 U are the lightest fermion in each column of the table. Why is the lightest correlated to the heaviest? Because the mass of 1 , 2 , 3 is in the same order as the mass of e , , , respectively. Let’s look at the formulas derived from (17.5) for orders of magnitudes comparison: 10 2 2 10703.41 2 e Wew e ew M MM M M , (18.6a) 22 2 10258.11 2 MM MM M M e Wewsews , (18.6b) 22 2 10559.91 2 MM MM M M e WGUTGUT . (18.6c) In which ew M, ews M, GUT M are the mass of 1 U, 2 U, 3 U, respectively. It is interesting to notice that, the numbers of second and third formulas for 2 U, 3 U ver- sus , are 2G grand numbers, while the number of first formula for 1 U versus e is close to 1G grand number. The apparent reason for such dif- ference is that, ew M is 13 10~ orders lighter than ews M. The mechanism of such difference is an open issue. De- spite this difference, (18.6) implies that, the reason for the lightest correlated to the heaviest has something to do with grand numbers related to random walk. It usually is the origin of hierarchy phenomena. If “the heaviest” is really made of a pair of “the light- est”, massons may play the role to fill the tremendous mass gaps between 1 U, 2 U ,3 U and 1 ~ , 2 , 3 . After all, the arrangement for 1 U, 2 U,3 Ucorrelated to 1 ~ , 2 , 3 in the SQS Elementary Particles Table is justified. Table 18.3 shows the numbers of three types particles in SQS theory. Table 18.3. Three categories of elementary particles in table 18.2 The three types particles are: Particles: This type includes 18 quarks r u, g u, b u, r d, g d, b d, r s, g s, b s, r c, g c, b c, r b, g b, b b, r t, g t, b t, 3 leptons e, , , and 3 gauge bosons W, 0 , 0 . Antiparticles: This type includes 18 anti-quarks r u, g u, b u, r d, g d, b d, r s, g s, b s, r c, g c, b c,r b, g b, b b, r t, g t, b t,3 anti-leptons e, , , and 3 anti-gauge-bosons W, 0 , 0 . Neutral particles: This type includes 3 neutral leptons 1 ~ , 2 , 3 . 9 neutral gauge bosons , 1 g, 2 g, 3 g, 4 g, 5 g, 6 g, 7 g, 8 g, and 12 neutral scalar bosons ,1 G, 2 G, 3 G, 4 G, 5 G, 6 G, 7 G, 8 G,1 U, 2 U, 3 U. Definition 18.1: Graviton is a scalar boson with spin zero. Explanation: In other quantum gravity theories, gra- viton is assigned with spin 2. Since graviton has not been found, there is no experimental confirmation. In the SQS theory Elementary Particles Table, there is no place for graviton as a tensor boson with spin 2. According to the Random Walk Theorem in Section 4 and the dis- cussion regarding electromagnetic force and gravitational force in Section 15, photon and graviton are two sides of the same coin. It is also shown in their models. Accord- ing to SQS theory, photon model is a closed single loop with circumferential length of P L2 corresponding to spin ; while graviton model is a cutoff loop with length of P L2. In essence, a graviton is a cutoff photon. A cutoff loop has zero spin. In terms of number parame- ters, as r q with 1 qr m, there is no way for rr qqg to make graviton with 4 g m required by spin 2. In short, graviton with spin 2 does not fit into SQS the- ory framework. There is also a philosophical reason. As shown in Section 15, gravity is the force to unify all forces. Gravity as the only force exerts to everything with mass or energy. In essence, gravity is the most fun- damental and universal force, and so is graviton. Ac- cording to natural philosophy, the most fundamental and universal thing should be the simplest one. Obviously, 0 fits this argument much better than 2. Is a scalar boson qualified as the mediator for interaction? Why not? with spin 0 is different from , W, 0 and )82,1( , igi with spin . It just means is unique. Let’s face it, gravity is unique in the first place. After all, there is no law forbidding the unique scalar boson serving as the mediator for the unique force gravity. Look at it the other way. A graviton center is at a discrete point i x, the two ends stretch to 1 i x and 1 i x. This scenario is closely related to the Random Walk Theorem. Starting from i x along the x-direction, the random walk has equal chance moving to 1 i x or 1 i x as the next step. The same is for y-direction and z-direction. In fact, there is a hidden question in the Random Walk Theorem: Why the step length is 1 not 2 or 3 etc? The graviton’s  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1287 cutoff model provides the answer: Because the length of graviton only allows each step moving to 1. Otherwise the Random Walk Theorem is in trouble. Graviton as a cutoff loop with length of P L2 fits the Random Walk Theorem naturally. Assume that, the middle point of three orthogonal straight lines each with normalized length 2 is attached at each discrete point ),,(kji zyxp with their six ends reaching to 1 i x, 1 j y, 1 k z along , y, directions, respectively. This ar- rangement not only fits the random walk process but also forms a network serving as the spatially quantized gravi- tational field. The three orthogonal straight lines repre- sent three gravitons serving as the quanta of gravitational field. This scenario is much more natural than what graviton with spin 2 can offer. Moreover, a topologi- cal theorem provides a definitive support for graviton having spin 0 as the only option, which will be given in Section 26, Most theories recognized graviton with spin 2. SQS theory probably is the only one recognizes graviton with spin 0. It is a bold and risky undertaking. But within SQS theory framework there is no alternative. From SQS the- ory perspective, graviton with spin 2 is a misunder- standing. As shown in Fig. 18.1(a), two head-to-tail con- nected gravitons form a closed loop with loop length P L4 corresponding to spin 2, which might be mistak- enly recognized as graviton. Actually it is merely a composite state made of two gravitons. Moreover, as shown in Fig. 18.1(b) and Fig. 18.1(c), when the loop area increases, the trajectory angular momentum in- creases in step of not in step of 2. So graviton with spin 2 is a misunderstanding. Of cause, the final proof has to wait until the discovery of graviton. Definition 18.1 serves as a prediction of SQS theory. Let’s wait for graviton show up to say the final word. Figure 18.1. Closed loops made of “head-to-tail” connected gravitons: (a) two gravitons, (b) three gravitons, (c) four gravitons. There are thirteen hypothetic bosons listed in Table 18.2, in which twelve of them are introduced in previous sections. The only one left is the neutral gauge boson0 . Like the W and 0 , according to SQS theory, the gauge boson 0 is also involved in weak interactions. As shown in Section 14, W and 0 are made of two fermion states 1 Y and 2 Y, which share the same m-parameters with two top quarks g t, b t: 53 1 tgY mm and 61 2 tbYmm. Similarly, the two fermion states 1f X and 2f X to make the 0 boson share the same m-parameters with two charm quarks g c and b c: 29 1 cgXfmm and 37 2 cbZf mm . It is inter- esting to find out that, these two sets of m-parameters have something in common: 3 285361 , 19321145361 , (18.7a) 3 282937 , 1132662937 . (18.7b) In fact, there are more similarities, which will be shown in Section 24. The mass of 0 boson is determined by the values of its 1 xand 2 xon x-axis. Let’s look at the special points c xon x-axis:73026452499871562.0 c xis a magic point. It is originated from the S-function of (2.11) and sets a slight deviation of anti-symmetry of )(xS with re- spect to the center 25.0 x of region 5.00 x. Point c xsets the boundaries of the gauge boson region cdc xxxx 5.0, and it sets a mass upper limit 2 /9732.4cGeVM Max for standalone fermions. More- over, c xdefined other two characteristic points a x ,b x, which determined the mass of two scalar bosons 1 U and 2 U for electro-weak and electroweak-strong unifications. As shown in Section 15, this approach is closely related to the other approach based on random walk and unifica- tion of electrostatic force with gravity. It provided the legitimacy of both approaches. Point a x and point b x succeeded for finding two scalar bosons owe gauge boson a favor. It is the time for them to pay back. Definition 18.2: Based on 10 10882111819946879.5 a x, -5 10918477191.18218617 b x and the S-function of (2.11): j jx exS 2 )( )( , define two characteristic points f x and g x on the x-axis. 25.0 0)()( f b ax x x dxxSdxxS , 36016352499871568.0 f x, (18.8a) fg xx 5.0 , 63983652500128431.0 g x. (18.8b) The summation index in )( xSis truncated at 1000 j, which is sufficient for convergence. Notice that, f x and g x both are in the gauge boson region:  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1288 25.0730262499871562.0 fc xx , (18.9a) 26973552500128437.025.0 dgxx . (18.9b) According to (6.18), the mass of two X-fermion states 1f X, 2f X with f xx 1, g xx 2 is: 2 12 /97345232.4 )(4)(4cGeV xx M xx M M fg ee Xf . (18.10) Because f xx 1 and g xx 2are in the boson re- gion and MaxXf MM , the X-fermion states 1f X and 2f X must appear in pair as a gauge boson 0 X with mass X M: 2 /94690465.92 cGeVMM XfX . (18.11) The gauge boson 0 is made of two fermion states 1f X and 2f X, which have the same mass and different before reduction numerical parameters. The gauge boson 0 has its anti-particle 0 X different from 0 X. 21 0ffXXX , (18.12a) 0 2121 0XXXXXX ffff . (18.12b) In the gauge boson region ],[ dc xx, 0 X boson has )(1 x and )( 2 x: 69111415926516.3)( 1f xx , (18.13a) 47381415050288.3)( 2g xx . (18.13b) It indicates that, the torus based model for 0 boson is spindle type with two branches like 0 bosons model. Look it closely, 1f X and 2f X having mass around 2 /97.4 cGeV are originated from g c and b c having mass around 2 /38.1 cGeV and 2 /34.1 cGeV, there is a mass gap between them. The gap is filled by massons. It is similar as W and 0 having the reversed mass gap with g t and b t filled by massons. The parameters of electroweak interaction are repre- sented by the GWS-triangle in charged particles’ model as shown by Figure 8.4. Figure 18.2 shows the GWS -triangle in extended region including the CKM-triangle. Besides the GWS-triangle of 2 AFO , there is another triangle FOO 21 similar to 2 AFO . It is called the S-triangle for SQS theory. The similarities of GWS -triangle and S-triangle are: 1) They both are compounded right-angled triangles including two small similar right-angled triangles. 2) They both share the common side FO2, which represents the 'g-type weak interaction. 3) They both have a long side: AO2 for SWG-triangle and 21OO for S-triangle. The similarities imply that the S-triangle also involves in some type of weak interactions. W and 0 serve for electroweak interactions represented by GWS -triangle. It is natural to assume that, 0 boson serves for the weak interactions represented by S-triangle. The S-triangle joints GWS -triangle on its right and links to CKM- trian- gle on its left. Noticed that, the a x and b x in the first integral term of (18.8a) served as two characteristic points to define 1 U and 2 U for electro-weak unification and electroweak-strong unification, respectively. Con- sider these factors as the clues to guess its function, 0 boson is probably involved in some type of weak interac- tions responsible for hadrons decay. Of cause, more supportive evidences are needed for sure. As shown in Figure 18.2, besides the common side FO2 shared with GWS -triangle, S-triangle has two other sides: FO1 labeled S g represents a g-like weak inter- action and labeled S q represents a charge of some kind. Figure 18.2. The S-triangle between GWS-triangle and CKM- triangle. According to trigonometry, the relations among e, S q, 'g, S g and angle 2 , W are: 'tantan 2ggg WS , (18.14a) ' coscos 2 g e q W S , (18.14b) 2 2coscos' WS geq . (18.14c) Based on the SQS theory Elementary Particles Table, the total number of particles and anti-particles is 72. Are all these particles elementary? At this level, yes! Is this the deepest level? It is a good question. Look back to history, in the early twenty century, only four “elementary” particles were known, i.e. electron, proton, neutron, and photon. Since then, so many parti- cles showed up; the numbers of particles kept growing. People started to think that so many particles cannot be all elementary; at a deeper level things could be simpli- fied. The quark model was introduced, which reduced the numbers of elementary particles by more than tenfold at that time. Now, we probably are in the same situation. Suppose there is a deeper level. What is it? To answer this question, let’s go back to the fundamentals. As indi- cated by the name: Stochastic Quantum Space. SQS the- ory is a theory of space. Vacuum is the ground level of space. According to SQS theory, everything including all  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1289 particles and interactions are originated from vacuum. Particles are excitations of vacuum, interactions are rip- ples through vacuum. In short, there is nothing but dif- ferent states of vacuum. As emphasized in Section 3, SQS theory treats vacuum as a continuum with Planck scale grainy structure. Now let’s take a step further to introduce the third fundamental postulation of SQS the- ory. Postulation 18.1, The Vacuon Postulation: Vacuum is a quantum field. All different fields for particles and interactions are originated from this Mother Field. Ulti- mately, vacuum field is the only field, vacuon as the par- ticle of vacuum field is the only elementary particle at the deeper level. Explanation: Vacuon as the ultimate elementary par- ticle has no dimension, no structure, no model, no mass, no spin, no charge of any kind, no anti-particle, no inter- action, and no parameters except its location and move- ment. In short, vacuon is nothing but itself. Yet every- thing in the universe ultimately is made of vacuons. Vacuon creates everything from nothing. It is the ulti- mate elementary particle of SQS theory. The closest thing for vacuon is a geometrical point. There are uncountable infinite numbers of it in the space continuum. Vacuons are free to move without interaction. It can be traced back to the first fundamental postulation of SQS theory, the Gaussian Probability Postulation. Gaussian probability is based on the precondition that, the events must be statistically independent. Otherwise, the probability is not Gaussian. Vacuons create events serving as the carriers of Gaussian probability. The events of Gaussian probability are independent, so are vacuons. Models and trajectories of all elementary particles are different patterns of moving vacuons. Vacuon movement is to reach evenness. In Section 2, Gaussian probability function is assigned to each discrete point i x. The su- perposition of all these probabilities is not evenly distrib- uted. It has peak at i x and trough in between peaks. The unevenness drives vacuons moving from peak to trough for temporally even distribution. But the momen- tum keeps vacuons going and the temporally even distri- bution becomes uneven again. Like a pendulum, the va- cuons oscillation goes on and on. Is the unevenness acting as an interaction for vacuons? For particle physicist, interaction is synonymous to force. The tendency for vacuons reaching evenness is not an external force per se. But if one like to call it force, that is the only one. Vacuon is the simplest thing you can think of, yet it has the capability to make all complex things in the uni- verse. The key is Gaussian Probability Postulation, which laid the foundation. Table 18.4 is the SQS theory Elementary Particle Ta- ble at the vacuon level. It serves as the foundation for all particles listed in the high level Elementary Particles Table of Table 18.2. Table 18.4. Elementary particle table at vacuon level. Vacuon With the help of vacuon, SQS theory reduced the numbers of elementary particles from 72 to 1 at a deeper level. Theorem 18.1: For a point particle such as vacuon moving with non-infinite speed, it has only 1-dimen- sional trajectories. Proof: Assume that, a point particle moving with a non-infinite speed has a trajectory other than 1-dimen- sional such as a 2-dimensional surface. A surface, no matter how small it is, contains uncountable infinite 1-dimensional lines. For the point particle with non-infi- nite speed to go through all lines on the surface, it re- quires infinite time to do so. That is impossible. Then the opposite must be true. QED Lemma 18.1: Theorem 18.1 is also valid for a set of point particles as long as all point particles in the set moving along the same trajectory. Proof: For a set of point particles moving in the same trajectory, the proof is the same as Theorem 18.1. QED Lemma 18.2: The 1-dimensional trajectory for point particles can only change its location by discrete steps. In other words, trajectories are quantized in the space. Changing course is only allowed by jumping trajectories, continuously shifting trajectory is prohibited. Proof: If the 1-dimentional trajectory were allowed to shift continuously, the shifting trajectory is no longer 1-dimensional. It violates Theorem 18.1. QED Theorem 18.1, Lemma 18.1 and Lemma 18.2 are based on geometry and point particle with non-infinite speed, which are universally valid. They serve as guide- lines for vacuons movements, which have important im- plications shown in later sections. In summary, SQS theory Elememtry Particles Table did its job. It provides a vacant cell for the gauge boson 0 related to the S-triangle for some type of weak inter- action. It confirms the eight massons and their scalar boson status. It reveals the correlations between fermions and bosons in general. In particular, without the table, the correlation of three scalar bosons 1 U, 2 U, 3 U to three eigenstate neutrinos 1 , 2 , 3 is not so obvious. It helps to define graviton with spin 0 instead of 2. It counts the total numbers of elementary particles at this level to be 72, no more and no less. Because 72 elemen- tary particles are too many, it leads to the concept of va- cuon at a deeper level.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1290 Section 19. Proton Neutron and Composite Particles In this section, proton, neutron and some simple compos- ite particles such as helium nucleon, deuterium nucleon and tritium nucleon are discussed based on quarks mod- els introduced in Section 11 and strong interactions in- troduced in Section 13. Proton, neutron and some simple composite particles such as helium nucleon etc are made of up quarks and down quarks. According to the values listed in Table 11.2, the numerical parameters of up quarks and down quarks are summarized in Table 19.1. Table 19.1. Numerical parameters of up quarks and down quarks. *Note: In the u and d columns, the numbers are the sum of three num- bers in the same row. A proton is made of uud and a neutron is made of udd and each flavored quark composed of three colored constituents with red, green and blue colors. The gluon connections diagrams of proton and neutron are shown in Figure 19.1 and Figure 19.2, respectively. The up quark and down quark with three colors are treated separately serving as the first level—colors level. The lines repre- sent gluon connections for the regular type strong force. As shown in Figure 19.1, proton has 40 connections for 9 colored quarks corresponding to 9 4 4 connections per colored quark. As shown in Figure 19.2, neutron has 31 connections for 9 colored quarks corresponding to 9 4 3 connections per colored quark. It is a fair comparison for proton and neutron, because they contain the some num- ber (9) of colored quarks. Under these conditions, the number of connections per constituent serves as an index for the relative strength of the strong force to bind con- stituents. So proton is more tightly bound than neutron. Helium nucleon is made of two protons and two neu- trons, which include 36 quarks with tree different fla- vors and three different colors. The gluon connections diagram of helium nucleon is shown Figure 19.3. To avoid over crowd lines, it only shows 86 connections for 6 different quarks as one sixth of total 516686 connections. As shown in Figure 19.3, r u has 24 connections, g u has 1 + 29 connections, b u has 1+47 connections, r d has 1 + 29 connections, g d has 6 connections, b d has 1 + 29 connections. The first number is for Figure 19.1. Gluon connections inside a proton at the first level. Figure 19.2. Gluon connections inside a neutron at the first level. Figure 19.3. The 86 connections as one sixth of 516 total gluon connections inside a helium nucleon at the first level.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1291 self-connection counted only once and the second num- ber is for connections between two quarks counted twice. The total number of connections and connections per constituent for helium nucleon are: Total number: 5166 2 29629472924 )1111( , (19.1a) Connections per constituent: 3 1 14 36 516 . (19.1b) The connections per constituent 3 1 14 for helium nu- cleon cannot directly compare to those for proton and neutron. It is not a fair comparison, because helium nu- cleon contains 36 colored quarks while proton and neu- tron each contains 9 colored quarks. In the case of gluon connections reaching the particle’s entire region, the more constituents involved, the more are the number of connections per constituent. For fair comparisons, the number of connections per constituent for helium nu- cleon should be weighted lighter than proton and neutron. Assuming the weighting factor is inversely proportion to the number of constituents. The weighted binding streng- ths (BS) of proton, neutron and helium nucleon for the first level are as follows. Proton: 494.0 81 40 9 1 9 40 p BS , (19.2a) Helium nucleon: ,398.0 1296 516 36 1 36 516 He BS (19.2b) Neutron: 383.0 81 31 9 1 9 31 n BS , (19.2c) Comparison: nHep BSBSBS. (19.2d) The first level comparison of (19.2) shows the right order of binding strengths: Helium nucleon is weaker than proton and stronger than neutron. Let’s consider the second level—flavors level, which treats flavored quark as a whole entity. As shown in Ta- ble 19.1, the corresponding numerical parameters are 9,21 nm for u-quark, 9,19 nm for d-quark. The second level gluon connections diagrams of proton and neutron are shown in Figure 19.4. In which, proton has 5 connections for 3 quarks corresponding to 3 2 1 connections per quark; neutron has 3 connections for 3 quarks corresponding to 1 connection per quark. Figure 19.4. Gluon connections inside a proton and a neu- tron at the second level. The corresponding gluon connections diagram of he- lium nucleon is shown in Figure 19.5. There are 57 gluon connections for 12 quarks corresponding to 4 3 412/57 connections per quark. Figure 19.5. Gluon connections inside a helium nucleon at the second level. Using the same weighting method as the first level, the weighted binding strengths (BS) of proton, neutron and  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1292 helium nucleon for the second level are as follows. Proton: 556.0 9 5 3 1 3 5 p BS , (19.3a) Helium nucleon: 396.0 144 57 12 1 12 57 He BS , (19.3b) Neutron: 333.0 9 3 3 1 3 3 n BS , (19.3c) Comparison: nHepBSBSBS . (19.3d) The results of (19.2) and (19.3) both show the right orders: nHep BSBSBS , which indicate that, the binding strength of helium nucleon is weaker than proton and stronger than neutron. In reality, proton and helium nucleon are stable, while neutron in stable nucleons is stable and freestanding neutron is unstable with a mean life of s8.07.885 . The results at two levels are quite reasonable. Both show that helium nucleon is a very tightly bound composite particle. Proton, neutron and helium nucleon also contain many gluons. These gluons m- parameters and n-parameters are not included in the diagrams. To ignore them is based on Theorem 13.2. It greatly simplifies the treatment for the numerical parameters of composite particles. The two level comparisons both make sense to explain proton, neutron and helium nucleon behaviors in terms of strong force binding strength, which serve as evidences to sup- port Theorem 13.2. Let’s consider the third level—elementary particles level, which treats elementary particles such as proton and neutron as a whole entity serving as the constituents of the composite particles such as the helium nucleon, deuterium nucleon, tritium nucleon etc. Proton is made of three flavored quarks duu and neutron is made of three flavored quarks udd . The “+” and “-”represent the sign of their numerical parame- ters. The numerical parameters are 9999,23192121 nm for proton, and 9999,17211919 nm for neutron. Figure 19.6 shows the gluons connections diagrams for helium nucleon, deuterium nucleon and tritium nucleon. For helium nucleon, there are 7 connec- tions for 4 constituents corresponding to 4 3 14/7 connections per constituent. For deuterium nucleon, there are 2 connections for 2 constituents corresponding to 12/2 connections per constituent. For tritium nu- cleon, there are 3 connections for 3 constituents corre- sponding to 13/3 connections per constituent. In case for the third level, the weighting method is different from the first and second levels. The difference is that, the nuclear force among protons and neutrons has limited range, which does not reach all constituents in the com- posite particles. As a first try, assuming the weighting factor for the third level is inversely proportional to the square root of constituents’ number. The weighted bind- ing strength (BS) for helium nucleon, deuterium nucleon and tritium nucleon for the third level are as follows. Helium nucleon: 875.0 4 1 4 7 He BS , (19.4a) Deuterium nucleon: 707.0 2 1 2 2 Det BS , (19.4b) Tritium nucleon: 577.0 3 1 3 3 Tri BS , (19.4c) Comparison: TriDetHe BSBSBS . (19.4d) The results of (19.4) shows the binding strengths are in the right orders: TriDetHe BSBSBS , which indicate deuterium nucleon is weaker than helium nucleon and stronger than tritium nucleon. In fact, helium and deute- rium are stable, while tritium is unstable with a fairly long lifetime of 12.32 years. The results make sense. It shows that, Theorem 13.2 also valid for the third level composite particles. Figure 19.6. Gluon connections inside helium nucleon, deu- terium nucleon and tritium nucleon at the third level.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1293 The assumption of weighting factor for the third level used for (19.4) can be generalized as follows. Helium nucleon: r He BS 4 1 4 7 , (19.5a) Deuterium nucleon: r Det BS 2 1 2 2 , (19.5b) Tritium nucleon: r Tri BS 3 1 3 3 , (19.5c) Comparison: TriDetHeBSBSBS for 5.00 r. (19.5d) For the generalized formulas (19.5), as long as 5.00r, the results for these three composite parti- cles all make sense. More examples of elements and iso- topes are needed to narrow down the value of r in for- mulas (19.5). The reasonable results of binding strengths at three le- vels serve as strong supportive evidences for Theorem 13.2. Moreover, the different type of weighting factor used for the third level indicates that the binding strength is different from the first and second levels. It clearly shows the restrict range of nuclear force among protons and neutrons in a composite particle comparing to the strong force among quarks. It is well known in nuclear physics that, nuclear force is the fringing effect of strong force with exponential decay behavior from the edges of protons and neutrons. Theorem 13.2 directly refers to m-parameters and n-parameters. Since gluons also contribute to composite particles’ mass, quarks’ np / ratio is no longer directly related to the mass of a composite particle. But quarks’ p-parameter may play some other roles. It is the reason for the sum of p values over three colors listed in the u and d columns of Table 19.1. Let’s take a step further to see how it behaviors for composite particles. Let’s treat proton and neutron. According to Table 19.1, the mp/ and mp /2 ratios of proton and neu- tron are: For proton )( duu : 1 1 23 23 192121 835353 m p, 2 2 m p; (19.6a) For neutron )( udd : 17 113 211919 538383 m p, 17 2262 m p. (19.6b) It shows that, the reduced m-parameters and p-para- meters for proton and neutron are: For proton: 1m, 1p; (19.7a) For neutron: 17 m, 113p. (19.7b) The next step is to treat the composite particle the same way with proton and neutron as constituents. For helium nucleon )( pnpn : 1 7 32 224 117117 11131113 m p, 14 2 m p; (19.8a) For deuterium nucleon )( pn : 1 7 16 112 117 1113 m p, 14 2 m p; (19.8b) For tritium nucleon )( pnn: 11 75 33 225 11717 1113113 m p, 11 1502 m p. (19.8c) For comparison, the 2p/m value of electron is: Electron: 1 1 )2/1(22 m p, (19.9) Summarizing the data of (19.7) and (19.8) seemingly implies a rule: Simple composite particles with mp /2 intege r are stable and with mp /2 integer are unstable. Which it valid for complex composite particles or not is an open issue. The rule is also valid for electron. However, it is not valid for other leptons and some quarks. Table 11.4 provides some clues for its selectiv- ity. The different behaviors of proton and neutron are ori- ginated from their difference in numerical parameters, which determine the gluons connections between them. For )( np : 1426 612 40 18 )17(23 )9(9 m n, 35 gg; (19.10a) For )( pp: 6104 244 46 18 )23(23 )9(9 m n, 12 4gg ; (19.10b) For )( nn : 14262 6230 34 18 )17(17 )9(9 m n, 382gg . (19.10c) It clearly indicates that, np and pp are tightly bound, while nn is loosely bound with weakened gluon connections indicated by the minus sign in 38 2gg . Dig it deeper, the difference is originated from the fact that, the up and down quarks have the same n-parameter, but they have different m-parameters. The sum of m-parameters is 211371 for up quark and 191153 for down quark. (19.10) shows that, the m-para- meters difference weakens the binding of nn . Therefore, ultimately the different behaviors of proton and neutron are originated from mathematics. Based on (19.10), some facts in nuclear physics can be  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1294 explained. For instance: 1) Why proton is the most tightly bound particle? 2) Why helium nucleon is the most tightly bound composite particle? 3) Why the strong force bindings for np and pp are tighter than nn ? 4) Why proton is stable, free neutron is not stable? 5) Why neutrons in some nucleons are stable, in other nucleons are not stable? 6) Why deu- terium is stable, tritium is not stable? 7) Why nucleons with Z indexes equal to multiples of 4 have more binding energy than others? Of cause, these are the well known facts observed in experiments and explained by various nucleon theoretical models. SQS theory contribution is to provide a simple and clear explanation based on mathe- matics. Theorem 13.2 plays a pivotal role for the sim- plicity and clearness demonstrated in this section. Gluons contribute to hadron’s mass evidenced by pro- ton and neutron. Does gluon also contribute to hadron’s spin? It is an interesting question. According to Theorem 13.2, the two gluons sequences sent by a pair of quarks (a pair of anti-quarks or a quark and an anti-quark) a q and b q are identical. In case of two gluons sequences sent by a q and b q simultaneously, their two aligned momen- tums with opposite directions cancel out and two oppo- site spins cancel out as well. So in this case, gluon does not contribute to hardron’s spin. On the other hand, in case of two gluons sequences sent by a q and b q at different locations, the displacement of a q and/or b q between the two events causes the two gluons sequences’ momentums no longer aligned, which produce a net an- gular momentum. It might contribute to a part of spin for the hadron. Nuclear physics is very complicated. Whether SQS approach can make more contributions or not, it remains to be seen. What presented in the section is just a start. More work along this line is needed. Section 20. Heisenberg Uncertainty Principle Heisenberg uncertainty principle is not universally valid for the microscopic space inside a Planck cube, because it inevitably leads to an energy paradox. A modified ver- sion of Heisenberg uncertainty principle is introduced in this section to eliminate the energy paradox. It stars with extensions of S-equation serving as the foundation and goes step by step. The 1-dimensional S-equation is the original one based on Gaussian Probability Postulation. According to Theo- rem 3.1, the solution of 1-dimensional S-equation for every x on the x-axis is a running constant )( x . 011)( 2 ))(( i i x xxx exS . (3.20) The original S-equation is valid along the x-axis. Definition 20.1: Define the S-equations along the y- axis and z-axis as: 011)( 2 ))(( j j y yyy eyS , (20.1a) 011)( 2 ))(( k k z zzz ezS . (20.1b) Explanation: According to Definition 20.1, the S- equation is extended from x-axis to y-axis and z-axis. 01)( yS and 01)( zS have the same form as 01)( xS and the same type of solutions )( y , )( z as )( x . Definition 20.2: Define three sets of S-equations par- allel to x-axis, y-axis and z-axis as: 011),;( 2 ))(( i i x xxx kjezyxS , ,,2,1,0, kj zy ; (20.2a) 011),;( 2 ))(( j j y yyy ik exzyS , ,,2,1,0, ik xz ; (20.2b) 011),;( 2 ))(( k k z zzz jieyxzS , ,,2,1,0, ji yx . (20.2c) Explanation: Definition 20.1 and Definition 20.2 ex- tend the original S-equation from the x-axis to three sets of S-equations along straight lines parallel to three or- thogonal axes to form a network. It is important to point out that, all these extended S-equations are 1-dimensional and along straight lines. They are exact duplicates of the original S-equation with the same form and the same type of solutions at different locations with different orienta- tions. According to quantum theory, pairs of conjugated va- riables x and x p , y and y p, and z p must satisfy the Heisenberg uncertainty principle: 42 h px x , (20.3a) 42 h pyy , (20.3b) 42 h pz z. (20.3c) In the microscopic space inside a Planck cube, the va- lidity of Heisenberg uncertainty principle is questionable. 1) Heisenberg uncertainty principle is based on quan- tum theory, which is a linear theory in flat space. Inside the Planck cube dominated by gravitation, the space is neither linear nor flat. 2) If Heisenberg uncertainty principle is universally valid, it inevitably leads to an energy paradox. Let 0 x, 0 y, 0 z, according to (20.3),  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1295 x p, y p , z p. When momentum approaches infinity, so does energy. In other words, there is infinite amount of energy hiding in an infinite small space. That is impossible. For the microscopic space inside a Planck cube, Hei- senberg uncertainty principle must be modified. The problem is lack of a valid quantum gravity theory serving as the foundation. In the meantime, there is no straight- forward way to modify Heisenberg uncertainty principle. Nevertheless, SQS theory provided some clues. The first clue comes from Theorem 3.2. It proved that, solution )( i x at i xof 1-dimensional S-equation is: )(i x at ,,2,1,0,1,2,, i x. (3.21) If the in the denominate of (20.3a) is replaced by )(i x , its right side value approaches to zero cor- responding to reduced uncertainty. The second clue comes from the Gaussian Probability Postulation. It introduced uncertainty in the first place. The S-equation based on it can play an important role for modifying Heisenberg uncertainty principle. Heisenberg uncertainty principle is fundamental for quantum theory, which has been verified by experiments enormous times. To touch it should be very careful. Be- fore doing so, some questions must be thought through. The first question is: If pi is not a constant, what hap- pens to particles’ spin? Since basic unit of spin is 4/2/ hh , if is replace with )(x , particles’ spin is no longer a fixed physics quantity. Is that possible? The answer is: No! Spin is not 1-dimensional, )( x cannot replace for cases other than 1-dimensional. In classic theory, spin as the angle momentum of a parti- cle’s interior movement is: )( vrmprs . (20.4a) Here m, , p and v are mass, radius vector, mo- mentum vector and velocity vector, respectively. For nonzero s , the two vectors and p or v must point to different directions, which do not fit the 1-dimensional condition for )(x to apply. In quantum theory, (20.4a) is in the operator form: y z z y ih sx 2 ˆ. (20.4b) There are also two dimensions y and z involved in right side of (20.4b). In both cases, spin is 2-dimensional, which prohibits )(x to replace . So spin is not a problem. The second question: What does )(x as a running constant mean? Originally, )(x is the solution of 1-dimensional S-equation. It serves as messenger carry- ing information to torus model to determine the location of characteristic points. In this case, )(x serves as messenger carrying 3-dimensional spatial curvature in- formation to the 1-dimensional system for Heisenberg uncertainty principle to apply. Rule 20.1: As the solution of 1-dimensional S-equa- tion, )(x is a 1-dimensional running constant carrying 3-dimensional spatial curvature information. Rule 20.1 serves as a guideline to dealing with Hei- senberg uncertainty principle. The other guideline is that, the energy paradox must be eliminated. Let’s take trial and error approaches to find the right way to modify Heisenberg uncertainty principle. Attempt-1: Define the r-sphere centered at a discrete point i P with radius P Lr 5.0. The intersection of the r-sphere and x-y plane is defined as the r-circle, which has the same center and the same radius as the r-sphere shown in Figure 20.1. Figure 20.1. The r-circle on the r-sphere. The ),( r on the r-circle is defined according to the following procedure: 1) Based on the fact that point 0 on r-circle is the same point on x-axis, take the 0 ),( r value on r-circle from the solution rx x )( of the 1-dimen- sional S-equation along x-axis: rx xrr )(),0(),( 0 , (20.5a) 011)( 2 ))(( n ni ixx exS . (20.5b) In (20.5), the original summation index i x is re- placed by i for simplicity. The truncation number n is sufficiently large to make )( xS converging to 1 for unitarity. 2) Assign the same value for ),( r at four points 0 A at 0 , 1 A at 2/ , 2 A at , 3 A at 2/3 along r-circle: rx A A A Axrrrr )(), 2 3 (),(), 2 (),0( 3 2 1 0 . (20.6)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1296 It is legitimate, because (20.5) is valid for -axis as well for y-axis. 3) Define the ),( r on the r-circle as the solution of the 1-dimensional S-equation along the circumference of r-circle: 011)( 3 0 2 22 ),( j M Mi rirjrr reCS . (20.7a) in which, C as the numerical factor for unitarity and as the truncation number of the summation index i are determined by: 0111)0( 3 0 2 22 ),0( 0 3 0 2 22 ),( j M Mi rirjr j M Mi rirjrr reCeCS . (20.7b) Explanation: Attempt-1 is to define the )( r S func- tion around r-circle based on the assigned value of ),( r at the four points: 0 A at 0 , 1 A at 2/ , 2 A at , 3 A at 2/3 , which are the intersection points of the r-circle with -axis and y-axis. The summation with index i is truncated at i. is selected to make the summation series converge according to certain criterion given latter. The summation with index 3,2,1,0j is to make ),( r and )( r S having a 4-fold symmetry with respect to angle around the r-circle center, which is required by geometrical symmetry of discrete points on the x-y plane. In essence, formula (20.7) is to analytically extend ),( r and )( r S from four intersection points to r-circle’s entire circumference. Based on (20.5), (20.6) and (20.7), the calculated re- sults are listed in Table 20.1. The value of ), 2 (rj (3,2,1,0 j) are the solutions of (20.5) and (20.6) serving as the base values for the extension. The value of ), 4 (rk (7,5,3,1 k) at intermediate angles are the solutions of (20.7) to show the maximum deviation from the base value. Table 20.1. Calculated values of c and ),( r at different points on r-circles*. *Summation index is truncated at a sufficient large number i , 6 10M for convergence. **The relative deviation is ),2/(/),4/(),2/( rjrkrj . The data of Table 20.1 show the following features. 1) For 25.05.0 r, the value of ), 4 (rk (7,5,3,1k) is different from the base value of ), 2 (rj (3,2,1,0j). 2) For 2 10125.0 r, the value of ), 4 (rk (7,5,3,1k) is the same as the base value of ), 2 (rj (3,2,1,0j). 3) For 621010 r, the value of ), 4 (rk (7,5,3,1k) is virtually the same as the base value of ), 2 (rj (3,2,1,0j). 4) The values of ),( r monotonically increase with decreasing as expected. 5) The values of C monotonically decrease with de- creasing as expected. Attempt-1 is to define )( r S by extending ),( r from four points to the entire r-circle. It lays the founda- tion for modifying the Heisenberg uncertainty principle. As a first trial, the Heisenberg uncertainty principle on the r-circle is redefined as: )(4 )(r h pr , (20.8a) 2 ),4/(),0( ),( 2 1 )( 2 0 rr drr . (20.8b) According to Table 20.1, the average value )(r increases with decreasing radius . The value on the right side of (20.8a) decreases corresponding to less un- certainty. It is encouraging. But is it sufficient to elimi- nate the energy paradox? According to (20.8), the energy 1 E for the r-circle with radius is: l E rr E rr hc cpE PP 4)(22)(4 1, (20.9a) 2 , rrl )(2 . (20.9b) In (20.9), length l is normalized with respect to Planck length mLP35 1061625.1 and JLhcE PP 10 1022905.1/ is the Planck energy. The values of l and 1 E calculated from (20.8),  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1297 (20.9) are listed in Table 20.2. Table 20.2. The calculated results from (20.9) and (20.10)* *The value of )( r is the average of the two values listed in Table 20.1 accord- ing to (20.8b). **The unit of energy is the Planck energy JE P10 1022905.1 . As shown in Table 20.2, the values of 1 E are in- crease rapidly with decreasing . The energy paradox is still there. The reason is that, the increasing rate of )(r is not sufficient to compensate the decreasing rate of , which makes the rrl )(2 in the denominator of (20.9a) approaching zero and the 1 E approaching in- finity. In Table 20.2, the summation index i is truncated at . Except for the case of 5.0r and 25.0r, the listed values of are determined by the “background noise” as criterion, which is determined by the sensitivity of 1) 4 ( r Sr from (20.7a) in 16-digit algorism used for numerical calculations. In the process to determine M, a sufficient large number of such as 6 10Mis used to deter- mine the value of C from (20.7b). After the value of C is determined, then gradually reduce the value of M and watch the converging of 1) 4 ( r Sr. when the increasing value of 1) 4 ( r Sr reaches 15 10~ with decreasing M, the truncation takes place at that value listed in Table 20.2. So the trun- cation number M is determined by the sensitivity of 1) 4 ( r Sr at 15 10~, which is determined by the 16-digit algorism not by physics as it should be. This pending issue of “background noise” will be discussed later in this sec- tion. Recall that, the index i in (20.5) is the replacement of the discrete length i x. In the )( r S of (20.7a), the equivalent of i x in the original S-equation of (20.5b) is 2/ r, which is a quarter of the r-circle’s circumferential length. As the radius decreases, so does 2/ r. The value of each term in the summation of (20.7b) increases with decreasing causing the number increase from 8 M for 5.0 r to 725320M for 6 10 r as shown in Table 20.2. Index i runs as Mi ,,3,2,1,0 and Mi ,,3,2,1,0 , in which the “+” and “–” signs are for clockwise and anti- clockwise directions around r-circle, respectively. For each turn around r-circle, the index i takes its value at four points: 0 A at 0 , 1 A at 2/ , 2 A at , 3 A at 2/3 . As the index i truncated at , it corresponds to run 4/MN turns around the r-circle for each direction. The number of turns 4/MN is also listed in Table 20.2. This scenario shows that, the internal movement journey takes 4/MN turns around the r-circle. Attempt-2: Define the energy N E for the internal movement journey around the r-circle with 4/MN turns as: L E rrN E N E EPP N 4)(24 1, (20.10a) rrNlNL )(2 , (20.10b) 4/MN . (20.10c) The calculated values of and N E are listed in Table 20.2. Starting from 5.0r, the values of N E increase with decreasing and peaked around 125.0 r, then it deceases monotonically with decreasing . The energy paradox goes away in this case. It is more encouraging. Attempt-3: Redefine (20.8) as: 24 h pL , (20.11a) rrNlNL )(2 . (20.11b) Take steps to generalize it as much as possible. Step-1: Define two types of lengths: Geometrical loop length: rrlLgeo )(2 , (20.12a) Effective jour ne y length: rrNlNNLLLgeoeff)(2 . (20.12b) The geometrical loop length geo L defined by (20.12a) is the r-circle circumferential length multiplied by a fac- tor of /)(r to recognize )( r different from . It represents the environment is curved space with )(x corresponding to positive curvature and )( x to negative curvature. The effective journey length eff Lis to recognize the journey taking 4/MN turns along the geometrical loop length for both direc- tions. Figure 20.2 shows three examples of geometrical loop length:  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1298 1) For 25.0r, )25.0( , rLgeo 2 is very close to r-circle circumferential length shown in red col- or at the middle of Figure 20.2. 2) For 1.0r, 16381.4)1.0( , 1.0 )(2 r geo rrL is 32538.1/)1.0( times longer than the r-circle circumferential length shown by the wave-shape red curve at Fig. 20.2 left. 3) For 5.0r, 7546.2)5.0( , 5.0 )(2 r geo rrL is 87682.0/)5.0( times shorter than the r-circle cir- cumferential length shown by the red small circle on top of the r-circle at Figure 20.2 right. It is important to point out that, Figure 20.2 is only for visual demonstration. In the real space, corre- sponds to positive curvature to shorten the geo L, while corresponds to negative curvature to elongate the geo L. Figure 20.2. Three examples of geometrical loop on r-sph- eres. Step-2: After the geometrical loop got its base value, it can detach from the four points. The detachment is an im- portant step, let’s look more closely. Recall in Section 8, )( 1 x and )(2 x are the messengers carrying informa- tion left the 1-dimensional S-equation and go to the torus model to determine its curvature. It shows that, messen- gers must leave and move, otherwise, the carried infor- mation cannot be sent to its destination. So the detach- ment of the geometrical loop is necessary. All three types of geometrical loops shown in Figure 20.2 are allowed to detach and to move around on corresponding r-sphere surface. Step-3: The next step is to generalize the correlated equations and formulas. Look at equation (20.7a) more closely. After parameters C and are determined, it can take a general form: 011)( 3 0 2 )( 00 j M Mi ij reCS . (20.13) The variable is the traveling distance along the geometrical loop. Step-3 laid the foundation for the next step of generalization. Step-4: For equations (20.13), the variable is not restricted to a circle. Instead, it is for a closed loop with arbitrary shape under the following conditions: 1) It must be a close loop on the r-sphere surface and must keep the same geometrical loop length rrlLgeo )(2 . 2) All parameters )0( , )(r , C, , and 4/MN keep the same. 3) Along the closed loop, the four points 0 A, 1 A, 2 A, 3 A divide the loop length into four equal parts. Besides these three conditions, there is another strict condition which will be given later in this section. As long as under these conditions, the geometrical loop is permitted to change forms and move on the r-sphere sur- face. After all these attempts and steps, SQS theory is ready to introduce its modified version of Heisenberg uncer- tainty principle. Definition 20.3: The modified Heisenberg uncertainty principle valid for inside the Planck cube is defined as: 2 pL , (20.14a) geoeff NLLL . (20.14b) In which p is the momentum along direction. It is interesting to notice that, the form of formula (20.14a) for the modified Heisenberg uncertainty is the same as the original Heisenberg uncertainty formula along 1-dimension. The change is to redefine the length difference geoeff NLLL . According to definition (20.14b), eff LL is the ef- fective journey length along the geometrical loop, which is 4/MN times the geometrical loop length. In other words, the real loop length is geo L, its internal movement journey takes 4/MN turns to form the effective jour- ney length serving as the L in (20.14). It comes a long way to get here. Is the effort worth it? The first and foremost test: Does the energy paradox go away? To check the energy paradox also takes steps. Step-1: For one loop on its corresponding r-sphere surface, according to the modified Heisenberg uncertainty princi- ple of Definition 20.3, the energy paradox is eliminated evidenced by the trend of N E data listed in Table 20.2. But that’s not enough, because it is for one loop on one r-sphere surface. Step-2: The question is: How many geometrical loops are there on an r-sphere surface? If the loop were allowed to continuously shifting, the answer is uncountable infinity. But that is not the case. According to Lemma 18.2, the  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1299 answer is a countable large number depending on the separation between adjacent trajectories. So the energy paradox may have a chance to survive. Step-3: The next question: Inside a sphere with radius 1 r, how many r-sphere surfaces with radius 1 0rr are there? According to Lemma 18.2, in order to prevent the geo- metrical loop shifting along the r-direction, the radius is only allowed to change discretely. The answer is a countable large number depending on the separation be- tween adjacent spherical surfaces. Compare to Step-2, the chance for the energy paradox to survive is increased tremendously. Step-4: According to the results of Step-2 and Step-3, the number of geometrical loops inside an r-sphere is in the order of two sets of countable many numbers combined. It seems troublesome. More guidelines are needed to dealing with the energy paradox, which come from physics insights we had already. As shown in Section 12, on its trefoil type model electron has two sets of count- able many possible trajectories to jump on. One set in- cludes trajectories with point A and point B at different locations, and the other set includes trajectories on dif- ferent models’ surfaces corresponding to multi-solutions of PS-equation. The number of possible trajectories is in the order of two sets of countable many numbers com- bined. The scenarios are virtually the same as for geo- metrical loops inside the r-sphere. The electron case can serve as a guideline to dealing with the multi-loop prob- lem for the r-sphere case. The key concept is that, the two sets of countable many possible trajectories are just for one electron to jump on. Likewise, the two set of countable many possible loops inside the r-sphere are just for one trajectory to jump on. It serves as the fourth strict condition for the generalized loop mentioned pre- viously. There are two types of jumping trajectory. One type is that, it jumps to a loop on the some r-sphere sur- face, the energy N Edoes not change. The other type is that, it jumps to a loop on a different r-sphere surface with different radiu and different energy, and then it jumps back. It is allow in a very short time interval by Heisenberg uncertainty principle with respect to energy and time. In either case, for a given time only one trajec- tory is effective. The energy paradox is eliminated evi- denced by the N E data listed in Table 20.2. Finally, the energy paradox goes away. It serves as a strong support for Definition 20.3. After all, the effort is worth it. Moreover, there are bonuses. 1) The understanding of Heisenberg uncertainty prin- ciple is deepened, which provides some clues for further investigations. (1) Inside a Planck cube, the valid Hei- senberg uncertainty principle is 1-dimensional. (2) Counting space curvature alone is not enough to elimi- nate the energy paradox evidenced by )(r alone not enough to compensate the 0 /1 r r rising rate. In order to eliminate the energy paradox, the internal movement journey should take multi-turns. (3) Outside the Planck cube, energy paradox does not exist. The original Hei- senberg principle is fine, no modification is needed. 2) The 1-dimension trajectory gets a strong support from Theorem 18.1, Lemma 18.1 and Lemma 18.2. It is not only for SQS theory. The proof is based on geometry and the non-infinite speed, which is general and may have impacts on other areas. 3) The jumping trajectory gets a strong support from Theorem 18.1, Lemma 18.1 and Lemma 18.2. Before that, the concept is based on the ad hoc PS-equation. With the help of Theorem 18.1, Lemma 18.1 and Lemma 18.2, the jumping trajectory gained a firm foundation based on geometry and the non-infinite speed. 4) The internal movement on a trajectory is determina- tive in nature; the uncertainty comes only from jumping trajectories. This is a very important concept, which needs explanation. Look at equation (20.13), even though the )( r S is the sum of probabilities, but the internal movement is represented by the function on the exponen- tial part, which is deterministic: 2 0 )()(o ijf . (20.15) The function )( f has one variable , a constant 0 and a running constant )( plus two integers i and . All of them are deterministic without probability involved. Therefore, as long as the particle is staying in a trajectory, once the initial conditions are determined, everything is exactly according to)( f without any un- certainty. The uncertainty only comes from jumping to another trajectory. Along the journey, the probability of jumping trajectory at is )( r S and the probability of staying on trajectory is )(1 r S. In any case, the uncertainty comes only from when to jump trajectory and jumping to which trajectory. The internal movement on trajectory is deterministic in nature. It supports the con- clusion for the electron and other elementary particles jumping trajectory and their deterministic internal move- ments in a trajectory. In Attempt-1, the r-circle is defined on x-y plane. It is equally valid to define other two r-circles on y-z plane and z-x plane. Accordingly, there are three r-circles in- stead of just one. If this is the case, at a given time, in- stead of only one, there are three effective geometrical loops. The three loops can independently move around, or they can combine into a Borromean-ring-type or a trefoil type acting as one. For either case, it does not change the conclusion of eliminating the energy paradox. There is one pending issue left. The “background noise” serving as the criterion for the index i truncated at is determined by the sensitivity of 1)4/( rSr  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1300 in (20.7b). In other words, it is the minimum change of 1)4/( rS r to trigger an action, which is difficult to derive from the first principle. But there is an indirect way to verify the “background noise” effects. As shown in Table 20.3. The M values are reduced from original values by a factor of %15~. As a result, for the cases from 125.0r to 6 10 r, the “background noise” is in- creased from 15 10~ to 12 10~ and the value of N E is increased by a factor of %15~ . It shows: (1) The three orders of magnitude “background noise” change only causes %15~ of M and N E changes; (2) The profile of N E keeps the same and the energy paradox is eliminated for sure. Table 20.3. The results of table 20.1 and table 20.2 based on reduced M values. From SQS theory standpoint, the Heisenberg uncer- tainty principle related issues are summarized as the fol- lows. 1) For elementary particles with displacements x , y, longer than the Planck length P L, the original Heisenberg uncertainty principle of (20.3) is valid. 2) Inside the Planck cube, Heisenberg uncertainty principle must be modified to eliminate the energy para- dox. 3) SQS theory provides a modified version of Defini- tion 20.3 based on extended S-equation. 4) According to Definition 20.3, for a single geomet- rical loop with energy N E listed in Table 20.2, the energy paradox is eliminated. It serves as a support for Definition 20.3. 5) For the r-spheres with radius 5.00 1r, the geo- metrical loop has many possible trajectories to jump on. At a given time, only one trajectory is effective. To treat all possible trajectories as a statistic ensemble, it has av- erage energy N E. The energy paradox is also elimi- nated. It serves as another support for Definition 20.3, in which L and pare replaced by their average val- ues over the statistic ensemble, L and p, respec- tively. 6) In any case, the point particles such as vacuons with non-infinite speed must have 1-dimentional trajectory and only allow jumping trajectory not shifting trajectory. In a trajectory, the point particles movement is determi- nistic. The uncertainty comes only from jumping trajec- tories. It seemingly raises a question: where does the uncertainty in the modified Heisenberg uncertainty prin- ciple come from? For the statistic ensemble, the uncer- tainty is obvious. For a particular geometrical loop, the internal movement is deterministic. For an observer without information of the initial conditions, the uncer- tainties are eff LL and pp 2 , because the ob- server does not know the particles’ location in the circle and the direction of is momentum. In other words, for a particular geometrical loop, objectively its internal movement is deterministic; subjectively it is uncertain for an observer due to lack of information. 7) The modified Heisenberg uncertainty principle of Definition 20.3 proposed by SQS theory is not derived from the first principle. Instead, the approach taken in this section is based on the extended S-equation with )( as a running constant to represent the space cur- vature inside the Planck cube. It is an indirect approach, but it does catch the essence and provides some useful information for the final version of the modified Heisen- berg uncertainty principle. The modified Heisenberg uncertainty principle pro- posed by SQS theory is subject to verification. Direct verification in the sub-Planck scale is unrealistic. How- ever, there is an indirect way. According to the original Heisenberg uncertainty principle, within extremely tiny space, the quantum fluctuations in vacuum caused by virtual particles pairs become extremely strong. Such quantum fluctuations with extremely high energy and momentum are rare. But for photons came from a star billions of light-years away, during the long journey, they could run into it and bounce off causing deflections. This effect makes the star’s image blurred. On the other hand, according to the modified Heisenberg uncertainty principle proposed by SQS theory, the blur effect is sig- nificantly reduced or virtually eliminated. Powerful tele- scope in obit may tell the difference. Section 21. Basic Constants and Parameters SQS theory is a mathematic theory with physics signifi- cance. In principle, all equations, formulas and parame- ters are based on three fundamental Postulations and de- rived from mathematics. The mathematical results are interpreted by three basic physics constants, Planck con- stant h, speed limit of light in vacuum c, and gravita- tional constant G. To reach this goal takes steps. Initially, SQS theory had two other physics inputs: electron mass and proton mass. In Section 15, a connec- tion between proton mass and Plank mass via unified interactions was discovered. Proton mass as a physics input for SQS theory is no longer needed. In Section 16, a connection between electron mass and Plank mass via logistic equation was discovered. Electron mass as a physics input for SQS theory is no longer needed. After  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1301 these two discoveries, SQS theory only needs three basic physics constants h, c, G and in principle no other physics input is needed. The three basic physics constants h, c, Gare re- lated to Planck length P L, Planck time P t, Planck en- ergy P E or Planck mass Planck M as: 3 2c hG LP , 5 2c hG tP ,G hc EP 5 2 , G hc MPlanck 2 . (21.1) P P t L c, PPtEh , 2 3 4 522 PPlanck P PP PtM L tE L G . (21.2) These two sets of basic constants are equivalent. From SQS theory standpoint, the set of P L, P t , P E or Planck M is preferred, because they are directly related to space, time, energy or mass. In fact, the Planck constants P L, P t, P E or Planck M are the basic length, basic time interval, basic energy or basic mass at Planck scale, re- spectively. Besides three basic physics constants, there are other physics parameters such as the mass of elementary parti- cles and various coupling constants etc. SQS theory standpoint is that, in principle all these physics parame- ters can be derived from particle’s model and traced back to mathematic parameters with three basic physics con- stants as interpreters. So far, SQS theory did part of them, the others are still open issues. The mass of a fermion is determined by its p/n ratio based on electron mass. The interaction parameters are related to the CKM-triangle, GWS-triangle and S-triangle of the particle’s model, which are determined by charac- teristic points on the model. The characteristic points are determined by )( 1 x and )( 2 x traced back to S-equation originated from Gaussian Probability Postula- tion. The derivation for other physics parameters from mathematical parameters is just a matter of time. The faith of SQS theory comes from this argument: If the geometrical models for elementary particles are real, everything should be derived from these models with characteristic points and triangles attached to them. If the physics parameters cannot be derived from these models, they are useless. SQS theory introduced three sets of numerical pa- rameters m, n, p for elementary particles. The nu- merical parameters of elementary fermions are listed in Table 21.1. According to SQS theory, elementary bosons are made of pairs of elementary fermion and anti-fermion, their numerical parameters are derived from these fer- mions as shown in previous sections. The total numbers of numerical parameters listed in Table 21.1 is 72. In which the 9 numerical parameters of neutrinos is the same as those of their companion leptons except the some sign changes and the constant 11 /103996.8 l R multiplication to p-parameters for neutrinos. The reduced m-parameters of leptons all equal to 1 for spin 2/. Substrate 9 + 3 = 12 from 72, the number of independent parameters is reduced to 60. For the quarks, their 18 m-parameters are uniquely deter- mined by a set of 18 least odd prime numbers; their n-parameters are selected from prime numbers and sub- ject to the tight constrain set by strong interactions leav- ing almost on room for alternative. Substrate 18 + 18 = 36 from 60, the number of independent numerical pa- rameters is reduced to 24. In addition, according to defi- nition e MMnp// , electron’s p-parameter must equal to its n-parameter. The number of independent numerical parameters for the current version of SQS theory is re- duced to 23. It is interesting to notice that, the number 23 is close to the number of handpicked parameters in the standard model. But there is a difference. The twenty some parameters in standard model are physics in nature cited from experimental data, while the 23 left numerical parameters of SQS theory are mathematics in nature. Table 21.1. The numerical parameters of elementary fer- mions. *11 /8.3996 10 l R . One of the final goals of SQS theory is to derive all physics properties of elementary particles and interac- tions from the first principle based on three fundamental postulations and three basic physics constants. We ha- ven’t reached the goal yet. The major obstacle is the p-parameters. In the current version SQS theory, an ele- mentary particle’s p-parameter is determined by its mass. In principle, it should be the other way around: p-parameter determines mass. It indicates that, there is a rule missing in the current version of SQS theory, which is an important open issue. Actually in the current version SQS theory, some par- ticles’ mass values are derived from the first principle already. In Section 15, the mass value of two scalar bos- ons 1 U and 2 U is derived from points a xand b x from special point c x originated from S-equation based  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1302 on Gaussian Probability Postulation. The mass value of the scalar bosons 3 U is derived from the converting factor at the grand unification scale, which is originated from the Random Walk Theorem based on Gaussian Probability Postulation. More importantly, the results of these two methods are correlated to fine structure con- stant )( Z M , which gives legitimacy to both methods. In Section 17, the mass value of the gauge boson is derived from points a x and b x also originated from special point c x. Is there a way to trace the mass value of other two gauge bosons W and 0 back to the special point 73026452499871562.0 c x? Let’s try: 01 25.0 0 )( 25.0 )( 22 dxedxe c f xN Nn xn x N Nn xn , (21.3a) 474772499988898.0 f x, (21.3b) 25.0 fc xx . (21.3c) Point 474772499988898.0 f x is used to determine two points on x-axis: 474772499988898.0 1 f xx , (21.4a) 525232500011101.05.0 2 f xx . (21.4b) Using the points 1 x and 2 x to define a fermion state f, according to (6.18) its mass is: 2 12 /5370162.57 4cGeV xx M Me f . (21.5) 2 /611049.1723cGeVMf. (21.6) 2 /3696287.812 cGeVM f. (21.7) To compare 2 /611049.1723 cGeVM f with top quarks mass 2 /)9.00.172( cGeVMqt cited from 2010-PDG data, the f M3 value is within its error range, and the relative deviation of f M3 from qt M medium value is 3 10553.3 . According the correlations of W, 0 and t q given by (14.2) and (14.3), the mass values of gauge bosons W, 0 can be calculated from the value of f M3 and Weinberg angle W as: 2 /7320308.91 cos1 3cGeV M M W f Z , (21.8a) 2 /879018.80cos cos1 3cGeV M MW W f W , (21.8b) 2 /611049.1723cGeVMMM fWZ , (21.8c) 15335581.28cos dataPDG Z W WM M ar . (21.8d) The values Z M, W M given by (21.8a), (21.8b) com- pare to 2010-PDG data, 2 /)0021.01876.91(cGeVM Z , 2 /)023.0399.80( cGeVMW, both have relative deviation of 3 1097.5 from medium values. Compare 2 /3696287.812 cGeVM f of (21.7) to 2 /)023.0399.80( cGeVMW , the relative devia- tion from its medium value is 2 102.1 . Notice that, f M and W M are the mass of a fermion state f and gauge boson W, respectively; while 2 is the nu- merical factor left unexplained in Section 16. It implies that, 2 may have something to do with the relation between fermions and bosons, which will be discussed in Section 22. In the meantime, it serves as a check point. Prediction 21.1: There is an electrically neutral scalar boson as a composite state of ffS MMM with mass: 22 /074032.115/)5370162.572(cGeVcGeVMMs . (21.9) If all of these are not by coincidence, the special point 73026452499871562.0 c x did it again. It not only de- termined the mass value for two scalar bosons W, 0 , but also for the top quark t q. It is the first quark with mass value traced back to the first principle. The three colored top quarks have slightly different mass values from their average value as listed in Table11.2, which are caused by color symmetry broken. If the 3 colored top quarks’ mass values are indeed traced back to the first principle, then the independent numerical parameters left is reduced from 23 to 20. In which there are 15 p-parameters of 15 quarks plus 2 p-parameters of muon and taon, the rest 3 parameters are the n-parameters of 3 leptons. Why does the special point c x determine top quark’s mass not other type quarks? Because top quark with mass MaxqtMM , it must appear with top anti-quark as boson state. Apparently the special point c x works only for bosons or boson states. The remaining question is: for qtfMM 3, where does the factor 3 come from? It is worthwhile to give a thought. Section 22. Space Structure and Symmetries The first fundamental postulation of SQS theory, Gaus- sian Probability Postulation, assigns Gaussian probability at each discrete point separated by Planck length, which makes continuous space with grainy structure. In previ- ous sections, the Planck cube as the building block of space is based on 3-dimensional Cartesian coordinate. The adoption of Cartesian coordinate system implies a hidden a priori assumption: Space has cubic lattice structure, which has no proof. What is the real structure of space? What are the inherent symmetries of space? These are the two basic questions of this section. To answer the first question, let’s go back to the fun- damental postulation. The 3-dimensional Gaussian pro-  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1303 bability distribution function has spherical symmetry like a ball with blurred boundary. The Gaussian probability distribution function converges rapidly toward zero with distance from its center. Let’s ignore its blurredness and treat the 3-dimensional Gaussian distribution function as a hard ball called “Gaussian sphere” with definitive boundary. In Section 2, the radius of Gaussian sphere is defined as: 932743535533905.0 22 1R. (2.9b) From SQS viewpoint to consider the structure of space, the question is: What is the preferred way for Gaussian spheres to arrange themselves? As the Gaussian sphere treated as hard ball, the question becomes: What is the most compact packing for balls? It is a classic topic known as Kepler conjecture. Kepler conjectured that, the face-centered arrangement is the most compact packing for balls, which has an average density: 74048049.0 18 cf D. (22.1) Kepler conjecture was proved by Thomas Hales in 1998 using the exhaust method with extensive numerical calculations. For comparison, the cubic arrangement for balls has an average density: 52359878.0 2 6 cf c D D . (22.2) Nature has a tendency to reach the lowest energy for stability. As gravity dominates, the most compact pack- ing is the one with lowest potential energy. The face- centered lattice is the preferred one for the space struc- ture. This is the first supportive evidence for the face- centered lattice structure of space. The ball packing argument is only a simulation. In re- ality, the spherical Gaussian probability distribution is not a hard ball with definitive boundary. Keep this in mind; let’s take a close look at face-centered lattice struc- ture. Figure 22.1 shows a sketch of the face-centered lattice structure within a Planck cube. It shows that, the face- centered lattice can be viewed as an octahedron embed- ded in a cube. The lattice length of cube and octahedron are Pcube Ll and 2/ Pocta Ll , respectively. The lattice lengths ratio of cube to octahedron is: 2/ octacube ll . (22.3) In (22.2) and (22.3), the number 2 looks familiar. It appeared in front of electron converting factor e N of equation (16.1) in Section 16. The definition of electron converting factor is: P eC eL N . (6.10) Figure 22.1. Face-centered lattice structure as an octahe- dron embedded in a cube. According to (6.10), multiplying 2 to PeCe LN / is equivalent to redefine Planck length P L' based on the octahedral lattice length 2/ Pocta Ll as: m c G c G LL PP35 33 1014286.1 2 2 1 2 1 ' . (22.4) The 2 factor appeared in equation (16.1) is not by coincidence. It can be interpreted as PP LL'/2. This is the second supportive evidence for the face-centered lat- tice structure of space. Moreover, in Section 15 and Section 16, there are two related converting factor formulas: For the scalar boson of grand unification: )( 2 Z GUT M N . (15.11) For electron as a fermion in Section 16, letting 0 r in equation (16.1) yields: )( 2 2 1 )0( e eM rN . (22.5) Despite the difference of )( Z M verses )( e M representing the difference of energy scales, the notable difference between (15.11) and (22.5) is the factor 2/1 . (15.11) is for boson and (22.1) is for fermion. Notice that, in (22.4), under the square root sign, 2/ in the rede- fined P L' is the basic spin for fermions, while in the original P L definition is the basic spin for bosons. These comparisons imply that, the difference between fermions and bosons may have something to do with 2/1 and the difference between octahedral part and cubic part of the space face-centered structure. It serves a possible explanation for the difference between (15.11) and (22.5). It also serves as the third supportive evidence for the face-centered lattice structure of space.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1304 Postulation 22.1: Space has face-centered lattice structure as shown in Figure 22.1. It contains two parts: the cubic part with unit length of P L and the octahedral part with unit length of 2/'PP LL . Explanation: Normalized to P L, 2/12/' PP LL . According to (2.9b): 22 2 ' 22 1PP LL R . (22.6) It explains the mathematical reason for the definition of the radius of Gaussian sphere . In reality, R is determined by the balance of attractive force and repul- sive force. According to Postulation 22.1, space has crystal struc- ture. It is well known in crystallography that, symmetry play an important rule to explain crystal properties. Let’s try to answer the second basic question. Definition 22.1: In the space with face-centered lattice structure, symmetry )(rO is defined as a set of vertexes on the spherical surface centered at an octahedral vertex with radius ; symmetry )(rC is defined as a set of vertexes on the spherical surface centered at a cubic ver- tex with radius . According to Definition 22.1, there are 18 symmetries for )(rO with 3r and 18 symmetries for )(rC with 3r. The parameters of 36 symmetries of )(rO and )(rC with 3r are listed in Table 22.1 and Table 22.2, re- spectively. In these tables, three sets of numbers are listed. In the column of “No. of vertexes TotalCubOct ..”, “.Oct” and “.Cub ” are the num- bers of octahedral and cubic vertexes in the symmetry, respectively. In the column of “No. of equilateral trian- gles TotalSeparConn .. ”, “.Conn” and “.Separ ” are the numbers of connected and separated equilateral triangles in the symmetry, respectively. In the column of “No. of squares with center Tota OffOn ”, “On” and “Off ” are the numbers of squares with center vertex of the symmetry on and off the square surface, respec- tively. Let’s start from the octahedral part listed in Table 22.1. )0(O is a basic symmetry represented by a single vertex, which has a rotational symmetry with any angle. It seems reasonable to identify )0(O related to the )1(U group. In the standard model, )1(U represents electromagnetic interaction mediated by photons. From SQS theory viewpoint, photon and graviton are two sides of the same coin. So )0(O is also related to graviton. In fact, the single vertex of )0(O has dual identity like two sides of the same coin. It is the vertex on its shrunk sphere sur- face and it also is the center vertex. It seems reasonable to identify the former with electromagnetic interaction and the letter with gravitation. All symmetries have center vertex not included in Table 22.1 and Table 22.2, which corresponds to gravity’s universality. Table 22.1. Symmetries centered at an octahedral vertex in the face-centered space. Note: The symmetries marked with * are the 6 essential symmetries. Table 22.2. Symmetries centered at a cubic vertex in the face- centered space. Note: The symmetries marked with *are the 6 essential symmetries. Symmetry )2/1(O is an important basic symmetry having 12 vertexes located at following Cartesian coor- dinates with origin at the center vertex.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1305 Cube vertexes: ) 2 1 , 2 1 ,0( 1 p, ) 2 1 , 2 1 ,0( 2 p,) 2 1 , 2 1 ,0( 3 p, ) 2 1 , 2 1 ,0( 4 p; (22.7a) Octahedral vertexes: )0, 2 1 , 2 1 ( 5 p)0, 2 1 , 2 1 ( 6 p, )0, 2 1 , 2 1 ( 7 p, )0, 2 1 , 2 1 ( 8 p; ) 2 1 ,0, 2 1 ( 9 p, ) 2 1 ,0, 2 1 ( 10 p,) 2 1 ,0, 2 1 ( 11 p,) 2 1 ,0, 2 1 ( 12 p. (22.7b) In which 4 vertexes are cubic type and 8 vertexes are octahedral type. The hybrid of octahedral and cubic ver- texes in )2/1(O may serve as a link between fermions and bosons. The 12 vertexes form 8 connected equilateral triangles, in which the 4 connected equilateral triangles in 0x part are shown in Figure 22.2. )2/1(O has 9 squares, in which 3 squares with center vertex on square surface and the other 6 squares with center vertex off square surface. The meaning of the equilateral triangles and the two types of squares will be given later in this section. In essence, symmetry )2(O is an enlarged version of )2/1(O. All symmetries are the same for )2/1(O and )2(O.The only difference is the linear scale of )2(O is enlarged by a factor of 2 comparing with )2/1(O. Figure 22.2. The vertexes of 2/1O with 4 vertexes lo- cated at 0x not shown. )1(O is an important basic symmetry. As shown in Table 22.1 and Figure 22.3, )1(O has 6 octahedral ver- texes, The 6 vertexes form an octahedron, which is one of two parts of the face-centered lattice structure of space with elongated length scale. The 6 vertexes are paired to form 3 orthogonal axes with 90 span angles at center. It is identified as )3(SO group. )3(SO is closely related to the )2(SU group. The elements of )3(SO and the elements of )2(SU are described by three parameters corresponding to the three Euler angles of a three dimen- sional rotation. The relation between )3(SO and )2(SU is that, each rotation in three dimensions of )3(SO corresponds to two distinct elements of )2(SU . In some sense, )2(SU is a dual version of )3(SO . It seems reasonable to relate )1(O with the )2(SU group. The 6 vertexes of )1(O form 3 squares with center ver- tex on square surface. A square with center vertex on square surface is a part of )3(SO and serves as a part of )2(SU representing weak interaction. As shown in Table 22.1 and Figure 22.3, )1(O has 8 connected equilateral triangles. The simplest representa- tion of )3(SU group is a triplet. It seems reasonable to relate the equilateral triangles in )1(O with )3(SU triplets such as bgr uuu ,, and bgrddd ,, . SQS the- ory searching for the )3(SU group comes from a long way. The first clue came from the 3-dimensional Gaus- sian probability standard deviation, 2/1 3. Its three roots provide one real number and two complex numbers, which define three axes separated by 120 on a complex plane as shown in Figure 3.2. The second clue came from the transportation route of electron mov- ing in the zigzagging path named “zitterbewegung” hav- ing 120 angle with x-axis on a complex plane shown in Fig. 3.4. The third clue is the fermions’ loop-2 tiny tilt angle deviated from 120 . Now, all these clues point at one origin, which is the triplet symmetrical structure in the face-centered lattice. It could serve as the geometrical foundation for )3(SU group in the real space. Figure 22.3. The 6 vertexes of 1O. In essence, the )1()0( OO is related to three groups )1(U, )2(SU , )3(SU plus gravitation as the center vertex, which represent all four types of interactions. As shown in Section 15, all four types of interactions are  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1306 united into one. So it should not be a surprise to find out that, )1()0( OO related to all four types of interac- tions. As shown in Table 22.1, symmetry )3(O has 8 oc- tahedral vertexes in which 4 of them in 0x region are shown in Fug. 22.4. The 8 vertexes of )3(O form a cube, which is one of the two parts of face-centered lat- tice space structure of space with elongated length scale. The 8 vertexes of )3(O form 8 connected equilateral triangles and 6 squares with the center vertex off surface. Since the )3(SU group has an eight-fold representation, octet, it seems reasonable to relate )3(O to the eight-fold. The 6 off center squares represent strong in- teraction to hold the 8 equilateral triangles representing 8 fermions. A possible physics interpretation is: The octet of )3(O represents the baryons octet as shown in Fig. 22.5. It includes 8 baryons:)( uudp , )(ddun , )(uus , )( dds , )( 0uss, )( dss , )( 0uds, )(uds, in which each baryon is made of 3 quarks in the first and second generations. Figure 22.4. The vertexes of 3O with 4 vertexes located at 0x not shown. There is a difference between two different types of squares. The squares with center vertex on square surface such as those in )1(O are related to part of )2(SU representing weak interaction. The squares with center vertex off square surface such as those in )3(O are related to a part of )3(SU representing strong interac- tion. The ratio of center to square distance over square edge is defined as EDR ED / /. For squares with center vertex on surface: 0 / D RED . (22.8a) For the squares with center vertex off surface: 0 / D RED . (22.8b) Figure 22.5. The baryons octet represented by 3O. Back to the )2/1(O symmetry, it has 3 squares with center vertex on surface and 6 squares with center vertex off surface. It seems that, both weak interaction and strong interaction are involved with its 8 equilateral tri- angles. A possible physics interpretation is: )2/1(O represents 8 fermions, r u, g u, b u, r d, g d, b d, e, e and their anti-particles of the first generation. The weak interactions among 8 fermions represented by 3 squares with center vertex on surface are understandable. The strong interactions among 6 quarks represented by squares with center vertex off surface are also under- standable. But there are squares with center vertex off surface connecting to equilateral triangles representing leptons and quarks. What does such type connection mean? Figure 22.6 shows the “Symmetries Family Tree” for )(rO symmetries. It includes all 18 octahedral symme- tries with radius 3 r. Symmetries are illustrated by squares with names. The vertical location of the square is raised according to increasing values of )(rO . Inside the square from top down, the numbers in three rows, TotalCubOct .. , TotalSeparConn .. , TotalOffOn are cited from Table 22.1. In Figure 22.6, there are three types of connecting lines: A vertical single solid line in- dicates that the connected two squares have the same type symmetry with different scales. The forked solid lines indicate that the top symmetry is a combination of two symmetries below. The dashed line indicates that the two connected symmetries are somehow correlated. In Table 22.1 and Fig. 22.6, the 6 symmetries marked with * belong to the essential type. In which, )0(O, )1(O)2/1(O are basic symmetries as mentioned pre- viously. The other three, )2/3(O, )2/7(O, )2/13(O, are the lowest symmetries having vertex numbers 24, 48, 72, respectively. 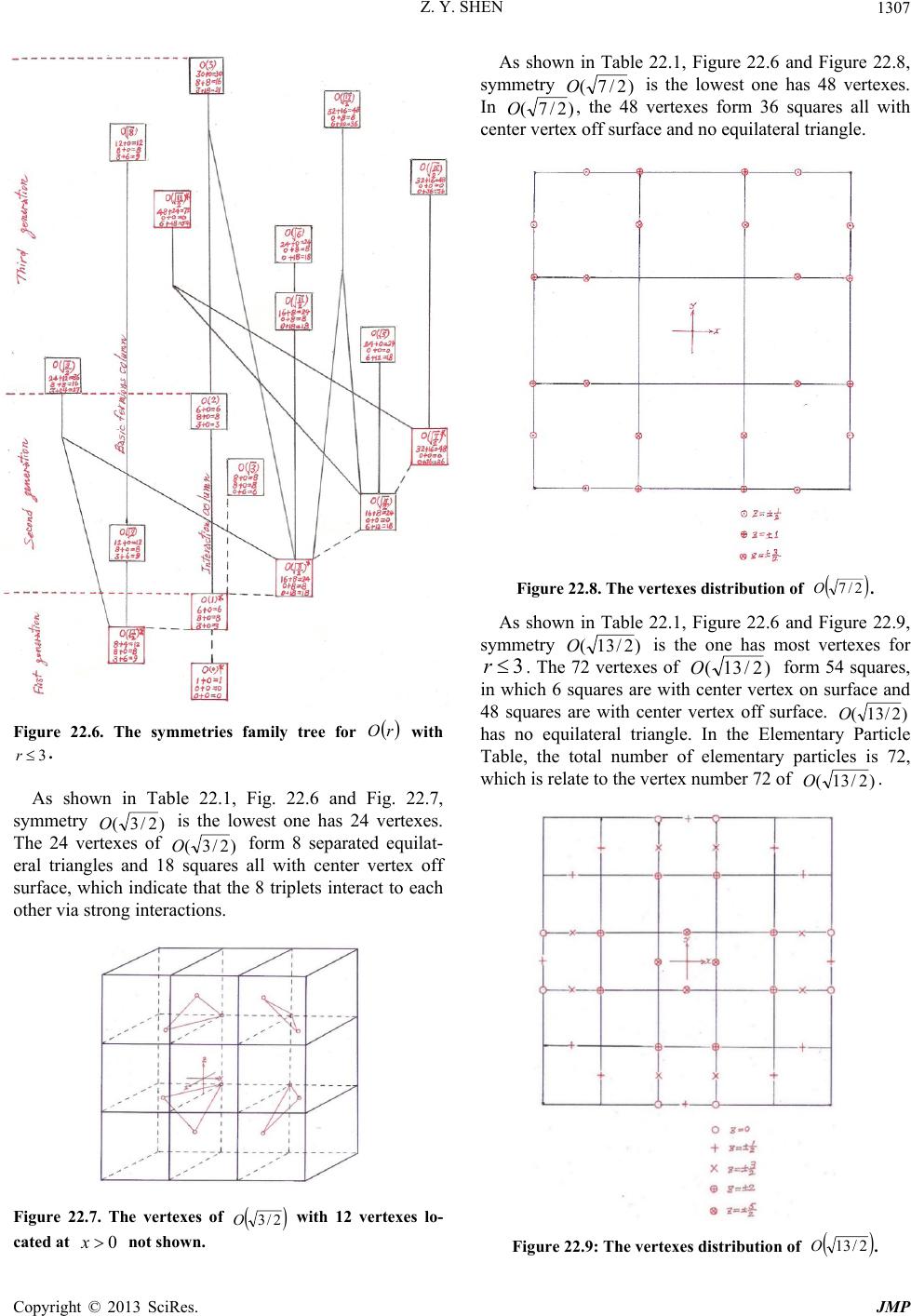 Z. Y. SHEN Copyright © 2013 SciRes. JMP 1307 Figure 22.6. The symmetries family tree for rO with 3r. As shown in Table 22.1, Fig. 22.6 and Fig. 22.7, symmetry )2/3(O is the lowest one has 24 vertexes. The 24 vertexes of )2/3(O form 8 separated equilat- eral triangles and 18 squares all with center vertex off surface, which indicate that the 8 triplets interact to each other via strong interactions. Figure 22.7. The vertexes of 2/3O with 12 vertexes lo- cated at 0x not shown. As shown in Table 22.1, Figure 22.6 and Figure 22.8, symmetry )2/7(O is the lowest one has 48 vertexes. In )2/7(O, the 48 vertexes form 36 squares all with center vertex off surface and no equilateral triangle. Figure 22.8. The vertexes distribution of 2/7O. As shown in Table 22.1, Figure 22.6 and Figure 22.9, symmetry )2/13(O is the one has most vertexes for 3 r. The 72 vertexes of )2/13(O form 54 squares, in which 6 squares are with center vertex on surface and 48 squares are with center vertex off surface. )2/13(O has no equilateral triangle. In the Elementary Particle Table, the total number of elementary particles is 72, which is relate to the vertex number 72 of )2/13(O. Figure 22.9: The vertexes distribution of 2/13O.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1308 In the Symmetries Family Tree shown by Fig. 22.6, there are five columns; the vertical line connections in- dicate their heritage, which is originated from the bottom symmetry of each column. Out of five, two columns are significant. The one called “interactions column” is made of )0(O, )1(O, )2(Oand )3(O; The other one called “basic Fermions column” is made of )2/1(O, )2(O and )8(O. The foundation of the interactions column is the )0(O symmetry representing electromagnetic interaction and gravitation as mentioned previously. As shown in Sec- tion 15, all interactions are finally unified to gravitation. The )0(O deserves to be the foundation of interactions column. From the foundation up, the next symmetry is )1(O. As mentioned previously, )1()0(OO represents gravitation, electromagnetic, weak, and strong interac- tions. Fig. 22.6 clearly shows that, all four types of in- teraction are in this column. Up further, there are two more symmetries, )2(O, )3(O. In which )2(O is an enlarged version of )1(O. As shown by the forked line, )2/3()2()3(OOO , the combination nature of )3(O is due to the fact that, its radius 3r is suffi- ciently large to accommodate the additional 24 vertexes in the enlarged version of )2/3(O. But the core of )3(O is an enlarged version of )1(O. Overall, )1(O, )2(O, and )3(O are the interaction symmetries for the 1st, 2 nd, and 3rd generations, respec- tively. It implies that, the radius values, 1, 2, 3 are related to the orders of three generations. )0(O is related to all symmetries corresponding to gravity’s universality, which was mentioned previously from another perspec- tive. The foundation of basic fermions column is )2/1(O, as mentioned previously, )2/1(O are related to the first generation 8 fermions of r u, g u, b u, r d, g d, b d,e, e and their anti-particles. Since 12/10 , 12/10 , 221 , and 382 , it seems natural to relate )2(O to the second generation 8 fermions of r s, g s, b s, r c, g c, b c, , and their anti-particles; to relate )8(O to the third generation 8 fermions of r b, g b, b b, r t, g t, b t, , and their anti-particles. The arrangement confirms the corre- lation between the values of and the orders of gen- erations. The column made of )2/3(O, )2/11(O and )6(O is based on )2/3(O. )2/11(O and )6(O have similar properties as )2/3(O. They all have the same vertexes number 24, the same structure of 8 sepa- rate equilateral triangles and 18 squares with center ver- tex off surface. The column made of )2/5(O and )5(O is based on )2/5(O. They all have 24 vertexes, and 18 squares in which 6 with center vertex on and 12 off surface. They have no equilateral triangle. The column made of )2/7(O and )2/15(O are based on )2/7(O. They all have 48 vertexes, 36 squares with center vertex off surface. They also have no equilateral triangle. The three columns based on )2/3(O, )2/5(O, )2/7(O with foundations all start from the second gen- eration. As shown in Fig.22.6, the columns based on )2/3(O, )2/5(O, and )2/7(O have 2, 1, and 1 symmetries in the third generation, respectively. The equilateral triangle and the square are two basic elements of the face-centered space lattice. The symme- tries in columns based on )2/5(O, )2/7(O and symmetry )2/13(O have no equilateral triangle. But the symmetry with a definitive radius is not alone. The eighteen symmetries in the Symmetries Family Tree live together as a family. From family perspective, more equilateral triangles can be found. For instance, in the combined symmetry )2/5()2/3(OO as shown in Fig. 22.10, besides the 8 equilateral triangles of )2/3(O, the combination adds 32 more equilateral tri- angles. )2/5()2/3(OO as a whole has 40 equi- lateral triangles. The same is true for some other symme- try. For instance, the combined symmetries of )5()2(OO , )2/7()2/3( OO ,)2/13()2/11( OO and )2/15()2/9(OO all add 8 more equilateral triangles. The numbers listed in Table 22.1 and Table 22.2 only count the equilateral triangles for each symme- try alone. Actually, the total number of equilateral trian- gles in )(rO and )(rC for 3r as two families are far more than the listed grand total of 224112112 . Figure 22.10. Additional equilateral triangles of 2/52/3 OO . 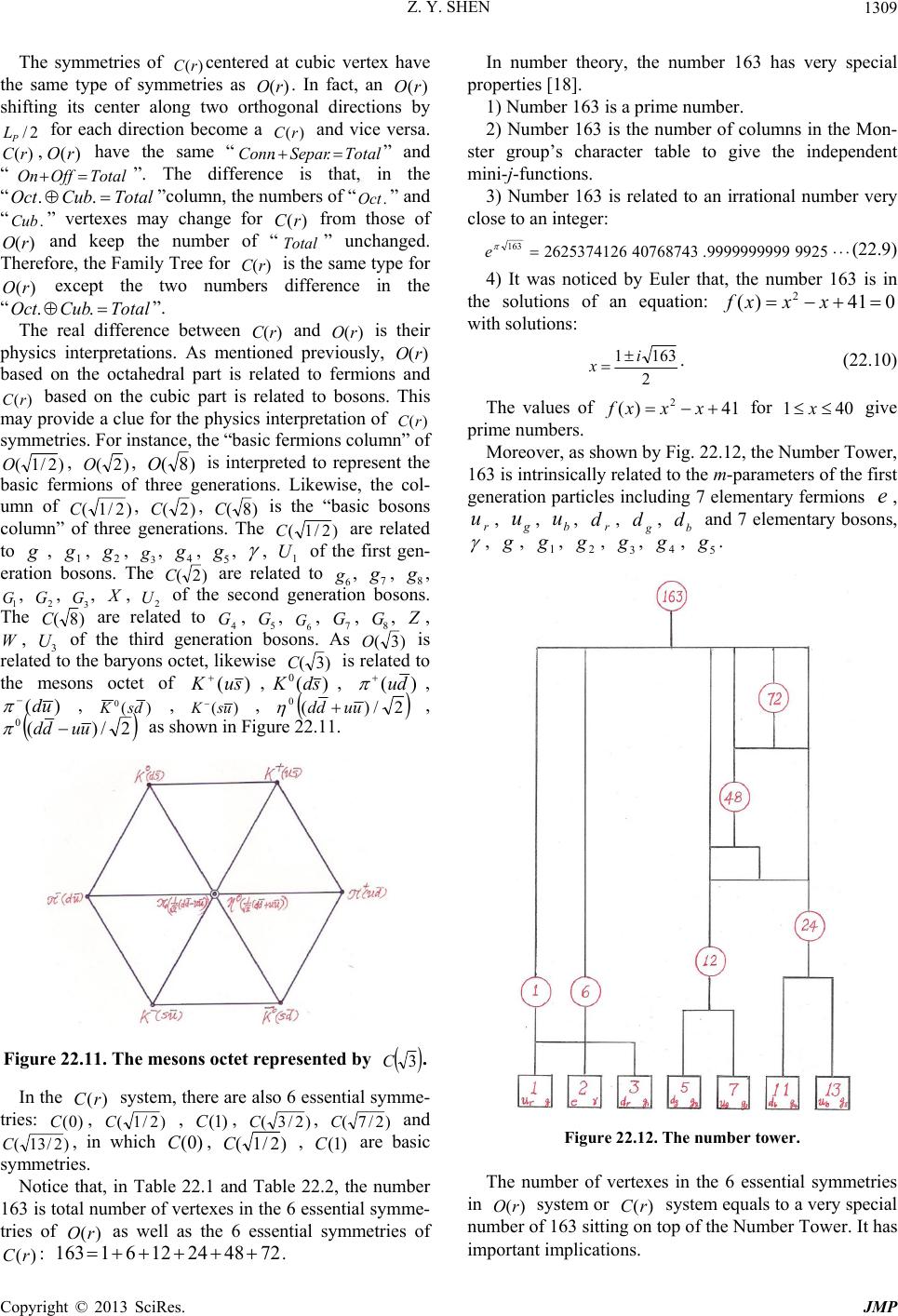 Z. Y. SHEN Copyright © 2013 SciRes. JMP 1309 The symmetries of )(rC centered at cubic vertex have the same type of symmetries as )(rO . In fact, an )(rO shifting its center along two orthogonal directions by 2/ P L for each direction become a )( rC and vice versa. )(rC ,)(rO have the same “Tota SeparConn .. ” and “TotalOffOn ”. The difference is that, in the “TotalCubOct .. ”column, the numbers of “.Oct ” and “.Cub ” vertexes may change for )(rC from those of )(rO and keep the number of “Total ” unchanged. Therefore, the Family Tree for )(rC is the same type for )(rO except the two numbers difference in the “TotalCubOct .. ”. The real difference between )( rC and )(rO is their physics interpretations. As mentioned previously, )(rO based on the octahedral part is related to fermions and )(rC based on the cubic part is related to bosons. This may provide a clue for the physics interpretation of )( rC symmetries. For instance, the “basic fermions column” of )2/1(O, )2(O, )8(O is interpreted to represent the basic fermions of three generations. Likewise, the col- umn of )2/1(C, )2(C, )8(C is the “basic bosons column” of three generations. The )2/1(C are related to g, 1 g, 2 g, 3 g, 4 g, 5 g, , 1 U of the first gen- eration bosons. The )2(C are related to 6 g, 7 g, 8 g, 1 G, 2 G, 3 G, , 2 U of the second generation bosons. The )8(C are related to 4 G, 5 G, 6 G, 7 G, 8 G, , , 3 U of the third generation bosons. As )3(O is related to the baryons octet, likewise )3(C is related to the mesons octet of )( suK,)( 0sdK, )(du , )(ud ,)( 0dsK ,)( usK, 2/)( 0uudd , 2/)( 0uudd as shown in Figure 22.11. Figure 22.11. The mesons octet represented by 3C. In the )(rC system, there are also 6 essential symme- tries: )0(C, )2/1(C , )1(C, )2/3(C, )2/7(C and )2/13(C, in which )0(C, )2/1(C , )1(C are basic symmetries. Notice that, in Table 22.1 and Table 22.2, the number 163 is total number of vertexes in the 6 essential symme- tries of )(rO as well as the 6 essential symmetries of )( rC: 7248241261163 . In number theory, the number 163 has very special properties [18]. 1) Number 163 is a prime number. 2) Number 163 is the number of columns in the Mon- ster group’s character table to give the independent mini-j-functions. 3) Number 163 is related to an irrational number very close to an integer: 99259999999999.407687432625374126 163 e(22.9) 4) It was noticed by Euler that, the number 163 is in the solutions of an equation: 041)( 2 xxxf with solutions: 2 1631 i x . (22.10) The values of 41)( 2 xxxf for 401 x give prime numbers. Moreover, as shown by Fig. 22.12, the Number Tower, 163 is intrinsically related to the m-parameters of the first generation particles including 7 elementary fermions e, r u, g u, b u, r d, g d, b d and 7 elementary bosons, , , 1 g, 2 g, 3 g, 4 g, 5 g. Figure 22.12. The number tower. The number of vertexes in the 6 essential symmetries in )(rO system or )(rC system equals to a very special number of 163 sitting on top of the Number Tower. It has important implications.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1310 1) The set of 6 essential symmetries is not an arbitrary selection. It is based on mathematics. 2) The total number of elementary particles is 72. It is the number of vertexes in )2/13(O or )2/13(C. It also is the largest vertexes number in any symmetry of )(rO or )( rC with radius 3r. The number 72 close relation with the magic number 163 is based on mathematics shown by the Number Tower. The SQS theory Elementary Particle Table given in Section 18 is based on mathematics. 3) It contains 72 elementary particles including 24 par- ticles, 24 anti-particles, 24 neutral particles. Notice that, 24, 48 = 24 + 24, 72 = 48 + 24 are the number of ver- texes for )2/3(O, )2/7(O, )2/13(O and their counterparts in the )(rC system, respectively. 4) There are only three generations of elementary par- ticles. It was supported by Prime Number Postulation in Section 11 and Conclusion 12.1 in Section 12, which are based on the prime numbers property in number theory. Here we have the second independent support from number theory and space symmetry. As the number 72 backed by the magic number 163, there is no room left for more generation beyond the existing three genera- tions. Otherwise, the total number of elementary particles would exceed 72, which is not supported by the Number Tower and the magic number 163 sitting on top of it. 5) As shown in the Number Tower, the first generation is the base of all three generations. This is also supported by the two basic columns in the Symmetries Family Tree, in which the first generation particles and interactions serve as the foundations. The second and the third gen- erations are the extensions of the first generation. This is also supported by Standard Model. SQS theory provides the mathematic interpretations based on number theory and symmetries of space. According to the above discussion, the 18 + 18 = 36 )(rO and )(rC symmetries with radius 3r cover all elementary particles and interactions for three genera- tions. What about the symmetries with radius 3r? The answer will be given in Section 24. Ideally, symmetries )(rO , )( rC all are perfect. In re- ality, the physics groups corresponding to )( rO, )(rC are not perfect caused by symmetry broken for particles to obtain mass. Take )2/1(O as an example. In its perfect symmetry form, the 8 fermions r u, g u, b u, r d, g d, b d, e, e all are mass-less to start with. Each of them obtains mass by broken symmetry in dif- ferent ways. The 12 vertexes of )2/1(Oare shown in Fig.22.13. Equilateral triangle 1171 ppp representing electron in- cludes a cubic vertex 1 p and two octahedral vertexes 7 p, 11 p. There are three squares 3421pppp , 7865pppp , 1112109 ppppwith center vertex on surface representing weak interaction connect to 1 p, 7 p, 11 p respectively. There are three squares 7251 pppp , 11391 pppp, 128117 pppp with center vertex off surface representing strong interaction connect to71 &pp , 111 &pp , 117 &pp respectively. For electron to obtain mass, the symmetrical triplet 1171 ppp must break under the con- ditions: (1) All three squares 7251 pppp , 11391 pppp , 128117pppp with center vertex off surface must break because electron has no strong interaction. (2) At least some of three squares 3421 pppp , 7865 pppp, 1112109 ppppwith center vertex on surface must retain because electron has weak interaction. There are two possible scenarios meet these requirements. Figure 22.13. The two triplets for e and e to demon- strate the retained symmetries and broken symmetries. Scenario-1:For an electron alone. Two vertexes 7 p, 11 p shift angles to break the triplet 1171 ppp for elec- tron to obtain mass. The results are: (1) All three squares 7251pppp, 11391 pppp , 128117 pppp with center vertex off surface are broken for no strong interaction. (2) One square 3421 pppp with center vertex on surface retains for weak interaction. Scenario-2:For electron and electron anti-neutrino e as a matched pair. Equilateral triangle 1064ppp representing e includes a cubic vertex 4 p and two octahedral vertexes 6 p, 10 p. There are three squares 3421pppp, 7865 pppp , 1112109 ppppwith center vertex on surface representing weak interaction connect to 4 p, 6 p, 10 p respectively. There are three squares 8364 pppp , 122104 pppp , 95106pppp with center vertex off surface representing strong interaction connect to 64 &pp,  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1311 104 &pp , 106 &pp respectively. Two vertexes 1 p, 7 p shift angles to break the triplet 1171ppp for electron to obtain mass. At the same time, two vertexes 4 p, 6 p shift the same angles with opposite directions to break the triplet 1064ppp for e to obtain mass. The re- sults are: (1) All six squares 7251 pppp , 11391pppp, 128117pppp , 8364 pppp , 122104 pppp , 95106pppp with center vertex off surface are broken for no strong interac- tion. (2) All three squares 3421pppp, 7865 pppp, 1112109 pppp with center vertex on surface retain for weak interaction. This scenario shows that, besides their ma- thematical correlation of n-parameter matching, there is a geometrical correlation between electron and its an- ti-neutrino e . It is conceivable that, Scenario-2 is for regular type weak interactions with electron and e as a matched pair. Scenario-1 is for rare type weak interactions with electron acting alone without e . Since Scenario-1 has only one square retained with center vertex on surface and Scenario-2 has all three squares retained with center vertex on surface, which serve as an explanation for the rarity of the rare type weak interaction for electron with- out e . The similar scenarios are also valid for e & and & which belong to the second and third genera- tions, respectively. In Figure 22.13, the other two triplets 1252ppp and 983ppp represent up quarks r u, g u, b u and down quarks r d, g d, b d. For them to break symmetries to obtain mass and keep strong interaction as well as weak interaction , the way to shift angles is under the condi- tions: (1) At least some of the six squares 7251 pppp, 11391pppp , 128117 pppp , 8364 pppp , 122104pppp , 95106 pppp with center off surface must retain for strong interaction. (2) At least some of three squares 3421 pppp, 7865 pppp , 1112109 pppp with center on surface must retain for weak interaction. The same requirements are also valid for triplets representing strange, charm, bottom and top quarks. These arrangements show the versatility and richness of the theory. In the meantime, the above discussions regarding to the correlations of the symmetries in )(rO and )(rC systems to physics groups of elementary particles are hyperbolic. The real correlations between the symmetries listed in Table 22.1, Table 22.2 and the particles’ groups such as )1(U, )2(SU , )3(SU require mathematical proof and more physical verification. But one thing is clear. If the face-centered space structure is the real space to accommodate all elementary particles and interactions, their symmetry groups must be originated from it. It is important to point out that, all symmetries in the face-centered space structure are represented by real numbers. On the other hand, most of particles’ groups are represented by complex numbers. This is a major differ- ence. But the difference is only superficial. So far, SQS theory hasn’t introduced intrinsic time as a variable yet. In essence, the intrinsic time can be represented by the phase angle of complex numbers. Once the intrinsic time variable is introduced, the major difference between these two systems will be resolved. In fact, intrinsic time represented by complex numbers’ phase angle is the key to understand the relation between symmetries )(rO , )(rC with 3 r in space and groups in particle physics. Postulation 22.2: All elementary particles’ groups are originated from the symmetries in )(rO and )(rC of space structure with face-centered lattice. Explanation: Lack of mathematical proof, this is the best thing one can offer. Table 22.1, Table 22.2 and the Symmetries Family Tree are useful for further investiga- tions on this topic. From SQS theory viewpoint, the physics groups of ba- sic fermions and bosons are presented in Fig 22.14. Quarks with different colors are treated as different par- ticles. Leptons are presented as trefoil model with three branches combined. The elementary fermions are repre- sented by 12 equilateral triangles. The 22 elementary bosons except and are represented by 8 equilat- eral triangles, in which the 6 equilateral triangles are combined into 2 hexagons. and are located at the center of equilateral triangle representing , , . Figure 22.14 is useful to identify the correlation between the symmetries in )(rO , )(rC systems and the groups in particle physics. Figure 22.14. Elementary particles organized in groups. Postulation 22.1 and Postulation 22.2 are here to stay for SQS theory. Hopefully mathematic proofs and more physics evidences will follow. In fact, they have supports already. One is the Gaussian sphere and the Kepler-Hales theorem. If gravitation dominates in the Planck scale microscopic space, the face-centered lattice structure  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1312 along with its symmetries is the only logical choice. The other is that, )( rO and )( rC symmetries with 3 r fit physics groups well. Inherited from the face-centered lattice structure, space has intrinsic symmetries, which serve as the origin of all groups of elementary particles. Postulation 22.2 is wait- ing for proof. From SQS theory standpoint, it is the way Mother Nature selected. In essence, space is like a crystal, but the macroscopic space is not a single crystal. Otherwise, the single crystal space with face-centered lattice is macroscopically ani- sotropic with preferred directions. That is impossible. Because theoretically space cannot be in such highly organized state with extremely low entropy; experimen- tally there is no evidence for such macroscopic space anisotropy. In fact, space is amorphous in large scale with single-crystal or poly-crystal domains. The system containing enormous identical Gaussian spheres with relative weak interactions fits well for the conditions of grand number phenomena. The number of Gaussian spheres in a typical domain can be estimated according to (16.13) as: G N11 10~ . (22.11) In which G is the rank number. The G N11 10~ Gau- ssian spheres fit in a volume with length scale of )22/(10~)( 311 P G dom LGL , (22.12a) For 1G:, mLL Pdom 323 10~10~)1( ,, (22.12b) For 2G: mLL Pdom296 10~10~)2( , (22.12c) For 3G: mLL Pdom2510 10~10~)3( . (22.12d) Such amorphous space is isotropic with grainy struc- tures on top of the Planck scale grainy structure. In the multi-layer grainy structure, the lowest layer with Gaus- sian sphere as basic building block is single-crystal or near single-crystal, which serves as the home for ele- mentary particles with their interactions. We will come back to this topic in later sections. The sum of 3-dimensional Gaussian probability ),,( 3zyxS for the cubic part alone was introduced by (2.24) with subscript changed for identification: ijk kji xyz zzyyxx cube ezyxSzyxS 222 ),,(),,( 3,3 . (22.13) The octahedral part lattice can be treated as three Car- tesian systems with 0.5 shifts along two orthogonal axes. In such coordinate system, the sum of the 3-dimensional Gaussian probability of the octahedral part alone is: ),5.0,5.0( 3 1 )5.0,,5.0( 3 1 )5.0,5.0,( 3 1 ,, 333,3 zyxSzyxSzyxSzyxS oct . (22.14) In which, the numerical factor 1/3 is for unitarity. According to (22.13) and (22.14), the overall sum of Gaussian probability for the 3-dimensional space with face-centered lattice structure is: ),5.0,5.0( 4 1 )5.0,,5.0( 4 1 )5.0,5.0,( 4 1 ),,( 4 1 ,, 33 33,3 zyxSzyxS zyxSzyxSzyxS cf . (22.15) In (22.15), the first term represents the cubic part and the other three terms combined represent the octahedral part. The numerical factor 4/1 for unitarity has a deep meaning. In a Planck cube with the face-cantered lattice structure, there are 8 Gaussian spheres centered at 8 cu- bic vertexes at 8 corners and another 6 Gaussian spheres centered at 6 octahedral vertexes at 6 face centers. For the cubic part, the 8 spheres at corners each one sharing with 8 cubes contribute 1 Gaussian sphere to the Planck cube. For the octahedral part, the 6 spheres at 6 surface centers each one sharing with 2 cubes contribute 3 Gaus- sian spheres to the Planck cube. Therefore, the filling ratio for cubic part versus octahedral part is 1:3 corre- sponding to unitarity factors 4 1and 4 1 4 1 4 1 4 13 . It confirms the reason for selecting the numerical fac- tor 4/1 for unitarity in (22.15). Actually formula (22.15) serves as a checkpoint for the consistency of the face-centered space structure. The face-centered structure is based on the most compact packing of Gaussian spheres. A hidden assumption is that, all Gaussian spheres in the space must be identical. In terms of profile and size, they are identical evidenced by 2/1 and )22/(1R for all Gaussian spheres. The four identical numerical factor 4/1 in (22.15) proved that, all Gaussian spheres also have the same va- cuons density. It shows that, no matter where they are located, all Gaussian spheres have the same profile, the same size and the same vacuons density. In short, they are identical. Moreover, the four identical numerical fac- tors also make the ),,( ,3 zyxS cf symmetry with re- spect to interchanges of three variables z ,, , which is required by the geometrical symmetry of the face- cen- tered lattice structure. So everything is consistent. According to Postulation 22.1, space has face-centered lattice structure, in which the cubic lattice structure serves as one of its two parts. The sums of probability data listed in Table 2.2 are based on ),,( 3zyxS of (2.24) for the cubic lattice structure. For the space with face-centered lattice structure, the sum of Gaussian probability formula is (22.15). The calculated sums of probability data based on (22.15) are listed in Table 22.3.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1313 Table 22.3: zyxS cf ,, ,3 values at 125 points in a Planck cube based on (22.15)* . *The summation index in (22.15) is truncated at a sufficient large number 1000,, kji As shown in Table 22.3, the maximum value and minimum value of ),,( ,3xyxS cf , is: 40660006652203.1)0,0,0(),,( ,3 max ,3 cfcf SzyxS , (22.16a) 594919993753280.0)5.0,5.0,5.0(),,( ,3 min ,3 cfcf SzyxS . (22.16b) The difference of maximum value and minimum value is in 4 10order. Compare to the values listed in Table 2.2: 59462823631158.1)0,0,0(),,( 3 max ,3 SzyxS cube , (22.17a) 985627624976706.0)5.0,5.0,5.0(),,( 3 min ,3 SzyxS cube .(22.17b) The difference between the difference of maximum value and minimum value is in 1 10 order. The comparison shows that, the sums of probability for the face-centered lattice structure are more evenly distributed due to more Gaussian probability distribution functions added at oc- tahedral vertexes. Theorem 22.1: In the face-centered space structure, the Random Walk Theorem is valid only for the cubic part of face-centered structure. It is not valid for the oc- tahedral part and the face-centered structure as a whole. In other words, all steps of the random walk zigzagging path only stop at the cubic vertexes. Proof: As shown in Section 4, the key to prove Ran- dom Walk Theorem is based on the fact that, the nu- merical factor in front of the exponential part of (4.3) and (4.4) is 1. Otherwise, the proof does not hold. The nu- merical factor in front of the exponential part in of (22.13) is 1 for the cubic part, which fits the requirement for random walk theorem proof. On the other hand, the nu- merical factors in front of the exponential part in zyxS oct ,, ,3 of (22.14) for the octahedral part and zyxScf ,, ,3 of (22.15) for the face-centered structure as a whole are 1/3 and 1/4, respectively, which do not fit the requirement for the random walk theorem. QED Theorem 22.1 has important physics significance. It reveals more insights from the Random Walk Theorem. The random walk process is the mechanism for interac- tions between particles mediated by bosons without mass, i.e. and . Moreover, as shown in Section 4 and Section 15, gravitational force and electrostatic force are related to the long path and short path, respectively, which are based on the converting factor originated from the Random Walk Theorem. These two forces belong to the long range type with strengths inversely proportional to the square of distance. The tremendous difference be- tween these two forces’ strengths is also originated from the difference between long path and short path. All of these features are originated from the Random Walk Theorem, which is only valid for the cubic part of space. The adding of octahedral part in face-centered space structure does not make difference for these two long range forces. Theorem 22.1 provides additional supports for Postu- lation 22.1 and to some extent for Postulation 22.2 as well. It indicates that, the theory based on face-centered space is consistent. Section 23: Cosmology Particle physics and cosmology are closely related. The topics of this section are cosmology and its correlation with particle physics based on prime numbers and the space structure introduced in Section 22 Let’s start from some related questions. According to prime numbers table and the Prime Numbers Postulation, there are only three generations of elementary particles in the current period of universe. Is it the only period? This is the first question. The electron converting factor 23 10501197.1 e N is close to a 2 G grand number. Is there a 1 G grand number related to electron? This is the second question. In Table 15.1, the mass or energy gap between 2 /7547.152 cGevMew and 215/1044708.8 cGevMews is thirteen orders of magnitude. Is this tremendous gap really empty? This is the third question. Let’ start from the first question. The way to search for other periods is to look at the prime numbers table. The odd prime numbers less than 1000 is listed in Table 23.1. To identify possible other periods and generations in a legitimate manner, the rules used to determine the three generations in the current period are summarized in a definition. Then a postulation is introduced to make the connections between generations of elementary particles and cosmic periods as well as space dimensions. Definition 23.1: A set of three consecutive even pairs of prime numbers is defined as one generation. A set of six consecutive even pairs of prime numbers is defined as two generations. A set of nine consecutive even pairs of prime numbers is defined as three generations. This defi- nition is also valid for other possible periods.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1314 Table 23.1: The odd prime numbers less than 1000* 1 3 5 7 11 13 17 1923 2931 3741 4347 53 59 61 67 71 73 79 83 89 97 101 103107 109113 127131 137 139 149 151 157 163 167 173 179 181 191 193 197 199211 223 227 229233239 241251 257 263 269 271 277 281 283 293 307 311 313 317 331337 347349 353359367 373 379 383 389 397 401 409 419 421 431 433439 443449457461463 467479 487 491 499 503 509 521 523 541 547 557 563569571 577 587593599601607 613 617 619 631 641 643 647 653 659 661 673677683691 701 709719 727733 739 743 751 757 761 769 773 787 797 809 811821 823827829839853 857859 863 877 881 883 887 907 911 919 929 937 941947953967971977 983991997 *Note: The prime number pairing is for quarks only. 1 for r u is included and 2 for r e is excluded. Postulation 23.1: The number of generations is intrin- sically related to elementary particles, cosmic periods and space dimensions. The first cosmic period has one generation of elementary particles in 1-dimensional space. The second cosmic period has two generations of elementary particles in 2-dimensional space. The third cosmic period has three generations of elementary parti- cles in 3-dimensional space. Lemma 23.1: In case the number of consecutive even prime numbers pairs is not a multiple of 3, it is defined as a period having fractional generations of elementary par- ticles in the space with fractional dimensions. Explanation: According to Definition 23.1 and Pos- tulation 23.1, the current period is the third cosmic period, in which there are three generations of elementary parti- cles in 3-dimensional space. The other periods are hypo- thetical and subject to verification and confirmation. With the help of Definition 23.1 and Postulation 23.1, let’s look at the prime numbers table and search for other possible cosmic periods. In Table 23.1, the m-parameters of 18 quarks started from 3&1 ended at 61&59 are listed in the first row. Since the before reduction m-parameters of leptons and bosons are related to their companion quarks’ m-parameters, the meaning for numbers of even prime numbers pairs is not just for quarks. In fact, the nine even pairs of prime numbers represent three generations of elementary particles for the current period in 3-dimen- sional space. It is defined as the cosmic third period. In the second row of Table 23.1, a set of six even pairs of prime numbers started from 103&101 ended at 157&151 is found to represent two generations of ele- mentary particles. According to Definition 23.1 and Pos- tulation 23.1, the two generations of elementary particles belong to the second cosmic period in 2-dimensional space. In the third row of Table 23.1, a set of four even pairs of prime numbers started from 173&167 ended at 197 & 199 is found. According to Postulation 23.1 and Lemma 23.1, it is defined as the first period with 3 1 1 generations of elementary particles in 3 1 1-dimensional space. In the third and fourth rows of Table 23.1, another set of nine even pairs of prime numbers started from 241&239 ended at347&337 is found to represent three generations of elementary particles. The newly found three generations are different from the three generations of current period. They belong to the pre-big-bang period in 3-dimensional space. The reason for the name of cosmic periods will be given later. In Table 23.1, the odd pair immediately before and af- ter a set of even pairs are underlined. They serve the function to start and to stop the set of even pairs. It is interesting to notice that, a single prime number, the spe- cial prime number 163, separates two sets of even prime number pairs representing the first and second cosmic periods. All pairs of prime members representing four periods are even pairs. The prime numbers in between periods are either a single prime number or pairs not qualified to form generation(s) represented by at least three consecu- tive even pairs. The newly found three cosmic periods along with their generations meets all rules. It is legitimate in mathematic sense. In the first cosmic period, the one generation is identi- fied as the first generation including six quarks r u, g u, b u, r d, g d, b d , two leptons , e and their an- ti-particles along with eight bosons , , i g)5,4,3,2,1( i and 1 U. In the second cosmic period, the two generations are identified as the first generation and the second genera- tion including twelve quarks r u, g u, b u, r d, g d, b d, r s, g s, b s, r c, g c, b c, four leptons, e, e , , and their anti-particles along with sixteen bosons , , i g)82,1( i, i G)3,2,1( i, and 1 U, 2 U. In the third cosmic period, the three generations are identified as the first generation, the second generation and the third generation including all elementary parti- cles listed in the Elementary Particles Table. This serves as an introduction for the first question, the  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1315 details will be given later. Let’s turn attention to the second question, which concerns electron converting factor e N as 2 G grand number. In essence, it is to search whether there is an electron intermediate state in existence corresponding to 1G grand number 11 10~ e N. Let’s go back to the lo- gistic equation of (16.1). Substitutinge N to replace e N and )(Z M to replace )(e M , a numerical calcula- tion found: 0104048421709430.2)(22 131 )(2 1 Z rx eMeN (23.1) 11 ,int 1056858745288094.3 eere NN , (23.2a) 200378771029244.3)125.0()(1 x, (23.2b) 6378494231955224.2r. (23.2c) The value given by (23.2a) falls into the range of 32 1 r. According to Table 16.1, for value in this range, the logistic recurrent process oscillates and converges to: 5873218.0/11 r. (23.3). This scenario fits the intermediate state well, in which the logistic recurrent process is in progress and about half way through toward the threshold. The 11 int, 1056858745288094.3 ee NNgiven by (23.2a) is a 1G grand number. The mass of the elec- tron intermediate state is: 228 int,int, /97323432.4/1097993553.1/cGeVMcGeVNMM MaxePe . (23.4) According to Rule 6.1, it cannot be a standalone fer- mion state, two intermediate states must appear in pair to form a scalar boson called “e-boson” with mass be M, converting factor be N and length scale be L: 28 int, /1095987106.32 cGeVMMebe , (23.5a) 11 int, 109372644.1 2 1 e be P beN M M N, (23.5b) m cM h L be be24 1013110359.3 . (23.5c) Now the second question regarding electron interme- diate state is answered. The mass of int,e M and be M fall into the middle of the tremendous gap between e M and ews M. The gap is not empty. So it answers the third question as well. Let’ turn attention to details of the first question. According to the cosmology standard model, the uni- verse started from a big bang with extremely high energy corresponding to extremely high temperature. From SQS theory perspective, there was a “pre-big-bang period” represented by a set of 9 prime number even pairs started from 241&239 and ended at 347&337 found in Table 23.1 as mentioned previously. The pre-big-bang universe was a 3-dimensional “overheated liquid state”. Its details will be given later. The overheated liquid state is unstable, any random stimulation causes evaporation. The Gaussian spheres were evaporated and free to fly as 0-dimensional objects in space represented by the prime numbers 211, 223, 227, 229, 233 between the two sets of prime number even pairs representing the pre-big-bang period and the first period. Let’s call it the “0-period”. The universe was born at the big bang. The cosmic time is set to zero: 0 0 t, and the new born universe started to evolve. During the 0-period, the flying around Gaussian spheres attracted each other by gravitational force and intended to gather as groups, which nurtured the first period. The first cosmic period started at time scale 1 t with length scale 1 L: mLLLPGUT 33 1101475.1~71 , (23.6a) scLtt GUTGUT 42 1108278.3~/ . (23.6b) At time 1 t, the first cosmic period started. The flying Gaussian spheres were gathered and organized into 1-dimensional array in 1-dimensional space. The 1-dimensional space was built as an array of Planck scale face-centered cubes. If the building block of array is a Planck cube centered at a cubic vertex includ- ing 12 octahedral vertexes, according to Table 22.1 and Table 22.2, only three symmetries )0(C, )2/1(C, )0(O are fully effective. There is no fermion in the three symmetries. This scenario is not acceptable. If the building block of array is a Planck cube centered at an octahedral vertex including 4 cubic vertex and 8 octahe- dral vertexes, according to Table 22.1 and Table 22.2, three symmetries )0(O, )2/1(O, )0(C are fully effective. It include 8 first generation fermions r u, g u, b u, r d, g d, b d, e, e and 8 anti-fermions in )2/1(O and 2 bosons , in )0(O responsible for electromagnetic interaction and gravitation. As shown in Section 15, the grand unification is to unify electromag- netic interaction into gravity. In (23.6b), 1 t is derived from GUT L originated from GUT M. At time 1 t, the re- verse process of grand unification happened, electro- magnetic interaction was separated from gravity. There- fore, in the first cosmic period after 1 t, the two bosons , in )0(O showed up is natural and fully ex- pected. For the symmetry )1(O representing the other 6 first generation bosons i g)5,4,3,2,1( i and 1 U, out of its 6 vertexes, only 2 of them are in the array counting for one third of its constituents. It indicates that, 2 out of 5 glu- ons such as 1 g and 2 g would be in effect. According to Table 13.2A and 13.2B , in the gluon links among r u,  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1316 g u, b u, 9 of the 12 links are made of 1 g and 2 g; in the gluon links among r d, g d, b d, 3 of the 6 links are made of1 g and 2 g. It means that strong interaction is partially in effect. Actually, the first cosmic period was in 3 1 1-dimen- sional space, which is a fractal space. The space dimen- sion was not fixed, instead, it was a developing process from 1-dimension gradually toward 2-dimension. Ac- cordingly, the cross section of the array gradually in- creases from PP LL11 to PP nLL 1. When the width number 2n, the symmetry )1(O has 4 out of its 6 vertexes in the wider array. As a result, 2 more gluons such as 3 g and 4 g would be in effect. According to Table 13.2A and 13.2B , in the gluon links among r u, g u, b u, all 12 links are made of 1 g, 2 gand 3 g; in the gluon links among r d, g d, b d, all 6 links are made of 1 g, 3 g and 4 g. It means that strong interaction for the first generation quarks is fully in effect. This scenario looks reasonable and is accepted by SQS theory. During the first period and other early cosmic periods, all particles are in their extremely high energy states cor- responding to extremely high temperature, which are quite different from their ordinary states. For instance, according to Figure 19.1 and Figure 19.2, the gluon links binding quarks to form proton and neutron all are made of 1 g, 2 g, 3 g and 4 g. But it does not mean that, proton, neutron were formed during the first cosmic pe- riod after the array cross section increased to PP LL 21 . Because of the extremely high temperature, it was im- possible to form any hadron. Instead, “quark-antiquark liquid state” would be formed from these first generation quarks and anti-quarks bound by strong interaction mediated by these in effect gluons1 g, 2 g, 3 g and 4 g. The second cosmic period started at 2 t with length scale 2 L: mLLMLL PPsewsew 311 2104678.1~9082)(71~ , (23.7a) stcLt Psew40 2108963.4~9082~/ . (23.7b) After 2 t, the second cosmic period started and the space became 2-dimensional, The 2-dimensional space is a membrane. In order to accommodate major symmetries of the first and the second generations, the thickness of membrane should be P L2. As shown in Table 22.1 and Table 22.2, the 2-dimensional membrane with P L2 thickness centered at a cubic vertex accommodates 7 fully effective symmetries )0(C, )2/1(C, )1(C, )2/3(C, )2(C,)0(O, )2/1(O, which does not in- clude the second generation fermions. This scenario is unacceptable. On the other hand, the 2-dimensional membrane with P L2 thickness centered at an octahedral vertex accommodates 7 fully effective symmetries )0(O, )2/1(O, )1(O, )2/3(O, )2(O, )0(C, )2/1(C, which include the first generation 8 fermions r u, g u, b u, r d, g d, b d, e, e and their anti-particles rep- resented by )2/1(O plus second generation 8 fermions r s, g s, b s, r c, g c, b c, , and their an- ti-particles represented by )2(O. Symmetry )2(O is not fully effective. Among its 6 vertexes, only 4 are in- cluded. The effective bosons for the second period are the first generation 8 bosons , , i g)5,4,3,2,1( i, 1 U plus second generation 6 bosons corresponding to two third of 9 bosons plus 1 anti-boson 0 in second generation. The second period started at length scale sew LL 2, which is the characteristic length of elec- troweak-strong unification. The scalar boson 2 U for that unification must be included. The strong interaction was separated and fully effective. All 8 gluons i g)8,,2,1( i must be included. There are two addi- tional second generation bosons as candidates selected from the remain second generation bosons: 3 massons i G)3,2,1( i, and anti-boson . Because , cannot be produced without its counterpart, there are only two possible selections. One is and , the other is two massons. The second period include the first and second genera- tions 16 fermions: r u, g u, b u, r d, g d, b d, r s, g s, b s, r c, g c, b c, e, e , , and 16 anti-particles along with 12 bosons for sure: , , i g)8,,2,1( i, 1 U, 2 U, plus 2 additional bosons or 1 boson and 1 anti-boson from one out of two choices. Ei- ther way sounds reasonable. This scenario is accepted by SQS theory. Conclusion 23.1: Weak interactions are not in effect in the second cosmic period with 2-dimensional space. Proof: The reason for Conclusion 23.1 is that, the ne- cessary mediators and intermediate states of weak inter- actions are not available in the second cosmic period. W and 0 as third generation gauge bosons are not available for the second cosmic period according to Pos- tulation 23.1. and X or two out of three massons i G)3,2,1( i are available depending on the choice. But the hypothetical gauge bosons and X serving as the intermediate state for some type of weak interactions have similar behavior as their counterpart W and 0 , they must have massons’ assistance to make the m-parameters match and the n-parameters match as well as to fill the mass gap described in Section 14. Unfortu- nately, the two choices can only provide either and or two massons but not both. The necessary media- tors and interstates are not in existence, weak interactions cannot perform. QED Conclusion 23.1 is important. It leads to a prediction given later. In the second comic period, all second generation par- ticles except perhaps and are unstable. Under normal conditions, they are subject to decay via weak  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1317 interactions. But the second cosmic period did not pro- vide normal conditions, in which things turned out quite differently. According to Conclusion 23.1, weak interac- tions are not in effect in second cosmic period. The un- stable particles in the 2-dimensional membrane cannot decay via weak interactions. They must hold until the third period, when the gauge bosons W, 0 , 0 and massons are effective, then decay in the 3-dimensional space. Moreover, the big bang produced equal amount of elementary particle and anti-particles. Some of them remained in the second period. Whether they had the chance to annihilate in second cosmic period is an inter- esting question, which will be discussed later. The third period started at 3 t with length scale be LL 3 of (23.5c): mLLL Pbe2411 3101311.3109373.1 , (23.8a) scLt 32 33 100444.1/ . (23.8b) After 3 t, the space became 3-dimensional. All parti- cles listed in the Elementary Particle Table showed up. All symmetries listed in Table 22.1 and Table 22.2 became fully effective. All four types of interactions were into full play. In fact, it is the universe started at 13.7 billion years ago we living in now. The transition from the 2-dimensional space to the 3-dimensional space was a phase transition, which trig- gered the cosmic inflation. The e-boson played a pivotal role in the cosmic infla- tion. It sets the length scale 3 L and time scales 3 t of the cosmic inflation. In addition, the logistic recurrent processes started at time 1 t, they reached about halfway at 3 t, which corresponds to the birth of the e-boson. More importantly, the scalar e-boson with mass of GeVM bs 8 109599.3 acted as the inflaton. Accord- ing to the cosmology standard model, during the rapid expansion period, the inflation was driven by a scalar boson called inflaton. Physicists are looking for the inflaton for some time without satisfaction. Here is the e-boson. It is a scalar boson; it is heavy and relatively stable. More importantly, it was born at the very begin- ning of the cosmic inflation and drove the space expan- sion to the very end of the inflation. Then it continued its journey toward the Compton scale and become a pair of ordinary electron and positron. The e-boson is not tailor made for the cosmic inflation; instead, it is the require- ment of logistic process, grand number, and Rule 6.1. In short, the e-boson fits the inflaton perfectly. The time scale of st32 3100444.1~ is roughly agreed with the time of the cosmic inflation proposed by cos- mology standard model. It is a good thing, but it raises questions. If 3 t corresponds the time of the cosmic in- flation, what about 1 tand 2 t? Were there two more inflations before the big one? These are very interesting questions. Space dimensions change is equivalent to phase transition, which releases energy causing inflation. The scale of inflation is determined by the amount of released energy. In this case, the released energy depends on three factors: the number of Planck cubes involved, the contraction depth of space elements, the total energy involved. The numbers of Planck cubes involved are 71, 9082, and 232 int,100048.6)2( e N for the phase transi- tions occurred at 1 t, 2 t, and 3 t, respectively. The ra- tios of contraction depth are estimated as 1~)71(~ 1/0 1 R, 95~)9082(~ 2/1 2 R,153/223 3101176.7~)100048.6(~ R for the transitions occurred at 1 t, 2 t and 3 t, respec- tively. If the potential energy released is proportional to the square of )3,2,1(,iRi, The ratios for the released energy is estimated as 312 3 2 2 2 110066.5:9082:1~:: RRR , for the phase transitions occurred at 1 t, 2 t and 3 t, respectively. In terms of scales, it seems no comparison between the two inflations occurred at 1 t, 2 t and the big one at 3 t. The two inflations at 1 t, 2 t were just mini rehearsals of the big show at 3 t. But there is an- other factor involved. According to the energy conserva- tion law, the total energy of three cosmic periods and the 0-period should be the same. The big difference in the numbers of Planck cubes involved is partially compen- sated by energy per Planck cube. It makes the released energy of three inflations quite different from 312 3 2 2 2 110066.5:9082:1~:: RRR . According to this argument, the difference of three inflations’ scales could be closer. In other words, there were two comparable scale rehearsals before the big show. But the three inflations scenario has a glitch. Phase transition is an abrupt event occurred in an extremely short time interval. Noticed that, the 1-dimensional space actually is 3 1 1-dimensional, which has fractal behaviors. The transition from 3 1 1-dimensional space to 2-dimensional space is not necessarily corresponding to a violent phase transition happened suddenly at 2 t. In- stead, it could be a gradual process. If this argument holds, there were only two cosmic inflations occurred at 1 t and 3 t. According to SQS theory, the phase transition hap- pened at 3 t corresponds to the big cosmic inflation proposed by cosmologist Ruth [19], which has been veri- fied by astronomy observations. According to SQS the- ory, there is at least one more phase transition happened at 1 t corresponding to a cosmic inflation before the big one happened at 3 t. It should also leave some footprints somewhere. The most like place is the cosmic microwave background radiation (MBR). From SQS theory perspective, the early cosmological history is the natural evolution of the space structure with Gaussian spheres as building blocks. The results derived  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1318 from it fit the cosmology standard model pretty well. SQS theory contributions are: (1) The cosmic periods and the generations of elementary particles are correlated to space dimensions; (2) It is determined by the prime numbers. In essence, everything is traced back to ma- thematics. Astronomical observations and measurements such as gravity lens effect and the cosmic MBR have found the evidence for dark matter. Astrophysics observations in- dicate that, the composition of universe is approximately 5% visible matter, 21% dark matter and 74% dark energy. What is dark matter made of? Physicists are looking for the answer for quite some time. The favorite candidates for dark matters are hypothetical particles such as axion and neutrarino etc. These dark matter candidates are hy- pothetic elementary particles and only interact with visi- ble matter via gravitation and weak interaction. Around the world, many underground experiments have been carried out to detect dark matter candidate particles rare interaction with visible matters. Despite the extensive efforts, so far, there is no confirmed positive result. It is the time for a second thought. Let’s look at the dark matter issue from SQS theory perspective. The Elementary Particle Table includes sev- eral undiscovered neutral heavy particles: i G, )8,2,1( i, , 1 U, 2 U, 3 U. But perhaps all of them are unstable particles, which do not fit the requirements for the dark matter. On the other hand, notice that, the reliable evidences for the existence of dark matter all are based on its gravitational effects. The idea for dark mat- ter as elementary particle having weak interaction with visible matters is hypothetical without experimental support. There is no reason to reject other types of dark matter candidates interacting with visible matters only via gravity. Moreover, there is no reason to reject radical ideas such as: dark matter is made of something other than undiscovered elementary particles. Hypothesis 23.1: At least part of dark matters in the universe is the debris left over from the cosmos inflation. The dominate part of this type dark matters is 2-dimen- sional membranes, which interact with visible matters only via gravity. Explanation: The cosmos inflation was a gigantic violent event happened in an extremely short time inter- val with tremendous amount of energy involved. It is inconceivable to assume that, the phase transition only produced the 3-dimensional space out from a 2-dimen- sional membrane. It is more natural to conceive that, the phase transition produced the 3-dimensional space along with many pieces of debris. Since the pre-state of phase transition is a 2-dimensional membrane, the dominate part of debris is relatively small pieces of 2-dimensional membrane. The phrase “part of dark matters” in Hy- pothesis 23.1 leaves room for other possible dark matter candidates. We haven’t found any dark matter, because we were looking for the wrong candidates. Dark matter may not be undiscovered elementary particles. According to Hy- pothesis 23.1, dark matters are left over debris from the comic inflation and most of them are 2-dimentional membranes flooding around in 3-dimentional space. The new type experiments for searching dark matter should be based on its gravitation effects. Astronomical observations have found that, dark matter is mixed with visible matter all over the universe. Therefore, it is pos- sible to design experiments for searching dark matter based on its gravitational effects. Suggestion 23.1: The new type of experiments for searching dark matter is to use extremely sensitive gravi- tation meter isolated from earthly interferences. As earth rotating around the sun, occasionally, a piece of 2-dimen- sional membrane passes through the meter, which will produce a signal to indicate its gravitational effect as the evidence of its existence. The signal can be recorded by monitoring apparatus and analyzed by computer with re- cognition software. There is another possibility to verify dark matter. A piece of relatively large 2-dimensional membrane is ca- pable to attract other membranes via gravity. When suf- ficient membranes get together in the right way, it is pos- sible to trigger a mini-inflation type of phase transition to transfer a piece of 2-dimensional dark mater into a chunk of 3-dimentional visible matter. From our perspective, the event is like that, a chunk of 3-dimensional visible mater suddenly appears from void. According to Conclu- sion 23.1, in the 2-dimensional membrane weak interac- tions are not in effect. The second generation unstable elementary particles such as muon, hadrons made of s-quarks, c-quarks and their anti-articles in the membrane hold their decay and wait for the chance. Immediately after the mini-inflation, in the new born 3-dimensional chunk, gauge bosons , , and massons become readily available and fully effective. These unstable par- ticles are eligible to decay. As a result, a shower of high energy particles is released, which can be detected and serve as the evidence of the mini-inflation and dark mat- ter. In addition, as mention previously, there were parti- cles and anti-particles left in the 2-dimensional mem- brane. If they did not have a chance to annihilate in the membrane, these particles and anti-particles should re- lease at once at the mini-inflation. If they were annihi- lated in the membrane already, the annihilation products remained in the membrane should release also. Either way, showers of high energy -rays and other particles and anti-particles should be detectable. Suggestion 23.2: The way to verify the mini-inflation is to monitor the primary high energy cosmic rays. If the components fit the pattern of decay modes branching  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1319 ratios of the second generation unstable particles or their annihilations products, these events serve as the evidence for the mini-inflation as well as for dark matter. Explanation: In fact, occasionally cosmic rays with extremely high energy has been observed coming from places such as the center of galaxy. If the branching ra- tios and products fit the right pattern, they can serve as the evidence of mini-inflation and dark matter. The key is to analyze the components whether fits the right pat- tern or not. So far, the cosmic history from big bang through infla- tion up to the current period is explained pretty well based on the prime numbers even pairs listed in Table 23.1 and the space structure and symmetries described in Section 22. It is natural to ask: What is the pre-big-bang history? What is the outlook for the cosmic future? The answers are also in the prime numbers table. As mentioned previously, in the third row and fourth row of Table 23.1, there is another set of 9 even pairs starting from 241&239 and ended at 347&337 . Ac- cording to Definition 23.1, it is qualified to be a 3-dimensional space corresponding to the pre-big-bang period. Its m-parameters are much larger than those of current 3-dimensional universe. It indicates that the ele- mentary particles in the pre-big-bang period had ex- tremely high energy to form the overheated quark- anti- quark liquid state. More details will be given in Section 24. Now let’s look at the future destiny of universe. The cosmic history from pre-big-bang period through the 0-period, first period, second period and the current third period indicate that, in the cosmic scale, the direction of time arrow is from the set with larger prime numbers toward the set with smaller prime numbers. It means that, to read the sets of prime numbers listed in Table 23.1 corresponding to cosmic history should be from bottom up and from right to left. In other words, the cosmic time sequence is from the period with the set of larger prime numbers to the period with the set of smaller ones. Now we are in the current third period corresponding to a set of 18 + 1 = 19 prime numbers, in which 18 prime numbers for quarks is listed in the first row of Table 23.1 plus the even prime number 2 for electron not listed. In the set of 19 prime numbers, the smallest one is 1. At first glance, it seems no prime number smaller than 1. If that is the case, our universe eventually will come to an end. But Mother Nature always has her ways. The num- ber axis centered at 0 has two wings, the right wing points toward positive numbers and the left wing points toward negative numbers. There is a set of negative prime numbers, which is exactly the same as ordinary prime numbers set with minus signs. Taking the negative prime numbers into account, there is a future for our un- iverse. Definition 23.2: The negative prime numbers are de- fined as the negative value of the ordinary prime num- bers, which correspond to the prime numbers listed in Table 23.1 with minus signs. Hypothesis 23.2: In terms of cosmology and elemen- tary particles, the negative prime numbers act the same way as their positive counterparts except that, all parti- cle’s m-parameters and n-parameters change signs. Definition 23.2 and Hypothesis 23.2 lay the theoretical foundation for the future and the pre-big-bang history of the universe. Astronomical observations found that, the universe currently is expanding with accelerating speed caused by the repulsive force of dark energy. Some cosmic models predicted that, the expansion will slow down and eventu- ally turn to contraction. The contracting universe re- verses its expansion process and finally back to a big crunch corresponding to the reverse of the big bang. Then the whole thing starts over again. The model is call- ed “oscillation model”. The universe cycles by itself over and over. Hypothesis 23.2 supports the oscillation model based on the negative prime numbers. The following is the scenario of universe future from SQS theory perspec- tive based on Hypothesis 23.2. The expansion of universe will slow down due to the dilution of dark energy density and eventually turn into a contraction. The evidence is in the extended prime num- bers table. As time passing by, the corresponding prime numbers become smaller. Finally it reaches 1, which is marked as the end of the current third period. But the cosmic evolution does not stop. It continues its journey. The number passes through 0, which is the m-parameter for the graviton. Then it enters into the negative territory. According to Hypothesis 23.2, the negative prime num- bers correspond to the m-parameter changing sign. Theoretically, here are two ways for the n-parameter to react: (1) The corresponding n-parameters also change its sign; (2) The corresponding n-parameters do not change sign. According to Definition 11.2, the second way means that all particles become anti-particles. All matters in the universe suddenly become anti-matters! This sce- nario is impossible. Then the only possibility is the first way as Hypothesis 23.2 stated. The simultaneously changing signs of both m-parameter and n-parameter indicate that, all particles change their handedness corre- sponding to change the direction of their momentum. This scenario is supported mathematically and physically. The mathematic support comes from prime numbers. At the time universe stop expansion, the prime number se- quence passes 0 and enters the negative territory causing m-parameters and n-parameters both changing their signs. The physical support is that, as universe stops expansion and starts to contract corresponding to all particles’ mo- mentum changing direction. This scenario is much easy  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1320 to be accepted than the other scenario, all particles sud- denly become anti-particles. Sine the negative prime numbers table is the same as the positive prime number table except the minus signs, as the universe starts to contract, it basically follow the reversed process of the expansion universe. It is like to play a video in the reverse order. The consecutive cosmic events sequence is like that, as the negative third period coming to its end, the universe enters to the negative second period, then the negative first period, the negative 0-period, the negative big bang, i.e. the big crunch, fi- nally reaches the negative pre-big-bang period, i.e. the post-big-crunch period, One cycle of universe oscillation is completed. The post-big-crunch period is the same as pre-big-bang period except that all m-parameters and all n-parameters change signs corresponding to time arrow in the opposite direction. To start the next cycle, the post- big-crunch period must transfer into the pre-big-bang period. This process can be realized through a “time tun- nel”. Since both periods possess extremely high energy, according to general relativity, the space-time is extre- mely curved providing the conditions to form time tunnel. Figure 23.1 shows a diagram to illustrate the evolution of the cyclic universe. Figure 23.1. Illustration of cosmic cycle based on prime numbers. The repetitive cycles of oscillation model are in the cosmological sense. It does not mean that, everything in the universe will repeat exactly. In fact, according to SQS theory, space is stochastic in nature, which prohibits absolute determinism at the fundamental level and upper levels. The cosmic history described in this section is based on the prime numbers table and the Prime Number Pos- tulation. It especially depends on the discovery of three sets of consecutive prime number even pairs serving as the mathematical bases for the first period, the second period and the pre-big-bang period. The correspondence of the original set of 18+1 prime numbers to the current third period is supported by many evidences. The ques- tion is: What is the mathematic relation between the newly found three sets of prime numbers and the original set of 18+1 prime numbers? Let’s start from the first prime numbers of the three sets, according to Table 23.1, which are 167, 101, and 239 for the first, second, and per-big-bang period, re- spectively. A simple arithmetical calculation found the following formulas. Period-I: )321(3129231917131175321167 , (23.9a) Period-II: 231917131175321101 , (23.9b) Period-III*: 41373129231917131175321239 . (23.9c) In which, Period-I, Period-II, and Period-III* are marked for first period, second period and pre-gig-bang- period, respectively. It is interesting to find some rules in (23.9). 1) The first prime number 101 corresponding to Pe- riod-II equals to the sum of the ten consecutive prime numbers from 1 to 23 in the set of 18+1 prime numbers for the current third period. 2) The first prime number 239 corresponding to Pe- riod-III* equals to the sum of the fourteen consecutive prime numbers from 1 to 41 in the set of 18+1 prime numbers for the current third period. 3) The first prime number 167 corresponding to Pe- riod-I equals to the sum of the twelve consecutive prime numbers from 1 to 31 plus (1 + 2 + 3) in the set of 18+1 prime numbers for the current third period. The repeat of three prime numbers (1 + 2 + 3) represents the fact that the space of Period-I is 3 1 1-dimensional, which is dif- ferent from Period-II and Period-III*. The last prime numbers of the three sets corresponding to period-I, period-II, and period-III* are, 199, 157, 347, respectively. Period-I: )321()7()13(535961199 , (23.10a) Period-II: )37(5961157 , (23.10b) Period-III*: )43(414347535961347 . (23.10c) There are also some rules in (23.10).  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1321 1) The order of summation in (23.10) is backwards from the last prime number 61 of the 18 + 1 prime num- bers set and consecutively takes the next one. 2) After the backwards consecutive summation ended, it jumps to the prime number(s) shown in parenthesis. 3) For Period-II, 37 is the prime number assigned to b c as the up type quark of the 2nd generation. For Pe- riod-III*, 43 is the prime number assigned to r t as the up type quark of the 3rd generation. 4) For Period-I, 13 and 7 are the prime numbers as- signed to b u and g u as the up type quarks of the 1st generation. (1 + 2 + 3) indicates that the space of Pe- riod-I is 3 1 1-dimensional, which is different from Pe- riod-II and Period-III*. The rest of prime numbers i P in the three sets corre- sponding to Period-I, Period-II, and period-III* are ex- pressed as follows. Period-I: yxPi 167 , 73,2 i; (23.11a) Period-II: yxPi101, 113,2 i; (23.11b) Period-III*: yxPi239 , 173,2 i. (23.11c) In which and y are two prime numbers selected from the set of 18 odd prime numbers from 1 to 61 cor- responding to the current third period. These rules answer the question. There are mathe- matical correlations between the three sets of prime numbers and the original set of 18 + 1 prime numbers. It implies that, the three periods in cosmic history are closely related to the current periods. It also serves as another supportive evidence for the Prime Number Pos- tulation and its roles in elementary particles and cosmol- ogy. Conclusion 23.2: Based on (23.9), (23.10), (23.11), the three sets of prime numbers even pairs corresponding to Period- I, Period-II, Period-III* are based on the orig- inal set of 18 + 1 = 19 prime numbers corresponding to the current Period-III. The selection of four sets of prime number pairs ac- cording to Definition 23.1, Postulation 23.1 and Lemma 23.1 is based on the Prime Numbers Postulation and the even pairing rule. There are so many things depending on it. It is necessary to ask the question: Is it by coincidence? Let’s try to answer. The odd prime numbers are divided into two catego- ries. The 14 n category: 14 1 nP , 3,2,1,0n; (23.12a) The 14 n category: 14 2 nP , 3,2,1n. (23.12b) For a pair of two prime numbers, there are four possi- ble combinations with average values as: evennnnnA )(22/)14()14(),( 2121 , (23.13a) evennnnnA )(22/)14()14(),( 2121 , (23.13b) oddnnnnA 1)(22/)14()14(),( 2121 , (23.13c) oddnnnnA 1)(22/)14()14(),( 2121 . (23.13d) The distribution of prime numbers seems random. It is natural to assume that, the four combinations of (23.13) each has equal probability of occurrence. In other words, for two consecutive prime numbers being even pair or odd pair each has fifty-fifty equal chance. Based on this assumption, it is possible to give some estimation. As listed in Table 23.1, for the first set with 9 consecutive even pairs from 3&1 to 61&59 plus an odd pair 71&67 at end as a specific prime numbers sequence to occur randomly, the probability is 1024/122 10)19( 19 p. For the second set with 9 consecutive even pairs from 241&239 to 347&337 plus two odd pairs 233&229 and 353&349 at both ends as a specific prime numbers sequence to occur randomly, the probability is 2048/122 11)29( 29 p. Likewise, for the two shorter sequences, the one with two generations has probability of 256/1228)26( 26 p, the one with one generation has probability of 64/122 6)24( 24 p. In average, 1024/1 19 p means that the event only occurs once per 1024 prime number pairs; for 2048/1 29 p, it only occurs once per 2048 prime num- ber pairs. These are the expected values according to statistics. But in fact, these two, not only one, sequences occurred in a set including only 71 odd prime numbers (35.5 pairs) from 1 to 353. The 71 odd prime numbers (35.5 pairs) also include the other two shorter sequences, and all four sequences are in the right order. Are all of these by coincidence? It is virtually impossible. Conclusion 23.3: The probability of four sets of prime number pairs occurred by coincidence in 71 least odd prime numbers sequence from 1 to 353 is in the order of 11 39 10305.4 23 71 )!4(2048102425664 2/71 coincid p. (23.14) The four sets of consecutive prime number pairs found in the prime numbers table shown in Table 23.1 based on the Prime Numbers Postulation and the even pairing rule  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1322 are not by coincidence. Explanation: It is only a rough estimate. 71 divided by 2 is for prime number pairs. )4321()!4( in denominator is for the 4 sets in the right order. The correlations of prime numbers to particle physics must have a deep origin. For instance, consider the ques- tion: Why the m-parameters and n-parameters of 18 quarks must be prime numbers? One possible reason is that, because prime numbers are not reducible, the 18 different prime numbers serving as m-parameters of 18 quarks prevent different quarks from mixed up by reduc- tions; the n-parameters of 18 quarks with prime numbers different from corresponding m-parameters prevent re- duction with m-parameters. In other words, the prime numbers serving as m-parameter and n-parameter give each quark unique mathematical identity to avoid mixed ups by reduction. There is another stronger reason based on number the- ory. For the cyclic arithmetic theory, it is well known that, only the p-cyclic-arithmetic with p as prime number is self-consistent for multiplication and division [18]. Since mand n determines the lengths of loop-1 and loop-2, respectively, the m-parameter and the n-para- meter equal to prime number have something to do with quark’s internal cyclic movements related to the p-cyclic- arithmetic. In terms of philosophy, prime numbers are the basic building blocks of numbers; likewise, quarks are the ba- sic building blocks of matters. In fact, it was the author’s original intuition to purposely look into the prime num- bers searching for possible physics significance. How- ever, the deeper reason for the roles of prime numbers in SQS theory is still an interesting open issue worthwhile to dig in. In summary, the cosmic models and history provided in this section is based on prime numbers listed in Table 23.1 and its extended version to the negative territory. The finding of three cosmic periods has its significance. It confirms the importance of the Prime Numbers Postu- lation for dealing with elementary particles as well as for identifying cosmic periods. It provides a chance to rec- ognize the meaning of intrinsic symmetries based on the geometry of the two parts of face-centered space struc- ture introduced in Section 22. It reveals cosmic history and links it to elementary particles. It provides natural explanations for the big bang, inflations, dark matters etc. It predicts the future destiny of universe. It also provides two suggestions for verification. The cosmic models and evolution according to SQS theory described in this section agreed with cosmological standard model pretty well. It serves as a supportive evi- dence of the face-centered space structure. Moreover, the classification of space symmetries as )(rO , )(rC and the Symmetries Family Tree provide the bases to identify the elementary particles and interactions in different cosmic periods, which are self-consistent and agreed well with particle physics and cosmological standard model. It cannot be by coincidence, which gives the credential for both. These agreements also serve as the supportive evi- dences for Definition 23.1 and Postulation 23.1 intro- duced at the beginning of this section. There is a pending issue to think about it. The expan- sion of universe corresponds to entropy increase. Then the contraction of universe corresponds to entropy de- crease. Is it a violation of the second law of thermody- namics? Section 24. The Monster and Two Other Sporadic Groups The finite Lie groups are classified into two categories, the classical groups and the sporadic groups. There are 26 sporadic groups in the second category [18]. Three sporadic groups M (Monster, E8) B (Baby monster) Suz (Suzuki) are closely related to the m-parameters and to some extent n-parameters of three generation elementary particles. It is a finding with important impacts on parti- cle physics and cosmology. The size of these three groups is factorized into prime numbers [18], which are listed in Table 24.1. The m-parameters of 18 quarks are also listed for comparison. Table 24.1. Factors of three sporadic groups size versus the m-parameters of quarks. *The prime numbers marked with under line are missing in the factors se- quence of corresponding group. Let’s take a closer look of the comparison between the M-group size factors and the m-parameters of 18 quarks. The size for M-group is factorized into 15 prime num- bers with different powers, in which 1 is not included. From SQS theory standpoint, the prime number 1 must be included with power nany integer:  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1323 715947413129231917131175321 32692046 n M F. (24.1) Except the last prime number 71, which will be dis- cussed later, there are 15 prime numbers left. In which 2 is the only even prime number assigned as the before reduction m-parameter of electron red branch r e. To compare the 14 odd prime numbers with the 18 prime numbers assigned as the m-parameters of three genera- tion quarks, there are 4 prime numbers 37, 43, 53, 61 missing in the M-group factors sequence. At first glance, the missing prime numbers seem a defect for the correla- tion between these two sets of prime numbers. Actually, it is just the opposite. The missing prime numbers have deep meanings. The missing prime numbers 53 and 61 are the m-parameters shared by g t, b t and 1 Y, 2 Y, which are the two components of gauge bosons W and . The missing prime number 37 is the m-parameter shared by b c and 2f X, which is one of the two com- ponents for the gauge boson 0 . So the three prime numbers 37, 53, 61 all have the common reason for missing inM F. They are the m-parameters of quarks serving as the constituents of bosons for weak interaction. The missing prime number 43 also has a meaning. The three prime number 43, 53, 61 are m-parameters for three top quarks r t, g t, b t, which have mass heavier than Max M. According to Rule 6.1, top quarks must appear in pair with anti-quarks as a boson state. Therefore, for the four missing prime numbers in the M-group, they all are involved in something related to bosons or boson states with more than one quark (anti-quark) involved. The size for the B-group is factorized into 12 prime numbers: 4731231917131175321 261341 n B F. (24.2) Except the last prime number 47, which will be dis- cussed later, there are 11 prime numbers left. The 10 odd prime numbers compare with the 12 prime numbers as- signed as the m-parameters of first and second generation quarks, there are two prime numbers 29, 37 missing in the B-group. According to the some rule, 29, 37 are the m-parameters shared by g c, b c and 1f X, 2f X, which are the two components of gauge boson 0 . The size for the Suz (Suzuki) group is factored into 7 prime numbers: 1311753212713 n Suz F. (24.3) In which the 6 odd prime numbers are the m-para- meters of first generation 6 quarks. There is no missing prime number in Suz F. Rule 24.1: The prime number factors sequence of three sporadic groups M, B, Suz are closely related to the m-parameters of three generation elementary particles. The correlation rules are: 1) The even prime number 2 is the before reduction m-parameter of electron red branch. 2) The odd prime numbers are related to quarks’ m-parameters of corresponding generations, all three generations, first generation plus second generation, and first generation for M-group, B-group, and Suz-group, respectively. 3) The missing prime number in the factors sequence corresponding to up type quark’s m-parameter is related to boson or boson state with more than one types of quark (anti-quark) involved. 4) The missing prime number in the factors sequence corresponding to down type quark’s m-parameter ends the previous generation(s). Explanation: The rules from No.1 to No.3 have been explained. Let’s talk about rule No.4. The M-group prime number factors sequence missed two prime numbers 61, 67, between 59 and 71, in which the missing of 67 cor- responding to the down type m-parameter ends all three generations. The B-group prime number factors sequence missed three prime numbers 37, 41, 43 between 31 and 47, in which the missing of 41 corresponding to the m-parameter of a down type quark r b ends two previ- ous generations. The Suz-group prime number factor sequence ends at 13, the missing of 17 corresponds to the m-parameter of a down type quark r s ends the first generation. In summary, the missing prime numbers in three sporadic groups’ factored sequences are classified into two categories: (1) The missing prime number cor- responding to the m-parameter of up type quark is related to boson or boson state with more than one types of quark (anti-quark) involved; (2) The missing prime number corresponding to the m-parameter of down type quark ends the previous generation(s). The correlation is one on one for every one without exception, which can- not be by coincidence. Rule 24.1 reveals the intrinsic correlation between three sporadic groups and three generations of quarks and the electron red branch. It clearly shows that, the assignment of 18 + 1 = 19 prime numbers as m-para- meters of 18 quarks and electron red branch is supported by three sporadic finite Lie groups. More importantly, it provides the third mathematic evidence for the conclu- sion of only three generations of elementary particles. The first evidence is the Prime Numbers Postulation based on number theory. The second evidence is the magic number 163 also based on number theory. Here comes the third independent evidence based on group theory. The M-group is the largest group. Its correlation to all three generations leaves no room for more genera- tion. No other group can change the conclusion, because no group is larger than the M-group. Moreover, the No. 3 rule of Rule 24.1 supports the as-  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1324 signment of up type quark’s m-parameter as m-parameter for the fermion constituents of gauge bosons W, Z and X. In addition, as shown in Table 24.2, the prime number factors of three sporadic groups also related to the n-parameters of quarks. Table 24.2. Factors of three sporadic group size versus n-parameters of quarks. *The prime numbers marked with under line are missing in the factors se- quence of corresponding group. As shown in Table 24.2, most quarks’ n-parameters are selected from the prime number factors sequence of corresponding sporadic group. There are exceptions marked with underline. The exceptions for up type of quarks r t, g t, b t and b c can be explained with the some rule for the m-parameters. There is one exception in a down type quark, which is 53 bb n for b b. What’s the implication for this down type exception? It is an open issue. In Table 24.3, the products of factors in orders of magnitude for three sporadic groups are listed. For com- parison, the products of quarks’ m-parameters for three generations along with the pre-big-bang period are also listed. Table 24.3. The products of factors for M, B, Suz groups and products of m-parameters. Note: G is the rank of the grand number. In the 7 products shown in Table 24.3, the 6 products either are grand numbers or close to a grand number. The only exception is the first generation. It shows that, grand numbers are common phenomena. They can be found in particle physics and cosmology as well as in mathematics such as group theory and number theory. It is interesting to point out that, 5~ M G, 3 B G and 1 Suz G are odd numbers, while 2 3G and 4 pre G are even numbers. Moreover, 4 pre G is the double of 2 3 G. It serves as a clue for the relation between these two pe- riods. So far in this section, all prime number factors of three sporadic groups M, B, Suz are covered with two prime numbers 47 and 71 left, which are the last prime number after corresponded generation ended. Let’s look at them closely. For the largest prime number 71 in M F, the first clue comes from GUT: 06279805.71 )( 2 Z GUT Planck GUT M M M N . (15.11) The relative deviation of 0627805.71 GUT Nfrom the prime number 71 is 4 10845.8 . In (15.11), GU N is the converting factor for the grand unification boson 3 U with mass 218 /1007948.1 cGeVMGUT , while )(Z M is the fine structure constant at Z boson mass 2 /1876.91cGeVMZ. The two very different energy scales do not match. Consider the asymptotic behavior of )( M as a running constant, it seems reasonable to use the prime number 71 to determine the value of )( 1GUT M : 69002169.127 2 71 )( 2 1 GUT M. (24.4) This is a new way to determine the value of at a particular mass scale, which is independent of the me- thod used in Section 9. More details will be given later in this section. Compare 69002169.127)( 1 GUT M with the experimental data from 2010-PDG (p.126): 016.0916.127)( 1 Z M , the value given by (24.4) seems reasonable. In other words, the grand unification of all interactions to gravity actually occurred at characteristic length scale: mLL PGUT 33 101475375.171 . (24.5) This is the reason to use PGUTLL 71 as 1 Lin (23.6a) for the length scale of first period. The prime number 71 serves as the characteristic length for the grand unification. It should also have other geometric and physics meanings.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1325 Definition 24.1: The M-sphere is defined as a sphere in space centered at a vertex with radius of mLLR PGUTM 33 1014754.171 . (24.6) It turns out that, the M-sphere is an important concept related to many issues. The spherical surface of M-sphere is the boundary between microscopic region and the intermediated region. According to SQS theory, space is divided into three regions: Inside of the M-sphere is the microscopic region, which is the territory of elementary particles, composite particles and their different states. The region with linear scale between mLR PM 33 10148.1~71 and Compton scale Mch C/ is defined as the intermediate region, which is the playground of the random walk and the logistic recurrent process discussed in Section 4 and Section 16, respectively. The region with linear scale larger than Compton scale is the macroscopic region. Take PMLR71 as radius and draw the M-circle on the surface of M-sphere with the same center. The circumferential length of the M-circle is: PPMLLL10615681.446712 . (24.7a) Taking P L as basic length unit, M L becomes a number: 10615681.446712 M L. (24.7b) In the following discussions, all lengths are numbers with P L as the basic length unit. In Figure 24.1(a), the intersections of two adjacent Gaussian spheres to the M-sphere surface are shown as two circles with radius )22/(1r. The distance between the two centers is 2/1 1d. The two circles are either centered at two adjacent octahedral vertexes representing two fermions or one centered at an octahedral vertex and the other centered at an adjacent cubic vertex represent- ing a fermion and a boson. The span angle of 1 d on the M-circle with respect to its center is: 57062302.0360 2712 1 360 1 M ML d . (24.8) As listed in Table 11.5, the average tilt angle for quarks and leptons from 120 is: 53410359.0 . (24.9) Comparing to M , the relative discrepancy is 2 104.6 . The near equality of M and has deep meanings. The arc length of 53410359.0 on the M-circle is: 661852 .0 360 53410359.0 712 360 MMLL . (24.10) As shown in Fig. 24.1(a), the center of the right Gaus- sian sphere shifts towards left and brings the Gaussian sphere with it to a new location shown by the red circle. M L is the distance between its original location and the new location after shifted. At its new location, the shifted Gaussian sphere overlaps with the Gaussian sphere at left. The distance between the centers of these two Gaussian spheres is: 0.0452542 2 1 1 MMLd. (24.11) As shown in Fig. 24.1(a), these two Gaussian spheres are almost entirely overlapped. Fig. 24.1(b) shows the case for two adjacent Gaussian spheres on the M-spherical surface centered at two adja- cent cubic vertexes representing two bosons. The dis- tance between them is 1 2d. The right Gaussian sphere shifts towards left with a distance of 6618525.0 M L. After shifted, its center is locates at a distance of 2M d from the center of its neighbor: 0.33814751 2 MM Ld . (24.12) As shown in Fig. 24.1(b), the center of shifted Gaus- sian sphere just gets into its neighbor’s boundary and overlaps with it about halfway. Figure 24.1. Pairs of adjacent Gaussian spheres intersect with m-sphere surface. The overlap of two Gaussian spheres means that, the vertexes at the center of Gaussian spheres are statistically no longer clearly distinguishable. As shown in Section 22, vertexes serving as elements of symmetries represent elementary particles. The overlapping Gaussian spheres are interpreted as two elementary particles represented by  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1326 two vertexes no longer clearly distinguishable. In particle physics, at extremely high energy, particles are no long distinguishable. Quarks and anti-quarks with extremely high energy form the “quark-antiquark liquid state”. The phenomenon has been demonstrated by phy- sicists working on RHIC at Brookhaven National Labo- ratories and LHC at CERN. They found that, the quarks and anti-quarks are bound relatively tight to form a liquid like state. The energy associated with particles increases rapidly with corresponding radius in the symmetrical space. As shown in Section 22, the first generation quarks, u and d, with mass less than 2 /10cMeV correspond to vertexes in the region with radius 1 . The top quarks t with mass of 25/1072.1 cMeV corresponds to ver- texes in the region with radius 3r. The 3 times radius increase causes the particles’ mass more that 4 10 times increase. Now, the M-sphere has a radius of 71 r, comparing with 3r is more than 23 times increase in radius. It pushes the energy well into the quark-antiquark liquid state territory. In fact, the energy scale of grand unification happened on the M-sphere surface is GeV 18 1007948.1 as listed in Table 15.1. Consider all of these facts, there are sufficient reasons to identify the region near the M-sphere inner surface as the region for the quark-antiquark liquid state. Now let’s deal with the largest prime number 47 in the B-group factors sequence. Definition 24.2: The B-sphere is defined as a sphere in space centered at the same center of the M-sphere with radius: mLR PB 34 10596375.747 . (24.13) Take 47 B R as radius and draw the B-circle on the B-sphere surface with the same center. The circumferen- tial length is: 30970944.295472 B L. (24.14) The arc length of 53410359.0 on the B-circle is: 43812771.0 360 53410359.0 472 360 BBLL. (24.15) Using the same method for calculation, the results on the B-spherical surface are: 0.26897907 2 1 1BB Ld , (24.16a) 0.561872291 2 BB Ld . (24.16b) As shown in Fig. 24.2(a), the center of right Gaussian sphere is shifted towards left at0.26897907 1 B dfrom the center of its neighbor and overlapped with its neigh- bor about half way. As shown in Fig. 24.2(b), the center of right Gaussian sphere is shifted towards left at 0.56187229 2B dfrom the center of its neighbor, and two spheres are marginally overlapped. It seems reasonable to call the region between B-sphere surface and M-sphere surface as the “quark- antiquark liquid region” or “liquid region” for short. But as shown by Fig. 24.2(b), the two Gaussian spheres are not detached yet. Inside the B-sphere, there are some liquid state remains left. Figure 24.2. Pairs of adjacent Gaussian spheres intersect with b-sphere surface. To find a clear cut for the liquid state region, let’s search for another sphere. The M-sphere and B-sphere are defined by the prime numbers 71 and 47 of the M-group and B-group, respectively. The number 47 is the largest prime number in the B-group factors sequence corresponding to the m-parameter 47 bg m of g b quark in the third generation. As shown in Table 24.1, for the Suz-group, there is no such prime number like 47 for the B-group. Look at it the other way, the first generation corresponding to Suz-group does relate to a prime num- ber at similar location as 47. The number is 23 sg m of g s quark in the second generation. Comparing with 47 bg m for the g bquark in the third generation, they sit at similar locations with a generation difference. Be- fore take 23 sg m seriously, let’s look at the three prime numbers in another way: 72171 , (24.17a) 48147 , (24.17b) 24123 . (24.17c) The three numbers on the right look familiar as shown  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1327 in Table 18.3. And these three numbers also serve as building blocks of the Number Tower to raise the magic number 163 to the top. The “1 ” term in (24.17) can be interpreted as adding the graviton, which is included in the Elementary Particle Table. If the three formulas of (24.17) are not by coincidence, they provide two implications: (1) They serve as the second support for the Elementary Particle Table and its classification for particles; the first support is the Num- ber Tower and the number 163 on top of it. (2) They provide the reason for using 23 to define a sphere like 47 to define the B-sphere and 71 to define the M-sphere. Moreover, look closely at the factors sequence of size for other sporadic groups, there are three groups called Conway groups labeled Co1, Co2, Co3 with similar structure as the Suzuki group Suz. The factors sequences of Co1, Co2, Co3 are: 2313117532 24921 1 Co F, (24.18a) 23117532 3618 2 Co F, (24.18b) 23117532 3710 3 Co F. (24.18c) The prime number 23 appears in 1Co F,2Co F,3Co F located at the right place corresponding to the down type quark g s with 23 sg m. These facts serve as the additional reasons for using the prime number 23 to define a sphere. Finally, there is another supportive fact: 47 3 714723 . (24.19) Definition 24.3: The S-sphere is defined as a sphere in space centered at the center of the M-sphere with radius of: mLR PS34 10717375.323 . (24.20) Take PS LR 23 as radius and draw the S-circle on the S-sphere surface with the same center. The circumferen- tial length of S-circle is: 51326207.144232 S L. (24.21) The arc length of 53410359.0 on the S-circle is: 21440292.0 360 53410359.0 232 360 SS LL . (24.22) Using the same method for calculation, the results on the S-sphere surface are: 0.49270386 2 1 1 SS Ld , (24.23a) 0.7855970 1 2 SS Ld . (24.23b) As shown in Fig. 24.3(a), the center of right Gaussian sphere is shifted towards left at a distance 0.49270386 1 S d from its neighbor and two spheres are overlapped mar- ginally. As shown in Fig. 24.3(b), the center of right Gaussian sphere is shifted towards left at a distance 0.7855970 2 S d from its neighbor and two spheres are detached. Figure 24.3. Pairs of adjacent Gaussian spheres intersect with S-sphere surface. Definition 24.4: The three regions inside the M-sphere are defined according to their radius ranges: The quark-antiquark liquid region: 7147 lqq r, (24.24a) The transition region: 4723 trans r, (24.24b) The particles region: 230 parti r. (24.24c) Explanation: In the quark-antiquark liquid region, the undistinguishable particles form the quark-antiquark liq- uid state having extremely high energy corresponding to extremely high temperature. In the transition region, in- dividual particles are barely distinguishable, and some liquid states remains left near the B-spherical inner surface. In the particles region, most particles are clearly distinguishable. The detachment shown in Fig. 24.3(b) indicates that, the two Gaussian spheres cen- tered at two adjacent vertexes representing two bosons are no longer mixed up. As shown in Fig. 24.3(a), the two adjacent Gaussian spheres with center to center dis- tance 2/1 1d always have some chance to mix up. In case the two Gaussian spheres centered at different types of vertexes, one at octahedral vertex presenting a fermion  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1328 and the other at cubic vertex representing a boson, the mix up does not blur their identity because they belong to different types. In fact, these two Gaussian spheres are touched at their boundary to begin with. Any shift no matter how tiny causes overlapping. It indicates that, fermions and bosons are intrinsically linked. In case the two Gaussian spheres centered at two adjacent octahedral vertexes represents two fermions, they have chance to mix up and to blur their identity. The Gaussian spheres shifting locations are caused by the tilt angle 5341.0 , which breaks the symmetry and provides mass for particles. It is possible to give some interpretations for the Gaussian spheres shifting. The two bosons represented by two detached spheres are interpreted as bosons without mass. The one sphere rep- resenting a boson overlapped with the other sphere rep- resenting a fermion is interpreted as the boson gained mass from its component fermions. The two overlapped spheres representing two fermions are interpreted as fer- mions with mass. In fact, all fermions have mass, while bosons such as , , )823,1(, igi have no mass; bosons such as , , , )823,1(, iGi, 1 U, 2 U, 3 U gained mass from component fermions. So the inter- pretations seem reasonable within the particles region inside the S-sphere. Let’s look at the scenario shown in Fig. 24.2 for the transition region. The overlapped spheres shown in Fig. 24.2(a) are overlapped more, which means the particles with mass gained more mass. Since the transition region has much high energy than the particle region, the mass gain sounds reasonable. The detached spheres shown in Fig. 24.3(b) are overlapped, which means the original massless boson gained mass. Is that possible? Recall the e-boson made of a pair of electron and positron having mass GeVMbe 8 1095987106.3 . Actually the e-boson is a “heavy photon” with zero spin. Why does the spin change? The reason is their numerical parameters com- bined in different ways. Regular photon: ee , 211 m, 02/12/1 n, 02/12/1p; 00)/( eeMMnpM , )2/(2)2/(ms . (24.25a) Heavy photon: eebosone , 011 m, 12/12/1 n, 1)2/12/1( p; ,int 22)/(2 eeeeebe MMNMnpNM , 02/ msbe . (24.25b) So the e-boson as heavy photon with zero spin is ex plained and consistent with the rules. This argument also explains the fact that, gluons have zero mass and spin , while 1 U, 2 U, 3 U and massons have mass and spin 0. So everything is consistent. It is important to point out that, the e-boson as heavy photon is not another elementary particle. It is just a high energy state of the photon listed in the Elementary Parti- cles Table, in which the heavy photon is not qualified to have its own seat. Inside S-sphere, the number of vertexes is estimated as: cf s SD V V N 0 . (24.26) The volume of Gaussian sphere: 3 022 1 3 4 V, (24.27a) The volume of S-sphere: 3 23 3 4 S V. (24.27b) The face-centered filling factor: 18 cf D. (22.1) Substituting (24.27) and (22.1) into (24.26) yields: 5 3 10039.2 18 2223 S N, (24.28a) For comparison: 6 3 1074.1 18 2247 B N, (24.28b) 6 3 10997.5 18 2271 M N. (24.28c) The S-sphere with 5 10039.2 S N vertexes has suf- ficient room to accommodate all different types of ele- mentary particles, composite particles and their different states. The term “liquid” of quark-antiquark liquid state is not just symbolic, it has real implications. As mentioned in Section 22, space has its crystal structure with face-centered lattice. In the particles region, space struc- ture is either single-crystal or poly-crystal akin to the solid. As energy and temperature rising, space in the transition region corresponding to very hot solid is start- ing to melt. After temperature rose to “melting point”, space becomes liquid. In the liquid region, even though temperature is extremely high, the binding force is strong enough to hold Gaussian spheres in the liquid state. It shows that, the term “liquid” is a good analogy to the space structure in quark-antiquark liquid region, which is also supported by experiments at RHIC and LHC.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1329 Let’s apply the analogy to the pre-big-bang period. As listed in Table 23.1, the pre-big-bang period prime num- bers sequence starts at 239, which is about 3.366 times of 71. It indicates that the lowest energy corresponding to 239 for the pre-big-bang period is many orders of mag- nitude higher than the highest energy in the liquid region of the M-sphere. In other words, the entire pre-big-bang sphere is in over heated liquid state. Any random stimu- lation causes the overheated pre-big-bang sphere to eva- porate into “gaseous state” with free Gaussian spheres flying around. This is exactly the big bang scenario de- scribed in Section 23. The 3-dimensional over heated liquid sphere serves as the origin of universe corre- sponding to the pre-big-bang period. Then the big bang consecutively developed into the first period, the second period, and the current third period as described in Sec- tion 23. It shows that, early cosmic history described in Section 23 is not only supported by the prime numbers table and the Prime Number Postulation but also supported by the category of regions for space based on three sporadic groups. Back to the tilt angle of 53410359.0 . The tilt an- gle deviated from 120 is calculated ac- cording to (8.38) based on AT-equation and PS-equation with the data cited from particles’ parameters of their models. Since AT-equation and PS-equation are not de- rived from the first principle, their ad hoc nature requires verification and accuracy needs to be determined. As mentioned previously, the relative discrepancy of 53410359.0 from 57062302.0M is 2 104.6 . 57062302.0 M is the angle for totally overlapping of two Gaussian spheres shown in Fig.24.1(a). Use it as a criterion, the relative error caused by AT-formula and PS-equation is estimated no more than 2 104.6 up on the upside. On the down side, as shown in Fig.24.1(b), use the right sphere center just touching to the left sphere surface as the criterion. The right sphere shifting distance is 64644661.0)22/(11 2 M Dcorresponding to a span angle on the M-cycle of 2M : 5216713.0360 2 2 2 M M MR D . (24.29) Compare to the tilt angle 53410359.0 , the down side relative error is estimated as 2 1038.2 down . It seems safe to say that, despite its ad hoc nature, the AT-equation and the PS-equation provide results in the ballpark. In Section 8, the AT-equation and the PS-equation as two independent equations with only one variable are satisfied simultaneously. It indicated that, there is something in it. Now the AT-equation and PS- equation have a second independent verification. These verifications are critical. Because so many things depend on it such as the f-modification, the effective parameters, and the signifi- cance of M-sphere, B-sphere, S-sphere etc. In fact, the AT-equation and the PS-equation catch the essence of elementary particles to break symmetry, to acquire mass and other related effects. This seems not an over state- ment. So far the correlations and meanings of all prime numbers in the factors sequence of size for three sporadic groups are covered. There is one issue left. Besides elec- tron’s red branch with m-parameter 2 er m, the other leptons’ m-parameters are not related to the sporadic groups. The before reduction m-parameters for charged leptons are even numbers. Except 2 er m as the only even prime number, all others are not prime numbers. This is the reason for them not listed in Table 24.1. But an even number can be factorized into prime numbers. The factorized prime numbers sequence of three charged leptons’ m-parameter with their branches as shown in Table 24. 4. The factors sequence M F of the M-group is also listed at the bottom for comparison. Table 24.4. The Factors of the before reduction m-para- meters for charged leptons. In the nine sets of prime number factors for three charged leptons with branches listed in Table 24.4, there are 6 prime numbers involved. In which 2 appears 11 times as 11 2, 3 appears 6 times as 6 3, 5 appears 3 times as 3 5, and 7 , 13, 17 each appears 1 time as 1 7, 1 13 , 1 17 , respectively. To inspect the prime number factors in a symmetric manner, some criteria are needed. The loose criterion: All prime number factors of charged leptons’ before reduction m-parameters must be included in the prime number factors inM F of the M-group. Notice that, 2, 3, 5, 7, 13, 17 all are included in the factors of M F. Apparently they meet the loose criterion. The strict criterion: All prime number factors of charged leptons’ before reduction m-parameters must be included in the prime number factors inM F of the M-group under the condition that, the number of times used for a prime number in the m-parameters of quarks and charged leptons does not exceed that prime number’s power number in M F factors. In the 171311753232692046 M Fsequence, the power numbers for 2, 3, 5, 7, 11, 13 have sufficient room to accommodate 111 2 , 16 3, 13 5, 11 7, 11 13 , in  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1330 which “+1” is to count they used once for the m-parameter of quarks already. But 17 inb F is a problem, because 17 appears inM F sequence only once and it has been used for the m-parameter of strange red quark r s already. It does not meet the strict criterion. There are ways to dealing with the problem. 1) The before reduction m-parameter of 2/)3731(34 b m is derived from the m-parameter of two quarks b s and b c with m-parameters of 31 sb m, 37 cb m. To switch the m-parameters forb c and g c, the new m-parameters of g ad b becomes: 532302/)3723(2/)'(' cgsgg mmm , (24.30a) 532302/)2931(2/)'(' cbsbb mmm . (24.30b) If the n-parameters and p-parameters are switched with the m-parameters, nothing else is changed except the colors green and blue switched accordingly. The problem goes away. But it raises another question: Why switch number parameters for these two quarks? Besides, the switched m-parameters of these two quarks violate the order of prime number sequence. This approach is ques- tionable. 2) The problem is originated from only one 17 in the factors ofM F. Multiplying 17 to theM F sequence yields a new sequenceM F' : 7159474131292319171311753217'232692046 MM FF . (24.31) The problem goes away. Multiplying M-group with another prime number sounds like a wild idea. But there is an additional merit: 5553 10374.11008.81717' MMFF. (24.32) Back to Table 24.3, unlike the other two sporadic groups with B F and Suz F as 1G and 3 G grand numbers, respectively,53 1008.8 M F is more than one order of magnitude away from 5G grand number, The 55 10374.1' M Fis a 5 G grand number, which puts it in line with the B-group and Suz-group in terms of grand number ranks. The number 17 also appears two times for the n-parameter of r b and g b as shown in Table 24.2. MM FF 17' resolves the similar prob- lem over there as well. So the multiplication of 17 toM F for the M-group may have some hiding reason in it. After all, it seems not a waste effort for taking the strict criterion and deliberately looking for problems. There is something special for the M-group. It defined the M-sphere, which provided many physics insights. Its largest factor 71 is a special prime number with many physics significances. The number 71 defined the M-sphere radius. The prime numbers table alone is not sufficient to make the decision. The M-sphere with radius 71 provided the span angle of 57062302.0 M . This angle is checked with the average tilt angle 53410359.0 to verify the AT-equation and PS-equation. Moreover, as shown by (15.11), the relative deviation of 06529795.71 GUT N from the prime number 71 is only 4 10845.8 , which leads to a impor- tant clue for a formula to define the fine structure constant at GUT scale: 69002169.127 2 71 )( 2 1 GUT M. (24.4) The as a constant in (24.4) is a special case for the boson 3 U with extremely heavy mass GUT M. For other particles, the general form of )( 1M is defined dif- ferently. Definition 24.5: The )( 1M of a fermion or a fer- mion state with mass is defined as: 2 1 2 71 )( M, (24.33a) . 2 )( 1dll L . (24.33b) In (24.33), 2 L is the fermion’s loop-2 length, is the average value of )(l around loop-2, which is re- lated to particle’s mass. Explanation: Definition 24.5 is a new way to define the fine structure constant based on a specific prime number 71 and geometry. It serves as an example to trace the mathematic origin of a physics constant, which fits SQS philosophy. Formula (24.4) for )( 1GUT M is a special case of the general definition (24.33). 218 /1007948.1 cGeVMGUT is the mass of 3 U for grand unification. For the scalar boson 3 U made of two constituent fermion states with such extremely heavy mass, the value of . 2 )( 1dll L is extremely close to . The reason is that, 3 U con- stituent’s spindle type torus model elliptic cross section on x-z plane with 1/ 22 ab is elongated so much to make . 2 )( 1dll L with negligible deviation. 69002169.127)2/71()( 21 GUT Mserves as an example for the validity of Definition 24.5 at the heaviest mass of mass spectrum.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1331 Take electron as another example. As shown in Sec- tion 8, the electron torus model loop-2 circular cross sec- tion on x-z plane is divided into two halves. The outer half has positive curvature with )(l; and the inner half has negative curvature with )(l. According to (24.31b), is calculated using the following formulas. For outer half: m mi m ib ody yb y b a m ib m 1 0 22 2 2 2 2 22 2 1 12 1 , (24.34a) For inner half: m mi id m i m ib a m 2 0 2 2 2 22cos1121 )12(2 1 , (24.34b) Overall average: 2 io . (24.34c) In (24.34), each of the cross section two halves is di- vided into12 mslices along y-axis and the values of )(y are calculated step by step. Then take a summa- tion to get the average value of o and i . (24.34c) is used for the overall average of . In (24.34b) for inner half, the term 2 2 2112 m i m ib a is the variation amplitude in a circle on the saddle-shape surface with radius of mibr / 2 , which is originated from (8.12a). The results of 16-digit numerical calculation based on (24.33) and (24.34) for the electron’s original version with 5.0 22 ba are listed in the first row of Table 24.5. As shown on Table 24.5 first row, the calculated value of )( 1e M based on the original 5.0 2a and 5.0 2b is agreed with the 2010-PDG data 035999084.137 1 with a relative deviation 5 10487.8 . The agreement is an important verification in many senses. 1) Definition 24.5 is verified not only for)( 1GUT M but also for )( 1e M . The mass GUT M of 3 U and the mass e Mof electron are at two ends of the mass spec- trum. It is hopeful that Definition 24.5 is also valid for particles with mass in between. 2) )( 1M as a physics running constant is origi- nated from the mathematic running constant . It serves as an example to support SQS theory philosophy. Ulti- mately, a valid unified theory should have no more than three basic physics constants and no other physics inputs. To convert )( 1M from a physics running constant to a mathematic one is an important step toward the right direction. 3) It confirms that, the prime number 71 originated from the M-group has many impacts on different issues. (24.33) is just one of them, but it is an important one. Because (24.33) is a very simple formula, it only has a prime number 71 and a geometrically originated math- ematic running constant . 4) It confirms that, the electron torus model is correct in terms of its shape, sizes and the characteristic points. Sine electron serves as the base for other elementary par- ticles, this confirmation has its significance. Table 24.5. The calculated )( 1M for electron, z and 3 U bosons with 7 10m*. *The results are based on 16-digit calculation, only 8 digits after decimal point are listed. **Relative deviation for )( 1e M is based on 2010-PDG data: 035999084.137 1 ; Relative deviation for )( 1Z M is based on 2010-PDG data: 916.137)( 1 Z M .***The electron orig. data are based on 5.0 2a, 5.0 2b; the electron f-modification data are based on 4443039836342346.0 a f, 39510162329200.1 b f. ****The data for )( 1Z M are based on9623340611307.1 2 a,504957482994050.10 2b. To compare theoretical value of04762893.137)( 1 e M with 2010-PDG data )51(035999084.137)( 1 e M , the relative deviation of 5 10487.8 is out of its error range. In the formulas of (24.34), except the summation index truncation determined by convergence, there is no adjustable parameter. The index truncated at 7 10m is sufficient for the converge with uncertainty less than 7 10. In fact, (24.34a) and (24.34b) are checked by tak- ing integrals to replace the summations, which are agreed to each other with 7 10~. Back to the electron model and parameters, there is no adjustable parameter either (for electron, before reduction number parameters 2 m, 1 n, 1 p are uniquely determined without alternative). Without adjustable parameter is a good thing for a theory. But it raises a question: Where does the 5 10487.8 relative deviation come from? One possi- ble clue is that, formulas (24.34a) and (24.34b) are based on the torus model; the real model for electron is trefoil type with three torus as branches. As shown in Fig. 12.2, a part of torus outer half is in the combined region, which may have some deformation. (24.34a) does not take it into account. It may cause minor error. It must point out that, formula (24.34b) is valid only  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1332 for torus model with circular x-z cross section. The inner half formula for elliptic cross section is complicated. The two equations (8.13a), (8.13b) with 22ab ,11 ab have two unknowns 1 a, 1 b, which are solved numeri- cally by trial and error method. A tailor made program for calculating i is not available in the meantime. When adequate numerical method is available, it can be used to calculate )( 1M for other particles as well. Fortunately, particles with mass2 /9732.4cGeVMM Max have spindle type torus model, its loop-2 cross section inner half does not have negative curvature. The problem with (24.34b) is irrelevant. For these particles, (24.34) is modified as: For outer half: m mi m ib ody yb y b a m ib m 1 0 22 2 2 2 2 22 2 1 12 1 , (24.35a) For inner half: oi , (24.35b) Overall average: 0 2 io . (24.35c) The modified formulas of (24.35) is used to calculate )( 1Z M for Z boson with mass 2 /18775548.91 cGeVM Z made of two fermion states 1 Y and 2 Y. The results are listed in Table 25.4 third row. The calculated value of 14067547.128)( 1 Z M is in between 916.127)( 1 Z M cited from 2010 PDG (p.126) and 957.128)( 1 Z M of reference [17] from Jegeriehner. It indicates that, the theoretical value is reasonable, which serves as the third checkpoint between )( 1e M and )( 1GUT M . The re- sults also serve as an indirect check for Z boson related data listed in Table 14.1 and Table 14.2. Since electron torus model cross section after f-modification is only slightly deviates from its original circular shape, formula (24.34b) serves as an approxima- tion. It is used along with (24.34a) and (24.34c) to calcu- late the data for electron f-modified version. The results are listed in Table 25.2 second row. The relative devia- tion from 2010-PDG data is 3 10498.3 with an opposite sign compared to the original version relative deviation of 5 10487.8 . It indicates that, the f-modification is in the right direction with overshoot. Since the calculation is based on approximate formulas, it is difficult to find the reason for the overshoot and to analyze the errors. But a rough estimate is possible. Be- cause of the overshot, the error of AT-equation and PS-equation used for the f-modification should be less than 33 10498.310498.3 . It is less than the esti- mated errors 2 104.6 up and 2 1038.2 down given previously. For ad hoc equations, to have mul- ti-checkpoints on different bases is important. In fact, these are very important checkpoints for SQS theory in terms of symmetry broken and the origin of particles mass both based on AT-equation and PS-equation. The estimated errors 2 104.6 up and 2 1038.2 down are from the M-circle, which is defined based on a spe- cific prime numbers 71. In the derivation processes, there is no adjustable variable. The estimate error of less than 3 10498.3 , is based on (24.33) and (24.34) according to electron parameters. As mentioned previously, there is no adjustment either. The results show that, despite their ad hoc nature, AT-equation and PS-equation yield reason- able results within adequate error range. It proves that the approach and framework are correct. In summary, the three sporadic groups, M, B, Suz, pro- vide important supports for SQS theory. The three groups’ size factors sequencesM F, B F, Suz F give strong support to Prime Number Postulation. The correlations between M F, B F, Suz F and the m-parameters of particles of three generations not only enhance their legitimacy but also reveal something behind scene such as missing prime number factors corresponding to bosons and boson states, the grand numbers with different ranks, the hidden meaning of three prime numbers 71, 47, 23 and the defi- nition for the M-sphere, B-sphere, S-sphere etc. These types of information were discovered by the author after the third draft of this paper completed and this section was added after that. There are some issues worthwhile to think about. Since the M-group is the largest finite Lie group, with no group in that category has larger size and all 26 sporadic groups’ size factorized sequences have factors less than 71, the question is: What is the group or groups corre- sponding to the pre-big-bang period? It is not just a ma- thematic issue; its answer might provide some insights for cosmology and particle physics like the three spo- radic groups did. There is a clue in Table 24.3 to start with: 22 310864.5 F of the third periods is a 2 G grand number, while 44 10686.1 pre Fof the pre-big- bang period is a 4 G grand number. Further discus- sions along this line will be given in Section 26. Section 25. SQS Theory Basic Equations General relativity theory is not compatible with quantum theory. General relativity theory is deterministic without uncertainty involved, whereas quantum theory is sto- chastic with uncertainty. This is the main reason for their incompatibleness. From SQS theory standpoint, intro- ducing uncertainty to original Einstein equations is the  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1333 way to make general relative theory compatible with quantum theory. The outcome turns out as the basic equ- ations of SQS theory serving as a new version of the uni- fied field theory. To reach the goal takes steps. Einstein equations in different terms are shown as fol- lows. The original with stress-energy term: ababab GTRgR 8 2 1 , (25.1a) The original without stress-energy term for vacuum: 0 2 1RgR abab, (25.1b) With add-on cosmological term and stress-energy term: ababababGTgRgR 8 2 1 . (25.1c) In which, G, ab g, ab R, , , ab T are Newtonian gravitational constant, gauge tensor, Ricci tensor, Ricci scalar, cosmological constant and stress-energy tensor, respectively. The parameters of Einstein equations (25.1) are: )()(gRggRR ab ab , (25.2a) ),()()()( 2 1 )()()()()()()()( 2222 gggg xx g xx g xx g xx g g gggggggRgRR c db d ac c dc d ab abcd dbac acbd dc ab cd c db d ac c dc d ab c acb c abc c acbabab (25.2b) , 2 )()( c db b cd d bc ad dbc ada bc a bc x g x g x g g ggg 3,2,1,0,,, dcba. (25.2c) In which, the “g” in parenthesis indicates ab g serving as variables. Postulation 25.1A: For a Gaussian sphere centered at a vertex point 0 P, gauge tensors ab g and ab g at point are redefined as: );( 0 PPpgG abab , (25.3a) );( 0 PPp g Gab ab , (25.3b) c a bc ab bc ab ggGG . (25.3c) The probability );(0 PPp introduced in (25.3) is Gaussian type: );( 2 );( 0 0 2 2 0 2 );( PPL PPL eePPp . (25.4) );( 0 PPL is geodesic length connecting point and point 0 P. Point is defined as: )(),(),();(03020100 xxxxP , (25.5a) 010110 xNxvtv , (25.5b) 22 1 1 )/(1 1 cv N. (25.5c) Explanation: Probability );( 0 PPp assigned to gauge tensors represents uncertainty. The probability );( 0 PPp in denominator of (25.3b) is to satisfy rule (25.3c). So (25.3b) is not a separate assumption. As shown in defini- tion (25.5), all four space-time variables )(),(),(),(03020100 xxxx are functions of intrinsic time v/ 0 , in which, v is speed. and are standard parameters of special relativity. is converting factor. According to Postulation 25.1A, the parameters of (25.2) are redefined as: )()(GRGGRab ab , (25.6a) ),()()()( 2 1 )()()()()()()()( 2222 GGGG xx G xx G xx G xx G G GGGGGGGRGR c db d ac c dc d ab ab cd db ac ac bd dc ab cd c db d ac c dc d ab c acb c abc c acbab (25.6b) , 2 )()( c db b cd d bc ad dbc ada bc x G x G x G G GGG3,2,1,0,,, dcba . (25.6c) In which, the “G” in parenthesis indicates gauge ten- sors redefined according to (25.3). In the vacuum, there is no additional energy besides vacuum energy. Based on original Einstein equations (25.1b) for vacuum without the stress-energy tensor: 0 ab T, Einstein equations are redefined according to Postulation 25.1A as: 0)( 2 1 )( GRGGR abab . (25.7a) Auxiliary equation is to determine geodesic length );(0 PPLL for );( 0 PPp . 0 2 2 ds dx ds dx ds xd cb a bc a, to i P. (25.7b) Substituting parameters of (25.6) into equations (25.7a), the derivation process is given in Part-A of Ap- pendix 6. According to (A6.9), the redefined Einstein equations (25.7a) are presented in two equivalent forms: 0 2 12 abababERgR , (25.8a) abababab GTgRgR 8 2 1 , (25.8b) in which the emerging part is: ababababab GTgRgRE 8 2 1 22 . (25.8c) The auxiliary equations to determine geodesic length are the same as (25.7b). As shown in Part-A of Appendix 6, the kinematic part RgR abab 2 1 of (25.8a) is the same and has the same contents as orig-  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1334 inal Einstein equation (25.1b). The emerging part RgRE ababab 2 1 22 is generated by probability, in which the emerging terms ab R 2 and R 2 are originated from corresponding ki- nematic terms ab R and , respectively. According to (A6.6) in Part-A of Appendix 6, the contents of emerging terms are: cd cd RgR 22 , (25.9a) ,)()12( )()12( )()12( )()12(2 2 2 2 2 2 2 2 2 222 c db d ac c dc d abab ab cd ba cd ab cd ab cd db db ac bd ac db ac db ac ac ac bd ca bd ac bd ac bd dc dc ab cd ab dc ab dc abab vv xx L Lg x L x g x L x g L x L x L gL vv xx L Lg x L x g x L x g L x L x L gL vv xx L Lg x L x g x L x g L x L x L gL vv xx L Lg x L x g x L x g L x L x L gLR (25.9b) b b cdd d bcc c db ada bc v x L gv x L gv x L gLg 3,2,1,0,,, dcba . (25.9c) As shown in Part-A of Appendix 6, probabilities in the emerging part cancel out, and probability is not included in the kinematic part. The redefined Einstein equations (25.8) for a single Gaussian sphere are deterministic. This is a distinguish feature with physics impact, which will be explained later. The emerging part of equations (25.8) is presented in 44 matrix form as: RgRE ababab 2 1 22 , 33323130 23222120 13121110 03020100 , (25.10) )/(),/(,),/(,,),( 22 xxLxLLxgggvv abab ; (25.11a) 33323130 23222120 13121110 03020100 , )/(),/(,),/(,,),( 22 xxLxLLxgggvv abab ; (25.11b) 33323130 23222120 13121110 03020100 , )/(),/(,),/(,,),( 22 xxLxLLxgggvv abab ; 3,2,1,0,,,,,,, ba. (25.11c) In which, the matrix with superscript “” represents transpose matrix. The speed products )( 2bavv in , , are presented in matrix form: 3323133 3222122 3121111 321 2 1 vvvvvvv vvvvvvv vvvvvvv vvv vv . (A6.8) The stress-energy tensor ab Tin (25.8b) in matrix form is related to matrix as: 16168 12 2 2 3 P Planck P P P ab tt L M G T. (25.12) In which, P L, P t, P M and 3 /PPPlanck LM are Planck length, Planck time, Planck mass and Planck den- sity, respectively. )/(2 23PPP tMLG of (21.2) is used in (25.12). To determine the contents of ab GT 8 and ab g in equations (25.8b), let’s start with a comparison serving as reference. The perfect fluid is characterized by density and pressure p. Set perfect fluid pressure equal to zero: 0 p, it becomes a collection of “dusts” with stress-energy tensor: 3323133 3222122 3121111 321 2 1 vvvvvvv vvvvvvv vvvvvvv vvv Tab ,.3,2,1,0, ba (25.13) The dusts’ vector velocity v is: 321 ,,,1 vvvv . (25.14) The elements )3,2,1,(, 2bavvba of ab Tare prod- ucts of two components of the vector velocity 321,,,1 vvvv . Comparing matrix of (25.11c) with ab T of (25.13), its elements ab also have corre- sponding speed products )3,2,1,(, 2bavv ba as shown in (A6.8), which are generated by derivation process with respect to space-time variables )(),(),(),(03020100 xxxx as functions of intrinsic time v/ 0 . Reference [20] provides a general formula of ab T for perfect fluid with pressure : )()( abbabaabbaab gvvpvvpgvvpT . (25.15) The 2 factor in (25.13) is absorbed by ba vv in (25.15). On (25.15) right side, the first term ba vv representing density contribution is already con- sidered. The second term )(abba gvvp represents pressure contribution. In the emerging part ab E 2 , the only covariant scalar is R . It seems reasonable to as- sume Rp 2 . But the product bavv with absorbed 2 factor in the term bavpv actually is bavv 2 . It makes the term )()(22 baba vvRvpv contains quar- tic terms 4 , which are not included in the emerging  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1335 part ab E 2 . Therefore, the term ba vpv shouldn’t be included in ab T. The pressure contribution is repre- sented only by one term abab gRpg )( 2 . Taking the reference into consideration, the contents of cosmological term and stress-energy terms of equa- tions (25.8) are determined as. Cosmological term: Rgg abab 2 1 2 , (25.16a) Stress-energy term: abababRRgGT 2 8 . (25.16b) Check for consistency: abababababGTgRgRE 8 2 1 22 . (25.16c) Step-1: Based on Postulation 25.1A, the redefined Einstein equa- tions for a single Gaussian sphere are presented as: abababab GTgRgR 8 2 1 . (25.17a) Auxiliary equation is to determine geodesic lengths );( 0 PPLL for );( 0 PPp . 0 2 2 ds dx ds dx ds xdcb a bc a, to 0 P. (25.17b) The cosmological term ab g and stress-energy term ab GT 8 in (25.17a) are determined by (25.16). There is no probability involved in all terms of rede- fined Einstein equations (25.17), which are deterministic equations without uncertainty. It started with introducing uncertainty in redefined Einstein equations (25.7) and ends up with redefined Einstein equations (25.17) as de- terministic equations without uncertainty. It is a surprise. But this is only half of the whole story; the other half will be told later. So far, it only dealt with a single Gaussian sphere cen- tered at one vertex. Actually space contains many Gaus- sian spheres arranged in face-centered lattice structure. Taking this factor into consideration, Postulation 25.1A must be generalized. Postulation 25.1B: For a collection of Gaussian spheres each centered at a vertex point i P in space with face-centered structure, gauge tensors ab g, ab g at point are redefined as: )(PpgGabab , (25.18a) )(Pp g Gab ab . (25.18b) c a bc ab bc ab ggGG . (25.18c) The function )(Pp is defined as: i PPL i PPL iii ii ii eePPpPp);( 2 );( 2 2 2 4 1 4 1 );()( , (25.19a) );( 2 4 1 );(iiPPL iiePPp , i PPL PPL ii ii ii e e Pp PPp );( );( 2 2 )( );( . (25.19b) Definition of the point is the same as (25.5a): )(),(),();( 03020100 xxxxP . (25.5a) Explanation: The function )(Pp is assigned at point with geodesic lengths );( ii PPL connected to vertex points i P. Summation index i covers all vertexes in- volved, which will be explained later. The face-centered space includes two types of vertexes, cubic type and oc- tahedral type. As shown by (22.15), the lattice structure is represented by four Cartesian coordinate systems with two 2/ P L shifts along two orthogonal directions. The factor 4/1 is for unitarity according to (22.15). The derivation process is given in Appendix 6 Part-B. Step-2: Based on Postulation 25.1B, according to (A6.15), the redefined Einstein equations for a set of Gaussian sph- eres are presented in equivalent form as: abababab GTgRgR 8 2 1 . (25.20a) Auxiliary equations are to determine geodesic lengths );( iiiPPLL for );( ii PPp . ,0 2 2 ds dx ds dx ds xd cb a bc a to i P. (25.20b) Cosmological term: Rgg abab 2 1 2 , (25.21a) Stress-energy term: abababRRgGT 2 8 , (25.21b) Emerging term: ababababab GTgRgRE 8 2 1 22 . (25.21c) Equations (25.20) serve as the foundation for SQS theory basic equations. The kinematic part RgRabab 2 1 of Equations (25.20a) is the same and has the same contents as original Einstein Equation (25.1b). As shown in Part-B of Appendix 6, probabilities in the emerging part RgREababab 2 1 22 do not cancel out. Equations (25.20a) are hybrid stochas- tic differential equations. The kinematic part RgR abab 2 1 without probability attached is deterministic, while the  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1336 dynamic part abababGTgE 8 2 with probabilities attached is stochastic. The mixed de- terministic and stochastic nature has important physics implications, which will be explained later. As shown in Part-B of Appendix 6, the merging part RgRE ababab 2 1 22 is generated by probability, in which emerging terms ab R 2 and R 2 are originated from terms ab R and , respectively. According to (A6.12), the contents of emerging terms are: cd cd RgR 22 , (25.22a) , )(2 )(2 )(2( )(2(2 2 2 2 2 2 2 2 2 222 c db d ac c dc d ab ab i i ab i icd i b i ii a cdi a i ii b cd i i a i b i cd i a i b i iicd db i i db i iac i b i ii d aci d i ii b ac i i d i b i ac i d i b i iiac ac i i ac i ibd i c i ii a bdi a i ii c bd i i a i c i bd i a i c i iibd dc i i dc i iab i c i ii d abi d i ii c ab i i d i c i ab i d i c i iiabab vv p p xx L Lg p p x L L x g p p x L L x g p p x L x L g p p x L x L Lg vv p p xx L Lg p p x L L x g p p x L L x g p p x L x L g p p x L x L Lg vv p p xx L Lg p p x L L x g p p x L L x g p p x L x L g p p x L x L Lg vv p p xx L Lg p p x L L x g p p x L L x g p p x L x L g p p x L x L LgR (25.22b) p p v x L Lg p p v x L Lg p p v x L Lggg i b ib i icd i id d i ibc i c ic i idb ad dbc ada bc , .3,2,1,0,,, dcba (25.22c) In (25.22), the ratio 2 2// j iL j L ieepp is the prob- ability associated with geodesic i L serving as the weighting probability for the parameters with subscript i: 2 2//)( j iL j L iw eeppip , (25.23a) 1/)( ppipii iw. (25.23b) The meaning of weighting probability )(ipw will be discussed later. For formulas (25.10), (25.11a), (25.11b), (25.11c), (A6.8) based on Postulation 25.1A, the equivalent for- mulas based on Postulation 25.1B are: RgRE ababab 2 1 22 , (25.24a) T ii ii ii ii ii ii ii ii ii ii ii ii ii iii ii ,33,32,31,30 ,23,22,21,20 ,13,12,11,10 ,03,02 1,01,00 , )/(),/(),/(,),/(,,),( 22 ,, ppxxLxLLxgggvv iiiiiabiab ; (25.24b) ii ii ii ii ii ii ii ii ii ii ii ii ii iii ii ,33,32,31,30 ,23,22,21,20 ,13,12,11,10 ,03,02 1,01,00 , )/(),/(),/(,),/(,,),( 22 ,,ppxxLxLLxgggvv iiiiiabiab ; (25.24c) ii ii ii ii ii ii ii ii ii ii ii ii ii iii ii ,33,32,31,30 ,23,22,21,20 ,13,12,11,10 ,03,02 1,01,00 , )/(),/(),/(,),/(,,),( 22 ,,ppxxLxLLxgggvv iiiiiabiab .3,2,1,0,,,,,,, ba (25.24d) 3323133 3222122 3121111 321 2 1 vvvvvvv vvvvvvv vvvvvvv vvv vv . (A6.14) Step-3A: To check the validity of redefined Einstein equations (25.20) is to convert into the form comparable to Ein- stein’s original equations. The way to do so is to take the average of variables in Equations (25.20). The average process irons out irrelevant microscopic details and re- tains their macroscopic contributions for comparison. The redefined Einstein Equations (28.20a) after aver- age are presented in the equivalent form as: ababababTGgRgR 8 2 1 , (25.25a) 0 2 1 ababab ERgR. (25.25b) The average process is not taken on ab R, , , ab T, ab E , instead, it is taken on their variables shown as follows: feab e ab ab ab abab xx g x g ggRR2 ,,, , (25.26a) fe ab e ab ab ab xx g x g ggRR 2 ,,, , (25.26b) ai fe i e i i e ab ab ab vpp xx L x L L x g gg ,,,,,,,, 2, (25.26c) ai fe i e i i e ab ab ab abab vpp xx L x L L x g ggTT ,,,,,,,, 2, (25.26d) ai fe i e i e ab iab ab abab vpp xx L x L x g LggEE ,,,,,,,, 2 . (25.26e) The average process of variables in (25.26) at discrete points );,,( 0llkji ctxzyxP is given as follows. a lkjiab Ax Ax Ay Ay Az Az Ax Ax abab gxzyxgxzyxgdxdzdydx A gi i j j k k l l );,,();,,( 10 2/ 2/ 2/ 2/ 2/ 2/ 2/ 2/ 00 4 0 0, (25.27a) ab lkji ab Ax Ax Ay Ay Az Az Ax Ax abab gxzyxgxzyxgdxdzdydx A gi i j j k k l l );,,();,,( 10 2/ 2/ 2/ 2/ 2/ 2/ 2/ 2/ 00 4 0 0, (25.27b)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1337 eablkjieab Ax Ax Ay Ay Az Az Ax Ax e ab e ab gxzyxg x xzyxg dxdzdydx Ax gi i j j k k l l / 0 / 2/ 2/ 2/ 2/ 2/ 2/ 2/ 2/ 0 0 4);,,( );,,( 1 0 0 , (25.27c) efablkjiefab Ax Ax Ay Ay Az Az Ax Ax fe ab fe ab gxzyxg xx xzyxg dxdzdydx Axx gi i j j k k l l / 0 / 2/ 2/ 2/ 2/ 2/ 2/ 2/ 2/ 02 0 4 2 );,,( );,,( 1 0 0 , (25.27d) ilkjii Ax Ax Ay Ay Az Az Ax Ax ii LxzyxLxzyxLdxdzdydx A Li i j j k k l l );,,();,,( 1 0 2/ 2/ 2/ 2/ 2/ 2/ 2/ 2/ 00 4 0 0, (25.27e) eilkjiei Ax Ax Ay Ay Az Az Ax Ax e i e iLxzyxL x xzyxL dxdzdydx Ax Li i j j k k l l / 0 / 2/ 2/ 2/ 2/ 2/ 2/ 2/ 2/ 0 0 4);,,( );,,( 1 0 0 , (25.27f) efilkjiefi Ax Ax Ay Ay Az Az Ax Ax fe i fe iLxzyxL xx xzyxL dxdzdydx Axx Li i j j k k l l / 0 / 2/ 2/ 2/ 2/ 2/ 2/ 2/ 2/ 02 0 4 2 );,,( );,,( 1 0 0 , (25.27g) pxzyxpxzyxpdxdzdydx A Pp lkji Ax Ax Ay Ay Az Az Ax Ax i i j j k k l l );,,();,,( 1 )( 0 2/ 2/ 2/ 2/ 2/ 2/ 2/ 2/ 00 4 0 0, (25.27h) ilkjii Ax Ax Ay Ay Az Az Ax Ax iipxzyxpxzyxpdxdzdydx A Ppi i j j k k l l );,,();,,( 1 )( 0 2/ 2/ 2/ 2/ 2/ 2/ 2/ 2/ 00 4 0 0, (25.27i) alkjia Ax Ax Ay Ay Az Az Ax Ax aa vxzyxvxzyxvdxdzdydx A vi i j j k k l l );,,();,,( 10 2/ 2/ 2/ 2/ 2/ 2/ 2/ 2/ 00 4 0 0. (25.27j) In (25.27), the integral range covers 5.32/ A, A=7. The reason for selecting A=7 is based on symme- tries )(rO, )( rC with 3r including all three genera- tion elementary particles and interactions as shown in Section 22. The additional 0.5 in 5.32/ A is to cover both octahedral and cubic vertexes involved. Av- erage values are assigned to each cubic vertex ),,( kji zyx with temporal variable ll vtx 0 in discrete space-time. The procedure is valid, because according Theorem 22.1, the random walk zigzagging path only stops at cubic vertexes. Space with face-centered lattice structure is symmet- rical with respect to 1 x,2 x, 3 x and vtx 0 axes. In the symmetrical space-time, integral of odd function over symmetrical range equals to zero by can- celation. Notice that, ab g, ab g, i L, p, i pand their second order derivatives with respect to the same vari- able are even functions; their first order derivatives and second order derivatives with respect to different vari- ables are odd functions. For integral over symmetrical range in symmetrical space-time, after average process only even functions retain and all odd functions equal to zero: 0);,,(0 // lkjieabeabxzyxgg , (25.28a) 0);,,( 0 // lkjiefabefab xzyxgg , fe , (25.28b) ,0);,,( 0 // lkjieeixzyxpL (25.28c) 0);,,( 0 // lkjiefefi xzyxpL. fe , (25.28d) 0);,,( 0lkjiaa xzyxvv , 0a. (25.28e) According (25.26), (25.27), (25.28), after average process, equations (25.25a) are presented as: abababab GTgRgR 8 2 1 , (25.29) Cosmological term: Rgg abab 2 1 2 , (25.30a) Stress-energy term: abababRRgGT 2 8 , (25.30b) Emerging part: abababababGTgRgRE 8 2 1 22 . (25.30c) The “bar” on top of parameters in Equations (25.29) is omitted for simplicity. It is important to notice that, the differential derivatives in (25.20a) become differences in (25.29) evaluated at discrete cubic vertexes. As shown in formulas (25.30), the emerging terms ab GT 8, ab g contain 2 factor. It makes speeds )3,2,1(, ava in the emerging terms superluminal, which is not acceptable for macroscopic equations. In addition, space-time variables in emerging part ababab GTgE 8 2 of equations (25.29) are converted to )(),(),(),( 03020100 xxxx and derivatives follow accordingly, but the space-time variables in kinematic part RgRabab 2 1 of Equations (25.29) are not converted. The different treatments create an imbalance of Equations (25.29) in terms of different types of space-time variables, which must be rebalanced. To rebalance Equations (25.29), both sides of Equa- tions (25.29) are divided by 2 factor. As results, the 2 factors in emerging part responsible for superluminal speed products )3,2,1,(, 2bavv ba are canceled out, and the separation between discrete points of difference Equ- ations (25.29) changes accordingly. Definition 25.1: SQS theory macroscopic basic eq- uations for gravity are defined as the difference equa- tions with parameters evaluated at cubic vertexes sepa- rated by Compton scale PC NLL , PC Ntt. abababab GTgRgR 8 2 1. (25.31)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1338 Cosmological term: Rggabab 2 1 , (25.32a) Stress-energy term: ababab RRgGT 8, (25.32b) Emerging part: ababababab GTgRgRE 8 2 1 . (25.32c) Explanation: Basic equations (25.31) are converted from equations (25.29) with two main differences: (1) Superluminal speeds in the emerging part are expelled, because 2 factors are canceled out; (2) The 2 factor in denominator of the kinematic part RgR abab 2 1 elongates the separation for each direction by a factor of . All parameters in equations (25.31) are evaluated at cubic vertexes separated by Compton scale: PC NLL , PCNtt . Notice that, the “double bar” on emerging terms of (25.32) ababababab GTgRgRE 8 2 1 indicating they are the averaged values of the second average process. The second average process is to take the summation over a “Compton cube” with Compton length C L as edge, which contains the first average val- ues of all cubic discrete points in the Compton cube. Then the sum is divided by the number of cubic discrete points in the Compton cube. Corresponding second av- erage is taken for temporal variable as well. The second average process is also applied to the kinematic part. The results of second average process are assigned to the center cubic vertex of the Compton cube. Second average is required by separation’s scale change from Planck scale to Compton scale. After the second average process, equations (25.31) are in the microscopic sense compara- ble with Einstein equations (25.1c). The features of basic equations (25.31) for gravity are as follows. 1) As results of average processes, the details of mi- croscopic effects are ironed out and their macroscopic contributions are assigned to cubic vertexes separated by Compton length. Differential equations (25.20a) be- come difference equations (25.31) with the merit of no singularity. 2) For vacuum without “real matter”, space-time is perfect symmetry. In equations (25.31), all odd terms are canceled out by average shown in (25.28) and only even terms remain. According to (25.28a) and (25.28b), in the kinematic part of equations (25.31), only )3,2,1,0,,(, 2 eba g eeab related terms remain. According to (25.28c), (25.28d) and (25.28e), in the emerging part of equations (25.31), no term in the part of c db d ac c dc d ab remain, and only 00 2 00 00 2 L vv Lii related terms remain. The contents of cosmological term ab g and stress-energy term ab GT 8 in equations (25.31) are significantly reduced. The re- mained terms still have nonzero values contributed by the even terms, which represent vacuum fluctuations. In essence, vacuum is matter with energy, there is no such thing as absol ute void. 3) For the real world with matters around, as shown in Section 22, elementary particles obtain mass by breaking symmetry. As a result, space symmetry is broken. In equations (25.31), the kinematic part RgR abab 2 1 along with the cosmological term ab g and stress-energy terms ab GT 8 have their full-brown contents, which serve the function as original Einstein equations (25.1c). In essence, broken symmetry provides mass for parti- cles, which in return serves as the mechanism for space-time curvature and the origin of gravity. It shows the consistency of the theory. 4) Basic difference equations (25.31) are evaluated as discrete cubic vertex with Compton scale separations. It has important physics implications. For instance, hydro- gen atom has a proton as its nucleon. The Compton length of proton is mcMhL pC 15 10321.1/ . Heavier atoms have even shorter Compton length. It shows that, according to equations (25.31), gravity has sufficiently fine resolution at atomic scale. More importantly, the cube with edge equal to Compton length serves as a shield to isolate the effect of microscopic mass. Other- wise, without the shielding effect, everything will be crushed by tremendous gravitational force produced by Planck mass. It shows the physics impact of separations’ elongation for difference equations (25.31) and the con- sistency of the theory. 5) As shown in (25.21a), the cosmological term Rgg abab 2 1 2 of microscopic Equations (25.20a) con- tains 2 factor, which is eliminated in the cosmological term Rgg abab 2 1 of macroscopic basic Equations (25.31). It provides a way to dealing with the annoying dark en- ergy problem. The one hundred twenty some orders of magnitude tremendous difference between theoretical value and observed data is a typical hierarchy problem. From SQS theory viewpoint, the way to dealing with such hierarchy problem is to apply appropriate convert- ing factor. One is readily available. According (5.5), the converting factor for photon with wavelength is: 2 )/(1 1 cv L N P. (25.33) For orders of magnitude estimation, cosmic Micro-  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1339 wave Background Radiation (MBR) frequency spectrum center wavelength m 3 01008.1 is used to calcu- late the value of converting factor . MBR photons are cosmically originated and their effects are elongated to cosmic scale by space expansion. As shown in Section 26, to consider their contribution should take long path wavelength to replace short wavelength. Based on cos- mic MBR photons with m 3 01008.1 and long path wavelength P LN / ˆ2 000 , the ratio of cosmological terms in microscopic equations (25.20a) and cosmologi- cal term in macroscopic equations (25.31) is: 127 4 0 2 010994.1 ˆ PP LL R . (25.34) The ratio of theoretical mass density versus observed data is: 123 10271.3 obserbed Planck R . (25.35) In which, 3973 /10239.3/mkgLM PPPlanck is the Planck density, 327 /109.9 mkg observed is observed cosmic mass density. Notice that, there is a subtle difference between gravity and electromagnetic force with the fac- tor 2 4/ shown in (4.19). Dark energy is based on gravity, while photon is generated by electromagnetic force. Taking this factor into account, the theoretical value of (25.34) with 036.137/1 becomes: 123 2 2 210685.3 4 ˆ 4 ' P L RR. (25.36) Compare to 123 10271.3 R of (25.35), the theo- retical result of (25.36) has a relative deviation of 12.6%. Other estimations on different basis will be given in Sec- tion 26 with similar results. 123 10271.3 R is the largest grand number in physics and cosmology and the most annoying hierarchy problem. It can be reduced to 12.6% relative discrepancy by a theory not tailored for such purpose. There must be something in it. 6) It seems a surprise that started with Einstein equa- tions (25.1b) for vacuum without stress-energy term and ended with basic equations (25.31) having stress-energy term automatically showed up from vacuum. After thought it over, it is really no surprise. By introducing probability, the stress-energy term generated by stochas- tic movement of vacuons in vacuum should be expected. Einstein reportedly said: The left side of my equation is marble while the right side is straw. Now, both sides of basic equations (25.31) are marbles. Einstein in heaven should be happy to hear the news. 7) Started with Einstein equations (25.1b) for vacuum without cosmological term and ended with basic equa- tions (25.31) having cosmological term automatically showed up from vacuum. The reason is the same as that for the stress-energy term. After the discovery of cosmic expansion, regarding his add-on cosmological constant , Einstein said: “It was the biggest brander in my life.” The authors of reference [20] correctly commented: “A great mistake was indeed! –– not least because, had Einstein stuck by his original equation, he could have claimed the expansion of the universe as the most trium- phant prediction of his theory of gravity.” Now, Ein- stein’s most triumphant prediction looks even more pro- found. Cosmological term showed up in basic equations (25.31) but not by add-on. It is generated naturally from stochastic movement of vacuons in vacuum. More im- portantly, dark energy represented by cosmological term does exist evidenced by accelerating expansion of the universe. 8) Notice that, there is no mass factor in the basic Eq- uations (25.31), which is consistent with the principle of inertial mass equal to gravitational mass. Basic Equations (25.31) are valid for gravity as one of two long range forces. The other one is electromagnetic force. SQS theory macroscopic basic equations also have a version for electromagnetic force. According to (4.19), the ratio of static electrical force and gravitational force is: 2 2 /4N f f R G E GE . (25.37) In equations (25.31), move the cosmological term ab g from left side to right side: ) 8 (8 2 1G g TGRgR ab ababab . (25.38) Multiplying 2 2 4N to both sides of equations (25.38) yields: ab ab abab T G g GNRgRN 8 2 2 1 4 22 2 .(25.39) According to (A4.1), (21.1), (4.15): hc e 0 2 2 , 2 2 P M hc G , M NP . The right side of equations (25.39) becomes: EM ab EM ab ab ab ab ab T M q M q T M e T G g M e T G g GN 2 2 1 1 0 2 0 2 2 0 2 2 22 8 2 8 2 . (25.40) In (25.40), the factor 22/Me is split to two factors 11 /Mq and 22 /Mq for two charged particles with elec- trical charge 1 q mass 1 M and charge 2 q mass 2 M, respectively. The equivalence of stress-energy tensor for electromagnetic (EM) force is defined as:  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1340 abababab ab EM ab E G RgR G T G g T 8 1 2 1 8 1 8 . (25.41) On left side of the difference equations (25.39), the multiplied factor 2 2 4N is absorbed by the kinematic part RgR abab 2 1 . The factor 2 N shrinks the Compton scale separation PC NLL , PC Ntt back to the Planck scale NLL CP/, Ntt CP /. According to (24.4), the factor 7171 1 42 elongates the shrunk separation from Planck scale to GUT scale: PMGUT LRL71 , PMGUTtcRt71/ . (25.42) PMGUT LRL71is M-sphere’s radius serving as the characteristic length for GUT. Definition 25.2: SQS theory macroscopic basic equ- ations for electromagnetic force are defined as the dif- ference equations with parameters evaluated at cubic vertexes separated by GUT scale PGUTLL 71, PGUT tt71: EM abababT M q M q RgR 2 2 1 1 0 2 2 1 . (25.43) Explanation: Left side of (25.43) is the kinematic part representing charged particles movements. Right side is the dynamic part serving as electromagnetic driving force for charged particles movements similar to the function of stress-energy term in equations (25.31) for gravita- tional force. The minus sign “-” on right side indicates the direction of force: 0 21 qq corresponds to attrac- tion force and 0 21 qq corresponds to repulsive force. Like the second average process for equations (25.31), the parameters of equations (25.43) are subject to a sec- ond average over the “GUT cube” with PGUT LL 71 as edge length. The features of basic equations (25.43) for the elec- tromagnetic force are as follows. 1) Spatial and temporal separations of the difference equations (25.43) set at GUT scalePGUT LL71, PGUTGUTtcLt 71/ are originated from the dynamic part converted from gravity to electromagnetic force. As shown in Section 15, PGUT LL 71 is the length scale of GUT for electromagnetic force unified with gravity. For distance longer than PGUT LL71, electromagnetic force separated from gravity becomes an independent force. It shows that, the adjustment of separation is valid and the theory is consistent. 2) The factor 22 N responsible for superluminal speed in the emerging part of equations (25.20a) is ex- pelled to build the basic equations (25.31) for gravita- tional force. As a result, the separations of difference equations were elongated from Planck scale to Compton scale for gravity. Then the factor 22 N is taken back along with the factor 7171 1 42 to build the basic equations (25.43) for electromagnetic force. As a result, the separation of difference equations is shrunk back to Planck scale then elongated to GUT scale. These processes are mathematically consistent and physically make sense. 3) The correlation between two versions of macro- scopic basic equations (25.31) and (25.43) serves as a support of the concept: Gravitational force and electro- magnetic force as two long range forces are two sides of the same coin. The microscopic effects of weak force and strong force as two short range forces are averaged out and their macroscopic contributions are included in cos- mological term ab g and stress-energy term ab GT 8 of equations (25.31) or the EM ab T M q M q 2 2 1 1 0 2 term of equations (25.43). It shows the richness and rig- orousness of the theory. 4) The distinctive feature of equations (25.43) is the mass factor21MM in denominator of the dynamic part at right. Actually the same mass factor also appeared in the dynamic part’s denominator of equations (25.31) for gravity, but it cancels out by the mass factor in nominator according to principle of initial mass equal to gravita- tional mass. Therefore, a fair comparison of the effects for electrical force E f and gravitational force G f should be 21 /MMfE versus 21 /MMfGeven thoughthe factor 21MM canceled out for the latter. Take the electromagnetic force between a pair of elec- tron as an example to show the two long range forces’ profiles varying with distance l. In (25.43), let 2 21 e MMM and 2 21eqq . As shown in Fig. 4.1 and discussed in Section 16, the converting factor e N as a function of distance l has two types of variation pro- files in two regions. Region-I: .const M M N e P e , foreC l ; (25.44a) Region-II: e GUT GUTe e P eN L l LN lM M lN )( )( )( , for eCeCGUT lL 71. (25.44b) In Region-II, the average length scale for the discrete variables of difference equations (25.31) is changing 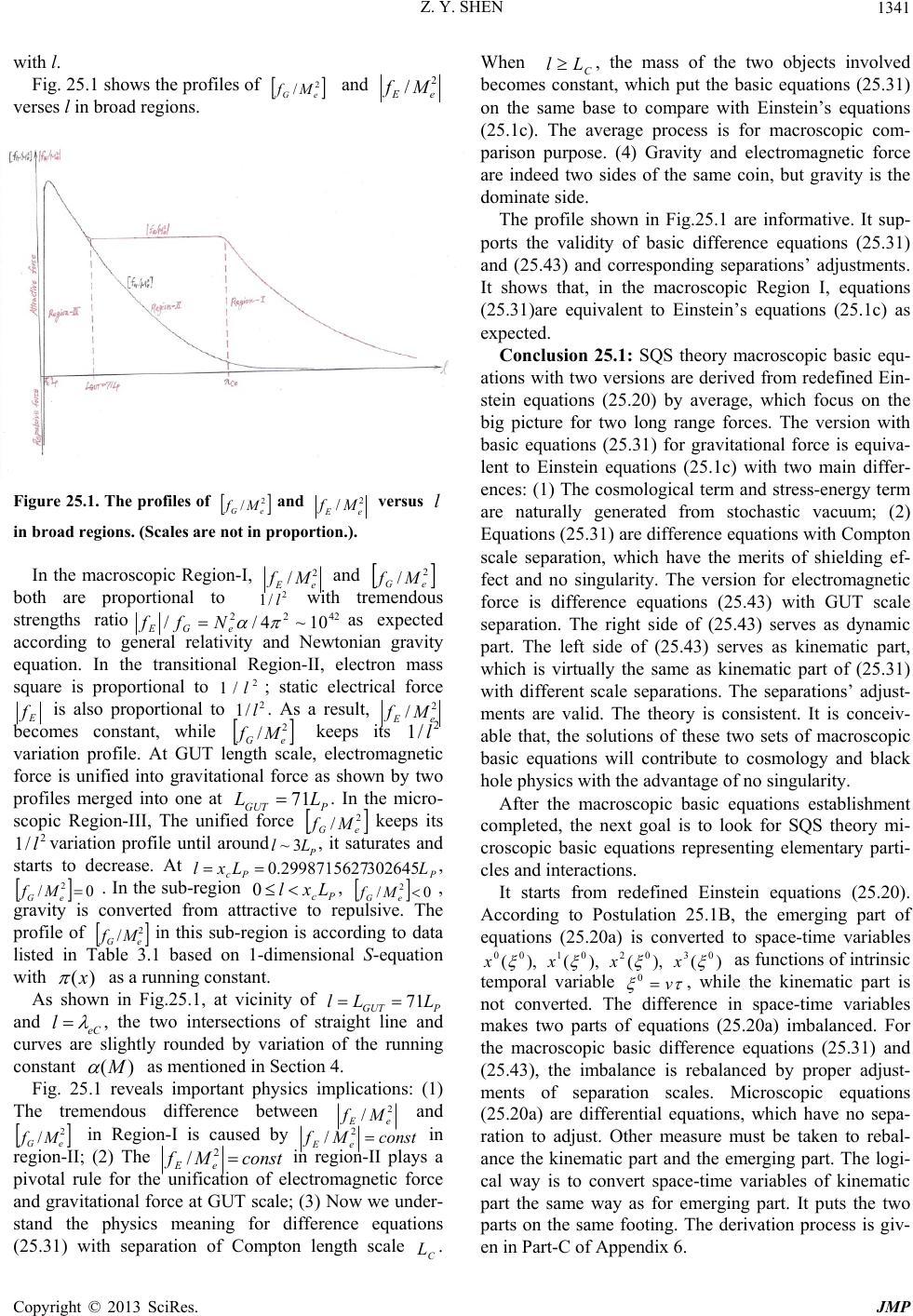 Z. Y. SHEN Copyright © 2013 SciRes. JMP 1341 with l. Fig. 25.1 shows the profiles of 2 /eG Mf and 2 /eE Mf verses l in broad regions. Figure 25.1. The profiles of 2 /eG Mf and 2 /eE Mf versus l in broad regions. (Scales are not in proportion.). In the macroscopic Region-I, 2 /eEMf and 2 /eGMf both are proportional to 2 /1 l with tremendous strengths ratio4222 10~4// eGENff as expected according to general relativity and Newtonian gravity equation. In the transitional Region-II, electron mass square is proportional to 2 /1 l; static electrical force E f is also proportional to 2 /1 l. As a result, 2 /eEMf becomes constant, while 2 /eGMf keeps its 2 /1 l variation profile. At GUT length scale, electromagnetic force is unified into gravitational force as shown by two profiles merged into one at PGUTLL 71. In the micro- scopic Region-III, The unified force 2 /eG Mfkeeps its 2 /1lvariation profile until aroundP Ll3~ , it saturates and starts to decrease. At PPc LLxl3026452998715627.0 , 0/ 2 eG Mf . In the sub-region PcLxl0, 0/ 2 eGMf , gravity is converted from attractive to repulsive. The profile of 2 /eG Mfin this sub-region is according to data listed in Table 3.1 based on 1-dimensional S-equation with )(x as a running constant. As shown in Fig.25.1, at vicinity of PGUT LLl 71 and eC l , the two intersections of straight line and curves are slightly rounded by variation of the running constant )(M as mentioned in Section 4. Fig. 25.1 reveals important physics implications: (1) The tremendous difference between 2 /eEMf and 2 /eG Mf in Region-I is caused by constMf eE 2 / in region-II; (2) The constMf eE 2 / in region-II plays a pivotal rule for the unification of electromagnetic force and gravitational force at GUT scale; (3) Now we under- stand the physics meaning for difference equations (25.31) with separation of Compton length scale C L. When C Ll , the mass of the two objects involved becomes constant, which put the basic equations (25.31) on the same base to compare with Einstein’s equations (25.1c). The average process is for macroscopic com- parison purpose. (4) Gravity and electromagnetic force are indeed two sides of the same coin, but gravity is the dominate side. The profile shown in Fig.25.1 are informative. It sup- ports the validity of basic difference equations (25.31) and (25.43) and corresponding separations’ adjustments. It shows that, in the macroscopic Region I, equations (25.31)are equivalent to Einstein’s equations (25.1c) as expected. Conclusion 25.1: SQS theory macroscopic basic equ- ations with two versions are derived from redefined Ein- stein equations (25.20) by average, which focus on the big picture for two long range forces. The version with basic equations (25.31) for gravitational force is equiva- lent to Einstein equations (25.1c) with two main differ- ences: (1) The cosmological term and stress-energy term are naturally generated from stochastic vacuum; (2) Equations (25.31) are difference equations with Compton scale separation, which have the merits of shielding ef- fect and no singularity. The version for electromagnetic force is difference equations (25.43) with GUT scale separation. The right side of (25.43) serves as dynamic part. The left side of (25.43) serves as kinematic part, which is virtually the same as kinematic part of (25.31) with different scale separations. The separations’ adjust- ments are valid. The theory is consistent. It is conceiv- able that, the solutions of these two sets of macroscopic basic equations will contribute to cosmology and black hole physics with the advantage of no singularity. After the macroscopic basic equations establishment completed, the next goal is to look for SQS theory mi- croscopic basic equations representing elementary parti- cles and interactions. It starts from redefined Einstein equations (25.20). According to Postulation 25.1B, the emerging part of equations (25.20a) is converted to space-time variables )(),(),(),(03020100 xxxx as functions of intrinsic temporal variable v 0, while the kinematic part is not converted. The difference in space-time variables makes two parts of equations (25.20a) imbalanced. For the macroscopic basic difference equations (25.31) and (25.43), the imbalance is rebalanced by proper adjust- ments of separation scales. Microscopic equations (25.20a) are differential equations, which have no sepa- ration to adjust. Other measure must be taken to rebal- ance the kinematic part and the emerging part. The logi- cal way is to convert space-time variables of kinematic part the same way as for emerging part. It puts the two parts on the same footing. The derivation process is giv- en in Part-C of Appendix 6.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1342 Step-3B: According to (A6.18), the redefined Einstein equations (25.20) are presented as: ababab ERgR 2 1, (25.45a) Emerging term: RgREE abababab 2 1 22 . (25.45b) Auxiliary equations are to determine geodesic lengths );( 0 PPLL ii for );( ii PPp : 0 2 2 ds dx ds dx ds xdcb a bc a, to i P. (25.46) According to (A6.17), the kinematic part of (25.45a) has the following contents: ab abRgR , (25.47a) , )()()()( 2 12222 2 c db d ac c dc d ab ab ab cd db db ac ac ac bd dc dc ab cd ab vv xx g vv xx g vv xx g vv xx g gR (25.47b) ,)()()( 2 c c db b b cd d d bc ad a bc v x g v x g v x g g 3,2,1,0,,, dcba . (25.47c) In which, the 2 factors are included and no probabil- ity attached. According to (A6.19), the speed product matrix in ki- nematic part of equations (25.45) is: 3323133 3222122 3121111 321 2 1 vvvvvvv vvvvvvv vvvvvvv vvv vv . (A6.19) In which, the 2 factors are included. The emerging terms of equations (25.45a) are the same of (25.22), in which, the 2 factors are included. The weighting probability 2 2//)( j iL j L iw eeppip serves as the weighting factor for parameters with subscript i as mentioned previously. According to (A6.14), the speed product matrix of the emerging part in equations (25.45) is: 3323133 3222122 3121111 321 2 1 vvvvvvv vvvvvvv vvvvvvv vvv vv . (A6.14) In which, the 2 factor are included. Definition 25.3: SQS theory primary basic equa- tions are defined as: ababab ERgR 2 1, (25.48a) Emerging part: RgREEabababab 2 1 22 . (25.48b) The parameters of kinematic part of (25.48) are given by (25.47) with the 2 factor included. Auxiliary equations are to determine geodesic lengths );( iii PPLL for );(iii PPpp . ,0 2 2 ds dx ds dx ds xdcb a bc a toi P. (25.48c) Explanation: The primary basic equations (25.48a) include ten independent differential equations for ten independent variables )3,2,1,0,(, bagg baab . The contents of kinematic part RRab 2 1 and emerging part ab E are given by (25.47) and (25.22), respectively. Einstein’s general relativity is based on two principles, the covariance principle and the equivalence principle. The essence of equivalence principle is that, acceleration is equivalent to gravitation and both are represented by space-time curvature. SQS theory primary basic equa- tions (25.48) are based on Einstein equations (25.1b) along with two principles of general relativity. According to Theorem 18.1, Lemma 18.1 and Lemma 18.2, vacuons movement is restricted in 1-dimensional discrete trajec- tories. Along a trajectory, variations of vacuons’ move- ment are represented by space-time curvature in terms of gauge tensors, which are consistent with equivalence principle. For vacuons with superluminal speed vv mov- ing in 1-dimensional trajectory, one spatial variable 3 x along trajectory’s longitudinal direction and temporal variable 0 x are selected as the effective variables. The speed product matrix V of (A6.19) for kinematic part are reduced as: 2 2 00 0000 0000 001 vv v vv . (25.49) The speed product matrix v of (A6.14) for emerging dynamic part in primary basic equations (25.48) for 1-dimensional trajectory in the selected coordinate sys- tem are reduced as: 2 2 00 0000 0000 001 vv v vv . (25.50) According to (25.49) and (25.50), the contents of ki- nematic part and dynamic part of primary basic equations (25.48) are significantly reduced. The original ten inde- pendent variables )3,2,1,0,(, bagg baab are reduced to three independent variables, )3,0,(, bagg baab . The reduc- tion significantly simplifies primary basic equations (25.48) and the solutions.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1343 The features of the primary basic equations (25.48) are as follows. 1) The primary basic equations (25.48a) are hybrid stochastic differential equations. The kinematic part RRab 2 1 with no probability attached is deterministic, while the emerging part ab E as dynamic part with probabilities attached is stochastic. The mixed states have important physics implications. 2) As the other half of the story, uncertainty shows up in the emerging part of primary basic equations (25.48) evidenced by the weighting probability )/( ppi in the emerging part (25.22). As shown in equations (25.17) for a single point with one geodesic length );(0 PPL connected to a single Gaussian sphere centered at vertex point 0 P, there is no uncertainty because of probability cancelation. In essence, the uncertainty comes from more than one geodesic lengths );( ii PPL involved repre- senting interaction. 3) Interactions are effective only for Gaussian spheres in the close vicinity. As shown in Section 22, The two sets of symmetries )(rO , )(rC with radius 3r are sufficient to serve as the origin of the groups representing all three generations particles and interac- tions. Question: Why 3r? The answer is hidden in primary basic equations (25.48). The next effective ra- dius longer than 3r is 2/19r . For orders of magnitude estimation, assume rrLi);0( and ignore temporal part’s effect. The derivative of ));(exp();( 2 4 1iiiiiPPLPPpp in iii PPpPp );()( 4 1is: .3,2,1, 3 2 4 1 2 4 1 2 4 1 4 1 4 1 )( 2 22 2 0 2);( ae r e r x re x r r x e x e x p rD r r a r aa r a PPL a ii (25.51a) The ratio of 2/19rD over 2/1rD represents their relative contributions: 12 2/1 2/19 2/1 2/19 1029.2~ 2/1 2/19 )2/1( )2/19( 2 2 2 2 e e re re rD rD r r r r (25.51b) As shown in (25.51b), the relative contribution of 2/19r term is in the order of 12 10, which is neg- ligible in most cases. Now we know the reason for 3r, because the Gaussian spheres centered at vertexes with 3r all have too long );( ii PPL and too low weighting probability ppi/ with negligible effects on interactions. In fact, the result of (25.51b) sets the back- ground noise floor for all elementary particles and inter- actions at 12 1029.2~ . It is comparable to the back- ground noise floor data estimated in Table 20.3 for re- duced 14 . The reciprocal of 12 1029.2 is 11 1037.4 as a 1 G grand number. Is it a coinci- dence? 4) Primary basic equations (25.48) include two parts: the kinematic part RgR abab 2 1 and the dynamic part ab E. The dynamic part serves as the cause of vacuons’ movement. The kinematic part represents state of vacuons’ movement as the result produced by the cause. These two parts are intrinsically interwoven. But they are different in terms of deterministic versus stochastic. The obvious question is: How does the stochastic cause of dynamic part produce the deterministic result for the kinematic part? According to Theorem 18.1, Lemma 18.1 and Lemma 18.2, vacuons’ movement is confined in discrete trajectory and change of movements is by jump- ing trajectories. In essence, vacuons’ movement along a trajectory is deterministic and uncertainty occurs only at jumping trajectories. The deterministic kine- matic part is to represent the state of movement in a tra- jectory without uncertainty involved, while the stochastic dynamic part causes jumping to different trajectories with uncertainty. It answers the question naturally. 5) The hybrid state of primary basic equations (25.48) has a deeper meaning. The quantization of vacuons’ tra- jectories is a necessity required by introduction of uncer- tainty in the first place. Otherwise, if there is no quanti- zation of discrete trajectories, the stochastic dynamic part as cause and the deterministic kinematic part as result would be head-on contradictory with no way out. 6) Take a close look at the geodesics. According to Lagrange principle, particle takes the path with shortest time interval from point A to point B. In general relativity, geodesic is the shortest distance connecting two points in curved space. As shown in previous sections, particle’s trajectory on torus model is determined by geodesics connecting characteristic point and point . All of these should come from the same origin. As shown in Fig. 25.2, in which Fig. 25.2(a) and Fig. 25.2(b) are for a sin- gle vertex V and for two vertexes V and C, respectively. Vertex V represents a particle with torus model, while vertex C is the center vertex representing interactions. Fig. 25.2 shows that the particle’s trajectory T and the roundtrip geodesic lengths i L2 are integrated into an overall closed loop with characteristic points A, B and vertexes V and C serving as junctions. The diagram for trefoil type model is similar to Fig. 25.2 with 3 branches and 6 characteristic points plus 3 V vertexes representing trefoil type model. 7) The factor 2 in speed matrixes (2.49) and (2.50) indicate that, the speed vv is superluminal. It is va- lid, because the vacuons movement in the overall loop is similar to the movement in the long path. In general, the solutions of primary basic equations 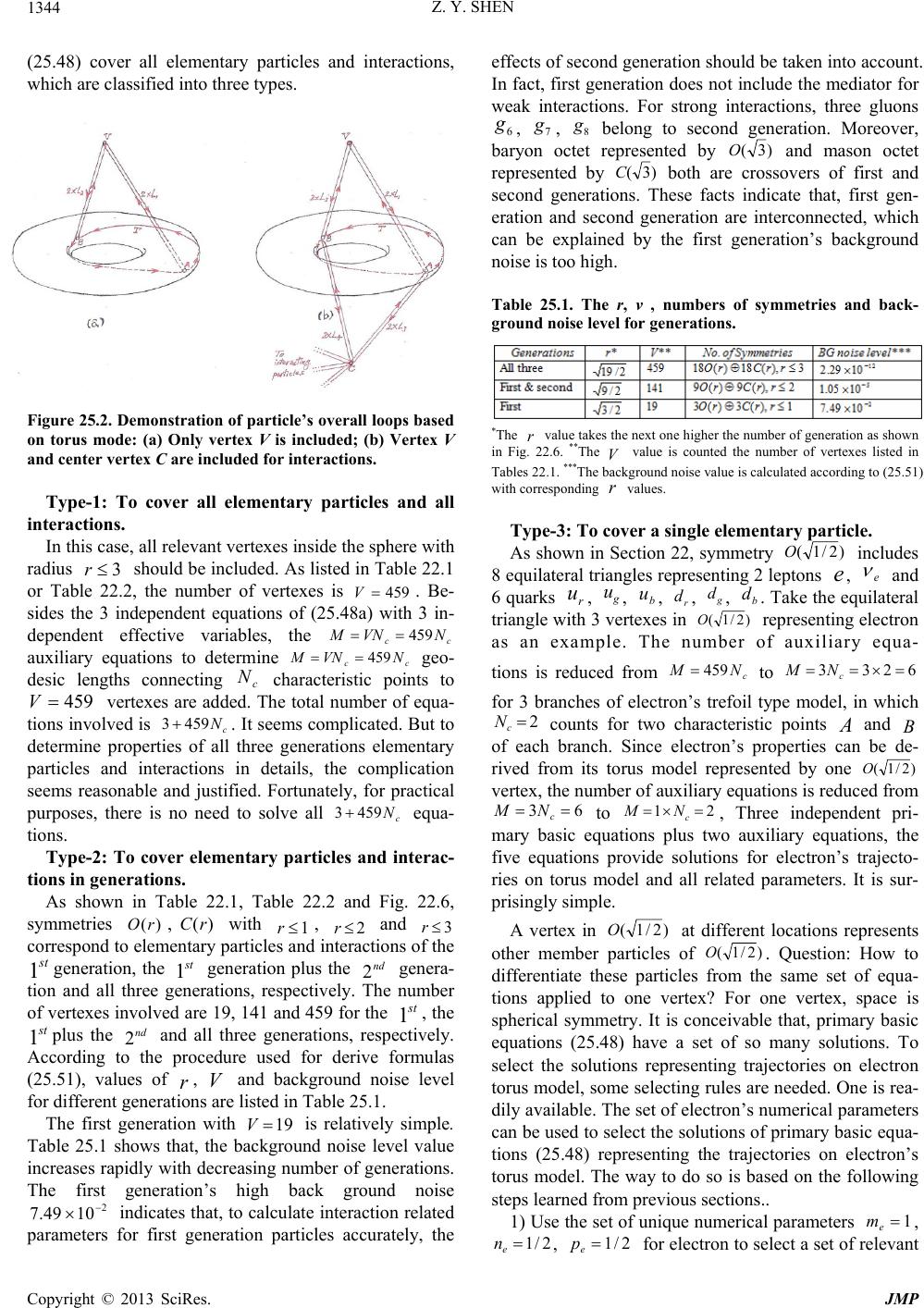 Z. Y. SHEN Copyright © 2013 SciRes. JMP 1344 (25.48) cover all elementary particles and interactions, which are classified into three types. Figure 25.2. Demonstration of particle’s overall loops based on torus mode: (a) Only vertex V is included; (b) Vertex V and center vertex C are included for interactions. Type-1: To cover all elementary particles and all interactions. In this case, all relevant vertexes inside the sphere with radius 3r should be included. As listed in Table 22.1 or Table 22.2, the number of vertexes is 459V. Be- sides the 3 independent equations of (25.48a) with 3 in- dependent effective variables, the cc NVNM 459 auxiliary equations to determine cc NVNM 459 geo- desic lengths connecting c N characteristic points to 459V vertexes are added. The total number of equa- tions involved is c N4593 . It seems complicated. But to determine properties of all three generations elementary particles and interactions in details, the complication seems reasonable and justified. Fortunately, for practical purposes, there is no need to solve all c N4593 equa- tions. Type-2: To cover elementary particles and interac- tions in generations. As shown in Table 22.1, Table 22.2 and Fig. 22.6, symmetries )(rO ,)( rC with 1 , 2 and 3 r correspond to elementary particles and interactions of the st 1generation, the st 1 generation plus the nd 2 genera- tion and all three generations, respectively. The number of vertexes involved are 19, 141 and 459 for the st 1, the st 1plus the nd 2 and all three generations, respectively. According to the procedure used for derive formulas (25.51), values of , V and background noise level for different generations are listed in Table 25.1. The first generation with 19 V is relatively simple. Table 25.1 shows that, the background noise level value increases rapidly with decreasing number of generations. The first generation’s high back ground noise 2 1049.7 indicates that, to calculate interaction related parameters for first generation particles accurately, the effects of second generation should be taken into account. In fact, first generation does not include the mediator for weak interactions. For strong interactions, three gluons 6 g, 7 g, 8 g belong to second generation. Moreover, baryon octet represented by )3(O and mason octet represented by )3(C both are crossovers of first and second generations. These facts indicate that, first gen- eration and second generation are interconnected, which can be explained by the first generation’s background noise is too high. Table 25.1. The r, v , numbers of symmetries and back- ground noise level for gener ations. *The value takes the next one higher the number of generation as shown in Fig. 22.6. **The V value is counted the number of vertexes listed in Tables 22.1. ***The background noise value is calculated according to (25.51) with corresponding values. Type-3: To cover a single elementary particle. As shown in Section 22, symmetry )2/1(O includes 8 equilateral triangles representing 2 leptons e, e and 6 quarks r u, g u, b u, r d, g d, b d. Take the equilateral triangle with 3 vertexes in )2/1(O representing electron as an example. The number of auxiliary equa- tions is reduced from c NM 459 to 6233 c NM for 3 branches of electron’s trefoil type model, in which 2 c N counts for two characteristic points and B of each branch. Since electron’s properties can be de- rived from its torus model represented by one )2/1(O vertex, the number of auxiliary equations is reduced from 63 c NM to 21 c NM , Three independent pri- mary basic equations plus two auxiliary equations, the five equations provide solutions for electron’s trajecto- ries on torus model and all related parameters. It is sur- prisingly simple. A vertex in )2/1(O at different locations represents other member particles of )2/1(O. Question: How to differentiate these particles from the same set of equa- tions applied to one vertex? For one vertex, space is spherical symmetry. It is conceivable that, primary basic equations (25.48) have a set of so many solutions. To select the solutions representing trajectories on electron torus model, some selecting rules are needed. One is rea- dily available. The set of electron’s numerical parameters can be used to select the solutions of primary basic equa- tions (25.48) representing the trajectories on electron’s torus model. The way to do so is based on the following steps learned from previous sections.. 1) Use the set of unique numerical parameters 1 e m, 2/1 e n, 2/1 e p for electron to select a set of relevant  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1345 solutions of equations (25.48). 2) Use characteristic point and point B to de- termine the overall loop including trajectory and round- trip geodesic lengths as shown in Fig. 25.2(a) to repre- sent electron. 3) Rotate point and point B to form circle- and circle-B, the trajectory rotates with point and point B to form the torus model supporting a set of discrete trajectories on its surface. 4) Add center vertex C representing interactions and additional roundtrip geodesic lengths as shown in Figure 25.2(b), then apply f-modification based on solutions of PS-equation to change the torus surface with slightly different 2 'a and 2 'b for a set of discrete surfaces. 5) Electron’s all physics parameters are derived from characteristic point , point and associated triangles: CKM-triangle, GWS-triangle and S-triangle. The same procedure is valid for electron’s trefoil type model represented by a triplet with three vertexes in )2/1(O. Comparing to torus model, the difference is that, there are 6 characteristic points involved instead of only 2 for torus model. Electron is just an example. The same procedure is va- lid for other member particles of )2/1(O. Applying primary basic equations (25.48) to different vertexes representing r u, g u, b u, r d, g d, b d, or e , the so- lutions are selected according to their unique set of nu- merical parameters as well as characteristic points. In general, there are three type interactions for ele- mentary particles. Does the center vertex represent all three type interactions? As shown in Section 15 and Sec- tion 22, all interactions are unified with gravity at GUT scale with characteristic length 71 GUT L. Inside the M-sphere with radius 71GUTM LR , gravity is the only effective interaction. The center vertex represents gravitational interaction. So the answer is: Yes. But it raises another question: How to distinguish three differ- ent type interactions? Section 22 already provided the answer: )0(O symmetry corresponding to )1(U group represents electromagnetic interaction; the square with center vertex on surface represents weak interaction; the square with center vertex off surface represents strong interaction. So these interactions are distinguishable. A particle ignored interaction is represented by a set of trajectories on a surface of its model corresponding to a set of selected solutions of primary basic equations (25.48). A particle with interactions is represented by a set of trajectories on a set of its model’s surfaces corre- sponding to another set of selected solutions of primary basic equations (25.48). In essence, trajectory is primary and model is secondary. If symmetry is perfect, the member particles all are massless. Particle’s mass is obtained by symmetry bro- ken caused by vertex shifting from its original location to break the symmetry as shown in Section 22. The above procedure learned from previous sections only serves as a reference to identify solutions of the primary basic equations (25.48) representing different elementary particles. The real procedure to identify solu- tions of equation (25.48) for different elementary parti- cles should be based on the characteristics of primary basic equations, in which shifting vertex to break sym- metry to obtain mass might play a pivotal rule. Symmetry )2/1(O is picked as an example. The same procedure is valid for other symmetries. It is con- ceivable that, primary basic equations (25.48) applying to different vertexes of symmetries )2/1(O, )2(O, )8(O and )2/1(C, )2(C, )8(C cover all three gen- eration elementary particles and interactions. It shows the versatility and richness of primary basic equations (25.48). The details will be revealed when solutions are available. The primary basic equations (25.48) are based on SQS theory three fundamental Postulations. The first one pro- vides Gaussian probability and Gaussian spheres. The second one correlates prime numbers to elementary par- ticles’ numerical parameters. The third one provides va- cuons. All seem reasonable. But look closely, there are open issues. One important open issue is the meaning of intrinsic time t 1 . The introduction of intrinsic time by (25.5) is phenomenological. It is conceivable that, intrinsic time serves as the “clock” for vacuons. It might play a pivotal rule for oscillation along the closed geodesic loop. Fur- ther work along this line is needed. Another important open issue is the origin of selecting rules. As mentioned previously, the set of numerical pa- rameters and characteristic points are used as selecting rules to choose the relevant solutions for a particle from primary basic equations (25.48). But if everything is ul- timately originated from primary basic equations, so are these rules. For instance, numerical parameters m, n, p are used to determine loop-1, loop-2 lengths and the os- cillation pattern along the closed loop. Their value should be determined by primary basic equations (25.48) not the other way around. The same argument is also valid for characteristic points. This is a very important open issue. Since the solution of primary basic equations (25.48) is not available yet, to get some ideas, let’s look at three special cases. Case-1: Mechanism of emitting and absorbing a photon by charged particles. For photon with spin , its trajectory p T is a circular loop with circumference length 222 PPp LC and radius /12/ p CR . All lengths are normalized with respect to Planck wavelength (Planck length)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1346 PP L . In Fig.25.3, is the vertex representing pho- ton and C is the center vertex, a, b, c are character- istic points, j L and k L are geodesic lengths connected to vertex V and vertex C, respectively. Figure 25.3. Overall closed loops represent photon’s emit- ting and absorbing mechanism: (a): 3k, 3/2 3L; (b): 2k,;1 2L(c) 1k, 2 3L. Photon as a stable particle, its internal movement in the overall loop including trajectory and roundtrip geo- desic lengths is exactly synchronized. If not, sooner or later, internal movement would fate away by cancelation. The synchronization condition of photon for trajectory and all roundtrip geodesic lengths included is: pkjkjppoverall IkLjLkLjLCL 22222 ,, (25.52a) kLj/1,kLLjk /22 ,3,2,1 k. (25.52b) poverall L, is the length of overall loop including trajec- tory p T and roundtrip geodesic lengths. The factor 2 is for counting roundtrip. p I are integers. j,3k, j,2 k, j,1kcorresponds to Fig.25.3(a), (b),(c), respectively. As shown in Fig. 25.3, the span angle of line aO1 at center vertex C is: k iL R arcsin , 3,2,1 k. (25.53) For a first trial, take 3k, 3/2/2 3 kLLk as shown in Fig.26.5(a). For 3/2/2,3 3 kLk : 51995651.28 2 3 arcsinarcsin 3 3 L R. (25.54) As listed in Table 8.1 and Table 8.2, electron’s origin- nal and effective Weinberg angles are 45987086.28 W and 47948454.28' W , respectively. The relative devia- tions of W and W ' from 51995651.28 3 are 3 1011.2 and 3 10419.1 , respectively. Formula (25.54) is based on flat space. In curved space, 3 L is the length of geodesic, which is slightly different from straight line aC . Taking this fact into account, the 3 10~ relative deviation is justified. It gives credit to identify 51995651.28 3 as the approximate value of Weinberg angle for electron. According to (25.52) and shown in Fig. 25.3(a), the total lengthpoverall L, of overall loop including a full circle of the trajectory p T plus roundtrips along six geodesic lengths connecting three characteristic points a, b, c to 2 vertexes and C is: pkjpoverall IkLjLL 83/2323/1322222 ,. (25.55) 8 , poverall L is an integer, which satisfies synchronization condition (25.52). Encouraged by the first trial positive results, let’s take more trials as shown in Fig. 25.3(b) and Fig.25.3(c). For 1/2,2 3kLk: 56074472.18 1 arcsinarcsin 2 2 L R, 84111708.27 2 3 2 . (25.56a) For 2/2,1 3 kLk : 15784951.9 2 1 arcsinarcsin 1 1 L R, 47354853.273 1 . (25.56b) Corresponding synchronization conditions are: For 2 k, 1/2 2 kL : Ppoverall IL 81222/1222 ,, (25.57a) For 1 k, 2/2 1 kL: Ppoverall IL 82121122 ,. (25.57b) The results of (25.57) also satisfy synchronization  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1347 condition (25.52). As shown in Section 11, formula (11.1) is used to cal- culate Weinberger angles for particles with fractional charges. Besides the factor W sin , another factor W cos is involved. Therefore, the values of 32 2 3 and 31 3 in (25.56) are understandable. Formula (11.1) is derived from (10.1b) and originated from (8.44) based on normalization1'22 gg , which is optional. According to (25.54) and (25.56), correspond- ing results are: 7192744 .0 cossin cossin 33 22 , instead of 66666667.03/2 , (25.58a) 37453391.0 cossin cossin 33 11 , instead of 33333333.03/1 . (25.58b) This approach not only provides results more accurate than those from formula (11.1) but also serves as a way to determine other parameters for charged fermions without normalization involved. According to (8.43a), 22 '/cossinggqiii , with the value of electrical charge i q determined from fine structure constant , the value of 22 'gg can be derived from i given by (25.54) or (25.56). Then all parameters value of GWS-triangle and S-triangle is determined without normalization involved. Based on the positive results of Weinberg angles, it is conceivable that, the cases for 1k, 2k and 3 k represent the mechanism of emitting or absorbing pho- tons by charged particles’ with electrical charges 3/eq , 3/2eq and eq , respectively. Let’s take a closer look at 3k case shown by Fig. 25.3(a), which represents the mechanism of emitting or absorbing photon by electron. As mentioned previously, the geodesic length i L and related parameters are weighted by the weighting prob- abilities: 2 2//)(j iL j L iw eeppip , (25.23a) 1/)( ppip ii iw. (25.23b) The weighting probability concept is also valid for the mechanism of emitting or absorbing photons, which represents these processes’ stochastic nature. Taking stochastic nature into consideration, the synchronization condition (25.52) is just a “snap shot” cut from the whole “movie”. It is a specific case for all roundtrip geodesic lengths are included in the overall loop. In reality, the six roundtrip geodesic lengths included or not included in the overall loop are determined by weighting probabili- ties )( ipw. In essence, the scenario is dynamic and sto- chastic in nature. Taking the stochastic effect into con- sideration, the synchronization condition of (25.52) is generalized as: p ipvia iippoverall ILCL w)( ,2, (25.59a) 2 2//)(j iL j L iw eeppip . (25.59b) In (25.59), the six geodesic lengths )62,1(, iLi are renamed and marked in blue color shown in Fig. 25.3(a). In which, three )3,2,1(,iLi attach to center vertex C and other three )6,5,4(, iLi attach to vertex V. The subscript “via )(ipw” in (25.59a) indicates that, synchronization condition (25.59) is stochastic with probability )(ipw involved. )(ipw is the probability for roundtrip geodesic lengths i L2 included in overall loop, while )(1 ip w is the probability for i L2 not included in overall loop. As shown in Fig. 25.3(a), there are 6 roundtrip geo- desic lengths i L2 involved. For each one of the 6 roundtrip geodesic lengths included or not included in the overall loop, the total number of overall loops’ dif- ferent patterns is 6426 p N. According to (25.59b), )(ipw is determined by its geodesic length i L in the nominator and all geodesic lengths in the denominator. For )3,2,1(, iLi attached to vertex C: 24752012.0 2 3 2 2 eep i L i, (25.60a) For )6,5,4(, iLi attached to vertex V: 70534668.0 2 3 1 2 eepi L i. (25.60b) Summation of all )62,1(, iLi: 85860041.23 6 1 3 1 3 222 2 j Leee i . (25.60c) According to (25.59b) and (25.60), the probabilities for the two types of roundtrip geodesic lengths included in the overall loop are given as follows: )3,2,1(, iLi included in poverall L,: 08658787.0/)3,2,1( 6 1 3 2 2 2 j L wj eep , (25.61a) )6,5,4(, iLi included in poverall L,: 246745463.0/)6,5,4( 6 1 3 1 2 2 j L wj eep , (25.61b) Check for unitarity: 1246745463.008658787.03)( 6 1 jwip . (25.61c) To get the idea, let’s look at some typical cases. 1) For all 6 roundtrip geodesics )62,1(, iLi in- cluded in the overall loop, the occurrence probability is: 6 33 11075256159.9)6,5,4()3,2,1( wwcase ppp .(25.62a)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1348 Synchronization condition (25.59a) is satisfied as: p ipvia iipoverallILCL w 8 3 1 23 3 2 2322 )( 1, . (25.63a) 2) For all 6 roundtrip geodesics )62,1(, iLi not in- cluded in the overall loop, the occurrence probability is: 32570587.0)6,5,4(1)3,2,1(1 33 2 wwcase ppp . (25.62b) Synchronization condition (25.59a) is satisfied as: p ipvia iipoverall ILCL w 2 3 1 20 3 2 2022 )( 2, . (25.63b) 3) For only 1 roundtrip geodesic )3,2,1(,iLi con- nected to C and only 1 roundtrip geodesic )6,5,4(, iLi connected to V included in the overall loop, the occur- rence probability is: 01011 .0)6,5,4(1 )6,5,4()3,2,1(1)3,2,1(22 3 wwwwcase ppppp . (25.62c) Synchronization condition (25.59a) is satisfied as: p ipvia iipoverall ILCL w 4 3 1 21 3 2 2122 )( 3, .(25.63c) 4) For only 2 roundtrip geodesic )3,2,1(, iLi con- nected to C and only 2 roundtrip geodesic )6,5,4(, iLi connected to V included in the overall loop, the occur- rence probability is: 4 22 4 1014066054.3 )6,5,4(1)6,5,4()3,2,1(1)3,2,1( wwwwcase ppppp. (25.62d) Synchronization condition (25.59a) is satisfied as: p ipvia iipoverall ILCLw 6 3 1 22 3 2 2222 )( 4, . (25.63d) 5) For only 1 roundtrip geodesic )3,2,1(, iLi con- nected to C and no roundtrip geodesic )6,5,4(, iLi connected to V included in the overall loop, the occur- rence probability is: 03087563.0)6,5,4(1)3,2,1(1)3,2,1( 32 5 wwwcase pppp .(25.62e) Synchronization condition (25.59a) is not satisfied as: p ipvia iipoverall ILCL w 3 1 3 3 1 20 3 2 2122 )( 5, . (25.63e) 6) For only 1 roundtrip geodesic )23,1(, iLi con- nected to C and only 2 roundtrip geodesic )23,1(, iLi connected to V included in the overall loop, the occur- rence probability is: 32 2 61031307079.3)6,5,4(1)6,5,4()3,2,1(1)3,2,1( wwwwcase ppppp . (25.62f) Synchronization condition (25.59a) is not satisfied as: p ipvia iipoverallILCLw 3 2 4 3 1 22 3 2 2122 )( 6,. (25.63f) The synchronization condition (25.59) must be satis- fied, for cases like No. 5 and No. 6, the way to do so is to change the values of p C and i L by adjusting gauge tensors ab g for reinstalling synchronization condition (25.59). It is legitimate according to background inde- pendence principle. Space structure is not a priori deter- mined, it emerges naturally with gauge tensors ab g de- termined by primary basic equations (25.48). In this case, synchronization condition is a necessary condition for primary basic equations (25.48) to have stable solutions. After the adjustment of tensors ab g completed, the probabilities change accordingly to satisfy synchroniza- tion. Not only cases like No. 5 and No. 6 request adjusting gauge tensors ab g. In fact, all 6426 p N cases re- quest adjusting gauge tensors ab g. For instance, case No. 3 and case No.4 both satisfy synchronization condition (25.59), but these two overall loops have different pat- terns with different ab g distributions in space. In gen- eral, for all 6426 p N overall loops’ different patterns, each one has its unique ab g distribution in space. The total number of different ab g distributions is 6426 p N. It is very important to point out that, the diagrams shown in Fig. 25.3, the synchronization conditions of (25.52), (25.59) and all related formulas are only for the mechanism of photon’s emitting and absorbing not for free flying photon. For free flying photon, the scenario is very simple. A free flying photon is represented by a circular trajectory with circumstance of P L2 with nothing attached. It is conceivable that, as shown in case No. 2, when all 6 roundtrip geodesics )62,1(, iLi are disconnected, the overall loop 2 , poverall L with nothing attached becomes the trajectory of a photon free to fly. The solution of primary basic equations (25.48) representing free flying photon should be very simple. In this case, the overall loop concept and the synchro- nization concept are verified for photon’s emitting and absorbing, which provide some insights for photon as well as for other particles. Case-2: Electron As shown in Section 12, electron is represented by trefoil trajectory with loop-1 and loop-2 combined movements on genus-3 trefoil type model. The situation is more complicated than photon. Details have to wait until the solutions of primary basic equations (25.48) available. But it is possible to take a bird-eyes view to get some ideas. For electron with spin 2/, its loop-1 is a circle with circumferential length 1 1 mL . Its loop-2 is a closed loop with circumferential length 2/1 2nL . For electron as a stable particle, the length of overall loop including trajectory and the roundtrip lengths of geodesics involved is determined by synchronization condition:  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1349 e ipvia M iieeoverall ILTL w )( 1 ,2, (25.64a) i L L ii i wi i e e p p ip 2 2 )( . (25.64b) In which, eoverall L, is overall loop length, e T is tra- jectory length, i L2 is roundtrip geodesic length, e I are integers. When multiple geodesic lengths are involved, weighting probabilities )(ipW are attached to parame- ters in the emerging part (25.22) of primary basic equa- tions (25.48). In (25.64), )( ipw is the probability for the roundtrip geodesic lengthi L2included in eoverall L,, while )(1ipw is the probability for the roundtrip geo- desic length i L2 not included in eoverall L,. The roundtrip length i L2 of each geodesic included or not included in the overall loop changes spontaneously by chances, the overall loop length eoverall L, changes accordingly. It shows that, electron’s internal movements are dynamic and stochastic in nature. Electron trefoil model with 3 branches has 632 characteristic points. Electron is represented by 3 ver- texes of 2/1O. The total number of roundtrip ge- odesics i L2 connecting 6 characteristic points to 3 ver- texes is 1836 1M. The number of possible overall loops is determined by each geodesic roundtrip i L2 in- cluded or not included in the overall loop as: 518 110621.222 1M N. (25.65) 5 110621.2N is number of solutions for primary basic equation (25.48) representing electron. As men- tioned in previous section, jumping trajectories on elec- tron model’s same surface corresponds to emit and ab- sorb a pseudo photon. 5 110621.2 N is the number of trajectories on electron’s trefoil type model’s same sur- face. This is the case for an electron ignored interactions. Electron is involved in electromagnetic interaction and weak interaction. Taking electromagnetic interaction into consideration, the center vertex C and the vertex V rep- resenting photon with its overall loop including relevant roundtrip geodesic lengths as shown in Fig. 25.3(a) is added to the diagram representing electron trefoil model. For the electron part, total number of geodesics in- volved including those connected to center vertex C is 24)13(6' e M. The number of possible overall loops determined by each roundtrip geodesic included or not included is: 724 '10678.122' e M N. (25.66) For the photon part, according to Fig. 25.3(a) in Case-1, total number of geodesics involved is 6 p M. The number of overall loops determined by each round- trip geodesic included or not included is: 6422 6 p M p N. (25.67) As shown in Case-1 for photon, the number of differ- ent gauge tensors ab g distributions is 6426 p N. Since electron and photon share the same space, as pho- ton adjusts gauge tensors ab g around its surroundings, which inevitably changes the gauge tensors ab g around electron’s surroundings. Electron trefoil type model’s 24)13(6' e M geodesic lengths i L change ac- cordingly. Taking this effect into account, 'N of (25.66) is changed to ''N as: 93062410074.1222''' p NNN . (25.68) It is important to notice that, the contribution of 6426 p N in ''N is not to combine photon’s overall loop to electron’s overall loop. It is counting the effects of photon’s ab g adjustments upon electron. Because of 642 6 p N different ab g distributions generated by photon’s overall loop different patterns, electron’s each original overall loop becomes 64 different loops caused by the values of geodesics i L changed according to 64 different ab g distributions. The same is true for other particle involved in interactions. Taking weak interaction into consideration, as shown in Section 14, electron epaired with electron an- ti-neutrino e via gauge boson for the regular type weak interactions. As shown in Fig. 17.2, e has trefoil type model with 3 branches similar to electron’s trefoil type model. Each branch has 2 characteristic points, total number of geodesic lengths is 241323 e M for the e part. Gauge boson 21 YYZ is made of two companion fermion states, which has ginus-2 type torus model with two branches. Each branch has 2 characteris- tic points, total number of geodesic lengths for the part is 121222 Z M.The numbers of possible overall loops are 24 22 e M e N and 12 22 Z M Z N for the e part and the Z part, respectively. Taking these effects into account, ''N of (25.68) is changed to for counting electromagnetic and weak interactions as: 196612243010379.72222'' Ze NNNN . (25.69) 19 10379.7N is the number of primary basic equa- tions’ solutions for electron with interactions. According to (25.65) and (25.69), on top of a set of 18 12N solu- tions, primary basic equations have another set of 12 /NNN solutions for electron: 14481866 12 10815.222/2/NNN . (25.70) Physics interpretation is that, electron’s trefoil type model has 14 12 10815.2/ NNN different surfaces with slightly different 2 'a and 2 'b caused by f-modifications. According to (8.41), electron’s torus model is estimated having 13 10544.7 N solutions of PS-equation, which is also valid for the trefoil model. The number 14 210815.2N is roughly in the same order of 13 10544.7N, The orders of magnitude  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1350 agreement serves as another theoretical verification for the PS-equation as well as for the validity of analysis in this case for primary basic equations (25.48) representing electron in terms of numbers of solutions. An electron has 19 10379.7 Nsolutions of primary basic equations (25.48). Is this scenario too complicated? The answer is: Not at all. For the 19 10379.7 N solu- tions, in which 5 110621.2 N solutions represent a set of the same type trajectories rotating around A-circle and B-circle to form trefoil type model with the same pa- rameters represented by the same CKM-triangle, GWS-triangle and S-triangle. The 5 110621.2N solu- tions have the same form with a parameter representing rotation angle. The 14 210815.2 N solutions represent a set of trefoil type surfaces caused by f-modification. The 14 210815.2 N solutions have the same form with slightly different values of parameters for 2 'a and 2 'b. This scenario is consistent with electron’s two sets of discrete trefoil trajectories and jumping trajectories. Pri- mary basic equations (25.48) are stochastic differential equations representing stochastic processes. Corre- sponding to members of statistic ensemble, multiple so- lutions are natural and fully expected. The situation is similar to quantum mechanics. The mixed state is a su- perposition of a set of enormous numbers of wave func- tions as solutions of Schrodinger equation; each one has probability for its occurrence. The mixed state of quan- tum mechanics is commonly accepted, so should be the multi-solution of equations (25.48). The vacuons moving with superluminal speed have the capability to go through all 19 10379.7 N overall loops many times within Planck time scale. The superposition of 19 10379.7 N solutions represents electron in stochastic sense, which corre- sponds to the “electron clouds” concept in Section 8. Each geodesics included or not included in the overall loop is a binary discrete event, which supports the dis- crete trajectory concept. Gauge tensors along overall loop adjust automatically to satisfy synchronization condition (25.64) under all circumstance. It shows that, the space-time continuum determined by primary basic equations (25.48) is dy- namic and stochastic in nature. In essence, microscopic space-time structure is not a priori determined. Back- ground independent is a natural request by primary basic equations (25.48) at Planck scale. The center vertex C serves as the junction to connect all particles involved in interactions. It confirms that, center vertex C represents all interactions as mentioned previously. Moreover, as shown in this case, center ver- tex C serves another function to distinguish different particles involved in interactions. If there is no center vertex C serving as partition, the overall loops represent- ing photon, e , and electron are directly connected to each other, the distinctions of these particles would be blurred. The center vertex C not only serves as junction but also as partition. In this case, the overall loop concept and the synchro- nization concept for particle’s stability are verified for electrons in principle. Hopefully, when solutions of pri- mary basic equations (25.48) for electron are available, these concepts can be confirmed Case-3: Unstable Particles The difference between unstable and stable particles is synchronization. As shown in Case-1 and Case-2, photon and electron as stable particles, synchronization condi- tions are exact with phase difference equal to zero pre- cisely. Otherwise, any nonzero phase difference no mat- ter how tiny, as cyclic movement goes on, sooner or later it will accumulate to 180 phase difference for cancela- tion corresponding to particle’s decay. For unstable particles, the quasi-synchronization con- dition is: kILCL u ipvia iiuuoverall w )( ,2, (25.71a) 11 2 2 )( i L L ii i wi i e e p p ip . (25.71b) In which, k is the number of turns around the overall loop, u I are integers. When 5.0 k corresponding to 180 phase difference, the particle has a chance to decay. Depending on each i L2 included or not included in utoverall L,, the values of uoverall L, are stochastic in nature, so are decay times. The scenario is consistent with the stochastic multiple decay-times for muon as an example described in Section 7. It is important to point out that, the synchronization condition and quasi-synchronization condition are not externally imposed; they belong to primary basic equa- tion (25.48) serving as the condition of stable solutions for stable particle or quasi-stable solutions for unstable particle. The same is true for numerical parameters and characteristic points, they are not externally imposed, instead, they are requested by primary basic equations (25.48) to have meaningful solutions. In essence, all se- lecting rules ultimately are originated from the set of primary basic equations (25.48). So it does tell the whole story. In principle, some information provided in the previ- ous twenty four sections before this section based on three fundamental postulations can be obtained from corresponding solutions of primary basic equations (25.48). Even though, these efforts are not wasted. They serve as very helpful and informative rehearsals. Imaging without these rehearsals, putting the set of primary basic equations (25.48) as the real show on the stage, one would be very hard to recognize what it is.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1351 The set of primary basic equations (25.48) tells the whole story. What is the whole story? From SQS theory perspective, it includes three parts. Bottom Part: Information of all elementary particles and interactions include trajectories, models, characteris- tic points, triangles and related parameters. Top Part: Information of universe, multiverse and anything on top of them include space dimensions, cos- mic periods and cosmic evolution. In-Between Part: Information of things in between the bottom part and the top part. The bottom part is governed by primary basic equa- tions (25.48). The top part is governed by basic equations (25.31) and (25.43), which have the same foundation (25.20) as the primary basic equations (25.48). The in-between part needs some explanation. If the set of primary basic equations (25.48) does unify general rela- tivity with quantum theory including standard model and quantum mechanics, it should provide information up to the molecules level. Further up to the upper levels, un- certainty plays a pivotal rule evidenced by the existence of freewill. The set of primary basic equations (25.48) is based on probability serving as the ultimate origin of uncertainty. It lays the foundation for things in upper levels. But, of cause, it cannot provide deterministic in- formation for things in upper levels. In fact, no theory can, because it violates freewill. In principle, the set of primary basic equations (25.48) cover all elementary particles and interactions in micro- scopic world and things on higher levels. In essence, it tells the whole story. The above statement is the final goal of SQS theory. We just get started. There is a long interesting journey to go. With the joint efforts of so many talented physicists and mathematicians, sooner or later we will get there. Conclusion 25.2: Equations (25.48) serve as the primary basic equations for SQS theory. The solutions of equations (25.48) under different circumstances pro- vide information of all elementary particles and interac- tions as well as things at higher levels. Basic equations (25.31) for gravity and basic equations (25.43) for elec- tromagnetic forces are macroscopic versions for two long range forces. Summary: The goal of this section is to establish SQS theory basic equations based on Einstein original equa- tions (25.1b) for vacuum with probability assigned to gauge tensors. What turn out are basic equations which cover things from universe down to elementary particles’ internal movements. The key is to introduce probability. It makes general relativity automatically quantized. Ein- stein original equations for vacuum are the right ones to begin with. The only thing lacking was probability . Unfortunately, Einstein did not like it with his famous saying: “God does not play dice.” But if God wants to create the world, he must play dice. Put it casually: Mr. SQS borrowed an equation from Dr. Einstein and added a rolling dice to develop the ba- sic equation. It paid back with interests: marbles for straws and everything in the universe. In this section, the foundation and framework of SQS theory basic equations are established based on Einstein equations for vacuum with probability assigned to gauge tensors. Since the solutions of basic equations are not available yet, more works along this line are needed. To reach the goal wouldn’t be easy, but it is definitely worth the effort. Section 26. Discussions This section provides an overview of SQS theory with emphasis on open issues. Originally, SQS theory was intended to be a theory of space. It turns out to cover many aspects of particle physics and cosmology. SQS theory as a mathematic theory with physics sig- nificances includes four parts. Part-1: The Foundation. It includes three fundamen- tal postulations: (1) Gaussian Probability Postulation; (2) Prime Number Postulation; (3) Vacuon Postulation. These three fundamental postulations serve as the first principle for SQS theory. Part-2: The Framework. Based on the foundation, SQS theory built a framework including a series of defi- nitions, additional postulations, theorems, lemmas, hy- pothesis, rules, equations, formulas and conclusions. Part-3: The Results. Based on Part-1 and Part-2, SQS theory produced many results in terms of space structure, symmetries, and elementary particles with their trajecto- ries, models, parameters, interactions as well as cosmic structure and evolution. SQS theory provided twenty five predictions for experimental verifications. Part-4: SQS Theory Primary Basic Equations. Based on Einstein Equations for vacuum of general rela- tivity and introduction of probability to redefine gauge tensors, SQS theory established the primary basic equa- tions, which turnout to be a new version of unified field Theory. Fig. 26.1 shows the SQS Theory Family Tree. Three fundamental postulations shown by three triangles serve as the roots of the Tree shown on the bottom. SQS theory primary basic equations (25.48) along with macroscopic basic equations (25.31) and (25.43) shown in red hexa- gons on the bottom serve as the foundation. The three basic constants P L, P t, P E in an octagon serving as the vocabulary to translate the mathematic results into physics are placed on the bottom alongside the three roots and basic equations. The major additional postula- tions, hypothesizes and rules are shown by 13 squares. The results and some intermediate steps serving as the  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1352 Figure 26.1. SQS theory family tree.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1353 elements of the Family Tree are shown by 158 circles. The solid line indicates that, the linked elements are based on logic deduction, mathematic derivation or fac- tual correlation. The dashed line indicates that, the linked elements are somehow correlated. As shown in the Family Tree, S-equations play impor- tant roles for SQS theory. The 1-dimensional S-equation, 01)( xS , is the most important one serving as the foundation. Other S-equations are derived or extended from this one. Its solutions )( 1 x , )( 2 x determine the location of characteristic points on particles’ model, which provide physics properties for the particle and its interactions with others represented by three triangles, GWS-triangle, CKM-triangle and S-triangle. More works along this line are needed to complete the task. What is the function of S-triangle? What does the triangle DBO 11 between CKM-triangle and S-triangle mean? These are open issues. The 1-dimensioanal S-equation is a growing point. Many branches of Family Tree grow from it. The )(xDS -equation is defined as an extension of the S-equation and Fourier transformed into )(kDSk -equation. The)(kDSk-equation on complex k-plane serves as the spectrum of particles. Fermions and bosons correspond to local minimums and local maximums of )( kDSk, respectively. The k-plane spectrum provides information of mass and a series of possible decay times for particles. But it leaves two open issues: The mass value is not uniquely determined; the correlation between decay times and lifetime is not clearly known. The )(kDSk-equation is extended by adding two sets of delta functions to define the )( kEDSk-equation, which is Fourier transformed back to complex x -plane as the )(xEDSx -equation. Comparing it to the )(xDS - equ- ation, the additional two summation terms are identified to represent interactions. In Section 15, these two terms are used for calculating suppression factors to determine the characteristic mass values ew M, ews M for two uni- fications based on )( a x , )(b x and proton mass proton M. It was a risk undertaking, because (15.2) is a bor- rowed formula not from SQS theory first principle and proton is a composite particle. Fortunately, it worked out well to provide the mass scales for two unifications. Moreover, formula (15.15) was found to link ews M and GUT M with )(Z M . It not only provider legitimacy to the borrowed formula (15.2) but also reveals the correlation between proton M and Planck M. It eliminates proton M as a physics input of SQS theory. In addition, it serves as an independent confirmation for the interaction terms in )(xEDSx -equation. The )(xDS -equation has a solution at 125.0 1x on the x-axis corresponding to electron. The )(xEDSx -equation no longer has this solution at 125.0 1 x. It is expected, because the adding of two interaction terms altered its function. To define )(xSSx -equation based on )(xEDS x -equation is an attempt to restore that function. A solution of )(xSSx -equation is found at a new location: W i exx 1 ' ,78213151240811255.0'1 x, 1384598708641.28 W . The fine structure constant 50359990834.137/1)( e M is derived from the value of 1 'x. The importance is the form of solution shows that, electron is a changed parti- cle with Weinberg angle W as a phase angle and the contribution of electromagnetic energy to its mass by (9.8) related to )(e M . It shows that, the theory is con- sistent and the extension of )(kEDSk,)(xEDSx and )(xSSx from )( kDSk are justified. The S -function 1)()( xSxS did an excellent job to find the special point730262499871562.0 c xand the slightly broken anti-symmetry of )(xS in the re- gion )5.0,0( from its center 25.0x. It is a very im- portant finding with many impacts. Point c x sets the boundary of the boson states region )5.0,( cdc xxx . Fermions’ 1 x and 2 x falling into this region must ap- pear in pair with anti-particle as a boson state, which is verified by top quarks’ pair production and e-boson serving as the inflaton. Point c x also defined two other special points a x and b x, which are used to calculate the values of )( a x , )( b x from the S-equation to de- termine the mass values for two unifications as mention previously. The deviation of 730262499871562.0 c xfrom 25.0 x is only 5 1028.1~ , but its impacts are huge. It shows the sensitivity, accuracy and power of the S -function and its origin, the S-equation based on SQS theory first principle. For the 3-dimensional Gaussian probability, its stan- dard deviation’s three values show 120 symmetry on the complex plane and set the three branch points on the Riemann surface to define the two cuts on two layers. The former provides the first clue for )3(SU group and the latter leads to the torus model and 4 characteristic points on its surface. An important trunk of the Family Tree is rooted from Gaussian Probability Postulation. The Random Walk Theorem plays a critical role for many important issues including converting rules, origin of hierarchy problems, photon dispersion, the route to GUT etc. In the convert- ing factor transition region, logistic recurrent process and random walk process both are in action. The former has a variable binary probability, while the latter has 6 prob-  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1354 abilities corresponding to directions along 3 dimen- sions for each step. A strict relation of these two proc- esses is needed to reveal more physics insights. It is an open issue. The Prime Number Postulation based on even-pairing rule is the key to correlate prime numbers with elemen- tary particles. It provides the mathematic foundation to recognize quarks with different colors as different parti- cles and to identify leptons trefoil type model with three branches. It serves as a backbone of the Elementary Par- ticle Table. In return, The Elementary Particles Table did its job including prediction of the boson along with other 12 bosons, , )82,1( iGi, 1 U, 2 U, 3 U. Its most important contribution is to determine 72 as total number of elementary particles at this level. The number 72 is supported by the Number Tower especially the magic number 163 on its top. In fact, there is a Second Number Tower shown in Fig. 26.2. Figure 26.2. The second number tower. Two number towers produce the number 48 in differ- ent ways. The first number tower is based on seven prime numbers from the m-parameters of first generation quarks and electron with “up + down” pairing. The second number tower includes two m-parameters of strange quarks to produce number 48 in a different way: 483117 sbsr mm with “red + blue” pairing. The prime number 23 sg m used to define the S-sphere is left out. Is it a coincidence? In the second number tower, the prime numbers assign to quarks with three flavors u, d, s, which are the members of isospin group )3(SU . Is it a coincidence? Both number towers provide the mathematic basis for six special numbers, 1, 6, 12, 24, 48, 72, and the number 7248241261163 on top as well as the classification of elementary particles in the Elementary Particles Table. In essence, SQS theory is a mathematic theory. If there is a mathematic inconsistency, it must be taken very se- riously. For example, from “common sense”, the three cells for electrical neutral leptons in Elementary Particles Table should be filled with the flavored version 3 neu- trinos and 3 anti-neutrinos. But it makes the total number of elementary particles equal to 75 instead of 72 not supported by two number towers especially the number 163 on top of them. The author tried many ways to re- solve the mathematic inconsistency without success. Then the only way out is to take eigenstate version three anti-neutrinos as Majorana type fermions to fill the three cells. Fortunately, it works well with a bonus— the fly- ing around eigenstate neutrinos 1 , 2 , 3 provide an opportunity to resolve the missing antimatters mystery. Another trunk of Family Tree is also rooted from fun- damental postulations. Gaussian sphere as an assembly of vacuons is defined based on Gaussian Probability Postulation and Vacuon Postulation. With the help of Kepler-Hales theorem, the face-centered lattice is identi- fied as the structure of 3-dimensional space. The two sets of symmetries )(rO , )(rC with 3r are identified and their vertexes are related to three generations ele- mentary particles and interactions as shown by the Symmetries Family Tree. The two sets of 6 basic sym- metries based on the vertexes numbers 1, 6, 12, 24, 48, 72 have important physics significances. The symmetries )(rO , )( rC with 3 r are correlated to physics groups such as )1(U, )2(SU , )3(SU , which give elementary particles another geometrical origin besides their models. But the strict mathematic proof of correlation between symmetries )(rO , )(rC with 3r and groups)1(U, )2(SU , )3(SU remains an open issue. In SQS theory current version, the selection of the p-parameter is from physics to mathematics. According to SQS theory philosophy, it should be the other way around. This controversy implies that, at least one rule is missing in the current version. When the missing rule is found, it will provide the way to select p- parameter from first principle to determine particle’s theoretical mass value. It remains as an important open issue. The solution is hidden in primary basic equations (25.48). Similar fluctuation behaviors are found in different areas of SQS theory. The first one is muon’s decay times determined by i k values at local minimums of )(kDSk. There are so many local minimums corresponding to so many possible decay times for muon originated from the fluctuation nature of )(kDSk. The second one is the  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1355 fluctuation nature of the complex x -plane, on which the value of )( e M is calculated from electron’s mass and Weinberg angle. The value of 50359990834.137/1)( e M listed in Table 9.1 is from one root of 0)( xSS. In fact, there is a serious of roots corresponding to different values, which indicates as a running constant. The third one is the fluctuation nature of the PS-equation. There is a serious of roots or minimums corresponding to slightly different tilting angles of loop-2 with slightly different effective parameters’ values. The three types of fluctuations have something in common. They all are random in nature, all vary in small steps, and all corre- spond to real physics parameters. These facts imply that, they have the same mechanism and come from the same origin. The mechanism is particles’ discrete trajectories proved by Theorem 18.1 and related lemmas. A particle and its parameters are represented by its trajectory on model surfaces. Jumping trajectories in discrete manner causes parameters changing responsible to these fluctua- tion behaviors. Ultimately it is originated from Gaussian Probability Postulation and stochastic nature of the quantum space. In Section 23, the finding of three more sets of prime number even pairs in prime numbers table is very impor- tant. Formulas (23.9), (23.10), (23.11) and Conclusion 23.1 indicate that, they are based on the original set of 18+1 prime numbers. With the help of Postulation 23.1, cosmic history and periods are correlated to elementary particles and traced back to prime numbers table. It pro- vides a mathematical explanation for cosmic evolution from the big bang through inflation(s) up to the current period. It also predicts the future of universe. Finally it reaches a conclusion: A cyclic universe oscillates with alternate expanding and contracting periods. All of these are built in prime numbers table based on even-pairing rule. It shows mathematics at work. As mentioned at the end of Section 23, the universe during its contracting period, entropy decrease seems contradictory to the second law of thermodynamics. The second law is such a fundamental physics law; any viola- tion is going to shake the foundation of physics. It must be dealt with. The precondition for applying second law is that, the statistic ensemble for second law to apply must be an isolated one. Then the questions become: Is the universe an isolated statistic ensemble? Is there any- thing on top of the universe? There are clues from grand numbers, as listed in Table 24.3, 22 310864.5 F as a 2G grand number is for universe current third period, 44 10686.1 pre F as a 4G grand number is for pre-big-bang period. For reference, the universe contain- ing 11 10~ galaxies with 22 10~ stars correspond to 1G and 2G grand numbers, respectively. Hypothesis 26.1: There is a multiverse including 22 10~ universes organized in two levels, each level has 11 10~ members. Our universe is one member of the lower level sub-multiverse. SQS theory is not the first one to propose the mul- tiverse concept. Other theory such as superstring theory did years ago. Despite the same name, there are differ- ences. The motivation of SQS theory to propose its mul- tiverse concept is trying to find a way to resolve the sec- ond law problem during cosmic contracting period. The clues are from two grand numbers. The 11 10~ universes in a sub-multiverse or the 22 10~ universes in the mul- tiverse correctively form a statistic ensemble for the sec- ond law to apply. Our universe is just an element akin to a molecule in the air. The entropy is counted for entire ensemble not for one element. Moreover, each universe in the sub-multiverse started from Gaussian spheres evaporated from pre-big-bang over heated liquid state at different times in a random fashion. From SQS perspec- tive, the overall scenario is like that, at a given time, dif- ferent universes are in their different periods. Some are expanding and others are contracting akin to six cylin- ders in a combustion engine. It provides a possible solu- tion for the second law problem. But it raises a question: What is the physics links among member universes in the sub-multiverse serving as the statistic ensemble? It may have something to do with neutrinos and photons. Table 26.1 shows mass, Compton wavelength, con- verting factor, long-path Compton wavelength and maxi- mum entanglement distance for three types of neutrinos. Mass values are sited from (17.4), converting factor and long-path values are calculated according to rules intro- duced in Section 4. Wavelength for photon as boson is replaced by Compton wavelength C for neutrinos as fermions. Maximum entanglement distance is changed accordingly to PCCLd/)4/12( ˆ )4/12(2 max for neutrinos. Table 26.1. Three type neutrinos related parameters*. * M, N are mass and converting factor; C , C ˆ are short path and long path Compton wavelengths. According to (17.23), the mass of 1 ~ and 2 ~ are close to the mass of e and , respectively, the mass of 3 ~ is close to one third of mass. For 1 with mass close to e , the 16 max 10228.1~ d light years maximum entanglement distance for a pair of entangled 1 is 5 10~ times longer than the 10 104.8~ light years visible universe size. It is capable to reach neigh- boring member universe territory in the sub-multiverse.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1356 For 2 ~ with mass close to , the 11 max 10872.2~d light years maximum entanglement distance is marginal to reach neighboring members of the sub-multiverse. For 3 with one third of mass, the 992 max 10139.9)10015.1(3~ d light years maximum entanglement distance is less than visible universe size. It is not capable to reach neighbor- ing members of sub-multiverse. If this is the case, a pair of entangled 1 is eligible to serve as the physics link between adjacent members of the sub-multiverse. There is an interesting twist: cross universes connected 1 ~ might only oscillate with 2 , which is a distinctive fea- ture different from its non-cross-universes counterpart. It provides a chance to verify the possible link between our universe and neighboring universes. Accordingly, a pair of entangled photons with wave- length longer than millimeter is also capable to do the job. The long wavelengths portion of the cosmic microwave background radiation (MBR) spectrum is in this range. It may leave some traces there. In ordinary flat space, max d sets a limit of the dis- tance between two entangled particles. But under ex- traordinary circumstance, things turn out differently. The edge of visible universe is like the event horizon of a black hole. The long path link between two entangled particles is capable to pass through event horizon. It is possible, because event horizon is defined based on speed does not exceed the speed of light, the superlu- minal speed along long path link does not subject to this restriction. In Section 25, cosmic MBR photons long-path wave- length P L/ 2 00 at frequency spectrum center wave- length m 3 01008.1 is used to deal with the dark energy hierarchy problem. For a double check, let’s use eigenstate neutrino 2 with long path wavelength m 27 ~ 2 ~10208.1 ˆˆ listed in Table 26.1 for an independent estimation: 123 2 2 ~10582.5 ˆ P L . (26.1) Since anti-neutrino 2 is electrically neutral, so the additional factor 2 4/ is not applicable. Comparing theoretical result 123 10582.5 of (26.1) with observed data 123 10271.3 R of (25.35), the relative discrepancy is 70.6%. The agreement from two independent sources provides additional support for using converting rule to deal with dark energy problem. Question: Why use long path wavelength of 2 not 1 in (26.1)? Answer: For an oscillating pair, the one with shorter wavelength sets the limit. The result of (26.1) is important in another sense. It confirms that, the factor 2 4/ is applicable only for the case with electromagnetic force and gravity involved. As universe keeps expanding in an accelerating rate, sooner or later, the distance between universe and its closest neighboring universe becomes too long exceeding the maximum entanglement distance of these particles made the cross universes physics link. Then the second law ensemble is in trouble. But look at it the other way, it might provide the cause to trigger cosmic contraction. It is a wild idea. But it doesn’t hurt to give a thought. There is another possible scheme to resolve the second law problem based on the definition of isolated statistic ensemble. During cosmic contracting period, the uni- verse boundary is shrinking. Does an ensemble with shrinking boundary qualified to be an isolated one for the second law to apply? It deserves a thought. But in any case, the second thermodynamic law always holds. In case the second law does not need entanglements to hold during cosmic contracting period, the multiverse concept still has a support from grand numbers: 22 310864.5F and 44 10686.1 pre F. It indicates that, there is something 22 10~ times bigger on top of our universe. Except the multiverse, what else can be? SQS theory provides a way to resolve the black hole information paradox. As Hawking suggested, a pair of virtual photons pops out from vacuum with one outside and the other inside event horizon. The outside one be- comes a real photon carrying out part of black hole’s energy/mass known as the Hawking radiation. Eventually, the black hole loses its entire energy/mass and vanishes. The paradox is that, after the black hole vanished, infor- mation in the back hole is lost. It contradicts to the con- servation of information according to quantum theory. From SQS theory standpoint, the two photons entangled as coherent states interact to each other with superlu- minal speed along long path link. Like the cosmic entan- glement case, long path link is capable to pass through event horizon and transmitting information along with energy/mass out of black hole via Hawking radiation. In this way, black hole does not lose any information. In- formation paradox is resolved. The key is the long path with superluminal speed. SQS theory supports its own version of the limited anthropic principle. Compare to the strong anthropic principle, it has an important difference. The strong an- thropic principle is based on the assumption: Physics laws and constants are different in different universes. According to SQS theory, there are two different types of physics laws and constants. The first type based on ma- thematics such as prime numbers does not change; while the second type based on geometry may change as the geometry changes. Any universe as a member of the multiverse in its third period is governed by 18 prime numbers serving as the m-parameters of 18 quarks and in some extent the n-parameters as well. These parameters cannot change, because they are based on the same sets  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1357 of 18 prime numbers. SQS theory standpoint is that, for any universe as a member of the multiverse in its third cosmic period corresponding to our current universe, the physics laws and constants may change, but they subject to strict limitations imposed by a set of unchangeable 18 prime numbers. Our universe nurtured human being on earth, some other universe in the multiverse with 22 10~ members should be capable to do the same. Su- perficially this argument seems to restrict the power of anthropic principle; actually it is to enhance the power of anthropic principle. If everything including all physics laws and constants can change arbitrarily, the 22 10~ member universes in multiverse are not sufficient to in- clude even one universe having the set of physics laws and constants for human being to exist. Then the an- thropic principle loses its power entirely. Mother Na- ture may change her mind but not arbitrarily. No one, not even God, can change the prime numbers. Back to the multiverse issue, 2 12/71)( M is defined by (24.33), its values depend on a prime number 71 and a running constant . For any universe in its third period, 71 as a special prime number in the M-group does not change, while depending on ge- ometry of particles model may change making )(M as a running constant. It supports the SQS theory limited anthropic principle. Prime number 71 defined the M-sphere for the current universe corresponding to a set of 9 even pairs of prime numbers listed in the first row of Table 23.1. The pre-big-bang period corresponds to another set of 9 even pairs of prime numbers listed in the third and fourth rows of Table 23.1. The prime number located at similar loca- tion as 71 is 353. Let’s look at (24.33a) for the pre-big-bang period universe, if 71 is replaced by 353 and kept unchanged, the value of )( 1M is in- creased about 2552 times. Sine fine structure con- stant is related to electrical charge, such big change is very unlikely. The alternative is: in denominator increases approximately 5 times to 5)25.0( for compensation. Since the 1-dimensional )(x carries information from 3-dimensional space, 5)25.0( means that pre-big-bang space has much larger area of negatively curvature corresponding to tremendous repul- sive force pushing everything outwards. It is a white hole. As mentioned in Section 23, after-big-crunch universe transfers into pre-big-bang universe via a time tunnel. The outlet of time tunnel is a white hole. Here is the white hole! The two comedies are matched so well. It was conducted by Mother Nature using mathematic lan- guage, the actress and actors were prime numbers. If this argument holds, it serves as another evidence for the roles played by 71 and 353 in specific and for the corre- lation between prime numbers and cosmic history in general. In fact, 71 is a special prime number in many senses. It is the largest prime number factor in the M-group factors sequence. It is in the non-even prime numbers pair 67&71 to end the three generations. It is the radius to define M-sphere and M-circle. It is the prime number in formula (24.33a) to define the running fine structure constant. Noticed that, the sum of three m-parameters for three strange quarks is: 71312317 sbsgsr mmm . (26.2a) Prime number 71 is also related to the Euclid number 7 n for )1!( n: 1)7654321(1!750417171 . (26.2b) This was a mathematic formula introduced by Greeks two thousand some years ago. Finally, 72171 is the total number of particles listed in Elementary Particles Table. All of these are based on mathematics; no wander 71 played an important role in physics. Some mathematicians do not recognize 1 as a prime number. Their definition of prime number is like that: A prime number is a natural number that has exactly two distinct natural number divisors: 1 and itself. For SQS theory, this definition is unacceptable. The first natural number 1 must be a prime number. There are mathematical reasons. (1) If 1 is not recognized as a prime number, the first even pair 3&1 does not exist. As a result, the first number tower no longer holds. (2) The second number tower no longer holds either. (3) The magic number 163 loses its foundation. (4) The symme- tries family trees lose their foundation. (5) Definition 23.1 and Postulation 23.1 no longer hold. Cosmic history and future based on it lose their foundation. There are physics reasons. (1) If 1 is not recognized as a prime number, up quark r u and down quark r d do not exist. The total number of quarks would be 16 instead of 18. A flavor triplet is in trouble and two color triplets no long exist. (2) Graviton as rruug does not exist. (3) Electron trefoil type model loses its red branch, because the only even prime number 2/)31(2 er m corre- sponding to electron red branch lost its foundation. (4) Photon as ee is “handicapped” due to the “wound” of eand e. (5) For the current cosmic pe- riod we live in, the space is 3 2 2-dimensional! What kind of world is that? SQS theory is obligated to provide a prime number de- finition. Definition 26.1, The Prime Number Definition: A prime number is a natural number that only has 1 and itself as its natural number divisor or divisors. Explanation: Definition 26.1 recognizes 1 as a prime number. For 1 as a prime number, two divisors happen to  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1358 be the same. This kind of degenerations is common in mathematics as well as in physics. Quantum theory is known for its uncertainty nature such as Heisenberg uncertainty principle. But the basic equation of quantum theory such as Schrodinger equation is deterministic. The uncertainty comes later from the statistic interpretation of its solution, the square of wave function’s magnitude * , serving as probability. SQS theory introduced uncertainty in the first place with the Gaussian Probability Postulation. Quantization comes later. After vacuon introduced in Section 18, Theorem 18.1 and Lemmas 18.1, 18.2 are proved to confirm tra- jectories’ discrete nature. It serves as the basic quantiza- tion for SQS theory. In essence, quantum theory is from quantization to probability, while SQS theory is from probability to quantization. These two approaches are quite different. According to SQS theory, particle’s spin is the angular momentum of its loop-1 internal cyclic movement. It is based by the fact that conservation of angular momen- tums is the sum of spin and trajectory angular momen- tums combined. Apples can’t add to oranges. Two add- able terms must belong to the same type. The formula to calculate a particle’s spin is: 2/ 444 11 m h m h L L h L s PP . (26.3) In which, P mL 1 is the loop-1 circumferential length, PP L is the Planck wavelength, mis the reduced m-para- meter. For bosons without mass, photon and gluons with 2m have spin s; graviton and massons with 0m have spin 0s. For charged leptons’ trefoil model three branches together with reduced m-parameter, 1)3/1(3 m, 2/)6/(3 s. Formula (26.3) is valid for these particles. For quarks, all 18 quarks have reduced m-parameter 1m, formula (26.3) is also valid. But it raises a ques- tion: Is reduction really applicable to quarks? Reduction means m-, n-, p-parameters reduced with some rate for a quark, which changes the values of quark’s m-parameter and n-parameter. As shown in Section 13, strong interac- tions are based on quarks’ original m-parameter and n-parameter versus gluons’ m-parameter and n-parameter. After quarks’ m- and n-parameters reductions, how does gluon “recognize” quark’s original parameters? In addi- tion, reduction makes quark’s n-parameter fractional. As shown in Section 14, leptons’ n-parameters are fractional. Does the reduction for quarks blur the distinction be- tween quarks and leptons and the distinction between strong and weak interactions? These are open issues. In fact, experiments have found that, some quarks such as u and d have spin problems. In the meantime, rather leaves quarks’ spin problem open. SQS theory does not use operators. It is not the first one to do so. Feynman’s path integral theory did it dec- ades ago. Feynman’s path integral equation is equivalent to Schrodinger’s equation, which shows that quantum theory can serve its functions without operators. It gives confidence to SQS theory to go its own way without op- erators. In Section 5, SQS theory provided the dispersion equ- ation (5.7) as a modification for special relativity based on Planck length P L. Later in Section 24, the M-sphere with radius P Lr 71 is introduced, which serves as a domain with linear scale longer than Planck length. Ac- cording to grand number phenomena, large domains with linear scale of P NL 11 10~ are possible as shown by (22.12). The multi-layer domain possibility raises a ques- tion: Should dispersion equation (5.7) change accord- ingly? The answer is: Yes. At least the M-sphere is le- gitimate evidenced by the fact that grand unification oc- curred on its surface. The dispersion equation (5.7) are generalized as: 2 /1)(cfLcfv domain , (26.4a) 2 /1)( domain Lcv . (26.4b) domain L is the length scale of the effective domain. Com- pare to (5.7), equation (26.4) makes dispersion stronger and relatively easier for experimental or observational verification. The results will provide information for ef- fective domain size. It is important to point out that, if an effective domain with Pdomain LL is found, it does not mean equation (5.7) is abolished and replaced by equa- tion (26.4). Photon dispersion equation (5.7) is funda- mental based on space basic grainy structure, which is always valid no matter higher level domain exists or not. This is the reason that equation (26.4) is defined as a generalization not a replacement of original dispersion equation (5.7). Quantum mechanics is a very successful theory in terms of extremely high accuracy and very broad practi- cal applications. But it has many contradict versions of interpretation and seemingly none of them is commonly accepted. SQS theory provides an opportunity for a new interpretation. The key is the meaning of locality. As discussed in Section 5, if locality means interactions and information transmission are restricted by speed of cv under any circumstances, the superluminal phe- nomena found by many experiments between entangled particles inevitably lead to “spooky action at a distance”. The long path provides a way out. Entangled particles are linked by long path. It is a physical entity for interactions and information transmission along it with superluminal speed cNcv ˆ seen by stationary observers. In this way, locality is reserved and many other “spooky actions” in quantum mechanics can be interpreted with common sense. This is a topic with very important phys-  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1359 ics and philosophical significances for further investiga- tions. SQS theory standpoint is clear: Einstein was right — “No spooky action at a distance.” General relativity is a beautiful theory. Based on two principles, general relativity provides a set of Einstein equations for gravity in terms of space-time curvature. It has been verified by many experiments and observations without even one failure. General relativity serves as one of two pillars for modern physics. The problem is that, general relativity is not compatible with quantum theory. For decades, there were many attempts to quantize gen- eral relativity and none of them is commonly accepted. From SQS theory viewpoint, it is the time to rethink the issue. In fact, this is the initial inspiration for the author to search SQS theory basic equations. As mentioned in Section 25, the key concept for SQS basic equations based on Einstein original equations (25.1b) is to introduce uncertainty to gauge tensors by Postulation 25.1. From SQS theory perspective, the con- cept is very clear to begin with: To unify general rela- tivity with quantum theory, uncertainty is primary and quantization is secondary. The other key concept is to introduce the intrinsic time by (25.5), which naturally leads to the superluminal speed for vacuons movements inside elementary particles and the appropriately adjust- ment of separation for the variable in difference equa- tions of (25.31) and (25.43) etc. Both concepts paid off tremendously as shown in Section 25. Standard Model (SM) is proved to be a successful ef- fective theory with enormous theoretical results agreed very well with experimental data. As shown in previous sections, many results from SQS theory are agreed well with experimental data. There must be a strict link be- tween SM and SQS theory. When the link is found, some open issues will settle down. On the other hand, there are some differences between SM and SQS theory. The first one is the difference ways to treat particles. SQS theory provides trajectories on models to represent elementary particles, while SM treats them as points. This is the reason that, SQS theory does not have diver- gence problem and does not need renormalization. There are deeper reasons for SQS theory to avoid divergence problem. For the long range force such as electrostatic force, its strength is inversely proportional to the square of distance. As distance approaches to zero, its strength and energy density approach to infinity causing diver- gence. According to SQS theory, electromagnetic force is unified into gravity at length scale PGUT LL 71 on M-sphere surface. So there are no infinity and no diver- gence for electromagnetic force. For gravity, its strength is also inversely proportional to the square of distance. It keeps that way until P Ll 3~ as shown in Fig.25.1. At PPcLLxl 3026452998715627.0 , gravitational force vanishes. In the region PcLxl 0, it becomes repul- sive. So there is no divergence for gravitational force. In fact, this is the way SQS theory eliminated singularity. Within the M-sphere, two short range forces are unified into gravity, so there is no divergence either. The second one is the different ways to introduce pa- rameters. SM has twenty some handpicked parameters from experimental data, while SQS theory has three sets of mathematical parameters. In which two sets mostly are determined prime numbers and the other set is deter- mined by particle’s mass in the current version. In es- sence, the second difference is originated from the first one. It is understandable that, one can derive parameters from a geometric model with trajectory and characteristic points, but no one can derive any parameter except its location and movement from a point. The third one is SM does not include gravity, SQS theory does. In fact, SQS theory unified all interactions to gravitational interaction as shown in Section 15. The fourth one is the number of elementary particles. As shown in Table 18.1 and Table 18.2, SM has 25 par- ticles not including anti-particles, while SQS theory has 72 particles. The difference is stemmed from SQS theory recognized quarks with different colors as different parti- cles. After the vacuon introduced, the difference becomes the other way around with only one ultimate elementary particle for SQS theory. SM is a well-developed theory. With decades of coop- erative efforts, it is capable to calculate the cross sections and branching ratios for particles and interactions from Feynman diagrams, which are agreed with experiments very well. SQS theory is a developing theory. It just gets started. It hasn’t done these type calculations yet but has the potential to do so. The potential is based on proper- ties of SQS theory. One is in the 1-dimensional S-equation, in general the probability at 1 x has excess and the probability at 2 x has deficit. For most particles, the excess does not match the deficit exactly. The mis- match provides the mechanism for the particle to interact with others or transfer to others. The other one is jump- ing trajectories, which also provide the opportunity for the particle interacting with others or transferring into others. These two properties are intrinsically correlated based on primary basic equations (25.48). For instance, as shown in Section 25, different elementary particle represented by different vertexes in 2/1O share the same center vertex. It serves as a junction of their overall closed geodesic loops, which provides the mechanism for interactions among particles. So SQS theory does have the potential to provide the method for calculating cross sections and branching ratios. This is an important open issue. It wouldn’t be easy and may require some tricks and extensive number crunching. But in principle it is  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1360 feasible. Hopefully, it can be done in the near future. SQS theory does not intend to compete with SM. It provides geometrical models and mathematical interpre- tations to support SM at a deeper level. It also provides a way to make SM as a quantum theory compatible with general relativity. There are similarity between super-symmetry theory and SQS theory. Both theories require fermions and bo- sons somehow matching to each other. But there is an important difference. All hypothetic particles predicted by super-symmetry theory such as the “s- ” for bosons and the “-o” for fermions are not discovered yet. In SQS theory Elementary Particles Table, there are no undis- covered fermions; for the 24 bosons, 13 of them are waiting to be discovered. If the 8 massons are indeed attached to W, Z, X bosons, the number of undiscovered bosons is reduced to 5. The difference between su- per-symmetry theory and SQS theory is stemmed from the different ways to match fermions and bosons. Su- per-symmetry theory does not look for possible matches in existing elementary particles, while SQS theory does. In fact, all fermions and bosons in Table 18.2 are matched, in which only 13 bosons are hypothetical. There are some similarities between SQS theory and string theory [21]. After all, strings and trajectories both are 1-dimensional objects representing elementary parti- cles. In this regard, these two theories do have some common grounds. In addition, for SQS theory the way to introduce mass by adding oscillating mass terms in the AT- equations and PS-equations is inspired by string the- ory. But there are major differences. The first difference is the number of space dimensions. Superstring theory is based on 9-dimensional or 10-dimentional space (the early version of string theory was based on 25-dimensional space), while SQS theory is based on 3-dimentional space. As shown in Sections 22, the physics groups are related to two set of symme- tries, )(rO and )( rC with 3 r, which are the intrin- sic property of the 3-dimensional space with face-centered lattice structure. It includes two parts, the cubic part and the octahedral part. The face-centered lat- tice structure can be viewed as an octahedron imbedded in a cube. Someone may interpret the imbedded octahe- dral part as the hidden space. For instance, )2/1(O symmetry centered at 1 octahedral vertex has 12 vertexes on the spherical surface. The 6212 pairs of ver- texes related to the center vertex form 6 non-orthogonal axes, which might be interpreted as a 6-dimensional space hidden in a 3-dimensional space represented by the cubic part. From SQS theory perspective, it is an illusion of the face-centered space structure. The argument is to state SQS theory viewpoint and by no means to criticize string theory. After all, what is the number of space di- mensions? 9? 10? 25? or 3? Only experiments can an- swer. The second difference is the nature of string and tra- jectory. String theory treats string as a vibrating thread with mass and elasticity. SQS theory treats trajectory as a path of vacuons movement. This difference makes the other difference. For some version of the string theories, except graviton, all other elementary particles are repre- sented by open strings; only graviton is represented by closed string. For SQS theory, except graviton, all other elementary particles’ trajectories are closed loops. The reason is that, in general, vacuons movement along tra- jectory cannot stop suddenly and revise directions ab- ruptly. As the only exception, graviton stops at cubic vertex i x and changes its directions. It has specific rea- sons based on Theorem 3.2, Theorem 4.1 and Theorem 22.1. The third difference is the topological structures of elementary particles. The particle models proposed by SQS theory are topological manifolds with genus num- bers of zero, one, two and three. String theory has so many different Calabi-Yao manifolds with possible numbers up to500 10 . If the model does represent an ele- mentary particle, it should provide particle’s all physics parameters from its geometrical parameters. SQS theory did so with models having genus number not exceeding three. The key is model having definitive shape and size plus characteristic points and related triangles. Model’s shape and size are determined by particle’s m-, n-, p-parameters; its characteristic points’ location and re- lated triangles are determined by )( 1 x and )( 2 x as messengers carrying information from the S-equation. In principle, the particle’s all physics parameters can be derived from these geometry parameters. On the other hand, if the topological manifold has no definitive shape, size and lack of characteristic points, the only way for it to represent an elementary particle with all physics pa- rameters is to increase its genus number. Again, it is by no means to criticize string theory. What type of strings or trajectories and models elementary particles really have, only experiments can tell. The fourth difference is fermions versus bosons. The original string theory based on 26-dimensional space- time had only bosons. Fermions were introduced later via super-symmetry to form the superstring theory. For SQS theory, fermions are primary, bosons made of a pair of fermion and anti-fermion are secondary. Boson or fer- mion, which one is primary? This is the question. A basic theory should answer. Over the years, string theory has accumulated so many mathematic achievements and some physics insights. It takes time for SQS theory to learn. Hopefully, more mu- tual understandings will benefit both theories. There are similarities between SQS theory and the  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1361 loop theory [22]. One similarity is obvious. Both theories are basically dealing with loops. There is another impor- tant similarity. One of the major merits of loop theory is background independence. Space structure is not a priori determined; instead, it emerges naturally. SQS theory supports background independence. In intermediate and macroscopic scales, the moving around M-spheres ar- range themselves according to distribution of mass and energy to satisfy basic equations (25.31) the same way as general relativity. Inside the M-sphere, Gaussian spheres arrange themselves in face-centered lattice structure to reach minimum potential energy. Inside the Planck cube, the primary basic equations (25.48) provide a mechanism for background independence based on the stochastic behavior of geodesics adjusting gauge tensors as shown in Section 25. Composite preons theory is based on preons triplets to form topological models for elementary particles [23,24]. In SQS theory, charged leptons and neutrinos trefoil tra- jectories have three branches. For quarks, there are flavor triplets and color triplets. In its current version, compos- ite preons theory does not provide detail information regarding elementary particles’ parameters for further comparison. Striking similarities between crystallography and par- ticle physics were found [25]. For SQS theory, it is not only similarity; the microscopic space is a crystal with face-centered lattice structure. All elementary particles, interactions and symmetries are originated from it. This area deserves further investigation based on the face-centered lattice structure. Hopefully, they will give SQS theory more supports and inspirations. Technicolor theory is proposed as an alternative of higgs mechanism to provide mass for particles with mass [26]. There are some similarities between technicolor theory and SQS theory. The eight hypothetic massons i G (82,1i) introduced in Section 14 are pure mass stuff. Massons contribute a portion of mass for gauge bosons W, Z and X. If 1 U, 2 U, 3 U are indeed made neutrino and anti-neutrino pairs, the tremendous mass gap between the “heaviest” and the “lightest” would be also filled by vast numbers of massons. From SQS theory perspective, massons provide a portion of mass to bosons with mass. Whither massons also play a role to provide a portion of mass for some fermions, it is an open issue. According to SQS theory, particles’ mass is determined by e MMnp// ratio and generated by sinusoidal oscil- lation of mass term )/2(sinmp along trajectory, which is ultimately originated from solutions of primary basic equations (25.48). It serves as the universal mecha- nism of particles’ mass for SQS theory. But it does not necessarily mean no common grounds for Higgs mecha- nism, technicolor theory and SQS theory. There are pos- sible correlations among these theories, which deserve a close look. The original Grand Unification Theory (GUT) in- tended to unify three interactions excluding gravity was based on )5(SU group [27, 28]. Despite the same name, it is different from SQS theory GUT including gravity. The GUT based on )5(SU is an elegant theory. Ac- cording to the minimal )5(SU model [28], protons are not stable and decay with lifetime of 7.129 10~ years. Unfortunately, this prediction was disproved by Ir- vine-Michigan-Brookhaven (I-M-B) experiment and later by Super-Kamiokande (S-K) experiment. It was such a disappointment, afterwards physicists moved on other directions. From SQS theory perspective, there are rea- sons to believe the original GUT based on )5(SU group might have a chance for revival. The protons predicted lifetime of 7.129 10~ years is based on )5(SU group. The obvious precondition is that, )5(SU group must be in existence in the first place. It is well known in crystallography that, 5-fold symmetry does not exist in single-crystal structure; it exists in the quasi-crystal structure with quasi-periodic lattice lengths [29, 30]. The quasi-crystal lattice must have at least two different spatial periods with irrational ratio. The face-centered space structure in its sin- gle-crystal form does not support )5(SU group. For )5(SU group to exist, the face-centered space structure must have defect to accommodate 5-fold spatial symme- try. As show in Fig. 26.3, icosahedron has 5-fold spatial symmetry. Like )2/1(O symmetry, icosahedron also has 12 vertexes on a spherical surface with radius: 2 95105652.0 5 2 sin 22 5210 4 1 cos p PP i L LL r . (26.5) The relative deviation of 2/95105652.0 cos pi Lr from 2/ )2/1( P OLr is 4.9%. The icosahedron has 20 connected equilateral triangles on its surface. It has sufficient room to accommodate quarks ),,( bgruuuu ,),,( bgr uuuu ,),,( bgrdddd and leptons participated in the proton )(uudp decay proc- ess. According to Kepler-Hales theory, space based on Gaussian spheres with face-centered lattice structure is the ground state of vacuum with lowest potential energy. An icosahedron as defect in face-centered space structure is in a quasi-stable state with higher energy. To accom- modate 5-fold symmetry, the 12 vertexes of )2/1(O must shift locations converting to icosahedron structure. The conversion process is governed by probability. Assume a vertex stays in )2/1(O and shifts to icosa- hedron with equal probability 2/1 . The probability for 12 vertexes of )2/1(O all shift to icosahedron is .4096/12/1 12 pFor a tank of water containing  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1362 3231101010~MN protons with lifetime 31 10~ years, one originally expected to detect 10M decay events per year. This expectation is based on the assump- tion that, )5(SUgroup is fully applicable to all pro- tons involved. But it is not true, because for N protons only protons are eligible for )5(SU group to apply. Take this effect into account, for the water tank contain- ing 3231 101010~ MN protons, the expected num- ber of proton decay events should be multiplied by probability p and become 00244.04096/11010 p per year. Instead 10 decay events per year, the real ex- pectation is ~2.4 events per 1000 years. According to this argument, I-M-B type and S-K type experiments should increase the number of protons in tank by at least 1000 times. Figure 26.3. Icosahedron with 12 vertexes and 20 equilat- eral triangles has 5-fold symmetry. There are also questions regarding the validity of I-M-B type and S-K type experiments. As shown in Sec- tion 7, in the time interval stt 13 min 10075.20 , muons have zero probability to decay. What is proton’s min t? If proton’s yearst 11 min 10~, even all protons were born at big bang 10 1037.1 years ago, none of them is eligible for decay yet. If this is the case, to increase the number of protons for I-M-B type and S-K type experi- ments would not help at all, the only way is to wait until . min tt In Section 15, SQS theory borrowed a method from GUT based on )5(SU group to calculate the character- istic mass for two unifications. This method is proved to be equivalent to the one with more credibility. It shows that, there is some truth in )5(SU group. For instance, )5(SU group breaks down to )1()2()3( USUSU , which are the right ones for elementary particles and in- teractions in the standard model. Moreover, )5(SU group contains 24 bosons, in which 13 of them called “X-bosons” are hypothetic. As shown in the Elementary Particles Table, SQS theory also has 24 bosons, in which 13 are hypothetical. Is this a coincidence? It is worth- while to investigate )5(SU group to find out its relations with )(rO and )(rC symmetries. The bottom line is that, as long as )2/1(O can convert to icosahedron with 5-fold symmetry, proton has a chance to decay. The question is: Under what condition and what’s the prob- ability? This is an interesting open issue worthwhile to explore. Elementary particles’ models proposed by SQS theory are listed in Table 26.2. Most models listed in Table 26.2 have been explained in previous sections. A few models need some explana- tion. The spindle type torus models are listed as genus-0, because their center hole(s) are covered. The topological manifold is allowed to continuously deform, but the heavy mass Max MM requires da 2 ' preventing the center hole to be uncovered. For gauge bosons W, Z, X and scalar bosons 1 U, 2 U, 3 U with heavy mass Max MM , their models belong to two joint spindle type torus with genus-0. Table 26.2. Summary of elementary particles models. In algebraic topology, Henri Poincare discovered the “hairy ball theorem” [31]. Imagine a ball with a hair growing out from every point on its surface. One tries to comb the hairs flat and smoothly around the ball. Put in mathematic terms. “Hairs” correspond to nonzero tangent vector field made of a set of tangent vectors. “Comb the hairs around the ball” is to arrange the tangent vectors around the closed surface. “Flat” means tangent vectors pointing only at tangential direction of the closed surface. “Smoothly” means tangent vectors arranged with conti- nuity without abruption. Poincare theorem proved that, no matter how to ar- range these tangent vectors (hairs), it always leaves some crown (bundle of hairs) stretched out from the ball sur- face. Poincare theorem is valid for any genus-0 closed surface topologically equivalent to the ball surface. Fig. 26.4 shows two crowns on a spherical surface.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1363 Figure 26.4. “Combed hairs” on spherical surface as ge- nus-0 manifold with two “crowns”. There are two closed surfaces, on which hairs can be combed flat and smoothly without crown. One is genus-1 torus with one center hole and the other is Klein bottle. In 3-dimensional space, closed surfaces are classified into two types: Type-1 surface with genus number equal to 1 and Type-2 surface with genus number other than 1. According Poincare theorem and related rules, Type-1 closed surface does not have crown and Type-2 closed surface has at least two crowns. From SQS theory perspective, Poincare theorem and related rules provide important clues for elementary par- ticles’ models, trajectories and interactions. As shown in previous sections, particle’s trajectories are on its mod- el’s closed surface (the small holes on torus surface are closed by filling points according to Penrose [2]). For a trajectory on model surface, the tangent vectors along its path are flat and smooth. For a set of trajectories on the model surface, the tangent vectors along these trajector- ies are arranged like combed hairs. According to Poin- care theorem and related rules, for the set of trajectories on the model’s Type-2 closed surface, there are always crowns for trajectories to jumping out or jumping in. Jumping literarily means vector must leave the surface, which makes it no longer tangential and abruptly chang- ing directions. This is what happens at the crowns. As described previously, jumping trajectories are equivalent to interactions. Therefore, a particle having interactions must be capable to jump trajectories and its model surface must have crowns. The requirement for crowns is met for Type-2 model with genus number other than 1. The problem is the fifteen quarks with genus-1 torus model: r u,g u,, b u,, r d,g d,b d,r s,g s,b s,r c,g c, b c,r b,g bb b.. The genus-1 torus belongs to Type-1, which has no crown. If this is really the case, there would be no electromagnetic interaction, no strong interaction and no weak interaction for these fifteen quarks. Obvi- ously, it is not true. One possible way to solve the prob- lem is to leave same of four tiny holes open on torus sur- face, which makes their model as open surface to have crowns. For instance, leaving two tiny holes open at characteristic points and creates two crowns. It serves as a working assumption for SQS theory. In topological terms, free flying photon with genus-1 model of Type-1 has no crown meaning no interaction among photons. In fact, electromagnetic interactions are linear and photons do not interact with each other. It is also evidenced by the fact that, Maxwell equations are linear equations. It serves as a supportive evidence for the effectiveness of Poincare theorem and related rules in particle physics. Gluon’s genus-2 model of Type-2 has crowns indicat- ing that, there is interaction among gluons. In fact, strong interaction mediated by gluons is nonlinear and gluons interact with each other as shown in Table 13.5. It also serves as another supportive evidence for the effective- ness of Poincare theorem and related rules in particle physics. Graviton’s genus-0 model of Type-2 has crowns. They should interact with themselves. In fact, as the mediator of gravity, graviton interacts with anything having mass and energy. The flying around gravitons have energy and dynamic mass for gravity to act upon. It is also evidenced by the fact that, Einstein equations of general relativity are nonlinear equations and nonlinearity represents self-interaction. The gravity among gravitons is ex- tremely feeble, but it does exist. It supports graviton with genus-0. Conclusion 26.1: Graviton is a scalar boson with spin 0. Explanation: Poincare theorem and related rules serve as the topological evidence for Conclusion 26.1, graviton must have spin 0. Let’s consider the opposite. If graviton has spin 2 or any other nonzero spin values, its closed loop model belongs to genus-1 of Type-1 without crown corresponding to no interaction among gravitons. It is obviously not true. This is a conclusive evidence for gra- viton having spin 0 as stated in Definition 18.1 based on other mathematic reasons. Black hole with closed event horizon is a genus-0 ma- nifold of Type-2. According to Poincare theorem, black hole must have crowns and hairs. Therefore, Hawking radiation is not only a possibility but also a necessity. It serves as a mathematic support for Hawking radiation and the solution for information paradox suggested by SQS theory. Poincare theorem and related rules also support an “absolute black hole” with no stretched out hair. Definition 26.2: Absolute Black Hole. A chuck of matter with total mass exceeding critical mass to form a manifold with genus-1 torus event horizon is defined as an absolute black hole. Explanation: The name “absolute black hole” is cho- sen to differentiate it from black hole. Black hole has Hawking radiations as stretched out hairs. Absolute black hole has no radiation and no stretched out hair.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1364 Theorem 26.1: No Radiation Theorem. Absolute black hole has no radiation of any kind. Proof: According to Poincare theorem with related rules and Definition 26.2, absolute black hole with ge- nus-1 torus event horizon has no crown and no stretched out hair which means no radiation. QED Lemma 26.1: Hawking Mechanism. Absolute black hole has no Hawking radiation, but it has Hawking me- chanism. A pair of virtual photons pops up in the vicinity of absolute black hole’s event horizon. One photon falls into absolute black hole, and the other photon is kept in the event horizon. This Hawking mechanism process keeps going on. As results, more and more photons are circulating in absolute black hole’s event horizon like “combed hairs”. Proof: The Hawking mechanism is the same as that occurred in the vicinity of ordinary black hole. The only difference is that absolute black hole has no “crown”, therefore photon cannot radiate. QED Lemma 26.2: When two absolute black holes collide in proper ways, they transfer into a regular black hole with genus-0 event horizon or a special black hole with genus-2 event horizon. Both subject to Hawking radia- tion. Proof: According to Poincare theorem with related rules and Theorem 26.1, the regular black hole with ge- nus-0 event horizon or the special black hole with ge- nus-2 event horizon has crowns and stretched out hairs — radiation. QED The boundary of visible universe like black hole’s event horizon is a genus-0 manifold of Type-2. Accord- ing to Poincare theorem, it must have crowns. Therefore, the cross universes connections via entangled 1 , 2 and cosmic MBR photons not only are possible but also are necessary. It serves as an independent mathematic support for the multiverse concept and the physics con- nections among its member universes. So far everything is consistent. It indicates that, Poin- care theorem in particular and topology in general play critical role for elementary particles’ models, trajectories and interactions as well as for cosmology. It is mathe- matics at work. According to Green et al [21], spinors may relate to the tangent vectors in Poincare theorem. Spinor is the basic concept of spinor theory [32]. The relation between spinor theory and SQS theory is an open area. Spinor theory is based on complex space, while SQS theory is based on real space except the abstract 3 complex planes associated with 3 axes introduced in Scheme-2 of Section 3. What is the implication of real space versus complex space is an interesting topic. SQS theory provided a framework for cosmology based on prime numbers with results agreed to cosmol- ogy standard model plus some new insights. But some important issues left open such as: (1) How many cosmic inflations did happen, one, two or three? (2) What is the mechanism of 3 1 1-dimensional space in the first period transferred into 2-dimensional space in the second period? (3) Based on mathematics, is there a way to reveal cos- mic history and to predict cosmic future in more details? (4) When will the current accelerating cosmic expansion end? (5) Are there more cosmic “secretes” hidden in prime numbers? In fact, there is one. It is interesting to find another set of 13 consecutive even paired prime numbers listed in Table 26.3. It starts from 2791&2797 and ends at 2999&3001. The two prime number odd pairs are 2777&2789 and 3011&3019 marked with underline to start and to stop the even paired prime number sequence at two ends. Table 26.3. The prime numbers between 2707 and 3083 and 13 consecutive even pairs 2707 2711 2713 2719 2729 2731 27412749 2753 2767 2777 2789 2791 2797 2801 2803 2819 2833 2837 2843 2851 2857 2861 2879 2887 2897 2903 2909 2917 2927 2939 2953 2957 2963 2969 2971 2999 3001 3011 3019 3023 30373041 3049 3061 3067 3079 3083 The set of 13 even prime numbers pair represents 3 1 4dimensional space without temporal dimension. The product of 26 prime numbers in this set is: .10642.9300129992971296929632957 2953293929272917290929032897288728792861 2857285128432837283329192803280127972791 89 S F (26.6) In the 13 consecutive even pairs representing 3 1 4di- mensional space, the one additional even pair served as fractal mechanism to change dimensions. Based on S F, two prime number products are defined as: 27 410948.328432837283328192803280127972791 S F, (26.7a) .10442.230012999297129692963295729532939 2927291729092903289728872879286128572851/ 62 49 SSS FFF (26.7b) In which, 4S F is the product of 4 consecutive even pairs in the beginning part of S F and 9S F is the prod- uct of the other 9 consecutive even pairs. As shown in Section 23, the product 22 310864.5 F  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1365 as a 2G grand number corresponds to the universe in current period. The product 44 10686.1 pre F as a 4G grand number corresponds to the multiverse in pre-big-bang period. It seems natural to assume that, the product 89 10642.9 S F as a 8G grand number corresponds to the precursor of the “super-multiverse”. Hypothesis 26.2: Super-Multiverse. There is a su- per-multiverse including 45 10/~ preS FF mul- ti-universes organized in two levels, each level has 22 10~ member multiverse. Our multiverse is one member of the lower level. The total number of universes in the super-multiverse is 67 310~/~ FFS. Hypothesis 26.2 serves as a foundation to explore pos- sible physics implications of S F related issues. Hypothesis 26.3: Big Start. The super-multiverse started at the big start, which is the beginning of time. Before the big start, everything was static without any variation. Time started at the big start, everything started to develop. Before the big-start, the 4 1 4dimensional space cor- responding to S F without temporal dimension wasstatic, in which everything was at a standstill without any movement. The mass/energy was “frozen”. The big start was the beginning of time, temporal di- mension split from the 4 1 4-dimensional space. The )13(-dimensional space-time corresponding to 4S F was born. The mass/energy carried out by 4S F became dynamic and the super-multiverse started to evolve. The mass/energy corresponding to 49 /SSSFFF served as the precursor of dark energy and dark matter. The mass/energy carried out by 4S F served as the precursor of ordinary matter/energy, which was the “raw material” of the ordinary elementary particles and energy to build the planets, stars and galaxies in the super-multiverse. The concept of changing space-time dimensions is checked with two ways. One way is given by9S F in (26.7b). The other comparative way is to treat spatial dimensions as the exponentials ofS F. As space changed from 3 1 4-dimensional to 3-dimensional: 62 4 3 89 4 3 1098.11042.93 1 3 1 S F. (26.8) Comparing to 62 910442.2 S F, the result of (26.8) has a relative deviation of 18.9%. For two large numbers difference with 62 orders of magnitude, the 18.9% rela- tive deviation serves as a check for the validity of changing space-time dimensions based on three products 4S F, 9S F and 94 FSS FFF . After the big-start, according to Hypothesis 26.2, the super-multiverse kept expanding and splitting to form multi-level multiverses and universes. The mechanism of space expansion is Planck cubes’ splitting. As the origi- nal one super Planck cube split into Planck cubes, the mass/energy in a Planck cube decreases according to 1 N rate, and the mass/energy density decreases accord- ing to 2 N rate. Correspondingly, the ratio of the super Planck density at big-start versus the ordinary mass/ en- ergy density in the current universe is estimated as: 124 2 9 2 4 10965.5 S S SF F F R. (26.9) Notice that, in the two previous estimations, the theo- retical values of (25.36), (26.1) and the observed ratio 123 10271.3 obserbed Planck R of (25.35) all are based on Planck density versus overall density including the contributions of ordinary matter, dark matter and dark energy. According to cosmic ob- servation and cosmic MBR data, the universe contains 4% ordinary matter, 23% dark matter and 73% dark en- ergy. Taking this factor into account, the value of (26.9) should be adjusted as: 123 2 9 2 4 10268.3 %73 %4 %73 %4 %73 %4 ' S S SF F F RR . (26.10) Compare the value of (26.10) with 123 10271.3 R of (25.35), the theoretical result 123 10268.3' R has a relative deviation of 4 1017.9 . Three theoretical results for the dark energy hierarch problem are listed in Table 26.4 to compare with ob- served data. Table 26.4. Theoretical results for dark energy hierarch problem compare to observed data. The comparison says all. As shown in Section 23, the legitimacy of three cos- mic periods, Period-I, Period-II and Period-III*, were verified by (23.9), (23.10), (23.11) and summarized in Conclusion 23.2. It shows that, the prime number corre- sponding to these three periods are closely correlated to the prime number corresponding to current period, Pe- riod-III. Let’s verify the legitimacy of the big start with prime number products S F. The following formulas are based on the prime numbers corresponding to cosmic periods listed in Table 23.1 and Table 26.3. The first prime number in product sequence S F is 2791, which is closely correlated to the prime numbers  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1366 corresponding to Period-III, Period-II, Period- and Period-III*. ).117()321( 263257251241239 197193191181179 113109107103101 1311753212791 * IIIPeriod IPeriod IIPeriod IIIPeriod (26.11) The rules in (26.11) are similar to the rules in (23.9). As shown on right of (26.11), prime number 2791 is the sum of 4 sets of beginning prime numbers in parenthesis for Period-III, Period-II, Period- and Period-III* plus (1 + 2 + 3) and (7 + 11). The repeat of three prime num- bers (1 + 2 + 3) represents the fact that, the space corre- sponding to product sequence S F is 3 1 4-dimen- sional. The repeat of two prime numbers (7+11) repre- sents the fact that, there is a temporal dimension hidden in the product sequence 4S F. For the Period- , the two prime numbers 167 and 173 at beginning of the sequence are omitted to transfer Period- with )1( 3 1 - dimen- sion space into Period- with 1-dimension space to avoid redundancy. Otherwise, the sum of Period-I and Period-II would be )3( 3 1 -dimension space contradic- tory to Period-III with 3-dimensional space. The last prime number in product sequence S F is 3001, which is closely correlated to the prime numbers corresponding to Period-III, Period-II, Period- and Period-III*. ).321()5()19()43( 317331337347 191193197199 139149151157 475359613001 * IIIPeriod IPeriod IIPeriod IIIPeriod (26.12) The rules in (26.12) are similar to the rules in (23.10). The order of summation in (26.12) is backwards from the last prime numbers 61, 157, 199, 347 of prime numbers sets corresponding to Period-III, Period-II, Period- , Period-III* and consecutively takes the next ones. After the backwards consecutive summation ended, it jumps to the prime number(s) shown in parenthesis. For Period-III, 43 is the prime number assigned to r t as the up type quark of the 3rd generation, 19 is the prime number as- signed to r c as the up type quark of the 2nd generation. Prime number 5 and the set of three prime numbers )321( is similar to the prime number 7 and )321( in formula (23.10). Besides 2791 and 3001, the rest 24 prime numbers in product sequence S F are expressed as the same form as (23.11). yxPi 2791 , .253,2 i (26.13) In which and y are two prime numbers selected from the set of odd prime numbers from 1 to 147 in two prime numbers sequences corresponding to Period-III and Period-II. Conclusion 26.2: Based on (26.11), (26.12), (26.13), the set of even paired prime numbers started from 2791&2797 ended at 2999&3001 corresponding to the big start are based on the original 4 sets prime numbers corresponding to Period-III, Period-II, Period- and Period-III*. Conclusion 26.2 supports Hypothesis 26.2 and related issues of the big start related toS F. From SQS theory perspective, some mathematical is- sues may have important physics implications. Examples are given as follows. 1) Besides the three finite sporadic Lie groups, M- group, B-group, and Suz-group, are there any other finite sporadic Lie groups also related to SQS theory? 2) What type group, sub-group or something else cor- relates to three sets of prime numbers corresponding to the first period, second period, pre-big-bang period and the precursor of the big-start? In fact, there are clues. One clue is related to S F and other even paired prime numbers sequences 3 FFIII , II F, I F, pre F: 200 10979.1 preIIIIIIS FFFFFA . (26.14) In which, 89 10642.9 S F for pre-big-start is given by (26.6), 22 310864.5 FFIII for current period and 44 10686.1 pre F for pre-gig-bang period are listed in Table 24.3, I F and II F are the products for two sets of prime numbers sequences corresponding to cosmic Pe- riod-I and Period-II: 18 10353.1199197193191181179173167 I F,(26.15a) 25 10534.1 157151149139137131127113109107103101 II F.(26.15b) The prime numbers product sequences for three spo- radic groups Suz-group, B-group and M-group as listed in Table 24.3 have the following products square: 200 210547.6' MBSz FFFB . (26.16) In which 55 10374.117' MM FF is given by (24.32) based on an argument to multiply an additional prime number factor 17 to the product sequence of M-group. The results of (26.14) and (26.16) only deviate by a fac- tor of 302.0/ BA for two grand numbers in the orders of 200 10 . If this is not a coincidence, it supports the cosmological roles played by newly found 13 even pairs of prime numbers corresponding to 89 10642.9 S F. Moreover, there are three additional clues. A: 110 10052.2 preIIIIII FFFF , (26.17a) B: 110 210887.1' M F, (26.17b)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1367 A/B: 087.1'/ MpreIIIIII FFFFF . (26.17c) A: 66 10887.9 preIIIFF , (26.18a) B: 67 210726.1 B F, (26.18b) A/B: 573.0/ 2BpreIII FFF. (26.18c) A: 22 10864.5 III F, (26.19a) B: 23 21001.2 Sz F, (26.19b) A/B: 292.0/ 2 SzIII FF . (26.19c) In which, A is the products of prime numbers sequence for different cosmic period(s) shown in Section 23; B is the squared product of corresponding sporadic Lie group(s) shown in Section 24; A/B is the ratio serving as the relative discrepancy factor. If all these are not by co- incidence, there are some implications: (1) There is a general relation between the products of prime numbers sequence(s) corresponding to cosmic period(s) and squared product(s) of sporadic Lie group(s); (2) Grand number phenomena show up in many different areas; (3) It seems reasonable to modify M F by multiplying 17 as MM FF 17' . But it raises interesting questions: Why the prime number 17 is so special? There is a clue: 2 cbaab , 2a, b, c are prime numbers. (26.20) Checked for 53b, only two sets of prime numbers fit (26.20). 3,1,2 cba : 31221 ; (26.21a) 17,3,2 cba : 173223 . (26.21b) So 17 is a special prime number. 3) What is the physics implication of the j-function closely related to M-group? 4) The Riemann conjecture has some hidden physics significance. Physicists have speculated: The zeros of the -function might relate to some particles’ spectrum. For SQS theory, )(kDSk serving as particles’ spectrum for mass and decay times also has a series of local mini- mums. Are they somehow correlated to -function? Riemann hypothesis is based on the zeta function: 1 1 )( ns n s . (26.22) In which, s are complex numbers. A connection between zeta function and prime num- bers was discovered by Euler, who proved the identity: primesp s nspn 1 11 1 . (26.23) In which, p are prime numbers greater than 1. Does it mean something for SQS theory? 5) Mathematics helped SQS theory tremendously. Are there any other mathematics related to SQS theory? For instance, golden ratio, fractals, Fibonacci numbers, Mor- ley theorem etc. It is important to point out that, except electron, the way to derive parameters from models for other particles is only for demonstration purpose. It is by no means the final version. In fact, the selection of p-parameters is still an open issue. Moreover, other than electron, the way to calculate particles geometrical parameters on the outer half of torus x-z cross section based on normalization 1'22 gg is optional. For the inner half, there are also some optional issues. For the primary basic equa- tions (25.48), solutions are not available yet. In essence, SQS theory is still a developing theory. The final version is waiting for these open issues and options to settle down. What this paper did is only scratching the surface. There are many open areas left to be explored. Simplicity is the guideline to develop SQS Theory. The phenomena in Physics world are complicated. The physics basic principle is simple. The deeper the level the simpler it is. At the deepest level, the basic principle should be the simplest. SQS Theory serving as a version of unified field theory has three fundamental postulation: the Gaussian Probability Postulation, the Prime Numbers Postulation and the Vacuon Postulation to begin with. After the establishment of SQS theory primary basic equation, the basic principles become even simpler. The Prime Number Postulation actually should derive from the set of primary basic equations (25.48) as the neces- sary condition for its stable or quasi-stable solutions. Moreover, since the vacuon serving as the basic unit of space and the carrier of Gaussian probability, the Vacuon Postulation can be combined with the Gaussian Probabil- ity Postulation. In other words, SQS theory ultimately has only one first principle, the Gaussian Probability Postulation, which provides our basic understanding of the space. The three basic physics units: Planck length, Planck time and Planck energy (Planck mass) are another example of simplicity. As its name implied, the key con- cept of unified field theory is the field. SQS theory as a unified field theory does not introduced a specific field, it utilizes the vacuum as the field of vacuon as the unified field to unify everything including all elementary parti- cles and interactions. Vacuum as the ground state of space is the simplest field for unified field theory. In essence, SQS theory is a mathematic theory. Its physics meaning is interpreted in terms of these three basic units. In principle, no more physics input is needed. In this regard, Planck contributed most. He not only was the one found the Planck constant h, but also was the one to point out that three Planck units can be defined by three basic physics constants: h, c and G. The final goal for SQS theory is to unify all interac- tions and all elementary particles into a self-consistent theory based on the first principle. It tells the whole story. It is exciting, but there is a long journey to go. A gold mine is out there. Let’s go for it.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1368 Section 27. Suggested Experimental Verifications for SQS Theory Predictions SQS theory is such a different theory from other particle physics and cosmology theories. Extraordinary claims re- quire extraordinary evidence. SQS theory provides 25 predictions for experimental and/or observational verifi- cations. 1) SQS theory predicts the mass of the scalar boson 1 U responsible for electroweak unification as: 2 /)5(754.152 cGeVMew . (27.1) The uncertainty of (27.1) comes from two sources: one is the relative accuracy of proton mass )23(272013.938 p M (PDG 2010 data) in 8 10 order, the other is the relative accuracy of )6(3701945.20)( b x limited by numerical calcula- tion, which is in 9 10order. So the uncertainty of ew Mgiven in (27.1) is a conservative one. The predicted value of ew M is within the energy range of LHC. 2) The hypothetical neutral gauge boson o with mass 2 /94690465.9cGeVM X probably has a very narrow width. It is worth the effort to find it; after all it is an elementary particle. After the o boson is found, the next thing is to find out the value of two parameters s g and s q defined as two sides of the S-triangle, which may provide some insights related to hadrons decay with the o boson involved. 3) The hypothetical scalar boson ffMs MMM is a neutral composite particle with predicted mass 2 /074032.115cGeVMMs . (27.2) The uncertainty of the mass value depends on the ac- curacy of electron’s mass in the order of 8 10~. 4) SQS theory predicted 8 hypothetical neutral scalar boson massons, i G, )83,2,1( i. The mass values listed in Table 14. 4 are within LHC capability. But there are some concerns of how to identify them. It is possible that, massons are attached to W , Z , X gauge bosons serving as part of their mass. If this is the case, massons are not detectable as individual particles. Nevertheless, there is a chance providing an indirect way to test the effects of two heavy massons, 7 G and 8 G each with mass values around 2 /342 cGeV. If they indeed attach to W or Z, it is conceivable to find two resonances around or higher than 2 /342 cGeV as the high energy states of W or Z. So there are two possibilities: One is to find all eight massons with their predicted mass listed in Table 14.4, the other is to find the effects of two heavy massons 7 G and 8 G attached to W or Z. Either way serves as the evidence of hypothetical massons. 5) More accurate experiments are needed to determine the mass and mixing angle of eigenstate neutrinos, which can be used to verify the three flavored neutrinos’ mass values of (17.4) as well as the estimated mass relations of (17.23) predicted by SQS theory. 6) As discussed in Section 5, photons’ speed varies with its frequency (energy) predicted by dispersion equa- tion (5.7). Since the dispersion effect is in the 56 10~ order for visible lights, it is virtually impossible to test by experiments in that wavelength range. The generalized dispersion equation (26.4) is relatively easier for experi- mental verification. Hopefully GRB090510 type of -ray bursts with much higher energy and longer dis- tance can provide chances for verification. 7) The long path concept originated from the Random Walk Theorem is very important in many senses. In case of entanglement, the extended long path makes the phys- ics link between entangled particles. Along the long path, interactions and information are transmitted with super- luminal speed many orders of magnitude faster than c, which was recently confirmed by experiment [9]. It serves as evidence for the superluminal speed. For direct evidence of the long path, one way is to confirm the maximum distance P Ld/)4/12( 2 0max between a pair of entangled photons. For an experimentally man- ageable distance kmd 1 max , required wavelength is in m 17 10475.8 range corresponding to -ray with energy of GeV629.14. The alternative way is to use a pair of entangled charged nucleons. The manageable distance can be increased by circulating the entangled nucleons in a ring with extremely high vacuum to pre- vent de-coherency. Such types of experiments are not easy, but it is worth the effort. Because so many things are based on the long path concept. 8) According to SQS theory, entangled photons have entanglement red shift and de-coherent blue shift. If some photons of the cosmic microwave radiation (MBR) were entangled to begin with, their entanglement red shifts and de-coherent blue shifts provide opportunities to verify them as well as for the stretched out long path for cross universes links. The cosmic MBR is the relic of high temperature radiations in the early universe with blackbody radiation spectrum. Due to the expansion of space, the MBR spectrum went through tremendous red shift and its temperature is lowered to 2.725k. The meas- ured cosmic MBR kept the blackbody spectrum. Ac- cording to the discussion in Section 5, the entanglement red shift is frequency (wavelength) dependent causing distortion to the blackbody spectrum. Comparing to the tremendous red shift caused by space expansion, the dis- tortion is extremely small even for the maximum red shift of 0max 5.1 according to (5.19). The de-coherent blue shift is unique. According to (5.22) and (5.24), the range of blue shifts for the photon far away from de-coherence location is from 1.5 times to 2 times  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1369 of its frequency. The red shifts and blue shifts have can- celation effect in the spectrum. It causes the difficulty to verify them. Fortunately, the highly raised peak of blackbody spectrum provides a mechanism to reduce the cancelation effect. Over all, the combination of entan- glement red shifts and de-coherent blue shifts causes the cosmic MBR spectrum deviated from the blackbody spectrum such that, its lower frequency portion has tiny gain due to entanglement red shifts and its higher fre- quency portion also has tiny gain due to de-coherent blue shifts, while its middle portion has deficit to pay for these gains. There are two ways for verification. One way is to compare the measurement cosmic MBR data with black- body radiation theoretical spectrum to find the deviation in different portions. The other way is based on statistic analysis of the measured cosmic MBR data. Since the stochastic nature of blackbody radiation and the ran- domness of measurements’ errors, the measured cosmic MBR data should have no statistic correlation among different frequency components. That is the scenario without counting the effects of entanglement red shift and de-coherent blue shift. The entanglement red shifts produce a correlation with gain for low frequency com- ponent and deficit for high frequency component in the spectrum’s lower and middle portions. The de- coherent blue shifts produce a correlation with deficit for low fre- quency component and gain for high frequency compo- nent in the spectrum’s middle and higher portions. The deviation overall effect upon the spectrum is to slightly lift up its two end portions and to slightly press down its middle portion. Due to the overwhelm effect of the space expansion red shift, the correlations and deviations are extremely small. It requires extremely sensitive and ex- tremely high precision measurements to verify. If the entanglement red shift deviation does exist, it indicates that some photons in the cosmic MBR are still entangled. If the de-coherent blue shift deviation does exist, it indi- cates that some originally entangled photons in the cos- mic MBR were de-coherent already. If none of these two deviations exist, it indicates that, either the photons in cosmic MBR were not entangled to begin with or the entangled photons were de-coherent shortly after their entanglement. In any case, it is worth the effort. 9) As discussed in Section 20, the difference between modified version and original version of Heisenberg un- certainty can be tested by looking into the images of stars at the edges of the visible universe. According to the original Heisenberg uncertainty principle, the blurred image can be detected. But so far no such blurred star image has been observed. According to the modified version of Heisenberg uncertainty principle proposed by SQS theory, the blurred image is not detectable. Use telescope with extremely high resolution and sensitivity to record the image of stars at the edge of visible uni- verse. If no blurred image is found, it serves as an indi- rect evidence to support the modified version of Heisen- berg uncertainty principle. The direct verification is vir- tually impossible, because it requires the high energy far beyond available technologies in the foreseeable future. 10) As shown in Section 17, The PDG-2010 data listed the upper limit 048.0 of “neutrino density” is close to the upper limit )4(044.0 b of baryon density in the universe, but the lower limit 0009.0 is far less than )4(044.0 b. From SQS theory standpoint, it is very important to narrow error range of the value of to determine the amount of 1 , 2 , 3 comparing to the amount of b . In addition, it is very important to measure the cosmology originated neutrinos’ handedness to determine the percentage of 1 , 2 , 3 , contribute to the “missing antimatters”. In case 1 , 2 , 3 contrib- ute only a part of the “missing antimatters”, it provides the opportunity for other types of antimatter candidates. 11) SQS theory would like to see more accurate ex- perimental data of the upper limit for flavored version neutrinos and anti-neutrinos electrical charge and mag- netic moment to verify whether they have remnant elec- trical charge or not. According to Conclusion 17.1, the three eigehstate anti-neutrinos 1 , 2 , 3 have no electrical charge. According to Theorem 17.1 and related discussions, for the flavored version e , , and e , , , SQS theory intends to favor no electrical change. Hopefully, further experiments will press the upper limits lower. 12) As discussed in Section 26, the cross-universes entangled eigenstate anti-neutrinos 1 oscillates only with 2 not with 3 , while the regular anti-neutrinos oscillate among all three members 1 , 2 , 3 . The dif- ferent oscillation patterns provide an opportunity for ve- rification. Of cause, 1 and 2 are not directly de- tectable, but their information can be extracted from the detected flavored neutrinos or anti-neutrinos based on the probability matrix of (17.26) and (17.27). The key is to make sure that, the neutrinos 1 , 2 are cross uni- verses originated. 13) According to SQS theory, part of dark matter is the debris left over from the cosmos inflation. In which the majority is 2-dimensional membranes flooding around in space. The right way to detect such dark matter should base on gravitation effects. As suggested in Section 23, gravity-meters with extremely high sensitivity isolated from earthly interferences fit the job. Recently, some experimental setups for verifying general relativity based on entangled atoms beam have very high sensitivity. Hopefully, they can be used to monitor the rare event of a piece of dark matter membrane passing by. 14) SQS theory predicts the mini-inflation caused by a piece of 2-dimensional dark matters membrane occa- sionally converting into a chunk of visible matters in the  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1370 3-dimensional space. As discussed in Section 23, the unstable particles’ decay modes and branching ratios are the same as the second generation particles’. In other words, the decay events happen in ordinary 3-dimen- sional space according to the same laws and rules. The way to verify this prediction is to detect the decay prod- ucts in the original cosmic ray and to see whether they fits the decay modes and branching ratios of second gen- eration particles. The most likely target of these cosmic rays source is the center region of galaxies, where the dark matter has higher density. Samuel Ting’s Alfa Magnetic Spectrometer fits this job perfectly. 15) SQS theory suggested that, there were more than one cosmic inflations happened after the big bang. These cosmic inflations should leave some traces on cosmic MBR. In Section 23, the first cosmic inflation and the third cosmic inflation happened at st42 1108278.3~ and st32 3100444.1~ after the big bang, respectively. It is worthwhile to look for possible traces. 16) SQS theory predicts that cosmic history went through three periods each with different dimensional spaces, 3 1 1-dimensional, 2-dimensional, 3-dimensional for the st 1 period, nd 2 period, rd 3 periods, respec- tively. The space with different numbers of dimensions should leave some traces on cosmic MBR map or some- where else. When more detailed data with better preci- sion and resolution are available, that is the place to look for. 17) According to the logistic recurrent process de- scribed in Section 16, in the intermediate scale from Compton length to GUT scale, the mass of a particle such as electron or muon increases continuously. This effect is testable. For instance, Randolf et al found that, to replace electron with muon in the hydrogen atom, some peculiar behaviors were observed including differ- ent values for proton’s size and the Rydberg constant [33]. In this case, the muon is much closer to the proton than electron. The changing mass effect due to random walk theorem may be responsible for these anomalies. It is worthwhile to check with existing experiments data and the future ones. 18) As shown in Section 7, SQS theory predicts that, muon has zero probability to decay in the time intervals stt 13 min 1020750 and the probability of decay at time st3 100933.8 or longer is less than 7 10, in which time 0t is set at the birth of the muon. When the muon factory is in operation, the two predictions should be relatively easy to check with experiments. If these predictions are confirmed, which serve as suppor- tive evidences for )(kDSk as particles spectrum. 19) SQS theory suggested that, quarks with the same flavor and different colors are different elementary parti- cles having different masses. The difficulty to confirm is due to the fact that, there is no isolated individual quark in existence. Fortunately, there is an indirect way. Nu- merical calculation methods such as the lattice QCD to analyze hadrons experimental data are capable to extract the mass values of their component quarks. Comparison of PDG-2010 data with PDG-2008 data found more dis- tinctive multi-peak behaviors of flavored quark’s mass curves, which support SQS theory. Hopefully more ex- perimental data and more powerful numerical computa- tion capability for lattice QCD will finally verify the mass values of 18 quarks listed in Table 11.2. 20) SQS theory proposed the multiverse with 22 10~ member universes organized into two levels. There are two possible ways to verify this hypothesis. One way is to look at the cross-universe entangled eigenstate an- ti-neutrino 1 and 2 oscillation pattern as suggested in Prediction No. 12. The other way is to look at the cosmic MBR map to search for the trace of cross uni- verses entangled photons. If such photon is found, it serves as evidence for cross universes entangled photons pair as well as for the neighbor universe in the multiverse. But one must make sure that the entanglement is cross universes. One possible way to verify is to observe the de-coherent blue shift. According to (5.24), for the de-coherence located at max dd in a neighbor uni- verse, the originally entangled photon in our universe shows a large blue shift as its frequency suddenly dou- bled to ff 2' max,0 . It also serves as evidence for the existence of long path. 21) According SQS theory, graviton is scalar boson with spin 0 instead of tensor boson with spin 2. The deci- sive proof is to find the graviton and to measure its spin. Graviton having spin 0 is based on mathematics sup- ported by two Number Towers and independently veri- fied by Poincare’s “hairy ball” theorem. SQS theory takes conclusion 26.1 seriously. There are many existing experimental setups designed to look for gravitational wave and gravitons. Perhaps all of them are based on the assumption of graviton having spin 2. Whether these types of setups eligible to find graviton with spin 0 or not? It is a question for experimenters and general relativity theorists to think about. The urgency is enhanced by the fact that, despite decades of extensive efforts, no gravita- tion wave or graviton have found. It is the time for a second thought. 22) According to Definition 26.2, Theorem 26.1 and Lemma 26.1, Lemma 26.2, when two absolute black holes collide in the proper ways, they transfer into a reg- ular black hole with genus-0 event horizon or a special black hole with genus-2 event horizon. Both are eligible to have Hawking radiations. As discussed in Section 26, absolute black hole with ginus-1 event horizon has Hawking mechanism without Hawking radiation. The absolute black hole holds half photons of virtual photon pairs produced by Hawking mechanism in its event ho-  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1371 rizon. After the collision, these held photons suddenly have the chance to release. The burst of Hawking radia- tions caused by collision is detectable. Moreover, since the gravity distribution pattern of absolute black hole with genus-1 event horizon is quite different from that of black hole with genus-0 event horizon, the different pat- terns provide another way to indentify the absolute black hole. 23) As shown in Section 26, GUT based on )5(SU group may have a chance to revival. The key is to reinterpret the results of I-M-B type and S-K type ex- periments. It is worthwhile to consider how to redo these experiments with larger water tank. For instance, if the linear size of water tank is increased by 20-fold corre- sponding to 8000 times more protons involved, it would be possible to see some proton decay events. But before doing that, one must make sure proton’s yearst 10 min 10from theoretical estimation. 24) A remote hope is to find the e-boson with pre- dicted mass GeVM be8 ,10959754.3 , which is roughly 4 10 times higher than the full scale energy of LHC. It is far beyond the current accelerator capability. But there is another way. Occasionally, a cosmic ray with extremely high energy hits earth. There is a chance that, it contains the trace for the leftover e-boson or its decay products from the big cosmic inflation. It is worthwhile to monitor and observe. The verification of the e-boson is significant. It not only will confirm electron having a high energy intermediate boson state but also will shed lights on de- tails of the cosmos inflation. Let’s keep hoping. 25) The author is confident to voluntarily offer a falsi- fied test for SQS theory. In our universe current period, if any experiment and/or observation find additional space dimension or dimensions beyond the existing three space dimensions, SQS theory is proved to be false. Hopefully some experimental physicists will be inter- ested and figure out the ways to carry out these proposed experiments. The author is standing by for assistance. Section 28. Conclusions The conclusions of SQS theory are summarized as fol- lows. 1) For current cosmic period, space is a 3-dimensional continuum with Planck scale face-centered lattice as the basic building block. 2) Space is stochastic in nature with Gaussian prob- ability distribution function attached at each discrete point, which serves as the ultimate origin of all physics uncertainties and stochastic behaviors. 3) Space is made of a collection of infinite point parti- cles called vacuons corresponding to infinite geometrical points. Vacuons serve as the event carriers of the Gaus- sian probability distribution function. 4) The Gaussian sphere is defined as a sphere with ra- dius )22/( P Lr . The separation between two adjacent Gaussian spheres is 2/2P Lr determined by the balance of gravity attractive and repulsive forces. 5) SQS theory is background independent. Space structure is not a priori determined. At upper level, rede- fined gauge tensors adjust simultaneously in according with mass and energy distribution governed by macro- scopic basic equations (25.31). Inside the M-sphere with radius PM LR 71 , Gaussian spheres governed by grav- ity arrange themselves to reach minimum potential en- ergy. At the Planck scale, redefined gauge tensors adjust simultaneously to satisfy microscopic primary basic equ- ations (25.48). 6) Space is classified into three regions: (1) The mi- croscopic region (2) The intermediate region (3) The macroscopic region. The classification is based on ma- thematics and physics. The boundary of the microscopic region is set by the GUT scale of P L71 , The boundary of the intermediate region is set by the Compton scale C , which have deep physics meanings and mathemati- cal foundation. 7) Inside the M-sphere, space has Planck scale face-centered lattice structure including two parts, the cubic part and the octahedral part. Space symmetries based on its face-centered lattice structure are classified into two types, )(rO and )(rC , each has 18 symmetries within 3 r, which serve as the origin of the symmet- rical groups for elementary particles and interactions. 8) The Random Walk Theorem is proved based on Gaussian Probability Postulation. It serves as the founda- tion of many important issues for SQS theory. For the two long rang forces, according to Theorem 22.1, the random walk zigzagging path each step stops only at cubic vertexes. 9) Based on the Random Walk Theorem, the short path and long path are defined. Short path is the distance between two points; long path is the random walk zig- zagging path connecting two points. The ratio of the long path and the short path is defined as the converting fac- tor. 10) Converting rules based on the Random Walk Theorem are used to treat hierarchy problems. The effec- tiveness of these converting rules serves as physics evi- dence for the Random Walk Theorem. 11) SQS theory supports locality. Einstein was right: “No spooky action at a distance”. A pair of entangled particles is physically linked by the stretched out long path. The transmitting speed of information and interac- tions along the long path between the entangled particles is superluminal but not infinite. 12) Photons have dispersion. Its speed varies with frequency (energy). The real meaning of c is a basic  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1372 physics constant. No photon travels with speed exactly equal to c. For the short path, photon travels with speed slightly less than c. For the long path, interactions and information transmit with superluminal speed cvLNvvP)/( ˆ . Dispersion equation is given by (5.7) and generalized by (26.4) serving as revision of special relativity. 13) The 1-dimensional S-equation is defined based on Gaussian Probability Postulation. It serves as the base for a series of secondary S-equations with impacts on dif- ferent areas. 14) In x-axis region 25.0,0 , the S-equation’s solution 730264 2499871562.0 c x is a very special point. It provides the mass value of two scalar bosons 1 U, 2 U, and to some extent the mass value of top quark and three gauge bosons , W, 0 . 15) For the 3-dimensional Gaussian probability distri- bution function, its standard deviation has three values, ,2/1 0 2/ 3/2 2 i e, 2/ 3/4 3 i e, corre- sponding to the three branch points on Riemann surface. According to Roger Penrose, the three branch points plus another one at infinity serve as the ends of the two pairs of cuts on Riemann surface two sheets. The edges of two pairs of cuts are glued together, it makes the two-sheet Riemann surface topologically equivalent to a torus with four tiny holes. The torus serves as the basic building block of models for Dirac type fermions and some bos- ons with mass. 16) Dirac type fermions have two components geo- metrically represented by two loops. Loop-1 is the torus center cycle, and loop-2 is perpendicular to loop-1 and has its center at the circumference of loop-1. 17) According to theorem 18.1, Lemma 18.1 and Lemma 18.2, the vacuons as point particles with non- infinite speed only take discrete 1-dimensional trajecto- ries. It serves as the basic quantization of space for SQS theory. 18) Dirac type elementary fermion is represented by a set of trajectories on its torus based model. Along a tra- jectory, there are three types of internal movements: a cyclic movement along loop-1, another cyclic movement along loop-2, and an oscillation along the trajectory path. 19) According to Theorem 18.1 Lemma 18.1 and Lemma 18.2, particle’s trajectory must be 1-dimensional and it changes trajectory only by jumping not by shifting. The movements in a trajectory are totally deterministic and the uncertainty only comes from jumping trajecto- ries. 20) A set of three numerical parameters, m, n, p is as- signed to each Dirac type fermion. The ratio of n/m equals to the length ratio of loop-2 to loop-1 for the fer- mion’s torus model. The ratio p/n equals to the ratio of fermion’s mass to electron’s mass. The value of numeri- cal parameters, m, n, p are ultimately determined by cor- responding solutions of primary basic equations (25.48). 21) According to Theorem 3.1, the 1-dimensional S-equation defined )( 1 x and )( 2 x serve as messen- gers carrying curvature information to the torus model to define the locations of characteristic points on its surface. 22) On the x-axis, region cdcxxxx 5.0 is de- fined as the gauge boson region. Fermion’s 1 x and 2 x in this region with mass 2 /97323432.4 cGeVMM Max must be paired with anti-fermion as a boson state. 23) Elementary particles are represented by trajecto- ries on models with genus numbers of 0, 1, 2, 3 as listed in Table 26.2. 24) On its model surface, fermion’s trajectory is made of two connected geodetics between two characteristic points and B defined by )( 2 x and )(1 x , re- spectively. The value of )( 1 x and )(2 x are deter- mined by fermion’s mass and the 1-dimensional S-equation. The values of these geometrical parameters are ultimately determined by corresponding solutions of primary basic equations (25.48). 25) On fermion’s torus model outer half surface, the characteristic points defines the GWS-triangle and S-triangle, which provide geometrical parameters for electromagnetic and weak interactions. On fermion’s torus model inner half surface, the characteristic points B defines the CKM-triangle corresponding to hadrons decay modes. These characteristic points and triangles represent the geometric parameters for the particle, which serve as the origin of particle’s physics parameters. The values of these geometrical parameters are ulti- mately determined by corresponding solutions of primary basic equations (25.48). 26) The AT-equation and PS-equation with the mass term )/2sin( mp to break the 120 symmetry, which serves as the mechanism to provide particle’s mass. Despite their ad hoc origin, the results derived from AT-equation and PS-equation are agreed to experi- ment data with reasonable accuracy. 27) According to Postulation 11.1, quarks with the same flavor and different colors are different elementary particles with different parameters. Accordingly, there are eighteen quarks instead of only six. It is supported by two independent experimental evidences. 28) The Prime Numbers Postulation along with even pairing rule plays pivotal roles in many areas including elementary particles and cosmology. The 18 least odd prime numbers 1, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61 paired as even pairs are assigned as the m-parameters of 18 quarks, r u, r d, g d, g u,b d, b u, r s,r c, g s, g c, b s, b c, r b, r t, g b, g t,b b, b t, respectively. Quarks n-parameters are also selected from prime numbers. 29) There are only three generations of elementary  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1373 particles. The fourth generation and beyond are strictly forbidden by mathematics. 30) Lepton’s before reduction m-parameter equals to the average value of corresponding up type and down type quarks m-parameters. All leptons reduced m-para- meters equal to 1 corresponding to spin 2/. Leptons’ reduced n-parameters are fractional, which play a pivotal rule for weak interactions and serve as mathematical dis- tinction between leptons and quarks. 31) The n-parameter for the flavored version neutrinos and anti-neutrinos, e , , , e , , , is de- termined by the matching rule of (17.1), which matches the n-parameter of corresponding charged lepton. The weak interactions are classified into two types. The ordi- nary type meets the matching rule and satisfies the lepton family numbers conservation law. The rare type violates the matching rule and the lepton family numbers conser- vation law. 32) According to SQS theory, the eigenstate neutrinos 1 ~ , 2 , 3 all are Marjorana type, which are the ones flying around in space. The flavored version neutrinos and anti-neutrinos e , , , e , , as Dirac type only exist at the birth or been detected. The relation between the eigenstate version and the flavored version neutrinos is determined by converting probability ma- trixes of (17.26) and (17.27). This scheme eliminated the chaser’s paradox and provided a candidate for the “miss- ing antimatters”. 33) Photon as a gauge boson with spin has single closed loop structure. 34) The eight gluons are made of corresponding quark and anti-quark of the same typejji qqg )8,2,1( i ),,,,,,,( bgrbbggr sssududdj . Strong interactions are me- diated by eight gluons and classified into two types. The ordinary type mediated by gluons with the same handed- ness and the weakened type mediated by gluons with different handedness. 35) Based on Theorem 13.2, SQS theory provided a simplified way to treat certain composite particles such as proton, neutron, and some light nucleons. It shows some promises in terms of interpretation for the binding forces for these composite particles based on simple ma- thematic rules. 36) Graviton has spin 0 represented by cutoff loop with length P L2, which is supported by Poincare’s “hairy ball” theorem. The cutoff loops move through the long-path and only stops at cubic vertexes serving as the building blocks for space with cubic lattice structure. 37) Bosons with mass are made of combination of their fermions constituents, and so are their trajectory and model. 38) The unifications for electro-weak, elec- troweak-strong, and grand unification of all four interac- tions including gravitation occur at energy scales of GeV7547.152, GeV 15 1044708.8 , GeV 18 1007948.1 , respectively. 39) Logistic recurrent process plays an important role to drive the converting factor as a running constant from grand unification scale to Compton scale with important impacts on elementary particles and interactions. 40) Grand number phenomena with rank-G based on G11 10~ (g37 2 ) are found in many areas including elementary particle physics and cosmology. Grand num- ber phenomena are intrinsically related to logistic process, random walk, group theory and Gaussian probability. 41) SQS theory provides the Elementary Particles Ta- ble including 72 particles. The number 72 is supported by two Number Towers with the special prime number 163 on top of it. It is an indication of mathematics at work. 42) In the deeper level, there is only one elementary particle, vacuon. All elementary particles and interac- tions are ultimately originated from different patterns of vacuons movements. 43) Heisenberg uncertainty principle is valid only for P Lzyx ,,. Inside Planck cube, Heisenberg uncer- tainty principle must be modified, otherwise the infinite energy paradox is inevitable. SQS theory provided a re- vised Heisenberg uncertainty principle (20.14) based on the extended 1-dimensional S-equation, for which the infinite energy paradox is eliminated and the quantum fluctuations with high energy is significantly reduced. 44) SQS theory provides a simple formula 2 71/)( M to determine the values of fine structure constant )(M at different mass scales. At three mass scale, e M, Z M and GUT M, it provided reasonably ac- curate results. )(M as a physics running constant is originated from as a mathematic running constant. 45) According to the Prime Numbers Postulation and Postulation 23.1, cosmic history is intrinsically related to elementary particles and both are based on prime num- bers. Three more sets of prime numbers were found cor- responding to three cosmic periods, the st 1-period, the nd 2-period, and the before-big-bang-period. The legiti- macy of three sets of prime numbers has additional sup- port from the correlations given by (23.9), (23.10), (23.11) and Conclusion 23.2. 46) According to SQS theory, started from the big bang, two or three space phase transitions occurred at st 42 1108278.3 , st 40 2108963.4 (optional), and st 32 3100444.1 . The one occurred at 3 t caused the big cosmic inflation suggested by cosmology standard model. 47) According to SQS theory, electron has an interme- diate boson state. The e-bosom, with mass 28 /1095987106.3cGeVM be serves as the inflaton to drive the cosmic inflation. 49) Based on the )(rO and )(rC symmetries in the  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1374 face-centered space, the elementary particles and interac- tions in the cosmic periods are explained naturally. The )(rO and )(rC symmetries also serve as the frame- work for primary basic equations (25.48). 49) At least part of dark matters is 2-dimensional de- bris left over from cosmic inflation, which only interact with ordinary matters via gravity. Two suggestions are given for verifications. 50) Based on Definition 23.2 and Hypothesis 23.2 and the “negative prime numbers table”, SQS theory pro- posed a cyclic universe model. In which the negative prime numbers sequences represent a cosmic contracting period ended up with the big crunch. The post-big-crunch universe transfers via a time tunnel into the pre-big-bang universe, and a new round of cosmic cycle starts. 51) SQS theory supported the multiverse concept as a possible way to resolve the second thermodynamic law problem during the cosmic contracting period. Based on grand numbers and the two prime numbers sequences, number of universes in the multiverse is estimated around 22 10 organized in two levels. 52) SQS theory proposed the limited anthropic princi- ple. For any member universe in the multivers during its third period, the change of physics laws and the variation of physics constants are not arbitrary; they subject to strict restrictions imposed by the same set of 18 prime numbers of our current universe. 53) Close correlation between the prime numbers se- quence of three finite sporadic Lie groups, M-group, B-group, Suz-group and the 18+1=19 prime numbers assigned as the m-parameters for the 18 quarks and elec- tron was found, in which the missing prime numbers in the sequence are correlated to some top type quark’s bo- son states. The correlation provides additional support to the Prime Numbers Postulation. 54) Based on the largest prime number 71 in the prime numbers sequence of M-group, the M-sphere with radius P Lr 71 is defined. Inside the M-sphere, two more spheres, the B-sphere with radius P Lr 47 and the S-sphere with radius P Lr23 are defined. Between M-sphere and B-sphere is the “quark-antiquark liquid state” region; inside the S-sphere all elementary particles are distinguishable. In between the B-sphere and S-sphere, it is the transition region. 55) Poincare’s “hairy ball” theorem and related rules play important roles for elementary particles in terms of trajectories, models and interactions as well as for cos- mology. As shown in Section 26, black hole has hairs and must have crowns, cross universes connections are necessary, and graviton must have spin 0. These are the conclusions supported by Poincare’s “hairy ball” theo- rem and related rules. It is mathematics at work. 56) Based on Poincare’s “hairy ball” theorem, SQS theory proposed the absolute black hole with no radiation of any kind and the suggestions for verification. 57) Another set of 13 even pairs of prime numbers as listed in Table 26.3 is found. According to Hypothesis 26.2, it corresponds to a super-multiverse including 45 10~ member multiverses organized in two levels, each level has 22 10~ member multiverse. Hypothesis 26.2 is supported by grand numbers as well as its esti- mates for dark energy hierarchy problem agreed with other estimates and observed data as listed in Table 26.4. 58) Based on Einstein equation (25.1b) for vacuum with redefined gauge tensors attached to probability, SQS theory established two sets of basic equations. The macroscopic set includes equations (25.31) for gravity and equations (25.43) for electromagnetic force. The microscopic set is equations (25.48), which serve as the primary basic equations representing all elementary par- ticles and interactions as well as things on upper levels. 59) In essence, SQS theory is a mathematic theory with physics interpretations. Based on three basic physics constants c, h, G or equivalently P L, P t, )(pPME. In principle, all physics parameters can be derived from mathematics with c, h, G or P L, P t,)( pPME as “interpreters”. Let’s end this paper with two famous ancient state- ments, one from East and one from West. East philosopher: “道生一,一生二,二生三,三生万物。” 老子 English translation: “Tao generates one, one generates two, two gener- ates three, three generates everything.” Laozi West philosopher: “Everything is numbers.” Pythagoras Acknowledgement First and foremost the author would like to thank the authors, editors and all contributors of Review of Particle Physics, Particle Data Group (PDG). The experimental data listed in PDG biannual report are extensively cited in this paper as supportive evidences for SQS theory. Without these experimental results, it is impossible to develop SQS theory. The author would like to thank Roger Penrose for his book The Road to Reality—A Complete Guide to the Laws of the Universe. It provides extensive mathematic background knowledge. Especially in Chapter 8, a short and comprehensive description of Riemann surface and correlations to torus gives the author confidence finally to nail down the torus model and the four characteristic points on its surface. The author would like to thank Mark Ronan for his book Symmetry and the Monster—One of the Greatest Quests of Mathema tics, and the mathematicians involved in study of the sporadic groups. The book provides an  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1375 overall and easy to understand summary of finite Lei groups with emphasis on M-group and other finite spo- radic groups. Without reading this book, the author would miss the opportunity to find the correlations be- tween M-group, B-group, Suz-group and three sets of prime number m-parameters for three generations of quarks, which serve as important checkpoints for the Prime Number Postulation and many related issues. The author would like to thank the JMP Editorial Board and staffs for their special effort to publish such long paper. The author would like to thank Leo Birenbaum, Char- lie Charter III, Xiao-Chun Gao (高孝纯), William Hol- stein, Fan Jin (靳蕃), Alan Lauder, Guang-Juang Ni (倪 光炯), Author Oliner, Cheng-Yi Pan (潘承毅), You-Xing Pan (潘友 星), John Radomsky, ShaoXue Ren (任绍绪), Kemin Sheng (盛克敏), Jian Song (宋健), Xiang-Bai Tan (谈祥柏), Qi-Dong Wang (王启东), Qing-Dong Yao (姚庆栋), Wen Zhou (周文 ), and Xue-Tian Zhu (朱雪天) for their helps, supports and en- couragements. During the six years long journey to de- velop SQS theory, their helps, supports and encourage- ments were very important to the author especially in difficult times. The author would like to thank Zhejiang University especially its Mathematics Department and Physics De- partment for providing basis science education for the author, which is very important to develop the SQS The- ory. The author would like to thank the DuPont Company and the US Government to provide the pensions for the au- thor to support the development of SQS Theory. References All experimental data cited in this paper unless stated otherwise are cited from Review of Particle Physics, Particle Data Group (PDG) 2010. [1] Shen, Zhiyuan (沈致远) (2007), “On Stochastic quantum space and related topics”, Frontier Science,4, 4-35. In Chinese with English abstract. [2] Penrose, Roger, The Road to Reality: A Complete Guide to the Laws of the Universe, Vintage Books, New York, 2007, 135-138. [3] Nanneke, D., Fogwell S. and Gabrielse G. (2008), Phys. Rev. Lett. 100, 120801. [4] Aoyama, T., Hayakawa M., Kinoshita T. and Nio M. (2008), Phys. Rev. D77, 053012. [5] Feynman, R. P. and Hibbs A. R., Quantum mechanics and path integrals, McGraw-Hill, 1965. [6] Abdo, A. A. et al. “Testing Einstein’s special relativity with Fermi’s short hard -ray burst GRB090510”, Aug. 13, 2009, available at: http://arxiv.org/abs/0908.1832v1. The supplementary material available at: at:http://gammaray.nsstc.nasa.gov/gbm/grb/GRB090510/ supporting_material.pdf [7] Abdo, A. A. et al. “A limit on the variation of the speed of light arising from quantum gravity effects”, Nature Letter, published on line, Oct. 28, 2009. [8] Supplementary Information, available at: http://www.nature.com/nature/journal/v462/n7271/extref/ nature08574-s1.pdf [9] Salart, D., et al. (2008), Testing the speed of ‘spooky action at a distance’, Nature, 454, 861. [10] Hestenes, David, (1990), “The Zitterbewegung Interpre- tation of Quantum Mechanics”, Found. Physica, 20, No. 10, 1213-1232. [11] Green,,M. B., J.H. Schwarz and E. Witten, String Theory, Cambridge Press, Vol.1, 27-42. [12] Penrose, Roger, The Road to Reality: A Complete Guide to the Laws of the Universe, Vintage Books, New York, 2007, 943-946. [13] Klinkhamer, F. R., Manton, N. S., (1984), “A Sad- dle-Point Solution of the Weinberg-Salam Theory”, Phys. Rev., D30, 2212-2220. [14] Lerner, R. G., and Trigg, G. L. (1990), Encyclopedia of Physics, Second edition, VCH Publishers, 445-448. [15] Georgi, H., Glashow, S. L., (1974), “Unity of All Ele- mentary Particle Forces”, Phys. Rev. Lett. 32, 438-441. [16] Shen, Zhiyuan (沈致远) (2008), “Correction and Pre- diction”, Frontier Science, 8, 86-87. In Chinese. [17] Jegeriehner, F., (2008), “The running fine structure con- stant )(E via the Adler function”, Nuclear Physics B-Proceedings Supplements Volumes 181-182, 135-140. [18] Ronan, Mark, Symmetry and the Monster, One of the Greatest Quest of Mathematics, Oxford University Press, 2006, 227-228. [19] Guth, Alan, The Inflationary Universe, Reading, Addi- son-Wesley, (1997). [20] Misner, C. W., Thorne, K. S. and Wheeler, J. A., Gravi- tation, Freeman and Company, New York, 2003. [21] Green, M. B., Schwarz, J. H. and Witten, E., Superstring Theory, Cambridge University Press. 1987. [22] Abhay, Ashtekar (1986), “New variables for classical and quantum gravity”, Phys. Rev. Lett. 57 (18): 2244-2247. [23] Sundance, O. Bilson-Thompson, “A topological model of composite preons”, arXiv:hep-ph/0503213v2 27 Oct 2006 and a preprint for Elsevier Science, May 19, 2006. [24] Bilson-Thompson, Sundance O., Markopoulou, Fotini, Smolin, Lee, “Quantum gravity and the stardand model”, arXiv:hep-th/0603022. [25] Wilczek, Frank, “Why are analogies between condensed matter and particle physics?” Physics Today, July 1998, 11-13. [26] Christopher, T. Hill and Elizabeth H. Simmons, (2003), “Strong dynamics and electroweak symmetry breaking”, Physics Reports, 381, 235-402. [27] Georgi, Howard and Glashow, S. L., (1974), “Unity of all elementary-particle Forces”, Phys. Rev. Lett.32, 438-441.  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1376 [28] Lerner, Rita G. and Trigg, George L., (1991), Encyclope- dia of Physics, second edition, VCH Publishers, 446-448. [29] Dyson, Freeman, (2008) “Birds and frogs”, Notice of AMS, 56 (2), 212-223. [30] Levine,Dov, Steinhardt, Paul J., (1984) “Quasicrystals: a new class of ordered structure”, Phys. Rev. Lett. 53, 2477-2480. [31] Elwes, Richard, Mathematics 1001, Firefly Books, 2010. [32] Penrose, Roger, The Road to Reality: A Complete Guide to the Laws of the Universe, Vintage Books, New York, 2007. 958-1003. [33] Randolf, P., et al. (2010), “The size of proton”, Na ture Letters, 466 (8), 213-217. doi:10.1038/Nature09250. Appendixes Appendix 1 The 1-dimensional Gaussian probability function of (2.4) is: 2 )(exp);( ii xxxxp ; ,,0,,x, ,2,1,0,1,2, i x. (2.4) Take Fourier transform of i xxp; with respect to variable : ii iiii iii ikx k dikx k ik xxd ik xx ik xx dxx ik xxdxikxxxpxkP exp 4 exp 2 1 expexp 4 exp 2 1 22 exp 2 exp 2 1 )(exp 2 1 )exp();( 2 1 ; 2 2 2 22 2 2 . (A1.1) The real part of (A1.1) is the probability distribution function in k-space: 4 2 2 1k ekP . (A1.2) The imaginary part of (A1.1) is the phase factor: i ikx iexkQ ;. (A1.3) As shown by (A1.2), kP is also Gaussian as ex- pected. For kP , the unitarity requirement is satisfied: 1 2 14 2 dkedkkP k . (A1.4) The standard deviation of kP is 2 k. (A1.5) Multiplying k with given by (2.3) yields: 1 k. (A1.6) Appendix 2 Three-dimensional geodesic coordinators in parametric form are: )( sxx ; .,, cba (A2.1) Here a x,b x,c x are 3-dimensional spatial coordina- tors, and s is the affine parameter. The solution sxx of following differential equation represents geodesic: 0 2 2 ds dx ds dx ds xdcb a bc a. (A2.2) In which, the Christoffel symbol of second type is: c db b cd d bc ad bcd ada bc x g x g x g gg 2 1. (A2.3) The components of a symmetrical gauge tensor satisfy: baabgg . (A2.4) Appendix 3 Let’s evaluate the effect on kDSk of disregarding the factor: iririr kkikkkik keeee 2)()( 222 2 4 1 4 1 4 1 . (A3.1) For the local minimums or local maximums of )(kDSk are evaluated by its absolute value kDSk, the second factor irkki e 2 of (A3.1) does not have effect, because 1 2 irkki e regardless the values of r k and i k. Since mass and decay times are determined by the location of local minimums or local maximums of kDSk on complex k-plane, the effect of 22irkk e is only related to the variation of r k and i k. i kk iir kk r i kk i r kk r kk kdekikdek kde k kde k ed irir iririr 2222 222222 22 . (A3.2) Substitute the muon data from Table 7.1 into (A3.2): 010~2 1000003 22 eek ir kk r ; (A3.3a) 010~2 10000014 22 eek ir kk i . (A3.3b) Substitute the taon data from Table 7.1 into (A3.2): 010~2100000004 22 eek ir kk r ; (A3.4a) 010~2 100000007 22 eek irkk i . (A3.4b) In both cases, the errors caused by disregarding the factor 22 irkk e are negligible. Appendix 4 The fine structure constant is: hc e 0 2 2 . (A4.1)  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1377 0 is permittivity of free space. Compton wavelength of electron is: cM h e eC . (A4.2) Classical electron radius is: 2 0 2 4cM e r e e , (A4.3a) Electron mass is: 2 0 2 4cr e M e e . (A4.3b) According to the converting rule given in Section 4, Compton wavelength eC is originated from Planck wavelengthPP L , which is the circumferential length of circular loop-1. On the other hand, e r is defined as radius. To be compare on the same base, eC should compare toe r 2. Since mass is inversely proportional to corresponding wavelength, the ratio of electron’s electromagnetic mass eM M to its total mass e M is: hc e cM h cM e r M M e e eC e e EM 0 2 2 0 2 2 4 2 2. (A4.4) The electromagnetic modification factor for mass is: 11 e EM e EMe M M M MM . (A4.5) (A4.5) is valid to other charged particles as well. Appendix 5 The origin of logistic equation is the following nonlinear difference equation: 2 1jjj xxx , 3,2,1j. (A5.1) In which parameters 0 and 0 represent the positive action (Type-P) for positive feedback and nega- tive action (Type-N) for negative feedback, respectively. Convert the variables in (A5.1) as: jixx ; 3,2,1i; 3,2,1j , (A5.2a) 11 ji xx ; 3,2,1i; 3,2,1j . (A5.2b) Substituting (A5.2) into (A5.1) yields the logistic equ- ation with parameter : )1( 1iii xrxx , 3,2,1i. (A5.3) . (A5.4) The logistic equation of (A5.3) represents a recurrent process. In (A5.3), and is absorbed. As value increases, Type-P action overwhelms Type-N action. (A5.3) is the logistic equation with constant parameter . In some cases, parameter also varies, which be- longs to the varying type logistic equation. In the logistic equation (A5.3), variables i x and )1( i x can be interpreted as a pair of binary prob- abilities. In this way, logistic equation represents a ran- dom recurrent process, in which the next step variable 1i x is determined by variables i x and )1( i x of the present step. The process evolves until it settles down or becomes chaotic depending on the value of parameter . Appendix 6 Part-A: For a Gaussian sphere centered at a vertex based on Postulation 25.1A. Based on Postulation 25.1A, the redefined parameters of equations (25.7) are: )()( GRGGR ab ab , (A6.1a) ),()()()( 2 1 )()()()()()()()( 2222 GGGG xx G xx G xx G xx G G GGGGGGGRGR c db d ac c dc d ab ab cd db ac ac bd dc ab cd c db d ac c dc d ab c acb c abc c acbab (A6.1b) c db b cd d bc ad dbc ada bc x G x G x G G GGG2 )()(, 3,2,1,0, ba . (A6.1c) In (A6.1), the terms containing derivatives of );( 0 PPpgG abab have two forms: (1) The product of two first order deriv, atives f cd e ab G G . (2) The second order derivative fe ab xx G 2. According to (25.3) and (25.4), the derivation process yields: e ab e ab L e ab e ab e ab e ab ab ee ab x L Lg x g pe x g x g p x p g x g ppg xx G 2)( 2, (A6.2a) .)12(2 22)12(22 22222 2)( 2 2 2 2 2 2 2 2 2 2 22 22 fe ab ef ab fe ab fe ab fe ab L ef ab fe ab fe ab fe ab fe ab L ef ab f ab L fe ab fe ab fe ab fe ab L f ab f ab e L ab fe ab fefe ab xx L Lg x L x g L x L x g L x L x L gLp xx g p e x L x g L xx L Lg x L x L gL x L x g L xx g e x L L x L Lg x g e xx L Lg x L x L g x L x g L xx g e x L Lg x g x eg xx pg xxxx G 3,2,1,0,,, feba . (A6.2b) In (A6.2a), the p factor is canceled by the p/1 factor of pgGabab/. After cancelation, the product of two first order derivatives is:  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1378 .22 22 1 2 2 fe ab cd ef cd ab fe cdab f cd e ab f cd f cd e ab e ab f cd e ab x L x g Lg x L x g Lg x L x L Lgg x g x g x L Lg x g x L Lg x g x G x G p 3,2,1,0,,,,, fedcba . (A6.3a) In (A6.3a), the first term serves as the term of original kinematic term in Einstein equations, which is in the )()()()( gggg c db d ac c dc d ab part of ab R and . The terms in the parenthesis serve as the terms in the emerging terms ab R and R . In (A6.2b), the probability p factor is canceled by the p/1 factor of pgG abab/. After cancelation, the second order derivative is: .)12(2 12 2 22 fe ab ef ab fe ab fe ab fe ab fe abxx L Lg x L x g L x L x g L x L x L gL xx g xx G p 3,2,1,0,,, feba . (A6.3b) In (A6.3b), the first term serves as the term of original kinematic term in Einstein equations, which is in the ab cd db ac ac bd dc ab cd xx g xx g xx g xx g g2222 2 1 part of ab R and R. The terms in the parenthesis serve as the terms in the emerging terms ab R and R . According to (A6.3), the emerging terms R and ab R are given as follows. ab abRgR , (A6.4a) .)12( )12( )12( )12(2 2 2 2 2 2 2 2 2 c db d ac c dc d ab ab cd ba cd ab cd ab cd db ac bd ac db ac db ac ac bd ca bd ac bd ac bd dc ab cd ab dc ab dc abab xx L Lg x L x g x L x g L x L x L gL xx L Lg x L x g x L x g L x L x L gL xx L Lg x L x g x L x g L x L x L gL xx L Lg x L x g x L x g L x L x L gLR (A6.4b) b cd d bc c db ad dbc ada bc x L g x L g x L gLgg ,.3,2,1,0,,, dcba (A6.4c) As shown in (A6.4), the emerging part includes three type terms: fe ab L g ,fe L L ,fe L 2 . According to (25.5), derivation process should be carried out further accord- ing to space-time variables )(),(),(),( 03020100 xxxx as functions of intrinsic temporal variable vtv 10 : )( )( 00 0e e e e e eee v x L x x x Lx x L x L x L (A6.5 a) )( )( 00 0e e ab e e ab e e ab e ab e ab v x g x x x g x x g x g x g , (A6.5b) )( )()(2 00 fe fe ab fe ab fe ab vv x L x g x L x g x L x g (A6.5c) fe fefefe vv x L x L x L x L x L x L2 00)()( , (A6.5d) )()()( )( )( 2 2 2 0 2 0 2 022 fe fe f e fe f e fe f fe f fefefe vv xx L v x x xx L v x xx L v x L x v x L xxx L xx L , 3,2,1,0,,,,, fedcba. (A6.5e) 1 0 0 0 x x v, 0 0 e x, (A6.5f) 0 x x va a , 0 00 e aa ee ax x xx x xx v,3,2,1, ea . (A6.5g) In (A6.5), sign “” and notation 0 in )( 0 ab g, )( 0 L indicate space-time variables change to )(),(),(),( 03020100 xxxx and the derivation process follows accordingly. In (A6.5g), e aa ex x xx x x00 , )3,2,1,( ea is based on a rule: Derivative operations e and 0 are commutable. Since spatial variables are independent, so 1 e a x )( ae , 0 e a x v)(ae , 0)( 0 e a x x x )3,2,1,( ea . Taking the converting of (A6.5) into account, the emerging terms R and ab R in (A6.4) are converted as follows: ab abRgRRR 220 )( (A6.6a) . )()12( )()12( )()12( )()12(2 )( 2 2 2 2 2 2 2 2 22 20 c db d ac c dc d ab ab ab cd ba cd ab cd ab cd db db ac bd ac db ac db ac ac ac bd ca bd ac bd ac bd dc dc ab cd ab dc ab dc ab ababab vv xx L Lg x L x g x L x g L x L x L gL vv xx L Lg x L x g x L x g L x L x L gL vv xx L Lg x L x g x L x g L x L x L gL vv xx L Lg x L x g x L x g L x L x L gL RRR (A6.6b) b b cdd d bcc c db ada bc a bc a bc v x L gv x L gv x L gLg )( 0, .3,2,1,0,,, dcba (A6.6c) In equations (25.7a), the kinematic part RgR abab 2 1 is the same of Einstein equations (25.1b), all other terms  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1379 generated by probability belong to the emerging part: RgRE ababab 2 1 22 . (A6.7) In which, the emerging terms ab R and R in (A6.6) are originated from the kinematic terms ab R and R, respec- tively. All emerging terms include the superluminal speed products, according to (A6.6), which can be pre sented in 44 matrix form as: 3323133 3222122 3121111 321 2 1 vvvvvvv vvvvvvv vvvvvvv vvv vv . (A6.8) As result of derivation process, the redefined Einstein equations (25.7a) are presented as: 0 2 12ababab ERgR , (A6.9a) Emerging Part: RgRE ababab 2 1 22 . (A6.9b) In (A6.9), the kinematic part RRab 2 1 is the same as Einstein equations (25.1b); the emerging terms ab R 2 and Rgrab 2 2 1 in emerging part RgREababab 2 1 22 are given by (A6.6). As shown in derivation process, probability is canceled out in all terms of equations (A6.9). Part B: For a set of Gaussian spheres each centered at a vertex based on Postulation 25.1B. The redefined parameters for Part-B have the same form of (A.6.1) for Part-A with different p(P) factors i PPL iii ii ePPpPp);( 2 4 1 );()( attached to redefined gauge tensors pgG abab , pgG abab/ of (25.18). As shown in (A6.1), the terms containing derivatives of pgG abab have two forms: (1) Product of two first order derivatives such as f cd e ab G G . (2) Second order deriva- tives such as feab G 2. For the first order derivatives, the derivation process yields: .2)2( 4 4 1 2 2 i i e i iab e ab i L e i i ab e ab i L e ab e ab e ab e ab ab ee ab p p x L Lg x g pe x L L p g x g p e x g x g p x p g x g ppg xx G i i (A6.10a) For the second order derivatives, the derivation pro- cess yields: , 22 22 22 422 4 2 4 1 4 1 2 44 1 )( 2 2 2 22 2 2 2 22 2 2 2 22 22 2 22 22 p p xx L Lg p p x L L x g p p x L L x g p p x L x L g p p x L x L Lgp xx g p e x L x L Lge xx L Lge x L x L g e x L L x g e x L L x g xx g p e x L x L L xx L L x L x Lg e x L L x g e xx g xx g p e x L L g x g p x e x g x g p x x p g x g p x pg xxxx G i ife iab i i e i i f ab i i f i i e ab ii i f i e i ab i f i e i iab fe ab i L f i e i iab L ii fe iab L f i e i ab i L f i i e ab i L e i i f ab fe ab i L f i e i i fe i f i e iab i L f i i e ab i L ef ab fe ab i L f i i ab f ab e i L f ab f ab e f ab f ab e ab fefe ab iii ii i ii ii 3,2,1,0,,, feba . (A6.10b) In (A6.10a), the factor is canceled by the p/1 factor of pgGabab/. After cancelation, the product of two first order derivatives is: .22 22 1 2 ji i e i i f cd ab i f j j e ab cd j j f j j i i e i icdab f cd e ab j j f j jcd f cd i i e i iab e ab f cd e ab p p x L L x g g p p x L L x g g p p x L L p p x L Lgg x g x g p p x L Lg x g p p x L Lg x g x G x G p 3,2,1,0,,,,, fedcba . (A6.11a) In (A6.11a), the first term serves as the term of kine- matic part, which is in the )()()()( gggg c db d ac c dc d ab part of ab R and . The three terms in the parenthesis are included in the )()()()( gggg c db d ac c dc d ab part of the emerging part RgR abab 2 1 . In (A6.10b), the p factor is canceled by the p/1 factor of pgG abab /. After cancelation, the second order derivative is: . 22 1 2 2 22 p p xx L Lg p p x L L x g p p x L L x g p p x L x L g p p x L x L Lg xx g xx G p i ife iab i i e i i f ab i i f i i e ab ii i f i e i ab i f i e i iab fe ab fe ab (A6.11b) In (A6.11b), the first term serves as the term of kine- matic part, which is in the ab cd db ac ac bd dc ab cd xx g xx g xx g xx g g2222 2 1 part of ab R and . The five terms in parenthesis are included in the emerging part RgR abab 2 1 . As shown in (A6.11), the emerging part includes three type terms: f i e ab L g , f i e i L L ,fe i L 2. According to Postulation 25.1B, the derivation process is carried out further the same way as (A6.5) based on space-time va- riables )(),(),(),(03020100 xxxx as functions of intrinsic time vtv 10 .  Z. Y. SHEN Copyright © 2013 SciRes. JMP 1380 According to (A6.1) and (A6.11), the emerging terms R and ab R are given as follows. cd cd RgRRR 220 )( , (A6.12a) . )(2 )(2 )(2( )(2(2 )( 2 2 2 2 2 2 2 22 20 c db d ac c dc d ab ab i i ab i icd i b i ii a cdi a i ii b cd i i a i b i cd i a i b i iicd db i i db i iac i b i ii d aci d i ii b ac i i d i b i ac i d i b i iiac ac i i ac i ibd i c i ii a bdi a i ii c bd i i a i c i bd i a i c i iibd dc i i dc i iab i c i ii d abi d i ii c ab i i d i c i ab i d i c i iiab ababab vv p p xx L Lg p p x L L x g p p x L L x g p p x L x L g p p x L x L Lg vv p p xx L Lg p p x L L x g p p x L L x g p p x L x L g p p x L x L Lg vv p p xx L Lg p p x L L x g p p x L L x g p p x L x L g p p x L x L Lg vv p p xx L Lg p p x L L x g p p x L L x g p p x L x L g p p x L x L Lg RRR (A6.12b) p p v x L Lg p p v x L Lg p p v x L Lggg i b ib i icd i id d i ibc i c ic i idb ad dbc ada bc , .3,2,1,0,,, dcba (A6.12c) The kinematic part RgR abab 2 1 is the same of Ein- stein equations (25.1b), all other terms generated by in- troducing probability belong to the emerging part: RgRE ababab 2 1 22 . (A6.13) In (A6.13), the emerging termsab R andR are originated from the kinematic termsab R and R, respectively. All emerging terms include the speed products, accord- ing (A6.12), which can be presented in 44 matrix form as: 3323133 3222122 3121111 321 2 1 vvvvvvv vvvvvvv vvvvvvv vvv vv . (A6.14) As result of derivation process, the redefined Einstein equations based on Postulation 25.1B are presented as: 0 2 12ababab ERgR , (A6.15a) Emerging Part: RgRE ababab 2 1 22 . (A6.15b) In (A6.15), the emerging terms ab R 2 and R 2 are given by (A6.12). Part-C: The spatial and temporal derivatives of gauge tensor ab g based on Postulation 25.1B for the kinematic part of basic equations. )( )( 00 0e e ab e e ab e e ab e ab e ab v x g x x x g x x g x g x g , (A6.16a) )( )()( 2 00 fe f cd e ab f cd e ab f cd e ab vv x g x g x g x g x g x g , (A6.16b) ).()()( )()( )( 2 22 0 2 0 2 022 fe fe ab f e fe ab f e fe ab f f ab e f f ab efe ab fe ab vv xx g v x x xx g v x xx g v x g x v x g xxx g xx g (A6.16c) In (A6.16c), the 0 x vf f moved out of derivation e is based on the same rule of derivative operations e and 0 are commutable and spatial variables are independent as shown in (A6.5f) and (A6.5g). Based on (A6.16), the parameters of kinematic part RgR abab2 1 are changed as: ab abRgRR 20 )( , (A6.17a) ,)()()()( 2 1 )( 2222 2 20 c db d ac c dc d abab ab cd db db ac ac ac bd dc dcab cd ababab vv xx g vv xx g vv xx g vv xx g g RRR (A6.17b) ,)()()( 2 )(0 c c db b b cd d d bc ad a bc a bc v x g v x g v x g g 3,2,1,0,,, dcba . (A6.17c) As a result, equations (25.20a) are presented as: ababab ERgR 2 1, (A6.18a) Emerging part: RgREE abababab 2 1 22 . (A6.18b) The emerging part in (A6.18) are the same of (A6.13) with simplified notation abab EE 2 , and 2 factors are included. The parameters of the kinematic part given by (A6.17) also have 2 factors included. The speed product matrix of the kinematic part is: 3323133 3222122 3121111 321 2 1 vvvvvvv vvvvvvv vvvvvvv vvv vv . (A6.19) The speed product matrix of emerging part is the same as (A6.14) with 2 factor included. The 2 factors included in (A6.18) indicate that, the vacuons move with superluminal speed.
|