Paper Menu >>
Journal Menu >>
 Applied Mathematics, 2011, 2, 123-130 doi:10.4236/am.2011.21014 Published Online January 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM Numerical Solution for a FG Cylinder Problem Using Finite-Difference Method Daoud S. Mashat Department of Mathematics, Faculty of Science, King AbdulAziz University, Jeddah, Saudi Arabia E-mail: dmashat@kau.edu.sa Received August 28, 2010; revised November 24, 2010; accepted Nove mber 28, 2010 Abstract A refined finite-difference approach is presented to solve the thermoelastic problem of functionally graded cylinders. Material properties of the present cylinder are assu med to be graded in the radial direction accord- ing to a power-law distribution in terms of the volume fractions of the metal and ceramic constituents. The governing second-order differential equations are derived from the motion and the heat-conduction equations. Numerical results for dimensionless temperature, radial displacement, mechanical stresses and electromag- netic stress are distributed along the radial directions. The effects of time parameter and the functionally graded coefficient are investigated. Keywords: Functionally Graded, Annular Cylinder, Electro-Magneto-Thermoelastic Field 1. Introduction Magneto-thermoelastic functionally graded material is a kind of magneto-thermoelastic material with material composition and properties varying continuously along certain directions. It is the composite material intention- ally designed so that they possess desirable properties for some specific applications. The advantage of this new kind of materials can improve the reliability of life span of magnetic devices. Recently, there has been growing interest in materials deliberately fabricated so that their electric, magnetic, thermal and mechanical properties vary continuously in space on the macroscopic scale. This research subject is so new that only a few results can be found in the literatures. In recent years the theory of magneto -thermo -elasticity that deals with the interactions among strain, temperature and electromagnetic fields has drawn the attention of many researchers. This theory is extensive uses in d iverse field such as geophysics for understanding the effect of the Earth’s magnetic field on seismic waves, damping of acoustic waves in a magnetic field, and emissions of electromagnetic radiations from nuclear devices. It is also developed a highly sensitive superconducting mag- netometer, electrical power engineering and optics. In the field of magneto-elasticity or magneto-thermo- elasticity, many studies have been conducted on an ana- lytical treatment of an interaction between elastic, elec- tromagnetic, and temperature fields (e.g., Paria [1], Wang et al. [2], Wang and Dai [3], Wang and Dong [4], Ba- nerjee and Roychoudhuri [5]). The magneto-thermoelastic problem of functionally graded material (FGM) hollow structures subjected to mechanical loads is considered by Dai and Fu [6]. Hou and Leung [7] analyzed the plane strain dynamic prob- lem of a magneto -electro -elastic hollow cylinder by virtue of the separation of var iab les, orthog on al exp ansion tech- nique and the interpolation method. Buchanan [8] consi- dered the free vibration problem of an infinite magne- to-electro-elastic cylinder. The frequency behaviour of clamped-clamped magneto -electro -el astic cylin drica l shel ls is analysed by Annigeri et al. [9] using the semi-ana- lytical finite element approach. Hou et al. [10] studied the transient responses of a special non-homogeneous magneto-electro-elastic hollow cylinder for axisymme- tric plane strain problem. The magnetother-moelastic problem in non-homogeneous isotropic cylinder in a primary magnetic field is discussed by Abd-El-Salam et al. [11]. The dynamic and quasi-static behaviors of mag- neto -thermo -elastic stresses in a conducting hollow circu- lar cylinder subjected to an arbitrary variation of mag- netic field are investigated by Higuchi et al. [12]. Bhangale and Ganesan [13] studied the free vibration on FGM magneto-electro-elastic cylindrical shells using a series solution. Kong et al. [14] presented an analytical method to investigate thermo -magneto-elastic stresses  D. S. MASHAT Copyright © 2011 SciRes. AM 124 and perturbation of the magnetic field vector in a con- ducting non-homogeneous hollow cylinder under thermal shock. Wang and Dai [15] presented magneto-thermo- dynamic stresses and perturbation of magnetic field vec- tor in an orthotropic thermoelastic cylinder. Dai and Wang [16] presented an analytical solution for magne- to-thermo-electro-elastic problems of a piezoelectric hol- low cylinder placed in an axial magnetic field subjected to arbitrary thermal shock, mechanical load and transient electric excitation. The objective of this investigation is to generate dis- placement, stresses, temperature, and magnetic field in a FGM annular cylinder. Material prop erties of the present cylinder are assumed to be graded in the radial direction according to a power-law distribution in terms of the volume fractions of the metal and ceramic constituents. The governing motion and the heat-conduction equations are obtained in conservation forms and solved numeri- cally using finite difference method. A refined finite- difference approach is presented to solve the present problem. Numerical results for the variation of tempera- ture, displacement and stresses are presented for a metal- ceramic FG cylinder. To make the study reasonably, temperature, displacement, and stresses are given for different homogenization schemes and exponents in the power-law that d escribes along- the- thick ness variation of the constituents. The effects of many parameters are in- vestigated. 2. Mathematical Model Let us consider an annular cylinder of outer radius r = b, inner radius r = a, and made of a functionally graded material. The cylindrical coordinates system ,,rz for the axially symmetric problem is used with z-axis coinciding with the axis of the cylinder. We have only the radial displacement r u which is independent of and z. The cylinder is placed in a constant primary mag- netic field 0 H as shown in Figure 1. In a generalized plane strain, we suppose that the planes perpendicular to the z-axis and r u is a function of the radial direction r and time t only. The Cauchy’s relations are ,, 0, rr rrzz zr rz uu eeeeee rr (1) where ij e are the strain components. The mechanical stress components rr and , and Maxwell’s elec- tromagnetic stress component rr are given, respec- tively, by 2 0 2, 2, . rr rrrr rr rr rr re ererT re ererT rH ee (2) (a) (b) Figure 1. Temperature distribution through the radial direction of the FGM annular cylinder at (a) different times, and (b) for different values the gradation exponent.  D. S. MASHAT Copyright © 2011 SciRes. AM 125 where T is the absolute temperature, and Lamé’s coefficients, the magnetic permeability, 32 the stress-temperature modulus, in which is the linear thermal expansion, and 0 H is the primary magnetic field. The magneto-elasto-dynamic equation in the radial direction of the FG annular cylinder is given by 2 2 1, rrrr r rr u r rrr t (3) where is the material density of the cylinder. The heat conduction equation in the absence of heat source can be written in the form [17] 22 10 22 11 , r rCrTrTu rrtr r rt (4) where 0 T is the reference temperature, Cc the specific heat at constant volume, and is the thermal conductivity. The material properties like , , , , , c, and of the FGM cylinder are assumed to be function of the volume fraction of the constituent materials. The functionally graded between the physical properties and the radial direction r for ceramic and metal FG cylinder is given by 1, j mc c ra PrP PP ba (5) where c P and m P are the corresponding properties of ceramic and metal, respectively, and j is the volume frac- tion exponent which takes values greater than or equal to zero. The value of j equal to zero represents a fully metal annular cylinder. The above power-law assumption re- flects a simple rule of mixtures used to obtain the effec- tive properties of the ceramic-metal FGM annular cy- linder. The rule of mixtures applies only to the radial direction. Note that the volume fraction of the metal is high near the inner surface of the cylinder, and that of ceramic high near the outer surface. In addition, Equa- tion (3) indicates that the inner surface of the annular cylinder is metal-rich whereas its outer surface is ceram- ic-rich. The density and other physical components of the annular cylinder according to the power law, and the power-law exponent may be varied to obtain different distributions of the component materials through the radial direction of the cylinder. 3. Solution of the Problem Introducing the following dimensionless variables may be simplifying the solving process: 00 11 222 000 ,, ,,, ,, 1 ,,,, r rr rr Trtu rt rat RAT U bbb TbT THT (6) where is dimensionless time and 0 is the linear thermal expansion constant. The effect of material prop- erties variation of the FG cylinder can be taken into ac- count in Equations (3) and (4) using Equation (5). The substitution of Equations (1) and (2) into Equations (3) and (4) with the aid of the dimensionless variables given in Equation (6) produces the governing equations for the FG cylinder as follows: 2 *2 2 2 *2 2 2 *2 2, mc mc UU U RRU RVR RR R T RV RURV RRT R U R (7) 22 12 22 11 ,TU RRR R R (8) where 22 00 2 0 * *0 12 ** 2, 2, 1 ,, 1 ,, mm mmcc cc j mc mc HH R HVR A T CC (9) where the letter in the expression *. mc c VR (10) is given instead of the parameters , , , C or . Note that, the prime () in Equation (7) denotes diffe- rentiation with respect to R. Also, p , p , p , p , p C, p and p (p = m or c) are Lamé’s constants, thermal modulus, thermal conductivity, specific heat, magnetic permeability, and density of the homogeneous metal or ceramic material, respectively, and the parame- ter in Equation (10) may be used to represent one of these constants. The dimensionless stresses induced by the temperature T and the electromagnetic stress are related to the dimen- sionless radial displacement U by *** 11 2, UUUT RR R (11) *** 22 2, UUUT RR R (12)  D. S. MASHAT Copyright © 2011 SciRes. AM 126 *. UU RR (13) Once again the letter in Equation (10) is given in- stead of the parameters , , , or . The elastic solution for the FG hollow cylinder is completed by the application of the initial and boundary conditions. The initial conditions can be expressed as 0,0 at0. TU TU (14) The boundary conditions at the inner and outer radii of the FG cylinder may be expressed as 11 11 e,0at , 0, 0at1, TRA TR (15) where is an exponent of the decayed heat flux. 4. Numerical Scheme A finite element scheme is used here to get the tempera- ture and radial displacement. The finite difference grids with spatial intervals h (mesh width) in the radial direc- tion and k as the time step for the maximum time max , and use the subscripts i and n to denote the ith discrete point in the R direction and the nth discrete time. A mesh is defined by max 1 ,0,1,2,,, . ,0,1,2,3,,, . i n A RAihiNh N knnK k K (16) The displacement and temperature may be given for positive integers N and K at any nodal location by ,,,. nn nn iiii URU TRT (17) The equation of motion and the heat conduction equa- tion, given in Equations (7) and (8), may be expressed in the finite difference as 11 11231 411 5 2 , nn nnn ii iii nn n ii i UfU fUfUU fT TfT (18) 11 112 31 11 2 1111 21111 21 2 , 2 nn nnn ii iii nnn iii nnnn iiii TgT gTgTT UUU Aih UUUU h (19) where 2* 1* 21 , 2imci i k f V hAih h (20a) 2* 2*2 2 21 , () ii i k f V Aih hAih (20b) 2* 3* 21 , 2imci i k f V hAih h (20c) 2 2* 45 ** ,, 2 mc ii ii k k f fV h (20d) 21 123 2 ,,1 ,1,1. 22 khh ggg A ihAih h (20e) Note that * 1 0 1 ,,0,1,2,, , 1 1,0, 0. 11 j imcici j iN Aih VVi N A jAih ViiNVV AA (21) The mechanical stresses and electromagnetic stress are given, accordingly, by *** * 111 1 2, 2 nnn n ii i ii iii UUU T kAih (22) ** ** 221 1 2, 2 nnnn ii iii iii UUUT kA ih (23) *11 . 2 nn n ii i i UU U kAih (24) The initial conditions in Equation (14) may be written as 0110 11 0, , 0, . iiiiii TTTUUU (25) Putting n = 0 in Equations (18) and (19), one obtains 10000 11 31 411 1, 2 iiiii UfUfUfTT (26) 1001 2 11 31 11 11 21111 1 2 , 4 iii i iiii TgTgT U Aih UUUU h (27) where 1, 2, 3,,1.iN The boundary conditions given in Equation (15) at R = A may be written as 011 00 2 e, , 2 nknnnn n mm mm h TUU UT A (28) and at R = 1, we get 11 2 0, . 2 nnnnn NNN cNcN cc h TUUUT (29)  D. S. MASHAT Copyright © 2011 SciRes. AM 127 Putting i = 0 in Equation (18) and using the forward difference approximation for the temperature’s derivative with the aid of Equation (28), one obtains 100 001 01312300 000 42 134 2 2 2 43e, 2 nn nn mm nn kn m mm h UffUffUU A h fT Tff (30) where 2 0 121 , 2m m k fhhA (31a) 2 0 222 21 2, m m k fhA (31b) 2 0 321 , 2m m k fhhA (31c) 2 0 4. 2m m k fh (31d) Putting i = N in Equatio n (18) and using the b ackward difference approximation for the temperature’s derivative with the aid of Equation (29), one obtains 121131 1421 2 2 4, nN NnNNn c NNN cc nNnn NNN h Uf fUffU UfT T (32) where 2 12 2, 2 c N c kh fh (33a) 22 22 2 2, c N c kh fh (33b) 22 34 2 2,. 2 2 c NN c c c kh k ff h h (33c) 5. Numerical Results The temperature, displacement and stresses for the present cylinder are obtained using the above finite ele- ment scheme. The results are presented in the non -di- mensional form: 68 1 211 22 10,,,10 .uU All results of this article are for aluminum as inner metal surface and alumina as outer ceramic surface. Generally, the magnetic permeability 0 p p K (p = m or c) is given in terms of the permeability of space 72 0410NA and the relative permeability for both aluminum m K and alumina c K . The material properties are assumed to be as: Metal (aluminum): 3 70 GPa,0.35,2700 Kgm, mmm E 6 23.110K,2.3,237 WmK. mmm K Ceramic (alumina): 3 116 GPa,0.33,3000 Kgm, ccc E 6 8.710K,1.0,1.78 WmK. ccm K Note that the properties of , , and for metal or ceramic are graded through the radial direction ac- cording to the following relations: ,, 112 21 32 ,,. pp p pp pp p pppp EE pmc Results are presented in Figures 1-5 for temperature, radial displacement, radial stress, circumferential stress and electromagnetic stress according to the fixed con- stants 5 00 1,0.25,27 K,210Oersted,2.5.bA TH The sensitivity of the ti me parameter and the FGM exponent j are discussed through the figures. Figure 1 represents the variation of the dimensionless temperature T through the radial direction of the FGM annular cy- linder. Four values of the time parameter with j = 3 are used in Figure 1(a), while four values of the FGM exponent j with 0.3 are used in Figure 1(b). Simi- lar results for the dimensionless displacement u, the radi- al stress 1 , the circumferential stress 2 and the elec- tromagnetic stress are plotted in Figures 2-5, re- spectively. Figure 1 shows that the absolute value of the temper- ature decreases as the time parameter increases and the FGM exponent j decreases. It is to be noted that the temperature is maximum for the homogeneous metal cylinders. The same behavior occurs for displacement and stress quantities. The solution satisfied the boundary conditions (see Figures 1 and 3) and the difference be- tween homogeneous and FGM cases is shown. The vari- ation of temperature, displacement, and stresses are due to the effect of inertia and magnetic field. It is seen that, the influence of the FGM on temperature, displacement and stresses is very pronounced. Finally, it is interested to see that all quantities my by vanished near and at the external ceramic surface of the annular cylinder.  D. S. MASHAT Copyright © 2011 SciRes. AM 128 (a) (b) Figure 2. Displace ment distribution through the radial direction of the FGM annular cylinder at (a) different times, and (b) for different values the gradation exponent. (a) (b) Figure 3. Radial stress distribution through the radial direction of the FGM annular cylinder at (a) different times, and (b) for different values the gradation exponent. 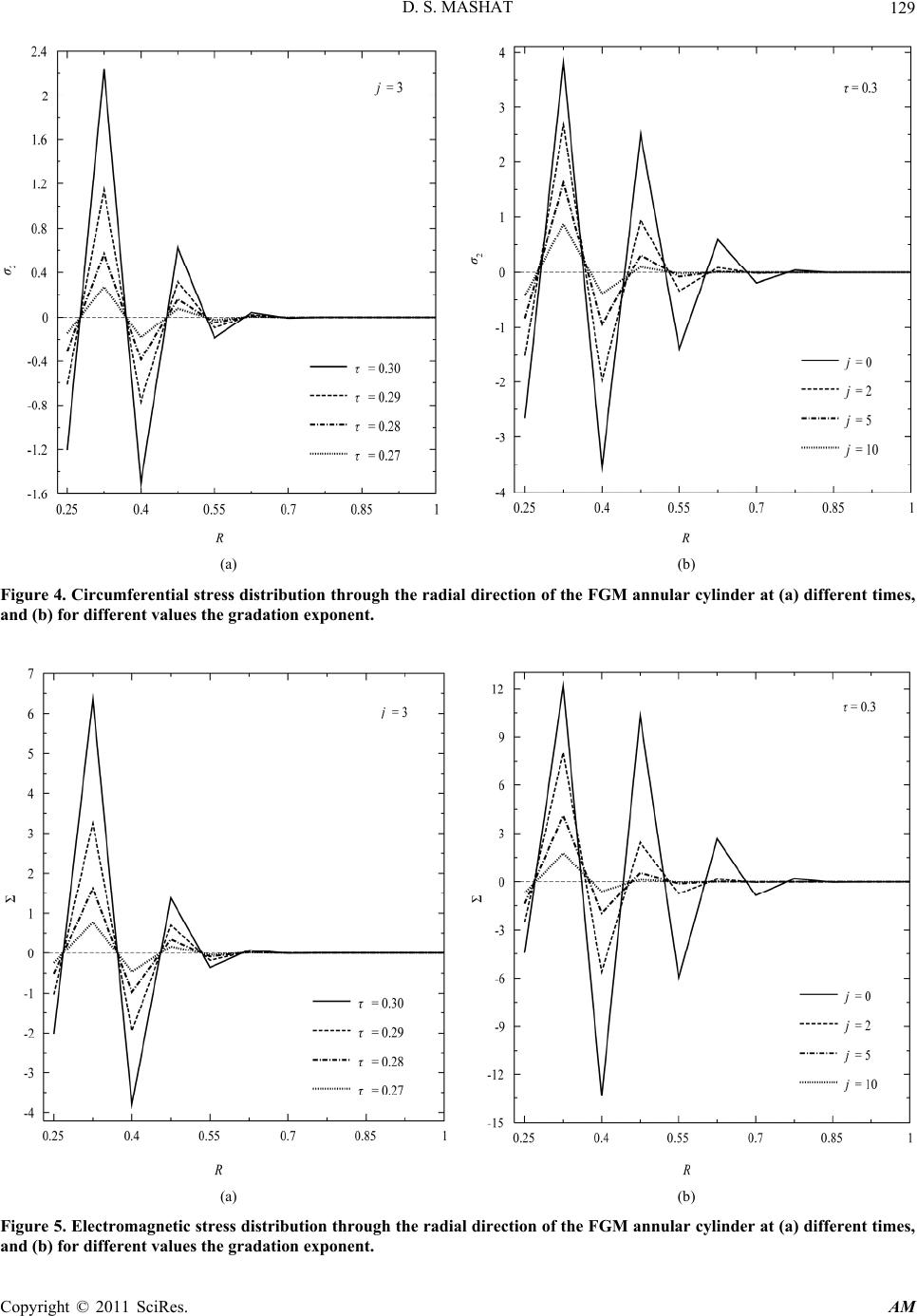 D. S. MASHAT Copyright © 2011 SciRes. AM 129 (a) (b) Figure 4. Circumferential stress distribution through the radial direction of the FGM annular cylinder at (a) different times, and (b) for different values the gradation exponent. (a) (b) Figure 5. Elec tromagnetic stress distribution thro ugh the radial direction of the FGM annular cylinde r at (a) different times, and (b) for different values the gradation exponent.  D. S. MASHAT Copyright © 2011 SciRes. AM 130 6. Conclusions The main contribution in this paper is to describe second- order explicit finite-difference scheme. This scheme helps us to solve the coupled hyperbolic equations on a uni- form grid, and is quite efficient for computation thermal stresses. The results obtained show that behavior of the temperature, displacement and stresses may change sig- nificantly by reason of influence of exponent heat flux and primary magnetic field in homogeneous and func- tionally graded cases. These results are specific for the example considered, but the example may have different trends because of the dependence of the results on the magnetic and thermal constants of the metal-ceramic functionally graded material. 7. References [1] G. Paria, “Magneto-Elasticity and Magneto-Thermo-Ela- sticity,” Advances in Applied Mechanics, Vol. 10, 1966, pp. 73-112. doi:10.1016/S0065-2156(08)70394-6 [2] X. Wang, G. Lu and S. R. Guillow, “Magnetothermody- namic Stress and Perturbation of Magnetic Field Vector in a Solid Cylinder,” Journal of Thermal Stresses, Vol. 25, No. 10, 2002, pp. 909-926. doi:10.1080/0149573029 0074397 [3] X. Wang and H. L. Dai, “Magnetothermodynamic Stress and Perturbation of Magnetic Field Vector in an Ortho- tropic Thermoelastic Cylinder,” International Journal of Engineering Science, Vol. 42, No. 5-6, 2004, pp. 539- 556. doi:10.1016/j.ijengsci.2003.08.002 [4] X. Wang and K. Dong, “Magnetothermodynamic Stress and Perturbation of Magnetic Field Vector in a Non- Homogeneous Thermoelastic Cylinder,” European Jour- nal of Mechanics-A/Solids, Vol. 25, No. 1, 2006, pp. 98- 109. doi:10.1016/j.euromechsol.2005.07.003 [5] S. Banerjee and S. K. Roychoudhuri, “Magneto-Thermo- Elastic Interactions in an Infinite Isotropic Elastic Cy- linder Subjected to a Periodic Loading,” International Journal of Engineering Science, Vol. 35, No. 4, 1997, pp. 437- 444. doi:10.1016/S0020-7225(96)00070-5 [6] H. L. Dai and Y. M. Fu, “Magnetothermoelastic Inter- actions in Hollow Structures of Functionally Graded Ma- terial Subjected to Mechanical Loads,” International Journal of Pressure Vessels and Piping, Vol. 84, No. 3, 2007, pp. 132-138. doi:10.1016/j.ijpvp.2006.10.001 [7] P. F. Hou and A. Y. T. Leung, “The Transient Responses of Magneto -Electro-Elastic Hollow Cylinders,” Smart Materials and Structures, Vol. 13, No. 4, 2004, pp. 762- 776. doi:10.1088/0964-1726/13/4/014 [8] G. R. Buchanan, “Free Vibration of an Infinite Magne- to-Electroelastic Cylinder,” Journal of Sound and Vibra- tion, Vol. 268, No. 2, 2003, pp. 413-426. doi:10. 1016/S0022-460X(03)00357-2 [9] A. R. Annigeri, N. Ganesan and S. Swarnamani, “Free Vibrations of Clamped-Clamped Magneto-Electro-Elastic Cylindrical Shells,” Journal of Sound and Vibration, Vol. 292, No. 1-2, 2006, pp. 300-314. doi:10.1016/j.jsv.2005. 07.043 [10] P. F. Hou, H. J. Ding and A. Y. T. Leung, “The Transient Responses of a Special Non-Homogeneous Magneto- Electro-Elastic Hollow Cylinder for Axisymmetric Plane Strain Problem,” Journal of Sound and Vibration, Vol. 291, No. 1-2, 2006, pp. 19-47. doi:10.1016/j.jsv.2005. 05.022 [11] M. R. Abd-El-Salam, A. M. Abd-Alla and H. A. Hosham, “A Numerical Solution of Magneto -Thermoelastic Problem in Non-Homogeneous Isotropic Cylinder by the Finite- Difference Method,” Applied Mathematical Modelling, Vol. 31, No. 8, 2007, pp. 1662-1670. doi:10.1016/j.apm. 2006.05.009 [12] M. Higuchi, R. Kawamura and Y. Tanigawa, “Dynamic and Quasi-Static Behaviors of Magneto-Thermo-Elastic Stresses in a Conducting Hollow Circular Cylinder Sub- jected to an Arbitrary Variation of Magnetic Field,” In- ternational Journal of Mechanical Sciences, Vol. 50, No. 3, 2008, pp. 365-379. [13] R. K. Bhangale and N. Ganesan, “Free Vibration Studies of Simply Supported Non-Homogeneous Functionally Graded Magneto -Electro - Elastic Finite Cylindrical Shell s,” Journal of Sound and Vibration, Vol. 288, No. 1-2, 2005, pp. 412-422. doi:10.1016/j.jsv.2005.04.008 [14] T. Kong, D. X. Li and X. Wang, “Thermo-Magneto - Dynamic Stresses and Perturbation of Magnetic Field Vector in a Non-Homogeneous Hollow Cylinder,” Ap- plied Mathematical Modelling, Vol. 33, No. 7, 2009, pp. 2939-2950. doi:10.1016/j.apm.2008.10.003 [15] X. Wang and H. L. Dai, “Magneto -Thermo-Dynamic Stress and Perturbation of Magnetic Field Vector in a Hollow Cylinder,” Journal of Thermal Stresses, Vol. 3, 2004, pp. 269-288. doi:10.1080/01495730490423900 [16] H. L. Dai and X. Wang, “Magneto-Thermo-Electro- Elastic Transient Response in a Piezoelectric Hollow Cy- linder Subjected to Complex Loadings,” International Journal of Solids and Structures, Vol. 43, No. 18-19, 2006, pp. 5628-5646. doi:10.1016/j.ijsolstr.2005.06.092 [17] S. B. Mukhopadhyay, “Thermoelastic Interactions with- out Energy Dissipation in an Unbounded Body with a Spherical Cavity Subjected to Harmonically Varying Temperature,” Mechanics Re search Communications, Vol. 31, No. 1, 2004, pp. 81-89. doi:10.1016/S0093-6413(03) 00082-X |

