Applied Mathematics, 2011, 2, 106-117
doi:10.4236/am.2011.21012 Published Online January 2011 (http://www.SciRP.org/journal/am)
Valuation of Credit Default Swap with Counterparty
Default Risk by Structural Model*
Jin Liang1*, Peng Zhou2, Yujing Zhou1, Junmei Ma3,4
1Department of Mathematics, Tongji University, Shanghai, China
2Deloitte Touche Tomatsu CPA Ltd., Shanghai, China
3Department of Applied Mathematics, Shanghai University of Finance and Economics, Shanghai, China
4Department of Applied Mathematics, Tongji University, Shanghai, China
Received June 19, 201 0; revised November 18, 2010; accepted November 23, 2010
Abstract
This paper provides a methodology for valuing a credit default swap (CDS) with considering a counterparty
default risk. Using a structural framework, we study the correlation of the reference entity and the counter-
party through the joint distribution of them. The default event discussed in our model is associated to wheth-
er the minimum value of the companies in stochastic processes has reached their thresholds (default barriers).
The joint probability of minimums of correlated Brownian motions solves the backward Kolmogorov equa-
tion, which is a two dimensional partial differential equation. A closed pricing formula is obtained. Numeri-
cal methodology, parameter analysis and calculation examples are implemented.
Keywords: CDS Spread, Counterparty Default Risk, Structural Model, PDE Method, Monte Carlo
Calculation
1. Introduction
A vanilla credit default swap (CDS) is a kind of insur-
ance against credit risk. The buyer of the CDS is the
buyer of protection who pays a fixed fee or premium to
the seller of protection for a period of time. If a certain
pre-specified “credit event” occurs, the seller pays com-
pensation to the buyer. The “credit event” can be a bank-
ruptcy of a company, called the “reference entity”, or a
default of a bond or other debt issued by the reference
entity. In this paper, the “credit event” also includes the
default of th e protection seller. If ther e is no credit event
occurs during the term of the swap, the buyer continues
to pay the premium until th e CDS maturity.
A financial institution may use a CDS to transfer credit
risk of a risky asset while continues to retain the legal
ownership of the asset. As the rapid growth of the credit
default swap market, credit default swaps on reference
entity are more actively traded than bonds issued by the
reference entities.
There are two primary types of models of default risk
in the literature: structural models and reduced form (or
intensity) models. A structural model uses the evolution
of a firm’s structural variables, such as an asset and debt
values, to determine the time of a default. Merton’s
model [1] is considered as the first structural model. In
Merton’s model, it is assumed that a company has a very
simple capital structure where its debt has a face value of
D and maturity of time T, provides a zero coupon. Mer-
ton shows that the company’ s equity can be regarded as a
European call option on its asset with a strike price of D
and maturity of T. A default occurs at T if the option is
not exercised. The second approach, within the structural
framework, was introduced by Black-Cox [2] and Long-
staff-Schwartz [3]. In this approach a default occurs as
soon as the firm’s asset value falls below a certain level.
In contrast to the Merton approach, the default can occur
at any time. Zhou [4,5] produces an analytic result for
the default correlation between two firms by this model.
Using this model, credit spread with jump is considered
by Zhou [6].
Reduced form models do not care the relation between
default and firm value in an explicit manner. In contrast
to structural models, th e time of default in intensity mod-
els is not determined via the value of the firm, but the
*This work is supported by National Basic Research Program of China
(973 Program )2007CB814903.

J. LIANG ET AL.
107
first jump of an exogenously given jump process. The
parameters governing the default hazard rate are inferred
from market data. These models can incorporate correla-
tions between defaults by allowing hazard rates to be
stochastic and correlated with macroeconomic variables.
Duffie-Singleton [7,8] and Lando [9] provide examples
of research following this approach.
There have been many works on the pricing of credit
default swaps. Hull - Wh ite [10] first considered the va l-
uation of a vanilla credit default swap when there is no
counterparty default risk. Their methodology is a two-
stage procedure. The first stage is to calculate the default
probabilities at different future times from the yields on
bonds issued by the referen ce entity. The second stage is
to calculate the present valu e of both the expected future
payoff and expected future payments on the CDS. They
extended their study to the situation where there is possi-
bility of counterparty default risk and obtained a pricing
formula with Monte Carlo simulation [11]. They argued
that if the default correlation between the protection sel-
ler and the reference entity is positive, the default of the
counterparty will result in a positiv e replacement cost fo r
the protection buyer.
Affection of the correlation on a CDS pricing remains
interesting. The valuation of the credit default swap is
based on computing the joint default probability of the
reference entity and the counterparty (protection seller).
Technically it is difficult because correlation b etween the
entities involved in the contract is hard to deal with. Jar-
row and Yildirim [12] obtained a closed form valuation
formula for a CDS based on reduced form approach with
correlated credit risk. In their model, the default intens ity
is assumed to be linear in the short interest rate. Jarrow
and Yu [13] also assumed an inter-dependent default
structure that avoided looping default and simplified the
payoff structure where the seller’s compensation was
only made at the maturity of the swap. They discovered
that a CDS may be significantly overpriced if the coun-
terparty default probability was ignored. Yu [14] con-
structed the default processes from independent and
identically distributed exponential random variables us-
ing the “total hazard” approach. He obtained an analytic
expression of the joint distribution of default times when
there were two or three firms in his model. Leung and
Kwok [15] considered the valuation of a CDS with
counterparty risk using a contagion model. In their model,
if one firm defaults, the default intensity of an other party
will increase. They considered a more realistic scenario
in which the compensation payment upon default of the
reference entity was made at the end of the settlement
period after default. They also extended their model to
the three-firm situation.
More studies on different kinds of CDS, such as a
basket reference entities, can be found from, e.x. [2,
15-23].
In this paper we develop a partial differential equation
(PDE) procedure for valuing a credit default swap with
counterparty default risk. In our model, a default event is
supposed to occur at most one time, which means either
reference entity or counterparty may default once. Our
work is based on the structural framework, where the
default event is asso ciated to whether the min imum value
of stochastic processes (value of the companies) have
reached their thresholds (default barriers). Usually we
choose the companies’ liability as the thresholds [1,24].
We show that the joint probability of minimums of cor-
related Brownian motions solves the backward Kolmo-
gorov equation, which is a two dimensional PDE with
cross derivative term. This equation can be solved as a
summation of Bessel and Sturm-Liouville eig enfunctions.
The defaultable CDS studied in this paper, sa me as Hull-
White’s, is a special case. More complicated features of
that kind of CDS are not considered.
The paper is organized as follows. In Section 2, we
present a CDS spread expression. In Section 3, we estab-
lish a partial differential equation model wh ich so lves the
joint probability distribu tion of two correlated companies
used in Section 2 under the some assumptions. We ob-
tain an explicit solu tion for this PDE. The main result of
the closed form of the pricing the CDS then follows and
shows in this section. Numerical calculation, example
tests and parameter analysis for our model are collected
in Section 4. We conclude the paper in Section 5.
2. CDS Spread w ith Counterparty Default
Risk
In this section, first, we analyze how to value a CDS with
counterparty default risk. Assume that party A holds a
corporate bond with notional principal of $ 1. To seek
insurance against the default risk of the bond issuer (ref-
erence entity B), party A (CDS protection buyer) enters a
CDS contract and makes a series of fixed, periodic pay-
ments of the CDS premium to party C (CDS protection
seller) until the maturity, or un til the credit event occurs.
In exchang e, party C promises to compensate party A for
its loss if the credit event occurs. The amount of this
compensation is usually the notional principal of the
bond multiplied by (1 )R

, where R is the recovery rate,
as a percentage of the notional. During the life time of
the CDS, a risk-free interest is applied.
Assume that the default event, the risk-free interest
rate and the recovery rate are mutually independent. De-
fine, for the credit default swap,

J. LIANG ET AL. 108
T: Maturity of the credit default swap;
R: Recovery rate on reference obligation;
:r Risk neutral interest rate;
:w Total payments per year made by the CDS
buyer (party A) per $ 1 of noti onal p ri ncipal ;

:t  Risk neutral probability density of default by
the reference entity and no default by the
counterparty;

:t  Risk neutral probability density of default by
the counterparty and no default by the refer-
ence entity.
A vanilla CDS contract usually specifies two potential
cash flow streams - a fixed premium leg and a contingent
leg. On the premium leg side, the buyer of protection
makes a series of fixed, periodic payments of the CDS
premium until maturity or until a cred it event occurs. On
the contingent leg side, the protection seller makes a sin-
gle payment in the case of the credit event. The value of
the CDS contract to the protection buyer at any given
point of time is the difference between the expected
present value of the contingent leg, which is the protec-
tion buyer expects to receive, and that of the fixed leg,
which he e x pects to pay , o r


= Value ofCDSEPVcontingentleg
EPVfixedpremium leg


 

(1)
Similar to the vanilla CDS, we assume that the pay-
ments are made at dates 12 <<<=
n
tt tT. Let t

be the time interval between payments dates, then the
payment made every time is wt. In practice the pay-
ments are usually made quarterly, therefore =0.25t.
The CDS payments cease when either the reference enti-
ty or the counterparty defaults. If a credit event occurs at
time

0< T  , denote the payments dates pre-
cisely before and after the default time

by n t

and
1n
t

. When this credit event occurs exactly at one of the
payments dates, let n t


. Then we have 1 <
nn
tt



.
First, we analyze the fixed premium leg side. As we
assumed, the credit event occurs at most once. That is,
there are three cases as follows.
Case 1. the credit event is that the reference entity de-
faults at time

. Then the pr esent value of all payments
is

 
1
=1 := .
nrt
rt n
i
n
i
wtew tewawe








Case 2. the credit event is that the counterparty de-
faults at time

. Then there is no final accrued payment
and the present value of all payments is
=1 =().
n
rti
i
wte wa





Case 3. neither the reference entity nor the counter-
party defaults prior to maturity time T. This time the
present value of the payments is

waT.
Using the default probability densities of


t

and


t  , the total expected present value of the premium
leg is
  
0.
T
wa eadwaT     


On the contingent leg side, if the reference entity de-
faults at time

, the present value of the payoff form the
CDS is given by


1,
r
Re

 

where

is the liquidation period. The expecte d payoff
is
 

01.
Tr
Re d






According to (1), the value of the CDS at time t is
 



 

1
.
Tr
t
T
t
Re d
wa eadwaT

 
  






The value of the swap at origination must be equal to
zero. The CDS spread s is the value of w which makes
the value of the CDS equal to zero. Thus
 

   
0
0
1
=.
Tr
T
Re d
s
ae adaT

 
  


  



(2)
The variable s is referred as the credit default swap
spread or the CDS spread. It is the total of the payments
per year, as a percentage of the notional principal.
In expression (2), the joint probability densities are
still unknown. We will focus on how to obtain these
probability densities in following sections.
3. Modelling and Solution
In this section, we present several mathematical theo-
rems which are necessary for the valuation of the CDS
with the counterparty default risk. In order to describe
the correlation between the reference entity and the
counterparty, we study the joint probability distribution
functions of the minimum values of two correlated
Brownian motions.
The following are Basic Assumptions for our model.
1) Interest rate r is constant;
2) Firm i’s asset value

i
Vt follows a geometric
Brownian process with constant drift r and volatility
i

under the risk neutral measurement,

J. LIANG ET AL.
109

 
=, =1,2,
i
ii
i
dV trdtdW ti
Vt
 
where
  
12
cov ,=dW tdWtdt

with

being a con-
stant;
3) Firm i defaults as soon as its asset value ()
i
Vt
reaches the default barrier i
D. In this paper, we use the
Black-Cox type default barrier, which is

=,
t
i
ii
Dt Fe
 
where i
F
and i

are given constants respectively (see
[2]);
4) The credit event occurs at most once.
3.1. Default Probability
Take
 

=ln 0
t
ii
i
i
Vt
Xt e
V
 




, then

0=0
i
X and
 
=,
iiii
dXtdtdW t  
where 2
1
=2
iii
r

  . The default barriers change to

 
0
=ln =ln0
00
ii
i
ii
DF
mVV





and a credit event oc-
curs when i
X
reaches i m.
Define the running minimum of

i
X
T by


=.
min
ii
tsT
X
TXs

In order to get the probability density needed in (2),
define





 
1 12 1
221 122
,,:=Prob< ,
>|=, =.
ux xtXTm
X
TmXtxXtx
(3)
Thus


12
,,ux x t is the probability of the event that
1
X
defaults (i.e. 1
X
reaches 1 m) and 2
X
does not
default till time T. Our main theorem displays th e proba-
bility distribution functions of the extreme values of two
correlated Brownian motions. The probability densities
of


t  and


t

can be obtained directly from


12
,,0uxx .
Lemma 1 The joint probability (3) satisfies backward
Kolmogorov equation

 

22 2
22
12 1212
22
12 12 12
12 12
1212 12
12
11
==0,
22
,,,,0,,
,,=1, ,,,,0,,
,,=0,
uu uuuu
utx xxx
xx
xxt mmT
umxtxxtmmT
uxmt
 
 

  



 
 
11
1212 12
,,0,,
,,=0, ,,,,
xt mT
uxxTxx mm











(4)
where 12 ,0.mm
Proof. Using Itô's formula (see, e.x. [25]), denote


=, =1,2,
iit
XtX i
 
12 12
22 2
22
12 1212
22
012 12
12
112 2
00
12
,,= ,,0
11
22
.
tt
t
tt
ss
uXXtuxx
uu uuuu
ds
sx xxx
xx
uu
dW dW
xx
 


 
  

 







Assume that u is the solution of backward Kolmogo-
rov equation (4), so
2
2
12 1
2
12 1
22
2
212
212
2
1
=2
1
2
=0.
uu uu
usx x
x
uu
xx x
 

 
 
 


 

Then
 
12121 1
01
,,=,,0 t
tt s
u
uXXtuxxdW
x




22
02
,
t
s
udW
x



 (5)
and




12 12
,,= ,,0.
tt
EuXXtux x

 (6)
Define the first passage time




12 12
=inf|, >, 0.sXsm Xsms  
Let =tT


, we find (6) is

 
121 2
,,0=, ,
tt
uxx EuXXt



J. LIANG ET AL. 110
 
 
 
1212 12
0
1212 12
0
12121212
12
=,,,,;,,0
,, ,,;,,0
,, ,,;,,0,
T
ss
T
ss
mm
umXs pmXsxxds
uX mspX msxxds
uTpTxxdd

 






(7)
where

12 12
,,;,,0
tt
pX X txx is the transition probabil-
ity of being at state

12
,
tt
X
X at time t, given that it
starts at

12
,
x
x at time 0.
Notice here, the above equation is also held for

120 0
,,, 0<<ux xttt , if only change the low limit of
the integration.
Because of the boundary and final-time conditions in
(4), we get

 
12121 212
0
,,0=,,=,,;,,0.
T
tt s
ux xEuXXtpmXsxxds



According to the definition of

12 12
,,;,,0
s
pm Xsx x
defined at the end of (7),

12
,,0ux x is the probability
defined in (3) at time 0.
Now, let us solve PDE (4).
First, we make the following transformation to elimi-
nate the drift terms. Let =Tt


and
 
112 2
12 12
,, =,,,
axaxb
ux xepx x




where
 
21 121221
12
222 2
12 12
=,=,
11
aa

 

 


22 22
11 2211121222
11
=.
22
ba a

  
Then

12
,,px x

satisfies




11 22
222
22
1212
22 12
12
12
12
12
11 =0,
22
,, =,
,,=0,
,,0=0.
ama xb
ppp p
xx xx
pm xe
pxm
px x






 










(8)
Next, we eliminate the cross-partial derivative and
normalize the Brownian motions by a suitable transfor-
mation of coordinates, this idea was introduced by He
etc. ([26]. Define new coordinates 1 z and 2 z as the
following
112 2
1212
1
=,
1
xmx m
z 



  


 

 

(9)
22
22
=.
x
m
z

 (10)
Then
  
112 21212
,, ,, =,,qzxxzxxpxx

 satis-
fies


 

112 222
22
22
12
1
2
12
1
=,
2
,=0,
,= ,
,,0=0,
am azmb
qqq
zz
qL
qL e
qzz





 





 






(11)
where



2
1 12221221
1
=,=0, =,=.L zzzLzzzz








Because the boundary conditions are more conve-
niently expressed in polar coordinates, we introduce


,r

corresponding to


12
,zz as
22 2
12 1
=,tan=,
z
rzz z   (12)
thus


0, 2   and obtain

,,qr

 satisfies





11 2 22
22
222
sin
111
=,
2
,0,=0,
,, =,
,,0=0.
am armb
qqqq
rr rr
qr
qr e
qr






 














(13)
Define a new function

 
11 2 22
sin
,, =,
am armb
fr e



 
  (14)
then



 
,, =,,,,gr qrfr

  solves




22
222
111
=,,,
2
,0,=0,
,, =0,
,,0=,,0.
gggg
bf r
rr rr
gr
gr
grf r










 








(15)
In order to solve PDE (15), we consider the Green’s
function


000
,,;, ,Gr r

 of this problem, which
satisfies
 

22
222
000
111
=,
2
,0,=, ,=0,
,, =.
GGGG
rr
rr
Gr Gr
Grr r


 




 








(16)
Lemma 2 The solution of PDE (16) is


0
0000
2
,,;, ,=r Gr r  





J. LIANG ET AL.
111

22
0
0
20
0
=1 0
sinsin.
rr
n
n
rr
nn
eI











 


 (17)
Proof. We try to find separable solutions to this equa-
tion in the form of



,, =,.GrM rT

 (18)
Plugging (18) into (16), we find that
 
22
222
11
,= .
2
TMMM
Mr Trr
rr

 




 

Divide the previous equation by



,Mr T


, we
find

 
222
222
111
==.
2, 2
TMM M
TMr rr
rr


 


 




(19)
Since the left side of (19) is a function of

and the
right side is a function of r and

, so it must be a
constant. Denote this constant by 2
2

 and we have

12
2
=.TKe




On the other hand,

,
M
r

satisfies equation

22
2
222
11 =0,
,0 =,=0.
MM M
M
rr rr
Mr Mr




 





(20)
This is a Sturm-Liouville problem. We try to find se-
parable solutions in the form of





,=Mr RrΘ

 .
Plugging this i nt o ( 16) we get
222
=,
RR Θ
rr r
RR Θ

 
  (21)
with boundary conditions
 


0= =0.RrΘRrΘ 
Let 2 =ΘΘ k
 , then

Θ

solves

2=0,
0= =0.
ΘkΘ
ΘΘ 
 



 (22)
It is easy to see that

=sin cos.Θ
A
kBk

 
Considering the boundary conditions, we have =0B
and sin= 0.Ak

Because

Θ

is non-zero solution,
we know that 0A and
=,=1,2,.
n
n
kn



Thus the eigenfunctions consistent with the boundary
conditions are
 
=sin,=1,2,.
n
n
ΘCn





Finally consider the radial part of the solution


Rr
which satisfies


2222
=0.
n
rRrRrk R 
 
 
Denoting =r

 , we get the standard form of Bes-
sel’s equation

2
222
2
dd =0.
d dn
RR kR




The well known fundamental solutions of this Bessel's
equation is
 
 
2
=0
1
=112
iik
n
knin
x
Jx Γki Γi





and


 

cos
=.
lim sin
pp
knpk
n
J
xpJx
Yx p





Since


0
kn
Y diverges and we require


0R to be
bounded, the solution


kn
Yy is not permitted. Hence
the general radial part of the solution is


,=. nk
n
RrJr


Sum up




,,nn
RrΘ


over n, we have
 
 
,,
=1
=1
,=
=sin.
nn
n
nn
n
MrR rΘ
n
CJr














Then




 
2
2
=1
,, =,
=sin.
nn
n
GrM rT
n
KCe Jr




 








Because K is a constant, we can define


=
n
A 


n
KC

. Integral the previous equation over

, we
obtain the general solution to PDE (16) for


,,Gr


as
 
2
2
0=1
,, =sin.
nn
n
n
GrAe Jrd













(23)
Now we try to find the coefficient

n
A

which fit
the initial condition






000
,, =Grrr

   . Mul-
tiply the previous equation at 0 =

 by sin m






and integrate over

, we find

J. LIANG ET AL. 112
  
2
0
2
00
0
sin=d.
2mm
m
rrAe Jr








 



(24)
Noticing the completeness relation of
 
0
1
d= ,
ss
x
JaxJbxx ab
a



multiply equation (24) by


m
rJ r



 and integrate over r
 
2
0
0200
2
=sin .
mm
rm
A
eJr











Plugging this expression into


,,Gr

 (23), we get


 
0
0
0
2
200
=1
2
,,=
sin sin.
nn
n
r
Gr
mn
eJrJrd




 


 












(25)
Using the fact [27] that

22
22 2
4
22
0
1
=,
22
ab
cx c
ss s
ab
xeJaxJbxdxeI
cc






(25) can be simplified into (17).
With Green’s function


000
,,;, ,Gr r

 and the
boundary and initial conditions, the solution of PDE (15)
can be expressed as



000000000
0
00000 0
,,=,,;,,, ,
,,;,,0,,0,
F
F
qrdGrrbfrdrd
Grrf rdrd



 



(26)
where
 
=,|0<, 0,Fr r



 (27)

11 2 22
((sin))
,, =.
am armb
fr e



 
  (28)
Then solution of PDE (13) is

,,=,,,, .qrgrfr

 
Returning to the original coordinates and variables

12
,,
x
xt, we get







112 2
112 2
112 2
12 12
12
,,= ,,
=,,
=,,,
axa xbTt
axaxbTt
axaxbTt
ux xtepx xTt
eqzzTt
eqrTt







(29)
where 1 z, 2 z, r,

are defined in (9), (10) and (12).
That is, we have
Theorem 1 The solution of the initial boundary prob-
lem (4) has a closed form solution (29) associated by
(26), (14) and (17).
By now, we have already obtained the probability of
that company 1 defaults and company 2 does not defaults
between time t and T. Change t into 0, T into t, here
comes the probability between time 0 and t.
In order to obtain the probability

12
,,vx x t of that
company 2 defaults and company 1 does not default, we
only need to change the positions of the parameters of
the two companies such as

,,,0
iiii
FV  in


12
,,ux x t.
Now apply our result to the spread Formula (2) when
=0

. In the valuation formula of (2), what we need are
the default probability density functions of



 and



 while we only have the probability functions.
Therefore, we need to modify (2). In fact, notice that


a

and


e

are piecewise continuous functions
and on every piece,
 
 

=0,==.
rr
n
ae teere



 




Integrate the numerator and denominator of (2) by
parts, and we have
 
 

0
0
=1
=1,
Tr
T
rT r
numeratorR ed
ReT red











 



   
 
 


0
0
1
=1
1
=1
1
=1
1
=
=
=|
T
T
nti
ti
i
nti
ti
i
nti
ti
i
ti
ti
denominatorae d
ad aT
aed
ad aT
ae

 






















 

 
1
=1
|,
r
nti
ti
i
ered
aaT












where




=,, =,,,u andv



 (30)
for u and v are solved in this subsection.
3.2. Survival Probability 12 ()πx,x,t
To calculate the credit default swap spread s, we still
need to study the joint survival probability of


12
,,
x
xt 
for 11 >
x
m, 22 >,
x
m

J. LIANG ET AL.
113


   
12
12 121122
,,
=Prob>,>|= ,=.
xxt
X
TmXTmXtxXtx

Same as Theorem 1, the probability of

12
,,
x
xt  is
the solution of PDE

 
 
 
22 2
22
1212 12
22
12 12
12
12 12
122 2
121 1
1212 12
11
==0,
22
,,,,0, ,
,,=0,,,0, ,
,,=0,,, 0,,
,, =1,,,,,
tx xxx
xx
xxt mmT
mxtxt mT
xmtxt mT
xxTxx mm
 
 




 
 











(31)
where 12 ,0.mm
In the previous section, we get the solutions to these two PDEs in the domain


12
,,0,,mm T  



22 2
22
12 1212
22
12 12 12
12
12
12
11
==0,
22
,,=1,
,,=0,
,, =0,
uu uuuu
utx xxx
xx
um xt
uxmt
ux x T
 
 
 
 









(32)
and



222
22
12 12 12
22
12 12 12
12
12
12
11
==0,
22
,,=0,
,,=1,
,, =0,
vv vvvv
vtxxxx
xx
vm xt
vxm t
vx x T
 
 
 










(33)
where 12 ,0.mm
Compare the boundary and final conditions of PDE
(31), (32), (33), the solution to (31) can be written as the
linear combination of the other two

1212 12
,,=1 ,,,,.
x
xtuxxt vxxt   (34)
Set =0t, we get the probability of

which was
defined in Section 2
 
12
=,,0=10 0.xx    (35)
Thus, the CDS spread (2) can be rewritten as
 


    

 
0
11
1
=1
1
= .
||
T
rT r
nt
tt
ir
ii
tt
it i
i
i
ReT red
s
aeeredaaT




 






 




(36)
Remark 1 It is a special case of our model that the
CDS with the counterparty default when the correlation
of the counterparty and reference entity are independent.
Remark 2 The same method can be used to the pric-
ing the CDS for a basket reference entities. In this case,
the PDE model is simpler as the boundaries condition
are all equal to 0. So that, it has no problem caused by
the singularity near (0,0). However, if the basket has a
big number of reference entities, the closed form solution
of the PDE is difficult to be obtained.
3.3. Main Result
Combine the previous two subsection, we obtain the all
probabilities required in Formula (36). Therefore we ob-
tain the main theorem of this paper presented as follows:
Theorem 2 (main theorem) Under the Basic As-
sumption (1)- (4), the credit default swap spread with
counterparty default risk is given by (36), where, in the
formula, the probability



 are given by (30) solving
the problem (4);



 are solved as

 in the same
way;

is given by (35).
4. Numerical Analysis
So far, we have derived the three probabilities in Section
2. With these, we can calculate the CDS spread by (29).
Even though we have a so called closed or semi-closed
form solution, but the calculation of the form is still not
trivial. The expression of the form includes integration

J. LIANG ET AL. 114
and infinite serial, as well as a special function. The di-
rect calculation is not easy to undertaken and the result is
usually not satisfying. This because that the value of the
integrand concentrates in a very small area and this area
is moving as the change of the time t. So that, the differ-
ence approximation, in general, will make the result val-
ue very small.
Here we introduce an algorithm of Monte Carlo method
to evaluate the form (29). It sounds that there is no dif-
ference from the one to calculate CDS spread by direct
Monte Carlo method, however, it is really different with
and without the closed form solution. We will see it in
the later.
Using Monte Carlo to calculate the closed form, in
fact, we only need to know how to calculate the first in-
tegration of the Formula (26). The steps to do it are as
follows:
1) Representing the integration with the exception of
the integrand.
Take


20sin
000000
,,,,Ar frcfr e


 

 as a den-
sity function, where 1221
212
=1 A





, c is a constant
such that

20sin
0000 00
0,, =1,
Ar
F
cd fredrd

 


where

000
,,fr

 , which is non-negative as


0, 2  ,
is defined in (28). By simple calculation, we obtain



112 2
22
2sin
=.
1
amamb
ba A
cee




 


Now rewrite the integration, E is measured respect to

f
:


20
000000000
0
sin
000
,,;,,, ,
=,,;,, ,
F
Ar
dGrrbfrdrd
b
EGrre
c



 
 




where G is defined in (25).
2) Random numbers fetching.
In our case, the three-dimensional random


,,
X
YZ
has a joint density


000
,,fr

 . We sample this random
variable

,,
ii i
X
YZ from


30,1U, for =1,2,i, in
the following way:
a) First, the marginal density function respect to 0 r is
 


22
100000 0
00
sin
0
22
=,,
=sin,
aA r
frfr dd
aA e









and the marginal distribution function is



22
220
sin
0
102 2
0
sin
()= sin
=1.
raA u
aA r
F
raAedu
e








Then generate uniform random number 1i U and set



12 2
=ln1 sin
ii
XUaA

  .
b) Secondly, for given 0
=
X
r, the conditional density
function





0
000 0
000 2
10
,, 2
,| ==.
1
b
b
fr be
fr
fr e


 
 





The marginal density function respect to 0

is
 
0
20000002
0
2
|=,|= ,fr frd






and its distribution function is

2
00
200 22
0
2
|= =.
u
Fr du






Then generate uniform random number 2i
U and set
22
=
ii
YU  .
c) Thirdly, the joint marginal distribution function
with respect to 0 r and 0

is
 


2
20
12000000
0
sin
2 02
2
,= ,,
2
=sin,
aA r
frfr d
aA e










then for given 00 =,=XrY

, the conditional densi-
ty function



0
000
3000 12 00
,,
|, ==,
,1
b
b
fr be
fr fr e



 




 and
its distribution function is

0
3000 1
|, =.
1
b
b
e
Fr e








Then generate uniform random number 3i U and set


3
1
=ln11b
ii
ZeU
b
 
 .
Therefore we generate the ith random sample


,,
ii i
X
YZ with density function

000
,,fr


.
3) By the method above, obtain three-dimensional
random sample


,,
ii i
X
YZ , then replace


000
,,r


and put it into the integ rand

20sin
000
,,;,,Ar
bGr re
c


  .
For =1,2,, ,in repeat the process n times (e.g.
=1000,10000n as required), then find the mean val-
ue, to find approximated the expectation.
It may argue that if use Monte Car lo method, why just
simulate directly on the original Formula (2)? The Fig-
ure 1 can answer this question.
Consider practical examples. Assuming there are two
companies B and C with initial values of


0=$70
B
V
million and


0= $100
C
V million; volatilities of them
are 12 ==0.2, ==0.3
BC

 respectively; recover
rate =0.3R; correlation =0.7

; =0
i

and the de-
fault barriers are $40 million and $60 million respectiv e-
ly.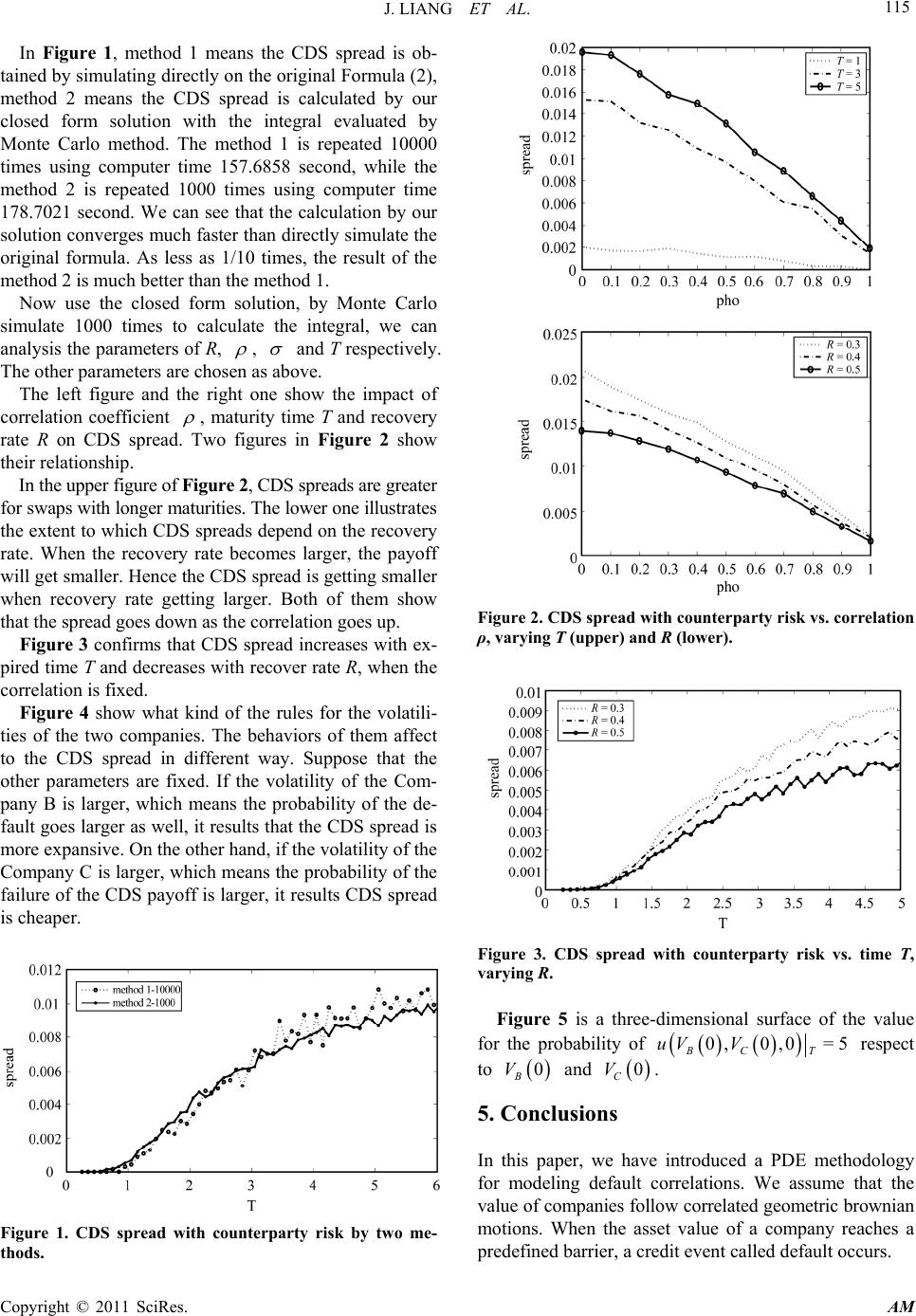

J. LIANG ET AL.
115
In Figure 1, method 1 means the CDS spread is ob-
tained by simulating d irectly on the o riginal Formula (2 ),
method 2 means the CDS spread is calculated by our
closed form solution with the integral evaluated by
Monte Carlo method. The method 1 is repeated 10000
times using computer time 157.6858 second, while the
method 2 is repeated 1000 times using computer time
178.7021 second. We can see that the calculation by our
solution converg es much faster than directly simulate the
original formula. As less as 1/10 times, the result of the
method 2 is much better than the method 1.
Now use the closed form solution, by Monte Carlo
simulate 1000 times to calculate the integral, we can
analysis the parameters of R,

,

and T respectively.
The other parameters are chosen as above.
The left figure and the right one show the impact of
correlation coefficient

, maturity time T and recovery
rate R on CDS spread. Two figures in Figure 2 show
their relationship.
In the upper figure of Figure 2, CDS spreads are greater
for swaps with longer maturities. The lower one illustrat e s
the extent to which CDS spreads depend on the recovery
rate. When the recovery rate becomes larger, the payoff
will get smaller. Hence the CDS spread is getting smaller
when recovery rate getting larger. Both of them show
that the spread goes down as the correlation goes up.
Figure 3 confirms that CDS spread increases with ex-
pired time T and decreases with recover rate R, when the
correlation is fixed.
Figure 4 show what kind of the rules for the volatili-
ties of the two companies. The behaviors of them affect
to the CDS spread in different way. Suppose that the
other parameters are fixed. If the volatility of the Com-
pany B is larger, which means the probability of the de-
fault goes larger as well, it results that the CDS spread is
more expansive. On the other hand, if the volatility o f the
Company C is larger, which means the probability o f the
failure of the CDS payoff is larger, it results CDS spread
is cheaper.
Figure 1. CDS spread with counterparty risk by two me-
thods.
Figure 2. CDS spread with counterparty risk vs. correlation
ρ, varying T (upper) and R (lower).
Figure 3. CDS spread with counterparty risk vs. time T,
varying R.
Figure 5 is a three-dimensional surface of the value
for the probability of
 


0,0,0 =5
BC T
uV V respect
to


0
B
V and


0
C
V.
5. Conclusions
In this paper, we have introduced a PDE methodology
for modeling default correlations. We assume that the
value of companies follow correlated geometric brownian
motions. When the asset value of a company reaches a
predefined barrier, a credit event called default occurs.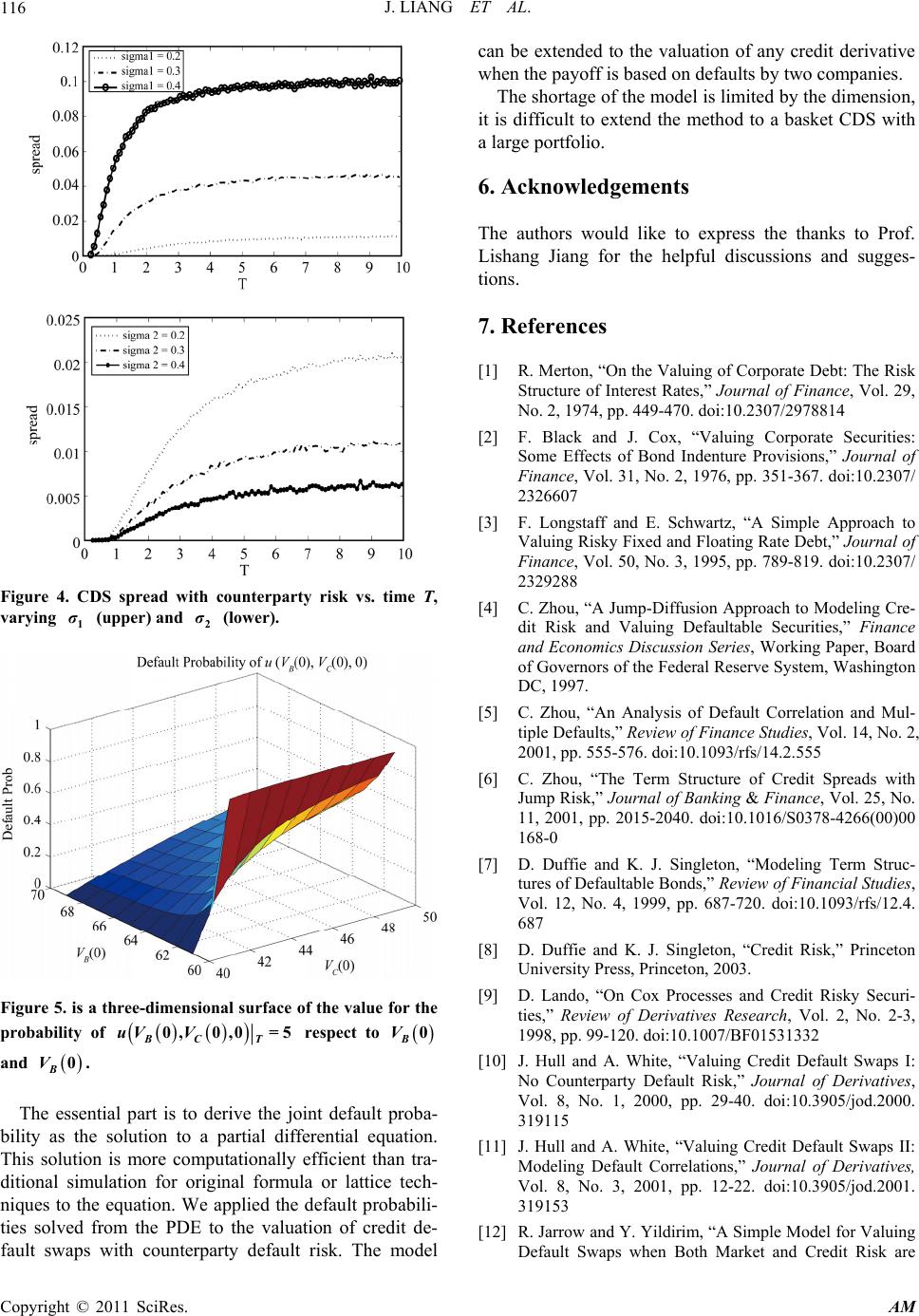

J. LIANG ET AL. 116
Figure 4. CDS spread with counterparty risk vs. time T,
varying 1
σ (upper) and 2 σ (lower).
Figure 5. is a three-dimensional surface of the value for the
probability of






0,0,0 =5
BC T
uV V respect to


0
B
V
and

0
B
V.
The essential part is to derive the joint default proba-
bility as the solution to a partial differential equation.
This solution is more computationally efficient than tra-
ditional simulation for original formula or lattice tech-
niques to the equation. We applied the default probabili-
ties solved from the PDE to the valuation of credit de-
fault swaps with counterparty default risk. The model
can be extended to the valuation of any credit derivative
when the payoff is base d o n de faul t s by tw o companies.
The shortage of the model is limited by the dimension,
it is difficult to extend the method to a basket CDS with
a large portfolio.
6. Acknowledgements
The authors would like to express the thanks to Prof.
Lishang Jiang for the helpful discussions and sugges-
tions.
7. References
[1] R. Merton, “On the Valuing of Corporate Debt: The Risk
Structure of Interest Rates,” Journal of Finance, Vol. 29,
No. 2, 1974, pp. 449-470. doi:10.2307/2978814
[2] F. Black and J. Cox, “Valuing Corporate Securities:
Some Effects of Bond Indenture Provisions,” Journal of
Finance, Vol. 31, No. 2, 1976, pp. 351-367. doi:10.2307/
2326607
[3] F. Longstaff and E. Schwartz, “A Simple Approach to
Valuing Risky Fixed and Floating Rate Debt,” Journal of
Finance, Vol. 50, No. 3, 1995, pp. 789-819. doi:10.2307/
2329288
[4] C. Zhou, “A Jump-Diffusion Approach to Modeling Cre-
dit Risk and Valuing Defaultable Securities,” Finance
and Economics Discussion Series, Working Paper, Board
of Governors of the Federal Reserve System, Washington
DC, 1997.
[5] C. Zhou, “An Analysis of Default Correlation and Mul-
tiple Defaults,” Review of Finance Studies, Vol. 14, No. 2,
2001, pp. 555-576. doi:10.1093/rfs/14.2.555
[6] C. Zhou, “The Term Structure of Credit Spreads with
Jump Risk,” Journal of Banking & Finance, Vol. 25, No.
11, 2001, pp. 2015-2040. doi:10.1016/S0378-4266(00)00
168-0
[7] D. Duffie and K. J. Singleton, “Modeling Term Struc-
tures of Defaultable Bonds,” Review of Financial Studies,
Vol. 12, No. 4, 1999, pp. 687-720. doi:10.1093/rfs/12.4.
687
[8] D. Duffie and K. J. Singleton, “Credit Risk,” Princeton
University Press, Princeton, 2003.
[9] D. Lando, “On Cox Processes and Credit Risky Securi-
ties,” Review of Derivatives Research, Vol. 2, No. 2-3,
1998, pp. 99-120. doi:10.1007/BF01531332
[10] J. Hull and A. White, “Valuing Credit Default Swaps I:
No Counterparty Default Risk,” Journal of Derivatives,
Vol. 8, No. 1, 2000, pp. 29-40. doi:10.3905/jod.2000.
319115
[11] J. Hull and A. White, “Valuing Credit Default Swaps II:
Modeling Default Correlations,” Journal of Derivatives,
Vol. 8, No. 3, 2001, pp. 12-22. doi:10.3905/jod.2001.
319153
[12] R. Jarrow and Y. Yildirim, “A Simple Model for Valuing
Default Swaps when Both Market and Credit Risk are

J. LIANG ET AL.
117
Correlated,” Journal of Fixed Income, Vol. 11, No. 4, 2002,
pp. 7-19. doi:10.3905/jfi.2002.319308
[13] R. Jarrow and F. Yu, “Counterparty Risk and the Pricing
of Defaultable Securities,” Journal of Finance, Vol. 56,
No. 5, 2001, pp. 1765-1799. doi:10.1111/0022-1082.003
89
[14] F. Yu, “Correlated Defaults and the Valuation of Defaul-
table Securities,” Proceedings of 2nd International Con-
ference on Credit Risk, Montréal, 15-16 April 2004, pp.
1-30.
[15] S. Y. Leung and Y. K. Kwok, “Credit Default Swap Val-
uation with Counterparty Risk,” The Kyoto Economic
Review, Vol. 74, No. 1, 2005, pp. 25-45.
[16] R. Jarrow and S. M. Turnbull, “Pricing Derivatives on
Financial Securities Subject to Credit Risk,” Journal of
Finance, Vol. 50, No. 1, 1995, pp. 53-86. doi:10.2307/
2329239
[17] J. Hull and A. White, “Valuation of a CDO and nth to
Default CDS without Monte Carlo Simulation,” Journal
of Derivatives, Vol. 12, No. 2, 2004, pp. 8-23. doi:10.
3905/jod.2004.450964
[18] J. Hull, M. Predescu and A. White, “The Relationship
between Credit Default Swap Spreads, Bond Yields, and
Credit Rating Announcements,” Journal of Banking &
Finance, Vol. 28, No. 11, 2004, pp. 2789-2811. doi:10.
1016/j.jbankfin.2004.06.010
[19] J. Hull, M. Predescu and A. White, “The Valuation of
Correlation-Dependent Credit Derivatives Using a Struc-
tural Model,” Journal of Credit Risk, Vol. 6, No. 3, 2010,
pp. 99-132.
[20] M. Kijima and Y. Muromachi, “Credit Events and the
Valuation of Credit Derivatives of Basket Type,” Review
of Derivatives Research, Vol. 4, No. 1, 2000, pp. 55-79.
doi:10.1023/A:1009676412322
[21] M. Kijima and Y. Muromachi, “Valuation of a Credit
Swap of the Basket Type,” Review of Derivatives Re-
search, Vol. 4, No. 1, 2000, pp. 81-97. doi:10.1023/A:
1009628513231
[22] M. Wise and V. Bhansali, “Correlated Random Walks
and the Joint Survival Probability,” Working Paper, Cal-
tech and PIMCO, pp. 1-13.
[23] P. Zhou and J. Liang, “Analysis of Credit Default Swap,”
Applied Mathematics-JCU, Vol. 22, 2007, pp. 311-314.
[24] K. Giesecke and L. R. Goldberg, “The Market Price of
Credit Risk,” Working Paper, Cornell University, New
York, 2003, pp. 1-29.
[25] J. Hull, “Options, Futures and Other Derivatives,” 7th
Edition, Prentice Education, Upper Saddle River, 2009.
[26] H. He, P. W. Keirstead and J. Rebholz, “Double Look-
backs,” Mathematical Finance, Vol. 8, No. 3, 1998, pp.
201-228. doi:10.1111/1467-9965.00053
[27] I. S. Gradshteyn and I. M. Ryzhik, “Table of Integrals,
Series, and Products,” Academic Press, New York, 1980.