Paper Menu >>
Journal Menu >>
 Journal of Signal and Information Processing, 2013, 4, 176-181 doi:10.4236/jsip.2013.43B032 Published Online August 2013 (http://www.scirp.org/journal/jsip) Study of Symmetry Process Behavior in Fractal Gray Image Compression by Traditional Method Eman A. Al-Hilo, Kawther H. Al-Khafaji College of Education for Girls, Physics Departments, Kufa University, Najaf, Iraq. Email: emanalhilo@yahoo.com Received June, 2013 ABSTRACT This paper studies the effect of symmetry process on the compression parameters of the fractal image compression tech- nique proposed by Jacquin. Two kinds of tests have been conducted. The first all kind of the symmetry operations [0-7] were taken; while the second tests were concentrated on studying the effect of the following parameters Block Size, Step Size, Domain Size on the probability distribution of symmetry operation. The results show that the higher value of PSNR and the lower value of ET occur at even symmetry operation only, but compression ratio is not affected with symmetry process. Also the occurrence probability of even symmetry is more than odd symmetry for all compression parameters. This behaviour can be utilized to reduce the encoding time to 50% with preserving PSNR. Keywords: Image Compression; Zero-Mean; Fractal Image Compression; Symmetry process 1. Introduction Image coding through fractal geometry has proven to be very effective, and fractal image compression is a prom- ising field that has gained efficiency in both memory consumption and high speed transmission. Fractal image coding introduced by Barnsley and Jacquin is the out- come of the study of the iterated function system devel- oped in the last decade [1]. By using IFS techniques and simple deterministic algorithms, images with spatial complexity can be encoded through certain fractal rela- tionships that describe mapping of blocks of images within themselves. This fractal image technique finds similar patterns that exist on different scales/orientations, and at different places in an image. Hence, it allows en- coding of an image file by systematically analyzing it and saving a much smaller set of instructions that can be used to iteratively reconstruct the entire image from those patterns. In fact, this compression technique can be thought of a method eliminating as much redundancy as possible. [2-3] Saup [4] represents selected studies about the influ- ence of symmetry on the quality of fractal codes. After- wards an empirically comparison of the efficiency of domain pools with same size with or without using symmetry blocks follows. The presented results show that the using of symmetry doesn't increase the efficiency of codes. The aim of our project is studding the behavior of symmetry process in the fractal gray image compression. 2. Fractal Image Coding The basic idea of fractal image compression is partition- ing the image into non overlapping range blocks. For every range block a similar but larger domain block is found. There are many ways to partition images. The fixed size partitioning are used in this research because it requires less computational time than the other.[5] For a range block with pixel values (ro,r1,…,rm-1), and the domain block (do,d1…,dm-1) the contractive affine approximation is [6]: osdr ii , (1) where, i r is the optimally approximated ith pixel value in the range block. di is the corresponding pixel value in the domain block. The symbols s,o represent the scaling and offset coefficients, respectively. The scale (s) and offset (o) coefficients are determined by applying the least mean square difference (χ2) criteria between ( r r ) and () values [7]. 12 2 11 0 1m i rr m , (2) 22 0, 0, so (3) The straightforward manipulation of the above equa- tion leads to: Copyright © 2013 SciRes. JSIP  Study of Symmetry Process Behavior in Fractal Gray Image Compression by Traditional Method 177 1 0 2 1 0 2 1 0 1 0 1 0 n i n i ii n i n i i n i iii ddn drdrn s, (4) 1 0 2 1 0 2 1 0 1 0 1 0 1 0 2 n i n i ii n i n i ii n i i n i ii ddn ddrdr o, (5) 1111 22 2 0000 1 0 22 2 nnnn iiii iiii n i i rssdrd od ono r i (6) 3. Symmetry Process In order to increase the size of domain pool and, conse- quently, to increase the probability of finding the best (near optimal) approximations for the range blocks, each domain block is transformed by using a set of symmetry transforms (i.e., rotation and flipping), such that eight versions (blocks) are produced for each domain block [8]. The eight symmetry mappings are (identity, rotation 90, rotation 180, rotation 270, reflection-x, reflection with rotation 90, reflection with rotation 180, reflection with rotation 270), (see Table 1). The number of bits required to represent the eight symmetry mapping cases is (3) bits. Table 1. The eight symmetry transformations. Sym Equations Results 0. Identity 0sin0cos yxx 0cos0sin yxy xx yy 1. Rot.(+90) 90sin90cos yxx 90cos90sin yxy yx xy 2. Rot.(+180) 180sin180cos yxx 180cos180sin yxy xx yy 3. Rot.(+270) 270sin270cos yxx 270cos270sin yxy yx xy 4. Ref. at x-axis 0sin0cos yxx 0cos0sin yxy xx yy 5. Ref.& Rot. (90) 90sin90cos yxx 90cos90sin yxy yx xy 6. Ref.& Rot. (180) 180sin180cos yxx 180cos180sin yxy xx yy 7. Ref & Rot. (270) 270sin270cos yxx 270cos270sin yxy yx xy The main disadvantage of using the symmetry map- pings in the encoding process is that more computational time will be required to perform the extra matching processes. 4. Encoding Process The encoding method could be summarized by the fol- lowing steps: 1) Load BMP image and put it in (2D arrays). 2) Establish the range image (array). 3) Down sample the range image to produce the do- main array. 4) Great range and domain pool by partitioning: a) The range array must be partitioned into non-over- lapping fixed blocks, to generate the range blocks (r1,….,rn). b) The domain must be partitioned into overlapping blocks, using specific step size, to generate the domain blocks (d1,…,dn). They should have the same size of range blocks. 5) Searching: For each range block do the following: a) Pick up a domain block from the domain pool. b) Perform one of the symmetry mappings that men- tioned in table (1). c) Calculate the scale (s) and offset (o) coefficient us- ing equations (4) and (5). d) Apply the following condition to bound the value of (s) and offset (o) coefficient: If s< s min then s=smin Else if s >smax then s=smax If o< o min then o=omin Else if o >omax then o=omax e) Quantize the value (s) and offset (o) using equations that referred in [9]. f) Compute the approximation error (χ2) using equa- tion (6). g) After the computation of IFS code and the sum of error (χ2) of the matching between the range and the tested domain block, the (χ2) is compared with registered minimum error (χ2 min); such that: If χ2< (χ2 min) then sopt=is; oopt=io, χ2 min= χ2 PosI=domain block index Sym=symmetry index End if h) If χ2 min < then the search across the domain blocks is stopped, and the registered domain block is considered as the best matched block. i) Repeat steps (4) to (10) for all symmetry states of the tested domain block. j) Repeat steps (3) to (11) for all the domain blocks listed in the domain pool. k) The output is the set of IFS parameters Copyright © 2013 SciRes. JSIP 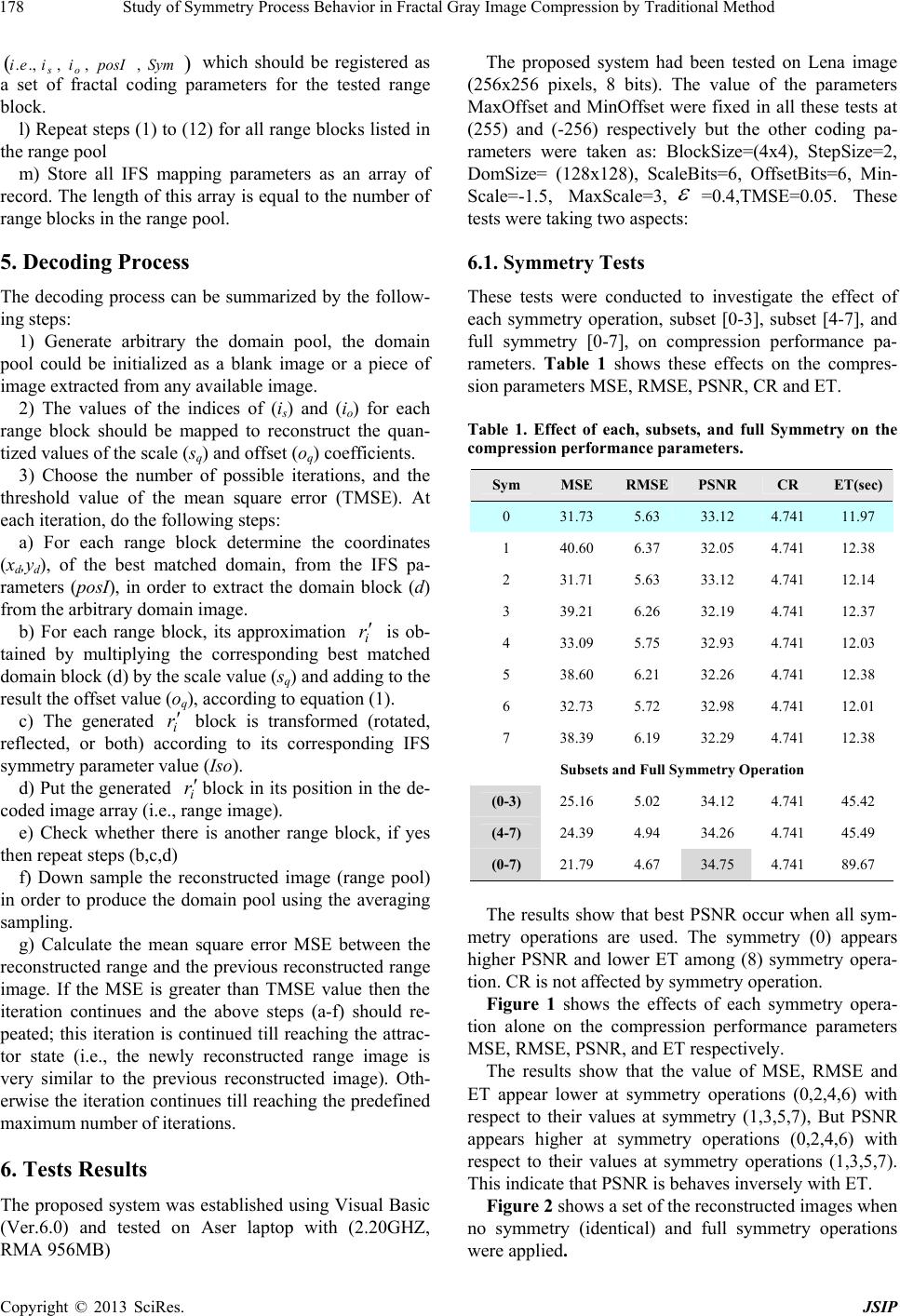 Study of Symmetry Process Behavior in Fractal Gray Image Compression by Traditional Method 178 SymposIiiei os ,,,.,. which should be registered as a set of fractal coding parameters for the tested range block. l) Repeat steps (1) to (12) for all range blocks listed in the range pool m) Store all IFS mapping parameters as an array of record. The length of this array is equal to the number of range blocks in the range pool. 5. Decoding Process The decoding process can be summarized by the follow- ing steps: 1) Generate arbitrary the domain pool, the domain pool could be initialized as a blank image or a piece of image extracted from any available image. 2) The values of the indices of (is) and (io) for each range block should be mapped to reconstruct the quan- tized values of the scale (sq) and offset (oq) coefficients. 3) Choose the number of possible iterations, and the threshold value of the mean square error (TMSE). At each iteration, do the following steps: a) For each range block determine the coordinates (xd,yd), of the best matched domain, from the IFS pa- rameters (posI), in order to extract the domain block (d) from the arbitrary domain image. b) For each range block, its approximation i r is ob- tained by multiplying the corresponding best matched domain block (d) by the scale value (sq) and adding to the result the offset value (oq), according to equation (1). c) The generated i block is transformed (rotated, reflected, or both) according to its corresponding IFS symmetry parameter value (Iso). r d) Put the generated iblock in its position in the de- coded image array (i.e., range image). r e) Check whether there is another range block, if yes then repeat steps (b,c,d) f) Down sample the reconstructed image (range pool) in order to produce the domain pool using the averaging sampling. g) Calculate the mean square error MSE between the reconstructed range and the previous reconstructed range image. If the MSE is greater than TMSE value then the iteration continues and the above steps (a-f) should re- peated; this iteration is continued till reaching the attrac- tor state (i.e., the newly reconstructed range image is very similar to the previous reconstructed image). Oth- erwise the iteration continues till reaching the predefined maximum number of iterations. 6. Tests Results The proposed system was established using Visual Basic (Ver.6.0) and tested on Aser laptop with (2.20GHZ, RMA 956MB) The proposed system had been tested on Lena image (256x256 pixels, 8 bits). The value of the parameters MaxOffset and MinOffset were fixed in all these tests at (255) and (-256) respectively but the other coding pa- rameters were taken as: BlockSize=(4x4), StepSize=2, DomSize= (128x128), ScaleBits=6, OffsetBits=6, Min- Scale=-1.5, MaxScale=3, =0.4,TMSE=0.05. These tests were taking two aspects: 6.1. Symmetry Tests These tests were conducted to investigate the effect of each symmetry operation, subset [0-3], subset [4-7], and full symmetry [0-7], on compression performance pa- rameters. Table 1 shows these effects on the compres- sion parameters MSE, RMSE, PSNR, CR and ET. Table 1. Effect of each, subsets, and full Symmetry on the compression performance parameters. Sym MSE RMSE PSNR CR ET(sec) 0 31.73 5.63 33.12 4.741 11.97 1 40.60 6.37 32.05 4.741 12.38 2 31.71 5.63 33.12 4.741 12.14 3 39.21 6.26 32.19 4.741 12.37 4 33.09 5.75 32.93 4.741 12.03 5 38.60 6.21 32.26 4.741 12.38 6 32.73 5.72 32.98 4.741 12.01 7 38.39 6.19 32.29 4.741 12.38 Subsets and Full Symmetry Operation (0-3) 25.16 5.02 34.12 4.741 45.42 (4-7) 24.39 4.94 34.26 4.741 45.49 (0-7) 21.79 4.67 34.75 4.741 89.67 The results show that best PSNR occur when all sym- metry operations are used. The symmetry (0) appears higher PSNR and lower ET among (8) symmetry opera- tion. CR is not affected by symmetry operation. Figure 1 shows the effects of each symmetry opera- tion alone on the compression performance parameters MSE, RMSE, PSNR, and ET respectively. The results show that the value of MSE, RMSE and ET appear lower at symmetry operations (0,2,4,6) with respect to their values at symmetry (1,3,5,7), But PSNR appears higher at symmetry operations (0,2,4,6) with respect to their values at symmetry operations (1,3,5,7). This indicate that PSNR is behaves inversely with ET. Figure 2 shows a set of the reconstructed images when no symmetry (identical) and full symmetry operations were applied. Copyright © 2013 SciRes. JSIP 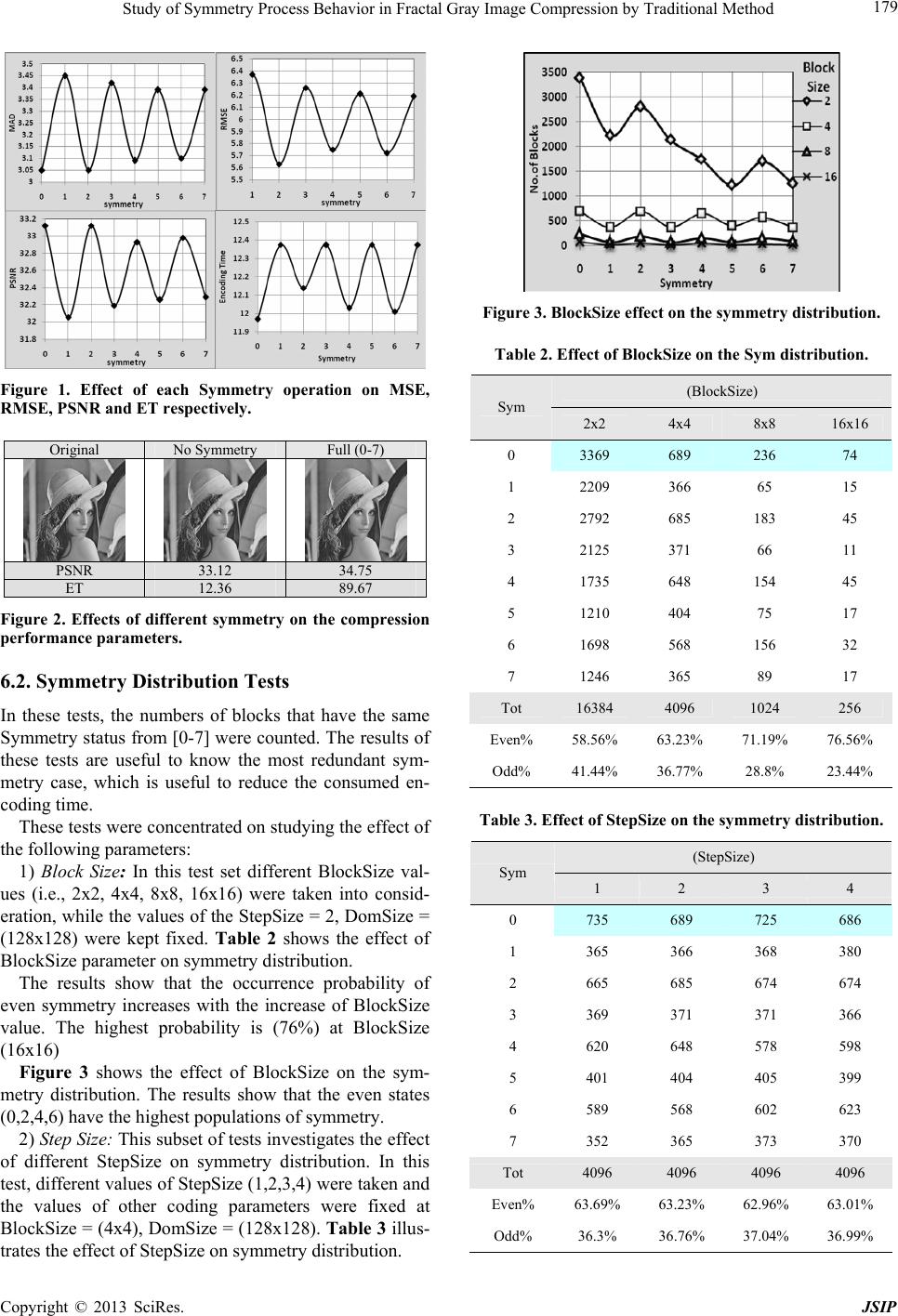 Study of Symmetry Process Behavior in Fractal Gray Image Compression by Traditional Method 179 Figure 1. Effect of each Symmetry operation on MSE, RMSE, PSNR and ET respectively. Original No Symmetry Full (0-7) PSNR 33.12 34.75 ET 12.36 89.67 Figure 2. Effects of different symmetry on the compression performance parameters. 6.2. Symmetry Distribution Tests In these tests, the numbers of blocks that have the same Symmetry status from [0-7] were counted. The results of these tests are useful to know the most redundant sym- metry case, which is useful to reduce the consumed en- coding time. These tests were concentrated on studying the effect of the following parameters: 1) Block Size: In this test set different BlockSize val- ues (i.e., 2x2, 4x4, 8x8, 16x16) were taken into consid- eration, while the values of the StepSize = 2, DomSize = (128x128) were kept fixed. Table 2 shows the effect of BlockSize parameter on symmetry distribution. The results show that the occurrence probability of even symmetry increases with the increase of BlockSize value. The highest probability is (76%) at BlockSize (16x16) Figure 3 shows the effect of BlockSize on the sym- metry distribution. The results show that the even states (0,2,4,6) have the highest populations of symmetry. 2) Step Size: This subset of tests investigates the effect of different StepSize on symmetry distribution. In this test, different values of StepSize (1,2,3,4) were taken and the values of other coding parameters were fixed at BlockSize = (4x4), DomSize = (128x128). Table 3 illus- trates the effect of StepSize on symmetry distribution. Figure 3. BlockSize effect on the symmetry distribution. Table 2. Effect of BlockSize on the Sym distribution. (BlockSize) Sym 2x2 4x4 8x8 16x16 0 3369 689 236 74 1 2209 366 65 15 2 2792 685 183 45 3 2125 371 66 11 4 1735 648 154 45 5 1210 404 75 17 6 1698 568 156 32 7 1246 365 89 17 Tot 16384 4096 1024 256 Even% 58.56% 63.23% 71.19% 76.56% Odd% 41.44% 36.77% 28.8% 23.44% Table 3. Effect of StepSize on the symmetry distri bution. (StepSize) Sym 1 2 3 4 0 735 689 725 686 1 365 366 368 380 2 665 685 674 674 3 369 371 371 366 4 620 648 578 598 5 401 404 405 399 6 589 568 602 623 7 352 365 373 370 Tot 4096 4096 4096 4096 Even% 63.69% 63.23% 62.96% 63.01% Odd% 36.3% 36.76% 37.04% 36.99% Copyright © 2013 SciRes. JSIP 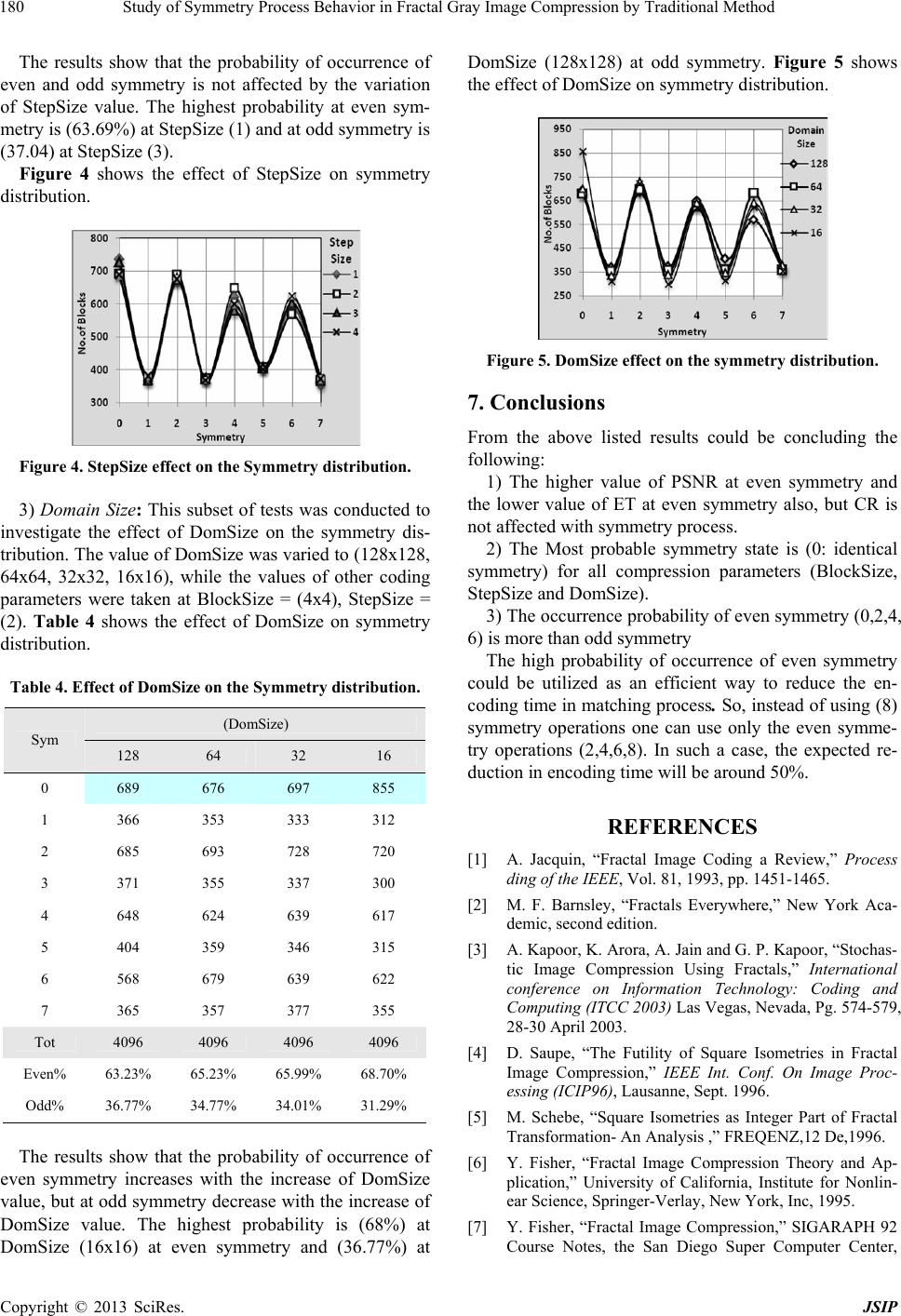 Study of Symmetry Process Behavior in Fractal Gray Image Compression by Traditional Method 180 The results show that the probability of occurrence of even and odd symmetry is not affected by the variation of StepSize value. The highest probability at even sym- metry is (63.69%) at StepSize (1) and at odd symmetry is (37.04) at StepSize (3). Figure 4 shows the effect of StepSize on symmetry distribution. Figure 4. StepSize effect on the Symme try distribution. 3) Domain Size: This subset of tests was conducted to investigate the effect of DomSize on the symmetry dis- tribution. The value of DomSize was varied to (128x128, 64x64, 32x32, 16x16), while the values of other coding parameters were taken at BlockSize = (4x4), StepSize = (2). Table 4 shows the effect of DomSize on symmetry distribution. Table 4. Effect of DomSize on the Symmetry distribution. (DomSize) Sym 128 64 32 16 0 689 676 697 855 1 366 353 333 312 2 685 693 728 720 3 371 355 337 300 4 648 624 639 617 5 404 359 346 315 6 568 679 639 622 7 365 357 377 355 Tot 4096 4096 4096 4096 Even% 63.23% 65.23% 65.99% 68.70% Odd% 36.77% 34.77% 34.01% 31.29% The results show that the probability of occurrence of even symmetry increases with the increase of DomSize value, but at odd symmetry decrease with the increase of DomSize value. The highest probability is (68%) at DomSize (16x16) at even symmetry and (36.77%) at DomSize (128x128) at odd symmetry. Figure 5 shows the effect of DomSize on symmetry distribution. Figure 5. DomSize effect on the symmetry distribution. 7. Conclusions From the above listed results could be concluding the following: 1) The higher value of PSNR at even symmetry and the lower value of ET at even symmetry also, but CR is not affected with symmetry process. 2) The Most probable symmetry state is (0: identical symmetry) for all compression parameters (BlockSize, StepSize and DomSize). 3) The occurrence probability of even symmetry (0,2,4, 6) is more than odd symmetry The high probability of occurrence of even symmetry could be utilized as an efficient way to reduce the en- coding time in matching process. So, instead of using (8) symmetry operations one can use only the even symme- try operations (2,4,6,8). In such a case, the expected re- duction in encoding time will be around 50%. REFERENCES [1] A. Jacquin, “Fractal Image Coding a Review,” Process ding of the IEEE, Vol. 81, 1993, pp. 1451-1465. [2] M. F. Barnsley, “Fractals Everywhere,” New York Aca- demic, second edition. [3] A. Kapoor, K. Arora, A. Jain and G. P. Kapoor, “Stochas- tic Image Compression Using Fractals,” International conference on Information Technology: Coding and Computing (ITCC 2003) Las Vegas, Nevada, Pg. 574-579, 28-30 April 2003. [4] D. Saupe, “The Futility of Square Isometries in Fractal Image Compression,” IEEE Int. Conf. On Image Proc- essing (ICIP96), Lausanne, Sept. 1996. [5] M. Schebe, “Square Isometries as Integer Part of Fractal Transformation- An Analysis ,” FREQENZ,12 De,1996. [6] Y. Fisher, “Fractal Image Compression Theory and Ap- plication,” University of California, Institute for Nonlin- ear Science, Springer-Verlay, New York, Inc, 1995. [7] Y. Fisher, “Fractal Image Compression,” SIGARAPH 92 Course Notes, the San Diego Super Computer Center, Copyright © 2013 SciRes. JSIP  Study of Symmetry Process Behavior in Fractal Gray Image Compression by Traditional Method Copyright © 2013 SciRes. JSIP 181 University of California, an Diego, 1992 [8] C. Frigaard, “Fast Fractal 2D/3D Image Compression, Report,” Institute of Electronic Systems, Alborg Univer- sity, Laboratory of Image Analysis, 1995. [9] E. A. Al-Hilo, “Loay E. George, "Fractal Color Image Compression,” 4th International Conference on Nov. 2008 (ICIMU’ 2008), Malaysia. |

