Journal of Signal and Information Processing, 2013, 4, 114-119
doi:10.4236/jsip.2013.43B020 Published Online August 2013 (http://www.scirp.org/journal/jsip)
Corner-Based Image Alignment using Pyramid Structure
with Gradient Vector Similarity
Chin-Sheng Chen1, Kang-Yi Peng1, Chien-Liang Huang1, Chun-Wei Yeh2
1Graduate Institute of Automation Technology, National Taipei University of Technology; 2Department of Electronic, Electrical &
Computer Engineering University of Birmingham, UK.
Received May, 2013.
ABSTRACT
This paper presents a corner-based image alignment algorithm based on the procedures of corner-based template
matching and geometric parameter estimation. This algorithm consists of two stages: 1) training phase, and 2) matching
phase. In the training phase, a corner detection algorithm is used to extract the corners. These corners are then used to
build the pyramid images. In the matching phase, the corners are obtained using the same corner detection algorithm.
The similarity measure is then determined by the differences of gradient vector between the corners obtained in the
template image and the inspection image, respectively. A parabolic function is further applied to evaluate the geo metric
relationship between the template and the inspection images. Results show that the corner-based template matching
outperforms the original edge-based template matching in efficiency, and both of them are robust against non-liner light
changes. The accuracy and precision of the corner-based image alignment are competitive to that of edge-based image
alignment under the same environment. In practice, the proposed algorithm demonstrates its precision, efficiency and
robustness in image alignment for real world applications.
Keywords: Corner-Based Image Alignment; Corner Detection; Edge-Based Template Matching; Gradient Vector
1. Introduction
In automatic optical inspection (AOI) systems, speed,
precision, and robu stness are the key requirements in real
world applications. The technique of image alignment
can be used to achieve these requirements. The common
image alignment technology can be categorized into two
kinds [1]: (1) area-based matching, and (2) feature-based
matching. In the area-based template matching, normal-
ized cross correlation (NCC) method is a popular one
that can be used to evaluate the degree of similarity be-
tween template and scene images. However, it is not ro-
bust against non-liner light changes and occluded objects
[2].
The main advantage of the feature-based image align-
ment is its efficiency. Chen et al. [1,3] proposed an im-
age alignment algorithm based on Fourier descriptor.
This is a kind of feature-based alignment algorithm,
so-called contour-based image alignment. Here, the Fou-
rier descriptor is used to describe the contour information
of an object. The contour information is extracted using
the maximally stable extremal regions (MSER) method.
The MSER method can be used to effectively extract the
contour information in an unstable environment. How-
ever, the contour-based alignment algorithm is based on
the contour information that has been strong ly influenced
by the results of segmentation. Thus, this algorithm is not
suitable for occluded object recognition.
To adapt the complicated environment for template
matching, Steger [4] presented a similarity measure
based on the difference of gradient direction in edges that
is robust against non-linear illumination changes, and it
can also be utilized to recognize occluded objects. How-
ever, the computation of this similarity measure is not
efficient enough for real-time applications.
To speed up the computation of the edge-based simi-
larity measure, we have presented a corner-based simi-
larity measure that is based on the difference of gradient
direction in corners instead of in edges. This corner-
based similarity measure has the same characteristic with
the edge-based similarity measure as mentioned before.
Additionally, we have further developed a corner-based
template matching algorithm based on the presented
similarity measure. A corner-based image alignment
combines two procedures of the corner-based template
matching and geometric parameter estimation.
In the presented corner-based template matching, the
stabilities of corners have been influen ced by the process
of corner detectio n. To addr ess the instab ilities of corn ers,

Co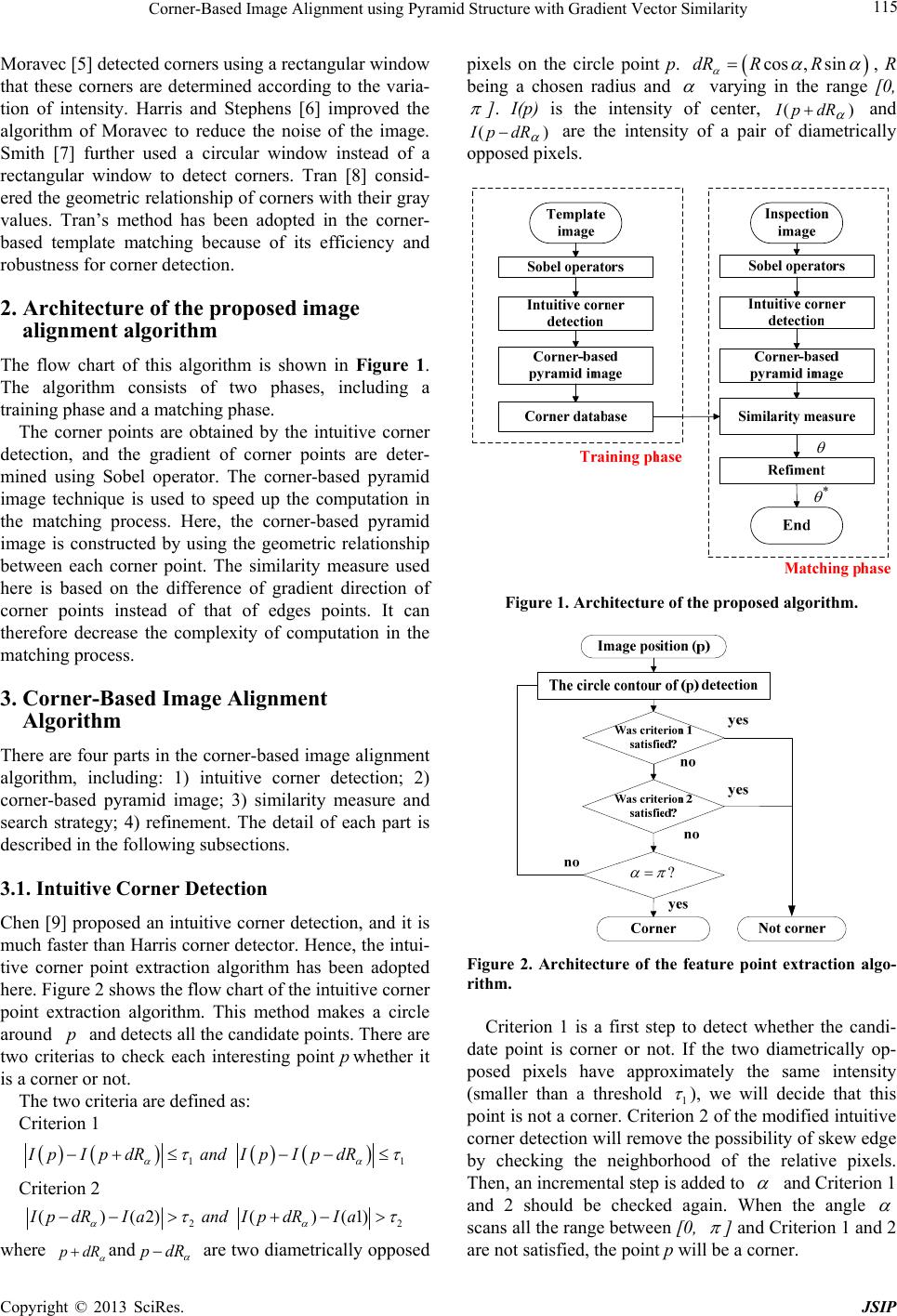rner-Based Image Alignment using Pyramid Structure with Gradient Vector Similarity 115
Moravec [5] detected corners using a rectangular window
that these corners are determined according to the varia-
tion of intensity. Harris and Stephens [6] improved the
algorithm of Moravec to reduce the noise of the image.
Smith [7] further used a circular window instead of a
rectangular window to detect corners. Tran [8] consid-
ered the geometric relationship of corners with their gray
values. Tran’s method has been adopted in the corner-
based template matching because of its efficiency and
robustness for corn er detection.
2. Architecture of the proposed image
alignment algorithm
The flow chart of this algorithm is shown in Figure 1.
The algorithm consists of two phases, including a
training phase and a matching phase.
The corner points are obtained by the intuitive corner
detection, and the gradient of corner points are deter-
mined using Sobel operator. The corner-based pyramid
image technique is used to speed up the computation in
the matching process. Here, the corner-based pyramid
image is constructed by using the geometric relationship
between each corner point. The similarity measure used
here is based on the difference of gradient direction of
corner points instead of that of edges points. It can
therefore decrease the complexity of computation in the
matching proces s.
3. Corner-Based Image Alignment
Algorithm
There are four parts in the corner-based image alignment
algorithm, including: 1) intuitive corner detection; 2)
corner-based pyramid image; 3) similarity measure and
search strategy; 4) refinement. The detail of each part is
described in the following subsections.
3.1. Intuitive Corner Detection
Chen [9] proposed an intuitive corner detection, and it is
much faster than Harris corner detector. Hence, the intui-
tive corner point extraction algorithm has been adopted
here. Figure 2 shows the flow chart of the intuitive corner
point extraction algorithm. This method makes a circle
around and detects all the candidate points. Th ere are
two criterias to check each interesting pointwhether it
is a corner or not.
pp
The two criteria are defined as:
Criterion 1








11
Ip IpdRandIp IpdR


   
Criterion 2
22
()(2) ()(1)IpdRI aandIpdRI a


  
where
p
dR

and
p
dR

 are two diametrically opposed
pixels on the circle point p.

cos ,sindR RR


 , R
being a chosen radius and

varying in the range [0,

]. I(p) is the intensity of center, and

)(

dRpI 
)dRp(I

are the intensity of a pair of diametrically
opposed pixels.
*


Figure 1. Architecture of the proposed algorithm.
?



Figure 2. Architecture of the feature point extraction algo-
rithm.
Criterion 1 is a first step to detect whether the candi-
date point is corner or not. If the two diametrically op-
posed pixels have approximately the same intensity
(smaller than a threshold 1

), we will decide that this
point is not a corner. Criterion 2 of the modified intuitiv e
corner detection will remove the possibility o f skew edge
by checking the neighborhood of the relative pixels.
Then, an incremental step is added to

and Criterion 1
and 2 should be checked again. When the angle

scans all the range between [0,

] and Criterion 1 an d 2
are not satisfied, the point p will be a corner.

Co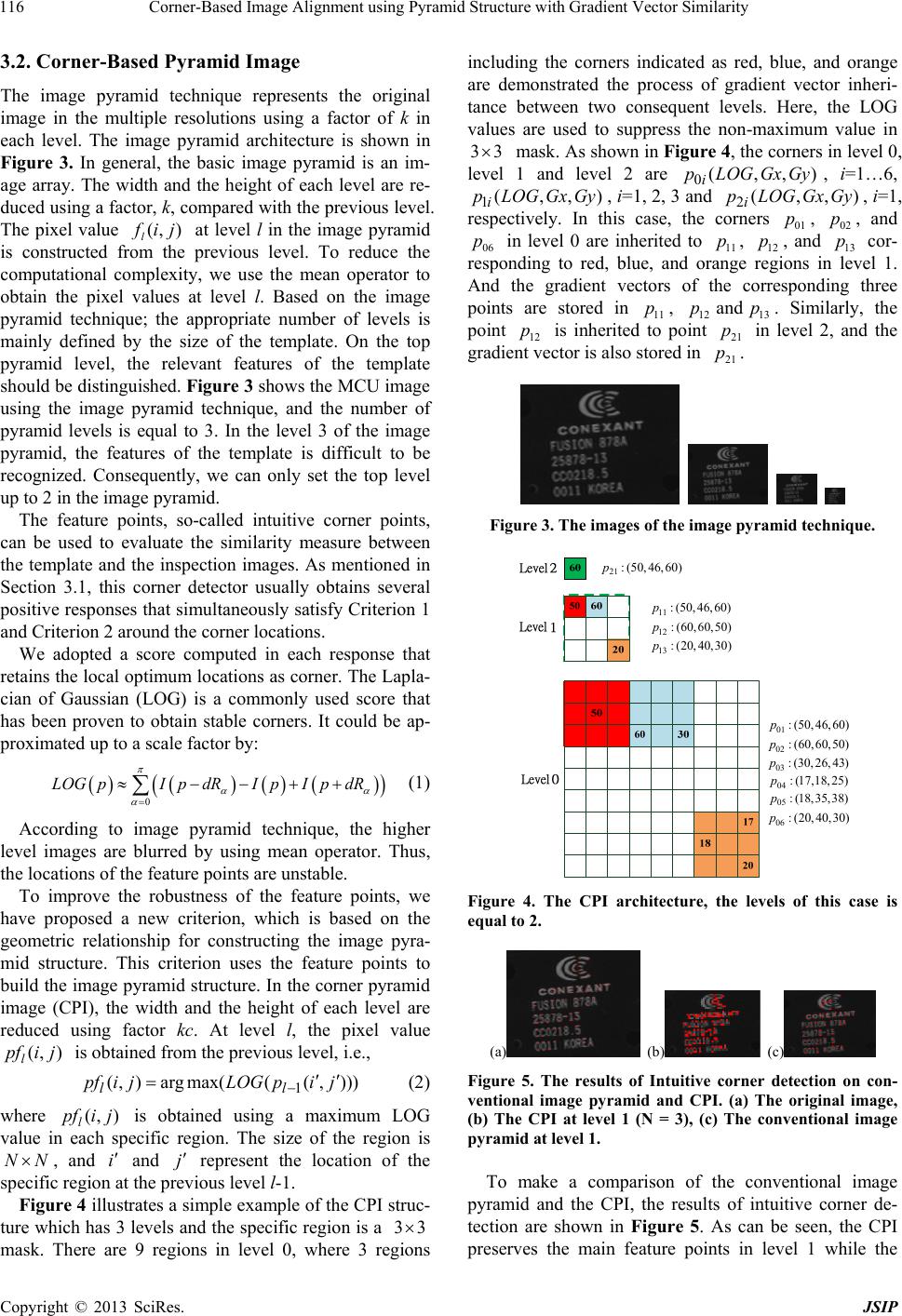rner-Based Image Alignment using Pyramid Structure with Gradient Vector Similarity
116
3.2. Corner-Based Pyramid Image
The image pyramid technique represents the original
image in the multiple resolutions using a factor of k in
each level. The image pyramid architecture is shown in
Figure 3. In general, the basic image pyramid is an im-
age array. The width and the height of each level are re-
duced using a factor, k, compared with the previous level.
The pixel value at level l in the image pyramid
is constructed from the previous level. To reduce the
computational complexity, we use the mean operator to
obtain the pixel values at level l. Based on the image
pyramid technique; the appropriate number of levels is
mainly defined by the size of the template. On the top
pyramid level, the relevant features of the template
should be distinguished. Figure 3 shows the MCU image
using the image pyramid technique, and the number of
pyramid levels is equal to 3. In the level 3 of the image
pyramid, the features of the template is difficult to be
recognized. Consequently, we can only set the top level
up to 2 in the image pyramid.
),( jifl
The feature points, so-called intuitive corner points,
can be used to evaluate the similarity measure between
the template and the inspection images. As mentioned in
Section 3.1, this corner detector usually obtains several
positive responses that simultan eously satisfy Criterion 1
and Criterion 2 around the corner locations.
We adopted a score computed in each response that
retains the local op timum locations as corner. The Lapla-
cian of Gaussian (LOG) is a commonly used score that
has been proven to obtain stable corners. It could be ap-
proximated up to a scale factor by:





0
LOGpIp dRIpIp dR


 



(1)
According to image pyramid technique, the higher
level images are blurred by using mean operator. Thus,
the locations of the feature points are unstable.
To improve the robustness of the feature points, we
have proposed a new criterion, which is based on the
geometric relationship for constructing the image pyra-
mid structure. This criterion uses the feature points to
build the image pyramid structure. In the corner pyramid
image (CPI), the width and the height of each level are
reduced using factor kc. At level l, the pixel value
is obtained from the previous level, i.e.,
(, )
l
pfi j
1
( ,)argmax(((,)))
ll
pfijLOG pij

 (2)
where is obtained using a maximum LOG
value in each specific region. The size of the region is
, and i and represent the location of the
specific region at the previous level l-1.
(, )
l
pfi j

NNj
Figure 4 illustrates a simple example of the CPI struc-
ture which has 3 levels and the sp ecific region is a 33

mask. There are 9 regions in level 0, where 3 regions
including the corners indicated as red, blue, and orange
are demonstrated the process of gradient vector inheri-
tance between two consequent levels. Here, the LOG
values are used to suppress the non-maximum value in
33

mask. As shown in Figure 4, the corners in level 0,
level 1 and level 2 are 0, i=1…6,
1, i=1, 2, 3 and 2, i=1,
respectively. In this case, the corners 01 , , and
06 in level 0 are inherited to 11 , 12 , and 13 cor-
responding to red, blue, and orange regions in level 1.
And the gradient vectors of the corresponding three
points are stored in 11, 12 and 13 . Similarly, the
point 12 is inherited to point in level 2, and the
gradient vector is also stored in .
(,,
i
pLOG Gx Gy
(,
i
pLOG Gx
p
p p
p p
21
p
21
p
)
) )(,,
OG Gx Gy
p
i
p L
p
,Gy
02
p
p
p
Figure 3. The images of the image pyramid technique.
01
:(50,
02
:( 60,
03
:(30,
04
:(17,
05
: (18,
06
:(20,
21
:(50,46,60)p
4p
60p
2p
18p
3p
4p
11
:(50,46,60)p
12
:(60,60,50)p
13
: (20,40,30)p
6,60)
,50)
6,43)
,25)
5,38)
0,30)
Figure 4. The CPI architecture, the levels of this case is
equal to 2.
(a) (b) (c)
Figure 5. The results of Intuitive corner detection on con-
ventional image pyramid and CPI. (a) The original image,
(b) The CPI at level 1 (N = 3), (c) The conventional image
pyramid at level 1.
To make a comparison of the conventional image
pyramid and the CPI, the results of intuitive corner de-
tection are shown in Figure 5. As can be seen, the CPI
preserves the main feature points in level 1 while the

Corner-Based Image Alignment using Pyramid Structure with Gradient Vector Similarity 117
conventional method abandons damages the original
structure. The CPI is more robust and stable to the con-
ventional one with the image pyramid technique.
These feature points will be considered in the deter-
mination of the similarity measure between the template
and the inspection image. The detail of the similarity
measure is described in next section.
3.3. Similarity Measure and Search Strategy
Similarity measure is used to recognize the template ex-
isted within the scene image. The use of the difference of
gradient direction shows its robustness to light changes.
The gradient of the selected corner points with the coor-
dinate information are stored as the template model
which contains a set of points . These
points are relative to the center of gravity, and th e feature
points of the template are represented using gradients
, . The points and their corre-
sponding gradients are respectively denoted as
and ,,
ii ii
ir crc
, , in the
candidate objects. If there is not rotation angle between
the template and the inspection image, the similarity
measure is defined as follows
(,)
T
iii
pxy 
)
T1, , i
(, )
T
iii
dtu
(, )
T
iii
qrc
1, , i
ev
n
n (,w

,,
222 2
1,,
1
,ii ii
ii ii
ni xrycixryc
iixryc ixryc
xy n 
 
 


tv uw
tuvw (3)
where n is the amount of the feature point.
In contrast, if there is a rotation angle between the
template and the search image, the similarity measure
should be modified by
,,
22 22
1,,
1
(,,) ii ii
ii ii
ni xrycixryc
eg iixrycixryc
xy n 
 
 
 
 




tv uw
tuvw (4)
where

is a rotation angle; the is the gradient
vectors after rotation. (, )
T
ii

tu
Perfect match corresponds to 1 in similarity measure.
The search strategy will be the subject of a separate pa-
per.
3.4. Refinement
The rotation angle

is obtained using the neighbor-
hood of

that notesopt

 -2 ,opt

 , opt

  and
opt

 2. The optimal rotation angle is defined as
1
2
cos 1
opt d
l







(5)
where is the maximum distance between the corner
point and the center, is the pixel displacement. The d
is equal to 1 here. The above five rotation angles and
their corresponding similarity coefficients are fed into the
fitting model to obtain the refinement angle. The compu-
tation of the best-fitting parabola is ach iev ed by solv ing a
system equation, where each rotation angle provides one
equation of the form
ld


2
, 1...5
iii
i    (6)
The whole system can be written as

 (7)
The three unknown parameters

,

and

, rep-
resented by vector in the Eq. 7, are calculated from
the known variables
X


i

 and i

(matrix

and
vector

in the Eq. 7, respectively). Taking the values
of i

for th e five nodes described above, the matr ix

and the vector

are filled with these
five nodes as:






222
211
2
211
222
21
11
, =1
11
21
nn
nn
nn
nn
nn
n
n
n
n
n










 




 


 




 




 
. (8)
The following equation yields the three unknown pa-
rameters

,

and

as:

1
TT











 (9)
After the determination of the parabola parameters

,

and

, the optimal refinement angle *

can be cal-
culated by
*/2

  (10)
4. Results and Discussion
The experiments are divided into three cases as (1) rota-
tion estimation, (2) computation cost and (3) robustness
for comparison. Figure 6 shows the two cases of the in-
spection images and their co rresponding template images.
The sizes of two template images are 160

120 and
120

110, respectively, and the inspection images are
640

480 and 512

512, respectively. These experiments
were performed with Visual C++ on Intel core i3 530
2.93 GHz with 4GB of memory.
4.1. Rotation Estimation
In this case, the inspection images were rotated from -20
to 20 for performance evaluation. Figure 7 describes the
comparison of the corner-based image alignment algo-
rithm and the edge-based image alignment algorithm
with the average error and the standard deviation error.
These two quantitative measures are used to verify the
accuracy and precision of the algorithms as listed in Ta-
ble 1. Figure 7 further shows the errors for each rotation

Corner-Based Image Alignment using Pyramid Structure with Gradient Vector Similarity
118
(a) (b)
Figure 6. The inspection image and template image: (a)
Case 1: PCB image, (b) Case 2: BGA image.
(a)
(b)
Figure 7. The comparison in accuracy for different cases in
the corner-based and edge-based alginment algorithms,
respectively: (a) Case 1: PCB image, (b) Case 2: BGA im-
age.
Table 1. The alignment results.
Proposed image
alignment Edge-based image alignment
Case 1 Case 2 Case 1 Case 2
Average error (o) 0.124 0.144 0.273 0.297
Standard deviation
error (o) 0.144 0.167 0.321 0.342
angle. As can be seen, the corner-based image alignment
outperforms the edge-based one in accuracy and preci-
sion estimation of Case 1 and Case 2.
This interprets that the corners obtained from the tem-
plates of Case 1 and Case 2 are more distinctive than the
edges. Although our algorithm demonstrates that it is
more accurate and precise than the edge-based one for
rotation estimation in these two cases, it wou ld be failure
when none or only fewer corners are obtained from the
images. This means that we have to select the template
image carefully in corner-based image alignment.
4.2. Computation Cost
Figure 8 shows the computation cost of the two com-
pared alignment algorithms. These figures clearly show
that our algorithm is more efficient than edge-based one
in these two cases. The average computation times of the
proposed algo rithm in Case 1 and Case 2 are 43.3 ms and
37.25 ms, respectively.
(a)
(b)
Figure 8. Executing time of case 1 and case 2 with the com-
peting method.
The computation cost of the corner-based and the
edged-based algorithms are both influenced by the
amount of feature points. Hence, the corner points are
used in similarity measure calculation and pyramid im-
age reconstruction instead of using edge points to speed
up the computation. Results interpret that this is an effec-
tive way to simultaneously reduce the computational
complexity and remain the accuracy for image align-
ment.
4.3. Robustness
To evaluate the robustness, the proposed algorithm was
utilized under the illumination changes. We used the
commercial software PhotoCap to simulate the illumi-
nant variation. The simulated light directions were di-
vided into 0 degree, 90 degree, 180 degree and 270 de-
gree. The exposure value was set from 1 to 2 for each
direction. Figure 9 shows the illu mination direction with
180 and 0 degrees. In Table 2, the proposed algorithm

Co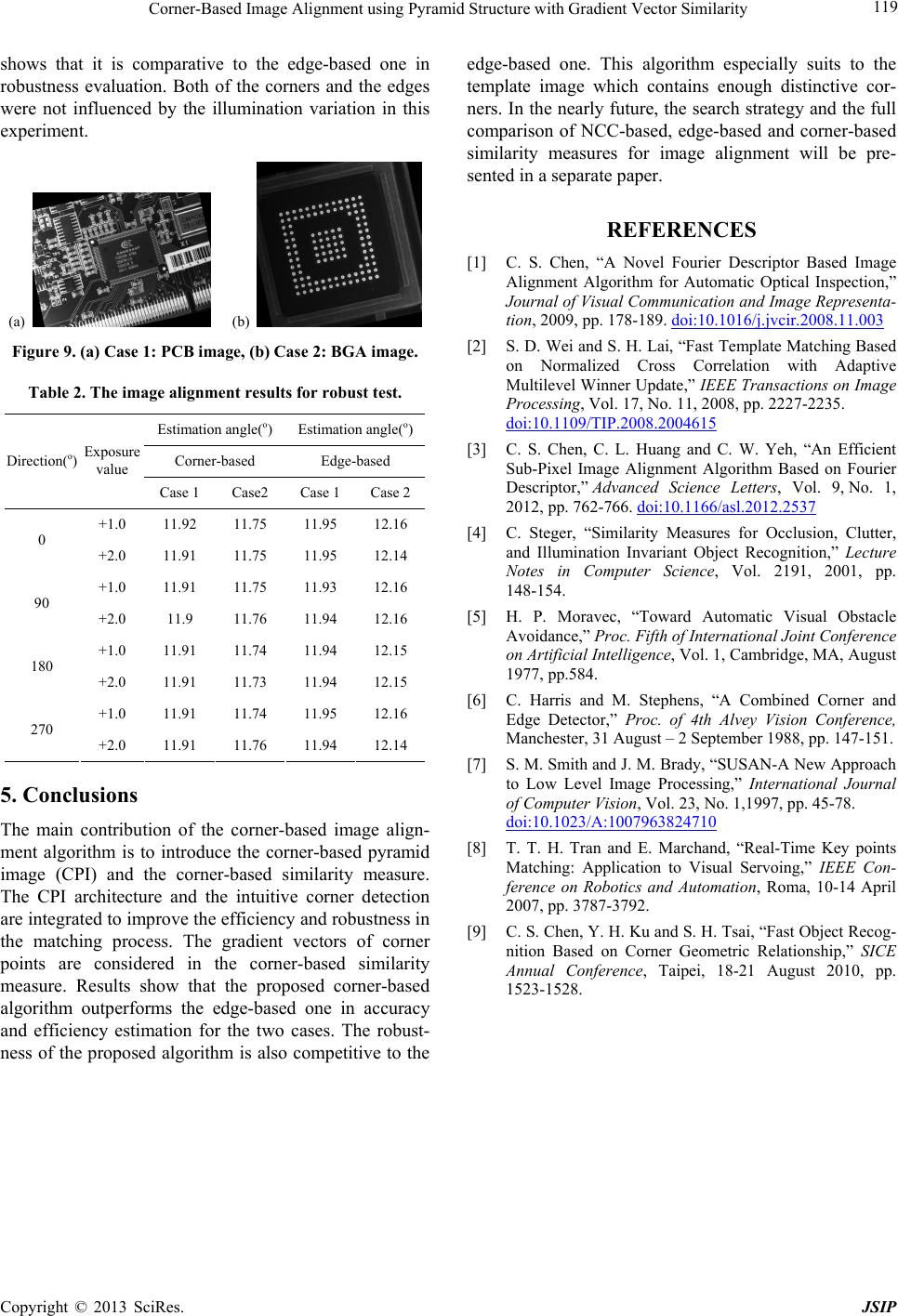rner-Based Image Alignment using Pyramid Structure with Gradient Vector Similarity
119
shows that it is comparative to the edge-based one in
robustness evaluation. Both of the corners and the edges
were not influenced by the illumination variation in this
experiment.
(a) (b)
Figure 9. (a) Case 1: PCB image, (b) Case 2: BGA image.
Table 2. The image alignment results for robust test.
Estimation angle(o) Estimation angle(o)
Corner-based Edge-based Direction(o) Exposure
value
Case 1 Case2 Case 1 Case 2
+1.0 11.92 11.75 11.95 12.16
0 +2.0 11.91 11.75 11.95 12.14
+1.0 11.91 11.75 11.93 12.16
90 +2.0 11.9 11.76 11.94 12.16
+1.0 11.91 11.74 11.94 12.15
180 +2.0 11.91 11.73 11.94 12.15
+1.0 11.91 11.74 11.95 12.16
270 +2.0 11.91 11.76 11.94 12.14
5. Conclusions
The main contribution of the corner-based image align-
ment algorithm is to introduce the corner-based pyramid
image (CPI) and the corner-based similarity measure.
The CPI architecture and the intuitive corner detection
are integrated to improv e the efficiency and robustness in
the matching process. The gradient vectors of corner
points are considered in the corner-based similarity
measure. Results show that the proposed corner-based
algorithm outperforms the edge-based one in accuracy
and efficiency estimation for the two cases. The robust-
ness of the proposed algorithm is also competitive to the
edge-based one. This algorithm especially suits to the
template image which contains enough distinctive cor-
ners. In the nearly future, th e search strategy and the full
comparison of NCC-based, edge-based and corner-based
similarity measures for image alignment will be pre-
sented in a separate paper.
REFERENCES
[1] C. S. Chen, “A Novel Fourier Descriptor Based Image
Alignment Algorithm for Automatic Optical Inspection,”
Journal of Visual Communication and Image Representa-
tion, 2009, pp. 178-189. doi:10.1016/j.jvcir.2008.11.003
[2] S. D. Wei and S. H. Lai, “Fast Template Matching Based
on Normalized Cross Correlation with Adaptive
Multilevel Winner Update,” IEEE Transactions on Image
Processing, Vol. 17, No. 11, 2008, pp. 2227-2235.
doi:10.1109/TIP.2008.2004615
[3] C. S. Chen, C. L. Huang and C. W. Yeh, “An Efficient
Sub-Pixel Image Alignment Algorithm Based on Fourier
Descriptor,” Advanced Science Letters, Vol. 9, No. 1,
2012, pp. 762-766. doi:10.1166/asl.2012.2537
[4] C. Steger, “Similarity Measures for Occlusion, Clutter,
and Illumination Invariant Object Recognition,” Lecture
Notes in Computer Science, Vol. 2191, 2001, pp.
148-154.
[5] H. P. Moravec, “Toward Automatic Visual Obstacle
Avoidance,” Proc. Fifth of International Joint Conference
on Artificial Intelligence, Vol. 1, Cambridge, MA, August
1977, pp.584.
[6] C. Harris and M. Stephens, “A Combined Corner and
Edge Detector,” Proc. of 4th Alvey Vision Conference,
Manchester, 31 August – 2 September 1988, pp. 147-151.
[7] S. M. Smith and J. M. Brady, “SUSAN-A New Approach
to Low Level Image Processing,” International Journal
of Computer Vision, Vol. 23, No. 1,1997, pp. 45-78.
doi:10.1023/A:1007963824710
[8] T. T. H. Tran and E. Marchand, “Real-Time Key points
Matching: Application to Visual Servoing,” IEEE Con-
ference on Robotics and Automation, Roma, 10-14 April
2007, pp. 3787-3792.
[9] C. S. Chen, Y. H. Ku and S. H. Tsai, “Fast Object Recog-
nition Based on Corner Geometric Relationship,” SICE
Annual Conference, Taipei, 18-21 August 2010, pp.
1523-1528.