Journal of Signal and Information Processing, 2013, 4, 91-95
doi:10.4236/jsip.2013.43B016 Published Online August 2013 (http://www.scirp.org/journal/jsip) 91
Optimal Design for MIMO Relay System
Fangni Chen
Department of Communication and Electronic Engineering, Zhejiang University of Science and Technology, Hangzhou, China.
Received May, 2013.
ABSTRACT
Recently, multiple-input multiple-output (MIMO) relay technique has been received great attention due to its prominent
ability to provide broad coverage and enhance the link reliability and spectral efficiency. In this paper, an overview of
optimal design for single user and multiuser non-regenerative MIMO relay systems is propos ed. We explore some key
designs of source node and destination node as well as relay node processing matrices using minimum mean square
error (MMSE) criterion under the transmit power constraints. Simulation resu lts compare different methods in terms of
the MSE and bit error rate (BER) performance.
Keywords: MIMO; Relay; Optimal Design; MMSE
1. Introduction
Multiple-input multiple-output (MIMO) relay communi-
cation, which incorporates relaying technology in MIMO
network, has attracted considerable attention in recent
years due to its potential ability to extend network cov-
erage and improve link reliability as well as spectral effi-
ciency. The aim of this paper is to provide an overview
of optimal design for single user non-regenerative MIMO
relay systems.
A MIMO relay can be regenerative or non-regenera-
tive, full-duplex or half-duplex, one-way or two-way [1].
A regenerative relay requires digital decoding and re-
encoding at the relay, which can cause a significant in-
crease of delay and complexity. A non-regenerative relay
does not need any digital decoding and re-encoding at the
relay, which is a useful advantage over regenerative re-
lays. The difference between full-duplex relay and half-
duplex relay depends on whether relays can transmit and
receive in the same time or same frequency or not. Full-
duplex relay is spectrally efficient but causes a problem
of self-interference and half-duplex relay is easy to im-
plement but not spectrally efficient as full-duplex. The
difference between two-way relay and one-way relay is
whether relays can relay information in two directions in
a single time or single frequ ency or not. In this paper we
will focus on non-regenerative, half-duplex, one-way
MIMO relay systems.
Initial research on MIMO relay began in single user
[2], where the capacity bounds of MIMO relay systems
were examined. It has been shown in [3] and [4] that
performing linear processing at the relay node can out-
perform the conventional AF relaying in a non-regenera-
tive, also known as amplify-and-forward (AF), MIMO
relay system. The optimal relay amplifying matrix which
maximizes the mutual information (MI) between source
and destination is derived in [5]. In [6], a minimum mean
square error (MMSE)-based iterative algorithm is pro-
posed for jointly designing the source, relay and destina-
tion processing matrices. A unified framework is devel-
oped in [7] to jointly optimize the source preceding ma-
trix and the relay amplifying matrix for a broad class of
objective functions.
In this paper, we focus on optimization for single user
non-regenerative MIMO relay systems where each node
is equipped with multiple antennas supporting multiple
data streams. We explore two design schemes to opti-
mize the transmitter and receiver aiming at minimizing
the MSE. First we introduce an iterative algorithm to find
the optimal source preceding matrix and relay amplifying
matrix. Considering the complexity in practical applica-
tions, we also introduce the simplified algorithm to solve
the same optimization problem. Simulation results show
the simplified algorithm has a comparable performance
with the iterative one.
The rest of this paper is organized as follows. In Sec-
tion II, we introduce the single user non-regenerative
MIMO relay system model and formulate the optimiza-
tion problem. Different optimization methods of obtain-
ing the source preceding matrix and relay amplifying
matrix structure under power constraints are analyzed in
section III. Simulation results are conducted to compare
the system performances of the different methods in Sec-
tion IV. Finally, extensions and future work are drawn in

Optimal Design for MIMO Relay System
92
Section V.
Notations: boldface letters represent matrices and vec-
tors. ()
H
, blkdiag, and tr stand for conjugate
transpose, the block diagonal matrix composed of
()I()()

,
the identity matrix and the trace, respectively. []e

in-
dicates the statistical expectation.
2. System Model
Consider a single user non-regenerative MIMO relay
system model, which is shown in Figure 1. This model
supports one source node (BS) transmitting the symbols
to one destination node (MS) and one relay node (RS)
assists the course of transmission between them, where
the BS, RS and MS have
s
N, r and d antennas,
respectively. The direct links between the BS and the MS
is neglected in order to simplify the analysis. The trans-
mission is comprised of four time slots. In the first time
slot, the
N N
M
×1 data stream vector is linearly pre-
coded at the BS by a x
s
N×
M
source preceding matrixT.
Then the preceded vector is transmitted to the RS, the
received signal at the RS can be written by
Figure 1. Single user MIMO relay system model.
r
yGTx+n
r
(1)
where is the r×GN
s
N
min
MIMO channel matrix be-
tween the source and the relay, is the r×1 additive
Gaussian noise vectors with at the relay
node. For a linear non-regenerative MIMO relay system,
there should be
r
n
[ enn
,
N
] I
H
rr 
, )(
s
rd
M
NNN, otherwise the
system can not support active M symbols in each trans-
mission.
In the second time slot, the BS remains silent and the
RS multiplies (linearly amplifies) the received signal
vector r
y
by a r×r relay amplifying matrix and
transmits the amplified signal vector to the MS. Hence
the received signal vector at the MS can be written as
N NW
d

r
rHWGTx+HWn n
)
(2)
where , , and dare the d×r MIMO channel
matrix between the RS and the MS, the received signal
and the additive Gaussian noise vectors at the MS, re-
spectively. Linear receiver is used at the MS to recover
the signals. Thus the estimated vector is eventually given
by
Hr nN N
ˆ(
()
rd


xDHWGTx + HWnn
DHWGTx n (3)
where D is the M × weight matrix.
is equivalent noise vector. We assume that the channel
matrices and are all quasi-static and known to the
BS, RS and MS through channel estimate method. We
also assume that all noises are independent and identi-
cally distributed (i.i.d.) complex circularly symmetric
Gaussian noise with zero mean and unit variance. An-
other two time slots are needed for the reverse link.
d
Nrd nHWn n
G
[(
H
)(
Follow the system model above, we can get the mean
square error matrix
ˆˆ) ]
()()
H
H
H
n
e

--x
DHWGT - IDHWGT - IDCD
Ex
n
xx
[(
H
(4)
Here we assumed that , means the trans-
mitted data are independent and identically distributed
(i.i.d.) and has the unit power. is the equivalent
noise covariance matrix given by
[]
H
Exx I
n
C
[]
)() ]
H
rd rd
HH
e
 
n
HWnn HWnn
HWWH+ I
e

Cn
H

HH
The weight matrix of the optimal linear receiver which
minimizes MSE is essentially the Wiener filter given by
1
(
HHH HHn

D THWGTTGWHC)GW
()
H (5)
where 1


denotes matrix inversion. Substituting
Equation (5) back into Equation (4) and using matrix
inversion lemma, we obtain
11
()
HH HH
n

WHCHWGTI  E
MMSE
T G
((
tr
(6)
The minimum MSE of the signal estimation at the des-
tination can be expressed as
11
()
) )
HH HH
n
tr 


E
TGWHCHWGT I (7)
Thus the source preceding matrix and the relay ampli-
fying matrix optimization problem can be formulated as
11
) )
) )
()
HH HH
n
HHH r
Hs
t P
tr P




TGWHCHWGT I
GTTG+ IW
((
(
tr
rW(
TT
min
..st
T,W
r
(8)
where and P
s
P are the power constraints at RS and
BS.
2. Optimization Algorithms
2.1. Iterative Algorithm
In [7], authors proposed a unified framework for opti-
mizing linear non-regenerative single user multicarrier
MIMO relay systems. We extend this algorithm to solve
our single user single carrier optimization.
First we denote the singular value decomposition

Optimal Design for MIMO Relay System 93
(SVD) of the channel between BS and RSand the
channel between RS and MS as G H
H
g
gg
GUΛV (9)
H
hhh
HUΛV (10)
where the dimensions of
g
U,
g
Λ,
g
V are r×r,
×N N
r
N
s
N,
s
N×
s
N, respectively, and the dimensions of
h, h,h are d×d, d×r, r×r, respec-
tively. We assume that the main diagonal elements of
UΛVN NNNNN
g
Λand h are arranged in decreasing order. The
closed-form of optimal and in (8) are given by
[7]
Λ
TW
,1
g
t
TVΛ (11)
,1 ,1
H
hwg
WVΛU (12)
where and ware M × M diagonal matrices,
t
Λ Λ,1
g
V,
and ,1,1h V
g
Ucontain the leftmost M columns from
g
V,
and
h
V
g
U, respectively.
Substitute (9)-(12) into (8), the problem is expressed
as
,,
2
,,,, 1
2
,1,,
22
,,,
1
2
,
1
()
min (1)
()1
..(() 1)
wi ti
Mhi wigi ti
ihi wi
M
wigi tir
i
M
ti s
i
s
t
P















P (13)
where ,, ,
g
ihi

 , denotes the i-th diagonal
element of 1
1,...,iM
g
Λand 1, which contain the largest M
elements inh
Λ
g
Λand . ,,ti
h
Λwi,

 are the main diagonal
elements of wand t, respectively. For the above
results, it follows that the non-regenerative MIMO relay
single user system becomes equivalent to a set of parallel
single-input single-out (SISO) channels [8].
Λ Λ
Since the problem (13) is non-convex, the global op-
timal solution is hard to obtain. In [9], a grid search-
based algorithm is designed to find the global optimal
solution for a multicarrier SISO relay system with the
MMI criterion. However, the computational complexity
of the algorithm in [9] is extremely high, since in order to
obtain a reasonably good solution, search over a high-
dense grid must be employed. In the following, we pro-
vide a numerical method [7] to obtain a local-optimal and
which has a much lower computational complexity than
that of [9].
To simplify notations, let us define
2,ig
ai

, i
2,ih
b


2
,it
xi

，, (14)
22
,,,
[() 1]
iwigiti
y  1,...,iM
Then the problem (13) can be equivalently rewritten as
,1
1
1
1
min 1
..
ii
Mii ii
xy iii iiiiii
M
ir
i
M
is
i
ax by
ax byabxy
sty P
xP










(15)
From (15), we see that the problem is symmetric in
i
x
and i, y1,...,iM

, and the power constraints are
decomposed. Thus, we can efficiently update i
x
and
i in an alternating way. First with fixed ,yi
y1, ...,iM

,
we can update i
x
by solving
1
1
1
min 1
..
i
Mii ii
xiiiiiiiii
M
is
i
ax by
ax byabxy
stxP







(16)
This is a convex optimization problem, using KKT
conditions we can obtain
1(
(1 )
ii i
i
iii
aby
xaby


1
)


 (17)
where () max(,0)


, and

is the solution to the
source power constraint.
In a similar way, we can update i with given i y
x
.
Moreover, i
x
and are symmetric, so we can easily
get i
y
1(
(1 )
iii
i
iii
abx
ybax


1 )


 (18)
where

is the solution to the relay power constraint.
Note that the conditional updates of i
x
and i may
either decrease or maintain but cannot increase the objec-
tive functions in (13). Monotonic convergence of i
y
x
and i follows directly from this observation. After the
convergence of the alternating algorithm,
y
,
,ti,wi

 can
be obtained from (14) as
,ti i
x
 , 2
,,
/( 1)
wiigi i
yx 

, (19)
1,...,iM
The procedure of optimizing source preceding matrix
and relay amplifying matrix is described in Ta-
ble 1.
TW
2.2. Simplified Algorithm
The iterative algorithm may still be computationally in-
tensive for practical systems. Note that if the objective
function in (15) can be decoupled for i
x
and i, then
the optimization of i
y
x
and i can be independently
conducted, since the constraints in (15) are already de-
coupled for i
y
x
and i[10]. With this inspiration, we
make an approximation of the objective function in (15)
y

Optimal Design for MIMO Relay System
94
Table 1. Procedure of Iterative Algorithm.
1) Set iterative number N, initialize the algorithm with
, set n=0；
(0) P/
ir
yM
2) Get the SVD of
H
g
gg
GUΛV and
H
hhh
HUΛV;
3) Using Equation (17) and giv en , obtain
()n
i
y
()
()
()
1(1
(1 )
n
nii i
in
iii
aby
xaby

)


;
4) Using Equation (18) and giv en ()n
i
x
, obtain
()
(1)
()
1(1

)
(1 )
n
niii
in
iii
abx
ybax


;
5) if , then go to step 6;
nN
Otherwise, n=n+1 and go to step 3;
6) Using Equation (19), (11), (12), we finally get the optimal
source precoding matrix and relay amplifying matrix. T W
1
1
1
1
1
2
1
11
11
Mii ii
iii iiiiii
Mii ii
iiiiiiiii
M
iii ii
ax by
ax byabxy
ax by
ax by abxy
ax by












(20)
Then, the problem (15) can be decomposed as two
problems as follows
1
1
1
min 1
..
i
M
xiii
M
is
i
ax
s
tx





P
(21)
and
1
1
1
min 1
..
i
M
yiii
M
ir
i
by
s
ty





P
(22)
Both problems (21) and (22) are convex optimization
problem, using KKT conditions, we can easily get
1(1)
i
i
i
a
xa


, 1(1) 1,...,i
i
i
i
b
yb


 M, (23)
where

and

are the solution to the constraints
in (21) and (22).
The procedure of this optimization is listed in Table 2.
Compare with Table 1, this is a non-iterative algo-
rithm and suboptimal because of the approximation in-
troduced in (20). Therefore, the proposed algorithm has a
substantially reduced computational complexity. Note
that the approximation (20) is tight when the transmis-
sion power
s
P and r are sufficiently high. Mean-
while in Section IV we will find that this simplify algo-
rithm yields only a slight MSE and BER increment
compared with the iterative algorithm Therefore, the
proposed simplified algorithm is very useful for practical
relay communication systems.
P
Table 2. Procedure of simplified algorithm.
1) Get the SVD of
H
g
gg
GUΛV and
H
hhh
HUΛV;
2) Using (14), (23), obtain i
x
and , ;
i
y1,...,iM
3) Using (19), (11), (12), we finally get the optimal source
precoding matrix and relay amplifying matrix. T W
3. Numerical Results
In this section, we study the performance of the two-hop
non-regenerative MIMO relay systems without direct
link. For all examples, we assume the elements of all th e
channels are i.i.d complex Gaussian with zero mean and
unit variance. We also assume that the power constraints
at source and relay are the same, i.e.
s
r
We compare the iterative optimal algorithm and the
simplified optimal algorithm in Section 3 (denoted as
Simplify I), another simplified optimal algorithm
proposed in [11] (denoted as Simplify II), and the naive
AF optimal algorithm (NAF). For the NAF relaying, we
set the source preceding matrix with the average power
PP.
allocation to be/
s
PMTIand the relay amplifying
matrix to be/( )
HH
r
PtrWGTTG+II.
We choose 2
srd
NNNM

 in example 1, and
4
s
NM

, 6
rd
NN

 in example 2. Figure 2 and
Figure 3 display the two examples of the MSE of dif-
ferent algorithms versus transmit power from 0dB to
40dB. It can be seen that the iterative algorithm consis-
tently yields the lowest MSE over the whole power range.
The performance of the two simplified algorithms is very
close to the iterative algorithm. Since for practical com-
munication systems the BER is an important criterion,
the performance of all algorithms of example 2 in terms
of BER versus transmit power is shown in Figure 4. The
QPSK constellations are used. In the simulation , after the
estimated vector is obtained by the linear MMSE re-
ceiver, a symbol-by-symbol demodulation is used to re-
trieve the source bits. Note the two simplified algorithms
have slightly higher MSE and BER than the iterative
algorithm at low SNR. But at high SNR, the three algo-
rithms have almost the same performance. It is reason-
able because in the simplified alg orithm, the approximate
objections are near the original one at high SNR. Con-
sidering the computation complexity, the simplified al-
gorithm is very useful for practical systems.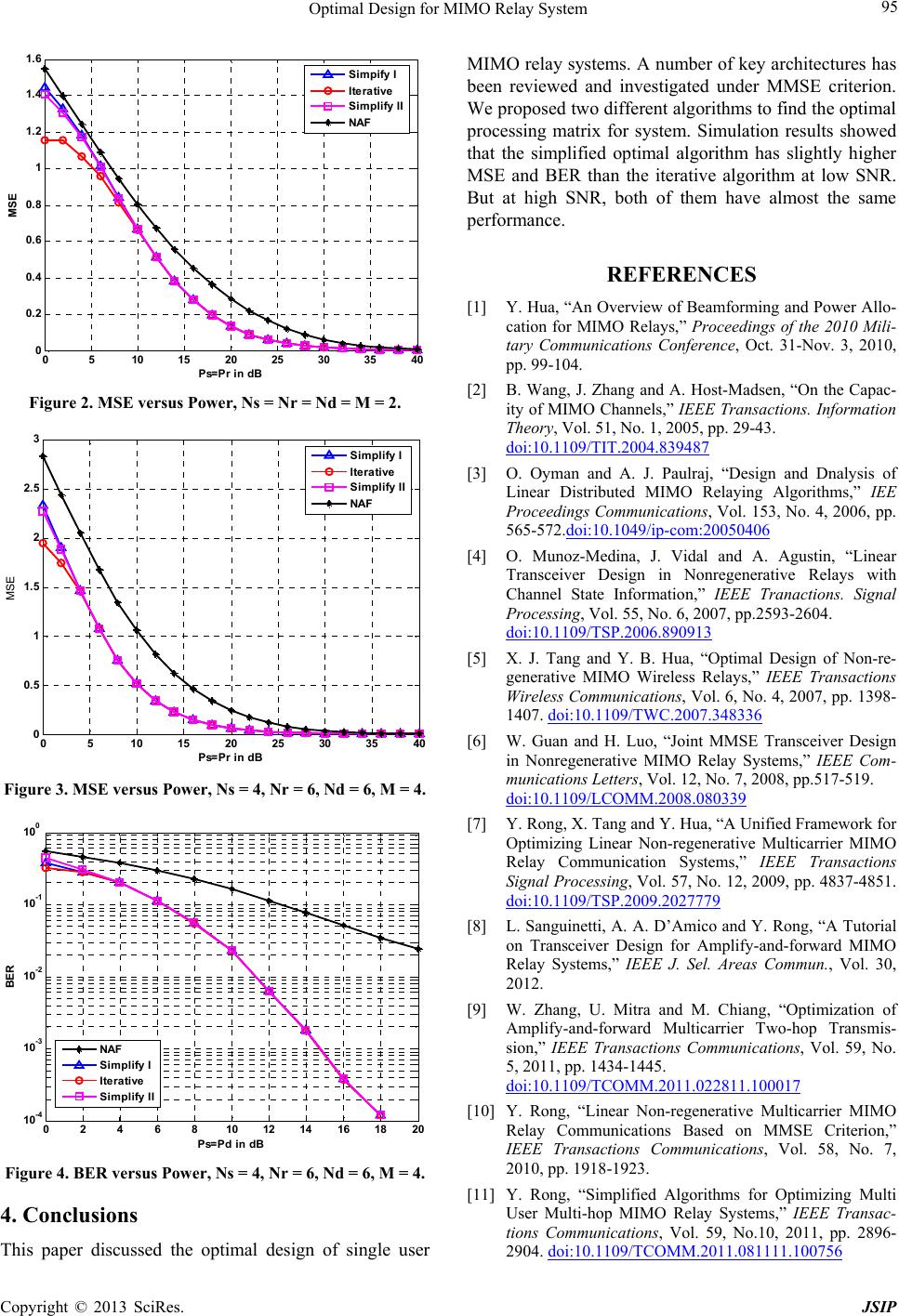

Optimal Design for MIMO Relay System
95
05 10 1520 25 30 35 40
0
0. 2
0. 4
0. 6
0. 8
1
1. 2
1. 4
1. 6
Ps=Pr in dB
MSE
Simpify I
Iterative
Simplify II
NAF
Figure 2. MSE versus Power, Ns = Nr = Nd = M = 2.
0510 1520 25 3035 40
0
0.5
1
1.5
2
2.5
3
Ps=Pr in dB
MSE
Simplify I
Iterative
Simplify II
NAF
Figure 3. MSE versus Power, Ns = 4, Nr = 6, Nd = 6, M = 4.
0 2 46 810 12 141618 20
10
-4
10
-3
10
-2
10
-1
10
0
Ps=Pd in dB
BER
NAF
Simplify I
Iterative
Simplify II
Figure 4. BER versus Power, Ns = 4, Nr = 6, Nd = 6, M = 4.
4. Conclusions
This paper discussed the optimal design of single user
MIMO relay systems. A number of key architectures has
been reviewed and investigated under MMSE criterion.
We proposed two different alg orithms to find the opti mal
processing matrix for system. Simulation results showed
that the simplified optimal algorithm has slightly higher
MSE and BER than the iterative algorithm at low SNR.
But at high SNR, both of them have almost the same
performance.
REFERENCES
[1] Y. Hua, “An Overview of Beamforming and Power Allo-
cation for MIMO Relays,” Proceedings of the 2010 Mili-
tary Communications Conference, Oct. 31-Nov. 3, 2010,
pp. 99-104.
[2] B. Wang, J. Zhang and A. Host-Madsen, “On the Capac-
ity of MIMO Channels,” IEEE Transactions. Information
Theory, Vol. 51, No. 1, 2005, pp. 29-43.
doi:10.1109/TIT.2004.839487
[3] O. Oyman and A. J. Paulraj, “Design and Dnalysis of
Linear Distributed MIMO Relaying Algorithms,” IEE
Proceedings Communications, Vol. 153, No. 4, 2006, pp.
565-572.doi:10.1049/ip-com:20050406
[4] O. Munoz-Medina, J. Vidal and A. Agustin, “Linear
Transceiver Design in Nonregenerative Relays with
Channel State Information,” IEEE Tranactions. Signal
Processing, Vol. 55, No. 6, 2007, pp.2593-2604.
doi:10.1109/TSP.2006.890913
[5] X. J. Tang and Y. B. Hua, “Optimal Design of Non-re-
generative MIMO Wireless Relays,” IEEE Transactions
Wireless Communications, Vol. 6, No. 4, 2007, pp. 1398-
1407. doi:10.1109/TWC.2007.348336
[6] W. Guan and H. Luo, “Joint MMSE Transceiver Design
in Nonregenerative MIMO Relay Systems,” IEEE Com-
munications Letters, Vol. 12, No. 7, 2008, pp.517-519.
doi:10.1109/LCOMM.2008.080339
[7] Y. Rong, X. Tang and Y. Hua, “A Unified Framework for
Optimizing Linear Non-regenerative Multicarrier MIMO
Relay Communication Systems,” IEEE Transactions
Signal Processing, Vol. 57, No. 12, 2009, pp. 4837-4851.
doi:10.1109/TSP.2009.2027779
[8] L. Sanguinetti, A. A. D’Amico and Y. Rong, “A Tutorial
on Transceiver Design for Amplify-and-forward MIMO
Relay Systems,” IEEE J. Sel. Areas Commun., Vol. 30,
2012.
[9] W. Zhang, U. Mitra and M. Chiang, “Optimization of
Amplify-and-forward Multicarrier Two-hop Transmis-
sion,” IEEE Transactions Communications, Vol. 59, No.
5, 2011, pp. 1434-1445.
doi:10.1109/TCOMM.2011.022811.100017
[10] Y. Rong, “Linear Non-regenerative Multicarrier MIMO
Relay Communications Based on MMSE Criterion,”
IEEE Transactions Communications, Vol. 58, No. 7,
2010, pp. 1918-1923.
[11] Y. Rong, “Simplified Algorithms for Optimizing Multi
User Multi-hop MIMO Relay Systems,” IEEE Transac-
tions Communications, Vol. 59, No.10, 2011, pp. 2896-
2904. doi:10.1109/TCOMM.2011.081111.100756