Applied Mathematics, 2011, 2, 23-32
doi:10.4236/am.2011.21003 Published Online January 2011 (http://www.SciRP.org/journal/am)
Risk Early-Warning Method for Natural Disasters Based
on Integration of Entropy and DEA Mod el*
Fengshan Wang, Yan Cao, Meng Liu
Engineering Institute of Engineering Corps, PLA University of Science & Technology, Nanjing, China
Received September 1, 2010; revised October 31, 2010; accepted November 5, 2010
Abstract
Risk early-warning of natural disasters is a very intricate non-deterministic prediction, and it was difficult to
resolve the conflicts and incompatibility of the risk structure. Risk early-warning factors of natural disasters
were differentiated into essential attributes and external characters, and its workflow mode was established
on risk early-warning structure with integrated Entropy and DEA model, whose steps were put forward. On
the basis of standard risk early-warning DEA model of natural disasters, weight coefficient of risk ear-
ly-warning factors was determined with Information Entropy method, which improved standard risk ear-
ly-warning DEA model with non-Archimedean infinitesimal, and established risk early-warning preference
DEA model based on integrated entropy weight and DEA Model. Finally, model was applied into landslide
risk early-warning case in earthquake-damaged emergency process on slope engineering, which exemplified
the outcome could reflect more risk information than the method of standard DEA model, and reflected the
rationality, feasibility, and impersonality, revealing its better ability on comprehensive safety and structure
risk.
Keywords: Entropy, Data Envelopment Analysis, Comprehensive Integration, Essential Attribute,
Risk Early-Warning, Natural Disaster
1. Introduction
Timely and exact early-warning of natural disasters, can
effectively reduce loss of life and property, which is an
important basis for emergency management and disaster
relief decision-making [1].
Risk early-warning is an extremely intricate and dy-
namic process, its early-warning object is the risk event
that was not certain and evident [2]. The relation among
the factors that influenced risk was intricacy and com-
plex [3], which often behaved fuzzy, certain, potential,
random, conflict, incompatible and other polymorphism
[4].
Data Envelopment Analysis (DEA) was brought for-
ward by A. Charnes, W. Cooper, and other scholars of
U.S. operations research, which evaluated the relative
effectiveness or probability of decision-making unit with
changing weight, as an important method for showing
relative efficiency evaluation [5]. DEA was strong in its
objectivity, and its conclusions from subjective human
personality, which presents a positive role on risk evalu-
ation [6,7], best selection and sort, effectiveness of fore-
casting combination, decision-making unit, and other
aspects. But, DEA evaluation is entirely dependent on
objective data, and can not reflect the preference of the
risk early-warning factors in the special risk environ-
ment.
Model and method of risk early-warning must adapt to
the requirement of natural disasters, as the characteristics
of natural disasters are polymorphism, contradictory and
incompatible. The comprehensive integration of DEA
theory and Information Entropy theory [8], was applied
into relational features, structure, function, organization
and regulatory mechanisms of complex early-warning
issues. It is useful for eliminating the subjective weight
when determining the indicator weight, and solving the
pivotal contradiction and incompatibility among indica-
tors.
This method of integrated DEA and Entropy was dif-
ferent from other comprehensive evaluation methods for
its unified mathematical model. It extracted information
entropy from risk early-earning samples, determined the
*This work is supported by the Chinese NSF grants 70971137.

F. S. WANG ET AL. 24
entropy weight preference of risk early-warning factors,
further carried on the evaluation about the relative risk
degree of risk early-warning sample, and finally realized
the impersonal, reasonable, accurate, scientific early-
warning decision about the risk natural disaster condi-
tions.
2. Risk Early-Warning Workflow Mode
about Natural Disasters
2.1. Early-Warning Characters of Risk Events
Set  as the abstract sign of earthquake, floods and
other natural disasters, and

denoted the potential
risk. And, i Cdenoted the general risk factor of potential
risk , whose factor set was denoted as C


|1,2,,
i
Ci m.
The movement and evolution of risk  is consistent
with the general laws of material movement and social
development, which is determined by internal factors,
objectively existed in the essential attributes of risk
events, such as rock integrity coefficient in the landslide
risk of rock slope engineering.
Risk  is random, disordered, which happened as
the essential attributes normally activated by a lot of un-
expected external factors, such as daily maximum rain-
fall in the landslide risk of rock slope engineering.
Therefore, the early-warning factors of risk

could
be differentiated into essential attributes and external
characters. Set i
X
as the signal risk early-warning ex-
ternal character, 1, 2,,ir, and i
Y as its signal es-
sential attributes, 1,, .ir m Then, the early-war-
ning factors of risk , formalized as:


12
12
,,,,,1
,,,,,
T
ir
T
rri m
X
XXXXi r
rim
YYYYY
CXY











(1)
where early-warning characteristic system was formally
denoted for risk . Here, X denoted the set about ex-
ternal characters, and Y denoted the set about essential
attributes.
2.2. Basic Mathematical Expression about Risk
Early-Warning Events
In accordance with the X and Y level classification of risk
early-warning factors, based on the low risk expectations
of psychological characteristics, the measuring require-
ment was designed, which provided rules for risk early-
warning samples.
Essential attribute measuring requirement: As ij y
denoting the value of risk early-warning sample
j
E on
the essential attribute i
C of Y, ij y satisfied the max
type, namely the greater measurement and the lower risk.
External character measuring requirement: As ij
x
denoting the value of risk early-warning sample
j
E on
the external character i C of X, ij
x
satisfied the min
type, namely the lower measurement and the lower risk.
Based on measuring requirement for risk ear-
ly-warning sample, risk early-warning was essentially to
distill risk sample, determine the risk early-warning im-
personal data, and further determine the measuring value
or the relative risk degree of risk early-warning sample,
and finally confirm the important risk early-warning po-
sitions.
Accordingly, risk early-warning was denoted formally:
::, ,optC EF (2)
Here, E denoted risk early-warning sample set, in-
cluding 1
E, 2 E, ···,
j
E, ···, n E. And, F formally de-
noted the risk early-warning mathematical methods, in-
cluding parametric, non-parametric methods, and intelli-
gent reasoning method.
In view of the min & max changing characteristics and
measuring requirements in risk early-warning factors,
risk early-warning function was designed formally, as
the following expression in (3).
1, 2,,
12
,,,
,,,
rj r jmj
max
j
jj rj
min
yy y
Fopx xx x





 









 (3)
where the inherent and external mechanism was indi-
cated through the formal mathematical logic, revealing
inherent stability of the risk early-warning sample. Here,
j
F
denoted the risk parameter of the risk early-warning
sample, ij
x
（1ir

）denoted the measurement of
sample
j
E on the external character i
X
, and ij y
（1rim

 ）denoted the risk estimation of sample
j
E on the essential attribute i Y.
2.3. Risk Early-Warning Workflow Model
According to the risk management requirements of natu-
ral disaster

, with the extraction the restraint require-
ment of risk early-warning, and the identification of po-
tential risk event and its related factors, the essential
attribute set Y and external character set X was estab-
lished for the risk early-warning of natural disasters.
Design risk early-warning workflow mode for natural
disasters on the integrated basis of Entropy and DEA
model, as shown in Figure 1.
Integration of Entropy and DEA model was carried
into the natural risk early-warning operations, which
mainly contained four stages.
1) Erect the risk early-warning indicator set C of natu-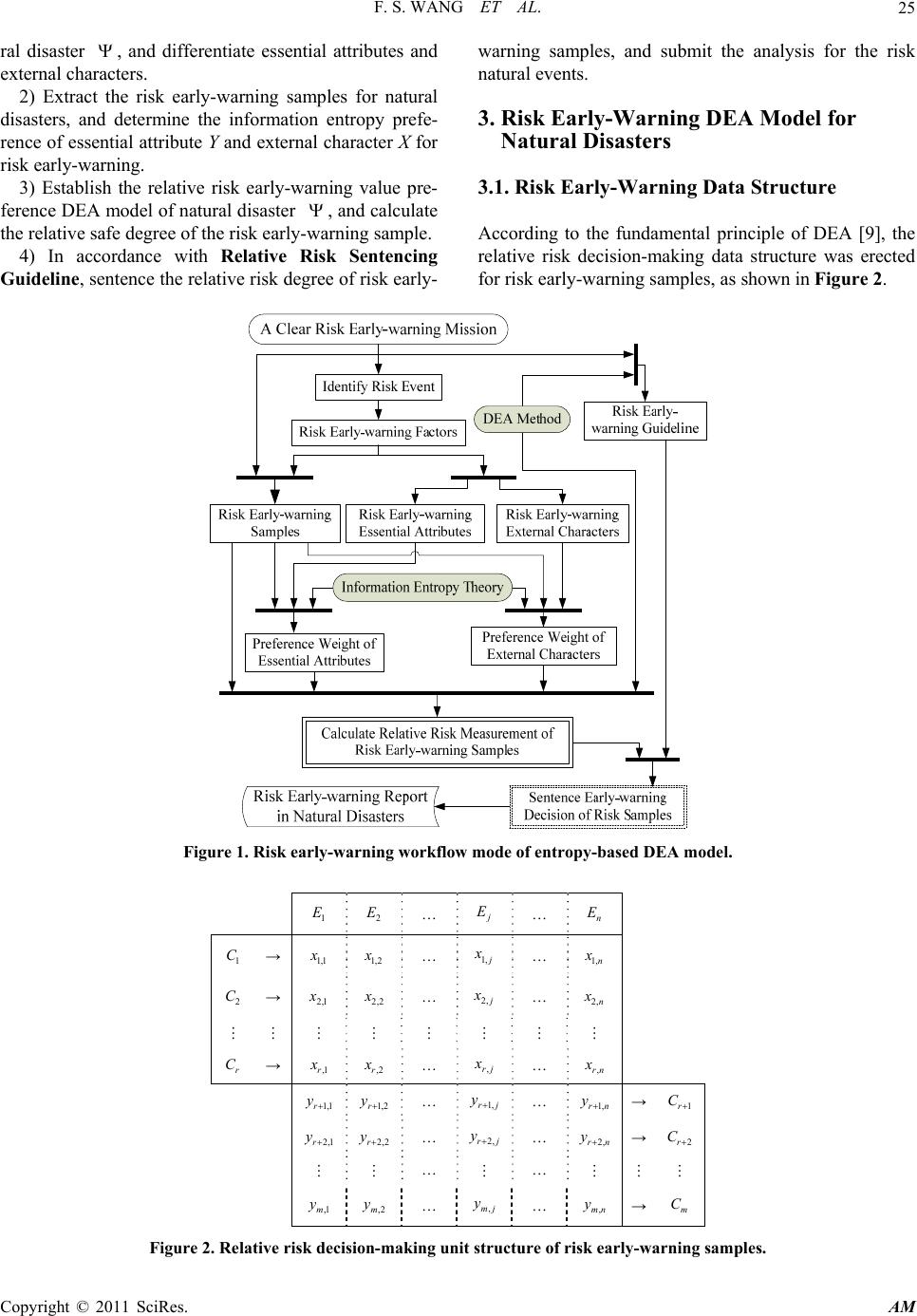

F. S. WANG ET AL. 25
ral disaster , and differentiate essential attributes and
external characters.
2) Extract the risk early-warning samples for natural
disasters, and determine the information entropy prefe-
rence of essential attribute Y and external character X for
risk early-warning.
3) Establish the relative risk early-warning value pre-
ference DEA model of natural disaster , and calculate
the relative safe degree of the risk early-warning sample.
4) In accordance with Relative Risk Sentencing
Guideline, sentence the relative risk degree of risk early-
warning samples, and submit the analysis for the risk
natural events.
3. Risk Early-Warning DEA Model for
Natural Disasters
3.1. Risk Early-Warning Data Structure
According to the fundamental principle of DEA [9], the
relative risk decision-making data structure was erected
for risk early-warning samples, as shown in Figure 2.
Figure 1. Risk early-warning workflow mode of entropy-based DEA model.
1
E 2 E …
j
E … n
E
1
C → 1,1
x
1,2
x
… 1,
j
x
… 1,n
x
2
C → 2,1
x
2,2
x
… 2,
j
x
… 2,n
x
       
r
C → ,1r
x
,2r
x
… ,rj
x
… ,rn
x
1,1r
y 1,2r y… 1,rj
y… 1,rn
y→1r C

2,1r
y 2,2r y… 2,rj
y… 2,rn
y→2r C

  …  …  
,1m
y ,2m y… ,mj
y… ,mn
y→m C
Figure 2. Relative risk decision-making unit structure of risk early-warning samples.

F. S. WANG ET AL. 26
In Figure 2, the risk early-warning sample
j
E was
converted into decision-making unit (
j
DMU ) in relative
risk decision-making system, and each
j
DMU had the
measurement about r external characters and mr

essential attributes.
With the relative decision-making unit structure of risk
early-warning sample, suppose that
j
X
denoted the
measurement of risk early-warning sample
j
E on ex-
ternal character, and
j
Y
 denoted its measurement on
essential attributes. Then, decision-making unit was de-
noted formally for the risk early-warning sample as in
(4).



1, 2,,
1, 2,,
,,,
,,,
,| 1,2,,
T
jjjrj
T
jrjrj mj
jjj
Xxx x
Yyy y
DMUX Yjn














 
(4)
where with decision-making unit model of DEA, deci-
sion-making data structure was established for risk ear-
ly-warning sample of natural disaster. Among them,
j
X

signed the characterization about the external risk input
vector of decision-making unit, and
j
Y
 signed the cha-
racterization about the essential safe output vector of
decision-making unit.
3.2. Basic Risk Early-Warning DEA Model
Formula (3) formally denoted the relative risk analysis
about risk early-warning samples, which was similar to
DEA efficiency evaluation expression.
Set the risk early-warning sample 1 E, 2 E, ···,
j
E, ···,
n
Eof natural disasters as DEA decision-making unit,
analyzing the relative risk of decision-making unit k E.
According to DEA model, basic mathematical DEA
model was established for natural risk early-warning
sample, such as the following formula.

max
0,
1
0,0,1, 2,,
T
kp
TT
jj
T
k
YV
vX Y
vX
vjn















(5)
In Formula (5), v denoted the weight vector of risk
early-warning external character measurement
j
X
, and

denoted the weight vector of risk early-warning es-
sential attribute measurement
j
Y
.
p
V signed the best
efficiency evaluation of risk early-warning decision-
making unit k E for natural disasters, namely the overall
safety degree of decision-making unit k E relative to
other decision-making units, and there 1
p
V.
3.3. Risk Early-Warning DEA Model with
Non-Archimedean Infinitesimal
Model (5), was known as standard DEA model, namely
2
CR model. Other related application showed [10,11],
there was often multi-effectiveness phenomenon, so it
was not easy to directly determine the effectiveness of
DEA. Charnes introduced the concept of non-Archime-
dean infinitesimal in his study on the degradation phe-
nomenon of linear programming, successfully solved the
difficulty in the calculation and technology of 2
CR
model.
Using the dual form of 2 CR model in DEA method,
non-Archimedean infinitesimal relative safe evaluation
model was established for risk early-warning samples,
such as model (6).
11
1
1
min
1, ,
1, ,
()
0,1,,
,0
rm
pii
iir
n
ij jiik
j
n
Iij jiik
j
j
ii
Vθ
xθxi r
yyirm
D
jn
θ,

 












 


 



 












(6)
where
p
V denoted the risk measurement of risk sample
k
E, namely risk early-warning decision-making unit
k
DMU , which was consistent with the
p
V expression
in model (5). Here, i


denoted the slack variable about
the external character, i


denoted the slack variable
about the essential attribute, and

signed the non- Arc-
himedean infinitesimal constant variable, which was less
than any positive number, but large than 0, usually taken
on 5 10 

.
3.4. Relative Risk Sentencing Guideline
Suppose that the optimal solution of model (6) was 0 θ,
0

, 0
i


, 0
i


, then the relative risk sentencing guide-
line was established for the early-warning sample k E
according to DEA model [6].
Guideline 1: If 01θ

, then the risk early-warning
decision-making unit k DMU was evaluated as weak
DEA efficiency, and it sentenced the risk early-warning
sample k E about natural disasters as relative weak effi-
ciency, namely the weak efficiency in relative safety.
Guideline 2: If 01θ

and 00
11
0
rm
ii
iir




 ,
then the risk early-warning decision-making unit k
DMU
was evaluated as DEA efficiency, and it sentenced the
risk early-warning sample k E as relative efficiency,

F. S. WANG ET AL. 27
namely the efficiency in relative safety for natural disas-
ters.
4. Improved DEA Model for Risk
Early-Warning Sample
Model (6), calculated relative safe degree of the objec-
tive risk early-warning sample data relative safety, which
played a positive role in the decision of risk warning
measurement; but it hadn’t made the best of objective
data, and could not reflect preference information of the
external character and essential attribute.
4.1. Standardization of Risk Early-Warning
Characteristics
In accordance with the data expression of decision-
making unit for risk early-warning sample, as the For-
mula (4), the initial risk early-warning matrix R
~
was
established for natural disasters in (7).
111 1,1,1
1
1221,2,2
2
11,,
rr m
rr m
nrnrnmn
n
xxyy E
xxy y
E
R
xxy y
E













 

(7)
With terminal minus, the initial risk early-warning
sample matrix R
 of natural disaster was standardized.
If the early-warning factor i C showed the external cha-
racter, namely the positive effect in natural disasters,
then:

'
111
ij ijijijij
jnjnjn
x
xminxmaxx minx
 
 
 
 
 
(8)
If the early-warning factor i
C showed the essential
attribute, namely the negative effect in natural disasters,
then:
 
'
111
ijij ijijij
jnjn jn
ymax yymax ymin y
 
 
 
 
 
(9)
Thus, under the natural disasters emergency, the initial
risk early-warning sample matrix R
 turned into the
standard matrix R:
''' '
1111 1,1,1
''' '
2122 1,2,2
''' '
11,,
rr m
rr m
nnrnrnmn
Exxy y
Exxy y
R
Exxy y














(10)
4.2. Preference Information Entropy Calculation
on Risk Early-Warning Factors
The weight value of early-warning factor was a con-
cernful information in early-warning structure for risk
natural disasters, which was easily impacted by human
personality. There was complexity and uncertainty, as
well as contradiction in the decision-making process, so
it was difficult to estimate the specific factor weight.
Entropy was a measure of uncertain due to the un-
known part of a message system [12]. With Entropy
theory, the weight value could be determined through the
inner components and relations in the risk early-warning
system. It was absolutely an impersonal weighting me-
thod. This method used entropy value to reflect the de-
gree of information disorder, which could effectively
reduce subjective bias on indicator weight.
According to the standard matrix R for risk early-
warning sample, suppose that ij
f
showed the propor-
tion of risk early-warning event
j
E on the risk early-
warning factor i C, then:
''
1
''
1
/1,2,,
/1,,
n
ij ij
j
ij n
ij ij
j
x
xi r
f
yyir m













(11)
In terms of the information entropy theory [8], the
natural disaster conditions and the risk entropy principles
[13], the Shannon entropy value of the early-warning
factor i C could be got with the following equation, as
shown in (12).



1
1ln
ln
n
iiij ij
j
eHCf f
n

 (12)
Here, i e said the entropy value of the risk early-
warning samples in natural disaster. As the entropy value
show greater, it reflected the greater degree of internal
disorder in the natural risk system. As 0
ij
f

, ij
f

0.00001 was set.
Thus, for natural disasters, the weight of risk early-
warning i C was calculated, as:


1
1
11
11,2,,
11,,
1
r
ii i
i
m
ii i
ir
rm
ii
iir
en eir
en eirm







 





 











 (13)
where i

said the weight value of risk early-warning
factor i C in natural disaster event.
4.3. Risk Early-Warning DEA Model with
Preference Entropy Weight
Make the risk early-warning sample k E of natural dis-

F. S. WANG ET AL. 28
aster as decision-making unit, and improve the non- Arc-
himedean infinitesimal risk early-warning DEA model
according to the preference weight of risk early-warning
factor for natural disasters. Then, risk early-warning
DEA model with preference entropy weight was estab-
lished on the risk early-warning sample k E, such as
model (14).
11
1
1
1, ,
1, ,
0,1,,
,0
rm
pii
iir
n
ij jiiki
j
n
ij jiikj
j
j
ii
min Vθ
xθ
x
ir
yyirm
jn
θ,
 
 
 













 



 












(14)
In model (14), the expression and significance of θ,

, i

, i

 and other variables, were consistent with
model (6). And, model (14) carried forward entropy
analysis in disaster information systems [14].
4.4. Risk Early-Warning DEA Sentencing
Guideline with Preference Entropy
Weight
Suppose that the optimal solution of model (14) was 0 θ,
0

, 0
i

, 0
i

, whose expression and significance was
consistent with model (6). Set

p
k
VE as the relative
safe measurement of risk early-warning sample k
E, and
establish risk early-warning entropy DEA sentencing
guideline.
Guideline 3: According to the formula (15), determine
the order of risk early-warning samples. Then, determine
the lowest value on the relative safe measurement of risk
early-warning samples, and sentence the corresponding
sample as the relative most risk sample unit.



min pj
jVE (15)
Guideline 4: Set


p
VE
 as the relative safe grade
threshold of risk early-warning samples. If the formula
(16) was true, the risk early-warning sample
j
E was
sentenced as key risk early-warning unit.




1, 2,,
pjp
VEVE jn
 (16)
5. Case study on Risk Early-Warning for
Slope Landslide
5.1. Initial Data for Risk Early-Warning Event
of Slope Landslide Case
For instance, in emergency response on earthquake-
damaged rock slope engineering, potential landslide was
the risk event. According to the multi-layer indicator
system for evaluating the overall safety on rock slope
engineering in reference [15-18], the risk early-warning
factors were given, as shown in Table 1.
Here, essential attributes included rock structure, rock
mass deformation modulus, rock integrity coefficient,
cohesion and internal friction angle; and external cha-
racters included slope height, slope angle, maximum
daily rainfall, monthly total rainfall, seismic level acce-
leration, maximum terra stress, surface deformation rate,
drainage capability, and others.
In the emergency response process on earthquake-
damaged rock slope engineering, it supposed that the risk
early-warning sample included 1 E, 2 E, 3 E, 4 E, 5 E
and 6 E, which needed more important focus, and its
relevant factors and value, as shown in Table 1.
Table 1. Value of the early-warning factor for slope landslide risk samples in earthquake-da m age d emergency response.
Sample
External factors ( minType） Essential attributes ( maxType)
Slope
height
Slope
angle
Daily
maximum
rainfall
Month
cumulative
rainfall
Seismic
horizontal
acceleration
Maximum
terra
stress
Surface
deformation
rate
Drainage
performance
Rock
structure
Rock mass
deformation
modulus
Rock
integrity
coefficient
Cohesion
Internal
friction
angle
1
E 0.85 26 56 290 0.15 12.8 0.08 0.25 71 2.7 0.43 0.12 24
2
E 1.15 39 28 245 0.09 14.7 0.26 0.49 54 6.9 0.39 0.18 39
3
E 1.06 12 89 212 0.13 4.1 0.17 0.35 29 7.5 0.75 0.26 14
4
E 0.79 21 63 229 0.07 4.3 0.09 0.21 89 20.5 0.64 0.21 27
5
E 0.54 51 47 192 0.31 11.8 0.32 0.83 86 11.4 0.20 0.29 12
6
E 1.21 28 19 264 0.24 5.7 0.13 0.52 32 8.4 0.54 0.15 25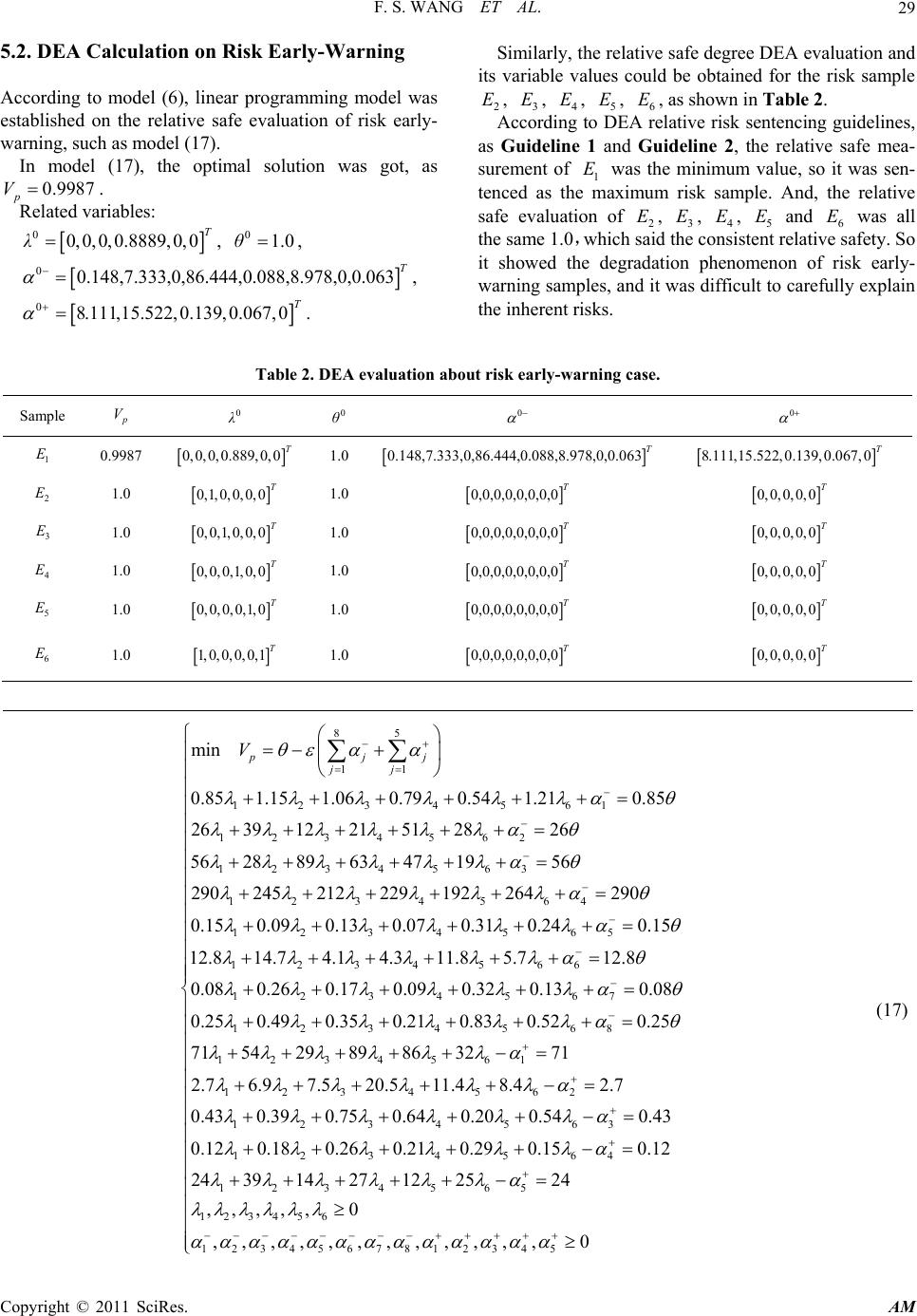

F. S. WANG ET AL. 29
5.2. DEA Calculation on Risk Early-Warning
According to model (6), linear programming model was
established on the relative safe evaluation of risk early-
warning, such as model (17).
In model (17), the optimal solution was got, as
0.9987
p
V.
Related variables:

00, 0,0,0.8889, 0, 0T
λ, 01.0θ,

00.148,7.333,0,86.444,0.088,8.978,0,0.063 T

,

08.111,15.522,0.139,0.067,0 T

.
Similarly, the relative safe degree DEA evaluation and
its variable values could be obtained for the risk sample
2
E, 3 E, 4 E, 5 E, 6 E, as shown in Table 2.
According to DEA relative risk sentencing guidelines,
as Guideline 1 and Guideline 2, the relative safe mea-
surement of 1 E was the minimum value, so it was sen-
tenced as the maximum risk sample. And, the relative
safe evaluation of 2 E, 3 E, 4 E, 5 E and 6 E was all
the same 1.0，which said the consistent relative safety. So
it showed the degradation phenomenon of risk early-
warning samples, and it was difficult to carefully explain
the inherent risks.
Table 2. DEA evaluation about risk early-warning case.
Sample
p
V 0
λ
0 θ 0


0


1
E 0.9987

0, 0,0, 0.889, 0, 0T 1.0

0.148,7.333,0,86.444,0.088,8.978,0,0.063 T

8.111,15.522, 0.139, 0.067, 0T
2
E 1.0

0,1,0, 0, 0, 0T 1.0

0,0,0,0,0,0,0,0 T

0, 0, 0,0, 0T
3
E 1.0

0, 0,1, 0, 0, 0T 1.0

0,0,0,0,0,0,0,0 T

0, 0, 0,0, 0T
4
E 1.0

0,0, 0,1,0, 0T 1.0

0,0,0,0,0,0,0,0 T

0, 0, 0,0, 0T
5
E 1.0

0,0, 0, 0,1,0T 1.0

0,0,0,0,0,0,0,0 T

0, 0, 0,0, 0T
6
E 1.0

1,0, 0, 0, 0,1T 1.0

0,0,0,0,0,0,0,0 T

0, 0, 0,0, 0T
85
11
123 4 561
1234562
1234563
1234564
min
0.85 1.151.060.790.541.210.85
2639 1221 51 2826
56 28896347 1956
290 245212229 192264290
pjj
jj
V  

 
 









 







1234565
1234566
1234567
1234568
0.15 0.090.130.070.31 0.240.15
12.8 14.74.14.311.85.712.8
0.080.26 0.17 0.090.32 0.130.08
0.250.490.35 0.210.830.520.2


 
 

 









1234561
1234 562
1234563
1234 564
123
5
71 542989863271
2.7 6.97.520.511.4 8.42.7
0.43 0.390.750.640.200.540.43
0.12 0.180.260.210.290.150.12
24 391427

 
 












45 65
123456
1234567812345
12 2524
,,,,, 0
,,,,,,,,,,,, 0




































(17)

F. S. WANG ET AL. 30
5.3. Risk Early-Warning DEA Model with
Entropy Weight
Risk early-warning samples were prepared in Table 1.
Firstly, standardize the initial risk early-warning data
according to Formulas (7), (8), (9) and (10). Then, cal-
culate the entropy value and weight value of the natural
risk early-warning indicator according to Formulas (11),
(12) and (13), Table 3 showed the entropy value and
weight value.
In Table 3, the entropy value reflected the amount of
useful information that the early-warning indicators pro-
vided for landslide early-warning system in the earth-
quake-damaged slope engineering. For example, “slope
height” showed the maximum entropy value, and its
weight value was 0.0803, which was the minimum weight
value in the risk indicators. Information effectiveness of
the entropy measurement denoted the changing rule,
which has the greater entropy value and the smaller
weight value of the risk early-warning factor.
According to model (14), the relative safe entropy
DEA evaluation model of risk early-warning sample 1 E
was erected, such as (18).
In model (18), the optimal solution was got, as
2.5362
p
V

.
Related variables:

00,0,0,0.186,0.048,0 T
λ, 02.5365θ,

02.537,0,0.253,1.487, 20.855,0.026,4.066,0T



00,3.991,0.041,0.029,1.759T

.
Similarly, the relative safe degree DEA evaluation and
its variable values could be obtained for the risk sample
2
E, 3 E, 4 E, 5 E, 6 E, as shown in Table 4.
Table 3. Entropy value and weight value of the risk early-warning factor for slope landslide risk case.
Sample Slope
height
Slope
angle
Daily
maximum
rainfall
Month
cumulative
rainfall
Seismic
horizontal
acceleration
Maximum
terra
stress
Surface
deformation
rate
Drainage
performance
Rock
structure
Rock mass
deformation
modulus
Rock
integrity
coefficient
Cohesion
Internal
friction
angle
Entropy 0.8623 0.8277 0.8131 0.8304 0.7564 0.71290.7279 0.7540 0.76030.8856 0.8322 0.83200.8684
Weight 0.0803 0.1004 0.1090 0.0989 0.1420 0.16740.1586 0.1434 0.29180.1392 0.2042 0.20450.1603
85
11
1234561
1234562
1234563
1234
min
0.851.151.060.790.541.210.85 0.0803
2639 1221 51 28260.1004
56288963471956 0.109
290 245212229
pjj
jj
V  

 
 
 







 







564
1234565
1234566
1234567
1922642900.0989
0.150.090.130.070.310.240.15 0.142
12.814.74.14.311.85.712.8 0.1674
0.080.26 0.17 0.09 0.32 0.130.080.1586
0.
 


 

 








1234568
12 34561
1234 562
1234563
250.490.350.210.830.520.25 0.1434
71542989863271 0.2918
2.76.97.520.511.48.42.70.1392
0.430.39 0.750.64 0.200.540.4

 
 










1234564
1234565
123456
1234567812345
30.2042
0.120.180.260.210.290.150.120.2045
24391427122524 0.1603
,,,,, 0
,,,,,,,,,,,, 0

 









































(18)

F. S. WANG ET AL. 31
Table 4. Entropy DEA assessment for risk early-warning case.
Sample
p
V 0

0

0


0


1
E 2.5362

0, 0, 0,0.186, 0.048,0T 2.5365

2.537, 0, 0.253,1.487, 20.855,0.026, 4.066,0T

0,3.991,0.041,0.029,1.759 T
2
E 2.7581

0,0.19,0,0.007,0.057,0 T 2.7582

0,0.337,0,7.785,0,3.29,0.045,0.052 T

0,1.136,0.01, 0.015, 2.028T
3
E 2.4959

0,0,0.169,0.041,0.003,0 T 2.4961

0,0,0,6.507,6.754,0.021,0.816,0.034,0.056 T

0.261,1.083,0,0,1.245 T
4
E 3.492

0, 0, 0,0.2529, 0.0402, 0T 3.4922

0,0,6.156,13.448,0.005,0.952,0.014,0.019 T

0, 2.79, 0.039, 0.022, 2.984T
5
E 3.6336

0, 0,0, 0,0.292, 0T 3.6339

0, 3.725, 4.902,12.977, 0.07, 3.735, 0.091,0.19T

0,1.74,0.018,0.025,1.58 T
6
E 2.5951

0,0.007,0,0,0.035,0.186 T 2.5952

0,0.03,0,10.187,0.032,0.902,0.016,0.064 T

0, 0.842, 0, 0.009,1.335T
According to risk early-warning entropy DEA sen-
tencing guideline, namely Guideline 3, the relative safe
order of the risk early-warning disaster samples could be
obtained as

3p
VE <

1p
VE <

6p
VE <


2p
VE
<

4p
VE <

5p
VE.
In accordance with Guideline 4, set the relative safe
threshold of the risk early-warning samples as

3.0
p
VE
, then sentence the risk sample 3
E, 1 E,
6
E, 2 E as the important risk early-warning units.
Comparing the calculation outcome of landslide risk
case of earthquake-damaged emergency response in Ta-
ble 2 and Table 4, entropy DEA model could explore
more information, whose conclusion was more reliable
than the standard DEA model, benefiting the sentencing
about the relative risk measurement of risk early-warning
samples for natural disasters.
6. Conclusions
1) Differentiate the risk early-warning factors of natural
disasters into essential attributes and external characters.
Using the integration of Entropy and DEA model, risk
early-warning model was erected. It made the best of
information, and had high reliability. This algorithm was
easy to realize by computer software, and had good re-
sults. It was a new way for risk early-warning of natural
disasters.
2) Determinating the weight value of natural risk early
warning indicator through entropy value, solved the con-
flicts and incompatibilities among indicators, and elimi-
nated the effect of random personality.
3) Risk landslide early-warning case in earthquake
emergency response testified, that entropy DEA model
explored more implicit preference information of essen-
tial attributes and external characters in early-warning
samples, whose outcome reflected more additional risk
information than the standard DEA model, effectively
improving the sentencing on relative risk degree of early-
warning samples for natural disasters.
4) Entropy DEA model integrated the objectivity of
DEA model and the information entropy of early-war-
ning samples, whose essence was the preference DEA
model based on entropy weight. And, its result was more
realistic and widely useful. But how to assess core fac-
tors in risk early-warning system needed further explora-
tion.
7. References
[1] M. Jarraud, “Reducing the Risk of Natural Disasters
through Early Warnings,” Bulletin of the American Me-
teorological Society, Vol. 86, No. 2, 2005, pp. 155-156.
[2] V. Selman, A. L. Selman and J. Selman, “Earthquake/
Quackery: The Science/Art of Predicting Natural Disas-
ters,” Simulation Series, Vol. 15, No. 1, 1985, pp. 113-
117.
[3] H. Yang and R. F. Adler, “Towards an Early-Warning
System for Global Landslides Triggered by Rainfall and
Earthquake,” International Journal of Remote Sensing,
Vol. 28, No. 16, 2007, pp. 3713-3719. doi:10.1080/
01431160701311242
[4] K. Kubo, “Prediction and Its Reliability,” Civil Engi-
neering in Japan, Vol. 26, No. 12, 1987, pp. 1-10.
[5] A. Charnes, W. W. Cooper and E. Rhodes, “Measuring
the Efficiency of Decision-Making Units,” European
Journal of Operational Research, Vol. 2, No. 6, 1978, pp.
429-444. doi:10.1016/0377-2217(78)90138-8
[6] J. K. Sengupta, “Measuring Dynamic Efficiency under
Risk Aversion,” European Journal of Operational Re-
search, Vol. 74, No. 1, 1994, pp. 61-69. doi:10.1016/
0377-2217(94)90203-8
[7] Z.-X. Ma and H.-L. Ren, “An Evaluation Method Based
on Some Sample Units and Its Applying on FSA,” Sys-
tems Engineering—Theory & Practice, Vol. 23, No. 2,
2003, pp. 96-100.
[8] Y. Horibe, “Entropy and Correlation,” IEEE Transactions
on Systems, Man and Cybernetics, Vol. SMC-15, No. 5,
1985, pp. 641-642.

F. S. WANG ET AL. 32
[9] J. K. Sengupta, “Efficiency Measurement in Stochastic
Input-Output Systems,” International Journal of Systems
Science, Vol. 13, No. 3, 1982, pp. 273-287. doi:10.1080/
00207728208926348
[10] Y.-M. Wang and Y. Luo, “DEA Efficiency Assessment
Using Ideal and Anti-ideal Decision-Making Units,” Ap-
plied Mathematics and Computation (New York), Vol.
173, No. 2, 2006, pp. 902-915.
[11] S. Mehrabian, M. R. Alirezaee and G. R. Jahanshahloo,
“Complete Efficiency Ranking of Decision-Making Units
in Data Envelopment Analysis,” Computational Optimi-
zation and Applications, Vol. 14, No. 2, 1999, pp. 261-
266. doi:10.1023/A:1008703501682
[12] L. S. Qu, L. M. Li and J. Lee, “Enhanced Diagnostic
Certainty Using Information Entropy Theory,” Advanced
Engineering Information, Vol. 17, No. 3-4, 2003, pp.
141-150. doi:10.1016/j.aei.2004.08.002
[13] J. J. Buckley, “Entropy Principles in Decision-Making
under Risk,” Risk Analysis, Vol. 5, No. 4, 1985, pp.
303-313. doi:10.1111/j.1539-6924.1985.tb00186.x
[14] S. Bilgi, C. Ipbuker, D. Ucar and M. Sahin, “Map Entro-
py Analysis of Topographic Data Used in Disaster In-
formation Systems,” Journal of Earthquake Engineering,
Vol. 12, No. S2, 2008, pp. 23-36.
[15] X. L. Tan, W. Y. Xu and G. L. Liang, “Application of
Extenics Method to Comprehensive Safety Evaluation of
Rock Slope,” Chinese Journal of Rock Mechanics and
Engineering, Vol. 28, No. 12, 2009, pp. 2503-2509.
[16] Y. P. Yin, F. W. Wang and P. Sun, “Landslide Hazards
Triggered by the 2008 Wenchuan Earthquake, Sichuan,
China,” Landslides, Vol. 6, No. 2, 2009, pp. 139-151.
doi:10.1007/s10346-009-0148-5
[17] G. Q. Chen, “Practical Techniques for Risk Analysis of
Earthquake-Induced Landslide,” Chinese Journal of Rock
Mechanics and Engineering, Vol. 27, No. 12, 2008, pp.
2395-2402.
[18] C.-T. Lee, C.-C. Huang, J.-F. Lee, K.-L. Pan, M.-L. Lin
and J.-J. Dong, “Statistical Approach to Earthquake-
Induced Landslide Susceptibility,” Engineering Geology,
Vol. 100, No. 1-2, 2008, pp. 43-58. doi:10.1016/j.enggeo.
2008.03.004