Applied Mathematics, 2011, 2, 1-10
doi:10.4236/am.2011.21001 Published Online January 2011 (http://www.SciRP.org/journal/am)
Study the Effect of Thermal Gradient on Transverse
Vibration of Non-Homogeneous Orthotropic Trapezoidal
Plate of Parabolically Varying Thickness
Arun K. Gupta, Shanu Sharma
Department of Mat hematics, M S College, Sahara npur, India
Received September 15, 2010; revised October 12, 2010; accepted October 15, 2010
Abstract
The present paper deals with the effect of linearly temperature on transverse vibration of non-homogeneous
orthotropic trapezoidal plate of parabolically varying thickness. The deflection function is defined by the
product of the equations of the prescribed continuous piecewise boundary shape. The non homogeneity of
the plate is characterized by taking linear variation of the Young's modulus and parabolically variation of the
density of the material. The non homogeneity is assumed to arise due to the variation in the density of the
plate material and it is taken as parabolically. Rayleigh Ritz method is used to evaluate the fundamental fre-
quencies. The equations of motion, governing the transverse vibrations of orthotropic trapezoidal plates, are
derived with boundary condition clamped-simply supported-clamped-simply supported. Frequencies corres-
ponding to first two modes of vibration are calculated for the trapezoidal plate for various combinations of
the parameters of the non-homogeneity, thermal gradient, taper constant and for different values of the aspect
ratios and shown by figures. All The results presented here are entirely new and are not found elsewhere.
Comparison can only be made for homogeneous plates, and in that cases the results have been compared
with those found in the existing literatures and are in excellent agreement.
Keywords: Thermal Gradient, Vibration, Orthotropic Trapezoidal Plate, Parabolically Thickness,
Non-Homogeneity
1. Introduction
Plate structures are fundamental elements in engineering
and are used in a variety of structural applications. Stru-
ctures like aircraft wings, satellites, ships, steel bridges,
sea platforms, helicopter rotor blades, space craft anten-
nae and subsystems of more complex structures can be
modeled as orthotropic plate elements. The practical im-
portance of plates has made vibration analysis essential
for avoiding resonance excited by internal or external
forces. Plate structures undergoing transverse deflection
can be classified into numerous regimes that describe the
nature of their behavior and thus the characteristics of the
mathematical problem. Plate theory has been applied to
reduce vibration and noise in structures since the end of
the 19th century where it began with the work of German
physicist Chladni, who discovered various modes of free
vibrations experimentally. Since then it has developed
into an escalating and expansive field with a wide variety
of theoretical and empirical techniques, dealing with
increasingly complicated problems. Also in recent years,
the development of solid propellant rocket motors, the
increased use of soft filaments in aerospace structure,
high speed runways, many practical solid structure inte-
raction problems such as floor slabs of multistory build-
ings or buildings activities in cold regions has intensified
the need for solution of various problems of plates and
other structure supported on elastic media.
In addition, the non-homogeneity of longitudinal to
transverse modules of these new materials demands im-
provement in the existing analytical tools. As a result, the
analysis of plate’s vibrations has attracted many research
workers, and has been considerably improved to achieve
realistic results. In the design of modern high-speed air-
craft and missile structures, swept wing and tail surfaces
are extensively employed. The literature on the free vi-
brations of plates is vast. A number of researchers have

A. K. GUPTA ET AL. 2
worked on free vibration analysis of rectangular, circular,
elliptical etc. plates and variable thickness. Little res-
earch work has been done on non uniform thickness tra-
pezoidal plates as compared to the other plates.
Trapezoidal plates are used commonly as structural
components in many engineering applications such as
ships, aircraft, engineering constructions etc. many res-
earcher have investigated the free vibration behavior of
trapezoidal plates. Leissa’s monograph [1-3] contains an
excellent discussion of the subject of vibrating plates.
Chopra and Durvasula [4] solved the problem of vibra-
tion of simple-supported trapezoidal plate symmetric
trapezoids. Vibration of skew plate was discussed by
Nair and Durvasula [5]. Thermal effect on axisymmetric
vibration of an orthotropic circular plate of variable thi-
ckness was discussed by Tomar and Gupta [6]. Tomar
and Gupta [7] solved the problem of vibration of ortho-
tropic rectangular plate of linearly varying thickness with
thermal gradient effect. Orris and Petyt [8] study of the
vibration of trapezoidal plate by using finite element me-
thod. Narita, Maruyama and Sonada [9] studied the tran-
sverse vibration of clamped trapezoidal plate having rec-
tangular orthotropy. Mirza and Bijlani [10] discussed the
vibration of triangular plates. Bhatnagar and Gupta [11]
solved the problem of thermal effect on vibration of vis-
co elastic elliptic plate of variable thickness. Transverse
free vibration of fully clamped symmetrical trapezoidal
plates was discussed by Sahba [12]. Laura, Gutierrez and
Bhat [13] studied the transverse vibrations of a trapezoi-
dal cantilever plate of variable thickness. Liew and Lam
[14] studied a Rayleigh-Ritz approach to transverse vi-
bration of isotropic and anisotropic trapezoidal plates
using orthogonal plate functions. Problem of variable of
symmetric laminated cantilever trapezoidal composite
plates was solved by Liew [15].Liew and Lim [16] stu-
died the transverse vibration of trapezoidal plates of va-
riable thickness: symmetric trapezoids. Qatu, Jaber and
Leissa [17] work out to analyze the natural frequencies
for completely free trapezoidal plates. Vibration of pret-
wisted cantilever trapezoidal symmetric laminates was
discussed by Lim and Liew [18]. Sakiyama and Hung
[19] studied the free vibration analysis of right triangular
plates with variable thickness. Lal [20] studied the trans-
verse vibration of orthotropic non uniform rectangular
plate with continuously varying density. Leissa [21] dis-
cussed the historical bases of the Rayleigh and Ritz me-
thods. Chi-Hung, Chien and Yen-Kuang [22] did expe-
rimental and numerical investigations for the free vibra-
tion of cantilever trapezoidal plates. Gupta, Johri and
Vats [23,24] work out to investigate the thermal effect on
vibration of non homogeneous orthotropic rectangular
plate having bi-directional varying thickness. Karami,
Shahpari and Malekzadeh [25] have applied Differential
Quadrature Method (DQM) for static, free vibration, and
stability analysis of skewed and trapezoidal composite
thin plates without hole. Recently, Gupta and Sharma [26]
solved the problem of thermally induced vibration of
orthotropic trapezoidal plate of linearly varying thick-
ness.
From the review of available literature it is observed
that the linearly temperature on transverse vibration of
non-homogeneous orthotropic trapezoidal plate of para-
bolically varying thickness with non-homogeneity effect
has not been studied. So it is necessary to analyze this
kind of problem using elasticity theory based Rayleigh
Ritz method to evaluate for the most accurate behavior of
frequencies of the plate. Therefore, a method is devel-
oped to study the problem both theoretically and experi-
mentally. In order to calculate natural frequencies for
first and second mode of vibration, Rayleigh Ritz method
is used. The frequencies for the first and second mode of
vibration are calculated for the trapezoidal plate having
C-S-C-S edges for the different values of taper constant ,
thermal gradient and aspect ratio and presented in graph-
ically form.
2 Method of Analysis
Let us assume that orthotropic trapezoidal plate under
consideration is subjected to steady one dimensional
temperature distribution

along the length, therefore
one can take

as,
0
1
12  







(1)
where 0

is the temperature at 1
2
  .
For most orthotropic materials modulus of elasticity
are described as a function of temperature as,




 
 
1
2
0
1
1
1
EE
EE
GG

















(2)
Using Equation (1), Equation (2) becomes
1
2
0
1
12
1
12
1
12
EE
EE
GG



































 







(3)
where 12 0
,EEandGare the values of moduli at some
reference temperature, i.e. 0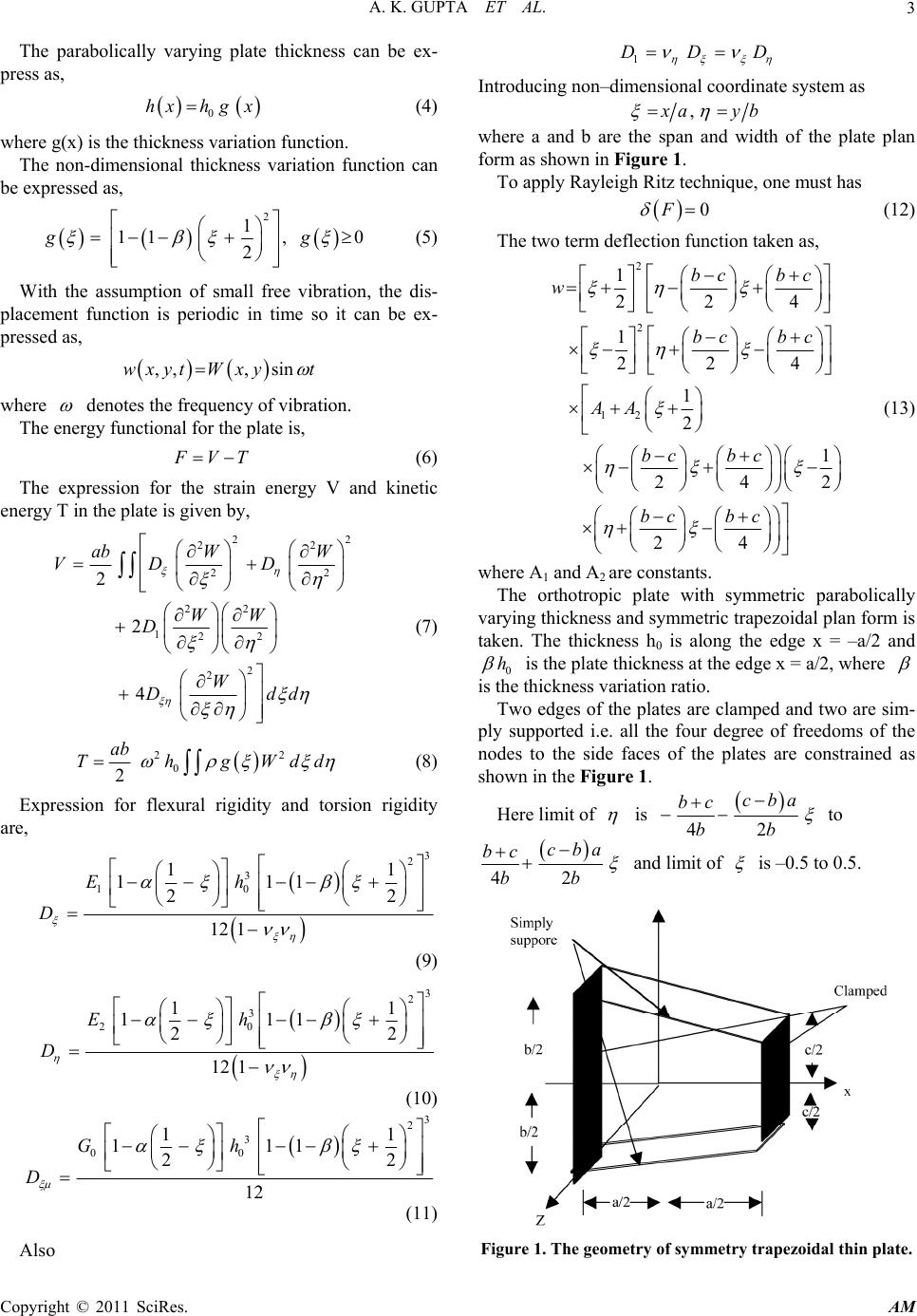

.

A. K. GUPTA ET AL. 3
The parabolically varying plate thickness can be ex-
press as,



0
hxhg x (4)
where g(x) is the thickness variation function.
The non-dimensional thickness variation function can
be expressed as,
 
2
1
11, 0
2
gg
 


 





(5)
With the assumption of small free vibration, the dis-
placement function is periodic in time so it can be ex-
pressed as,



,,, sinwxyt Wxyt


where

denotes the frequency of vibration.
The energy functional for the plate is,
F
VT (6)
The expression for the strain energy V and kinetic
energy T in the plate is given by,
22
22
22
22
122
2
2
2
2
4
ab WW
VD D
WW
D
W
Ddd






 

 
 

 










 



(7)

22
0
2
ab
ThgWdd

   (8)
Expression for flexural rigidity and torsion rigidity
are,


3
2
3
10
11
111
22
12 1
Eh
D


 



 
 

 

 




(9)


3
2
3
20
11
111
22
12 1
Eh
D


 



 
 

 

 
 


(10)

3
2
3
00
11
111
22
12
Gh
D

 


 
 

 

 
 


(11)
Also
1
DDD






Introducing non–dimensional coordinate system as
,
x
ayb



where a and b are the span and width of the plate plan
form as shown in Figure 1.
To apply Rayleigh Ritz technique, one must has


0F 

(12)
The two term deflection function taken as,
2
2
12
1
224
1
224
1
2
1
242
24
bc bc
w
bc bc
AA
bc bc
bc bc
 
 







 












 









 
 

 

 
 



 

 





(13)
where A1 and A2 are constants.
The orthotropic plate with symmetric parabolically
varying thickness and symmetric trapezoidal plan form is
taken. The thickness h0 is along the edge x = –a/2 and
0
h

is the plate thickness at the edge x = a/2, where

is the thickness variation ratio.
Two edges of the plates are clamped and two are sim-
ply supported i.e. all the four degree of freedoms of the
nodes to the side faces of the plates are constrained as
shown in the Figure 1.
Here limit of

is

42
cba
bc
bb



 to


42
cba
bc
bb


 and limit of

is –0.5 to 0.5.
Figure 1. The geometry of symmetry trapezoidal thin plate.

A. K. GUPTA ET AL. 4
Assume that the density varies parabolically in x di-
rection.

2
1
11 0.5
ox
 

 

where α1 is the non homogeneity of the plate.
Substitute Equations (5), (9) to (11) and (13) in Equa-
tions (7) and (8), one has





3
01
4
32
22
2
3
02
4
32
22
2
3
01
22
1
12
24 1
1
112
1
12
24 1
1
112
1
61
habE
Va
Wdd
habE
b
Wdd
hE
ab






 



 















 





 




 






 




 






3
222
22
3
00
22
32
22
1
2
1
112
1
12
3
1
112
WW
dd
hG
ab
Wdd





 




 






 




 












 
 


 


 




(14)
 
2
00
2
22
1
2
1
110.5 112
ab
Th
x
Wdd


 





  








(15)
Using Equations (14) and (15) in (6) we have,

2
11
0VT   (16)
Where

3
2
1
22
22
2
22
1
22
2
22
1
2
2
0
1
11
111
22
2
(1 )
4
V
E
WW
E
EWW
E
GWdd
E


 


 




 
 


  
 





 



 

 

















2
11
2
2
11 0.5
1
112
Tx
Wdd




 



 





and


25
0
2
2
10
12 1a
Eh






 is a frequency parameter.
Equation (16) contains two unknown constants A1 and
A2 which can be evaluated as
2
11
()
0, 1,2
n
VT n
A
  
 (17)
The Equation (17) simplifies to the form
112 20, 1,2 nn
cA cAn

 (18)
where cn1 and cn2 (n = 1,2) involves parametric constants
and frequency parameter.
For a non-zero solution, the coefficient matrix of Equ-
ation (18) must be zero. In this way the frequency equa-
tion must comes out to be
11 12
21 22
0
cc
cc
 (19)
From Equation (19) one can obtain a quadratic equa-
tion in 2

from which two values of 2

can be found.
3 Results and Discussion
Numerical results are obtained for the first two modes of
vibrations for transverse vibration of non-homogeneous
orthotropic trapezoidal plate of parabolically varying thi-
ckness with thermal gradient effect and non-homo- gene-
ity effect for different values of aspect ratios. Frequency
(19) is quadratic in 2

, so it will give two roots.
The parameters for orthotropic material have been
taken as [3]:

0 22
111
0.32,0.04, 10.09
G EE
EEE

 
These results are plotted in Figures 2-9.
A study will now be presented for a set of trapezoidal
plate configurations by varying c/b and a/b values.
In Figure 2, results have been displayed for the fol-
lowing values:
a/b = 1.0, c/b = 0.5,
α = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0
β = 0.0, 0.2
α1 = 0.0, 0.2
It can be concluded that with the increase in thermal
gradient, frequency decreases for both the modes.
Result have been displayed for the following values
a/b = 1.0, c/b = 0.5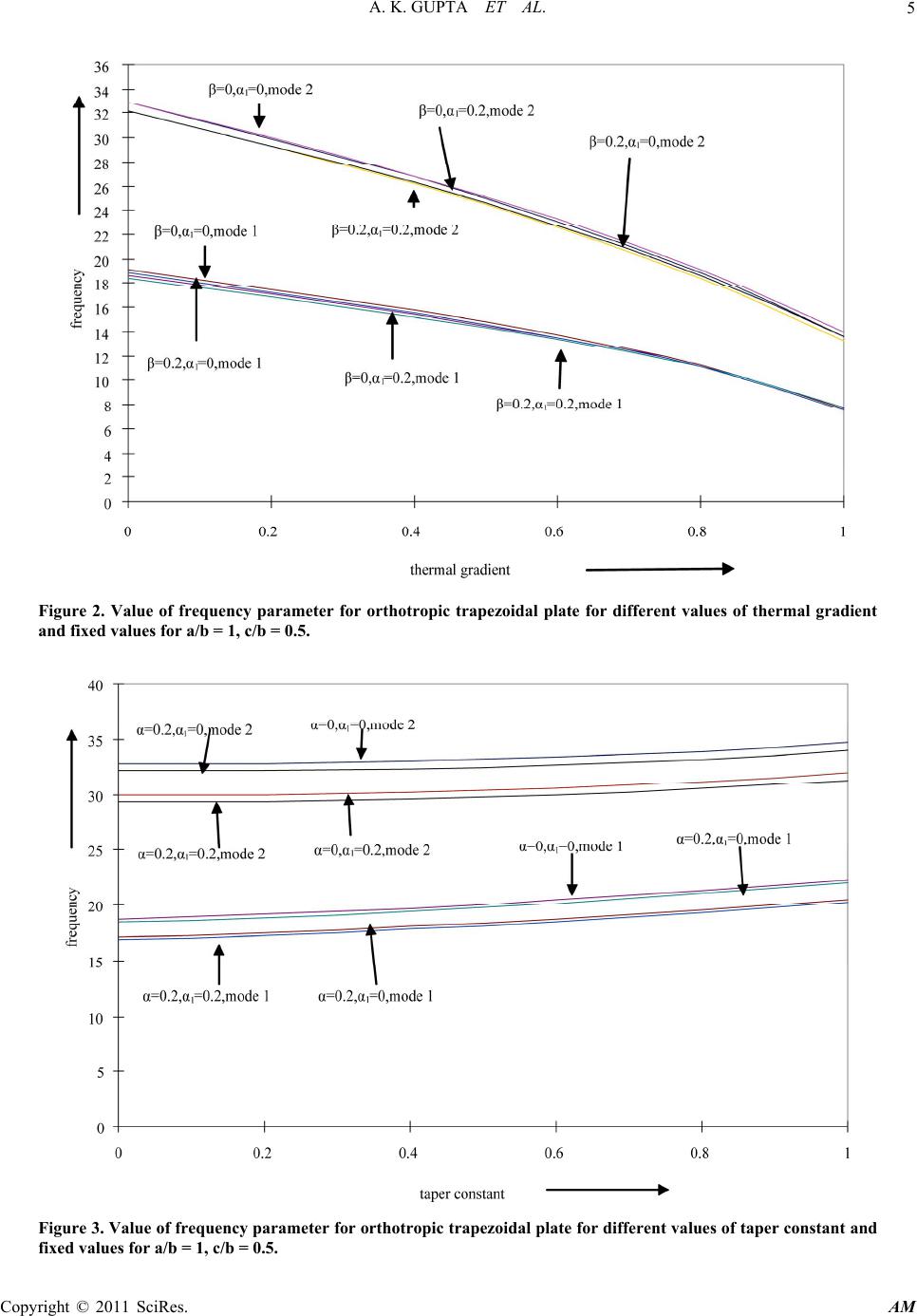

A. K. GUPTA ET AL. 5
Figure 2. Value of frequency parameter for orthotropic trapezoidal plate for different values of thermal gradient
and fixed values for a/b = 1, c/b = 0.5.
Figure 3. Value of frequency parameter for orthotropic trapezoidal plate for different values of taper constant and
fixed values for a/b = 1, c/b = 0.5.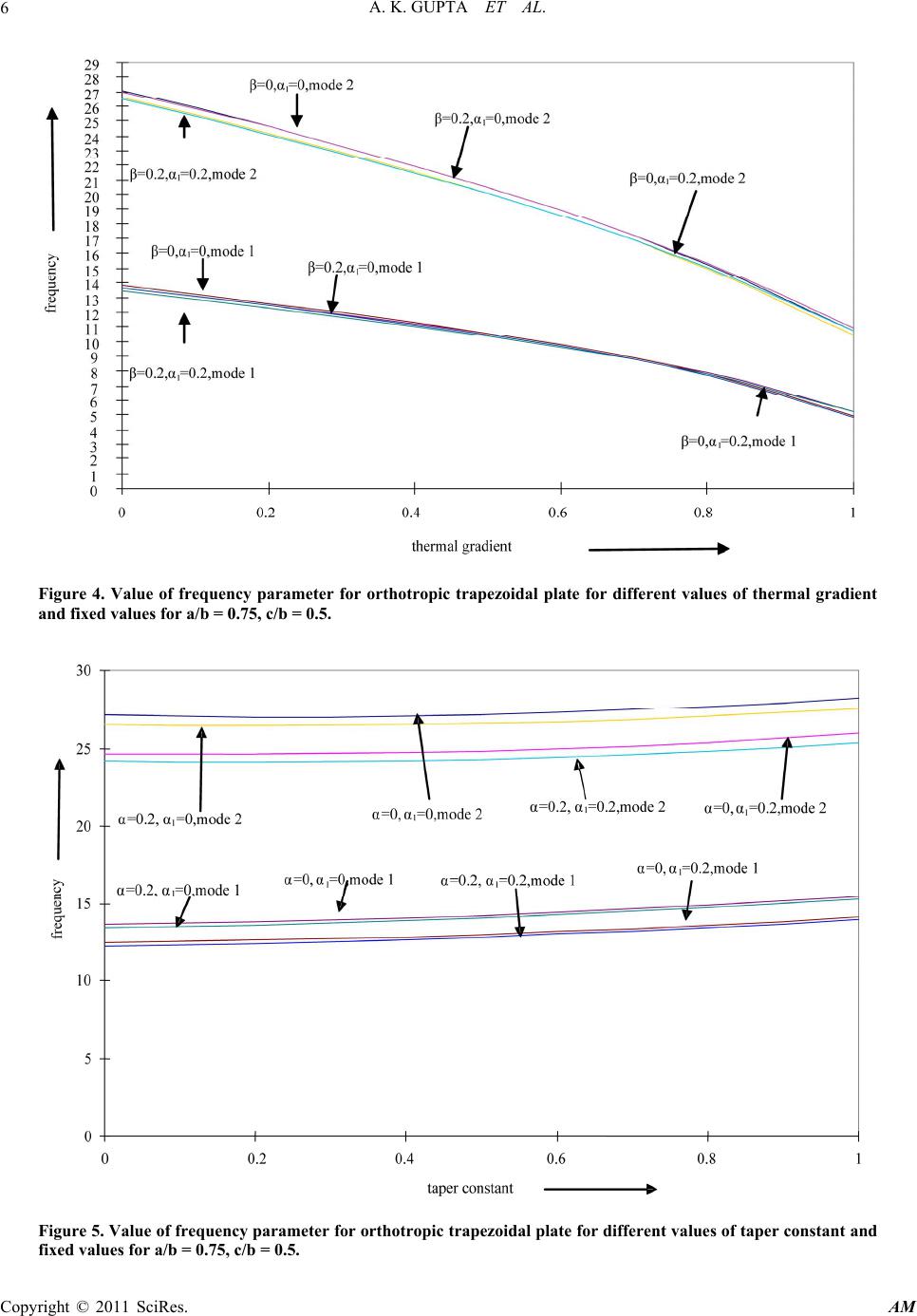

A. K. GUPTA ET AL. 6
Figure 4. Value of frequency parameter for orthotropic trapezoidal plate for different values of thermal gradient
and fixed values for a/b = 0.75, c/b = 0.5.
Figure 5. Value of frequency parameter for orthotropic trapezoidal plate for different values of taper constant and
fixed values for a/b = 0.75, c/b = 0.5.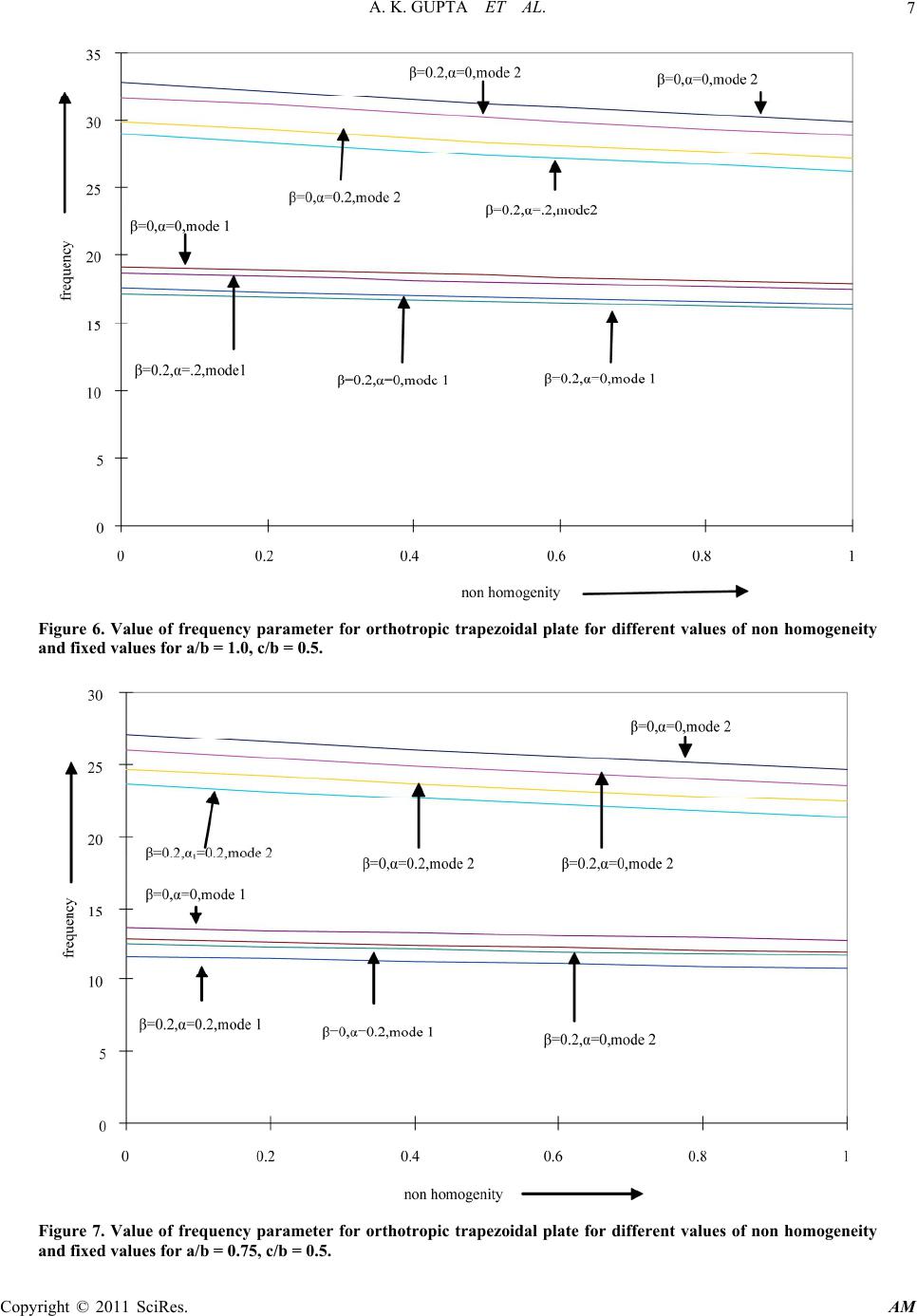

A. K. GUPTA ET AL. 7
Figure 6. Value of frequency parameter for orthotropic trapezoidal plate for different values of non homogeneity
and fixed values for a/b = 1.0, c/b = 0.5.
Figure 7. Value of frequency parameter for orthotropic trapezoidal plate for different values of non homogeneity
and fixed values for a/b = 0.75, c/b = 0.5.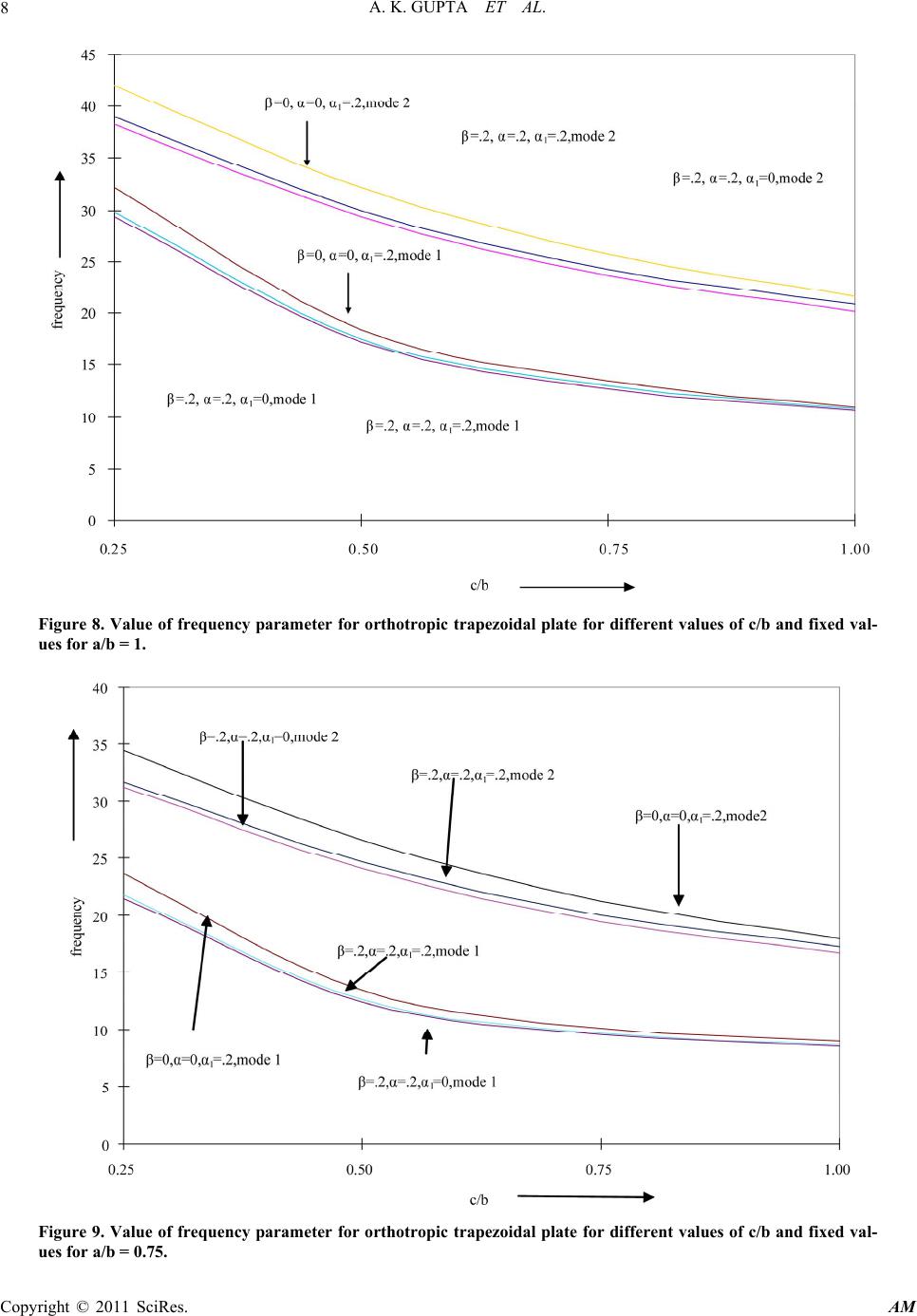

A. K. GUPTA ET AL. 8
Figure 8. Value of frequency parameter for orthotropic trapezoidal plate for different values of c/b and fixed val-
ues for a/b = 1.
Figure 9. Value of frequency parameter for orthotropic trapezoidal plate for different values of c/b and fixed val-
ues for a/b = 0.75.

A. K. GUPTA ET AL. 9
β = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0
α = 0.0, 0.2
α1 = 0.0, 0.2
In Figure 3. It can be concluded that with the increase
in taper constant, frequency increases for both the modes.
In Figure 4, results have been displayed for the fol-
lowing values:
a/b = 0.75, c/b = 0.5
α = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0
β = 0.0, 0.2
α1 = 0.0, 0.2
It can be concluded that with the increase in thermal
gradient, frequency decreases for both the modes.
Figure 5 show the results for the following values:
a/b = 0.75, c/b = 0.5
β = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0
α = 0.0, 0.2
α1 = 0.0, 0.2
and it can be concluded that with the increase in taper
constant ,frequency increases for both the modes.
In Figure 6, results have been displayed for the fol-
lowing values:
a/b = 1.0, c/b = 0.5
α1 = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0
β = 0.0, 0.2
α = 0.0, 0.2
It can be concluded that with the increase in non ho-
mogeneity, frequency decreases for both the modes.
In Figure 7, results have been displayed for the fol-
lowing values:
a/b = 0.75, c/b = 0.5
α1 = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0
β = 0.0, 0.2
α = 0.0, 0.2
It can be concluded that with the increase in non ho-
mogeneity, frequency decreases for both the modes.
In Figure 8, results have been displayed for the fol-
lowing values:
a/b = 1.0; c/b = 0.25, 0.5, 0.75, 1.0;
β = 0.0, 0.2;
α = 0.0, 0.2
α1 = 0.0, 0.2
It can be concluded that with the increase in the value
of c/b, frequency decreases for both the modes and for all
combinations of α, α1 and β.
In Figure 9, results have been displayed for the fol-
lowing values:
a/b = 0.75; c/b = 0.25, 0.5, 0.75, 1.0;
β = 0.0, 0.2;
α = 0.0, 0.2
α1 = 0.0, 0.2
It can be concluded that with the increase in the value
of c/b, frequency decreases for both the modes and for all
combinations of α, α1 and β.
4. Conclusions
The paper presented a comprehensive review for the ana-
lysis of the linear vibration characteristics of orthotropic
trapezoidal plates. The review covered numerical proce-
dures by using Ritz method. The influence of various
parameters as non homogeneity, taper constant, thermal
gradient etc, affecting the frequency was also discussed.
Accurate data has obtained by varying the length ratios
a/b and c/b. The results for orthotropic trapezoidal plates
of parabolically varying thickness are verified by the
literature [3,16]. It has been shown that the method pro-
vides accurate results.
The frequencies presented in this paper are considera-
ble accurate in order that these should be useful in sub-
sequent research carried out for these plates.
5. References
[1] A. W. Leissa, “Recent Studies in Plate Vibration 1981-
1985 Part II, Complicating Effects,” The Shock and Vi-
bration Digest, Vol. 19, No. 3, 1987, pp. 10-24. doi:
10.1177/058310248701900304
[2] A. W. Leissa, “Recent Studies in Plate Vibration: 1981-
1985. Part Classical Theory,” The Shock and Vibration
Digest, Vol. 19, No. 2, 1987, pp. 11-18. doi:10.1177/
058310248701900204
[3] A. W. Leissa, Vibration of Plates, NASA SP-160, 1969.
[4] I. Chopra and S. Durvasula, “Vibration of Simple-Sup-
ported Trapezoidal Plates. I: Symmetric Trapezoids,”
Journal of Sound and Vibration, Vol. 19, No. 4, 1971, pp.
379-392. doi:10.1016/0022-460X(71)90609-2
[5] P. S. Nair and S. Durvasula, “Vibration of Skew Plate,”
Journal of Sound Vibration, Vol. 26, No. 1, 1973, pp.
1-20. doi:10.1016/S0022-460X(73)80201-9
[6] J. S. Tomar and A. K. Gupta, “Thermal Effect on Axi-
symmetric Vibration of an Orthotropic Circular Plate of
Variable Thickness,” American Institute of Aeronautics
and Astronautics, Vol. 22, No. 7, 1984, pp. 1015-1017.
[7] J. S. Tomar and A. K. Gupta, “Thermal Effect of Fre-
quencies of an Orthotropic Rectangular Plate of Linearly
Varying Thickness,” Journal of Sound and Vibration, Vol.
90, No. 3, 1983, pp. 325-331. doi:10.1016/0022-460X(83)
90715-0
[8] R. M Orris and M. Petyt, “A Finite Element Study of the
Vibration of Trapezoidal Plates,” Journal of Sound and
Vibration, Vol. 27, No. 3, 1973, 325-344. doi:10.1016/
S0022-460X(73)80349-9
[9] Y. Narita, K. Maruyama and M. Sonada “Transverse
Vibration of Clamped Trapezoidal Plates Having Rec-
tangular Orthotropy,” Journal of Sound and Vibration,
Vol. 85, No. 3, 1982, pp. 315-322. doi:10.1016/0022-
460X(82)90257-7

A. K. GUPTA ET AL. 10
[10] S. Mirza and M. Bijlani, “Vibration of Triangular Plates,”
American Institute of Aeronautics and Astronautics, Vol.
21, No. 10, 1983, pp. 1472-1475.
[11] N. S. Bhatnagar and A. K. Gupta, “Thermal Effect on
Vibration of Visco Elastic Elliptic Plate of Variable Thi-
ckness,” Proceedings of International Conference on
Modelling and Simulation, Melbourn, 1987, pp. 424-429.
[12] H. T. Sahba, “Transverse Free Vibration of Fully Cla-
mped Symmetrical Trapezoidal Plates,” Journal of Sound
and Vibration, Vol. 126, No. 2, 1988, pp. 237-247. doi:
10.1016/0022-460X(88)90238-6
[13] P. Laura, R. Gutierrez and R. Bhat, “Transverse Vibra-
tions of a Trapezoidal Cantilever Plate of Various Thick-
ness,” AIAA, Vol. 27, No. 7, 1989, pp. 921-922. doi:
10.2514/3.10201
[14] K. M. Liew and K. Y. Lam, “A Rayleigh-Ritz Approach
to Transverse Vibration of Isotropic and Anisotropic
Trapezoidal Plates Using Orthogonal Plate Functions,”
International Journal of Solids and Structures, Vol. 27,
No. 2, 1991, pp. 189-203. doi:10.1016/0020-7683(91)
90228-8
[15] K. M. Liew, “Variable of Symmetric Laminated Canti-
lever Trapezoidal Composite Plates,” Journal of Me-
chanical Sciences, Vol. 34, No. 4, 1992, pp. 299-308. doi:
10.1016/0020-7403(92)90037-H
[16] K. M. Liew and M. K. Lim, “Transverse Vibration of
Trapezoidal Plates of Variable Thickness: Symmetric
Trapezoids,” Journal of Sound and Vibration, Vol. 165,
No. 1, 1993, pp. 45-67. doi:10.1006/jsvi.1993.1242
[17] M. S. Qatu, N. A. Jaber and A. W. Leissa, “Natural Fre-
quencies for Completely Free Trapezoidal Plates,” Jour-
nal of Sound and Vibration, Vol. 167, No. 1, 1993, pp.
183-191. doi:10.1006/jsvi.1993.1328
[18] C. W. Lim and K. M. Liew, “Vibration of Pretwisted
Cantilever Trapezoidal Symmetric Laminates,” Acta Me-
chanica, Vol. 111, No. 3-4, 1995, pp. 193-208. doi: 10.
1007/BF01376930
[19] T. Sakiyama and M. Hung, “Free Vibration Analysis of
Right Triangular Plates with Variable Thickness,” Jour-
nal of Sound and Vibration, Vol. 234, No. 5, 2000, pp.
841-858. doi:10.1006/jsvi.2000.2903
[20] R. Lal, “Transverse Vibration of Orthotropic Non Uni-
form Rectangular Plate with Continuously Varying Den-
sity,” Indian Journal of Pure and Applied Mathematics,
Vol. 34, No. 4, 2003, pp. 587-606.
[21] A. W. Leissa, “The Historical Bases of the Rayleigh and
Ritz Methods,” Journal of Sound and Vibration, Vol. 287,
No. 4-5, 2005, pp. 961-978. doi:10.1016/j.jsv.2004.12.021
[22] C.-H. Huang, C.-H. Hsu and Y.-K. Lin, “Experimental
and Numerical Investigations for the Free Vibration of
Cantilever Trapezoidal Plates,” Journal of the Chinese
Institute of Engineers, Vol. 29, No. 5, 2006, pp. 863-872.
[23] A. K. Gupta, Johri Tripti and R. P. Vats, “Thermal Effect
on Vibration of Non Homogeneous Orthotropic Rectan-
gular Plate Having Bi-directional Parabolically Varying
Thickness,” Proceedings of International Conference on
Engineering and Computer Science, San Francisco, 2007,
pp. 784-787.
[24] A. K. Gupta, Johri Tripti and R. P. Vats, “Thermal Gra-
dient Effect on Vibration of a Non-Homogeneous Ortho-
tropic Rectangular Plate Having Bi-direction Linearly
Thickness Variation,” Meccanica, Vol. 45, No. 3, 2010,
pp. 393-400. doi:10.1007/s11012-009-9258-3
[25] G. Karami, S. A. Shahpari and P. Malekzadeh, “DQM
Analysis of Skewed and Trapezoidal Laminated Plates,”
Computer Structures, Vol. 59, No. 3, 2003, pp. 393-402.
doi: 10.1016/S0263-8223(02)00188-5
[26] A. K. Gupta and S. Sharma, “Thermally Induced Vibra-
tion of Orthotropic Trapezoidal Plate of Linearly Varying
Thickness,” Journal of Vibration and Control (Accepted
for publication).