 Journal of Signal and Information Processing, 2013, 4, 25-29 doi:10.4236/jsip.2013.43B005 Published Online August 2013 (http://www.scirp.org/journal/jsip) 25 Semi-Rigid Registration of 3D Points Baowei Lin, Kouhei Sakai, Toru Tamaki, Bisser Raytchev, Kazufumi Kaneda, Koji Ichii Graduate School of Engineering, Hiroshima University, Higashi-Hiroshima, Japan. Email: lin@eml.hiroshima-u.ac.jp Received April, 2013. ABSTRACT In this paper, we proposed a method for semi-rigid changed 3D point clouds registration. We first segment the point clouds into individual segments and then the alignment energy costs of each segment are calculated. The rough initial transformation is estimated by minimizing the energy cost using integer programming. The final registration results are obtained by rigid alignments of separated corresponded segments. Experimental result with simulated point clouds demonstrate that the concept of semi-rigid registration works well. Keywords: Semi-Rigid Registration; Segmentation; Integer Programming; Rigid Alignment; Energy Minimization 1. Introduction In this paper, we propose a method for semi-rigid regis- tration. Rigid and non-rigid 3D registration methods have been widely studied for many useful applications such as 3D shape reconstruction and visualization [1,4,5,7], medical image analysis [9], robot navigation [19,21] and augmented reality [25]. Registration of 3D data is the process to align two sets of 3D points, which are called point clouds. This process is useful in many situations, for example, for stitching them tog ether to obtain a larg er point cloud which covers wider area, or for merging them to fill holes or cracks and obtain complete 3D mod- els of objects or scenes. Rigid registration is the process to align two 3D point clouds of a rigid object or a static scene: the target is as- sumed to be static and there is no change. Hence rigid registration methods find exactly the same overlapping part by estimating a rigid transformation between them. This is reasonable in cases that targets are stones, houses or furniture [15]. In contrast, non-rigid registration methods deal with non-rigid objects: the target shape is changed and hence the transformation is no longer rigid. Typical target objects of non-rigid registration include human organs [26], skin [2,27], and clothes [3]. However, there is another situation, we call it semi- rigid, which more frequently happens in real situations: the target scene has several rigid objects that have moved or changed position and orientation. Consider an office, for example, where desks and chairs exist. These are rigid objects but might be moved after the 3D scene has been captured as a point cloud. In this case, rigid meth- ods would not work well because the scene has been changed, and also, non-rigid methods could not capture the differences as expected because the scene is made of rigid objects. It is very important to deal with these kinds of scene changes for navigating robots in the environ- ments [6] or for surveillance of outdoor scenes for pre- venting collapse in case of disaster [8]. In this paper, we propose a semi-rigid registration method to align two 3D point clouds of the same scene, which contains rigid objects, and some of them are not in the same position or orientation. Our approach first di- vides a point cloud into many rigid segments. Then cor- respondences between segments of two point clouds are calculated based on energy minimization by using integer programming. These correspondences provide an initial rigid transformation between two point clouds as a whole. Then transformations between each corresponding seg- ments are estimated separately. The rest of the paper is organized as follows. Related work on registration is reviewed in section 2. In section 3, we will introduce the proposed method. Experimental results are given in section 4. 2. Related Work Rigid registration generally computes correspondences and then finds the transformation pose. Besl et al. [12] proposed a method called Iterative Closest Point (ICP) which is the most widely used method to align two 3D point clouds. ICP iterates two steps: in each iteration, closest points are selected, and a rigid transformation between them is estimated. This estimation is usually called the orthogonal Procrustes problem [13]. An alternative for registration is to use non-rigid Copyright © 2013 SciRes. JSIP  Semi-Rigid Registration of 3D Points 26 Figure 1. Segmentation result for small blocks. (Top) Some images used for 3D reconstruction. (Bottom) Segments of the point cloud visualized in different colors. Note that the ground plane is excluded. methods. Sclaroff et al. [14] proposed a method to com- pute the correspondences in 2D images or 3D point clouds by using modal analysis. However, it requires complete shapes and a discretization suitable for finite element analysis. Also, some researches [10,11,15,16,17] focused on deformation model to determine deformation assumptions of a 3D shape. Obviously, deformation is suitable when our research target is semi-rigidly changed scenes. 3. Proposed Semi-Rigid Registration Method In this section, we describe the details of the proposed method. Since our main focus is to establish correspon- dences between 3D segments, we first introduce the segmentation and pose estimation steps briefly. 3.1. Segmentation The first step is to segment a point cloud into many rigid segments. To this end, we use the distances between the neighboring 3D poin ts as well as the angle of the normal vectors of those points in order to cluster the points into different clusters (or rigid segments). Also we detect and segment the ground plane [18] in order to decide whether the segment is an object which is potentially able to be removed. Figure 1 shows a typical result of our simple dataset of some small blocks. In this case, the blocks are well separated and each segment can be seen as a rigid object in the scene. 3.2. Segments Correspondence The next step is to establish correspondences between the 3D segments of the two point clouds. Our method is based on minimizing energies which represent the similarity between 3D segments. In addition to energies between two 3D segments, we define energies between two pairs of 3D segments too: if correspondences are correct, a pair of 3D segments in one point cloud is similar to another pair in the other point cloud. In the following sections, we explain the proposed energy method in the same manner as introduced by [23]. 3.3. Formulation Suppose that we have two point clouds andQ. The point cloudis segmented into segments as PP{P} where 1, 2,, and cloud {QQ} where 1, 2,,.N R We express each correspondence be- tween the segments as[1,2,, M][1,2,, N] . We use a binary valued vector {0 ,1} N x to repre- sent correspondences of all of the segments. Each corre- spondence is denoted by, an index of an entry a aR in the vector . We say a correspondenceais ac- tive if x 1 a x . In order to make sure that each segment only has one (or no) corresp on de nce, we use the following constraints: (i,j),i1,2,,M 1 a a x and (i,j),1,2, , 1 a aj N x (1) Then we define an energy function Ex to repre- sent the relations between the individual segments which will be introduced in the next section. In our energy function, we define the energy terms. 3.4. Energies The first term 1 is the similarity in terms of 3D key- point correspondences; in other words, how many of the 3D keypoints in E P have corresponding points in Q . A 3D keypoint is a representative poin t in a 3D segment, and it has a descriptor which can be used to find its cor- responding point [8]. If P and Q are similar to each other, many 3D keypoints in P have corre- sponding points in Q . Let C be the number of correspondences between P and Q . Then the total number of correspondences of 3D keypoints in P is 1 NC . The value 1 C N becomes larger when P and Q actually correspond to each other. Therefore, we use the reciprocal of the ratio as energy: 1 E Copyright © 2013 SciRes. JSIP  Semi-Rigid Registration of 3D Points 27 1 1 11a aR ECC xx. (2) The second term2uses similarity between the de- scriptors of the corresponding 3D keypoints. While the first term finds how many keypoints are corresponding between E P andQ , this term evaluates whether the de- scriptors of those corresponding points are really similar to each other. We use the sum of distances between the corresponding descriptors as follows: 21 ,a aR EDPQ xx , (3) where 1is the distances between the descriptors of 3D keypoints of DP andQ . The third term3uses the rigid registration error be- tween each pair of 3D segments. If the correspondences are correct, a pair of 3D segments must have its corre- sponding pair. In other words, two 3D segments 1 E P and 2 P in correspond to the segments 1 PQ and 2 Q in We evaluate this pair of correspondences by using the residual error after rigid registration. Al- though we have assumed that the scene is semi-rigid, nevertheless, it is reasonable to assume that a pair of segments is rigid. We defineas follows: .Q 3 E 32121 (1,1) , (2,2) ,;, ab aR bR 2 DPPQQ xx x (4) where is the rigid registration error from ICP. 2 The last term4 Eimposes a penalty when there are no correspondences. If only the three energy terms above are used, a trivial solution will be obtained: all elements in are zero and the energy becomes 0. This is obviously not the case we want to estimate. Therefore, to avoid this case, we add the following term: D x 41a aR x x, (5) where is a penalty constant. If manya are zero, i.e. many segments do not find their corresponding segment, this term becomes larger and hence such a solution will be less important. By combining Equations (2)-(5), we get the finial en- ergy functio n. 1234 +++EEEEExxxxx . 6) This energy can be written as follow: , , min( )aa abab aR abR ExE xx x, (7) subject to the constraints in Eq. (1) where variables a are binaries. This optimization problem is called a 0 - 1 integer programming [24]. We used a dual decomposi- tion approach [23] to solve this integer programming problem. Once the solutionis obtained, we can find an initial rigid transformation between two point cloudsandQ. Of course we have assumed that the scene is semi-rigid, so this rigid transformation is not the final solution. xP 3.5. Rigid Registration for Each Segment The final step performs rigid registration between corresponding 3D segments. After the initial rigid registration between the two point clouds, the corresponding 3D segments are now close to each other like in the example shown in Figure 3. In this step, each 3D segmentP in the first point cloudis registered to its counterpartQP in the other point cloudHere, the correspondence .Q (,)a is active (a) in the solution obtained by solving the 0-1 integer programming explained above. 1x 4. Experimental Results We demonstrate by simulation that the concept of the proposed method effectively works on 3D point clouds. The dataset was generated from artificial small blocks. After the generation of one point cloud, one block was moved, and then another point cloud was reconstructed. Two point clouds with 15,804 and 25,178 points are shown in Figure 2 which are computed by 3D recon- struction with the Bundler [20] followed by Patch-based Multi-view Stereo [22]. The rough initial transformation calculated based on the correspondences in section 3.2 is shown in Figure 3. The semi-rigid registration result shown in Figure 4 shows that the proposed method can estimate accurate transformation for each block. In con- trast, the result when using ICP directly sho wn in Figure 5 was not successful. The energies between the two point clouds are show n in Figure 6. The energy of our method is much smaller than that of ICP, which clearly shows that the proposed semi-rigid registration outperforms the rigid ICP. Figure 2. Experiment point clouds. Red block is moved between two point clouds. Copyright © 2013 SciRes. JSIP 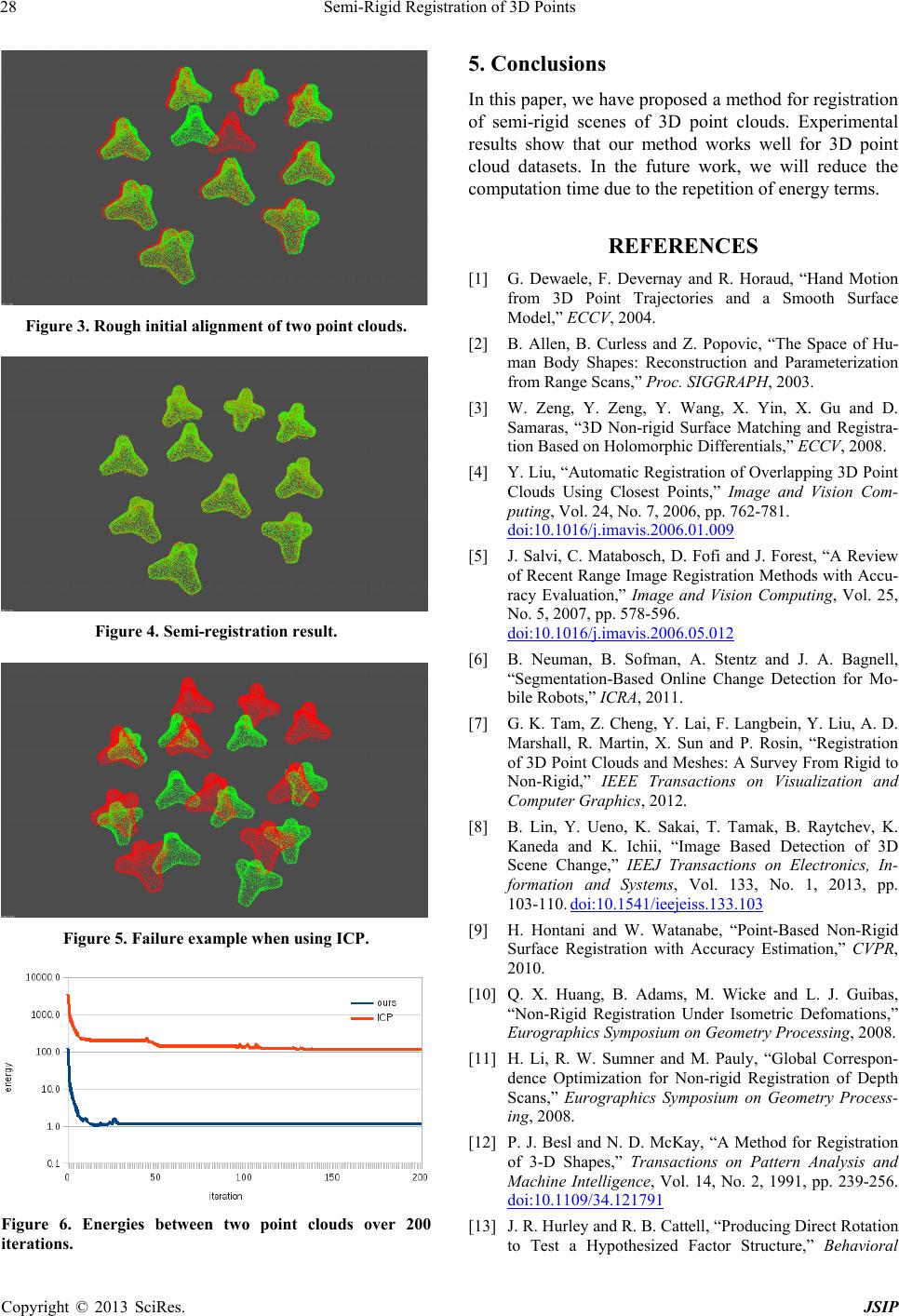 Semi-Rigid Registration of 3D Points 28 Figure 3. Rough initial alignment of two point clouds. Figure 4. Semi-registration result. Figure 5. Failure example when using ICP. Figure 6. Energies between two point clouds over 200 iterations. 5. Conclusions In this paper, we have proposed a method for registration of semi-rigid scenes of 3D point clouds. Experimental results show that our method works well for 3D point cloud datasets. In the future work, we will reduce the computation time due to the repetition of energy terms. REFERENCES [1] G. Dewaele, F. Devernay and R. Horaud, “Hand Motion from 3D Point Trajectories and a Smooth Surface Model,” ECCV, 2004. [2] B. Allen, B. Curless and Z. Popovic, “The Space of Hu- man Body Shapes: Reconstruction and Parameterization from Range Scans,” Proc. SIGGRAPH, 2003. [3] W. Zeng, Y. Zeng, Y. Wang, X. Yin, X. Gu and D. Samaras, “3D Non-rigid Surface Matching and Registra- tion Based on Holomorphic Differentials,” ECCV, 2008. [4] Y. Liu, “Automatic Registration of Overlapping 3D Point Clouds Using Closest Points,” Image and Vision Com- puting, Vol. 24, No. 7, 2006, pp. 762-781. doi:10.1016/j.imavis.2006.01.009 [5] J. Salvi, C. Matabosch, D. Fofi and J. Forest, “A Review of Recent Range Image Registration Methods with Accu- racy Evaluation,” Image and Vision Computing, Vol. 25, No. 5, 2007, pp. 578-596. doi:10.1016/j.imavis.2006.05.012 [6] B. Neuman, B. Sofman, A. Stentz and J. A. Bagnell, “Segmentation-Based Online Change Detection for Mo- bile Robots,” ICRA, 2011. [7] G. K. Tam, Z. Cheng, Y. Lai, F. Langbein, Y. Liu, A. D. Marshall, R. Martin, X. Sun and P. Rosin, “Registration of 3D Point Clouds and Meshes: A Survey From Rigid to Non-Rigid,” IEEE Transactions on Visualization and Computer Graphics, 2012. [8] B. Lin, Y. Ueno, K. Sakai, T. Tamak, B. Raytchev, K. Kaneda and K. Ichii, “Image Based Detection of 3D Scene Change,” IEEJ Transactions on Electronics, In- formation and Systems, Vol. 133, No. 1, 2013, pp. 103-110. doi:10.1541/ieejeiss.133.103 [9] H. Hontani and W. Watanabe, “Point-Based Non-Rigid Surface Registration with Accuracy Estimation,” CVPR, 2010. [10] Q. X. Huang, B. Adams, M. Wicke and L. J. Guibas, “Non-Rigid Registration Under Isometric Defomations,” Eurographics Symposium on Geometry Processing, 2008. [11] H. Li, R. W. Sumner and M. Pauly, “Global Correspon- dence Optimization for Non-rigid Registration of Depth Scans,” Eurographics Symposium on Geometry Process- ing, 2008. [12] P. J. Besl and N. D. McKay, “A Method for Registration of 3-D Shapes,” Transactions on Pattern Analysis and Machine Intelligence, Vol. 14, No. 2, 1991, pp. 239-256. doi:10.1109/34.121791 [13] J. R. Hurley and R. B. Cattell, “Producing Direct Rotation to Test a Hypothesized Factor Structure,” Behavioral Copyright © 2013 SciRes. JSIP  Semi-Rigid Registration of 3D Points Copyright © 2013 SciRes. JSIP 29 Science, 1962. [14] S. Sclaroff and A. Pentland, “Modal Matching for Corre- spondence and Recognition,” Compyter society, Vol. 17, No. 6, 1995, pp. 545-561. doi:10.1109/34.387502 [15] M. Pauly, N. J. Giesen, M. H. Gross and L. J. Guibas, “Example-based 3D Scan Completion,” Eurographics Symposium on Geometry Processing, 2005. [16] B. Allen, B. Curless and Z. Popovic, “The Space of Hu- man Body Shapes: Reconstruction and Parameterization from Range Scans,” Proc. SIGGRAPH, 2003. [17] I. Eckstein, J. P. Pons, Y. Tong, C. C. J. Kuo and M. Desbrum, “Generalized Surface Flows for Mesh Process- ing,” Eurographics Symposium on Geometry Processing, 2007. [18] D. Holz, S. Holzer, R. B. Rusu and S. Behnke, “Real-Time segmentation using RGB-D Cameras,” Proc. of RoboCup International Symposium, 2011. [19] T. Stoyanov, M. Magnusson and A. J. Lilienthal, “Point Set Registration through Minimization of the L2 Distance between 3D-NDT Models,” ICRA, 2012. [20] N. Snavely, S. M. Seitz and R. Szeliski, “Modeling the World from Internet Photo Collections,” International Journal of Computer Vision, Vol. 80, No. 2, 2008, pp. 189-210. doi:10.1007/s11263-007-0107-3 [21] J. Ryle and N. Hillier, “Alignment and 3D Scene Change Detection for Segmentation in Autonomous Earth Mov- ing,” ICRA, 2011. [22] Y. Furukawa and J. Ponce, “Accurate, Dense and Robust Multi-View Stereopsis,” Transactions Pattern Analysis Machine Intelligence, Vol. 32, No. 8, 2010, pp. 1362- 1376. doi:10.1109/TPAMI.2009.161 [23] L. Torresani, V. Kolmogorov and C. Rother, “A Dual Decomposition Approach to Feature Correspondence,” Transactions Pattern Analysis Machine Intelligence, Vol. 35, No. 2, 2013, pp. 259-271. doi:10.1109/TPAMI.2012.105 [24] S. P. Bradley, A. C. Hax and T. L. Magnanti, “Applied Mathematical Programming,” Addison-Wesley, 1977. [25] G. Klein and D. Murray, “Parallel Tracking and Mapping for Small AR Workspaces,” ISMAR, 2007. [26] Y. Sawada and H. Hontani, “A Study on Graphical Model Structure for Representing Statistical Shape Model of Point Distribution Model,” MICCAI, 2012. [27] B. Amberg, S. Romdhani and T. Vetter, “Optimal Step Nonrigid ICP Algorithms for Surface Registration,” CVPR, 2007.
|