iBusiness, 2013, 5, 7-10
doi:10.4236/ib.2013.52B002 Published Online June 2013 (http://www.scirp.org/journal/ib)
7
Performance Measurement of the Fourth Part y Logi stics
Provider s
Yu-Wei Chang
Department of Air Transportation Management, Aletheia University, Tainan 721.
Received April, 2013
ABSTRACT
This paper presents a multicriterica decision making method (MCDM) to evaluate the performance of the fourth-party
logistics providers. The four indexes of balanced scorecard (BSC) are used as the evaluation indexes. AHP (ana-lytical
hierarchy process) is used fo r rating the we ights of criteria and alternatives. MCDM method of SAW (Simple Additive
Weighting) is used for ranking the companies. Results show that the approach is applicable for the performance me a-
surement problem.
Keywords: MCDM; AHP; S AW
1. Introduction
To cost down and increase core competence, many com-
panies deal with their logistics activities by the third-
party logistics provider (3 PL). With the developme nt o f
electronic commercial, a new logistics provider which is
called the fourth party logistics (4 PL) is more and more
popular in Taiwan. The concept of the 4PL is that it
integrates the resources, capabilities, and technology of
its own organization and other organizations to design,
build, and run comprehensive supply chain solutions.
The main difference between the 3 PL and 4 PL lies in
that firms o wn t heir o wn a sset s in t he 3 P L, a nd th ey per-
form more than one or more logistic s service s. However,
firms do not own any type of assets in the 4 PL. The 4 PL
only arrange the logistics services and serve as an inter-
mediar y between the firm and the service provider. With
the help of the 4 PL, the companies can manage the 3
PLs, truckers, forwarders, custom house agents, and
others, essentially taking responsibility of a complete
process for the customer .
Many traditional methods nowadays are used for the
performance evaluation (i.e. data envelopment analysis,
DEA; regression method and ration analysis). The dra w-
back of the traditional methods focuses on the financial
performance and ignores the non-financial performance.
To solve the disadvantages of the above approaches,
Kaplan and Norton (1992) proposed the Balanced Scored
Card (BSC) concept to evaluate the performance of a
company by four perspectives [1]. The four perspectives
include financial, customer, internal business pr oc ess and
learning and growth. With the help of BSC evaluation,
both financial and non-financial performance can be
overall measured.
Analytic Hierarchy Process (AHP) is a multi-attribute
decision making method proposed by Satty in 1971 [2].
It is a widely used method, providing a rational frame-
work for solving a complex decision problem. The ma in
ideal of the AHP is that it derives ratio scales by pairwis e
comparisons of attrubutes. It is a popular method utilized
in a multicriteria de c ision making (MCDM) problem.
Many methods have been developed for solving the
MCDM problems (i.e. Weighting Product, WP; Simple
Additive Weighting, SAW; Technique for Order Pre-
ference by Similarity to Ideal Solution, TOPSIS) . Each
method has its own aim and advantages. For example,
the concept of SAW is to obtain a weighted sum of the
performance ratings of each alternative over all attributes.
The concept of W eighte d P rod uct method is to obtain the
performance ratings by multiplying contributions from
attributes. The concept of TOPSIS is to obtain the per-
formance rating by the concept that the alternative to be
chose n sho ul d have t he ne ar e s t d ist anc e fr o m the p o siti ve
ideal solution and the farthest distance from the negative
ideal solution.
This paper presents a hybrid model that combines both
AHP and BSC for performance measurement of the
fourth-party logistics providers. In the model, the four
indexes of BSC will be used as evaluation criteria. AHP
is used for the weights of criteria, sub-criteria and alter-
natives. Rank of the fourth-party logistics providers is
determined by the help of SAW. The advantage of the

Performance Measurement of the Fourth Party Logistics Providers
8
method is that both final and non-final perspectives are
considered for the performance measurement problem of
the fourth-party logistics provider at the same time.
2. Methodology
2.1. AHP
Analytic Hierarchy process (AHP) is originall y proposed
by Saaty in 1971 to deal with complex problems by de-
composing a complex problem into a structured decision
hierarchy. The first step of AHP is to establish hierar-
chial structure and decompose into different levels (i.e.
the goal) and each level is further decomposed into sub-
levels (i.e. criteria) until the lowest levels of the hierar-
chy.
After the hierarchial structure of the problem is fin-
ished, the next step is to use pairwise comparison to de-
te rmin e the priority. T he decision maker uses a nine
point scale to assess the priority score. The procedure
focuses on two factors at a time and their relation to each
other with the scores 1, 3, 5, 7, a nd 9. The score 1 refers
to equal importance, 3 refers to slight more importance, 5
refers to strong more importance, 7 refers to very strong
importance and 9 denotes extremely more importance.
The scores of 2, 4, 6, and 8 are intermediate scores be-
tween the two judgments. If there are n attributes and m
alternatives, the matrix judgment will lead to an n × m
matrix and there are n * m (m − 1)/2 pairwise compari-
sons to be performed. The pairwise comparison maxtrix
has t he following form:
11 1
12
22 2
12
12
...
...
...
n
n
nn n
n
ww w
ww w
ww w
ww w A
ww w
ww w





=





(1)
where
1
2
w
w
is the relative importance of the 1-th crite-
rion over the 2-th attribute. After the pairwise compari-
son matrix is obtained, the we ights need to be calculated.
Satty (1977) ustilizes the maximal eigenvalue method to
find the va lue vecto r of w. The exact values of w1, w2, …,
wn are computed and fi nally normalized as follows:
w1 + w2 + … + wn =1 (2)
The consistency property of the matrix needs to be
checked to ensure the consistency of judgments in the
pairwise comparison. Both the consistency index (C.I.)
and consistency ratio (C.R.) are defined as follows:
max
1
C.I ()
1n n
λ = −
− (3)
max
λ
: The maximal e igenvalue
n: The number of items being compared in the matrix
The closer the C.I. val ue is to 0, the greater the consis-
tency and acceptable. The C.I. value less than 0.1 is ge n-
erally acceptable. After checking the consistency index,
the consiste ncy ratio is t hen examined.
C.R. =
..
..
CI
RI
(4)
R.I. = The average consistency index.
when C.R. ≤ 0.1, the weights obtained by the eigen- val-
ue method are acceptable.
2.2. The Simp le Ad d i tiv e We ightin g (SAW)
The SAW method is one of the mo st widely used
MADM method [3]. The basic concept of the SAW is to
obtain a weighted sum of the performance ratings of each
alternative over all attributes. One need to scale the
scores, apply weights and sum up the values for each
alternative. The SAW method requires normalizing the
decision matrix (y) to allow a comparable scale for all
ratings in X by
, if is a benefit attribute
max
min , if is a cost attribute
1, 2,,;1, 2,,
ij
ij
i
ij ij
i
ij
yj
y
ryj
y
i mj n







=…=…
= (5)
where rij (0 ≤ rij ≤ 1) is defined as the normalized per-
formance rating of alternative Ai on attribute Cj. This
normalization process transforms all the ratings in a pro-
portional way, so that the relative order of magnitude of
the ratings remains equal. The overall preference value of
each alternative (Vi) is obtained by
1
1,2,,
ij ij
n
j
Vwr im
=
== …
∑
(6)
The greater the value (Vi), the more preferred the al-
ternative (Ai). Rese ar ch r e s ul ts ha ve s hown t hat t he l i near
form of trade-offs between attributes used by the SAW
method produces extremely close approximations to com-
plicated nonlinear forms, while maintaining far easier to
use and understand (Hwang and Yoon 1981).
3. Empirical Results
To illustrate how the proposed method can be used to
evaluate the performance measurement of the fourth-
party logistics, an empirical case will be used to explain
it. In the case, five decision makers (D1, D2, …, D5) are
formulated as a team to evaluate the performance of 6
logistics providers. The DMs decide to evaluate the per-
fo rman ce of logistics providers based on BSC. The best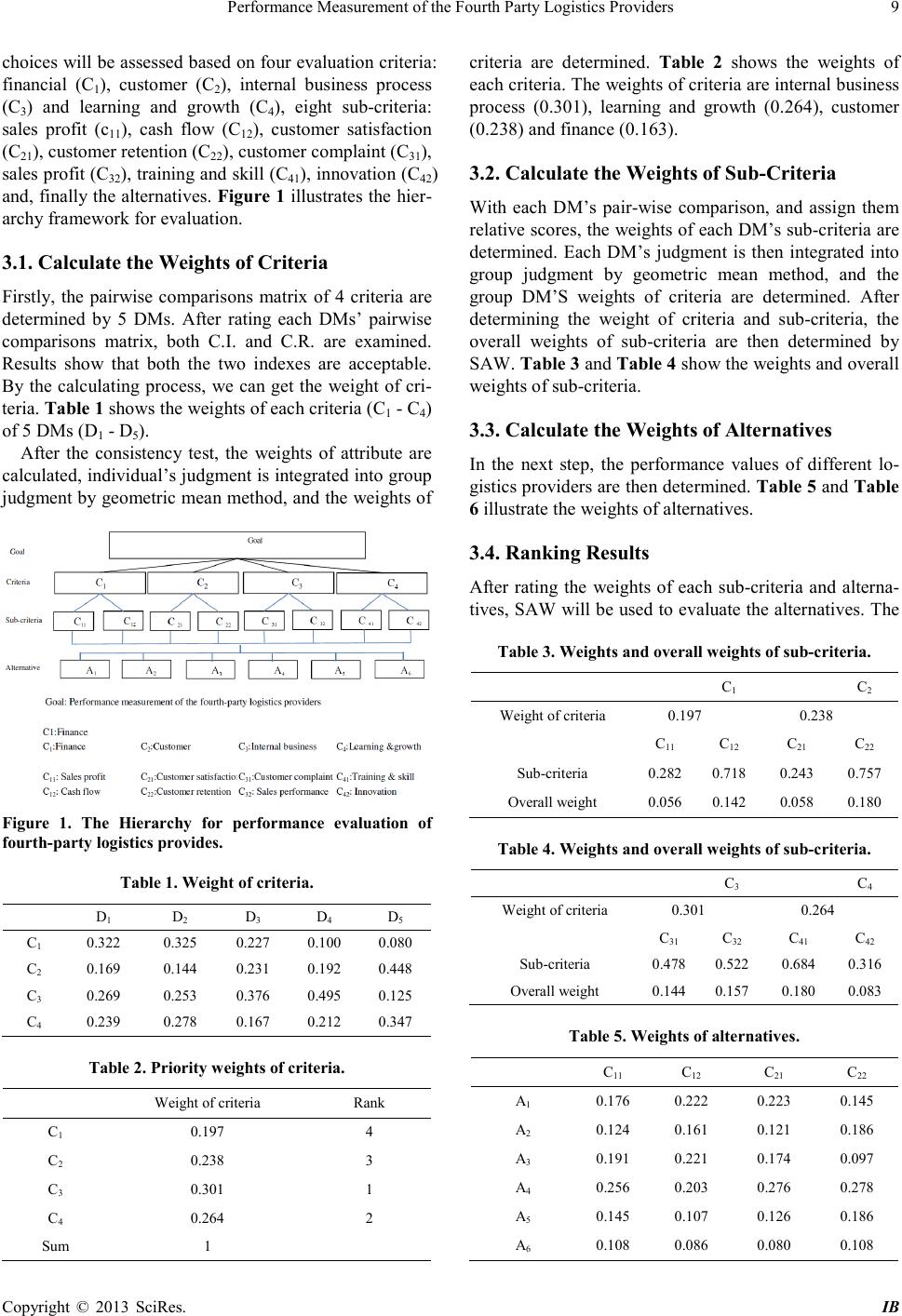

Performance Measurement of the Fourth Party Logistics Providers
9
choices will be assessed based on four evaluation criteria:
financial (C1), customer (C2), internal business process
(C3) and learning and growth (C4), eight sub-criteria:
sales profit (c11), cash flow (C12), customer satisfaction
(C21), customer rete ntion (C22), customer complaint (C31),
sales profit (C32), training and skill (C41), in novatio n (C42)
and, finally the alternatives. Figure 1 illustrates the hier-
archy framework for evaluation.
3.1. Calculate the Weights of Criteria
Firstly, the pairwise comparisons matrix of 4 criteria are
determined by 5 DMs. After r ating each DMs’ pairwise
comparisons matrix, both C.I. and C.R. are examined.
Results show that both the two indexes are acceptable.
By the calculating process, we can get the weight of cri-
teria. Table 1 shows the weights of each criteria (C1 - C4)
of 5 DMs (D 1 - D5).
After the consistency test, the weights of attribute are
calculated, individual’s judgment is integrated into group
judgment by geometric mean method, and the weights o f
Figure 1. The Hierarchy for performance evaluation of
fourth-party logisti cs provides.
Table 1. Weight of criteria.
D1 D2 D3 D4 D5
C1 0.322 0.325 0.227 0.100 0.080
C2 0.169 0.144 0.231 0.192 0.448
C3 0.269 0.253 0.376 0.495 0.125
C4 0.239 0.278 0.167 0.212 0.347
Table 2. Priority wei ghts of criteri a.
Weight of criteria Rank
C1 0.197 4
C2 0.238 3
C3 0.301 1
C4 0.264 2
Sum 1
criteria are determined. Table 2 shows the weights of
each criteria. The weight s of criteria are inter nal b usi ness
process (0.301), learning and growth (0.264), customer
(0.238) and finance (0.163).
3.2. Calculate the Weights of Sub-Criteria
With each DM’s pair-wise comparison, and assign them
relative scores, the weights of each DM’s sub-criteria are
determined. Each DM’s j udgment is then integrated into
group judgment by geometric mean method, and the
group DM’S weig h ts of criteria are determined. After
determining the weight of criteria and sub-criteria, the
overall weights of sub-criteria are then determined by
SAW. Table 3 and Table 4 s ho w the weights and overall
weights of sub-criteria.
3.3. Calculate the Weights of Alternatives
In the next step, the performance values of different lo-
gistics provid ers are then deter mined. Table 5 and Table
6 illustrate the wei ght s of alternatives.
3.4. Ranking Results
After rating the weights of each sub-criteria and alterna-
tives, SAW will be used to evaluate the alternatives. T he
Table 3. We ights and ov erall weights o f sub-criteria.
C1 C2
Weight of criteria 0.197 0.238
C11 C12 C21 C22
Sub-criteria 0.282 0.718 0.243 0.757
Overal l wei gh t 0.056 0.142 0.058 0.180
Table 4. Weights and o v erall weights of su b-criteria.
C3 C4
Weight of criteria 0.301 0.264
C31 C32 C41 C42
Sub-criteria 0.478 0.522 0.684 0.316
Overal l wei gh t 0.144 0.157 0.180 0.083
Table 5. Weights o f alternatives.
C11 C12 C21 C22
A1 0.176 0.222 0.223 0.145
A2 0.124 0.161 0.121 0.186
A3 0.191 0.221 0.174 0.097
A4 0.256 0.203 0.276 0.278
A5 0.145 0.107 0.126 0.186
A6 0.108 0.086 0.080 0.108

Performance Measurement of the Fourth Party Logistics Providers
10
Table 6. Weights of alternat ives.
C31 C32 C41 C42
A1 0.169 0.193 0.164 0.196
A2 0.121 0.208 0.141 0.224
A3 0.288 0.220 0.194 0.172
A4 0.259 0.206 0.264 0.184
A5 0.090 0.091 0.149 0.131
A6 0.074 0.081 0.088 0.093
final score for each alternative is as follows,
1
A0.056*0.176 0.142*0.222 0.058*0.223
0.180*0.145 0.144*0.169 0.157*0.193
0.180*0.1640.083 *0.196 0.181
=++
+++
++=
2
A0.056*0.1240.142*0.161 0.058*0.121
0.180*0.1860.144*0.121 0.157*0.208
0.180*0.1410.083 *0.224 0.073
= ++
+++
++=
3
A0.056*0.191 0.142*0.221 0.058*0.174
0.180*0.0970.144*0.288 0.157*0.220
0.180*0.1940.083 *0.172 0.069
=++
+++
++=
4
A0.056*0.256 0.142*0.203 0.058*0.276
0.180*0.278 0.144*0.259 0.157*0.206
0.180*0.264 0.083*0.1860.184
=++
+++
++=
5
A0.056*0.145 0.142*0.107 0.058*0.126
0.180*0.186 0.144*0.090 0.157*0.091
0.180*0.149 0.083*0.1310.131
=++
+++
++=
6
A0.056*0.1080.142*0.086 0.058*0.080
0.180*0.1080.144*0.074 0.157*0.081
0.180*0.088 0.083*0.0930.093
=++
+++
++=
Based on the results of S AW, we can conclude that the
ranki ng o rd er o f six c o mpanie s is A4, A1, A5, A6, A2, and
A3. In the case, the A4 is the best one.
4. Conclusions
This paper proposes an effective method that combines
both the AHP and SAW for the performance measure-
ment of the fourth party logistics provider. In the evalu-
ate context, t he AHP is utilized to rate the weight of cri-
teria, sub-criteria and alternatives. The SAW is used to
rank the performance order. We can observe that the
ranking of the six logistic providers is A4(0.184) >
A1(0.181) > A5(0.131) > A6(0 . 093) > A2(0.073) >
A3(0.069). Results show that the proposed model is
comprehensible for the problem. Future research can use
this model for evaluatio n of other ind ustries.
REFERENCES
[1] R. S . Kap lan and D. P. Norton, “The Balanced Scorecard:
Measures the Drive Performance, In Harvard Business
School,” Harvard Business Review on Measuring Corpo-
rate Performance, Boston, MA: Harvard Business School
Press, 19 92.
[2] T. L. Saat y, “The Anal ytic Hiera rchy Process, ” NY: New
York,” McGraw-Hill, 1980.
[3] K. P. Yoon and C. L. Hwang, “Multiple attribute decision
making: An introduction,” Sage publication, 1995.