Received 7 April 2016; accepted 24 May 2016; published 27 May 2016

ABSTRACT

Cognitive radio systems are helpful to access the unused spectrum using the popular technique, referred to as spectrum sensing. Spectrum sensing involves the detection of primary user (PU) signal using dynamic spectrum access. Cooperative spectrum sensing takes advantage of the spatial diversity in multiple cognitive radio user networks to improve the sensing accuracy. Though the cooperative spectrum sensing schemes significantly improve the sensing accuracy, it requires the noise variance and channel state information which may lead to transmission overhead. To overcome the drawbacks in conventional cooperative spectrum sensing, this paper proposes a fuzzy system based cooperative spectrum sensing. Selection combining (SC) and maximum ratio combining (MRC) are used at fuzzy based fusion center to obtain the value of the sensing energy. These energy values are utilized in finding the presence of PU, results in improved sensing accuracy. In addition, an intelligent fuzzy fusion algorithm determines the PU presence without the channel state information based on multiple threshold values. Simulation results show that the proposed scheme outperforms the existing schemes in terms of sensing accuracy.

Keywords:

Cognitive Radio (CR), Spectrum Sensing, Fuzzy System, Dynamic Spectrum Access, Energy Detection Scheme

1. Introduction

Cognitive Radio (CR) technology has been introduced to alleviate the spectrum scarcity in wireless communication. Using this technology, secondary users (SUs) or CR users are allowed to opportunistically access the licensed spectrum band of primary users (PUs). In a CR network, SUs must accurately sense the vacant spectrum (spectrum holes) for their transmissions and vacate the frequency band as soon as the Primary Users (PUs) start their transmissions [1] - [3] . The main challenge in such systems is to avoid the harmful interference from SUs imposed on the PUs in their locality through spectrum sensing. The basic idea behind the spectrum sensing is to detect the weak signal of a PU. To overcome some practical concerns of spectrum sensing such as multipath fading and hidden PUs, cooperative spectrum sensing has been proposed [4] . In centralized cooperative spectrum sensing, each SU sends its local sensing results to a fusion center. The fusion center combines the received local information and makes a final decision to detect the absence/presence of the PU. In recent years, cooperative spectrum sensing schemes have been extensively studied in cognitive radio networks [5] [6] .

Various schemes have been proposed in the literature for spectrum sensing. Based on the signal detection, two broad categories of sensing techniques are: coherent and non-coherent detection. In coherent detection, the PU presence is determined by comparing the received signal with a priori knowledge of PUs. However, non-cohe- rent detection techniques do not require any prior knowledge. Figure 1 provides the classification of sensing techniques. Three most popular sensing techniques in cooperative sensing are energy detection, cyclostationary feature detection, and compressed sensing [6] .

Cyclostationary feature detection techniques detect the PUs using the periodicity in the received primary signal [7] . The periodicity is embedded in sinusoidal carriers, spreading code, hopping sequences, or cyclic prefixes of the PUs which is not present in stationary noise and interference. Due to this periodicity feature, it is robust to noise uncertainties. Though it requires a priori knowledge about the characteristics of signals, CR transmissions from various types of PU signals can be distinguished in this scheme [8] . The drawbacks of this technique are high computational complexity and long sensing time. Energy detection is a non-coherent detection technique that identifies the PU presence using sensed energy [9] . Since the energy detection scheme does not require a priori knowledge of PU signals, it is the widely preferred sensing technique in cooperative spectrum sensing. However, energy detection has the following limitations. i) The sensing time is usually more to attain a good probability of detection. ii) The detection performance may be affected due to uncertain noise power. In spite of these shortcomings, energy detection is most popular, because noise uncertainty issues can be minimized by the diversity gain achieved due to cooperation. In compressed sensing, wideband sensing consumes large sensing delay and requires high computational complexity.

In most detection techniques, the noise power is supposed to be known for fixing a specific threshold value [10] . However the noise power variations cause ambiguity in the process of signal detection. In general, the sensing information about the spectrum availability from different SUs is combined at a fusion center (FC). The status of the PU signal is decided at this fusion centre. The existing literature on cooperative spectrum sensing is based on two important assumptions: i) SUs and FC are familiar about the signal-to-noise ratio (SNR) information of the PU signal ii) the detailed information about noise at the SUs. However, it is not easy for SUs to estimate these parameters due to their variation over time. Furthermore, though the SUs are in a position to estimate and obtain the information exactly, transmitting local observations to the FC is very much expensive. To overcome this expensive transmission, the soft combination scheme has been proposed in the literature [11] [12] . It assumes that the noise at the SUs has unit variance. Moreover, FC needs to obtain instantaneous SNR of the PU signal to make a global decision. This information is necessary to determine the weights and the decision

threshold but represents a significant transmission overhead. However, soft combining schemes simply perform like maximal ratio combining schemes in low SNR conditions. Some of the soft computing based algorithms require full idea about SNR and noise level of at all SUs [13] . Some programming based optimal fusion rules depend on clear knowledge of noise variance and instantaneous SNRs at energy detectors [14] .

Authors in [15] presented spectrum sensing techniques for different fading channels. Visotsky et al. [16] proposed AND logic operation for hard decision and likelihood ratio test for providing soft decisions respectively. They have proved that the fusion of soft decisions provide better results than the hard decisions. Throughput performance of secondary users in cognitive radio network is analyzed in [17] . A single-objective particle swarm optimization (PSO) has been proposed by Zheng et al. (2010) for cooperative spectrum sensing with higher probability of detection [18] .

The PSO and soft combining approaches require more information about the detected signals. To reduce the amount of transmission information overhead in energy detection schemes, a fuzzy logic can be utilized which can process noisy and incomplete input information [19] [20] . For example, a fuzzy inference system has been utilized to make soft spectrum sensing decision based on the observed energy at the SUs [21] . The final decision is made at the FC on the basis of the local soft decisions of the SUs. In the proposed scheme, each SU measures the energy of its received signal in the frequency band of interest and then transmits its observation to the FC without any additional information. The FC performs data fusion with an adaptive fuzzy system using online learning to determine the fuzzification parameters from the data received. The remainder of this paper is organized as follows: the fuzzy based system model is introduced in Section 2. Section 3 presents the proposed spectrum sensing scheme. Results are provided and discussed in Section 4. Finally, the conclusion of the proposed work is provided in Section 5.

2. Fuzzy Based System Model for Hypothesis Test

The effective cooperative spectrum sensing can be achieved by the CR system which utilizes the fuzzy logic concept. In this section, a fuzzy inference system is introduced that can be useful for spectrum sensing systems and system model is explained based on fuzzy hypothesis test.

i) Fuzzy inference system for Spectrum Sensing

In cognitive radio networks, fuzzy logic based spectrum sensing is preferred over conventional mathematical methods. The fuzzy rule based fusion process provides better results in comparison with conventional AND/OR fusion rule is presented in [22] [23] .

Fuzzy based decision making is performed the fuzzy inference system, shown in Figure 2. It comprises of fuzzification process, inference engine, knowledge/rule base and defuzzification process. The fuzzification process usually converts the given crisp input into fuzzy quantity. In the proposed model, spectrum sensing process is accomplished using fuzzy inference system which detects the spectrum hole from the received signal energy and PU activity. The fuzzifier provides the available information to inference engine so that the efficient spectrum sensing is carried out. The membership form of inputs is evaluated by fuzzy sets and rule base. The fuzzy rule base has if-then statements which provide various possible spectrum access options. These fuzzy rule set are given to a fuzzy inference system to decide about the spectrum hole.

ii) System model and Fuzzy Hypothesis Test

Performance evaluation of Spectrum sensing techniques is carried out in [24] . In hypothesis test, H0 repre- sents the absence of PU signal whereas H1 represents the presence of PU signal, which is given by

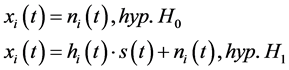(1)

In the hypothesis H₀, x_i(t) represents the signal received by ith SU and n_i(t) is additive white Gaussian noise. In the hypothesis H₁, s(t) is PU signal and h_i(t) is channel impulse response. Spectrum sensing scheme using energy detection is presented in [25] to detect PU in the network. Figure 3 shows the CR system that can be utilized for spectrum sensing with the help of basic energy detection schemes.

The traditional energy detection problem decides between two crisp hypotheses H₀ (null hypothesis) and H₁ (alternative hypothesis). In real time situations, it is not a wise choice to go with crisp hypotheses due to the problems and practical difficulties associated with uncertainty. Fuzzy set theory concepts have been discussed in the literature to consider the uncertainty issues. The hypothesis test utilizes these fuzzy set theory is called as fuzzy hypothesis test (FHT).

Suppose µ is mean parameter of a normal probability density function, the crisp hypothesis can be defined as

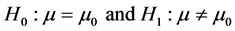(2)

However the fuzzy hypotheses are defined for realistic models as

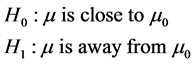(3)

The flowchart for conventional energy detection scheme is shown in Figure 4. The detection decision is made by comparing the energy spectrum of the received PU signal with the threshold energy to declare the presence and absence of PU signal.

3. Proposed Fuzzy Based Energy Detection Scheme

The main objective of this work is to propose an intelligent fuzzy logic based data fusion algorithm at the fusion centre (FC). The important contribution of the proposed work is to identify the PU signal without prior information. Some of the information are the noise variance, SNR of the PU signal at the SUs. In the proposed scheme, each SU measures the energy of its received signal in the frequency band of interest and then transmits its observation to the FC without any additional information. The FC performs data fusion with an adaptive fuzzy system using online learning to determine the fuzzification parameters from the data received. Consequently, the FC can make a global decision based on local observed energies without the knowledge of instantaneous SNR and noise variance at the SUs. Figure 5 shows the block diagram of the proposed cooperative spectrum sensing approach.

In the proposed spectrum sensing energy detection is performed at secondary users followed by the fuzzy based fusion for decision making. Based on the energy detection at SUs, local observations are transmitted to the fusion centre (FC). The global decision can be made at the FC using the local observations by means of adaptive Sugeno’s fuzzy system [26] . It is well known that energy detection method is ideal when prior information of the PU signal is unavailable. In the energy detection, the energy of the signal in the frequency band from a band-pass filter (BPF) is converted into discrete samples with the help of an analog-to-digital converter (A/D). Each SU measures PU signal energy using the PU signal x(j). The received PU signal energy detection at the kth SU user is given by

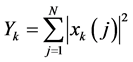(4)

where x_k(j) is the jth sample of the received signal at the kth SU.

The Sugeno’s fuzzy system comprises of fuzzification unit, inference engine, rule base and defuzzification unit as shown in Figure 2 to make the global sensing decision. The observed energy is applied to fuzzification unit to convert low and high energy values. The membership functions are bell shaped. The threshold value is fixed by comparing the global decision threshold with the local threshold values set the observed energy values. Here the energy of the received signal based on the threshold values, the output is classified into four membership functions as strongly present, moderately present, weakly present and not present. Cognitive base station uses the multiple ratio combining (MRC) strategy based on the weighted combination of the energy for sensing signals. The particular combining strategy is determined based on the operating average SNR value.

Cognitive base station finds the strongest PU signal using the weighted combination of PU signal energy measured from the sensed energy of individual SUs. Fuzzy logic is utilized in energy detection using multilevel threshold values based on cooperative spectrum sensing. Membership functions are formed to fix the optimal set of thresholds. The received PU signal energy can be classified into different categories such as PU strongly present, PU moderately present, PU weakly present and PU not present using four different membership functions. The objective is to determine the optimal combination of these parameters that would maximize the fuzzy function which allow representation in flexible and adaptive form.

Based on the fuzzified energy, the inference rules are used to gain information on the present status of the PU

signal. Let pd_i denote the private decision reflecting the possibility that the PU signal is present based on the observation of the ith SU. Then, the fuzzy inference rule set can be proposed as follows [23] :

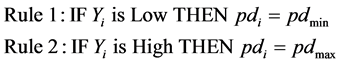(5)

Based on the private decisions obtained from the weighted averaging procedure, the global decision can be made based on the majority rule. The global decision is given by

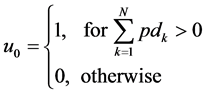(6)

Figure 6 shows the flowchart for the proposed fuzzy based spectrum sensing scheme. The global decision is made by comparing the energy spectrum of the received PU signals at SUs to determine presence and absence of PU signal. Fuzzy fusion center is used for decision making.

4. Results and Discussion

In the simulation scenario, we assumed equal SNR for all the nodes in the cognitive radio network. Here each node will calculate the energy of the received signal and based on the threshold values it decides on the output as strongly present, moderately present, weakly present and not present This information is passed on to neighboring nodes as two bit information. Each node will take the result of two neighboring nodes, own decision and SNR value to make final decision. Performance of this decision fusion method is evaluated at various SNR values and it is compared with conventional AND/OR rule based single node decision. The presence and absence of the primary user is found using the time domain and frequency domain plots of the received signal. These plots are shown in Figure 7. It is observed that PU can be detected in the frequency slots (4, 5), (10, 11) and (15, 16).

To validate the proposed cooperative spectrum sensing scheme, a Monte-Carlo simulation was carried out to analyze the ROC characteristics, probability of detection under the following conditions: the number of SUs is M = 7; the number of samples is N = 1000; the PU signal is a zero mean signal with 6 MHz bandwidth; the

noises at SUs have SNRs of −20, −19, −18, −17, −16, −15, −14 respectively. All the simulations are performed using Matlab version 7.12 with communication toolbox. To identify the best PU signal energy values and weighted energy values for MRC, the variability in sensing channels are considered. It is assumed that the distances from the PU to the SUs are significantly large compared to the distances between the SUs. Let p(H₁) and p(H₀) represent the probabilities that PU is present and absent, respectively. It is given by

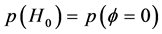(7)

and

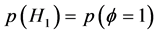(8)

p(H₁) and p(H₀)are taken as 0.5 and 0.5 initially. Energy values are first averaged over 1000 Monte Carlo simulations and then is normalized dividing by the maximum average energy value. The performance of the proposed scheme was first evaluated in terms of the receiver operating characteristic (ROC) under both non-fading and Rayleigh fading channels with the learning rate a fixed at 0.05.The probability of detection was computed the same way as that of probability of false detection and the same thresholds are been used. Performance comparison of the proposed scheme and conventional method is shown in Figure 8.

The proposed scheme provides better probability of detection, reduced probability of false alarm and probability of miss detection and thus outperforms the existing hard decision based technique for varied SNR conditions. The ROC plot between Probability of false alarm and probability of detection (Pd) for SNR=-10 dB is shown in Figure 9. The Pd is nearly 0.99 when the probability of false alarm (Pfa) is 0.1.

If the spectrum is free or not utilized by the licensed PU, then these situations are indicated by false detection. The probability of false detection was computed by running the program 100 times and counting the number of times the PU was falsely detected when it was not using the spectrum.

The ROC plot between Probability of false alarm (Pfa) and probability of miss detection for SNR = −10 dB is shown in Figure 10. The probability of miss detection is very low compared with the existing scheme.

5. Conclusion

An intelligent and reliable cooperative spectrum sensing based on fuzzy system based data fusion has been proposed. The main contribution of the work is that an intelligent fuzzy fusion algorithm is developed based on multiple threshold values at the fusion centre (FC) without the channel state information of the PU signal. Simulation results have been provided for spectrum sensing, probability of detection in different SNR conditions. The proposed method outperforms the existing energy detection schemes in terms of probability of detection and probability of false alarm.

Cite this paper

Sitadevi Bharatula,Meenakshi Murugappan, (2016) An Intelligent Fuzzy Based Energy Detection Approach for Cooperative Spectrum Sensing. Circuits and Systems,07,1042-1050. doi: 10.4236/cs.2016.76088

References