Energy and Power Engineering, 2013, 5, 219-225
doi:10.4236/epe.2013.54B043 Published Online July 2013 (http://www.scirp.org/journal/epe)
Research on Parallel Interleaved Inverters with
Discontinuous Space-Vector Modulation*
Feng Yang1, Xu Zhao1, Cong Wang1, ZhiFei Sun2
1China University of Mining & Technology (Beijing), Beijing, China
2Chongqing Research Institute of China Coal Technology & Engineering Group Corporation, Chongqing, China
Received April, 2013
ABSTRACT
Parallel converter can significantly increase the capacity of the converter and improve the power quality of AC side, but
the circulation which can lead to high switching loss and even damage the devices will easily exist in the direct parallel
converters. In this paper, the average model of parallel interleaved inverters system to analyze the circulation current is
shown, and the cross current is relevant to DC-bus voltage and the overlap time of zero vectors in the switching period.
Based on this observation, a discontinuous space vector modulation without using zero vectors (000) is eliminate and
suppress the zero-sequence current to entire system. Finally, the effectiveness of modulation strategy is verified by the
simulations in this paper.
Keywords: Interleaved Inverters; Circulating Current; Discontinuous Space-vector Modulation; Zero- sequence
Current
1. Introduction
With the increasing demand for power equipment capac-
ity and quality, how to improve the capacity of the power
electronic converters and improve its output performance
is an important development direction of modern power
electronics technology. High-frequency inverters due to
the switching frequency and the power devices loss limit,
the single component of the inverter only suitable for low
or medium capacity occasions. In recent years, in the
application of high power applications, the multi-level,
mixed topologies, or parallel multiple methods is an ef-
fective way for expansion of the capacity of the inverters.
Three-phase inverter parallel system has many advan-
tages, such as the system can achieve high current level,
the current and voltage ripple is small, the parallel sys-
tem has higher bandwidth. Previous research on parallel
systems are mainly concentrated in the UPS, motor
drives, as well as to improve the power factor occasions
[1-2,4-6]. With the development of IGBT and other
power semiconductor device of intelligent control to the
integrated structure, now more and more application
modules are directly connected in parallel, especially
where a high power density integration is required, such
as power sources, traction systems, uninterruptible power
supplies, power factor correction circuits and active
power filters (APF), and high power photovoltaic power
generation system [3,8], through parallel technology to
improve converter power and current levels, and enhance
the redundancy of the system. therefore, parallel PWM
inverter technology is of great significance for the pro-
motion of high-power photovoltaic, wind power applica-
tions。
Putting modules in parallel, however, is not risk free.
One of the major concerns for the parallel operation of a
three-phase system is the cross-coupling between the
three-phase system parallel modules, i.e., when each
module in a certain switching state, the inverter module
is connected with a DC bus at the same time to a com-
mon power supply or load, to increase the system does
not require the circulation loop. In order to avoid this
problem, the traditional method is to use an isolation
transformer [4-5]. However, the use of transformer will
undoubtedly increase the size and cost of the inverter
system, especially in the high power and low switching
frequency occasions, this problem more prominent.
Therefore, the power converter modules are directly
connected in parallel is required[3].
Through a comprehensive system analysis using the
averaged model, this paper shows the mechanism of how
the zero-sequence current is produced with the inter-
leaved technology, and the peak of zero-sequence current
is related to DC voltage and the overlap time of zero
vectors in a switching period. The discontinuous space
*National Natural Science Foundation of China. (51077125); The
Fundamental Research Funds for the Central Universities. (2010YJ03).

F. YANG ET AL.
220
vector modulation without using zero vectors is used to
eliminate the cause of pure zero-sequence current for
parallel operation. Simulation results are discussed which
are obtained to validate the theoretical analysis.
2. The Principle of Interleaved Modulation
2.1. General Description
The system to be analyzed is shown in Figure 1.
It is composed of two three-phase inverters connected
in parallel. Each phase(A, B, C) is composed of two
commutation cells (a and b) which DC input side directly
connected to the DC bus , and AC side output connected
to the grid through inductors.
The interleaved modulation of two inverter modules is
shown in Figure 2, module 1 and module 2 using the
same three-phase sine-wave voltage as a modulated wave,
and the carrier phase shift 1800, each phase has the same
fundamental wave. When the switching frequency is high
enough (and the Carrier ratio is large), the three-phase
modulated wave can be regarded as a DC constant in a
switching period, the driving waveform of right bridge in
phase A can be regarded as a half shift in carrier cycle to
the left bridge. The driving waveform of two modules
can be obtained from Figrue 2 [1].
Figure 1. Typical configur ations of inte rle a ve d invert er s.
Figure 2. The principle of interleaved modulation.
We take the phase A as an example, a simplified dia-
gram is shown in Figure 3.
Ua1 and Ua2 are the voltage of phase A between the
two interleaved inverter modules, two inverters will
transmit power to the grid together, at the same time as
Ua1, Ua2 and inductance L has a circulation path, when
the two inverters output voltage Ua1 and Ua2 are
inconsistent or the two inverter parameters is inconsistent,
it will produce cross-current, when the two inverters
output voltage Ua1 and Ua2 are inconsistent or the two
inverter parameters are inconsistent, the crossing current
is IH. We assumed that the parameters of the two invert-
ers is completely consistent, from Figure 3 we can ob-
tain the output voltage Uao of the interleaved inverter
[2,3].
Uao=(Ua1+Ua2)/2 (1)
Even two modules of the system parameters, dead-
time entirely consistent, due to the interleaved modula-
tion, it will also cause the two inverter output voltage
instantaneous value are inconsistent, the difference volt-
age in the same phase between the output voltages of the
two inverter modules are inherent[8,9], the differential
mode component will be the formation of crossing cur-
rent IH
IH=(Ua1-Ua2)/2XL (2)
2.2. Analysis of the Circulating Current
With interleaved parallel technology, it can greatly
reduce the output current ripple of high-frequency inverter
[1-3,6]. In high-power applications, using interleaved
parallel technology, the single tubes resistance can be
reduced by half, in the same current ripple requirement,
the size of the inductor can be greatly reduced, and the
dynamic response of the entire system can be improved
accordingly[3,7]. However, since the inverter is directly
connected in parallel, in addition to the common mode
component power supply for load or grid, while the two
interleaved parallel modules generate the differential
mode component, and this component will flow between
the two modules, this is circulation current, the circulation
current performance for zero-sequence component, inhibit
the Zero Sequence circulation current is conducive to
improve the current stress of the inverter module switchs.
Figure 3. The simplified diagram of two interleaved invert-
ers.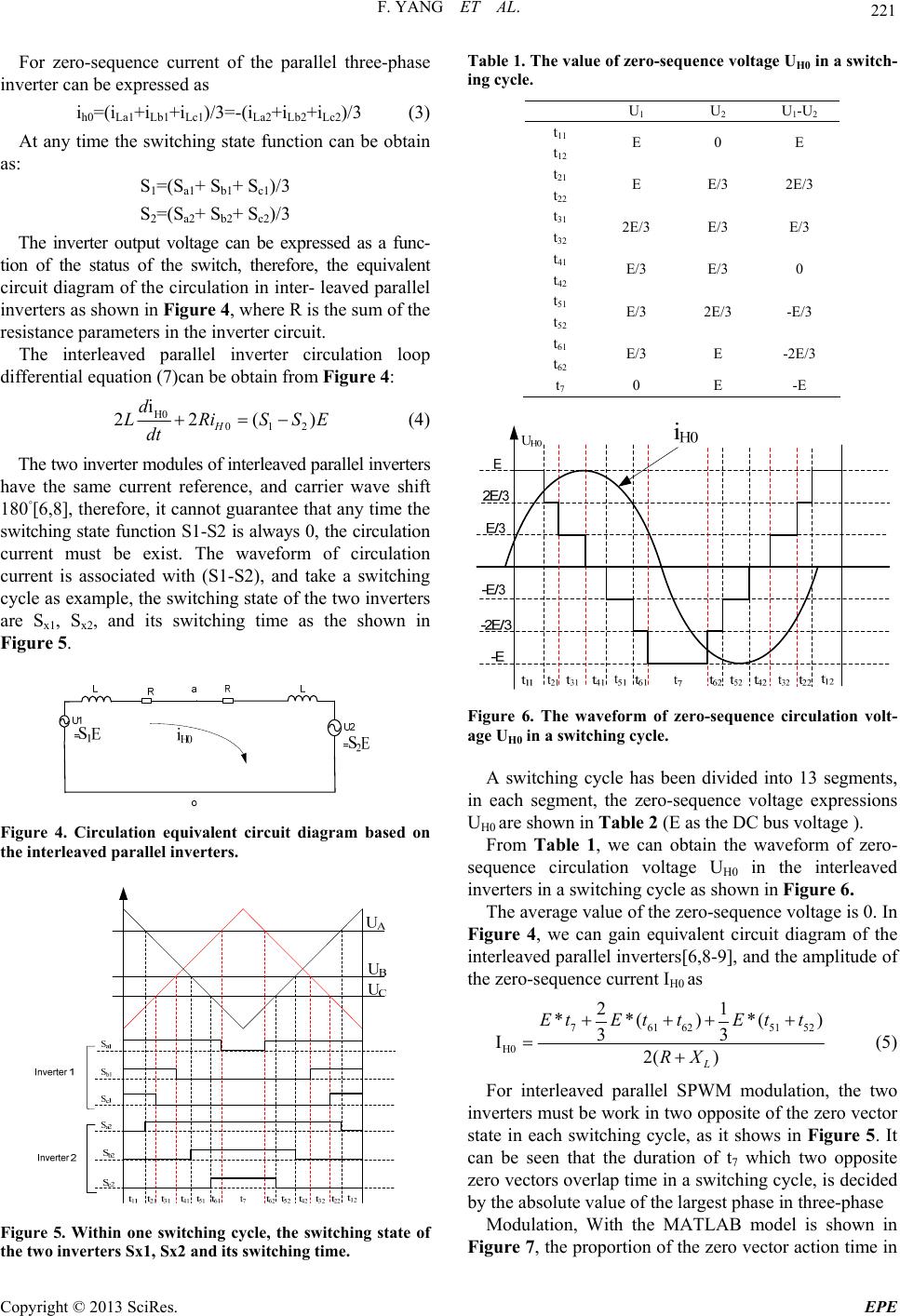

F. YANG ET AL. 221
For zero-sequence current of the parallel three-phase
inverter can be expressed as
ih0=(iLa1+iLb1+iLc1)/3=-(iLa2+iLb2+iLc2)/3 (3)
At any time the switching state function can be obtain
as:
S1=(Sa1+ Sb1+ Sc1)/3
S2=(Sa2+ Sb2+ Sc2)/3
The inverter output voltage can be expressed as a func-
tion of the status of the switch, therefore, the equivalent
circuit diagram of the circulation in inter- leaved parallel
inverters as shown in Figure 4, where R is the sum of the
resistance parameters in the inverter circuit.
The interleaved parallel inverter circulation loop
differential equation (7)can be obtain from Figure 4:
H0
012
i
22(
H
d
LRiSS
dt )E (4)
The two inverter modules of interleaved parallel inverters
have the same current reference, and carrier wave shift
180◦[6,8], therefore, it cannot guarantee that any time the
switching state function S1-S2 is always 0, the circulation
current must be exist. The waveform of circulation
current is associated with (S1-S2), and take a switching
cycle as example, the switching state of the two inverters
are Sx1, Sx2, and its switching time as the shown in
Figure 5.
Figure 4. Circulation equivalent circuit diagram based on
the interleaved parallel inverters.
Figure 5. Within one switching cycle, the switching state of
the two inverters Sx1, Sx2 and its switching time.
Table 1. The value of zero-sequence voltage UH0 in a switch-
ing cycle.
U
1 U2 U1-U2
t11
t12 E 0 E
t21
t22 E E/3 2E/3
t31
t32 2E/3 E/3 E/3
t41
t42 E/3 E/3 0
t51
t52 E/3 2E/3 -E/3
t61
t62 E/3 E -2E/3
t7 0 E -E
Figure 6. The waveform of zero-sequence circulation volt-
age UH0 in a switching cycle.
A switching cycle has been divided into 13 segments,
in each segment, the zero-sequence voltage expressions
UH0 are shown in Table 2 (E as the DC bus voltage ).
From Table 1, we can obtain the waveform of zero-
sequence circulation voltage UH0 in the interleaved
inverters in a switching cycle as shown in Figure 6.
The average value of the zero-sequence voltage is 0. In
Figure 4, we can gain equivalent circuit diagram of the
interleaved parallel inverters[6,8-9], and the amplitude of
the zero-sequence current IH0 as
76162 51
H0
21
**()*(
33
I2( )
L
EtE ttE tt
RX



52
)
(5)
For interleaved parallel SPWM modulation, the two
inverters must be work in two opposite of the zero vector
state in each switching cycle, as it shows in Figure 5. It
can be seen that the duration of t7 which two opposite
zero vectors overlap time in a switching cycle, is decided
by the absolute value of the largest phase in three-phase
Modulation, With the MATLAB model is shown in
Figure 7, the proportion of the zero vector action time in

F. YANG ET AL.
222
a switching cycle is shown in Figure 8.
3. Mitigation of the Circulation Current
We can obtained this conclusion from the formula (5)
and Figure 8: the zero sequence circulation current is
ralated to the DC voltage E and the duration of two op-
posite zero vectors overlap time. Reducing the overlap
time of two zero vectors of the inverter module can be
reduced the amplitude of the circulation current, and in-
creasing the filter inductors also can weaken the size of
the circulation current, coupled inductor is a good choose
to reduce the the circulation [2,8]. From Figure 8 can be
seen : the duration of two opposite zero vectors overlap
time is inversely proportional to the modulation ratio,
while the higher modulating ratio, the higher the utilize-
tion of the DC-bus voltage, which can also reduce the
circulation current.
The inverter with high-frequency SPWM modulation,
has high quality of the output waveform, but high
switching frequency with more switching losses, and
with low utilization of DC voltage. While the inverter
with SVPWM modulation, it can get better output volt-
age waveform with not very high switching frequency,
and maintaining a higher utilization rates of DC voltage.
It gives the proportion of zero vector time within one
Sine Wave2
Sine Wave1
Sine Wave
Scope
max
MinMax 2
Gai n
1
Constant
Add
|u|
Abs2
|u|
Abs1
|u|
Abs
Figure 7. Simulation model of the proportion of zero vector
action time.
Figure 8. Simulated the proportion of zero vector for a si-
nusoidal reference voltage modulated in a switching cycle.
switching cycle with different modulation method and
modulation ratio in [4]. So SVPWM together with inter-
leaving paralleled technology would be a better method
to mitigate the circulation current.
In the formula (5), t7 is the overlap time for the two
opposite zero vector in the two inverter modules with
interleaved parallel technology, When this is happening,
the top switches of one module are connected to the posi-
tive dc rail and the bottom switches of the other module
are connected to the negative dc rail. The three-phase
currents will flow simultaneously from the dc bus ca-
pacitor through the top switches of one module, the filter
inductors, the bottom switches of the other module, and
back to the dc bus capacitor, as shown in Figure 9.
Theoretically, the zero-vectors (000 and 111) can be
split apart and arranged appropriately in one switching
cycle with other SVM schemes so that the effect of
zero-vector overlap would be minimized or eliminated in
a switching cycle. Uncertainties, however, exist in sys-
tem transients and sector transition, where transition
chattering is likely to occur because of the current ripple.
Once the overlap is created, the zero-sequence will exist
in at least one switching cycle before it can be corrected.
Because the current loop operates as a feed back loop
based on the existing current to perform the following
actions, it can not be so fast as to eliminate the switching
frequency current. And the overlap time between zero
vectors (000 and 111) is decided to vector 000. Therefore,
discontinuous space-vector modulation without using
zero vector(000) to eliminate the zero vectors overlap
time is an effective method for interleaved parallel sys-
tem. Figure 10 shows the principle of this modulation
method, in a switching cycle, zero vector(000) using the
two of the other switching cycle modulation vector and
the inverse vector to synthesized. In the first sector, for
example, the modulation vector of the inverter 1 is
111,110,100,000, and the effective time of each vector is
Figure 9. Example of the cross-current circulation when
inverter 1 uses the zero vector v0(000) and inverter 2 uses
v7(111).

F. YANG ET AL. 223
t1, t2, t3, t4, a switching cycle of the zero vector effective
time for the t1, t4, and a switching cycle within the
modulation vector symmetrical distribution, while mak-
ing t1=t4=t0, select the effective time of the zero vector is
divided into four equal periods of time and rearrange the
duty cycles as the following,
0
22
0
33
0
1
4
4
2
t
tt
t
tt
t
t



In the t0 period, the vector(000) synthesize as shown in
Figure 10.
Take the first sector as example, rearrange the order
and the active time of space vector based on discontinu-
ous space vector modulation without using zero vector
(000) as shown in Figure 11.
With the application of discontinuous space vector
modulation without using zero vector(000) in the first
sector, a switching cycle is symmetrically divided into 14
segments, in each segment, the expression of zero se-
quence circulation voltage UH0 as shown in Table 2.
Figure 10. The principle of discontinuous space-vector modu-
lation without using zero vector(000).
Figure 11. Switching signal of discontinuous space-vector
modulation without using zero vector(000).
Table 2. The value of zero-sequence voltage UH0 in a switch-
ing cycle within discontinuous space vector modulation
without using zero vector(000).
U
1 U2 U1-U2
t11 E 2E/3 E/3
t21 E E/3 2E/3
t31 2E/3 E/3 E/3
t41 E/3 E/3 0
t51 E/3 2E/3 -E/3
t61 E/3 E -2E/3
t71 E/3 E -2E/3
t72 2E/3 E -E/3
t62 E/3 E -2E/3
t52 E/3 2E/3 -E/3
t42 E/3 E/3 0
t32 2E/3 E/3 E/3
t22 E E/3 2E/3
t12 E E/3 2E/3
From Table 2, we can obtain the waveform of zero-
sequence circulation voltage UH0 with discontinuous
space vector modulation without using zero vector(000)
in a switching cycle as shown in Figure 12
Comparing Figure 6 and Figure 12, the peak of zero-
sequence circulation voltage UH0 in a switching cycle has
been eliminated.
In addition to the switching circulation, the average of
the cross-current theoretically is zero during a funda-
mental period, any small difference between the inverters
determines a lower frequency circulation between them.
The lower frequency zero-sequence current is removed
by a current controller placed on zero-axis, which keeps
a null average of the zero sequence current [7,10].
4. Simulation Results
In order to validate the proposed discontinuous SVM
without using zero vector(000) in two parallel interleaved
inverters, simulation has been built in Simulink. Figure
13(a) shows FFT analysis of the AC-side current in
phase A as a single inverter, and Figure 13(b) illustrates
FFT analysis of the AC-side current in phase A based on
parallel interleaved inverters with discontinuous SVM
without using zero vector(000).
Figure 14(a) shows the circulation waveform of phase
A in two parallel inverters, and Figure 14(b) illustrates

F. YANG ET AL.
224
the circulation waveform of phase A in parallel inverters
based on interleaved discontinuous SVM without using
zero vector(000).
5. Conclusions
The parallel interleaved technology in high-power appli-
cations, a single switch tube flow resistance value re-
duced by half, with the same current ripple request, the
inductor size can be reduced by about 40%, it can also to
improve the dynamic response time of the entire system.
When two or more modules are connected directly to a
dc bus and a three-phase source/load without using
transformer isolation, the intended PWM interleave will
cause the cross current in all the phases. This paper first
introduces the cross current is ralated to the DC voltage
E and the duration of two opposite zero vectors over-
lapped time. And then proposed the SVM without using
Figure 12. The waveform of zero-sequence circulation volt-
age UH0 in a switching cycle.
(a)
(b)
Figure 13. FFT analysis of AC-current in phase A. (a)
Phase-A currents for single inverter. (b) Phase-A currents
for two parallel interleaved inverters.
(a)
(b)
Figure 14. The circulation waveform of phase A (a) Phase-A
currents for two parallel interleaved inverters without the
proposed SVM . (b) Phase-A currents for two parallel in-
terleaved inverters with the proposed SVM.
zero vector(000), The simulation results have shown that
the proposed SVM is feasible. It effectively eliminates
the circulation current and simultaneously reduces the
harmonic current. Simulation results validate the pre-
sented analysis.
REFERENCES
[1] Y. L. Cai, Y. Zhang and L. L. Fei, “The Analysis of Cur-
rent Ripple in the AC Side of High-Frequency Rectifier
Based on Interleaving Technology,” Telecom Power
Technology, Vol. 28, No. 3, 2011.
[2] B. Cougo, G. Gateau, T. Meynard, M. Bobrowska-Rafal
and M. Cousineau, “PD Modulation Scheme for
Three-Phase Parallel Multilevel Inverters,” IEEE Trans-
actions on Industrial Electronics, Vol. 59, No. 2, 2012.
[3] F. J. Liu, “Multi-level inverter technology and its applica-
tions. Beijing. China Machine Press 2007.
[4] L. Asiminoaei, E. Aeloiza, P. N. Enjeti and Frede Blaab-
jerg, “Shunt Active -Power-Filter Topology Based on
Parallel Interleaved Inverters,” IEEE Transactions on In-
dustrial Electronics, Vol. 55, No. 3, 2008.
[5] Z. H. Ye, D. S. Boroyevich, J. Y. Choi and F. C. Lee,
“Control of Circulating Current in Two Parallel
Three-Phase Boost Rectifiers,” IEEE Transactions on
Power Electronics, Vol. 17, No. 5, 2002.
[6] K. Xing, F. C. Lee, D. S. Borojevic, Z. H. Ye, and Sudip
Mazumder, “Interleaved PWM with Discontinuous
Space-Vector Modulation,” IEEE Transactions on Power
Electronics, Vol. 14, No. 5, 1999.

F. YANG ET AL.
225
[7] L. A. Moran, J. W. Dixon and R. R. Wallace, “A
Three-phase Active Power Filter Operating with Fixed
Switching Frequency for Reactive Power and Current
Harmonic Compensation,” IEEE Transactions on Indus-
trial Electronics , Vol. 42, No. 4, 1995, pp. 402-408.
doi:10.1109/41.402480
[8] P.-W. Lee, Y.-S. Lee, D. K. W. Cheng, and X.-C. Liu,
“Steady-state Analysis of an Interleaved Boost Converter
with Coupled Inductors,” IEEE Transactions on Indus-
trial Electronics, Vol. 47, No. 4, 2000, pp. 787-795.
doi:10.1109/41.857959
[9] J. M. Guerrero, L. Garcia de Vicuna, J. Matas, M. Castilla,
and J. Miret, “Output Impedance Design of Parallel-
Connected UPS Inverters with Wireless Load-sharing
Control,” IEEE Transactions on Industrial Electronics,
Vol. 52, No. 4, 2005, pp. 1126-1135.
doi:10.1109/TIE.2005.851634
[10] Y. H. Zhi, D. Boroyevich, C. Jae-Young and F. C. Lee,
“Control of Circulating Current in Two Parallel
Three-phase Boost Rectifiers,” IEEE Transactions on
Power Electronics, Vol. 17, No. 5,2002, pp.
609-615.doi:10.1109/TPEL.2002.802170