Energy and Power Engineering, 2013, 5, 97-101
doi:10.4236/epe.2013.54B019 Published Online July 2013 (http://www.scirp.org/journal/epe)
Dual-loop Control Strategy for Grid-connected
Inverter with LCL Filter
Qiubo Peng, Hongbin Pan, Yong Liu, Lidan Xiang
Key Laboratory of Intelligent Computing & Information Processing of Ministry of Education,
Xiangtan University, Xiangtan, China
Received February, 2013
ABSTRACT
As to the concrete topology of three-phase LCL type grid-connected inverter with damping resistance, mathematical
model was deduced in detail, using method of equivalent transformation to the structure diagram, damping resistance
was virtualized, mathematical model under the DQ frame that can realize decoupling control was established, a
dual-loop control strategy for grid-connected inverter with LCL filter was proposed, the system stability was analyzed
and the design method of controller was given. The proposed method overcame the flaws of loss increase, efficiency
reduce and cost increase which were caused by damping resistance in LCL type grid-connected inverter, the system
efficiency and power supply quality of the output were improved. Feasibility and effectiveness of the new method were
validated by simulation and experimental results.
Keywords: Virtual Damping; LCL Filter; Three-phase Grid-connected Inverter; Decoupling Control
1. Introduction
LCL filter compared with the traditional L filter, it needs
smaller inductance value and it is more effective for re-
straining higher harmonic when they achieve the same
filtering effect, but resonance problem exists in LCL fil-
ter itself, it will cause system instability [1-3]. There are
two common methods to solve it [4, 5]: one is passive
damping, that is, a damping resistance is connected with
the capacitor branch in series to inhibit resonance [6,7].
This method is simple and reliable, but the LCL filter’s
ability of restraining higher harmonic was reduced, it will
also bring extra system loss for the damping resistor;
another one is active damping, namely the modified con-
trol algorithm was adopted to inhibit resonance and make
sure the system stability [8, 9].
According to the principle of inhibiting resonance by
using damping resistance, and using equivalent transfor-
mation, a dual-loop control strategy for grid-connected
inverter with LCL filter was proposed in this paper, this
new method was used to inhibit resonance, ensure system
stability. A detailed description about the process of
proposing control strategy, mathematical modeling and
decoupling control of grid-connected inverter in the DQ
coordinate system, and the design method of controller
parameter was given in this paper. Then system stability
was analyzed, finally, the effectiveness and feasibility of
the new method have been verified by simulate and ex-
perimental ways.
2. The Topology and Mathematical Model of
Grid-connected Inverter with LCL Filter
2.1. The Mathematical Model of LCL Filter with
Damping Resistance
The topological structure of LCL grid-connected inverter
with damping resistance is shown in Figure 1. Where,
1 is inductance on the side of inverter, 1 is parasitic
resistance; 2 is inductance on the side of grid, 2 is
parasitic resistance; C is filter capacitor, is damping
resistance connecting with C in series; dc is DC-bus
voltage, are three-phase output voltages of
inverter, 1a1b1c, 2a2b2c and Ca Cb Cc are three-
phase currents on the side of inverter, three-phase cur-
rents on the side of grid and three-phase currents flowing
L R
c
R
V
i
L
a b
u
i
R
u
ic
u
ii i ii i
1a
i 2a
i
Ca
i
1 b
i
1 c
i
Cb
i
Cc
i
2b
i
2c
i
Figure 1. Grid-connected inverter with LCL filter based on
damping resistance.

Q. B. PENG ET AL.
98
through filter capacitor, respectively,
g
a
u
g
b
u
g
c
u are
three-phase grid voltages.
1a
iu1b i1c i
u, 2a2b2c and voltages of filter capacitor
Ca Cb Cc are selected as state variables to obtain state
equation in the three phase static coordinate system.
Transfer functions in the αβ coordinate system were ob-
tained by using Laplace transform and Clarke transform
to the state equation, then, transfer functions in the DQ
coordinate system were obtained by using Park transform
to the frontal transfer functions, it is as follows:
i i i
u
11
1
11
22
2
22
12
(1)
dCd q
d
Cd gdq
d
Cdd d
CCdCCq
Cd
UU wLI
ILs R
UUwLI
ILs R
III
R CsIwR CIwCU
UCs









 


Cq
(1)
11
1
11
22
2
22
12
(1)
qCq d
q
Cq gqd
q
Cqq q
CCqCCd
Cq
UU wLI
ILs R
UUwLI
ILs R
III
R CsIwR CIwCU
UCs









 


Cd
(2)
where, 1d
I
, 2d
I
, Cd
I
, Cd , d and U U
g
d
U is D-axis
current on the side of inverter, current on the side of grid,
the output voltage of inverter and grid voltage, respec-
tively. Similar tagging method to D-axis variables is
adopted for Q-axis variables.
The block diagram of LCL filter with damping resis-
tance and blocking capacitance can be obtained from
transfer functions in the DQ coordinate system, D-axis
structure diagram is shown in Figure 2 as example:
2.2. Equivalent Transformation of the System
Block Diagram
The equivalent transformation is as follows: 1) Moving
signal comparing point of the feedback loop Cq
I
to the
left side of the signal comparing point of the feedback
loop Cd by equivalent transformation and shown in
Figure 3(a); 2) Doing equivalent transformation to
U
c
wR C
1
wL wC
2
wL
11
1
L
sR
1
Cs
22
1
L
sR
1
c
R
Cs 
1d
I
2d
I
Cd
I
Cd
U
d
U
g
d
U
Cd
U
1q
I
Cq
I
2q
I
Cq
U
2d
I
Figure 2. D-axis block diagram of LCL filter based on
damping resistance.
1
wL wC
11
1
L
sR

1
Cs
22
1
L
sR
1
c
R
Cs

1d
I
2d
I
Cd
I
Cd
U
g
d
U
Cd
U
1q
I
Cq
U
2 d
I
d
U
2
wL
2q
I
Cq
I
11
1
cc
L
sR
wR C
R
Cs


(a)
1
wL wC
11
1
L
sR

1
Cs
22
1
L
sR
1d
I
2d
I
Cd
I
Cd
U
g
d
U
Cd
U
1q
I
Cq
U
2 d
I
d
U
1
c
c
R
Cs
R
Cs

2
wL
2q
I
Cq
I
11
1
cc
L
sR
wR C
R
Cs


(b)
1
wL wC
11
1
L
sR

1
Cs
22
1
L
sR
1d
I
2d
I
Cd
I
Cd
U
g
d
U
Cd
U
1 q
I
Cq
U
2 d
I
d
U
2
11
1
cc
c
L
RCs RRCs
RCs


2
wL
2 q
I
Cq
I
11
1
cc
L
sR
wR C
R
Cs


(c)
Figure 3. Equivalent transforms of LCL filter based on
damping resistance.
“1
c
RCs

” as Figure 3(b); 3) Moving signal comparing
point of the equivalent part of “(2)”to the left side of the
signal comparing point of the feedback loop Cd U by
equivalent transformation, finally, the equivalent block
diagram is obtained and shown in Figure 3(c).
Equivalent transforms in the above paragraphs was
called “virtualization process of damping resistance”,
whereas the dotted portions in the figure can be called
“virtual damping resistance”. The remaining solid por-
tions are the block diagram of LCL filter without damp-
ing resistance. The conclusion that it needs capacitance
current and grid-connected current double closed loop
control in order to achieve the same filtering effect as
before the equivalent transforms is obtained from the
transform results.
3. Current Dual-loop Control Strategy
3.1. Control Strategy
The output current of three-phase grid-connected inverter
with LCL filter will have higher quality, but it demands
higher requirement of control. The system is unstable if
using typical grid-connected current direct feedback
closed loop control. Conclusion that is obtained from the
block diagram in the above paragraphs is that: it can
achieve the same effect of inhibiting resonance as using a
damping resistance in the filter capacitor branch in series
by adopting the filter capacitor current feedback as well
as proper control strategy.
If “virtual damping resistance” that is from the equiv-
alent transformation is directly used in controlling, due to
the order of its transfer function numerator is higher than

Q. B. PENG ET AL. 99
that of the denominator, feedback quantity is the filter
capacitor current, the current harmonic is high and the
control is more difficult, it is difficult to achieve the ef-
fect of inhibiting resonance and system stability and this
is verified by simulation result.
Now that the control effect is not good by using “vir-
tual damping resistance” directly that is from the equiva-
lent transformation, only the feedback quantity is taken
in the control that is simplified in this paper. Current
double closed loop control strategy is used in three-phase
grid-connected inverter with LCL filter and the feedback
quantity is the filter capacitor current C
I
and the grid-
connected current 2
I
on the grid side. A P control is
applied in the filter capacitor current inner loop and a PI
control is applied in the grid-connected current outer
loop.
3.2. System Performance Analysis and
Controller Parameter Design
Current double closed loop control for grid-connected
inverter consists of capacitor current inner loop and grid-
connected current outer loop. Voltage-current double
closed loop control for grid-connected inverter consists
of grid-connected current inner loop and grid voltage
outer loop. Because the control principle is different be-
tween the two, it cannot adopt a similar method to the
latter to design current double closed loop controller in
this paper [10]. The setting value of the current double
closed loop control in this paper is current instruction,
the reference current of the capacitor current inner loop
will be obtained after flowing through outer PI controller,
then, the voltage instruction will be obtained after flow-
ing through inner P controller and it will be sent to in-
verter. The inner or outer loop cannot be designed inde-
pendently because of the interdependence between the
two, only the inner and outer loop controllers were de-
signed synchronously in order to ensure system per-
formance.
Due to the duality between D-axis and Q-axis, only
taking D-axis controller design for example in what fol-
lows. The system control block diagram is shown in
Figure 4.
Where, Inverter Bridge is equivalent to proportional
component
p
wm , 1
K
K
is the feedback coefficient of
capacitor current inner loop and 2
K
is the feedback
coefficient of grid-connected current outer loop.
11
1
L
sR

1
Cs
22
1
L
sR
1d
I
2d
I
Cd
I
Cd
U
d
U
g
d
U
Cd
U
2d
I
Ii
Ip
K
K
s

p
wm
K
Up
K
1
K
2
K
*
2d
I
2d
I
*
Cd
I
Cd
I
Figure 4. Control block diagram of D-axis.
According to the control block diagram and ignoring
the parasitic resistance 1 and 2 of the inductance,
the open loop transfer function of the system can be ob-
tained as follows:
R R
22
22
12121 2
() ()
Up IppwmUp Iipwm
Up pwm
KK KKsKK KK
Gs sLLCsKKKLCs LL







The closed loop transfer function is:
10
432
4321
() bs b sas asas asa


0


where,
412
aLLC

, 31 2Up pwm aKKKLC

, ,
21
aLL
2
12 Up Ippwm
aKKKK

, ,
02UpIipwm
aKKKK
1Up Ippwm
bKKK

, .
0UpIi pwm
bKKK
The system stability condition can be obtained as fol-
lows by using Routh stability criterion.
1
11 221
22
11221 2
() 0
()Ip
Ip
IpUp Iipwm
KL LKKL
KKLLKKLKKK KLC
 


0




Therefore, it can ensure the system stability as long as
satisfying the above identities when designing controller.
From the open loop transfer function of the system, it
can be seen that this system is a Ⅱ type system and
contains a second-order system. Let be the open loop
transfer function1
222
22
(1)
() (2
KTs
Gs sTs Ts



1)
, where
2
12
Up Ii pwm
KK KK
KLL , 1
I
p
I
i
K
T
K
, 2
212
12
LLC
TLL 

,
1
2
12
2Uppwm 2
K
KK LC
TLL  ,

is damping coefficient.
Using the design method of controller based on ex-
pected logarithmic frequency characteristic in what fol-
lows: They can be calculated from the open loop transfer
function: 12
2
21
1LLC
TwLL  2 , 212
12
2( )
Up pwm
TL L
K
K
KLC
 
,
also 21
12
wT
hwT  , selecting middle-frequency width
coefficient h, 1
1
1
T
w

2
h T can be calculated; selecting
a suitable K that satisfies
12
11
K
TT
 ,
12
2
(
Ii Up pwm
)
K
LL
KKK K

 can be calculated; finally,
1
I
pIi
K
TK

can be calculated.
By substituting system parameters11.6LmH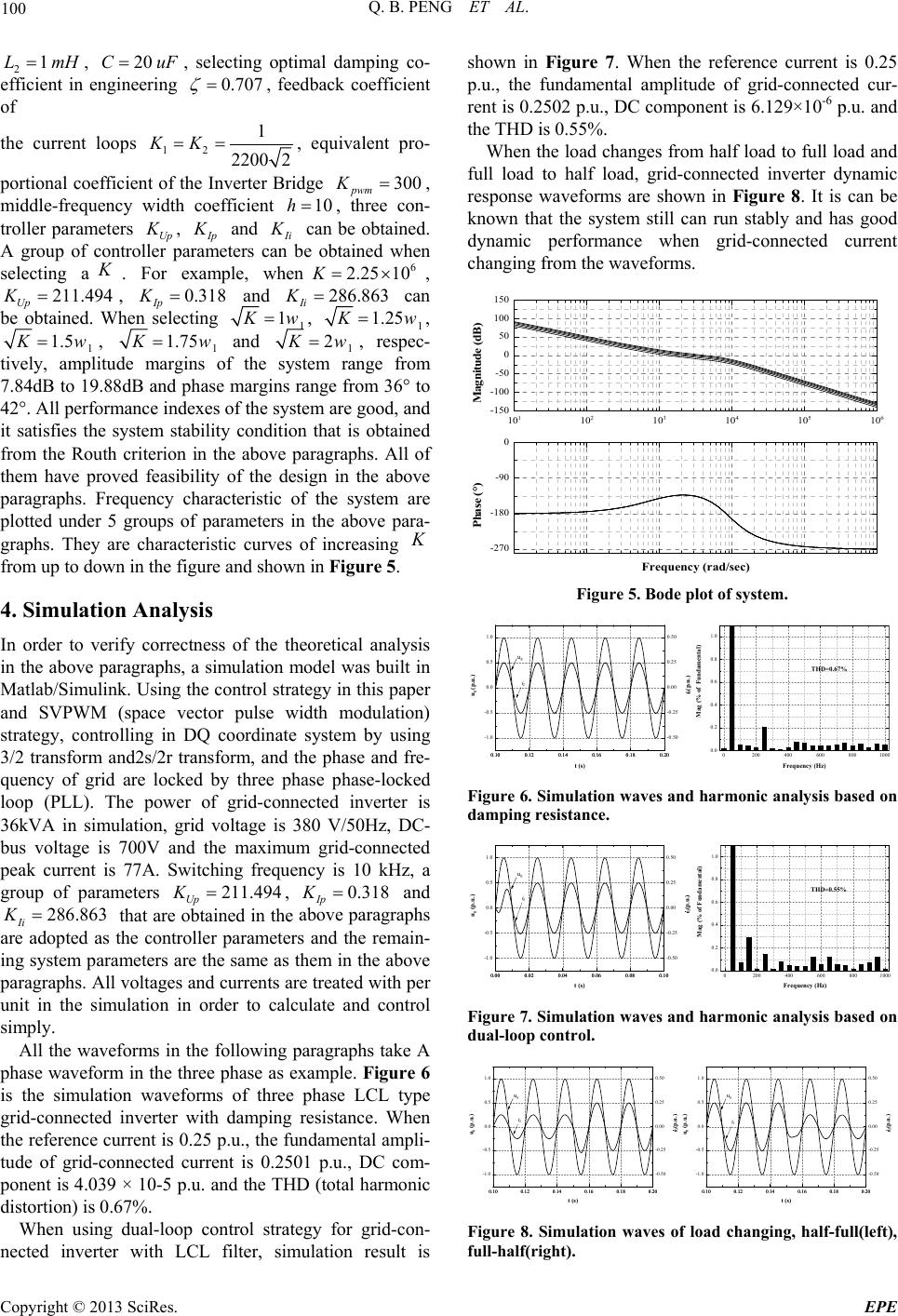

,

Q. B. PENG ET AL.
100
2, , selecting optimal damping co-
efficient in engineering
1LmH20CuF
0.707

, feedback coefficient
of
the current loops 12
1
2200
 2 KK , equivalent pro-
portional coefficient of the Inverter Bridge 300
pwm
K

,
middle-frequency width coefficient , three con-
troller parameters Up
10h
K
,
I
p
K
and
I
i
K
can be obtained.
A group of controller parameters can be obtained when
selecting a
K
. For example, when,
Up , Ip and can
be obtained. When selecting
6
2.25 10
286.863
K
Ii
K21K1.494 0.318K
1
1
K
w, 1 1.25
K
w,
1
1.5
K
w, 1 1.75
K
w and 1 2
K
w, respec-
tively, amplitude margins of the system range from
7.84dB to 19.88dB and phase margins range from 36° to
42°. All performance indexes of the system are good, and
it satisfies the system stability condition that is obtained
from the Routh criterion in the above paragraphs. All of
them have proved feasibility of the design in the above
paragraphs. Frequency characteristic of the system are
plotted under 5 groups of parameters in the above para-
graphs. They are characteristic curves of increasing
K
from up to down in the figure and shown in Figure 5.
4. Simulation Analysis
In order to verify correctness of the theoretical analysis
in the above paragraphs, a simulation model was built in
Matlab/Simulink. Using the control strategy in this paper
and SVPWM (space vector pulse width modulation)
strategy, controlling in DQ coordinate system by using
3/2 transform and2s/2r transform, and the phase and fre-
quency of grid are locked by three phase phase-locked
loop (PLL). The power of grid-connected inverter is
36kVA in simulation, grid voltage is 380 V/50Hz, DC-
bus voltage is 700V and the maximum grid-connected
peak current is 77A. Switching frequency is 10 kHz, a
group of parameters , and
that are obtained in the above paragraphs
are adopted as the controller parameters and the remain-
ing system parameters are the same as them in the above
paragraphs. All voltages and currents are treated with per
unit in the simulation in order to calculate and control
simply.
211.494
Up
K0.318
Ip
K
286.863
Ii
K
All the waveforms in the following paragraphs take A
phase waveform in the three phase as example. Figure 6
is the simulation waveforms of three phase LCL type
grid-connected inverter with damping resistance. When
the reference current is 0.25 p.u., the fundamental ampli-
tude of grid-connected current is 0.2501 p.u., DC com-
ponent is 4.039 × 10-5 p.u. and the THD (total harmonic
distortion) is 0.67%.
When using dual-loop control strategy for grid-con-
nected inverter with LCL filter, simulation result is
shown in Figure 7. When the reference current is 0.25
p.u., the fundamental amplitude of grid-connected cur-
rent is 0.2502 p.u., DC component is 6.129×10-6 p.u. and
the THD is 0.55%.
When the load changes from half load to full load and
full load to half load, grid-connected inverter dynamic
response waveforms are shown in Figure 8. It is can be
known that the system still can run stably and has good
dynamic performance when grid-connected current
changing from the waveforms.
-270
-180
-90
0
Phase (°)
Frequency (rad/sec)
10
1
10
2
10
3
10
4
10
5
10
6
-150
-100
-50
0
50
100
150
Magnitude (dB)
Figure 5. Bode plot of system.
0200400 600 8001000
0.0
0.2
0.4
0.6
0.8
1.0
Mag (% of Fundamental)
Frequency (Hz)
THD=0.67%
0.10 0.12 0.140.16 0.18 0.20
-1.0
-0.5
0.0
0.5
1.0
0.10 0.12 0.140.16 0.18 0.20
-0.50
-0.25
0.00
0.25
0.50
t (s)
u
g
(p.u.)
u
g
i 2
i
2
(p.u.)
Figure 6. Simulation waves and harmonic analysis based on
damping resistance.
0200400 6008001000
0.0
0.2
0.4
0.6
0.8
1.0
Mag (% of Fundamental)
Frequency (Hz)
THD=0.55%
0.00 0.02 0.04 0.06 0.08 0.10
-1.0
-0.5
0.0
0.5
1.0
0.00 0.02 0.04 0.06 0.08 0.10
-0.50
-0.25
0.00
0.25
0.50
t (s)
u
g
(p.u.)
i
2
(p.u.)
u g
i 2
Figure 7. Simulation waves and harmonic analysis based on
dual-loop control.
0.10 0.12 0.14 0.16 0.18 0.20
-1.0
-0.5
0.0
0.5
1.0
0.10 0.12 0.14 0.16 0.18 0.20
-0.50
-0.25
0.00
0.25
0.50
t (s)
u
g
(p.u.)
u
g
i
2
i
2
(p.u.)
0.10 0.12 0.14 0.16 0.18 0.20
-1.0
-0.5
0.0
0.5
1.0
0.10 0.12 0.14 0.16 0.18 0.20
-0.50
-0.25
0.00
0.25
0.50
t (s)
u
g
(p.u.)
u
g
i
2
i
2
(p.u.)
Figure 8. Simulation waves of load changing, half-full(left),
full-half(right).

Q. B. PENG ET AL.
101
5. Experimental Results power supply quality of the output: low harmonics, espe-
cially has a stronger ability of high harmonic suppression,
and has solved the system unstable problem caused by
resonance; b) system sufficiency was improved further:
the real damping resistance has been canceled, it has no
extra loss caused by real damping resistance.
An experimental prototype for 3 kVA output power has
been successfully implemented based on the theoretical
analysis and simulation experiments in the above para-
graphs by using TM320F2812 DSP as the digital con-
troller. Figure 9 is the experimental waveforms of three
phase LCL type grid-connected inverter with damping
resistance. In this case, grid-connected current is 4.54 A
and THD is 3.54%. When using dual-loop control strat-
egy for grid-connected inverter with LCL filter, experi-
mental result is shown in Figure 10. By this method,
grid-connected current is 4.52 A and THD is 3.68%. It
can be obtained from the experimental results. When
using the new control strategy, it can achieve the same
inhibiting resonance as the method of using real damping
resistance. At the same time, good power supply quality
of the output can be ensured.
7. Acknowledgements
This work is supported by the Key Laboratory of Intelli-
gent Computing & Information Processing (Xiangtan
University), Ministry of Education and the construct
program of the key discipline in hunan province.
REFERENCES
[1] Y. Q. Wang, F. J. Wu, L. Sun, et al., “Optimized Design
of LCL Filter for Minimal Damping Power Loss,” Pro-
ceedings of the CSEE, Vol. 30, No. 27, 2010, pp. 90-95．
[2] M. Liserre, A. Dell'Aquila and F. Blaabjerg, “Stability
Improvements of an LCL-filter Based Three-phase Active
Rectifier,” IEEE Annual Power Electronics Specialists
Conference, Cairns, 2002．
6. Conclusions
The dual-loop control strategy for grid-connected in-
verter with LCL filter in this paper can be used to control
the currents of three phase grid-connected inverter, and it
will let grid-connected inverter has a stronger ability of
harmonic suppression. A detailed description about
theoretical basis of the control strategy and design me-
thod of the controller were given in this paper, the effec-
tiveness of the new control strategy has been verified by
simulation and prototype experiment.
[3] X. H. Wang, X. B. Ruan and S. W. Liu, “Control Strategy
for Grid-connected Inverter to Suppress Current Distor-
tion Effected by Background Harmonics in Grid Volt-
age,” Proceedings of the CSEE, Vol. 31, No. 6, 2011, pp.
7-14.
[4] C. H. Zhang, Y. Ye, A. Chen, et al., “Research on
Grid-connected Photovoltaic Inverter Based on Output
Current Control,” Transactions of China Electrotechnical
Society, Vol. 22, No. 8, 2007, pp. 41-45．
Compare with the control method of inhibiting reso-
nance by using damping resistance, the new control me-
thod in this paper has characters as follows: a) good [5] T
. C. Y. Wang，Z. H .Ye，G. Sinha，et al., “Output
Filter Design for a Grid-interconnected Three-phase In-
verter,” IEEE PESC’03, Acapulco, Mexico, 2003．
t (15ms/grid)
U
g
(200V/grid) i
2
(5A/grid)
U
g
i
2
[6] Z. Y. Xu, A. G. Xu and S. J. Xie, “Dual-loop Grid Cur-
rent Control Technique for Grid-connected Inverter Using
an LCL Filter,” Proceedings of the CSEE, Vol. 29, No. 27,
2009, pp. 36-41．
[7] M. Malinowski and S. Bernet, “A Simple Voltage Sen-
sorless Active Damping Scheme for Three-phase PWM
Converters with an LCL Filter,” IEEE Transactions on
Industry Electronics, Vol. 55, No. 4, 2008, pp.
1876-1880．
Figure 9. Experimental waves based on damping resistance. [8] Ji Bao-jian, F. Hong and J. F. Zhao, “A Non-isolated
Three-level Dual Buck Photovoltaic Grid-connected In-
verter,” Proceedings of the CSEE, Vol. 32, No. 12, 2007,
pp. 7-13．
t (15ms/grid)
U
g
(200V/grid) i
2
(5A/grid)
U
g
i
2
[9] B. C. Wang, X. Q. Guo, Q. Mei, et al., “DC Injection
Control for Transformerless PV Grid- connected Invert-
ers,” Proceedings of the CSEE, Vol. 29, No. 36, 2009, pp.
23-28.
[10] F. Liu, S. X. Duan and X. M. Zha, “Design of Two Loop
Controller in Grid-connected Inverter with LCL Filter,”
Proceedings of the CSEE, Vol. 29, No. S1, 2009, pp.
234-240.
Figure 10. Experimental w ave s based on dual-loop co ntr ol.