Advances in Ma terials Physics and Che mist ry, 2012, 2, 270-273
doi:10.4236/ampc.2012.24B069 Published Online December 2012 (htt p://www.SciRP.org/journal/ampc)
Simulation of Thermophysical Processes at Laser Welding of
Alloys Containing Refractory Nanoparticle s
Anatoly N. Cherepanov1, Vasily P. Shapeev1, Guangxun Liu2, Lamei Cao2
1Khristianovich Institute of Theoretical and Applied Mechanics SB RAS; Novosibirsk State University, Novosibirsk, Russia
2Beijing Institute of Aeronautical Materials, Beijing, China
Received 2012
ABSTRACT
Mathematical model is formulated for description of thermophysical processes at laser welding of metal plates for the case when
modifying nanoparticles of refractory compounds (nanopowder inoculators – NPI) are introduced into the weld pool. Specially pre-
pared n anoparti cles of refractor y compo und s serve here as cr ystallizatio n cent ers, i.e. in fact th ey are exogeno us ino culants o n which
surface clu st ers are gro uped . This can be us ed to contro l the melt cryst alli zatio n proces s and formatio n of its stru ctur e, and, ther efore,
properties of the weld seam. As an example, calculation results of the butt welding of aluminum alloy and steel plates are p resent ed.
The results of calculation and experimen tal data compariso n are shown.
Keywords: Mathematical Model; Laser Welding; Nanopowder Inoculators; Crystallization Process; Calculation Results
1. Introduction
In the last years increasing attention has been paid to develop-
ment of technology for laser welding of metal products. In this
connection, development of appropriate mathematical models
and numerical algorithms for their implementation is a pressing
problem [1,2].
A mathe matical model is developed in this work for descrip-
tion of thermophysical processes at laser welding of metal
plates for the case when modifying nanoparticles of refractory
compounds (nitrides, oxides, etc) are introduced in the molten
pool. The mathematical model proposed is based on
non-equilibrium birth and growth of crystal phase on the in-
oculants, which are the nanoparticles, with use of the Kolmo-
gorov’s theory for calculation of the solid phase fraction. At
that, the homogeneous nucleation can be neglect ed.
2. Physicomathe ma tical Mod el o f the Process
Let us consider a steady-state process of two plates butt weld-
ing. We introduce the Cartesian coordinate system with x axis
lying on the plates upper surface, z axis coinciding with the
symmetr y axis an d direction of the laser beam operation, and y
axis perpendicular to the joint. The coordinates origin lies on
intersection of the beam axis and the plates upper surfaces
(Figure 1). The beam moves along the joint in negative direc-
tion of x axis with constant welding speed v=const. The metal
of the welded plates is protected from oxidation by an inert gas
blow that carries away a part of the metal vapors. We assume
the thermophysical parameters to be constant and equal to their
average values in the temperature range under consideration.
Due to the small concentration of the dispersed nanoparticles
(~0.05% by mass), their influence on the physical parameters of
the alloy can be neglected. The alloy is considered to be a bi-
nary system. With these assumptions, the three-dimensional
equation of heat transfer in the weldpool and solid metal in the
moving coordinate system takes the form:
2 22
1
2 22s
ii i
TT TTf
cv v
x xyzx
ρ λδκρ
 ∂∂ ∂∂∂
=++ −

∂ ∂∂∂∂

(1)
where ci,
λ
i,
ρ
i are specific heat, heat conductivity, and density
of the i-th phase, respectively (indices i = 1, 2, 3 denote para-
meters of solid, two-phase, and liquid states of the metal); δ = 0
in the melting zone; δ = 1 in the crystallization zone; fs is a
share of the solid phase; fl =1–fs is a share of liquid phase in the
two-phase zone. In variant of the model used in this paper, all
particles of the product in movable coordinate system move
parallel to x axis with the welding speed. The process of melt-
ing is considered in Stefan problem approximation, considering
the phase transition boundary to be a smooth surface, on which
the conditions of thermodynamic equilibrium and heat balance
are fulfilled:
21 1
21
,( ),
TT
TT
mnn
λλ κρ
∂∂
=−+=⋅
∂∂ vn
where
0
( )/2
ml s
TTT= +
is fictitious melting temperature,
0
,
ls
TT
are temperatures of equilibrium values of liquidus and
Figure 1. T he weld zone la yout: 1 – laser beam, 2 – st eam c hannel,
3 – liquid phase (molten pool), 4 – two-phase zone , 5 – solid phase.

A. N. CHEREPANOV ET AL.
271
solidus, respectively, n is unit normal to the phase transition
boundary, κ is the melting heat (heat of crystallization),
( )
11
/T λ ∂∂n
and
( )
22
/T λ −∂∂n
are the heat flu xes calculated
on the sides of the solid and liquid phases, respectively. This
approximation is reasonable, because at high temperature gra-
dients, zone of the phase transition at melting is a thin layer,
which thickness is much less than the weld pool characteristic
size. Considering
0
( )/2
ml s
TTT= +
to be the melting temper-
ature, we can uninterruptedly proceed to modeling of nonequi-
librium heterogeneous crystallization on active superdispersed
seeds in region of the alloy solidification (
0el
TTT≤<
). Here, Te
is temperature of solidification completion, determined from
kinetic equation
( )
/
l
T TCK
e eee
ξ =− 
where
,,CK
eee
ξ

are velocity of the solidification boundary
movement, impurity concentration on i t, and the kinetic co effi-
cient, respectively. For the problem's simplification, the kinetic
overcooling (/
ee
K ξ
) is neglected due to its smallness, and the
temperature of solidification completion, similarly to the theory
of quasi-equilibrium two-phase zone [3], is considered equal to
the eutectic temperature (
()
e le
T TC=
, where
e
C
is impurity
concen tration in the eutectic po int). In th e area of solid ification
(i = 2), the crystallization rate is defined by the processes of
origin and growth of solid phase in overcooled alloy on seeds,
which are refractory activated nanoparticl es . Con s id ering all th e
nanoparticles to be centers of crystallization, we can define
section of the solid phase, using the formula of Kolmogorov
N.E. [4,5]:
1,
s
fe
−Ω
= −
(2)
where
( )
0
3
4
,, 3l
x
u
pp x
K
xy zNrTd
v
πξ

Ω =+∆


∫
is volu me o f the cr ystal p hase for med in o vercoo led melt. H ere,
p
N
is the number of nanoparticles in volume unit; xl0 is the
coordinate of point x on isotherm with the temperature of li-
quidus Tl0 ,
0
()
ll
fT
=
4 /3
1
p
N
e
π −
≈
, p r is the radius of nanopar-
ticles; Ku is the constant of crystal growth in kinetic law [4-6]
u =Ku [Tl(C)
−
T]n,
where u is the growth rate, n is a physical constant (n = 1 at
normal mechanism of growth, n = 2 at dislocation one); Tl(C) is
the liquidus temperature, which is approximated by linear de-
pendenc e on di s sol v e d (a lloy ing) component С:
Tl(C) = Tl0 – β (C – C0 ),
where C0 is initial concentration of the dissolved component,
β
is coefficient module of the liquidus line slope on the state dia-
gram of corresponding binary alloy,
T∆
is local overcooling,
defined by equation
( )
–
l
T TCT∆=
(3)
According to (1), (2) and (3), in the crystallization zone
(
0el
TTT≤<
) appear s a source o f heat, connected with heat gen-
eration during the melt crystallization. Due to nonlinear depen-
dence of
()
l
fT
, contribution of this heat generation can be
taken into account by solving the equation of heat conduction
iteratively, specifying on iterations
l
f
and, consequently, T in
the zo ne of crystallizat ion.
Boundary conditions. At infinite distance from the radiation
source
, xy→∞ →∞
we assume
( )
0
,, .T xyzT=
On the
plates upper and lower surfaces
(0, )z zh= =
blown by the
inert gas, outside the steam channel, are fulfilled conditions of
complex con vective and radiat ion heat exchange with th e envi-
ronment
0, 0,
( ).
iт zh g zh
TTT
z
λα
Σ= =
∂−
∂
=
(4)
Here, Tg is the gas temperature,
m
α
Σ
is the total coefficient
of heat transfer defined by expression
( )( )
22
00 0
,
mkmmzg zg
TTTT αα εσ
Σ==
=+ ++
m
ε
is reduced emissivity of the heat transfer surf aces, m=0,
1 for the upper and lower surfaces, respectively;
0
σ
is Ste-
phan–Boltzmann constant,
km
α
is coefficient of convective
heat transfer [7]
1/2 1/3
0,646Re Pr,
/
kmmg l
αλ
=
where
Re/; P/; r
mgmgg g
va νν ==
gm
v
is the gas flow ve-
locity; l is the characteristic length of the cooling zone;
ν
g, ag,
λ
g are the gas kinematic viscosity, temperature conductivity,
and heat conductivity, respectively.
In the laser radiation impact zon e (on the steam channel su r-
face z = Zc(x y) is fulfilled the heat balance condition:
.
3T Lm
λ − ∇⋅=⋅−  n qn
(5)
Here,
m

is mass velocity of the substance evaporation from
the surface unit, related to the vapors excessive pressure P(z)
necessary for keeping the channel walls from collapse. It is
defined by relation v ()m Pz ρ =
,
v
ρ
is the vapor density; L
is specific heat of the alloy evaporation, q is the absorbed heat
flux with the re-reflecti on taken int o account,
n
is unit normal
to the ch annel surface. In numerical simulat ion , the last relat ion
determines t he h eat flu x on the stea m chann el su rface and is the
boundary condition for equation (1). We assume, that the
welding is realized by CO2laser radiation with wavelength λ
0 =
10,6 μm. The radiation intensity is described by Gaussian normal
distribution
( )
22
0
,,exp( 2)
z
I xyzIrr= −/
where
( )
2
0
2/ ;
z
IWr π =
W is the las er power, rz is the radius of the laser beam at depth z
of the steam chann el, det er min ed by relation [8]
2
20
,
F
zFF
zZ
rr r λ
π

−
=+ 

where rF is the laser beam radius i n focal plane; ZF is lo cation
of the focus relative t o the upper surface s of the details welded.
For density distribution of the absorbed radiation power on
the surface of the steam channel with coordinates z=Zc(x, y) in
the zo ne of direct i nteraction we have expressi on
( ) ( )
( )
22
2
2
, ,,exp2/
ef
z
z
AW
qxyZ xyrr
r
π
=−
Here,
(1 )
ef
A AAA
e
=+−
is the absorption effective coeffi-
cient. The first member in this coefficient takes into account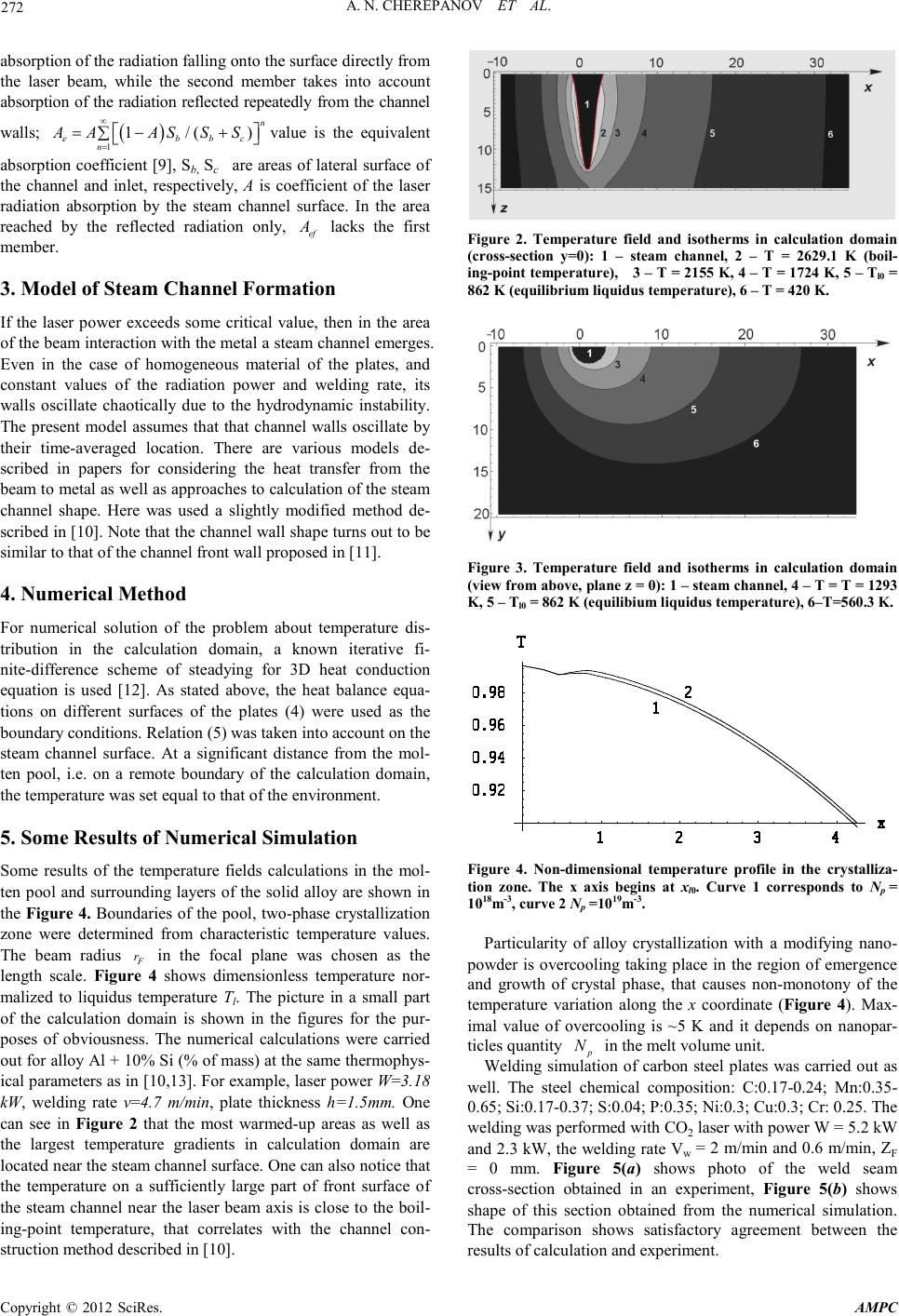

A. N. CHEREPANOV ET AL.
272
absorption of the radiation fallin g onto th e surface di rectl y fro m
the laser beam, while the second member takes into account
absorption of the radiation reflected repeatedly from the channel
walls;
( )
11n
eb bc
n
A AASSS
∞
=
=−/ (+)
∑
value is the equivalent
absorption coefficient [ 9], S b, Sc are areas of lateral surface of
the channel and inlet, respectively, A is coefficient of the laser
radiation absorption by the steam channel surface. In the area
reached by the reflected radiation only,
ef
A
lacks the first
member.
3. Model of Steam Channel Formation
If the laser power exceeds some critical value, then in the area
of the b eam interactio n with the metal a stea m channel emerges.
Even in the case of homogeneous material of the plates, and
constant values of the radiation power and welding rate, its
walls oscillate chaotically due to the hydrodynamic instability.
The present model assumes that that channel walls oscillate by
their time-averaged location. There are various models de-
scribed in papers for considering the heat transfer from the
beam to metal as well as ap pro aches to calculat ion of the stea m
channel shape. Here was used a slightly modified method de-
scribed in [10]. Note that the channel wall shape turns out to be
similar to that of the channel front wal l proposed i n [11].
4. Numerical Method
For numerical solution of the problem about temperature dis-
tribution in the calculation domain, a known iterative fi-
nite-difference scheme of steadying for 3D heat conduction
equation is used [12]. As stated above, the heat balance equa-
tions on different surfaces of the plates (4) were used as the
boundary conditions. Relation (5) was taken into account on the
steam channel surface. At a significant distance from the mol-
ten pool, i.e. on a remote boundary of the calculation domain,
the temperat ure was set equal to that of the environment.
5. Some Results of Numerical Simulation
Some results of the temperature fields calculations in the mol-
ten pool and surrounding layers of the solid alloy are shown in
the Figure 4. Boundaries of the pool, two-phase crystall ization
zone were determined from characteristic temperature values.
The beam radius
F
r
in the focal plane was chosen as the
length scale. Figure 4 shows dimensionless temperature nor-
malized to liquidus temperature Tl. The picture in a small part
of the calculation domain is shown in the figures for the pur-
poses of obviousness. The numerical calculations were carried
out for alloy Аl + 10% Si (% of mass) at the same thermophys-
ical paramet ers as in [ 10,1 3]. For exampl e, laser p ower W=3.18
kW, welding rate v=4.7 m/min, plate thickness h=1.5mm. One
can see in Figure 2 that the most warmed-up areas as well as
the largest temperature gradients in calculation domain are
located n ear th e steam chan nel surface. One can also n ot ice that
the temperature on a sufficiently large part of front surface of
the steam channel near the laser beam axis is close to the boil-
ing-point temperature, that correlates with the channel con-
struc ti o n method des c r ibe d i n [1 0 ].
Figure 2. Temperature field and isotherms in calculation domain
(cross-section y=0): 1 – steam channel, 2 – T = 2629.1 K (boil-
ing-point temperature), 3 – T = 21 55 K , 4 – T = 1724 K, 5 – Tl0 =
862 K (equilibrium liquidus temperature), 6 – T = 420 K.
Figure 3. Temperature field and isotherms in calculation domain
(view from above, plane z = 0): 1 – ste am cha nnel, 4 – T = T = 1293
K, 5 – Tl0 = 862 K (equilibium liquidus tem p eratu re) , 6 –T=560. 3 K .
Figure 4. Non-dimensional temperature profile in the crystalliza-
tion zone. The x axis begins at xl0. Curve 1 corresponds to Np =
1018m-3, curve 2 Np =1019m-3.
Particularity of alloy crystallization with a modifying nano-
powder is overcooling taking place in the region of emergence
and growth of crystal phase, that causes non-monotony of the
temperature variation along the x coordinate (Figure 4). Max-
imal value of overcooling is ~5 K and it depends on nanopar-
ticles quantity
p
N
in the melt volume unit.
Welding simulation of carbon steel plates was carried out as
well. The steel chemical composition: С:0.17-0.24; Mn:0.35-
0.65; Si:0.17-0.37; S:0.04; P:0.35; Ni:0.3; Cu:0.3; Cr: 0.25. The
welding was performed with CO2 laser with po wer W = 5. 2 kW
and 2.3 kW, the welding rate Vw = 2 m/min and 0.6 m/min, ZF
= 0 mm. Figure 5(a) shows photo of the weld seam
cross-section obtained in an experiment, Figure 5(b) shows
shape of this section obtained from the numerical simulation.
The comparison shows satisfactory agreement between the
results of calculation and experiment.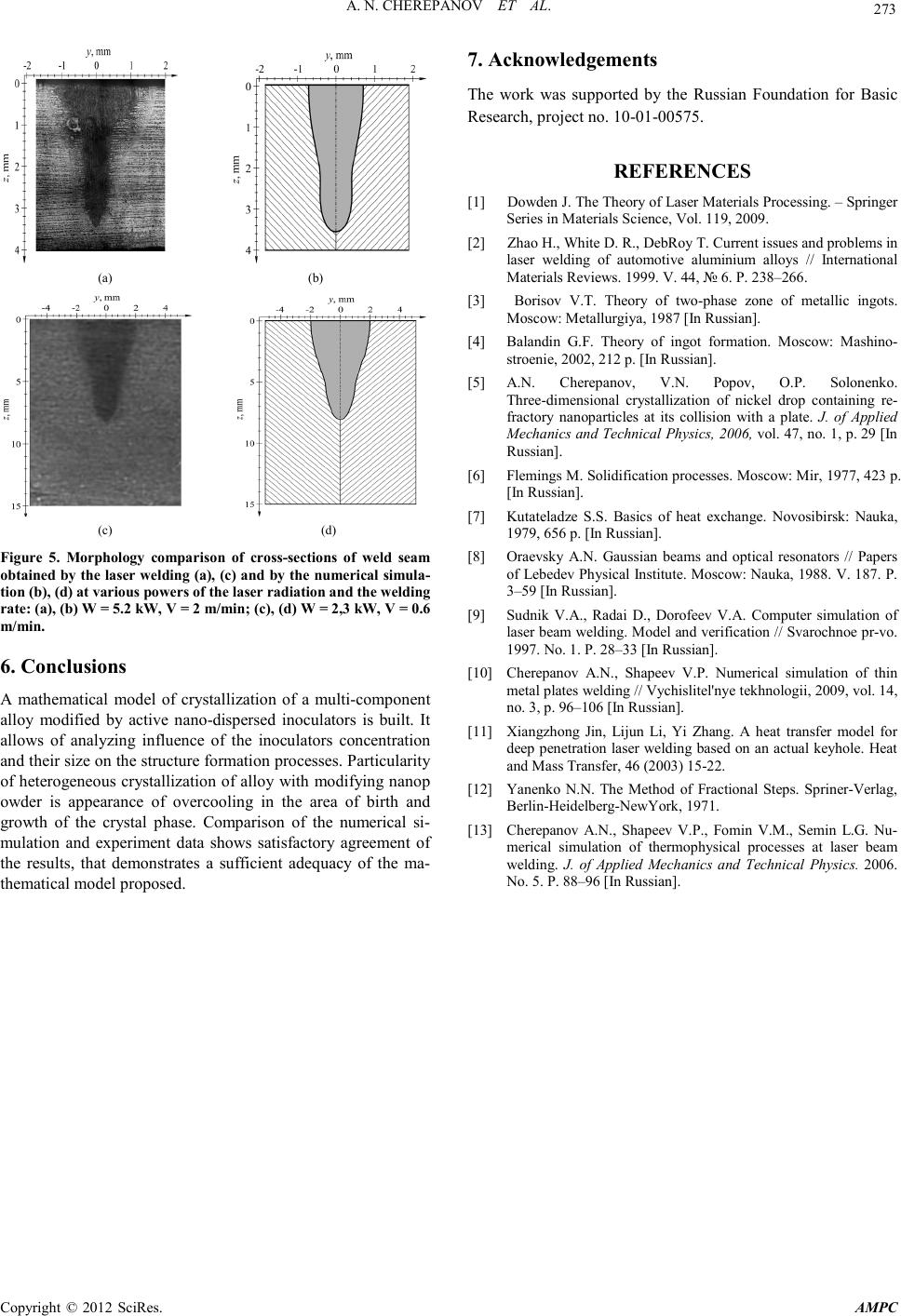

A. N. CHEREPANOV ET AL.
273
(a) (b)
(c) (d)
Figure 5. Morphology comparison of cross-sections of weld seam
obtained by the laser welding (a), (c) and by the numerical simula-
tion (b), (d) at various powers of the laser radiation and the welding
rate: ( а), (b) W = 5.2 kW, V = 2 m/min; ( с), (d) W = 2,3 kW , V = 0.6
m/ mi n .
6. Conclusions
A mathematical model of crystallization of a multi-component
alloy modified by active nano-dispersed inoculators is built. It
allows of analyzing influence of the inoculators concentration
and t hei r size o n the stru ctu re formati on p rocesses. Part icu larit y
of heterogeneous crystallization of alloy with modifying nanop
owder is appearance of overcooling in the area of birth and
growth of the crystal phase. Comparison of the numerical si-
mulation and experiment data shows satisfactory agreement of
the results, that demonstrates a sufficient adequacy of the ma-
thematical model proposed.
7. Acknowledgements
The work was supported by the Russian Foundation for Basic
Research, project no. 10-01-00575.
REFERENCES
[1] Do wden J . Th e Theory of Laser M a t eri a ls P roc es si n g. – Springer
Series in Materia l s Scienc e, Vol. 119, 2009.
[2] Zhao H., White D. R., DebRoy T. Current issues and problems in
laser welding of automotive aluminium alloys // International
Mat er ial s Reviews. 199 9 . V. 44, № 6. P. 238–266.
[3] Borisov V.T. Theory of two-phase zone of metallic ingots.
Moscow: Metallurgiya, 1987 [In Russian].
[4] Balandin G.F. Theory of ingot formation. Moscow: Mashino-
stroenie, 2002, 212 p. [In Russian].
[5] A.N. Cherepanov, V.N. Popov, O.P. Solonenko.
Thre e-dimensional crystallization of nickel drop containing re-
fractory nanoparticles at its collision with a plate. J. of Applied
Mechanic s and Technical Physics, 200 6, vol. 47, no. 1 , p . 29 [In
Russian].
[6] Flemin gs M . Solidi ficat i on proc esses. M osc ow: Mir, 1977, 4 23 p.
[In Russian].
[7] Kutateladze S.S. Basics of heat exchange. Novosibirsk: Nauka,
1979, 656 p. [In Russian].
[8] Oraevsky A.N. Gaussian beams and optical resonators // Papers
of Lebedev Physical Institute. Moscow: Nauka, 1988. V. 187. P.
3–59 [In Russian].
[9] Sudnik V.A., Radai D., Dorofeev V.A. Computer simulation of
laser bea m welding. Model and verific ation // Svaroc hnoe pr-vo.
1997. No. 1. P. 28–33 [I n Russ i an].
[10] Cherepanov A.N., Shapeev V.P. Numerical simulation of thin
meta l plat es weld in g // Vych i slit el'n ye tek hn ologii , 2009, vol. 14,
no. 3, p. 96–106 [In Russian].
[11] Xiangzhong Jin, Lijun Li, Yi Zhang. A heat transfer model for
deep penetration laser welding based on an actual keyhole. Heat
and Ma s s Transfer, 46 (2003) 15-22.
[12] Yanenko N.N. The Method of Fractional Steps. Spriner-Verlag,
Berlin-Heidelberg-NewYork , 1971.
[13] Cherepanov A.N., Shapeev V.P., Fomin V.M., Semin L.G. Nu-
merical simulation of thermophysical processes at laser beam
welding. J. of Applied Mechanics and Technical Physics. 2006.
No. 5. P. 88–96 [In R uss ian].