Communications and Network, 2013, 5, 634-640
http://dx.doi.org/10.4236/cn.2013.53B2114 Published Online September 2013 (http://www.scirp.org/journal/cn)
Performance E valu a tion of Fl o ws with Di vers e Traffic and
Transmission Rates in IEEE 802.11 WLAN
Yiru Wu, Yinghong Ma, Hongyan Li, Jiandong Li
State Key Laboratory of Integrated Service Networks, Xidian University, Xi’an, China
Received July 2013
ABSTRACT
IEEE 802.11 WLAN cannot guarantee the QoS of applications, thus admission control has been proposed as an essen-
tial solution to enhance the QoS. Packet delay and throughput are commonly employed as assessment criterions to de-
termine whether a new connection can be admitted into the WLAN. Considering the real network condition, the analyt-
ical model is presented in this paper, which is aimed to evaluate the packet delay and throughput performance of IEEE
802.11 WLAN in nonsaturated conditions, taking into account diverse transmission rates and diverse traffic flows (i.e.
flows with differ ent packet sizes and arrival rates) simultaneously. This model is based on Markov chain and the theo-
retical predictions are verified by simulation in OPNET 14.5. We also analyze the influences of transmission rate diver-
sity and traffic flow div ersity on th roughput performance. It is observed that, the presence of even one station with low-
er transmission rate can cause a considerable degradation in throughput performance of all the stations when they have
the same packet size and arrival rate. Higher system throughput can be achieved if lower transmission rate stations
transmit packets with smaller size or arrival rate.
Keywords: IEEE 802.11 DCF; Transmission Rate Diversity; Traffic Flow Diversity; Packet Delay; Throughput
Performance
1. Introduction
In recent years, the IEEE 802.11 based wireless LANs
(WLANs) have gained great popularity due to high band-
width, low cost and simple deployment. The fundamental
mechanism to access the medium in 802.11 is called dis-
tributed coordination function (DCF), based on the carri-
er sense multiple access with collision avoidance (CSMA/
CA) protocol. The contention-based random access na-
ture of the CSMA/CA protocol leads to the result that
achieving a satisfactory Quality of Service (QoS) in
WLANs is challenging. To enhance QoS support in
WLANs, the IEEE 802.11e standard is proposed which
introduces prioritization to the legacy DCF by allowing
different traffic classes [1]. Nevertheless, 802.11e cannot
guarantee the QoS all the time for the existence of con-
tentions among flows of the same priority, especially
under heavy load conditions [2].
Admitting a new connection can cause severe degrada-
tion in the QoS of the legacy connections in a WLAN,
which can be seen from the simulation results by OPNET
14.5. In the simulation, multiple wireless stations were
associated with the same 802.11b AP, which is connected
to a 100 Mbps Ethernet. The setup was used to make
full-duplex VoIP calls between a wireless station and a
wired station using IP phones. For each call, we used the
ITU G711 a-Law codec where frames are sent out every
10 milliseconds. We tested the number of VoIP connec-
tion with acceptable voice quality by successively estab-
lishing new calls in addition to the ongoing calls. As
shown in Figures 1 and 2, as soon as the seventh call
was placed, the average packet delay of every VoIP con-
nection became too high and there was a sharp decrease
in total throughput.
Admission control has been proposed as an essential
Figure 1. Average packet delay of VoIP connection.
34567
0
500
1000
1500
2000
2500
3000
3500
4000
4500
Number of VoIP connection
Dela y (ms )

Y. R. WU ET AL.
635
Figure 2. Total throughput.
solution to provide QoS guarantees for applications over
WLANs. Packet delay and throughput are commonly
employed as assessment criterions to determine whether
a new connection can be admitted into the WLAN [3-5,
7]. A loose estimation of delay or throughput is harmful
for admission control, because once traffic load exceeds
the network capacity, the quality of all ongoing connec-
tions will be jeopardized as shown in Figures 1 and 2.
Consequently, the accuracy of predicting delay or through-
put is of great significance.
Numerous efforts have been made to model the behav-
ior of the DCF of IEEE 802.11 and analyze the delay and
throughput performance of WLAN. Bianchi [6] firstly
develops a bidimensional discrete-time Markov chain mod-
el to calculate the system throughput in saturated condi-
tions, meaning that the stations always have packets to
transmit. The nonsaturated condition is considered in
[7-10]. In [7], a modification of [6] is put forward where
a probability is introduced that represents a station hav-
ing no packet ready for transmission. The model is not
predictive as this probability is not known as a function
of traffic load and must be estimated from simulation. In
[8], idle states are added after a successful packet trans-
mission where a station waits for the following packet
from upper layers. The delay in the idle states is distri-
buted geometrically with a parameter
λ
; nevertheless,
no relationship is given between
λ
and the traffic load
on the system. In [9,10], the probability of a sta tion hav-
ing at least one p acket ready for transmissio n is expressed
as a function of traffic load, which takes into account the
packet arrival rate diversity.
In the previous work, different stations are assumed to
have the same transmission rate or packet size for simpli-
fication. In order to accurately predicting delay or through-
put, we consider the traffic flow diversity (i.e. packet size
diversity and arrival rate diversity) and the transmission
rate diversity simultaneously, and derive the formulas for
delay and throughp ut in non-saturated cases. Specifically,
our contributions presented in this paper are the follow-
ing,
• We present a discrete Markov chain model to calcu-
late the probability τ of a station transmitting in an ar-
bitrary time slot in nonsaturated conditions. The Mar-
kov chain model utilized considers suspension of the
backoff time counter when the channel is sensed
busy.
• To determine τ, we express the probability q that
represents a station having at least one packet ready
for transmission in a randomly chosen time slot. q is
related to the length of the time slot which may be
occupied by a successful transmission, a collision, or
being idle. To precisely calculate the length of the
time slot occupied by a collision, we take into account
both the packet size diversity and the transmission
rate diversity.
• The packet delay is defined as the delay from the time
instant when a packet is at the head of the queue to
the time instant when the packet is successfully trans-
mitted, which is a stochastic variable. We assume the
distribution of packet delay to be a geometric distri-
bution and derive the average packet delay of hetero-
geneous f l ows.
• We formulate the individual throughput and system
throughput respectively. By simulation in OPNET 14.5,
it is verified that these formulas can closely approx-
imate the throughput performance in WLAN.
• We also analyze the influences of transmission rate
diversity and traffic flow diversity on throughput per-
formance and draw the conclusion that, the system
throughput can be increased if lower transmission rate
stations transmit packets with smaller size or arrival
rate.
2. Analytical Model
In this paper, we consider only the basic access mechan-
ism and assume that: 1) the network consists of N con-
tending stations, labeled i=1, 2, …, N; 2) packets arrive
at the MAC layer of station i based on Poisson process
with arrival r ate
i
λ
, where
[ ]
1, iN∈
; 3) packets of sta-
tion i have constant size Li and transmission rate Ri,
where
[ ]
1, iN∈
.
Let
i
S
T
be the time the channel is sensed busy be-
cause of a successful transmission from station i; and w e
have
i
S ii
T LR=
,
[ ]
1, iN∈
. Suppose that there are M
different values of
i
S
T
(due to the diversity of packet
size and transmission rate) labeled
1
S
T
,
2
S
T
, …,
M
S
T
with the relation
12 M
SS S
TT T> >>
holding and that
l
n stations have the same value of
i
S
T
that equals to
l
S
T
(
[ ]
1, lM∈
), thus having
1
Ml
lnN ==
∑
.
2.1. Per-Station Markov M ode l
The Markov chain model presented in this paper is de-
picted in Fig u r e 3. In the model, each station is modeled
34567
0
0.2
0.4
0.6
0.8
Number of VoIP connection
Throughput (Mbps)

Y. R. WU ET AL.
636
Figure 3. Non-saturated Markov chain model for IEEE 802.11.
by pair of stochastic processes b(t) and s(t), representing
the backoff time counter and the backoff stage respec-
tively. For convenience, the simplified notations ( j, k) are
used instead of (s(t), b(t)) to represent each state in this
model.
The backoff stage j starts at 0 at the first attempt to
transmit a packet and is increased by 1 every time a
transmission attempt results in a collision, up to a maxi-
mum value m. Initially, the backoff time counter k is
chosen uniformly between
0, 1
j
W  −

, where typically
0
=2
j
j
WW
is the range of the counter and W0 is the
802.11 parameter CWmin. At the beginning of each slot,
the counter is decremented if the channel is sensed idle
and frozen if a transmission is detected on the channel.
When the counter reaches zero, the station attempts to
transmit.
A new state E is introduced for a station to check
whether there is at least one packet to transmit or not
after a successful transmission. If there is none packet
awaiting transmission, the station remains in this state;
otherwise, the 802.11 MAC begins another stage-0
backoff.
We represent by
i
p
the conditional collision proba-
bility of a packet transmitted by station i, where
[ ]
1, iN∈
. The probability
i
p
is assumed to be constant
and independent, regardless of the number of retransmis-
sions already suffered. Under the assumption, we have
for
0 -1
j
kW≤≤
[ ]
[ ]
[ ]
+1
(j+1,k)|(j,0)= 0<
(j,k)|(j,0)= =
E|(j,0)=1 0
i
j
i
j
i
p
P jm
W
p
P jm
W
Pp jm
≤
− ≤≤
(1)
Furthermore,
i
p
also stands for the probability of
detecting the channel busy. For
0jm≤≤
and
0< -1
j
kW≤
, we have
[ ]
[ ]
(j,k1)|(j,k) =1
(j,k)|(j,k)=
i
i
Pp
Pp
−−
(2)
i
q
represents the probability of a station having at
least one packet ready for transmission. We have for
0
0 -1kW≤≤
[ ]
[ ]
0
E|E =1
(0,k)|E =
i
i
Pq
q
PW
−
(3)
Let
,,ijk
b
be the stationary distribution of the Markov
chain for station i. We can obtain a closed-form solution
for this chain. First, note that
, -1,0, ,0,j,0,0,0
,m-1,0,m,0 ,m,0,0,0
,0,0
,s,0
s=0
== 0< j<
=(1)= 1
(1 )==
j
ijiijii im
i
i iiiii
i
mi
iiEiE
i
bpbbpbm
p
b ppbbb
p
b
bp bqbq
⋅→
⋅− →−
⋅− ⋅→
∑
(4)
pipipipi
0,0 0,W0-2 0,W0-1
1-pi
0,1 0,2
1-pi. . .
1-pi1-pi
pi /W1. . .. . .. . .. . .. . .. . .
j-1,0
pipipipi
j,0 j,Wj-2 j,Wj-1
1-pi
j,1 j,2
1-pi. . .
1-pi1-pi
pi /Wj+1 . . .. . .. . .. . .. . .. . .
pi /Wj
pipipipi
m,0
m,W
m
-2 m,W
m
-1
1-pi
m,1 m,2
1-pi. . .
1-pi1-pi
pi /Wm
pi /Wm
qi /W0
1-qi
1-pi
1-pi
1-pi
1-pi
E

Y. R. WU ET AL.
637
Owing to the chain regularities, the following relations
hold, for
0< 1
j
kW≤−
( )
, s,0
s=0
, ,, 1,0
, m1,0, ,0
(1 )0
10
1
m
ii
j
ijki ij
ji
i iim
pb j
Wk
bpb jm
Wp
p bbjm
−
−
−=


−
=⋅⋅ ⋅<<

−
⋅+ =


∑
(5)
From relations (4), we can obtain
( )
, ,0,0,0
j0
=1
m
ij ii
bb p
=
−
∑
. Then rewrite (5) as
, , , ,0
1
=0, 0< 1
1
j
ijk ijj
ji
Wk
bbjm kW
Wp
−⋅⋅≤≤≤ −
−
(6)
Thus, all the stationary probabilities
,,ijk
b
can be ex-
pressed in terms of
,0,0i
b
, and
,0,0i
b
is finally deter-
mined by imposing the normalization condition
1
, ,
=0 =0
+ =1
j
W
m
i jkE
jk
bb
−
∑∑
(7)
from which
()( )
()()( )
( )
()( )
,0,0
2
2
00
2 121
=12+1+1 2+2121
i
i ii
m
iiiiii i
b
qpp
qpWq pWppp
−−
−− −−
(8)
As any transmission attempt occurs when k = 0, irres-
pective of the backoff stage, we can now express the
probability
i
τ
that station i transmits in a randomly
chosen slot time, that is
()( )
()()()
( )
()( )
,0,0
, ,0
j=0
2
00
==
12 121
=12+1+1 2+2121
mi
i ijiiii
m
iiiiiii
b
bpqpp
qpWq pWppp
τ
−−−
−− −−
∑
(9)
A collision occur s if more than one station is trans mit-
ting in the same time slot. As station i transmits with
probability
i
τ
, the conditional collision probability can
be ex pressed as
=1
=1(1)
N
iu
u
ui
p τ
≠
−−
∏
(10 )
With m and W0 given in 802.11 standard, in order to
determine τi and pi, we must determine qi first.
2.2. Probability q with Traffic Flow Diversity
and Transmissi on Rate Diversity
Under our assumption of Poisson process for packet ar-
rival, the probability qi can be expressed as
=1
iS
E
i
qe
λ −
−
(11)
where ES is the average length of a time slot. The length
of the virtual time slot is not a fixed value, and each time
slot may be occupied by a successful transmission, a col-
lision, or the medium being idle, which gives
11
=+ +
ii
NM
ll
SidleS Scc
il
E PPTPT σ
= =
⋅∑∑
(12)
where,
σ
is the duration of an empty slot tim e;
idle
P
is
the probability the channel is sensed idle (i.e., none sta-
tion transmitting);
=1
= (1)
N
idle u
u
P τ −
∏
(13)
i
S
T
is the time the channel is sensed busy because of a
successful transmission from station i;
i
S
P
is the proba-
bility station i successfully transmits (i.e., only station i
transmitting);
u=1
(1 )
i
N
Si u
ui
P ττ
≠
= −
∏
(14)
l
c
T
is the time the channel is sensed busy during a
collision, i.e., the longest transmission time of stations
involved in a collision; then
l
c
T
has M possible values
that are
[ ]
1,
ll
cS
TT lM= ∈
(15)
l
c
P
is the probability of
l
c
T
being equal to
l
S
T
, for
[ ]
1,lM∈
( )( )
0
0
0
1
111
1 11
l
Nj N
n
l
ci Nji
jiiN j
P ττ τ
+−
+
=== ++

=− ⋅⋅−−


∑∏∏
(16)
where
1
01
lk
k
Nn
−
=
=∑
.
The set of Equations (9)-(11) (i=1, 2, …, N) represent
a nonlinear system with 3N unknowns τi, pi and qi, which
can be solved by numerical techniques.
2.3. Average Packet Delay
We approximate the random length of the virtual time
slot by its average value ES given by (12). Suppose Xi is a
random variable that represents the number of time slots
that station i needs for a successful transmission, then the
packet delay of station i is also a random variable given
by
i Si
T EX= ⋅
. Assume that the distribution of Xi is a
geometric distribution, and that the probability of station
i successfully transmitting in a random slot is
i
S
P
given
by (14). Thus, the distribution of packet delay is a geo-
metric distribution given as follows,
{ }
( )
1
1
i
ii
x
i siSS
PTE xPP
−
=⋅=− ⋅
(17)
from which the average packet delay of station i, E[Ti],

Y. R. WU ET AL.
638
derives,
[ ][]
1
i
iS iS
S
ETE EXEP =⋅=⋅
(18)
2.4. Throughput Formulation
We are now able to express the throughput of station i as
the ratio of the time that the medium is occupied by sta-
tion i for successful transmission to the average packet
delay of station i.
[ ]
==
i ii
S SS
i
iS
T PT
SET E
(19)
As a result, the system throughput is
=1
=N
i
i
SS
∑
(20)
3. Model Verification
Suppose there are 6 stations and two possible trans-
mission rates of 1 Mbps and 11 Mbps in the WLAN. The
other parameters are summarized in Table 1.
We first evaluate the throughput when different sta-
tions have different transmission rates but the same
packet size
==1024 bytes
i
LL
(including MAC, IP, UTP
and RTP headers) and the same arrival rate λi = λ = 100
packets/sec. Starting with all stations at 1 Mbps, we in-
crease the transmission rate of one of them to 11 Mbps in
each step. Eventually all six stations have the rate of
11Mbps. We simulate this setup in OPNET 14.5. Figure
4 shows that the analytical formulas (19) and (20) can
closely approximate the individual throughput and the
system throughput respectively. It is obvious from the
figure that even one lower transmission rate can cause a
considerable degradation in throughput performance of
all the stations. This degradation is a consequence of the
DCF mode which guarantees equal packet transmission
probability to all stations. As a result, lower data rate
stations receive more time to transmit and unfairly bring
down the throughput of the higher data rate stations. This
degradation was previously observed in [11] under satu-
rated conditions. Then we exploit different packet sizes
and arrival rates in the analysis.
Table 1. System parameters.
Slot Time 20 μs
PHY header 192 μs
Propagation Delay 1 μs
DIFS 50 μs
SIFS 10 μs
ACK 112 bit + PHY header
CWmi n 32
m 5
On the one hand, we reduce the packet size of stations
with rate 1Mbps to
L′
= 102 bytes, but the packet ar-
rival rate remains to be 100 packets/sec. As seen from
Figure 5, the system throughput and throughput of 11
Mbps stations are improved, whereas the 1 Mbps stations
are worse off. In this case, lower data rate stations and
higher data rate stations receive the same amount of time
to transmit.
On the other hand, we reduce th e packet arrival rate of
stations with rate 1 Mbps to
λ
′
= 15 packets/sec, but the
packet size remains to be 1024 bytes. The throughput
performance plotted in Figure 6 resembles that in Figure
5, which shows that the throughput performance of sys-
tem and high data rate stations can be enhanced by sacri-
ficing that of low data rate stations. By reducing the
packet arrival rate of lower data rate stations, the packet
transmission probability of lower rate stations is reduced.
Figure 7 shows the throughput performance when 1
Figure 4. Throughput with transmission rate diversity (L =
1024 bytes, λ = 100 packets/sec).
Figure 5. Throughput with diversity of transmission rates
and packet sizes (λ = 100 packets/sec).
0123456
0
1
2
3
4
5
6
7
8
Number of stati ons wi th 11M bps out of 6 s tat i ons, t he rest wi t h 1M bps
Throughput (M bps)
A nal y ti cal 11M STA
A nal y ti cal 1M STA
A nal y ti cal System
S i m ulati on 11M STA
S i m ulati on 1M STA
S i m ulati on System
0123 456
0
1
2
3
4
5
6
7
8
Num ber of st ations with 11Mbps out of 6 st ations , the rest with 1Mbps
Throughput (Mbps)
11M ST A
1M STA
System
Opt im ized 11M STA ( L=1024 bytes)
Opt im ized 1M STA ( L′ =102 bytes)
Opt im ized Sys tem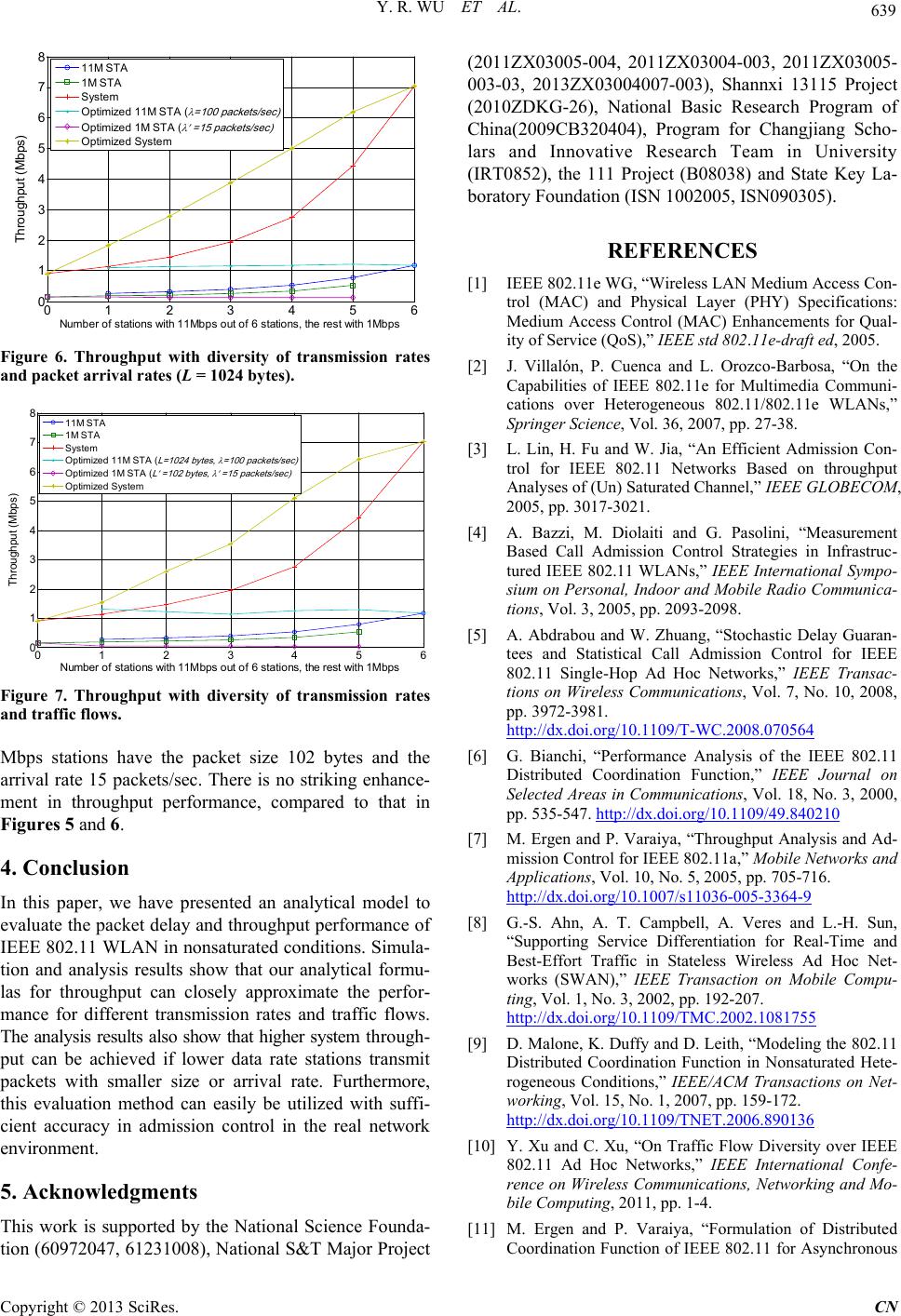

Y. R. WU ET AL.
639
Figure 6. Throughput with diversity of transmission rates
and packet arrival rates (L = 1024 bytes).
Figure 7. Throughput with diversity of transmission rates
and traffic flows.
Mbps stations have the packet size 102 bytes and the
arrival rate 15 packets/sec. There is no striking enhance-
ment in throughput performance, compared to that in
Figures 5 and 6.
4. Conclusion
In this paper, we have presented an analytical model to
evaluate the packet delay and throughput performance of
IEEE 802.11 WLAN in nonsatur ated conditions. Simula-
tion and analysis results show that our analytical formu-
las for throughput can closely approximate the perfor-
mance for different transmission rates and traffic flows.
The analysis results also show that higher system through-
put can be achieved if lower data rate stations transmit
packets with smaller size or arrival rate. Furthermore,
this evaluation method can easily be utilized with suffi-
cient accuracy in admission control in the real network
environment.
5. Acknowledgments
This work is supported by the National Science Founda-
tion (609720 47, 61231008 ), National S&T Ma jor Project
(2011ZX03005 -004, 2011ZX03004-003, 2011ZX03005-
003-03, 2013ZX03004007-003), Shannxi 13115 Project
(2010ZDKG-26), National Basic Research Program of
China(2009CB320404), Program for Changjiang Scho-
lars and Innovative Research Team in University
(IRT0852), the 111 Project (B08038) and State Key La-
boratory Foundation (ISN 1002005, ISN090305).
REFERENCES
[1] IEEE 802.11e WG, “Wireless LAN Medium Access Con-
trol (MAC) and Physical Layer (PHY) Specifications:
Medium Access Control (MAC) Enhancements for Qual-
ity of Service (QoS),” IEEE std 802.11e -draft ed, 2005.
[2] J. Villalón, P. Cuenca and L. Orozco-Barbosa, “On the
Capabilities of IEEE 802.11e for Multimedia Communi-
cations over Heterogeneous 802.11/802.11e WLANs,”
Springer Science, Vol. 36, 2007, pp. 27-38.
[3] L. Lin, H. Fu and W. Jia, “An Efficient Admission Con-
trol for IEEE 802.11 Networks Based on throughput
Analyses of (Un) Saturated Channel,” IEEE GLOBECOM,
2005, pp. 3017-3021.
[4] A. Bazzi, M. Diolaiti and G. Pasolini, “Measurement
Based Call Admission Control Strategies in Infrastruc-
tured IEEE 802.11 WLANs,” IEEE International Sympo-
sium on Personal, Indoor and Mobile Radio Communica-
tions, Vol. 3, 2005, pp. 2093-2098.
[5] A. Abdrabou and W. Zhuang, “Stochastic Delay Guaran-
tees and Statistical Call Admission Control for IEEE
802.11 Single-Hop Ad Hoc Networks,” IEEE Transac-
tions on Wireless Communications, Vol. 7, No. 10, 2008,
pp. 3972-3981.
http://dx.doi.org/10.1109/T-WC.2008.070564
[6] G. Bianchi, “Performance Analysis of the IEEE 802.11
Distributed Coordination Function,” IEEE Journal on
Selected Areas in Communications, Vol. 18 , No. 3, 2000,
pp. 535-547. http://dx.doi.org/10.1109/49.840210
[7] M. Ergen and P. Varaiya, “Throughput Analysis and Ad-
mission Control for IEEE 802.11a,” Mobile Networks and
Applications, Vol. 10, No. 5, 2005, pp. 705-716.
http://dx.doi.org/10.1007/s11036-005-3364-9
[8] G.-S. Ahn, A. T. Campbell, A. Veres and L.-H. Sun,
“Supporting Service Differentiation for Real-Time and
Best-Effort Traffic in Stateless Wireless Ad Hoc Net-
works (SWAN),” IEEE Transaction on Mobile Compu-
ting, Vol. 1, No. 3, 2002, pp. 192-207.
http://dx.doi.org/10.1109/TMC.2002.1081755
[9] D. Malone, K. Duffy and D. Leith, “Modeling the 802.11
Distributed Coordination Function in Nonsaturated Hete-
rogeneous Conditions,” IEEE/ACM Transactions on Net-
working, Vol. 15, No. 1, 2007, pp. 159-172.
http://dx.doi.org/10.1109/TNET.2006.890136
[10] Y. Xu and C. Xu, “On Traffic Flow Diversity over IEEE
802.11 Ad Hoc Networks,” IEEE International Confe-
rence on Wireless Communications, Networking and Mo-
bile Computing, 2011, pp. 1-4.
[11] M. Ergen and P. Varaiya, “Formulation of Distributed
Coordination Function of IEEE 802.11 for Asynchronous
0 123 4 56
0
1
2
3
4
5
6
7
8
Num ber of st ations with 11Mbps out of 6 stations , the rest with 1Mbps
Throughput (Mbps)
11M ST A
1M STA
S ystem
Opt im ized 11M S T A ( λ=100 packets/sec)
Opt im ized 1M S T A ( λ′ =15 packets/sec)
Opt im ized System
0 123 456
0
1
2
3
4
5
6
7
8
Number of stations with 11Mbps out of 6 stations, the rest with 1Mbps
Throughput (Mbps)
11M STA
1M STA
System
Opt imized 11M STA ( L=1024 bytes, λ=100 packets/sec)
Opt imized 1M STA ( L′ =102 bytes, λ′ =15 packets/sec)
Opt imized Syst em

Y. R. WU ET AL.
640
Networks Mixed Data Rate and Packet Size,” IEEE
Transaction on Vehicular Technology, Vol. 57, 2008, pp. 436-447. http://dx.doi.org/10.1109/TVT.2007.901887