Compression of MR Images Using DWT by Comparing RGB and YCbCr Color Spaces
Open Access JSIP
368
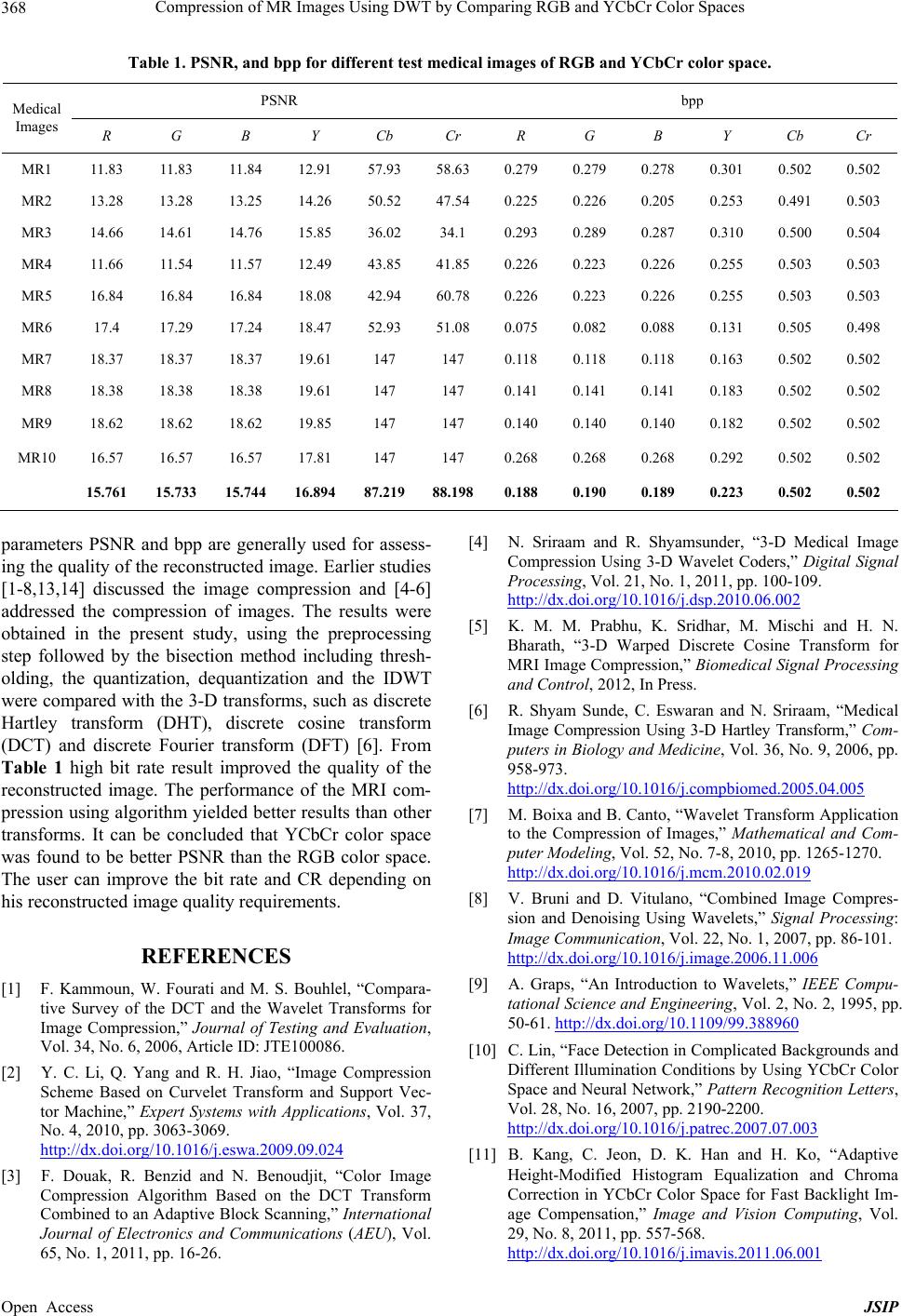
Table 1. PSNR, and bpp for different test medical images of RGB and YCbCr color space.
PSNR bpp
Medical
Images R G B Y Cb Cr R G B Y Cb Cr
MR1 11.83 11. 83 11. 84 12.91 57.93 58.63 0.279 0.279 0.278 0.301 0.502 0.502
MR2 13.28 13.28 13.25 14.26 50.52 47.54 0.225 0.226 0.205 0.253 0.491 0.503
MR3 14.66 14.61 14.76 15.85 36.02 34.1 0.293 0.289 0.287 0.310 0.500 0.504
MR4 11.66 11. 54 11. 57 12.49 43.85 41.85 0.226 0.223 0.226 0.255 0.503 0.503
MR5 16.84 16.84 16.84 18.08 42.94 60.78 0.226 0.223 0.226 0.255 0.503 0.503
MR6 17.4 17.29 17.24 18.47 52.93 51.08 0.075 0.082 0.088 0.131 0.505 0.498
MR7 18.37 18.37 18.37 19.61 147 147 0.118 0.118 0.118 0.163 0.502 0.502
MR8 18.38 18.38 18.38 19.61 147 147 0.141 0.141 0.141 0.183 0.502 0.502
MR9 18.62 18.62 18.62 19.85 147 147 0.140 0.140 0.140 0.182 0.502 0.502
MR10 16.57 16.57 16.57 17.81 147 147 0.268 0.268 0.268 0.292 0.502 0.502
15.761 15.733 15.744 16.894 87.21988.1980.188 0.190 0.189 0.223 0.502 0.502
parameters PSNR and bpp are generally used for assess-
ing the quality of the reconstructed image. Earlier studies
[1-8,13,14] discussed the image compression and [4-6]
addressed the compression of images. The results were
obtained in the present study, using the preprocessing
step followed by the bisection method including thresh-
olding, the quantization, dequantization and the IDWT
were compared with the 3-D transforms, such as discrete
Hartley transform (DHT), discrete cosine transform
(DCT) and discrete Fourier transform (DFT) [6]. From
Table 1 high bit rate result improved the quality of the
reconstructed image. The performance of the MRI com-
pression using algorithm yielded better results than other
transforms. It can be concluded that YCbCr color space
was found to be better PSNR than the RGB color space.
The user can improve the bit rate and CR depending on
his reconstructed image quality requirements.
REFERENCES
[1] F. Kammoun, W. Fourati and M. S. Bouhlel, “Compara-
tive Survey of the DCT and the Wavelet Transforms for
Image Compression,” Journal of Testing and Evaluation,
Vol. 34, No. 6, 2006, Article ID: JTE100086.
[2] Y. C. Li, Q. Yang and R. H. Jiao, “Image Compression
Scheme Based on Curvelet Transform and Support Vec-
tor Machine,” Expert Systems with Applications, Vol. 37,
No. 4, 2010, pp. 3063-3069.
http://dx.doi.org/10.1016/j.eswa.2009.09.024
[3] F. Douak, R. Benzid and N. Benoudjit, “Color Image
Compression Algorithm Based on the DCT Transform
Combined to an Adaptive Block Scanning,” International
Journal of Electronics and Communications (AEU), Vol.
65, No. 1, 2011, pp. 16-26.
[4] N. Sriraam and R. Shyamsunder, “3-D Medical Image
Compression Using 3-D Wavelet Coders,” Digital Signal
Processing, Vol. 21, No. 1, 2011, pp. 100-109.
http://dx.doi.org/10.1016/j.dsp.2010.06.002
[5] K. M. M. Prabhu, K. Sridhar, M. Mischi and H. N.
Bharath, “3-D Warped Discrete Cosine Transform for
MRI Image Compression,” Biomedical Signal Processing
and Control, 2012, In Press.
[6] R. Shyam Sunde, C. Eswaran and N. Sriraam, “Medical
Image Compression Using 3-D Hartley Transform,” Com-
puters in Biology and Medicine, Vol. 36, No. 9, 2006, pp.
958-973.
http://dx.doi.org/10.1016/j.compbiomed.2005.04.005
[7] M. Boixa and B. Canto, “Wavelet Transform Application
to the Compression of Images,” Mathematical and Com-
puter Modeling, Vol. 52, No. 7-8, 2010, pp. 1265-1270.
http://dx.doi.org/10.1016/j.mcm.2010.02.019
[8] V. Bruni and D. Vitulano, “Combined Image Compres-
sion and Denoising Using Wavelets,” Signal Processing:
Image Communication, Vol. 22, No. 1, 2007, pp. 86-101.
http://dx.doi.org/10.1016/j.image.2006.11.006
[9] A. Graps, “An Introduction to Wavelets,” IEEE Compu-
tational Science and Engineering, Vol. 2, No. 2, 1995, pp.
50-61. http://dx.doi.org/10.1109/99.388960
[10] C. Lin, “Face Detection in Complicated Backgrounds and
Different Illumination Conditions by Using YCbCr Color
Space and Neural Network,” Pattern Recognition Letters,
Vol. 28, No. 16, 2007, pp. 2190-2200.
http://dx.doi.org/10.1016/j.patrec.2007.07.003
[11] B. Kang, C. Jeon, D. K. Han and H. Ko, “Adaptive
Height-Modified Histogram Equalization and Chroma
Correction in YCbCr Color Space for Fast Backlight Im-
age Compensation,” Image and Vision Computing, Vol.
29, No. 8, 2011, pp. 557-568.
http://dx.doi.org/10.1016/j.imavis.2011.06.001