 Journal of Signal and Information Processing, 2013, 4, 351-358 Published Online November 2013 (http://www.scirp.org/journal/jsip) http://dx.doi.org/10.4236/jsip.2013.44044 Open Access JSIP 351 Multi-Level Halftoning by IGS Quantization Tadahiko Kimoto Faculty of Science and Engineering, Toyo University, Kawagoe, Japan. Email: kimoto@toyo.jp Received August 19th, 2013; revised September 15th, 2013; accepted September 24th, 2013 Copyright © 2013 Tadahiko Kimoto. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT Improved gray-scale (IGS) quantization is a known method for re-quantizing digital gray-scale images for data com- pression while producing halftones by adding a level of randomness to improve visual quality of the resultant images. In this paper, first, analyzing the IGS quantizing operations reveals the capability of conserving a DC signal level of a source image through the quantization. Then, a complete procedure for producing a multi-level halftone image by IGS quantization that can achieve the DC conservation is presented. Also, the procedure uses the scanning of source pixels in an order such th at geometric patterns can be prevented from occurring in the resulting halftone image. Next, the per- formance of the multi-level IGS halftoning is evaluated by experiments conducted on 8-bit gray-scale test images in comparison with the halftoning by error diffusion. The experimental result demonstrates that a signal level to be quan- tized in the IGS halftoning varies more randomly than that in the error diffusion halftoning, but not entirely randomly. Also, visual quality of the resulting halftone images was measured by subjective evaluations of viewers. The result in- dicates that for 3 or more-bit, in other words, 8 or more-level halftones, the IGS halftoning achieves image quality comparable to that by the error diffusion. Keywords: Digital Halftone; Multi-Level Halftone; Improved Gray-Scale Quantization; Error Diffusion; Subjective Testing 1. Introduction Digital halftoning is a technique to re-quantize a digital image to fewer bits while preventing the image appear- ance from being corrupted by producing continuous- looking tones, that is, so-called halftones [1]. For in- stance, for being printed with a black-and-white printer, an 8-bit gray-scale image is to be re-quantized to one bit or two possible levels. Thus, halftoning with two levels is still indispensable in printing. Also, halftoning with more than two levels is useful for output devices that can pro- duce many levels, such as electro static printers and com- pact LED displays. Generally in a halftoning method, some kind of signal is added to each pixel of a source image and then, the resulting signal is re-quantized to fewer bits. These sig- nals determine the resulting image appearance. A variety of halftoning methods to generate the additional signals can yield good halftone quality in the resulting images that have bee n p r oposed. Error diffusion is a well-known halftoning method that can produce halfton e images of good quality. In the error diffusion, the additional signals are generated by distrib- uting error signals, which are the difference of a source pixel level and the re-quantized pixel level, by a digital filter. Thus, the resulting halftone quality depend s on the digital filter. The improved gray-scale (IGS) quantization [2] is re- garded as a halftoning method where the additional sig- nals are generated from the low-order bits of neighboring pixels. The low-order bits in a natural scene image are generally a random variable depending on the image characteristics, and also, they are more random as the bit orders are lower. Consequently, the additional signals become a random variable with these properties. In this paper, we consider the use of the IGS quantiza- tion for multi-level halftoning. By evaluating the per- formance of multi-level quantization and the visual qual- ity of the resulting halftone images, a manner of using the IGS halftoning instead of the error diffusion halfton- ing is investigated . The rest of this paper is organized as follows: Section 2 defines the IGS halftoning. First, the IGS quantization is formulated on the basis of the literature. From an analysis of the recursion formula, it is proven that the DC  Multi-Level Halftoning by IGS Quantization 352 component of a source image can be conserved through the quantization. Then, a co mplete algorith m to apply the quantization to gray-scale images while achieving the DC conservation is presented. In Section 3, stochastic performance of IGS halftoning is evaluated through an experiment conducted on 8-bit test images. The extent of randomness of the additional signals is measured and compared between three IGS methods and two error dif- fusion methods. In Section 4, visual quality of IGS half- tone images is evaluated through a subjective testing conducted to measure image quality by the subjective evaluations of human observers. From the result, a num- ber of halftone bits can be yielded as good image ap- pearance as that achieved by error diffusion that is esti- mated. Section 5 concludes the paper. 2. IGS Halftoning 2.1. Principle of IGS Quantization The procedure of the IGS quantization from M-bit sig- nals to N-bit ones, , is expressed as follows. Here, we suppose that source pix els are of M bits withou t stating it clearly in the rest of this paper. Let 1NM n v denote the n least significant bits of the binary expression of v. Also let n denote a value that consists of the n most significant bits same as those of v and the other bits of zero. Then, an M-bit value v can be expressed as Uv NMN vU vLv . (1) For an M-bit pixel value i in a scanning order, , where T is the number of pixels in the im- age, an M-bit value Si is defined by the recursion relation p 1, 2,,iT 1iiMNi SpL S (2) where S0 is supposed to be 0. To ensure that 2 i S, if 212 NM i p N i , we use instead of Equation (2) i Sp . (3) The N-bit result of quantizing pi, denoted by Ni Qp , is given by the N most significant bits of Si. In other words, 2 N Ni Ni Qp US . (4) Figure 1 shows the relationship between source lev els and output levels of the IGS quantizer. In summary, Ni Qp is given by the relation eithe r or 1, if 212 for in the range 0,1,,22 ,if 2 for in the range 0,1,,21 21, if 2122. MN MN iN MN Ni iN N NMN M i kk kpk k k Qp pk k p (5) Figure 1. Input-output level relationship of IGS quanti zer. In this relation, for 212 NM i kpk N 2 and 02 N k , N has two possible values, which b o th de p e nd on i Qp 1MN i S . 2.2. Mathematical Properties A sum of the quantized pixels can be described as fol- lows: Expressing 1i S in the form of Equation (1), then, substituting 1iMN S into Equation (2) and using Equation (4) for 1Ni US yield the relation 11 2MN iNi i SQpS p i . (6) The summation of each side of Equation (6) for i from 1 to T yields 1 11 2 TT MN TNi ii SQp i p (7) Since 00S and hence, . Substituting the form of Equatio n (1) for ST yields the final relation: 00 N Qp 11 2 TT MN NTN ii ii LSQp p . (8) Dividing both sides of Equation (8) by T gi ves 2 MN TMN Ni i LS Qp p T (9) where represents the average of a sequence of x. Because NT S takes a value of at most 21 MN , the first term of the left-hand side of Equation (9) can be neglected for large T’ s ; thus, we obtain 2MN Ni i Qp p . (10) This relation means that a level of direct current (DC) of the source image is left almost unchanged in the quan- tized image. Also, because Equation (8) holds for any T, the DC level changes by at the most 21 MN T at any pixel during the quantizing of the image. Note that given by Equation (3) are excluded in deriving Equation (8). ' i Ss Open Access JSIP  Multi-Level Halftoning by IGS Quantization 353 2.3. Implementing of IGS Halftoning 1) Source signal range The DC conservation described above is achieved un- der the condition that all of are given by Equation (2). This condition can be satisfied by limiting the input signals of the quantizer in the range associated with Equation (2). To limit the source pixel lev els in the range, we apply a level transformation that maps the whole M- bit range onto the range to a source image before carrying out the IGS quantiza- tion. For simplicity of implementation, a linear mapping is used in the transformation in this paper. ' i Ss 0,2 1 M 0,21 2 NMN On the other hand, the level distribution in an image is likely to be distorted due to both the above level trans- formation and the following IGS quantization. On the assumption both that all the pixel levels in the range 0,2 1 M occur uniformly in an M-bit source image and that 1MN i S of Equation (2) takes on equally likely random values, it is derived from stochastic analy- sis that in the resulting N-bit image, both the occurrence frequency of level 0 and that of level 2 N1 are 122 1 N, and those of the other levels are 12 1 N. Image areas of pixel levels in the range 212 ,21 NMNM N 1 1 are painted over in the solid level after the IGS quantization. Such areas pos- terized in the highest level may degrade the resulting halftone quality. The abov e level transformation prev ents the posterization from occurring while ensuring that the source level is always quantized to 2 2 M21 N . 2) Scanning order The scanning order in an image during the IGS quan- tization affects the results according to the recursion rela- tion of Equation (2). Such processing dependent on the scanning direction is likely to produce visible artifacts in the resulting image. Scanning in a more complicated order than the raster order can reduce a relation between the scanning result and the image content [3]. Such scanning is implemented by, for example, the Hilbert path. Figure 2 illustrates an Figure 2. An example of Hilbert scanning path. example of Hilbert path through a squared image with one side of integer-power-of-2 pixels, where the path starts at the upper-left pixel and ends at the lower-left pixel. Figure 3 shows the system diagram of IGS halftoning process. This diagram involves scanning the whole of a source image once and works in point processing: For every source pixel extracted in the scanning order, first, the level transformation described in the preceding sec- tion is carried out and then, the resultant pixel value is quantized by the IGS m a nne r . 3. Stochastic Performance of IGS Quantization 3.1. Measuring Randomness of Additional Signals In this section, we evaluate the properties of the addi- tional signals, that is, 1MNi S of Equation (2) as a random variable by an experiment with real images. For a given N, let s represent a variable that produces Ni S for i1,2,,T and also, let s be regarded as a random variable in the range 0,2 1 MN . As measures of randomness of s, the following two quanti- ties are used: 1) The memory-less entropy of 12 ,,, T ss, de- noted b y , given by 21 0 log MN Ns Ps Ps (11) Figure 3. Diagram of IGS halftoning. Open Access JSIP  Multi-Level Halftoning by IGS Quantization 354 where s is the probability of s. 2) The Entropy of 12 ,,, T ss conditional on pix- els 12 ,,, T pp p, denoted by , given by 2121 00 log Nps PpPspPsp MMN (12) where Psp is the conditional probability that, given that a pixel level is p, a signal of level s is added to it, and p represents the occurrence probability of level p. These quantities are compared between the following five methods: 1) Method IGS-RAS implements the IGS quantization by raster scanning. 2) Method IGS-HIL implements the IGS quantization by the Hilbert scanning described in Section 2.3 (2). 3) Method IGS-RND uses an N-bit uniform random number, which is actually generated by a pseudo-random number generator with a computer, in- stead of 1MNi S in Equation (2). 4) Method EDF-FS implements the error diffusion scheme with the error filter proposed by Floyd and Steinberg [4]. 5) Method EDF-JJN implements the error diffusion scheme with the error filter proposed by Jarvis, Judice and Ninke [5]. In EDF-FS and EDF-JJN, the error diffusion scheme works to quantize M-bit pixels to N bits, 1NM . Because the additional signal that plays the role of 1MNi S of Equation (2) takes on fractional values in the error diffusion, itis to be digitized to M-bit levels in calculating and . 3.2. Experimental Results Experiments of the above methods were conducted on 256-gray scale (that is, 8M ) images with various values of N. The source images used in the experiments include vertical and horizontal ramp images shown in Figures 4(a) and (b), respectively, and two natural scene images Barbara and Lena shown in Figures 4(c) and (d), respectively. Note that the image Barbara includes striped regions easy to see, and Lena includes wide smooth regions. For each given N, the source images were transformed by the level transformation described in Section 2.3 (1) prior to undergo ing any of the halfton- ing methods. Figure 5 shows the measurements of the entropy N that were taken in performing each method by varying N for three of the source images. As this figure shows, the entropies in IGS-HIL are almost the same as those in IGS-RND, and consequently, the additional signals in IGS-HIL preserve a nearly uniform randomness for any N as far as the memory-less entropy is concerned. (a) (b) (c) (d) Figure 4. Examples of 8-bit source images of 256 by 256 pixels used in the experiments: (a) Vertical ramp with 1- level per pixel gradation; (b) Horizontal ramp with 1-level per pixel gradation; (c) Barbara and (d) Lena. Figure 6 shows the measurements of the entropy N for the three source images. The result indicates that in the three IGS methods, the additional signals in IGS-HIL have more randomness for source pixels than those in IGS-RAS and less randomness than those in IGS-RND, and also, more randomness than those in the two error diffusion methods. In addition, we can observe a differ- ence between the two error diffusion methods due to the error filters; the additional signals are more constrained in EDF-JJN than in EDF-FS. As regards IGS-RAS, a large difference between the measurements of the entropy of the vertical ramp image and the entropy of th e horizontal ramp image is ob served from Figure 6. This result demonstrates that the proper- ties of the additional signals in IGS-RAS are apt to de- pend on the scanning direction. Figure 7 reveals a visual difference between the IGS results of raster scanning and those of Hilbert scanning. We observe that the IGS quantization yields geometrical patterns from regions of a uniform level gradation through the raster scanning, and the generated patterns depend on the relation between the direction of raster scanning and that of gradation. On the contrary, the Hil- bert scanning is effective in inhibiting such patterns from being produced regardless of the direction of gradation. 4. Visual Quality of Halftones 4.1. Subjective Evaluation In this section, we consider appearances of multi-level Open Access JSIP  Multi-Level Halftoning by IGS Quantization Open Access JSIP 355 (a) (b) (c) Figur e 5. Entropies N of additional signals in halftoning. (a) The vertical ramp image; (b) The horizontal ramp image; and (c) Barbara. (a) (b) (c) Figur e 6. Entr opies N of additional signalsin halftoning. (a) The vertical ramp image; (b) The horizontal ramp image; and (c) Barbara. 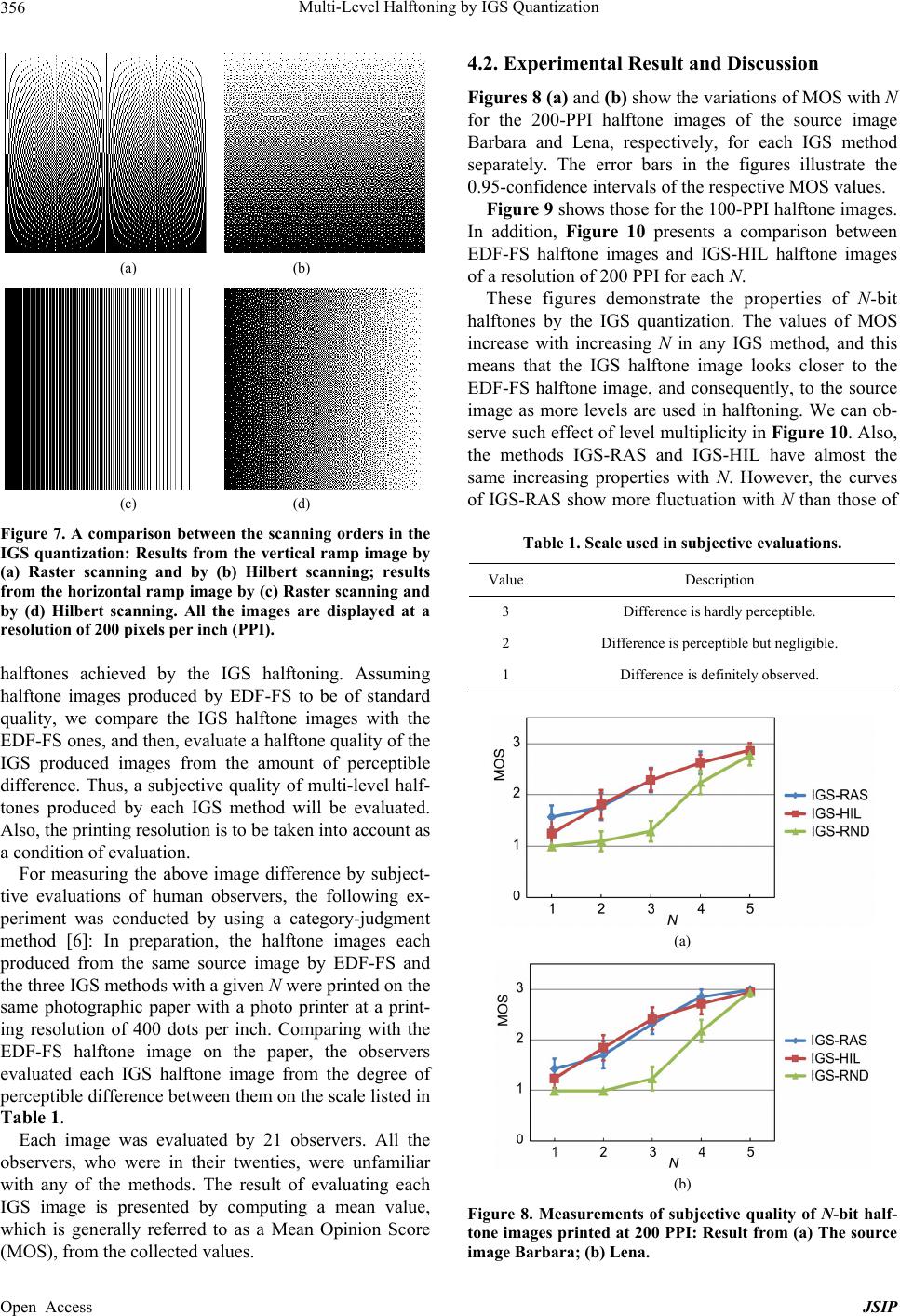 Multi-Level Halftoning by IGS Quantization 356 (a) (b) (c) (d) Figure 7. A comparison between the scanning orders in the IGS quantization: Results from the vertical ramp image by (a) Raster scanning and by (b) Hilbert scanning; results from the horizontal ramp image by (c) Raster scanning and by (d) Hilbert scanning. All the images are displayed at a resolution of 200 pixels per inch (PPI). halftones achieved by the IGS halftoning. Assuming halftone images produced by EDF-FS to be of standard quality, we compare the IGS halftone images with the EDF-FS ones, and then, evaluate a halftone quality of the IGS produced images from the amount of perceptible difference. Thus, a subjective quality of multi-level half- tones produced by each IGS method will be evaluated. Also, the printing resolu tion is to be taken into account as a condition of evaluation. For measuring the above image difference by subject- tive evaluations of human observers, the following ex- periment was conducted by using a category-judgment method [6]: In preparation, the halftone images each produced from the same source image by EDF-FS and the three IGS methods wit h a give n N were printed on the same photographic paper with a photo printer at a print- ing resolution of 400 dots per inch. Comparing with the EDF-FS halftone image on the paper, the observers evaluated each IGS halftone image from the degree of perceptible difference between them on the scale listed in Table 1. Each image was evaluated by 21 observers. All the observers, who were in their twenties, were unfamiliar with any of the methods. The result of evaluating each IGS image is presented by computing a mean value, which is generally referred to as a Mean Opinion Score (MOS), from the collected values. 4.2. Experimental Result and Discussion Figures 8 (a) and (b) show the variations of MOS with N for the 200-PPI halftone images of the source image Barbara and Lena, respectively, for each IGS method separately. The error bars in the figures illustrate the 0.95-confidence intervals of the respective MOS values. Figure 9 shows those for the 100-PPI halftone images. In addition, Figure 10 presents a comparison between EDF-FS halftone images and IGS-HIL halftone images of a resolution of 200 PPI for each N. These figures demonstrate the properties of N-bit halftones by the IGS quantization. The values of MOS increase with increasing N in any IGS method, and this means that the IGS halftone image looks closer to the EDF-FS halftone image, and consequently, to the source image as more levels are used in halftoning. We can ob- serve such effect of lev el multiplicity in Figure 10. Also, the methods IGS-RAS and IGS-HIL have almost the same increasing properties with N. However, the curves of IGS-RAS show more fluctuation with N than those of Table 1. Scale used in subjective evaluations. Value Description 3 Difference is hardly perceptible. 2 Difference is perceptible but negligible. 1 Difference is definitely observed. (a) (b) Figure 8. Measurements of subjective quality of N-bit half- tone images printed at 200 PPI: Result from (a) The source image Barbara; (b) Lena. Open Access JSIP 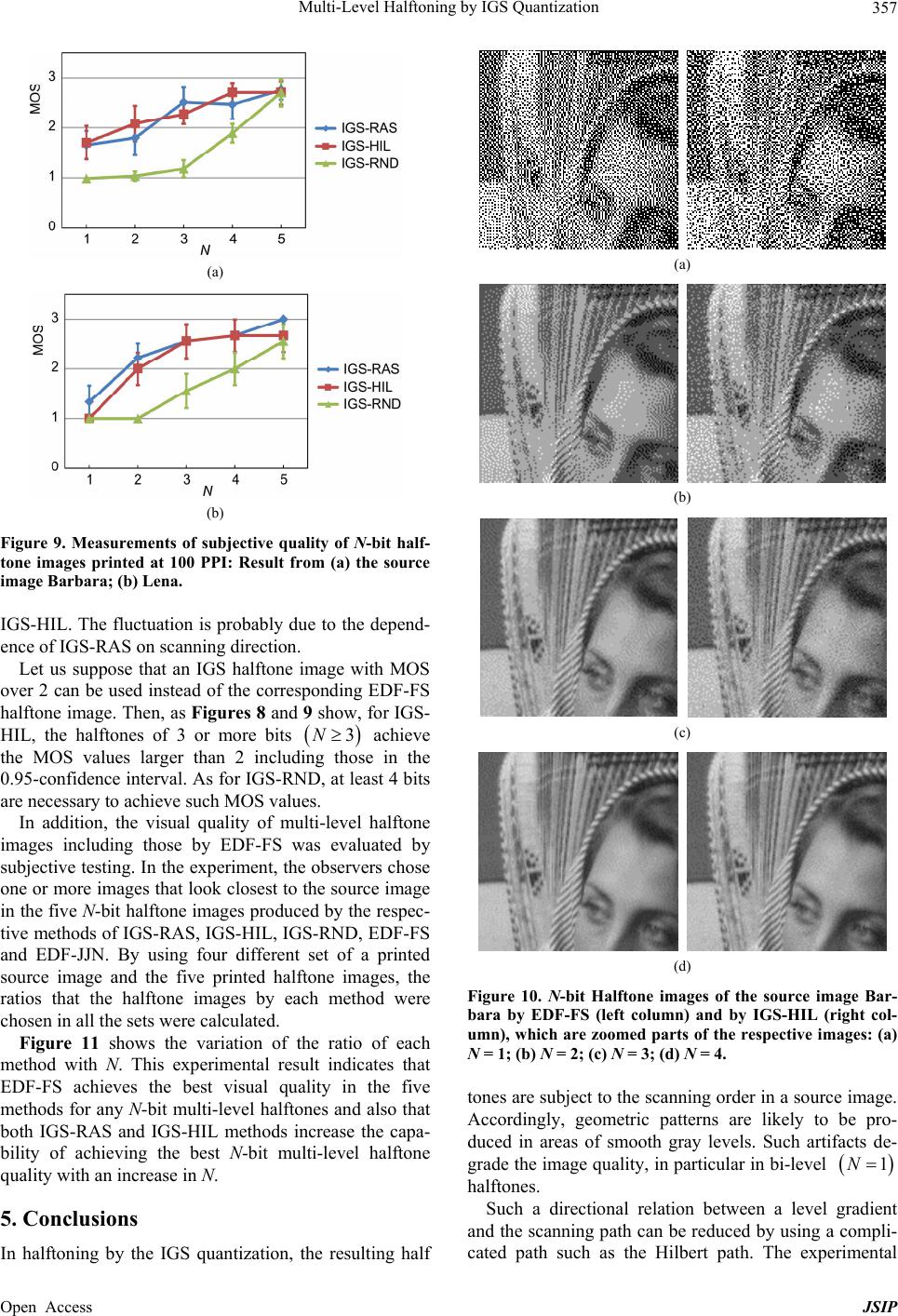 Multi-Level Halftoning by IGS Quantization 357 (a) (b) Figure 9. Measurements of subjective quality of N-bit half- tone images printed at 100 PPI: Result from (a) the source image Barbara; (b) Lena. IGS-HIL. The fluctuation is probably due to the depend- ence of IGS-RAS on scannin g di rect io n. Let us suppose that an IGS halftone image with MOS over 2 can be used instead of the corresponding EDF-FS halftone image. Then, as Figures 8 and 9 show, for IGS- HIL, the halftones of 3 or more bits 3N achieve the MOS values larger than 2 including those in the 0.95-confidence interval. As for IGS-RND, at least 4 bits are necessary to achieve suc h MOS v alues. In addition, the visual quality of multi-level halftone images including those by EDF-FS was evaluated by subjective testing. In the ex periment, the observers chose one or more images that look closest to the source image in the five N-bit halftone images produced by the respec- tive methods of IGS-RAS, IGS-HIL, IGS-RND, EDF-FS and EDF-JJN. By using four different set of a printed source image and the five printed halftone images, the ratios that the halftone images by each method were chosen in all the sets were calculated. Figure 11 shows the variation of the ratio of each method with N. This experimental result indicates that EDF-FS achieves the best visual quality in the five methods for any N-bit multi-level halftones and also that both IGS-RAS and IGS-HIL methods increase the capa- bility of achieving the best N-bit multi-level halftone quality with an increase in N. 5. Conclusions In halftoning by the IGS quantization, the resulting half (a) (b) (c) (d) Figure 10. N-bit Halftone images of the source image Bar- bara by EDF-FS (left column) and by IGS-HIL (right col- umn), which are zoomed parts of the respective images: (a) N = 1; (b) N = 2; (c) N = 3; (d) N = 4. tones are subject to the scanning order in a source image. Accordingly, geometric patterns are likely to be pro- duced in areas of smooth gray levels. Such artifacts de- grade the image quality, in particular in b i-level 1N halftones. Such a directional relation between a level gradient and the scanning path can be reduced by using a compli- cated path such as the Hilbert path. The experimental Open Access JSIP  Multi-Level Halftoning by IGS Quantization Open Access JSIP 358 Figure 11. Experimentally measured ratios of each N-bit halftone image looking closest to the source image between those generated by the five methods. result demonstrated that the Hilbert scanning makes the additional signals for the IGS quantization independent of level gradients, and also, increases their randomness. Consequently, the IGS halftone image by Hilbert scan- ning looks a little grainier with high-frequency signal components somewhat degraded than that by simple raster scanning. Bi-level halftone images by IGS-HIL probably look worse than those by the error diffusion scheme. Using multi-level halftones improves v isual quality of IGS-HIL halftone images. By using three or more bits, that is, 8 or more levels for a halftone level, the IGS-HIL images look comparable to the EDF-FS images. Such 8-level halftone images are supposed to be printed at a resolution of one pixel per dot with a printer of a capability of eight levels per dot. Otherwise, they can be printed with a bi-level printer, by expressing one 8-level halftone pixel by a set of bi-level dots by using another halftoning method such as clustered-dot ordered dithering [7]. For instance, a set of 3 × 3 bi-level dots can represent a 10-gray scale pixel. The IGS quantizing is one of what we call point proc- essing. Hence, the operation of the quantization is obvi- ously simpler than that of the convolution of filtering in the error diffusion. Although the IGS quantization may be an old-fashioned method, the operational simplicity as well as the above quality comparability to EDF-FS makes the IGS multi-level halftoning useful in recent image output devices. REFERENCES [1] R. Ulichney, “Digital Halftoning,” MIT Press, Cambridge, 1993. [2] R. C. Gonzalez and R. E. Woods, “Digital Image Proc- essing,” Addison-Wesley, Boston, 1993. [3] N. D. Venkata, B. L. Evans and V. Monga, “Color Error Diffusion Halftoning,” IEEE Signal Processing Magazine, Vol. 20, No. 4, 2003, pp. 51-58. http://dx.doi.org/10.1109/MSP.2003.1215231 [4] R. W. Floyd and L. Steinberg, “An Adaptive Algorithm for Spatial Grayscale,” Proceedings of the Society of In- formation Display, Vol. 17, No. 2, 1976, pp. 75-77. [5] J. F. Jarvis, C. N. Judice and W. H. Ninke, “A Survey of Techniques for the Display of Continuous-Tone Pictures on Bilevel Displays,” Computer Graphics and Image Processing, Vol. 5, No. 1, 1976, pp. 13-40. http://dx.doi.org/10.1016/S0146-664X(76)80003-2 [6] A. N. Netravali and B. G. Haskell, “Digital Pictures,” Plenum, 1988. http://dx.doi.org/10.1007/978-1-4684-1294-9 [7] P. G. Roetling and R. P. Loce, “Digital Halftoning,” In: E. R. Dougherty, Ed., Digital Image Processing Methods, Marcel Dekker, New York, 1994, pp. 363-413.
|