Vol.4, No.10, 536-540 (2013) Agricultural Sciences
http://dx.doi.org/10.4236/as.2013.410072
Technical efficiency analysis of hybrid maize
production using translog model case study in
District Chiniot, Punjab (Pakistan)
Syed Asif Ali Naqvi*, Muhammad Ashfaq
Institute of Agricultural and Resource Economics, University of Agriculture, Faisalabad, Pakistan;
*Corresponding Author:
Received 9 January 2013; revised 10 February 2013; accepted 15 March 2013
Copyright © 2013 Syed Asif Ali Naqvi, Muhammad Ashfaq. This is an open access article distributed under the Creative Commons
Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is
properly cited.
ABSTRACT
In Pakistan, maize accounts for 5.93 percent of
the total cropped area and 4.82 percent of the
value of agricultural production. Given high cost
of the production, there is a belief that it is dif-
ficult to boost profitability without enhancing use
of pricey inputs. Maximum likelihood estimates
of stochastic frontier model were estimated and
determinants of technical efficiency were calcu-
lated. Using Cobb Douglas model estimated ma-
ximum likelihood coefficients for all inputs were
significant and showed signs according to ex-
pectations. The evaluation with the different mo-
dels gives different technical efficiencies, which
shows that technical efficiency estimations are
extremely sensitive to the functional form speci-
fied.
Keywords: Maize; Tran slog Model; Maximum
Likelihood Co ef ficie nts
1. INTRODUCTION
Maize (Zea mays L.) is the third cereal for Pakistan
after wheat and rice and it accounts for 5.93 percent of the
total cropped area and 4.82 percent of the value of agri-
cultural production. Maize being the highest yielding ce-
real crop in the world is of significant importance for
countries like Pakistan, where rapidly increasing popu-
lation has already out stripped the available food supplies
output. Area under maize occupies the third position after
wheat and rice, 98% of which is grown in Punjab and
N.W.F.P. It is intensely grown on worldwide bases and
often referred as “king of grain crops” [1]. It is grown on
an area of 1083 thousand hectares with a yearly pro-
duction of 4271 thousand tones and it has 3944 kg/hec-
tare yield per hectare [2].
Mostly the farms with the same resources are produc-
ing different per acre output, because of management in-
efficiency. The scanty or no role of extension services,
poor right of entry to credit, tenant cultivation, low lite-
racy rate, poor communications facilities, and long dis-
tance from markets [3] characterize inefficient farms. At
present yield level is still up to some extent lower than
the potential of our existing varieties. Main constraints to
enhance maize productivity are unfavorable weather con-
ditions, unavailability of input at proper time, suboptimal
plant density, late sowing, inadequate fertilizer use, ina-
dequate water supply, weed infestation, insect pest attack
and the selection of unsuitable cultivars under a given set
of environments. Consequently, a farmer’s ability to in-
crease his income and productivity level is constrained
by a number of factors of which many fall out of his con-
trol. Pakistani maize farmers are constrained with many
such factors as acquisition of inputs with limited re-
sources.
Normally, the efficiency levels are low when compar-
ed to the international per acre productivity: no doubt,
some of the factors contributing towards the low produc-
tivity are out of control. This inefficiency is also termed
as technical inefficiency and Farrel [4] developed its con-
cept. Broadly speaking, technical inefficiency is the fail-
ure to produce maximum output from a given level of in-
puts.
This efficiency has two components: technical and al-
locative. Technical efficiency is the ability of a firm to
produce a maximal output from a given set of inputs or it
is the ability of a firm to use as modest inputs as possible
for a given level of output. The former is called input ori-
ented measures and the latter is known as output-oriented
measures of technical efficiency. Productivity can be in-

S. A. A. Naqvi, M. Ashfaq / Agricultural Sciences 4 (2013) 536-540 537
creased through more efficient utilization of resources of
farmers and inputs with current technology. In this study,
efficiency of maize producers of District Chiniot is eva-
luated. Interrelationship between efficiency level and va-
rious firm specific factors provides useful policy related
information. Main objective of the study is to calculate
the technical efficiency and determinants of inefficiency of
maize growers. A particular objective of the study is to
identify the factors causing technical inefficiency by exa-
mining the relationship between efficiency level and va-
rious firm specific factors.
2. MATERIALS AND METHODS
The primary data was used in this study, which was
collected from District Chiniot during the year 2010-11.
In order to collect data, random sampling technique was
used. The sampling procedure involved the three stages:
selection of tehsils, selection of villages, and selection of
farmers (respondents). Three tehsils were selected for
collecting data and three villages were selected from
each selected Tehsil. A sample of 120 farmers was taken
as total by dividing equally into three groups (large, me-
dium and small) by farm size. A farm was considered
small if farm size is less than or equal to 12.5 acres, me-
dium if farm size was more than 12.5 acres and less than
25 acres, and large if farm size is equal to or greater than
25 acres. Three sampling frames were designed at village
level by making strata of small, medium and large far-
mers. Five farmers were selected from each stratum ran-
domly.
2.1. Statistical Analyses
The Cobb-Douglas and Translog production frontier
functions defined and the inefficiency model were jointly
projected by the maximum-likelihood (ML) method us-
ing FRONTIER 4.1 [5]. By taking the same indicators
for the both models, it is clear from the results that Trans-
logrithmic function has a more robustness over the Cobb-
Douglas because the mean technical efficiency from the
of prior was up to 94% while for subsequent model it was
81.06%.
At this juncturevariant of the stochastic function ap-
proach proposed by Battese and Coelli [6] and continu-
ed by Greene [7], Hassan [8] and Dey et al. [9] in which
technical inefficiency effects in a stochastic frontier are
an explicit function of other farm specific explanatory
variables, and all parameters are estimated in a single-
stage maximum likelihood (ML) procedure. The stocha-
stic production frontieris,



0
ln ln,
ijiji
Yv   
i
u

Here, Yi is the yield of maize for the i-th farm, xi is a
vector of inputs (or cost of inputs),
 is a vector of i-th
unknown parameters, (vi − ui) is an error term. The
stochastic frontier is also called composed error model,
because it shows that the error term (vi − ui) is decom-
posed into two components: a stochastic random error
component (random shocks) vi and a technical ineffici-
ency component ui. Where Vi is a symmetrical two sided
normally distributed random error that contains stocha-
stic effects which are uncontrolled. It is assumed to be
independently and identically distributed

2
0, v N

. The
term

i, is one side (

I > 0) efficiency component. The
two error component (v and
 ) are also assumed to be in-
dependent of each other. The variance parameters of the
model are parameterized as:
2
222
2
; and 01
u
svu
s

 


 
2.2. Cobb-Douglas Function




 
011 2233
4455
lnln lnln
ln ln
i
ii
YXX
XXVU
 

 

X
i
where, Yi is the quantity of output (Kg): X1 is the land
preparation cost (Rs); X2 is N, P, and K nutrients applied
(Kg); X3 is the total irrigation (number); X4 is the total
chemical cost counting both weeding and insecticide cost
(Rs) and X5 is thetotal threshing cost (Rs).
Inefficiency regression equation can be written as,
,1
iii
uZ





where, Zi are farm-specific variables that may cause in-
efficiency and δο and all δi are coefficients to be estimated.
Z1 is farming experience (year); Z2 is the education (year);
Z3 is the credit it is in the form of dummy variable it has
value 1 if farmer avails credit otherwise it would be equal
to 0; Z4 is the extension facilities, dummy variable as-
suming value 1 if farmer avails extension facilities, other-
wise 0; Z5 is the maize cropped area (acre); Z6 is the dum-
my variable for sowing time assuming value 1 if farmer
sow timely, otherwise 0.
2.3. Translogrithmic Model
 
ln lnln
1, 2, 3,1, 2, 3
itititjtit it
YXXXV
intn

 

 




Inefficiency model and variables were same as the
Cobb-Douglasmodel.
3. RESULTS AND DISCUSSION
The summary statistics related tothe variables used in
analysis is given in Table 1.
It is clear from the table the mean yield was 3570 kg,
farming experience was 22.7 year, up to 15 irrigations

S. A. A. Naqvi, M. Ashfaq / Agricultural Sciences 4 (2013) 536-540
538
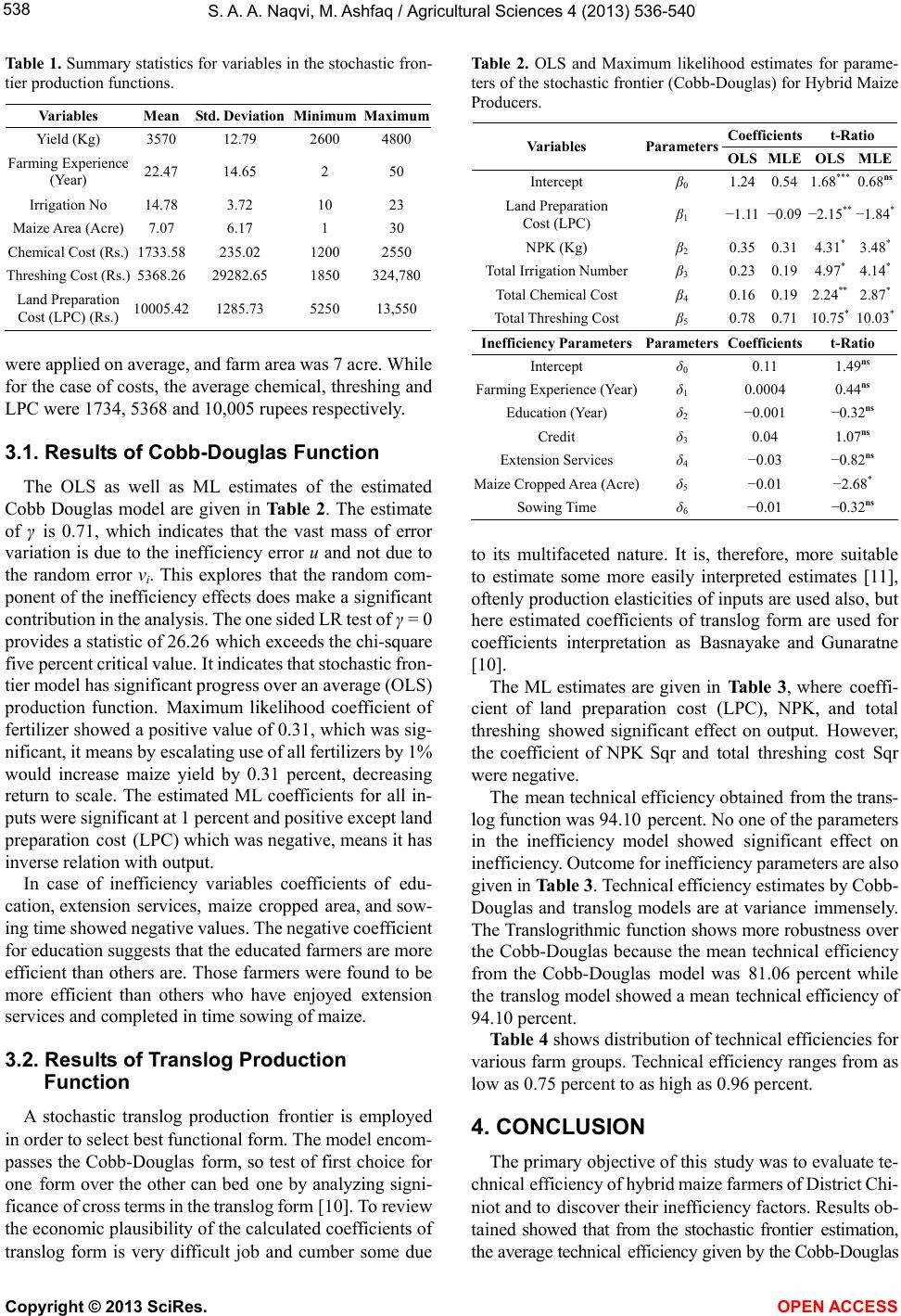
Tabl e 1 . Summary statistics for variables in the stochastic fron-
tier production functions.
Variables Mean Std. Deviation MinimumMaximum
Yield (Kg) 3570 12.79 2600 4800
Farming Experience
(Year) 22.47 14.65 2 50
Irrigation No 14.78 3.72 10 23
Maize Area (Acre) 7.07 6.17 1 30
Chemical Cost (Rs.) 1733.58 235.02 1200 2550
Threshing Cost (Rs.) 5368.26 29282.65 1850 324,780
Land Preparation
Cost (LPC) (Rs.) 10005.42 1285.73 5250 13,550
were applied on average, and farm area was 7 acre. While
for the case of costs, the average chemical, threshing and
LPC were 1734, 5368 and 10,005 rupees respectively.
3.1. Results of Cobb-Douglas Function
The OLS as well as ML estimates of the estimated
Cobb Douglas model are given in Ta bl e 2. The estimate
of γ is 0.71, which indicates that the vast mass of error
variation is due to the inefficiency error u and not due to
the random error vi. This explores that the random com-
ponent of the inefficiency effects does make a significant
contribution in the analysis. The one sided LR test of γ = 0
provides a statistic of 26.26 which exceeds the chi-square
five percent critical value. It indicates that stochastic fron-
tier model has significant progress over an average (OLS)
production function. Maximum likelihood coefficient of
fertilizer showed a positive value of 0.31, which was sig-
nificant, it means by escalating use of all fertilizers by 1%
would increase maize yield by 0.31 percent, decreasing
return to scale. The estimated ML coefficients for all in-
puts were significant at 1 percent and positive except land
preparation cost (LPC) which was negative, means it has
inverse relation with output.
In case of inefficiency variables coefficients of edu-
cation, extension services, maize cropped area, and sow-
ing time showed negative values. The negative coefficient
for education suggests that the educated farmers are more
efficient than others are. Those farmers were found to be
more efficient than others who have enjoyed extension
services and completed in time sowing of maize.
3.2. Results of Translog Production
Function
A stochastic translog production frontier is employed
in order to select best functional form. The model encom-
passes the Cobb-Douglas form, so test of first choice for
one form over the other can bed one by analyzing signi-
ficance of cross terms in the translog form [10]. To review
the economic plausibility of the calculated coefficients of
translog form is very difficult job and cumber some due
Table 2. OLS and Maximum likelihood estimates for parame-
ters of the stochastic frontier (Cobb-Douglas) for Hybrid Maize
Producers.
Coefficients t-Ratio
Variables Parameters
OLS MLE OLSMLE
Intercept β0 1.24 0.54 1.68*** 0.68ns
Land Preparation
Cost (LPC) β1 −1.11 −0.09 −2.15** −1.84*
NPK (Kg) β2 0.35 0.31 4.31*3.48*
Total Irrigation Numberβ3 0.23 0.19 4.97*4.14*
Total Chemical Cost β4 0.16 0.19 2.24** 2.87*
Total Threshing Cost β5 0.78 0.71 10.75*10.03*
Inefficiency ParametersParameters Coefficients t-Ratio
Intercept δ0 0.11 1.49ns
Farming Experience (Year)δ1 0.0004 0.44ns
Education (Year) δ2 −0.001 −0.32ns
Credit δ3 0.04 1.07ns
Extension Services δ4 −0.03 −0.82ns
Maize Cropped Area (Acre)δ5 −0.01 −2.68*
Sowing Time δ6 −0.01 −0.32ns
to its multifaceted nature. It is, therefore, more suitable
to estimate some more easily interpreted estimates [11],
oftenly production elasticities of inputs are used also, but
here estimated coefficients of translog form are used for
coefficients interpretation as Basnayake and Gunaratne
[10].
The ML estimates are given in Ta b l e 3 , where coeffi-
cient of land preparation cost (LPC), NPK, and total
threshing showed significant effect on output. However,
the coefficient of NPK Sqr and total threshing cost Sqr
were negative.
The mean technical efficiency obtained from the trans-
log function was 94.10 percent. No one of the parameters
in the inefficiency model showed significant effect on
inefficiency. Outcome for inefficiency parameters are also
given in Table 3. Technical efficiency estimates by Cobb-
Douglas and translog models are at variance immensely.
The Translogrithmic function shows more robustness over
the Cobb-Douglas because the mean technical efficiency
from the Cobb-Douglas model was 81.06 percent while
the translog model showed a mean technical efficiency of
94.10 percent.
Tab le 4 shows distribution of technical efficiencies for
various farm groups. Technical efficiency ranges from as
low as 0.75 percent to as high as 0.96 percent.
4. CONCLUSION
The primary objective of this study was to evaluate te-
chnical efficiency of hybrid maize farmers of District Chi-
niot and to discover their inefficiency factors. Results ob-
tained showed that from the stochastic frontier estimation,
the average technical efficiency given by the Cobb-Douglas

S. A. A. Naqvi, M. Ashfaq / Agricultural Sciences 4 (2013) 536-540 539
Table 3. Maximum likelihood estimates for parameters of the stochastic frontier (translog) for hybrid maize producers.
Variables Parameters Coefficients t-Ratio
Stochastic Production Function
Intercept β0 13.03 12.67*
Land Preparation Cost (LPC) β1 7.03 2.78*
NPK (Kg) β2 3.76 3.90*
Total Irrigation Number β3 −1.42 −0.88ns
Total Chemical Cost β4 3.31 1.32ns
Total Threshing Cost β5 5.36 4.53*
LPC Sqr. β6 0.14 1.36ns
NPK Sqr. β7 −1.38 −3.21*
Total Irrigation Number Sqr. β8 0.11 0.11ns
Total Chemical Cost Sqr. β9 0.31 0.94ns
Total Threshing Cost Sqr. β10 −0.32 −0.82ns
LPC * NPK β11 1.71 4.06*
LPC * Total Irrigation Number β12 −0.68 −3.21*
LPC * Total Chemical Cost β13 −0.34 −1.06ns
LPC * Total Threshing Cost β14 −0.02 −0.05ns
NPK * Total Irrigation Number β15 1.23 2.85*
NPK * Total Chemical Cost β16 −1.13 −2.10**
NPK * Total Threshing Cost β17 1.09 1.34ns
Total Irrigation Number * Total Chemical Cost β18 1.28 3.87*
Total Irrigation Number * Total Threshing Cost β19 −1.11 −3.87*
Total Chemical Cost * Total Threshing Cost β20 −0.28 −3.28*
Technical Inefficiency Function
Intercept δ0 0.069 1.28ns
Farming Experience (Year) δ1 0.001 4.93*
Education (Year) δ2 0.006 2.31**
Credit δ3 0.008 0.24ns
Extension Services δ4 0.038 1.11ns
Maize Cropped Area (Acre) δ5 −0.012 −4.68*
Sowing Time δ6 0.030 0.84ns
Variance Parameters
σ2 0.05 7.89
Γ 0.72 2.88
Note: * and ** show significance at 1 and 5 percent.
Table 4. Frequency distribution of technical efficiency range according to small, medium and large farmers.
Efficiency Range Small Farmers % age of Farmers Medium Farmers% age of FarmersLarge Farmers % age of Farmers
0.75 - 0.85 5 4.16 2 1.67 1 0.83
0.86 - 0.95 15 12.5 5 4.16 1 0.83
0.96 - 100 20 16.67 33 27.5 38 31.66
Total 40 33.33 40 33.33 40 33.33
model is 81.06 percent which shows that 18.94 percent
output can be increased without increasing the levels of
inputs, and this is due to input oriented technical ineffi-
ciency. According to the results, older farmers appeared to
be more efficient than younger farmers. This is perhaps
due to their good managerial skills, which they have learnt
over time. Hence, it is necessary to increase educational
facilities in the area. It was also discovered that the te-

S. A. A. Naqvi, M. Ashfaq / Agricultural Sciences 4 (2013) 536-540
540
chnical efficiency estimates are highly responsive to the
functional form specified because the Cobb-Douglas and
translog models resulted in dissimilar technical efficien-
cies. Although Cobb-Douglas specification gives constant
returns to scale, it is widely accepted in the literature.
REFERENCES
[1] Tahir, M., Tanveer, A., Ali, A., Abbas, M. and Wasaya, A.
(2008) Comparative yield performance of different maize
(Zea mays L.) hybrids under local conditions of Faisala-
bad-Pakistan. Pakistan Journal of Life and Social Scienc-
es, 6, 118-120.
[2] Government of Pakistan (GOP) (2012) Pakistan Econo-
mic Survey 2011-12. Economic Advisor’s Wing, Finance
Division, Islamabad.
[3] Parikh, A. and Shah, M.K. (1994) Measurement of tech-
nical efficiency in the north-west frontier provinces of Pa-
kistan. Journal on Agricultural Economics, 45, 132-138.
http://dx.doi.org/10.1111/j.1477-9552.1994.tb00384.x
[4] Farrell, M. (1957) The measurement of productivity effi-
ciency. Journal of the Royal Statistical Society. Series A
(General), 120, 253-290.
http://dx.doi.org/10.2307/2343100
[5] Coelli, T.J. (1996) A guide to frontier version 4.1 a com-
puter program for stochastic frontier production and cost
function estimation. CEPA Working Papers, 96/07, Uni-
versity of New England, New England, 135.
[6] Battese, G.E. and Coelli, T.J. (1995) A model for technical
efficiency effects in astochastic frontier production func-
tion for panel data. Empirical Economics, 20, 325-332.
http://dx.doi.org/10.1007/BF01205442
[7] Greene, W.H. (2003) Econometric analysis. 5th Edition,
Prentice Hall, Upper Saddle River.
[8] Hassan, S. (2004) An analysis of technical efficiency of
wheat farmers in the mixed farming system of the Pun-
jab Pakistan. Ph.D. Thesis, Department of Environmental
and Resource Economics (Farm Management), Univer-
sity of Agriculture, Fasialabad.
[9] Dey, M.M., Paraguas, F.J., Kambewa, P. and Pemsl, D.E.
(2010) The impact of integrated aquaculture-agriculture
on small-scale farms in Southern Malawi. Agricultural
Economics, 41, 67-79.
http://dx.doi.org/10.1111/j.1574-0862.2009.00426.x
[10] Basnayake, B.M.J.K. and Gunaratne, L.H.P. (2002) Esti-
mation of technical efficiency and it’s determinants in the
tea small holding sector in the mid country wet zone of
Sri Lanka. Sri Lankan Journal of Agricultural Economics,
4, 137-150.
[11] Ngwenya, S.A., Battese, G.E. and Fleming, E.M. (1997)
The relationship between farm size and the technical in-
efficiency of production of wheat farmers in the Eastern
Free State. Agrekon, 36, 283-301.
http://dx.doi.org/10.1080/03031853.1997.9523466