Hybrid Designing of a Neural System by Combining Fuzzy Logical Framework and PSVM for Visual Haze-Free Task

doi:10.4236/ijis.2013.34016

Paper Menu >>

Journal Menu >>

International Journal of Intelligence Science, 2013, 3, 145-161

http://dx.doi.org/10.4236/ijis.2013.34016 Published Online October 2013 (http://www.scirp.org/journal/ijis)

Hybrid Designing of a Neural System by Combining Fuzzy

Logical Framework and PSVM for Visual Haze-Free Task

Hong Hu, Liang Pang, Dongping Tian, Zhongzhi Shi

Key Laboratory of Intelligent Information Processing, Institute of Computing Technology,

Chinese Academy of Sciences, Beijing, China

Email: huhong@ict.ac.cn, pangl@ics.ict.ac.cn, tiandp@ics.ict.ac.cn, shizz@ics.ict.ac.cn

Received June 28, 2013; revised August 25, 2013; accepted September 5, 2013

permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Brain-like computer research and development have been growing rapidly in recent years. It is necessary to design large

scale dynamical neural networks (more than 106 neurons) to simulate complex process of our brain. But such a kind of

task is not easy to achieve only based on the analysis of partial differential equations, especially for those complex neu-

ral models, e.g. Rose-Hindmarsh (RH) model. So in this paper, we develop a novel approach by combining fuzzy logi-

cal designing with Proximal Suppo rt Vector Machine Classifiers (PSVM) learning in the designing of large scale neural

networks. Particularly, our approach can effectively simplify the designing process, which is crucial for both cognition

science and neural science. At last, we conduct our approach on an artificial neur al system with more than 108 neurons

for haze-free task, and the experimental results show that texture features extracted by fuzzy logic can effectively in-

crease the texture information entropy and improve the effect of haze-removing in some degree.

Keywords: Artificial Brain Research; Brain-Like Computer; Fuzzy Logic; Neural Network; Machine Learning;

Hopfield Neur al Network; Bounded Fuzzy Operator

1. Introduction

Driven by rapid ongoing advances in computer hardware,

neuroscience and computer science, artificial brain re-

search and development are blossoming [1]. The repre-

sentative work is the Blue Brain Project, which has

simulated about 1 million neurons in cortical columns

and included considerable biological detail to reflect spa-

tial structure, connectivity statistics and other neural

properties [2]. The more recent work of a large-scale

model for the functioning brain is reported in the famous

journal Science, which is done by the group of Chris Eli-

asmith’s group [3]. In order to bridge the gap between

neural activity and biological function, Chris Eliasmith’s

group presented a 2.5-million-neuron model of the brain

(called “Spaun”) to exhibit many different behaviors.

Among these large scale visual cortex simulations, the

visual cortex simulations are most concerned. The two

simulations aforementioned are all about the visual cor-

tex. The number of neurons in cortex is enormous. Ac-

cording to [4], the total number in area 17 of the visual

cortex of one he mispher e is close to 160,000,0 00. Fo r the

total cortical thickness th e numerical density of synapses

is 276,000,000 per mm 3 of tissue. It is almost impossible

to design or analyze a neural network with more than 108

neurons only based on partial differential equations. The

nonlinear complexity of our brain prevents our progress

from simulating useful and versatile functions of our

cortex system. Many studies only deal with simple neural

networks with simple functions, and the connection ma-

trices should be simplified. The visual functions simu-

lated by “Blue Brain Project” and “Spaun” are so simple

that they are nothing in the traditional pattern recogni-

tion.

On the other hand, logic inference plays a very impor-

tant role in our cognition. With the help of logical design,

the things become simple, and this is the reason why

computer science has made great progress. There are

more th an 108 transistors in a CPU today. Why don’t we

use similar techniques to build complex neural networks?

The answer is yes. As our brains work in the non Turing

computable way, fuzzy logic rather than Boolean logic

should be used. For this purpose, we introduce a new

concept-fuzzy logical framework of a neural network.

Fuzzy logic is not a new topic in science, but it is really

very fundamental and useful. If the function of a dy-

namical neural network can be described by fuzzy logical

formulas, it can greatly help us to understand behavior of

H. HU ET AL.

146

this neural network and design it easily.

For neural systems, the basic logic processing module

to be used as a bu ilding module in the logic arch itectures

of the neural network comes from OR/AND neuron [3,5],

also referred by [6]. The ideal of hybrid design neural

networks and fuzzy logical system is firstly proposed by

[7]. While neural networks and fuzzy logic have added a

new dimension to many engineering fields of study, their

weaknesses have not been overlooked, in many applica-

tions the training of a neural network requires a large

amount of iterative calculations. Sometimes the network

cannot adequately learn the desired function. Fuzzy sys-

tems, on the other hand, are easy to understand because

they mimic human thinking and acquire their knowledge

from an expert who encodes his knowledge in a series of

if/then rules [7].

Neural networks can work either in dynamical way or

static way. The former can be described by partial dif-

ferential equations and denoted as “dynamical neural

networks”. Static points or stable states are very impor-

tant for dynamical analysis of a neural network. Many

artificial neural networks are just abstract of static points

or stable states of dynamical neural networks, e.g. per-

ception neural networks, such a kind of artificial neural

networks work in a static way and are denoted as “static

neural networks”. There is a natural relation between a

static neural network and a fuzzy logical system, but for

dynamical neural networks, we should extend the static

fuzzy logic to dynamic fuzzy logic. A novel concept de-

noted as “fuzzy logical framework” is defined for this

purpose.

At last, we give out an application of our hybrid de-

signing approach for the visual task about image mat-

ting-haze removing from a single input image. Image

matting refers to the problem of softly extracting the

foreground object from a single image. The system de-

signed by our novel hybrid approach has a comparable

ability with ordinary approach proposed by [8]. Texture

information entropy (TIE) is introduced for roughly

evaluating the effect of haze removing. Experiments

show texture features extracted by fuzzy logic can effec-

tively increase TIE.

The main contributions of this paper include: 1) we

develop a novel hybrid designing approach of neural

networks based on fuzzy Logic and Proximal Support

Vector Machine Classifiers (PSVM) learning in the arti-

ficial brain designing, which greatly simplifies the de-

signing of large scale artificial brain; 2) a novel concept

about fuzzy logical framework of neural network is

firstly proposed; 3) in stead of the lin ear mapping in [8], a

novel nonlinear neural fuzzy logical texture feature ex-

tracting, which can effectively increase TIE, is intro-

duced in the task of haze free application. The experi-

ments show that our approach is effective.

2. Hopfield Model

There are many neuron models, e.g. Fitz Hugh (1961),

Morris, Lecar (1981), Chay (1985) and Hindmarsh, Rose

(1984) [9-1 1 ]. W h ether th e f uzzy logical approach can be

used in all kinds of neural networks for different neuron

models? In order to answer this question, we consider a

simple neuron model- Hopfield model [12] (see Equation

(1.1)) as a standard neuron model, which has a good

character of fuzzy logic. We have proved that Hopfield

model has universal meaning, such that almost all neural

models described by first order differential equations can

be simulated by them with arbitrary small error in an

arbitrary finite time interval [13], these neural models

include all the model s summarized by H D I [14].



;

iii ijjik

iii

UaU wVwI

VSUT





 







(1.1)

where sigmoid function





S can be a piecewise linear

function or logistic function. Hopfield neuron model has

a notable biological characteristic and has been widely

used in visual cortex simulation. One example of them is

described in [7,10,15-17]), (see Equation (1.2)). Such

cellos membrane potential is transferred to output by a

sigmoid-like function. Only the amplitude of output pluses

carries meaningful information. The rising or dropping

time







of output pluses conveys no useful informa-

tion and is always neglected. According to [15], the neu-

ral networks described by Equation (1.2) are based on

biological data [18 -23] .

In such kind neural networks, cells are arranged on a

regular 2-dimensional array with image coordinates





inm

and divided into two categories: excitatory

cells



and inhibitory cells i



. At every position





inm, there are

cells with subscript t



that

are sensitive to a bar of the angle



. Equation (1.2) is

the dynamical equation of these cells. Only excitatory

cells receive inputs from the outputs of edge or bar

detectors. The direction information of edges or bars is

used for segmentation of the optical image.







 



;

ixiyicxic

yiijxj i

iyixixicijxj

xaxgyJgxI

gyJ gxI

yaygxgxI Wgx

 

 



 







 

 







 

 

 







(1.2)

where





x and





x are sigmoid-like activation

functions, and



is the local inhibition connection in

the location , and ,ij





and ,ij



 are the synaptic

connections between the excitatory cells and from the

excitatory cells to inhibition cells, respectively. If we

represent the excitatory cells and inhibitory cells with

H. HU ET AL.

147

same symbol i and summarize all connections (local U



, global exciting ,ij



 and global inhibiting ,ij





)

as ij, the Equation (1.2) can be simplified as Hopfield

model Equation (1.1).

w

3. Fuzzy Logical Framework of Neural

Network

Same fuzzy logical function can have several equivalent

formats; these formats can be viewed as the stru ct ure of a

fuzzy function. When we discuss the relationship be-

tween the fuzzy logic and neural network, we should not

only probe the input-output relationship but also their

corresponding structure. Section 3.1 discusses this prob-

lem. Section 3.2 discusses the problem about what is the

suitable fuzzy operator, and in Section 3.3, we prove

three theorems about the relationship between the fuzzy

logic and neural network.

3.1. The Structure of a Fuzzy Logical Function

and Neural Network Framework

In order to easily map a fuzzy formula to a dynamical

neural network, we should define the concept about the

structure of a fuzzy logical function.

Definition 1. [The structure of a fuzzy logical function]

If is a set of fuzzy logical functions(FLF), and a

FLF





xx x can be represented by the

combination of all FLFs in with fuzzy operators

“” and “”, but with no parentheses, then the FLFs in

is denoted as the 1



t layer sub fuzzy logical

functions (1

t FLF) of





xx x; similarly, if a

variable in a FLF in is not just a variable, i.e.



, then



n112

yyy has its

own 1

t layer sub FLnoted as the

layer sub FLFs of Fs which are dend





,,,

fxx x, and every th

layer non variable sub FLub fuzzy logical

functions. In this way, F can have its s





,,,

xx x has a layered

structure of sub fuzzy logical functi suchons,

he structure o we denote

layered structure as t



,,,

xx x.

For example





1234

,,, Figure 1 can be

xxxx in





2 2

11 1

xx xxrepred by esent and









2 2342

fyy y

3 4

xxxxxx







 as





12 234

, ,

1 2

xx fxx,

so x





2 234

xxx are the 1

t layer





1 21

xx and

FLFs i1





,,,

xx x m equivalent formats,

so the struc

ay have several





,,,

xx x is not unique, for

ture of

example,





1234

,,,xxx



Figure 1



1 22 3

12 2

x xxx

xx xx

 

 



d (b) in

nctio







12 23 4

xx xx x

can be represented as trees (a) an. If a

sub fun is just



,,,

zzy logical fu

xx x itself,

then





n12

,,,

xx a recurrent structux hasre, 





otherwis 12

xx ,

xkind structure.

 has a tree





,,,

xx x has a recurrent structure, then it

can be representes Equa time needed

for output isd a

ttion (1.3), and the

and 1





,,,

xx x

changed to is linearly





,,,

tt n

xx x

  then



,,,

xx x

can create a time serial output and can be written in

pafferential fortial dirm as Equation (1.4).









,,xx 12

,,,,

nn12

,,,

xgxxx fxx x (1.3)











,,, 1212 1212

,,,,,, ,,,,,,,

tdt t

nn nnn

xxfxx xxx xxx xfxx xdtt



 



 x



gf (1.4)

hwere 12

,, n

xx

an i

k c

is a stab

iti



le input vector wh

networ

ich can

be viewal condition of a dynamical system

and 0dt t. Suppose the dynamical behavior of a

neuralan be describ ed as

ed as n







Fxtyt



where



 t at time is the inpu

and



 is the

output at

. If



G is a FLF with same dynamical

variables in





, we again define













the dynamical behavior of a fuzzy logical function,

where



G

 and



 are input and output at

respectand the idomain for



ively, nput

 is D.

The definition 2 is the measure abhe diout tfference

between a fuzzy logical function and a neural network.

Definition 2. [Difference error between a fuzzy logical

function and a neural network] If



 is input, and the

region of input



 is D. Tdifference error

network

between a fuzzy logical function and a neural

is defis:

Dynamical case:

ned a



aerrGxtF t t

 (1.5)

Static case:





GxD

errG xFx







 (1.6)

where









lis the fixe d point of F.

a n approximately Usualeural model can onl

simulatzzy operator, so it is ne

y, y

e a fucessary to find the

most similar fuzzy function for a neural network, which

is denoted as the fuzzy logical framework of a neural

network, the definition 3 gives out the concept of the

fuzzy logical framework.

Definition 3. [The fuzzy logical framework] Suppose

H. HU ET AL.

148

(a) (b)

Figure 1.





xx x

,,, may have several equivalent

formats, so the structure of





fxx x

,,, is not unique.

 is a set of fuzzy logic fuzzy logical al functions, a

mework for a neural network fra

is the best fuzzy

log

ical function G in  satisfied the constrain that

G has smallest G

err i.e. m

errerr 



. If there is a

one to one onto appi from neurons in a neural

twork

m ng

to th layercal functions

in a G’s structure, such kind fuzzy logical framework is

denoted as structure keeping fuzzy logical framework.

3.2. The Suitable Fuzzy Operator

e alls sub logifuzzy

After the theory of fuzzy logic was co

many fuzzy logical systems have beenceived by [24],

n presented, for

example, the Zadeh system, the probability system, the

algebraic system, and Bounded operator system, etc.

According to universal approximation theorem [25], it is

not difficult to prove that q-value weighted fuzzy logical

functions (5) can precisely simulate Hopfield neural

networks with arbitrary small error, or vice versa, i.e.

every layered Hopfield neural network has a fuzzy logi-

cal framework of the q-value weighted bounded operator

with arbitrary small error. This means that if the sigmoid

function used by Hopfield neurons is a piecewise linear

function, such kind fuzzy logical framework is structure

keeping. Unfortunately, if the sigmoid function is logistic

function, such kind fuzzy logical framework is usually

not structure keeping. Only in an approximate case(see

Appendix A), a layered Hopfield neural network may

have a structure keeping fuzzy logical framework.

Definition 4. [Bounded Operator



F ]

Bounded product:





1, max 0,

xy xy 

and Bounded sum:





min 1,

yx , y

where 10,

y.

In order to simulate neural cells, it is necessary to ex-

e Boundederator to Weighted Bounded Op-

tend th Op

ator. The fuzzy formulas defined by q-value weighted

bounded operators is denoted as q-value weighted fuzzy

logical functions.

Definition 5. [q-value Weighted Bounded operator



F ] q-va





1212

,,,

pp Fppww







11 2212

max 0,1wpwpw wq

(1.7)

q-value Weighted Bounded sum:





12 1212

ppFpqww



 



(1 )

where

112

,,, min,qwpwp

0,pp q



association and

Fordistribution rules, we define:











12 312123

,,, ,,1,

pppFFppww pw





and











12312323 1

,,,,,

ppFpFppwww



 , ,1

Here

,or

lue Weighted Bounded product:



 . We can prove that



and



follow the associative condition (see Appe

B) ndix

and

123 1

min ,

fffn ii

xxx qwx



 







 (1.9)



(1.10)

For more above q-value weighted bounded operator

123

max 0,1

ffffn

ii i

in in

xxx x

wxw q

 





















 follows the Demorgan Law, i.e.





23fffn

x xx



 

123

min ,

max 0,

max 0,1

ii i

in in

ffff

qqwx

qwx

wq xwq

Nx NxNxNx



 





 

























n

(1.11)

But for the q-value weighted bounded operator









ho , the distribution condition is usually not

equal to 1, f

ld, and the boundary condition is hold only all weights











1,, ,max0,1

pqFpqwwwpwq





112111

and





111211

,, ,min ,

pqFpqww qwpwq



 .



Three Important Theorems about the

Relationship between the Fuzzy Logic and

H Dn

modinclude [9,11,26-35] and inte-

3.3.

Neural Network

I [14] studied the synchronization of 13 neuro

els. These models

grate-and-fire model [36] [see Equation (1.14), the rest

H. HU ET AL. 149

11 neuron models are all the special cases of the

generalized model described by the ordinary differential

Equation (1.16).



22 2.

iaiiai

aiiji j

xpxgx ft

 

xx x







 (1.12)



22 2

iai iai

aiiji j

xpygx ft

xx x







 







 (1.13)



dext syn



  (1.14)

where and

0v

 

0ifvt vt









. Usually



syn

t is defined by Equation (1.15).







syn spike

spikes

Itg ftt

 

exp expft A tt



















(1.15)

In fact, if we introduce a new variable ii





change, the

Van-der-Pol generator [28] model can bed to

Eqf Equuation (1.13) which is just a special case oation

(1.16); for the integrate-and-fire model, if we use logistic

function



1exp





to replace the step

function, th model can also has the e integrate-and-fire

form of the Equation (1.16). So the Equation (1.16) can

be viewed as a general representation of almost all

neuron models, if we can prove the Equation (1.16) can

be simulated by a neural network based on the Hopfield

neuron model [see Equation (1.1)], then almost all

neuron models can be simulated in the same way.



11111121

,,,



22212

,,,

nnnn

axwfx xxu

 







 









  



(1.16)

where every



,,, ,1

xxxi n

rtial differential in the fin, has the

continuous paite hypercubic

domain













112 2

,, n

b aba

 

,,, :0

xt xttT.

(1.17) is the fixed point



tof

Da of its

trajectory space





TR x

The Equationth i





a Hopfield

neural circuit which only has one cell winput k



,1exp 1

iikkii ii

UwIaV UT









(1.17)

At the fixed poin t, every neuron works just lik

ron in a perception neural network. Theorem 1 tries to

e a neu-

ow the condition of Equation (1.17) to simulate dis-

junctive normal form (DNF) formula. The fixed point of

Equation (1.17) can easily simulate binary logical opera-

tors; on the other hand, a layered neural network can be

simulated by a q-value weighted fuzzy logical function.

Theorem 1 Suppose in Equation (1.17), 1



, and

every ,0,0,1

ikk iki

wTTkK





, for more,





1, ,

Si L is a class of index sets,every

index ,

Cset i

S is a s and

ubset of



1,2,3,

, then we

1. If

have:



12 1, ,

,,, i

klL

fxxx 













 is a d

noform (DNF) formula,

isjunctive

rmal and the class





1, ,

CSi L is the class which has the following

two characters: (1). for every ,

SS C,ijk

SS SC





for all and



(this condition assures that





,,,

xx x has a simple

the character

st form); (2). every i

S has





j



, where i

SC, and any index

sets SC





have character 1





, or if 1







jS







there must be an index set such that

SC

SSS





 (this condition a is the larg, ssures est)

xed point of the neural described by

formu

cellthen the fi

Equation (1.17) can simulate the DNFla



12 1, ,

,,, i

klL

fxxx 













z

with arbitrary small error, where , if the corres-

ponding input ii



, or ii

z if 1

z

on (1

2. If a ne described by.17) can ural cell Equati

simulate the Boolean formula 2



xx x with

arbitrary small error, and









is an item in the



disjunctive normal form of



,,,

xx x, i.e.





,,, 1fxx x

12 k



 at xr all jS1

j fol



and



for all l



, then i







dex and 2

S ound



3. If a couple of insets can be f

in the formula



,,,

1, , ,

lk l

xx x



x







, such that



tS tS









 xed point

 





fals



, thhe fi

of the neural cell described by Equation (1.17) can’t

simulate the formula

en t





,,,

xx x.

Proof

1. If 1



, for all l



, and 0

I, for all l



because 1





iS



, th see ind ext l

S is a subseten for th

H. HU ET AL.

150



1,2,3, ,

, we have







1exp1









1exp1 1,

ik ki

wI T

















 





































lim1, ,,

Vfxxx



  . If 1,



 ;





condition of th and , then acce

is thSC



eorem: if ording to th









,



, ,k





if 1





, then there is an i

lim 0,

Vf x

  ;

ndex set such that

, then



i

SC

SSS







lim1, ,,

Vfxxx



  k

. Shen o w



 static error defined by Equat6) trends to

0. , theion (1.

2. If thepoint of the neural cell de

Eqauti fixed scribed by

on (1.17) can simulate the Boolean formula



,,,

xwhich is not a constant with arbitrary x x

small error, and for a definite binary input 12

,,,

xx,

then the arbitrary small error is achieved when



trends

to infinite and





ii ikki

UT wIT



 

 where l

S is

the set of the labels and 1

I, for all l

iS, and

I, for all ition suppses

that every wT K

iS

. The ’s condotheorem

,0,

i0,1

k ikT k



 , and

,,,

xx are binary nr 0 or so if



umbe1,



xx xs not a constant, when



,,,

fxx x





0, ther lime must be0



; and

when



,, 1

xx , it is necessary for lim 1







fx,



ii i













 trends to minus



lim 0



 

infinite and

needs th

lim1



 

ii i







trends to plus infinite. So ,,

needs that

if 1

,fx











21x



 at

x for all l

jS and 0

x for all l



, in

order to guarantee



e hol



is the static error

ween the neural cell

kki



1 must bd, here





12 ,1 ,2,

lim,, ,,0,

ii i

fxx

errw wwT



 













12 ,1 ,2,

,,,,,,,

kii iki

fxx x

errw wwT



defined by Equation (1.6) bet

described d by Equat ion (1. 17) an



,,,

xx x

is based on the si

mple

fact that for a single neuron

3. The third part of the theorem

iis monotone on every

input i

which can be i

z or 1i

z.

An example of above theoreme is that th

e ed byquation (1.1) has a

la he

nction can’t be simulated by the neuron described by

Equation (1.17).

If thneural network dscribe E

yered structure, the fixed point of a neuron at t

non-input layer l is



,,,1,

liliklii

li li

UwVa

VSUT









(1.18)

Equation (1.18) is just a perception neur al network, so

a perception neural network can be view

of static points or stable states of a real

described by Equat i o n ( 1. 18 ).

red neural network can be

ed as an abstract

neural network

Theorem 2 shows the fact that a continuous function

can be simulated by a layered Hopfield neural network

just like a multi layered perception neural network with

arbitrary small erro r, and a laye

mulated by a q-value weighted fuzzy logical function.

Theorem 2 is directly from the universal approximation

theorem [25,37]’s proof.

Theorem 2 If





1,,

xx is a continuous mapping

from



0,1 m to



0,1

, for any 0, we can build a

layered neural network



defined by Equation (1.18),

and its fixed point can be viewedontinuous map as a c







 





1 1

,,, ,,

mqm11

,, ,

xx FFxx from



0,1m1xx

to 0,



, such that









,, ,,

Fx x fx x





, here 12

,,,

xx are

k inputs of the neural network. For more, for an

ned by

on (which has

arbitr

Equaary layer

ti1 ed neur

) al netwo

ark

fixe  defi

d point func

tion .17





xx, we can find a q-value fuzzyction logical fun







 





111 1

,,,, ,,,,

mmqm

xx FxxmFxx



 

weighted Bounded operator , such that



 

,,,, .

x xFxxF









nt neu

networks described by the Equation (1.1

Theorem 3 tries to prove that all kind recurreral

6) can be simu-

lated by Hopfield neural networks described by Equation

(1.1). The ordinary differential Equation (1.16) has a

strong ability to describe neural phenomena. The neural

network described by Equation (1.16) can have feedback.

For the sake of the existence of feedback of a recurrent

neural network, chaos will occur in such a neural net-

work. As we known, the important characteristics of

chaotic dynamics, i.e., aperiodic dynamics in determinis-

tic systems are the apparent irregularity of time traces

and the divergence of the trajectories over time (starting

from two nearby initial conditions). Any small error in

the calculation of a chaotic deterministic system will

cause unpredictable divergence of the trajectories over

time, i.e. such kind neural networks may behave very

differently under different precise calculations. So any

small difference between two approximations of a tra-

jectory of a chaotic recurrent neural network may create

two totally different approx imate results of this trajectory.

Fortunately, all animals have only limited life and the

H. HU ET AL. 151

domain of trajectories of their neural network are also

finite, so for most neuron models, the Lipsch itz condition

is hold in a real neural system, and in this case, the simu-

lation is possible.

Theorem 3 If





0, ,0TT , is an arbitrary finite

time interval, and the partial differential for all



,,,

xx x and

in Equation (1.16),

,1,2,,ij n are continuous in th

pace then every

e finite domain

Hopfield neural

the time interv

its trajectory sneural network NC

described by Equation (1.16) can be simulated by a

netwodescribed by Equation

al ][0,T and the finite domain D w

an arbitrary small error 0

.1) in

ith



.

Proof The detail is showed in [13].

Neural networks described by Equation (1.16) can in-

clude almost all l models found nowada. [13]

uses 1251 neurons Hopfeura

neura ys

ield nl network to simulate

Rg to Theorem 3.

e of pages, in this paper only layered neural

nug fuzzy logical frameworks

log

ts weters are time coefficients

to the logical relation

ab ons; (2)

ose-Hindmarsh (RH) neuron accordin

ose-Hindmarsh (RH) neuron is much more complicate

than Hopfield neurons. To simulate a complicate neuron

by simple neurons is not a difficult task, but the reverse

task is almost impossible to complete, i.e., it is almost

impossible to simulate a Hopfield neuron by a set of RH

neurons.

4. Hybrid Designing Based on the Fuzzy

Logic and PSVM

For the sak

networks are discussed. For a layered neural network

if the number of neurons at every layer is fixed

mber of structure keepin

the

N is fixed, so the number of the fuzzy logical frame-

works of a neural network is also fixed. When the coeffi-

cients of N are continuously changed, the neural net-

work N is shifted from one structure keeping fuzzy

ical framework to another.

There are two different parameters in a dynamical lay-

ered neurnetwork. The first kind parameters are

weighhich represent the connection topo logy of neu-

ral network. The second param

hich control the time of spikes.

Time coefficients should be decided according to the

dynamical behavior of the whole neural network.

There are two ways to design weights of a layered

neural network: (1) according

out this neural network, we can design the weights

based on the q-value weighted fuzzy logical functi

ccording to the input and output relation function



123

,,,,

xxx x, we use machine learning

approaches ,e.g. Back Propagation method, to learn

weights for



123

,,,,

xxx x. In order to speed up the

learning process, for a layered neural network, we

esigning with PSVM [15],

called as “Logical support vector machine (LPSVM)”.

LPSVM a

 Step 1: Except for the last output layer’s weights,

designing the layers’ weights according to the logical

relations;

Step 2: If

is the input train set, computing the last

combine logical dwhich is

lgorithm:

 inner layers’ output





X based on

;

 Step 3: Using PSVM to compute the output layer’s

weights according to the target set ;

e input

e output

zation

is ic, we

ca similar to design binary digit

boundary detection by

reground object

image matting

 Step 4: Back propagate the error to the inner layers by

the gradient-based learning and modify th

layers’ weights.

 Step 5: Repeat the step 2 to step 4, until th

error is small enough.

5. Hybrid Design of Columnar Organi

of a Neural Network Based on Fuzzy

Logic and PSVM

In the neural science, the design of nonlinear dynamic

neural networks to model bioneural experimental results

an intricate task. But with the help of fuzzy log

n design neural models

networks. In our Hybrid designing approach(LPSVM),

we firstly design neural networks with the help of fuzzy

logic, and then we use PSVM to accomplish the learning

for some concrete vi sual tasks.

Although there are already many neural model to

simulate the functions of the primary visual cortex, they

only focus on very limited function. Early works only try

to address the problem of

mbining ideas and approaches from biological and

computational vision [39-41], and the most recent works

[1,3] are only for very simple pattern recognition tasks.

In this experiment, we try to hybrid design a model of a

columnar organization in th e p rimary visu al co rtex wh ich

can separate haze from its background.

5.1. The Theory of Image Matting

According to Levin A et al. (2008), image matting refers

to the problem of softly extracting the fo

from a single input image. Formally,

methods take

as an input, which is assumed to be a

composite of a foreground image

and a background

B in a linear form and can be written as







 . Closed form solution assumes that



is a linear nction of the input image fu

in a small

window w:,

aIbi w





. Tn to solve a spare

ear system to get the alpha matte. Our

gets rid of the linear assumption

ween

lin

bet

neural fuzzy

logical appro ach



and

. Instead, we try to introduce

nonlinearla re btionetween



and





 (1.19)

here w

W is the image block included in the small win-

dow w. We take color or tture in o cal exlwindow as our

H. HU ET AL.

152

input feature, and the trimap image

map” means three kinds of regions, white denotes defi-

fore

e primary visual cortex are still un-

tood.

rma-

tion primary visual cortex

nt areas of

as the target. “Trip-

nite ground region, black denotes definite back-

grounregion and gray denotes undefined region. After

training, the neural fuzzy logical network will generate

the result of alpha matte. In the application of alpha mat-

ting, our method can remove the haze using dark channel

prior as the tr imap.

5.2. Neural System for Haze-Free Task with

Columnar Organization

Many functions of th

known, but the columnar organization is well unders

The lateral geniculate nucleus (LGN) transfers info

from eyes to brain stem and

(V1) [42]. Columnar organization of V1 plays an impor-

tant role in the processing of visual information. V1 is

composed of a grid



11mm of hypercolumns (hc).

Every hypercolumn contains a set of minicolumns (mc).

Each hypercolumn analyzes information from one small

region of the retina. Adjacent hypercolumns analyze in-

formation from adjace the retina. The recogni-

tion of our hypercolumns’ system (see Figure 2) is

started with the recognition orientation or simple struc-

ture of local patterns, then the trimap image is computed

based on these local patterns. The hypercolumns is de-

signed by LPSVM, the weights of 1st and 2nd layers are

are designed by PSVM to learn the trimap image.

5.2.1. The 1st Layer

Every minicolumn (Figure 3) in the 1st layer tries to

change a 33 pixels’ image block into a binary33



alized.

cus a

The

pixels’ texattern. The input image is norm

Hopfield neurons to fo

ture p

there

This process needs 33

33 small window, every neuron focuses only one

pixel, and are two kinds of fuzzy processing.

t processing directly transforms every pixel’s value to

a fuzzy logical one bsigmoid function, and the 2nd

ssing is also completed by a sigmoid function, the

difference is that every boundary pixel’s value subtracts

h the center pixel’s value before sending it to a sig-

moid function. Such processing emphasizes the contrast

of texture, and our experiments support this fact. These

two processing scan be viewed as some kind preprocess-

ing of input image. Every neuron in a 1st layer’s mini-

column has only one input weight ij

w in Figure 3,

which equals 1; when

y a

proce

wit



, the coefficient



Equation (1.17) ch anges the outpu ts from fuzzy values to

binary numbers(see Figure 4).

5.2.2. The 2nd Layer

Every minicolumn in the 2nd layer works in the way

described by Hopfield neuron equation as Equation (1.18)

or Equation (1.17) and can be viewed as a hypercolumn

columns, which focuses on same of the 1st layer mini

small 33



window, and has some ability to reco gnize a

definite shape (see Figure 5). If there are total q local

small patterns, a hypercolumn in the 2nd layer contains

q (in our system 256q



or 512) minicolumns of the

2nd layhich have same receptive field, and try to

recognize q local small patterns from q miniclumns

of the 1st layer. For a mn

er, wo



image, if adjacent windows

e overlapped, thenar



 

2n2m



 hypercolumns are

needed. In the plane of



 

22mn hypercolumns,

similar 2nd inicolumns’ outputs create small images

sized mq









22mn



 defined as “minicolumn-

images”; if an image 6, then 254 254

and

size is 256 25



hypercolumns are used fo or G or B.

The input of every 2nd-layer minicolun comes from

the ouyer’s minicolumn and has three

different ways:

1. In a local image pattern recognition way(LIPW):

r every color Rm

tput of a la

m a 1st–layer’s minicolumn which

ery 2nd layer hypercolumn contains 512 2nd–layer’s

minicolumns, and inputs of these 2nd–layer’s mini-

columns come fro

cuses on a 33



small window and applies the first

kind processing. Every 2nd–layer’s minicolumn tries to

classify the image block in this window into 512 binary

texture patterns(BTP), e.g. eight important BTPs are

shown in Figu . The pixel value is “1” for white and

“0” for black. In this mode, 33 Hopfield neurons of

the st

1 layer output a 33

re 6



vector, i.e., a 33



fuzzy

logical pattern of a BTP, which is computed by a

Sigmoid function. When the coefficient



in Equation

(1.17) is large enough, after enh cycles, the output of

the nral model in Figu changes a gray pattern to a

binary pattern of LIPW.

2. In a local Binary Pattern operator simulating way

(LBPW). Every 2nd–layer’s hypercolumn in LBPW is

similar to a 2nd–layer’s hypercolumn in above LIPW,

except that its focused 1st

oug

eu re 3

–layer’s minicolumns apply the

second kind processing. A 2nd–layer’s hypercolumn

contains 256 2nd–layer’s minicolumns which can be

labeled by





LBP xy in Equation (1.20). [43]

introduced the Local Binary Pattern operator in 1996 as a

mean of summarizing local gray-level structure. The

operator takes a local neighborhood around each pixel,

thresholds theneighborhood at the value of

the central pixel and uses the resulting binary-valued

image patch as a local image descriptor. It was originally

defined for neighborhoods, giving 8 bit codes based on

the 8 pixels around the central one. Formally, the LBP

operator takes the form:

 

CCnC

LBP xyS ii

 (1.20)

pixels of the

0n

H. HU ET AL.

153

Figure 2. A 4 layers’ structure of a columnar organization of V1 for haze-background separation.

where in this case runs over the 8 neighbors of the

ngle color ed

e R

central pi

si l c, ,ck

i and ,nk

i in Equation (1.20) are

valu







or Gree





Blue







at and , and is a sigmid

0 otherwise.

In thst mn outputs a

, a 1

layer’s min



icolu

function or step function, i.e. 1 if 0u and

is mode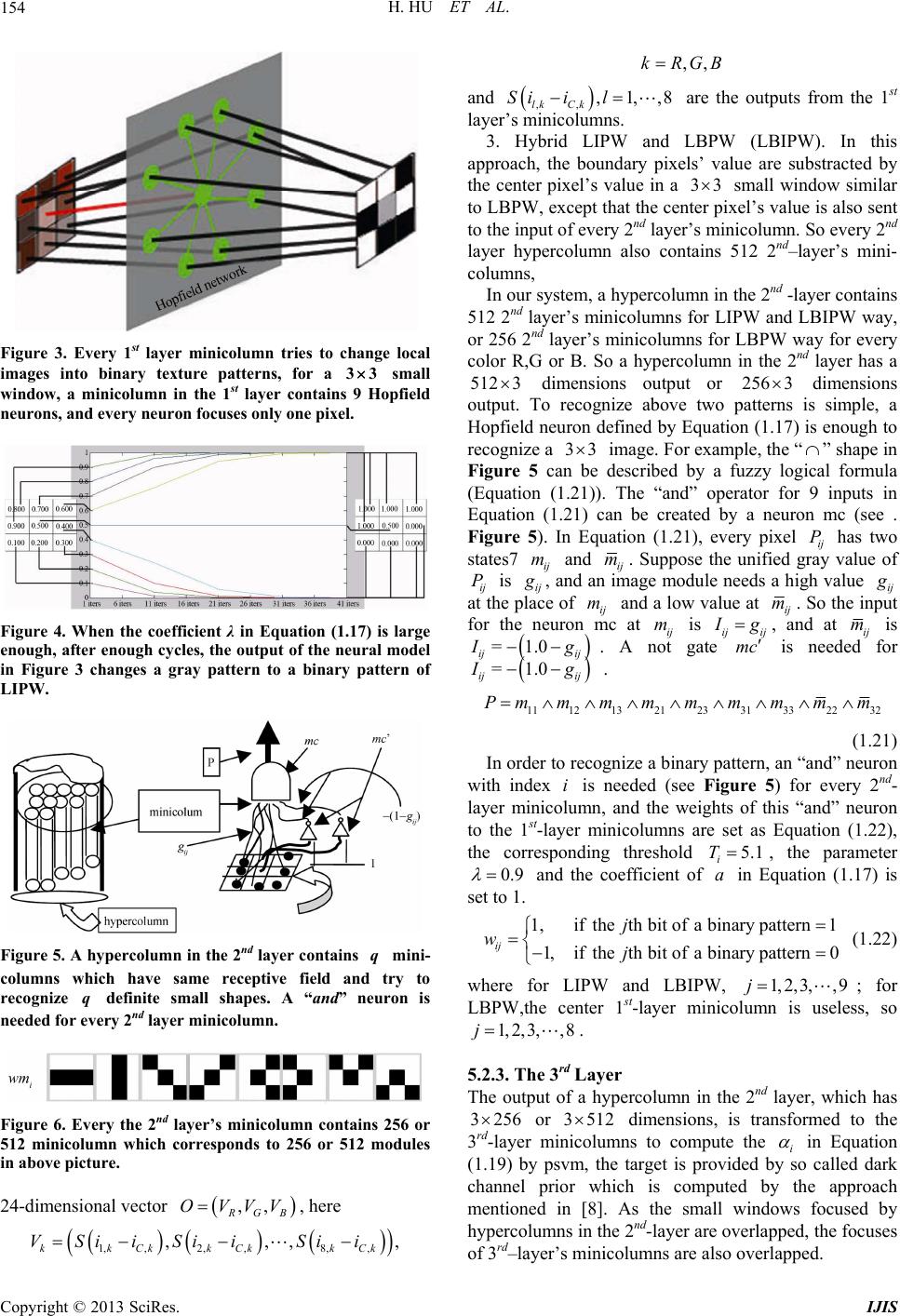

H. HU ET AL.

154

Figure 3. Every 1st layer minicolumn tries to change local

images into binary texture patterns, for a 33



small

window, a minicolumn in the 1st layer coeld

neurons, and eve ry neuron focuses only one pi xel.

ntains 9 Hopfi

Figure 4. When the coefficient λ in Equation (1.17) is large

enough, after enough cycles, the output of the neural model

in Figure 3 changes a gray pattern to a binary pattern of

LIPW.

Figure 5. A hypercolumn in the 2nd layer contains mini-

columns which have same receptive field and try to

recognize

definite small shapes. A “and” neon is

needed for ry 2nd layer minicolumn .

eve

Figure 6. Every the 2nd layer’s minicolumn contains 256 or

512 minicolumn which corresponds to 256 or 512 modules

in above picture.

24-dimensional vector



OVVV, her e







1, ,2, ,8, ,

,,,

kkCkkCk kCk

VSiiSiiSii 

,,kRGB



and





,1,,8

lkCk

Si il

layer’s minicolumns. are the outputs from the 1st

he center pixel’s value is also sent

layer’s minicolery 2nd

ntains 512 2ini-

columns,

In our system, a hypercolumn inhe 2nd -layer contains

512 2nd layer’s minicolumns for LPW and LBIPW way,

6 2nd layer’s minicolu

percolumn in the 2nd layer has a

3. Hybrid LIPW and LBPW (LBIPW). In this

approach, the boundary pixels’ value are substracted by

the center pixel’s value in a 33 small window similar

LBPW, except that tto

to the inpu t of ev ery 2 nd u mn. So ev

layer hypercolumn also cond–layer’s m

or 25mns for LBPW way for every

color R,G or B. So a hy

512 3



dimensions output or 256 3 dimensions

output. To recognize above two patterns is simple, a

Hopfield neuron defined by Eion (1.17) is enough to

recognize a 33quat



image. For example, the “” shape in

Figure 5 can be described by a fuzzy logical formula

(Equation (1.21)). The “and” operator for 9 inputs in

Equation (1.21) can be created byc (see . a neuron m

Figure 5). In Equation (1.21), every pixel ij

P has two

states7 ij

m and ij

m. Suppose the unified gray value of

P is ij

, and an image module needs a high value ij

at the place of ij

m and a low value at ij

m. So the input

neuron mc at ij

m is ij ij

Id at for the g, anij

m is





=1.0

ij ij

g . A not gate mc is needed for





=1.0

ij ij

g .

1112 1321 2331 33 2232

Pmmmmmmmmm





(1.21)

In order to recognize a binary pattern, an “and” neuron

with index i is needed (see Figure 5) for every 2nd-

layer micolumn, and the weights of this “and” neuron

to the 1-layer minicolumns are set as Equation (1.22),

the corresponding threshold 5.1T, the parameter

0.9





and th coefficient of a quation (1.17) is e

set to 1. in E

1,iftheth bit ofabinary pattern1

1,ifthethbit ofabinarypattern0











 (1.2

where for LIPW and LBIPW,

1, 2, 3,,9j; for

PW,the center 1st-layer minicolumn is useless, so

1, 2, 3,,j8



.

5.2.3. The 3rd Layer

The output of a hypercolumn in layer, which has the 2nd

3256



or 3512



dimensionsis transformed to the

3rd-layer ,

mns to compute the inicolumi



in Equation

psarget is providedso calle

channel prior which is computed by the a

mentioned in [8]. As the small windows focused by

rlapped, the fo

(1.19) byvm, the t by d dark

pproach

hypercolumns in the 2nd-layer are ovecuses

of 3rd–layer’s minicolumns are also overlapped.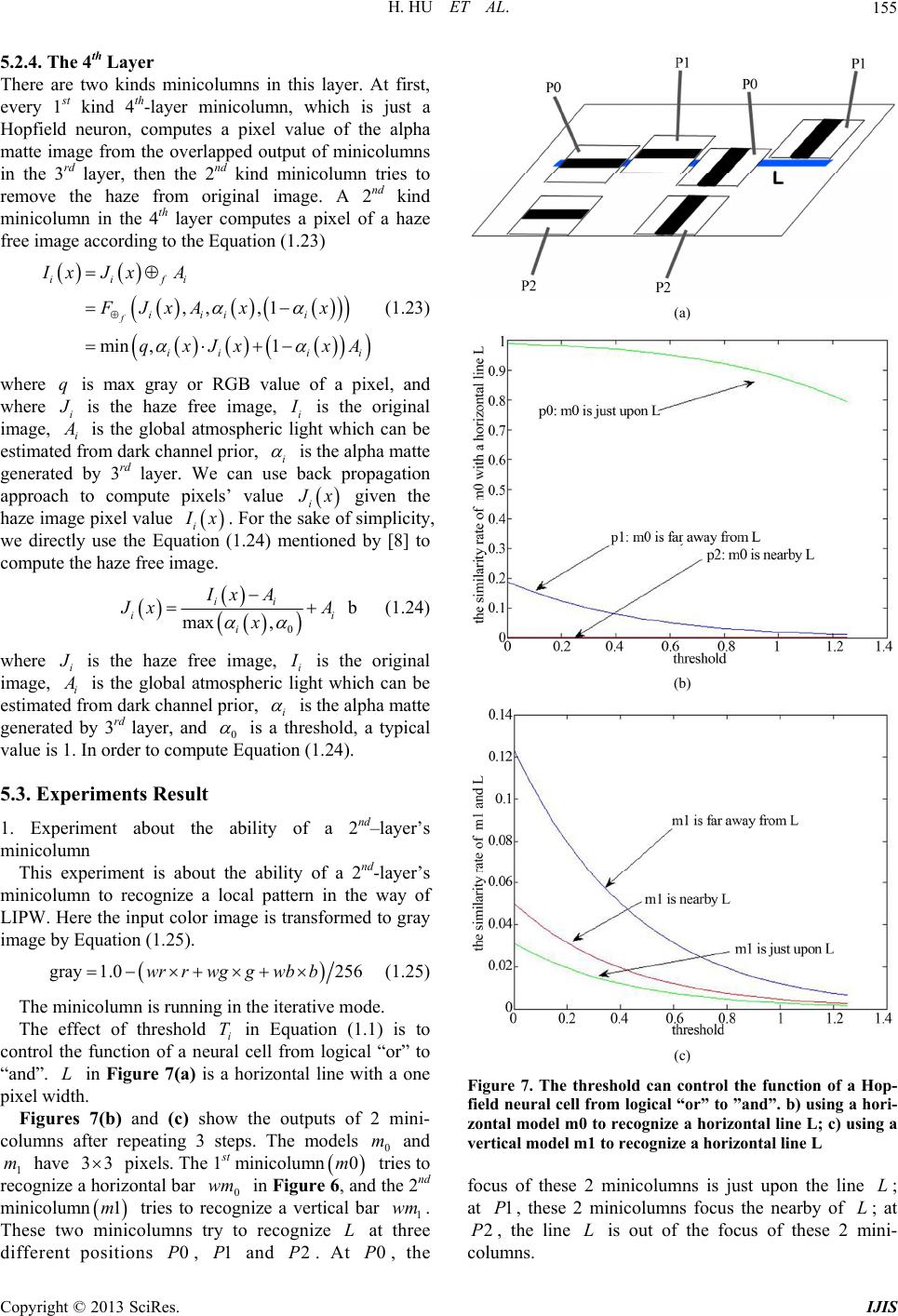

H. HU ET AL. 155

5.2.4. The 4th

There are two kinds minicolumns in this layer. At first,

yer minicolumn, which is just a

matte imfrom tco



(1.23)

Layer

every 1st kind 4th-la

Hopfield neuron, computes a pixel value of the alpha

age he overlapped output of minicolumns

in the 3rd layer, then the 2nd kind minilumn tries to

remove the haze from original image. A 2nd kind

minicolumn in the 4th layer computes a pixel of a haze

free image according to the Equation (1.23)

 

iifi

Ix JxA









 



,, ,1

xAxx





 



min ,1

i i

ii ii

JxxA







where q is max gray or RGB value of a pixel, and

where i

is the haze free image, i

is the original

image, i

A is the global atmospheric light which can be

estimated from dark channel prior, i



is the alpha matte

generated by 3rd layer. We can use back propagation

approach to compute pixels’ value



x given the

haze image pixel value



uation (1

. Foof simp licity,

we di use the Eq.2b

compute the haze free image.

r th

4) m

e sak

ent e

ioned rectlyy [8] to









max ,

Ix A



 b (1.24)



where i

is the haze free image, i

is the original

image, i

is the global atmospheric light which can be

estimated from dark channel prior, i



is the alpha matte

generated by 3rd layer, and 0



is a threshold, a typical

value is 1. In order to compute Equation (1.24).

5.3. Experiments Result

1. Experiment about the ability of a 2nd–layer’s

minicolumn

This experiment is about the ability of a 2-layer’s

minicolun to recognize a local pattern in the way of

LIPW. Hre the inpu t color image is transformed to gray

image by Equation (1.25).



gray1.0256wrrwgwbb  (1.25)

The minicolumn is running in the iterative mo

g

de.

in Equation (1.1) is to

cell from logical “or” to

Figure 62

icolu tries toize a ve

se twcolumns recogniz

The effect of threshold

control the function of a neui

ral

“and”. L in Figure 7(a) is a horizontal line with a one

pixel widt h .

Figures 7(b) and (c) show the outputs of 2 mini-

columns after repeating 3 steps. The models 0

m and

m have 33 pixels. The 1st minic o l u mn



0m tries to

recognize a horizontal bar nd

recogn

try to

, and the

min

The

mn 1m

o min



irtical b

e Lar 1

wm .

at three

fferent positions 0P, 1

and 2

. At 0P, the

(a)

(b)

(c)

Figure 7. The threshold can control the function of a Hop-

field neural c ell from logical “or” to ”and”. b) using a hor i-

zontal model m0 to recognize a horizontal line L; c) using a

vertical model m1 to recognize a horizontal line L

focus of these 2 minicolumns is just upon the line ;

at L

, these 2 minicolumns focus the nearby of L; at

, the line is out of the focus of these 2-

columns. L mini

H. HU ET AL.

156

These two minicolumns are constructed by a fuzzy

formula similar to Eqaution (1.21). In the experiment, th e

threshold changes from 0.0 to 1.26. The threshold

can co function of a neural cell from logical “or”

to “and”, when is too small, the neuron works in the

way of looo two minicolumns both output high

value at

Same as Equation (1.21), the minicolumn of has

a inhibit region when the weights of haveive

values. At position

The





pi denote the rate of each pattern in histo-

gram. In general





pi define in Eqaution (1.28). Here

ntrol the

gic “

r”, s

tterns we use are the LBPs in Equaiton (1.20), where





Si i



, if 10

ii else



Si i









,0,1,,1pihi NMiG



 (1.28)

In Figures 8 (a)-(e) are the results of LBPW, LBIPW,

becomes vaguer from

LBPW, LBIPW, LIPW to LMKH. For the sakend

kind processing in the 1st-layer’s minicolumns p

m ttentihe h

n of them,a similar as the linear

proposed by

According to the results showed in the Tab

negat

PW, the linear mode by [8], and the original image

respectively. From Figure 8, we can see that the texture

structure in the waist of a mountain

, L is droppeto thhibit

region of model has a l mate

at p1 wher than and . As

“vertical” has meaning

curve of m0 at ifferenwith the of

n izedcan

zontal bar and a vertical bn be viewed as a couple of

Equation

d in

owest

of “

be selected.

e in

ching rat

horizontal”, the

e curv

As a hori

e L is

a re

thre

, so

verse

is to

shol

arby

tally d

d T

1mA0p.

optim

of the 2

ays much

ore aon to the contrast, LBPW has the highest

ability to remove taze, LBPW and LIPW are com-

plementary approaches, LBIPW, which is the coopera-

tio has bility aapproach

[8].

caar

opposite shapes, the output of the minicolumn 0m is

opposite to m1’s output in the task of recognize a hori-

zontal bar or a vertical bar, so the most suitable threshold

for logical operator “and” can be selected by

le 1, wh ich

e about texture information entropy of the image, we

can see that the texture information entropy is increased

after haze-free processing, so our approaches have higher

ability to increase the texture information entropy than

the linear approach proposed by [8]. Theoretically speak-

ing, LBPW is a pure texture processing, so LBPW has a

highest value, LIPW is much more weaker than LBPW,

LBIPW is the hybrid of LBPW and LIPW, so it has a

average ability. The texture information entropy of the

Area1 correctly reflects this fact. But for the Area2, as it

already has a clearest texture structure in the original

(1.26).







0.6

argmax

Tfrmfrm



 ( .26)

Here





rm is the fitting rate (output) at the place

P1 of the minicolumn i

2. The Haze-Free Experiment Result

(a) The Haze-Free and texture information entropy

Texture information can give out a rough measure

about the effect of haze-freeing, we use the entropy of

the texture histogram to measure the effect of deleting

haze from images. The entropy of the histogram is de-

age, the deleting of haze may cause overdone. The

texture information is over emphasized by LBPW in the

Aera2, so it has a lowest texture information entropy and

almost becomes a dark area. This fact means that over-

treatment is more easier to appear in a non linear proc-

essing than a linear one in the haze-free task.

(b) The effect about the degree of fuzzyness (Figure 9)

Just as the theorem 1 mentioned above, the parameter



in Eqa ution (1.17) ca n contr ol the fuzzyness of a Hopfield

ribed in Equation (1.27).

Haze makes the texture of an image unclear, so

theoretically speaking, haze removing will increase the

entropy of the texture histogram.

 

Entropy: log

pi pi





 



 (1.27)

(a) (b) (c) (d) (e)

Figure 8. The processing result of neural system for visual haze-free task. a) LBPW; b) LBIPW; c) LIPW; d) LMKH; e)

Original.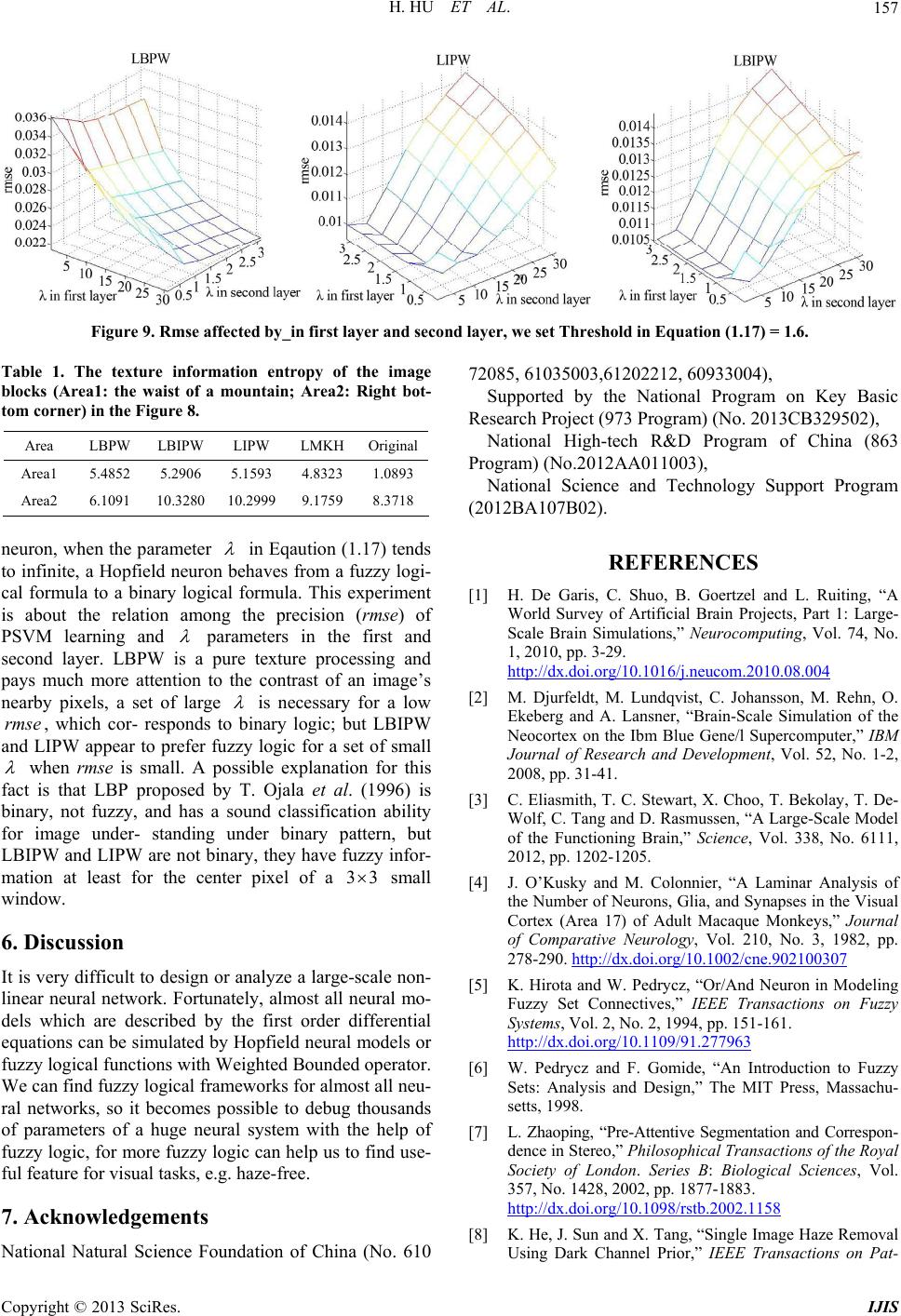

H. HU ET AL. 157

Fig 1.6.

ea1: the waist of a mountain; Area2: Right bot-

tom corner) in the Figure 8.

Area LBPW LBIPW LIPW LMKH Original

ure 9. Rmse affected by_in first layer and second layer, we set Threshold in Equation (1.17) =

Table 1. The texture information entropy of the image

blocks (Ar

Area1 5.4852 5.2906 5.1593 4.8323 1.0893

Area2 6.1091 10.3280 10.2999 9.1759 8.3718

neuron, when the parameter



cal fo

g t

in Eqaution (1.17) tends

to infinite, a Hopfield neuronhaves from a fuzzy logi-

cal formula to a binary logirmula. This experiment

is about the relation amonhe precision (rmse) of

PSVM learning and



meters in the first and

second layer. texture processing and

ays much

para

reLBPW is a pu

n more attention to the contrast of an image’s

earby pixels, a set of large



is necessary for a low

rmse, which cor- responds to binary logic; but LBIPW

and LIPW appear to prefer fuzzy logic for a set of small



when rmse is small. A pos

a s

nary

sible explanation for this

hat rjal (s

otany

- stbinatet

nd a hazr-

fac

bin

for im

t is t LBP poposed T. Oa et al.1996) i

ary, n fuzzy, d has ound classification abilit

age u

IPW ander

LIPW anding

re not binder

, theyry pat

ve fuzrn, bu

y infoLB

mation at least for the center pixel of a 33



small

window.

6. Discussion

It is very difficult to desn or analyze a large-scale non-

linear neural network. Fortunately, almost all neural mo-

dels which are described by the first order differential

equations can be simulated by Hopfield neural models or

logical functions with Weighted Bounded operator.

We can find fuzzy logical frameworks for almost all neu-

networks, so it becomes possible to debug thousands

of parameters of a huge neural system with the help of

fuzzy logic, for more fuzzy logic can help us to find use-

ful feature for visual tasks, e.g. haze-free.

7. Acknowledgements

National Na

fuzzy

ral

tural Science Foundation of China (No. 610

Supported by the National Program on Key Basic

Research Project (973 Pr ogram) (No. 2013CB329502),

National High-tech R&D Program of China (863

Program) (No.2012AA011003),

National Science and Technology Support Program

(2012BA107B02).

REFERENCES

[1] H. De Garis, C. Shuo, B. Goertzel and L. Ruiting, “A

World Survey of Artificial Brain Projects, Part 1: Large-

Scale Brain Simulations,” Neurocomputing, Vol. 74, No.

1, 2010, pp. 3-29. 4

72085, 61035003,61202212, 60933004),

http://dx.doi.org/10.1016/j.neucom.2010.08.00

[2] M. Djurfeldt, M. Lundqvist, C. Johansson, M. Rehn, O.

Ekeberg and A. Lansner, “Brain-Scale Simulation of the

the Ibm Blue Gene/l Supercomputer,” IBM

ch and Development, Vol. 52, No. 1-2,

Neocortex on

Journal of Resear

2008, pp. 31-41.

[3] C. Eliasmith, T. C. Stewart, X. Choo, T. Bekolay, T. De-

Wolf, C. Tang and D. Rasmussen, “A Large-Scale Model

of the Functioning Brain,” Science, Vol. 338, No. 6111,

2012, pp. 1202-1205.

[4] J. O’Kusky and M. Colonnier, “A Laminar Analysis of

the Number of Neurons, Glia, and Synapses in the Visual

Cortex (Area 17) of Adult Macaque Monkeys,” Journal

of Comparative Neurology, Vol. 210, No. 3, 1982, pp.

278-290. http://dx.doi.org/10.1002/cne.902100307

[5] K. Hirota and W. Pedrycz, “Or/And Neuron in Modeling

IEEE Transactions on Fuzzy

4, pp. 151-161.

Fuzzy Set Connectives,”

Systems, Vol. 2, No. 2, 199

http://dx.doi.org/10.1109/91.277963

[6] W. Pedrycz and F. Gomide, “An Introduction to Fuzzy

/10.1098/rstb.2002.1158

Sets: Analysis and Design,” The MIT Press, Massachu-

setts, 1998.

[7] L. Zhaoping, “Pre-Attentive Segmentation and Correspon-

dence in Stereo,” Philosophical Transactions of the Royal

Society of London. Series B: Biological Sciences, Vol.

357, No. 1428, 2002, pp. 1877-1883.

http://dx.doi.org

[8] K. He, J. Sun and X. Tang, “Single Image Haze Removal

Using Dark Channel Prior,” IEEE Transactions on Pat-

H. HU ET AL.

158

tern Analysis e, Vol. 33, No. 12and Machine Intelligenc,

2011, pp. 2341-2353.

http://dx.doi.org/10.1109/TPAMI.2010.168

[9] R. FitzHugh, “Impulses and Physiological States in Theo-

retical Models of Nerve Membrane,” Biophysical Journal,

Vol. 1, No. 6, 1961, pp. 445-466.

http://dx.doi.org/10.1016/S0006-3495(61)86902-6

[10] H. R. Wilson and J. D. Cowan, “Excitatory and Inhibitory

Interactions in Localized Populations of Model Neurons,”

Biophysical Journal, Vol. 12, No. 1, 1972, pp. 1-24.

http://dx.doi.org/10.1016/S0006-3495(72)86068-5

[11] J. Hindmarsh and R. Rose, “A Model of Neuronal Burst-

ing Using Three Coupled First Order Differential Equa-

tions,” Proceedings of the Royal Society of London. Se-

ries B. Biological Sciences, Vol. 221, No. 1222, 1984, pp.

87-102. http://dx.doi.org/10.1098/rspb.1984.0024

[12] J. J. Hopfield, D. W. Tank, et al., “Computing with Neu-

ral Circuits: A Model,” Science, Vol. 233, No. 4764, 1986,

pp. 625-633. http://dx.doi.org/10.1126/science.3755256

[13] H. Hu and Z. Shi, “The Possibility of Using Simple Neu-

ron Models to Design Brain-Like Computers,” In: Ad-

vances in Brain Inspired Cognitive Systems, Springer,

Shenyang, 2012, pp. 361-372.

http://dx.doi.org/10.1007/978-3-642-31561-9_41

[14] H. Abarbanel, M. I. Rabinovich, A. Selverston, M. Baz-

henov, R. Huerta, M. Sushchik, and L. Rubchinskii, “Sy n-

chronisation in Neural Networks,” Physics-Uspekhi, Vol.

39, No. 4, 1996 pp. 337-362.

http://dx.doi.org/10.1070/PU1996v039n04ABEH000141

[15] Z. Li, “A Neural Model of Contour Integration in the

Primary Visual Cortex,” Neural Computation, Vol. 10,

No. 4, 1998, pp. 903-940.

http://dx.doi.org/10.1162/089976698300017557

[16] E. Fransen and A. Lansner, “A Model of Cortical Asso-

ciative Memory Based on a Horizontal Network of Con-

nected Columns,” Network

tems, Vol. 9, No. 2, 1998, pp. 235-264.

: Computation in Neural Sys-

http://dx.doi.org/10.1088/0954-898X/9/2/006

[17] H. Sun, L. Liu and A. Guo, “A Neurocomputational Mo-

del of Figure-Ground Discrimina

ing,” IEEE Transactions on Neural Networks, V

tion and Target Track-

ol. 10,

No. 4, 1999, pp. 860-884.

http://dx.doi.org/10.1109/72.774238

[18] H. B. Barlow, C. Blakemore and J. D. Pettigrew, “

Neural Mechanism of Binocular Depth DiscriminThe

tion,”

The Journal of Physiology, Vol. 193, No. 2, 1967, p. 327.

[19] D. H. Hubel and T. N. Wiesel, “Stereoscopic Vision in

Macaque Monkey: Cells Sensitive to Binocular Depth in

area 18 of the Macaque Monkey Cortex,” Nature, Vol.

225, 1970, pp. 41-42.

http://dx.doi.org/10.1038/225041a0

[20] K. S. Rockland and J. S. Lund, “Intrinsic Laminar Lattice

Connections in Primate Visual Cortex,” Journal of Com-

parative Neurology, Vol. 216, No. 3, 1983, pp. 303-318.

http://dx.doi.org/10.1002/cne.902160307

[21] C. D. Gilbert and T. N. Wiesel, “Clustered Intrinsic Con-

nections in Cat Visual Cortex,”

ence, Vol. 3, No. 5, 1983, pp. 1116-1133.

The Journal of Neurosci-

/S0042-6989(00)00044-4

[22] R. von der Heydt, H. Zhou, H. S. Friedman, et al., “Rep-

resentation of Stereoscopic Edges in Monkey Visual Cor-

tex,” Vision Research, Vol. 40, No. 15, 2000, pp. 1955-

1967. http://dx.doi.org/10.1016

8188-8198.

ets, Vol.

An Active

[23] J. S. Bakin, K. Nakayama and C. D. Gilbert, “Visual Re-

sponses in Monkey Areas v1 and v2 to Three-Dimensio-

nal Surface Configurations,” The Journal of Neuroscience,

Vol. 20, No. 21, 2000, pp.

[24] L. A. Zadeh, “Information and Control,” Fuzzy S

8, No. 3, 1965, pp. 338-353.

[25] S. S. Haykin, “Neural Networks: A Comprehensive Foun-

dation,” Prentice Hall Englewood Cliffs, 2007.

[26] J. Nagumo, S. Arimoto and S. Yoshizawa, “

Pulse Transmission Line Simulating Nerve Axon,” Pro-

ceedings of the IRE, Vol. 50, No. 10, 1962, pp. 2061-

2070. http://dx.doi.org/10.1109/JRPROC.1962.288235

[27] A. L. Hodgkins and A. F. Huxley, “A Quantitative De-

scription of Membrane Current and

Conduction and Excitation in Nerve, Its Application to

from Crustacean Ax-

No. 1, 1977, pp. 81-

” American Journal

of Physiology, Vol. 117, No. 4, 1952, pp. 500-544.

[28] V. der Pol B, “The Nonlinear Theory of Electrical Oscil-

lations,” Proceedings of the Institute of Radio Engineers,

Vol. 22, No. 9, 1934, pp. 1051-1086.

[29] J. A. Connor, D. Walter and R. McKowN, “Neural Repe-

titive Firing: Modifications of the Hodgkin-Huxley Axon

Suggested by Experimental Results

ons,” Biophysical Journal, Vol. 18,

102. http://dx.doi.org/10.1016/S0006-3495(77)85598-7

[30] C. Morris and H. Lecar, “Voltage Oscillations in the Bar-

nacle Giant Muscle Fiber,” Biophysical Journal, Vol. 35

No. 1, 1981, pp. 193-213. ,

http://dx.doi.org/10.1016/S0006-3495(81)84782-0

[31] T. R. Chay, “Chaos in a Three-Variable Model of an Ex-

citable Cell,” Physica D: Nonlinear Phenomena, Vol. 16,

No. 2, 1985, pp. 233-242.

http://dx.doi.org/10.1016/0167-2789(85)90060-0

[32] T. R. Chay, “Electrical Bursting and Intracellular Ca2+

Oscillations in Excitable Cell Models,” Biological Cyber-

netics, Vol. 63, No. 1, 1990, pp. 15-23.

http://dx.doi.org/10.1007/BF00202449

[33] D. Golomb, J. Guckenheimer and S. Gueron, “Reduction

of a Channel-Based Model for a Stomatogastric Ganglion

/10.1007/BF00226196

Lpneuron,” Biological Cybernetics, Vol. 69, No. 2, 1993,

pp. 129-137. http://dx.doi.org

Thalamic

[34] H. R. Wilson and J. D. Cowan, “A Mathematical Theory

of the Functional Dynamics of Cortical and

Nervous Tissue,” Kybernetik, Vol. 13, No. 2, 1973, pp.

55-80. http://dx.doi.org/10.1007/BF00288786

[35] F. Buchholtz, J. Golowasch, I. R. Epstein and E. Marder,

“Mathematical Model of an Identified Stomatogastric

al Cy-

Ganglionneuron,” Journal of Neurophysiology, Vol. 67,

No. 2, 1992, pp. 332-340.

[36] A. Burkitt, “A Review of the Integrate-and-Fire Neuron

Model: I. Homogeneous Synaptic Input,” Biologic

bernetics, Vol. 95, No. 1, 2006, pp. 1-19.

http://dx.doi.org/10.1007/s00422-006-0068-6

[37] H.-X. Li and C. P. Chen, “The Equivalence between

Fuzzy Logic Systems and Feedforward Neural Networks,”

H. HU ET AL.

159

IEEE Transactions on Neural Networks, Vol. 11, No. 2,

2000, pp. 356-365. http://dx.doi.org/10.1109/72.839006

[38] G. Fung and O. L. Mangasarian, “Proximal Support Vec-

tor Machine Classifiers,” Proceedings of the Seventh

ACM SIGKDD International Conference on Knowledge

Discovery and Data Mining, New York, 2011, pp. 77-86.

http://dx.doi.org/10.1145/502512.502527

[39] D. Wielaard, M. Shelley, D. McLaughlin and R. Sh

“How Simple Cells Are Made in a Nonlinear Neapley,

twork

dings o

Model of the Visual Cortex,” The Journal of Neurosci-

ence, Vol. 21, No. 14, 2001, pp. 5203-5211.

[40] J. Wielaard and P. Sajda, “Simulated Optical Imaging of

Orientation Preference in a Model of V1,” Procee

First International IEEE EMBS Conference on Neural

Engineering, Capri Island, 20-22 March 2003, pp. 499-

502.

[41] Kokkinos, R. Deriche, O. Faugeras and P. Maragos,

“Computational Analysis and Learning for a Biologically

Motivated Model of Boundary Detection,” Neurocom-

puting, Vol. 71, No. 10, 2008, pp. 1798-1812.

http://dx.doi.org/10.1016/j.neucom.2007.11.031

[42] V. B. Mountcastle, “The Columnar Organization of the

Neocortex,” Brain, Vol. 120, No. 4, 1997, pp. 701-722.

http://dx.doi.org/10.1093/brain/120.4.701

[43] T. Ojala, M. Pietikäinen and D. Harwood, “A Compara-

7-4

tive Study of Texture Measures with Classification Based

on Featured Distributions,” Pattern Recognition, Vol. 29,

No. 1, 1996, pp. 51-59.

http://dx.doi.org/10.1016/0031-3203(95)0006

H. HU ET AL.

160

Appendix A

A Hopfield neuron can approximately simulate Bounded

operator.

Bounded operato r



F

max

pq

Bounded product ,



0, 1pq



min 1,pq pq 

Bounded sum .

Based on Eqaution (1.1)), the membrane potential’s

fixed poin t under input is

Iiikk

UwIi

a and the

output at the fixed point is



1exp 1

VUT



 .

If there are only two inputs







12 12

,,0,1IIII

21.0w and

we set , and , then

1.0

a11.0w

I



Now we try to prove that the Bounded operator



F is the best fuzzy operator to simulate neural

cells described by (3) and the threshold Ti can change the

neural cell from the bounded operator

 to



analyzing the output at the fixed point







1exp 1

iii

. If is a constant and VUT 0C

12i

UIIC , then







1exp1 1V

When CT

12i

UII

1

V, so in this case, if

is large enough, C

V. If 12

I I

CU C , then



1exp1 1exp1

ii i

CT VCT

according to equation (a). We can select a , that

makes i



!1exp _

iii i

TUTj kUT





 

 i

small enough, then 1i

VII









1exp 1

1exp 1exp

11 !

1exp _

1exp_ .

iii

ii ii

VUT

UT kUT

UTUT j

kUT

UTUT j

kUT























 

 

 



 



So in this case,



12 12

min 1,

VI III .

Similarly, if  21

=IIUi 0

V. So when

is large enough and

C12 0

UII C, then

V. When 12i

CUI IC , if we select a

suitable which makes





!1exp

iii ii

TUTj kUT











then



12 12

max 0,1

VI III.

Based on above analysis, the Bounded operator fuzzy

system is suitable for neural cells described by Equation

(1.1) when 1.0



,1 and 2. For

arbitrary positive i,1 and 2, we can use corres-

ponding q-value weighted universal fuzzy logical func-

tion based on Bounded operator to simulate such kind

neural cells. If a weight is negative , a N-norm

operator

1.0ww

1.0w

a w





1xNx



 should be use d.

Experiments done by scanning the whole region of





I in



to find the suitable coefficients for



0,1



and



show that above analysis is sound. We

denote the input in (5b) as

 







tItIt

. The

“error” for



and “errAnd” for



are shown in

Figure A as the solid line and the dotted line resp ectively.

In Figure 10, the threshold is scanned from 0 to 4.1

with step size 0.01. The best i in Equation (4) for



is 2.54 and the best in Equation (4) for



is 0,

when 1.0a



, 11.0w



and . In this case the

“errOr” and “errAnd” is less than 0.01. Our experiments

show that suitable i can be found. So in most cases,

the bounded operator

1.0=









<0w

mentioned above is

the suitable fuzzy logical framework for the neuron

defined by Equation (3). If the weight 1 and



, we should use a q-value weighted bounded

operator







 to represent above neuron.

Appendix B

It is easily to see



follows the associative condition

and

123 1

min ,

fffn ii

xxxqwx











.

For



, we can prove the associative condition is

Figure 10. Simulating fuzzy logical and-or by changing

thresholds of neural cells. The X-axis is the threshold value

divided by 0.02, the Y-axis is errG. The real line is

perrAndq between



and

V, and the dot line is

the perrorq between



and

H. HU ET AL. 161

hold also. The proof is listed as below:

If , we have:



11 221 21wpwpw wq0















12 3

1212 33

11 221 233

11 221 2

33 3

11 22331 23

,,, ,,1,

1, ,1,

max 0,1

pp p

FFppwwpw

Fwpwp wwqpw

wpwpw wq

wpwq

wpwpwpw wwq















;





11 221 21wp wpw wq0



, we have



12 3

1212 33

33 3

for 03

33 3

11 22331 23

,,, ,,1,

0, ,1,

max 0,011

max 0,0

max 0,1

pp p

FFppwwpw

Fpw

wpwq

wp wq

wpwpwpw wwq



















;







12 3123

11 22331 23

max 0,1

ff ff

pppp pp

wpwpwpw wwq





By inductive approach, we can prove that



also

follows the associative condition and

123

max 0,1

ffffn

ii i

in in

xxx x

wxw q

 



















For more if we define (usually, a

negative weight i corresponds a N-norm), above

weighted bounded operator



Npq p



F follows the

Demorgan Law, i.e.







 

123

min ,

max 0,

max 0,1

ffffn

iii

in in

fff

Nx xxx

qqwx

qwx

wq xwq

Nx NxNxNx









 



















  







n