P. P. LI ET AL.
Copyright © 2013 SciRes. CN
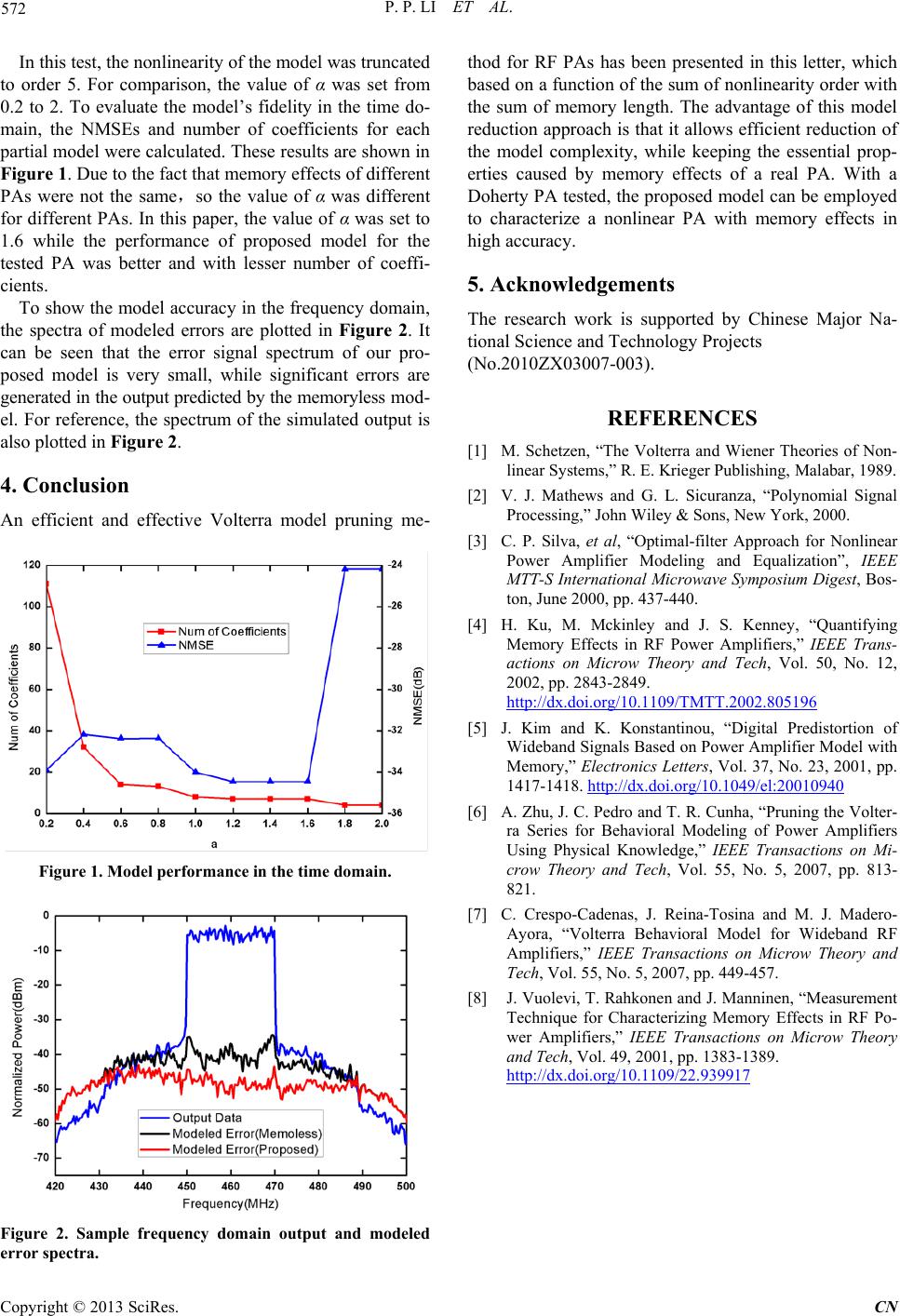
In this test, the nonlinearity of the model was truncated
to order 5. For comparison, the value of α was set from
0.2 to 2. To evaluate the model’s fidelity in the time do-
main, the NMSEs and number of coefficients for each
partial model were calculated. These results are shown in
Figure 1. Due to the fact that memory effects of different
PAs were not the same,so the value of α was different
for different PAs. In this paper, the value of α was set to
1.6 while the performance of proposed model for the
tested PA was better and with lesser number of coeffi-
cients.
To show the model accuracy in the frequency domain,
the spectra of modeled errors are plotted in Figure 2. It
can be seen that the error signal spectrum of our pro-
posed model is very small, while significant errors are
generated in the output predicted by the memoryless mod-
el. For reference, the spectrum of the simulated output is
also plot t e d in Figure 2.
4. Conclusion
An efficient and effective Volterra model pruning me-
Figure 1. Model performance in the time domain.
Figure 2. Sample frequency domain output and modeled
error spectra.
thod for RF PAs has been presented in this letter, which
based on a function of the sum of nonlinearity order with
the sum of memory length. The advantage of this model
reduction approach is that it allows ef ficient reduction of
the model complexity, while keeping the essential prop-
erties caused by memory effects of a real PA. With a
Doherty PA tested, the proposed model can be employed
to characterize a nonlinear PA with memory effects in
high accuracy.
5. Acknowledgements
The research work is supported by Chinese Major Na-
tional Science and Technology Projects
(No.2010ZX03007-003).
REFERENCES
[1] M. Schetzen, “The Volterra and Wiener Theories of Non-
linear Systems,” R. E. Krieger Publishing, Malabar, 1989.
[2] V. J. Mathews and G. L. Sicuranza, “Polynomial Signal
Processing,” John Wiley & Sons, New York, 2000.
[3] C. P. Silva, et al, “Optimal-filter Approach for Nonlinear
Power Amplifier Modeling and Equalization”, IEEE
MTT-S International Microwave Symposium Digest, Bos-
ton, June 2000, pp. 437-440.
[4] H. Ku, M. Mckinley and J. S. Kenney, “Quantifying
Memory Effects in RF Power Amplifiers,” IEEE Trans-
actions on Microw Theory and Tech, Vol. 50, No. 12,
2002, pp. 2843-2849.
http://dx.doi.org/10.1109/TMTT.2002.805196
[5] J. Kim and K. Konstantinou, “Digital Predistortion of
Wideband Signals Based on Power Amplifier Model with
Memory,” Electronics Letters, Vol. 37, No. 23, 2001, pp.
1417-1418. http://dx.doi.org/10.1049/el:20010940
[6] A. Zhu, J. C. Pedro and T. R. Cunha, “Pruning the Volter-
ra Series for Behavioral Modeling of Power Amplifiers
Using Physical Knowledge,” IEEE Transactions on Mi-
crow Theory and Tech, Vol. 55, No. 5, 2007, pp. 813-
821.
[7] C. Crespo-Cadenas, J. Reina-Tosina and M. J. Madero-
Ayora, “Volterra Behavioral Model for Wideband RF
Amplifiers,” IEEE Transactions on Microw Theory and
Tech, Vol. 55, No. 5, 2007, pp. 449-457.
[8] J. Vuolevi, T. Rahkonen and J. Manninen, “Measurement
Technique for Characterizing Memory Effects in RF Po-
wer Amplifiers,” IEEE Transactions on Microw Theory
and Tech, Vol. 49, 2001, pp. 1383-1389.
http://dx.doi.org/10.1109/22.939917