Communications and Network, 2013, 5, 485-492
http://dx.doi.org/10.4236/cn.2013.53B2089 Published Online September 2013 (http://www.scirp.org/journal/cn)
Efficient Implementations of NTRU in Wireless Network
Xin Zhan, Rui Zhang, Zhilong Xiong, Zhaoxia Zheng, Zhenglin Liu
School of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan, China
Received April 2013
ABSTRACT
NTRU is a lattice-based public key cryptosystem featuring reasonably short, easily created keys, high speed, and low
memory requirements, seems viable for wireless network. This paper presents two optimized designs based on the en-
hanced NTRU algorithm. One is a light-weight and fast NTRU core, it performs encryption only. This work has a
gate-count of 1175 gates and a power consumption of 1.51 μW. It can finish the whole encryption process in 1498 μs at
500 kHz. As such, it is perfect for wireless sensor network. Another high-speed NTRU core is capable of both encryp-
tion and decryption, with delays of 16,064 μs and 128,010 μs in encryption and decryption respectively. Moreover, it
consists of 25,758 equivalent gates and has a total power consumption of 59.2 μW (it will be reduced greatly if low
power methods were adopted). This core is recommended to be used in base stations or servers in wireless network.
Keywords: Wireless Network; Public key Cryptosystem; NTRU ; Eff icient Implementations
1. Introduction
The wireless network is b eing exp ected to be widely used
in various fields. Although wireless network offers low-
cost deployment and convenience, security implementa-
tion is considered essential because of its inherent vuln e-
rability. The public key cryptosystem using two different
keys, such as RSA and ECC, has profo und consequences
in the areas of confidentiality, key distribution and au-
thentication, but its common conception is complex, slow
and power hungry [1]. The relatively new lattice-based
public key cryptosystem—NTRU that features reasona-
bly short, easily created keys, high speed, and low mem-
ory requirements [2], seems viable for wireless network.
O’Rourke first implemented the NTRU core with a
gate count of minimum 1483 gates (N = 503) [3]; but it
performs star multiplication only. Another design is rea-
lized in Kaps’s p aper (N = 167) [4]; it performs only en-
cryption w ith an area of 2850 gates and power consump-
tion of 15.1 μW at 500 kHz. The most detailed low-cost
implementation of NTRU is realized by AC Atici’s [5].
The author presented two compact NTRU architectures
(N = 167), one is for encryption only with an area of
2800 gates and a dynamic power consumption of 1.72
μW at 500 kHz. Another is capable of both encryption
and decryption, and it consists of 10,500 gates and con-
sumes 6 μW dynamic power. Several other papers focus
on the optimization of area and power consumption, but
only a few works are related to studies on the optimiza-
tion of speed.
In Jeffrey Hoffstein’s paper [6], an alternative of
NTRU is proposed with a new form
1f pF= +
to
create private key f that speeds both the key generation
and the decryption. Unfortunately, there is little research
on the im plementation of the enhanced NTR U.
The rest of this paper is organized as follows: Section
2 summarizes the basic of enhanced NTRU algorithm;
Section 3 presents the architecture of an encryption-only
enhanced NTRU optimized for small area and fast speed;
in Section 4, an architecture of enhanced NTRU opti-
mized for high speed is presented, it is capable of both
encryption and decryption; in Section 5 we give synthe-
sis results on an ASI C technology library; Section 6 co n-
cludes this paper.
2. Algorithm of Enhanced NTRU
NTRU is a parameterized family of lattice-based public
key cryptosystems. Its basic operations are realized in a
truncated polynomial ring
[] /(1)
N
R ZXX= −
. Polyno-
mials in the ring have a degree of N-1 and all the coeffi-
cients are integers. Polynomial
aR∈
can be presented
as:
2 21
01 221
1
0
NN
NN
Ni
i
i
a aaX aXaXaX
aX
−−
−−
−
=
= +++⋅⋅⋅++
=
∑
. (1)
The addition in the ring R is just as the same as general
polynomial addition. But the multiplication in R is re-
ferred to star multiplication (see [2] for details) and de-
noted as a
∗
symbol.

X. ZHAN ET AL.
486
The NTRU cryptosystem depends on three parameters,
where a large prime N limits the degree of polynomials
in the ring and
(,)pq
satisfies
gcd( ,)1pq=
. It is also
possible to consider p as a polynomial, for example
2pX= +
.
In order to speed up both the key generation and the
decryption process, a new form of enhanced NTRU is
suggested [6]. In enhanced NTRU, users choose f to have
the form
1f pF= +
. Notice that this form has the
property of
1
(mod )1 pff p
−
= =
, so it is not necessary to
compute the inverse modulo p, and the second multipli-
cation in the decryption process disappears. Some other
optimizations presented in the rest of this paper are all
based on enhanced NTRU.
Before we give an outline of enhanced NTRU algo-
rithm, four sets of binary polynomials
, ,,Fgrm
need to
be specified first. Some notations are used to specify the
sets of polynomials:
R
The set of binary polynomials in
[] /(1)
N
R ZXX= −
.
()Rd
The set of binary polynomials in R with d ones
and N-d zero s.
Then the polynomials
, ,,Fg rm
are selected in the
specified set:
() F F Rd∈
,
( ), g g Rd∈
( ), r r Rd∈
m∈
() m Rd
.
 Key Generation: the user must first choose two ran-
dom polynomials
() F F Rd∈
and
( ), g g Rd∈
pri-
vate key is computed as:
1f pF= +
. (2)
Besides,
1
(mod ) q ff q
−
=
must exist. Then the fol-
lowing computation is performed:
(mod ). qh pf gq≡∗
(3 )
Now h is the public key and f is the private key.
 Encryption: To encrypt a plaintext
() m m Rd∈
, the
user should select a random polynomial
() r r Rd∈
at
first. Then the cipher e is formed:
(mod ).ehr mq≡∗+
(4 )
 Decryption: In order to decrypt the cipher e using
private key f, the user first calculates:
(mod ).a feq≡∗
(5)
Then the user chooses
aR∈
to satisfy this congru-
ence and to lie in a pre-specified subset of R. Finally,
a binary polynomial m should be fou nd out to sat isfy
( 2)( 2)(mod21).
N
ma−=− +
(6)
It can be proved that m equals the plaintext.
3. Light-Weight and Fast NTRU
(Encryption-Only)
In order to meet the requirements in ultra-low cost envi-
ronments like wireless sensor network, we proposed a
light-weight NTRU structure based on the enhanced NTRU
algorithm. It performs encryption only and is optimized
for both fast speed and small area. The parameter set we
have chosen is
(, )(107,64),Nq=
and
5 r d=
, which
was the lowest security recommended in [2].
Figure 1 shows the architecture of light-weigh t N TRU
engine. It consists of a control engine, a 6 bits result buf-
fer, a multiplication module, a look up table (LUT) and a
non-zero coefficients sequence generator (NCSG).
The control engine manages the process of encryption.
The result buffer is used to store final result and current
sum in star multiplication process. The multiplication
module performs star multiplication operation. Public
key h is pre-computed and stored in the LUT. NCSG is
designed to generate and rotate the degrees of non-zero
terms of random polynomial r.
Due to NCSG, one operand in multiplication operation
is bounded to 1’b1 (see Section 3.1 below), the multiplier
is needless and multiplication module only consists of a
6bits adder and a router.
3.1. Non-Zero Coefficients Sequence Generator
(NCSG)
In NTRU encryption process, the computation of
hr∗
is not time-efficient. In fact, r is a quite sparse binary
polynomial that has only
rd
non-zero coeff icients . As a
result, most of the multiplicatio ns in a star multiplication
process are unnecessary.
In this paper, we introduce a structure of non-zero coef-
ficients sequence generator (NCSG), which could record
the degrees of non-zero terms in polynomial r when the
coefficients of r loaded one by one. Then the non-zero
coefficients sequence is rotated during the computation
of star multiplication. According to this, the control en-
gine generates the corresponding address of h for LUT.
As F ig u re 2 shows, NCSG consist of a
7 r d
bits circu-
lar register, a 7 bits counter, a 7 bits adder, a 2-input rou-
ter, an AND gate and an OR gate.
Input of the right hand 7-bit register is composed of 2
paths and determined by a ctrl signal. Path 1 is from the
most significant 7 bits during the computation of star
multiplication, the register performs as a general shift
register and the degree of current non-zero term is output
to control engine by left-hand 7 bits register. During load-
ing polynomial r, the output of the 7 bits counter is as
one source of path2, it is added to the least significant 7
bits (where the degree of current term is stored). The
counter counts the zero from
_r in
and resets if a one is
input. Then the degree of next term is computed by the
adder and loaded to the circular register. After N clocks,
non-zero coefficients sequence is generated in the circu-
lar register.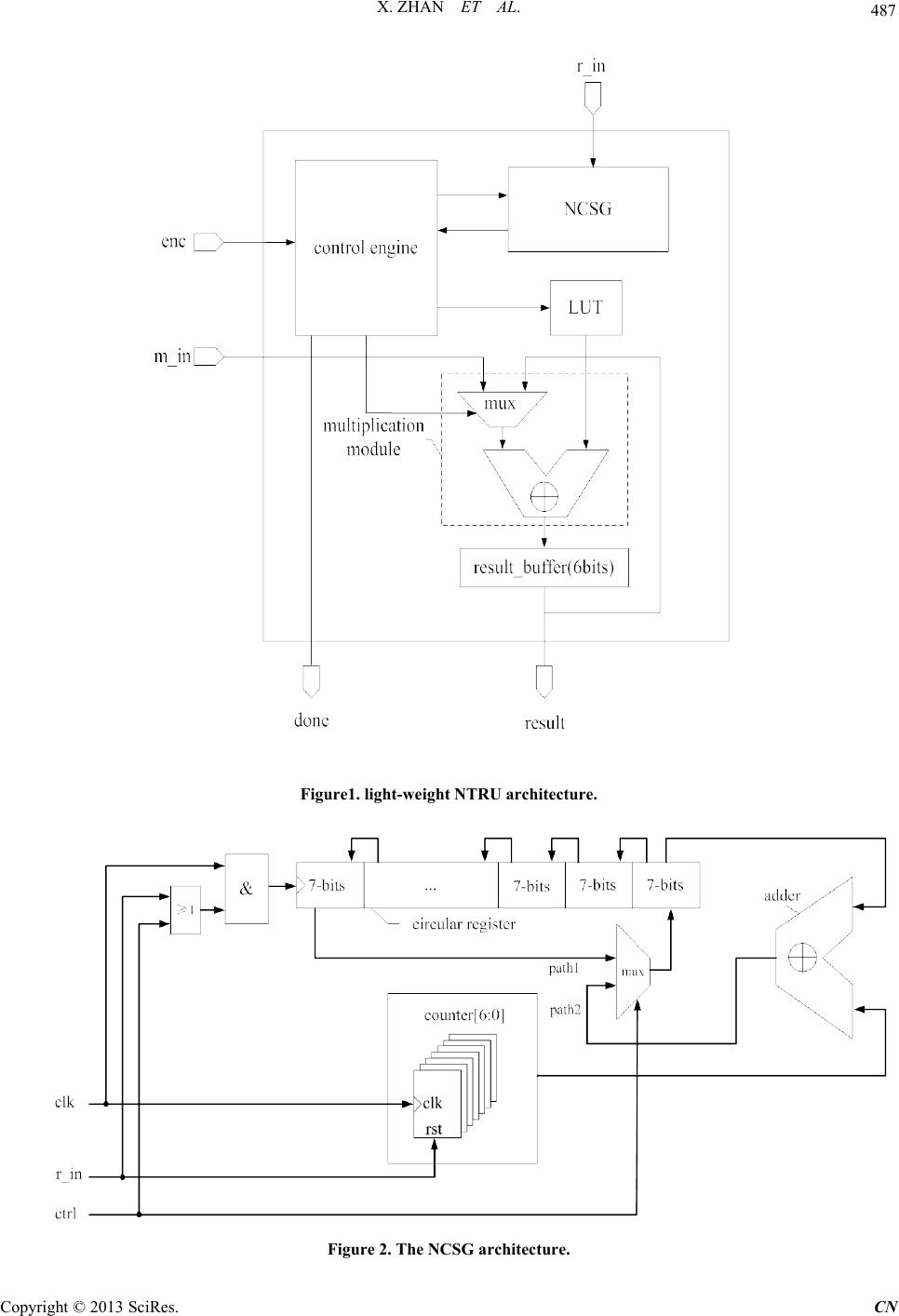

X. ZHAN ET AL.
487
Figure1. light-weight NTRU architecture.
Figure 2. The NCSG architecture.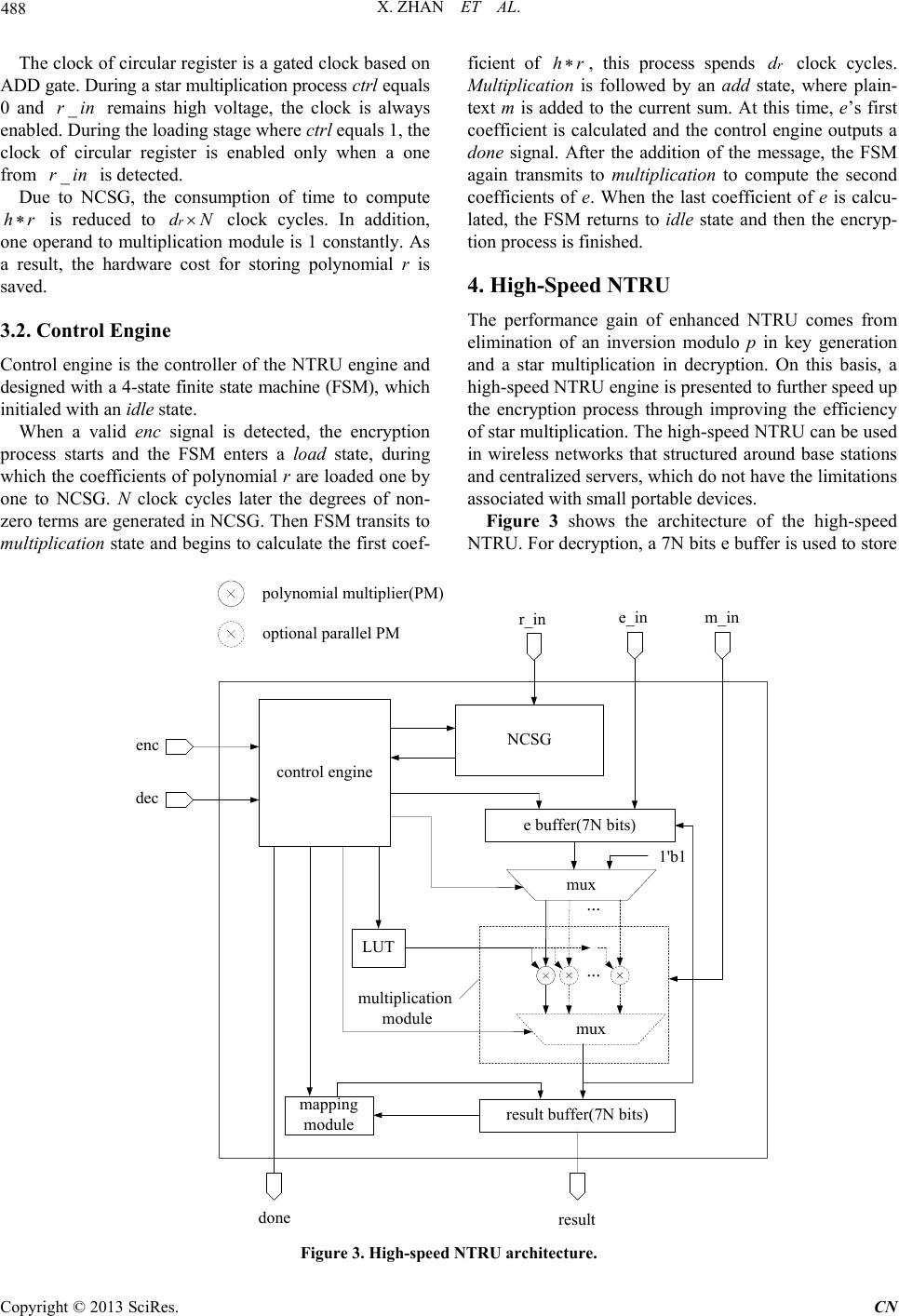

X. ZHAN ET AL.
488
The clock of circular register is a gated clock based on
ADD gate. During a star multiplication process ctrl equals
0 and
_r in
remains high voltage, the clock is always
enabled. During the loading stage where ctrl equals 1, the
clock of circular register is enabled only when a one
from
_r in
is detected.
Due to NCSG, the consumption of time to compute
hr∗
is reduced to
r dN×
clock cycles. In addition,
one operand to multiplication module is 1 constantly. As
a result, the hardware cost for storing polynomial r is
saved.
3.2. Control Engine
Control engine is the controller of the NTRU engine and
designed with a 4-state finite state mach ine (FSM), which
initialed with an idle state.
When a valid enc signal is detected, the encryption
process starts and the FSM enters a load state, during
which the coefficients of polynomial r are loaded one by
one to NCSG. N clock cycles later the degrees of non-
zero terms are generated in NCSG. Then FSM transits to
multiplication state and b egins to calculate the first coef-
ficient of
hr∗
, this process spends
rd
clock cycles.
Multiplication is followed by an add state, where plain-
text m is added to the current sum. At this time, e’s first
coefficient is calculated and the control engine outputs a
done signal. After the addition of the message, the FSM
again transmits to multiplication to compute the second
coefficients of e. When the last coefficient of e is calcu-
lated, the FSM returns to idle state and then the encryp-
tion proce s s is finis hed.
4. High-Speed NTRU
The performance gain of enhanced NTRU comes from
elimination of an inversion modulo p in key generation
and a star multiplication in decryption. On this basis, a
high-speed NTRU engine is presented to further speed up
the encryption process through improving the efficiency
of star multiplication. The high-speed NTRU can be used
in wireless networks that structured around base stations
and centralized servers, which do not have the limitations
associated with small portable devices.
Figure 3 shows the architecture of the high-speed
NTRU. For decryption, a 7N bits e buffer is used to store
Figure 3. High-speed NTRU architecture.
enc
dec
...
LUT
result buffer(7N bits)
control engine
mapping
module
done result
r_in e_in m_in
1'b1
NCSG
mux
e buffer(7N bits)
multiplication
module
...
mux
polynomial multiplier(PM)
optional parallel PM

X. ZHAN ET AL.
489
cipher e and another 7N bits result buffer is for the final
result. Multiplication module and mapping module per-
form the main arithmetic function, the former is for star
multiplication (parallel polynomial multiplier is optional
to further speed up the process) and the latter is used to
recover plaintext m from the intermediate variable a.
Moreover, LUT stores both f and h.
In our design, we have chosen
(, )(251,128)Nq=
,
2pX= +
,
72Fgrddd== =
and
125. m d=
This para-
meter set of NTRU is considere d with high level of secu-
rity and extremely low decryption failure probability [8].
4.1. Mapping Module
After we calculated
(mod )a feq= ∗
in the decryption
process, we need to recover binary plaintext m from a.
The Binary polynomial m satisfies Equation [6].
According to [6], the transformation in the mapping
algorithm can be summarized as：
12 12
(,,)( ,2,),
ii iii
a aauavwavw
++ ++
→ +−+−
(7)
where u, v and w are obtained as:
[ ]
12
[0];
{1'0,[6: 1]};
min{() / 2,}.
i
i
ii
ua
v ba
wav av
++
=

=

=++


(8)
We denote this transformation as below:
12 12
( ,,)Algorithm( ,,).
ii iii i
aa aaa a
++ ++
→
(9)
The mapping module can be implemented in a com-
pletely combinational way, it performs the following
function:
( ,,),&{0,1};
(,,) Algorithm( ,,),,
iii i
ooo
iii
xyz iNx
xyz x y zotherwise
≥∉


=


(10)
where i is the value of a 7 bits counter increasing every
clock cycle till i equals 2N.
The connection of the mapping module and the result
buffer is shown in Figure 4. When the control signal sel
SASA equals zero, a mapping operation is executed and
ox
is connected to the input of the right-hand 7 bits reg-
ister; when sel equals 1, the resu lt o f star multiplication is
loaded to the result buffer and data is as the input to the
circular register.
According to the above description, the entire mapping
process takes 2N clock cycles totally.
4.2. Small Hamming Weight Product
To further decrease the consumption of time in computa-
tion of the product
hr∗
, an alternative form is suggested
that takes advantage of sparse polynomials [6,7]. The sug-
gested form is:
12 3rrr r=∗+
, where the three sparse
binary polynomials
1r
,
2r
and
3r
have
1r d
,
2r d
and
3r d
non-zero coefficients (one in this case) respec-
tively. When it satisfies
12 3rr rrdd dd+=
, the constructed
polynomial r has approximately
rd
ones (occasional
non-binary coefficients are mixed in with the ones and
zeros, but don’t affect matters very much). Then the com-
putation of
hr∗
is divided to three steps by
1hr∗
,
(1) 2hr r∗∗
and
3hr∗
. When combined with NCSG
mentioned previously, the operation times of computing
hr∗
are reduced to
123()rr rdddN++
clock cycles.
For the case
72 r d=
, we have chosen
123rr r ddd= =
= 8. As the result, the efficiency of star multiplication in
NTRU encryption tripled without changing the level of
security.
4.3. Control Engine
Control engine in this design has 6 states and begins with
an idle state.
Figure 4. The mapping unit.

X. ZHAN ET AL.
490
On detection of a high signal of enc, the encryption
process starts and the FSM enters a load state. We divide
the whole encryption process into three steps, as shown
in Figure 5.
 Step1: computing
1hr α = ∗
. During load state, the
coefficients of
1r
are loaded one by one to NCSG.
After N clock cycles the degrees of non-zero terms
are generated in NCSG. FSM transits to multiplica-
tion state to calculate the first coefficient of
α
, this
process takes
1r d
clock cycles, it should be noted
that one multiplier is constant “1” during this state.
The following state is result, during which the first
coefficient of
α
is loaded to the e buffer. Then FSM
returns to multiplication state to compute
α
’s second
coefficient and stores it in result state. After repeats
this process N times, all coefficients of intermediate
variable
α
are calculated and stored in e buffer,
then Step1 is finished and FSM enters Step2. S t ep1
costs
1 ( 1) r d NN++
clock cycles totally.
 Step2: computing
2.rm βα =∗+
Step2 starts with
load state, during which the coefficients of
2r
are
loaded one by one. Then FSM transits to multiplica-
tion state and begins to calculate the first coefficient
of
2r α ∗
, this process spends
2r d
clock cycles.
Multiplication is followed by add state, where plain-
text m is added to current sum. At this time,
β
’s first
coefficient is calculated, it is loaded to the result buf-
fer in result state. After this, FSM begins to compute
and store the second coefficients of
β
. When the last
coefficient of
β
is stored in the result buffer, S t ep3
is followed. Step2 takes
2 ( 2) r d NN++
clock cycles.
 Step3: computing
3ehr β =∗+
. Like in Step1 and
Step2 , polynomial
3r
is loaded in load state first.
The following state is multiplication and the compu-
tation of
3hr∗
’s first coefficient starts. After this
FSM transmits to add state,
β
is added to calculate
the first coefficient of cipher e. In result state, the re-
sult is loaded to the result buffer. After repeats N
times, the whole coefficients o f e are stored in the re-
sult buffer. Finally control engine outputs a done sig-
nal and the FSM back to idle state. Step3 takes
3
( 2) r d NN++
clock cycles.
So the whole process of encryption requires a total of
123 ( 8) rr r Nd dd+++
clock cycles.
When dec signal is valid, NTRU engine performs de-
cryption operation. Firstly, the FSM transmits to lo ad
state, coefficients of cipher e are loaded to the e buffer
one by one. During the following multiplication state, the
first coefficient of
a
is calculated; this state takes N
clock cycles. Then FSM transmits to resu lt state and
a
’s
first coefficient is loaded into result buffer. After this
FSM begins to compute and store the second coefficients
of
a
. When the last coefficient of
a
is computed, FSM
enters map state, the plaintext binary polynomial m is
recovered from
a
in 2N clock cycles. Finally, control
engine outputs a done signal indicating the end of de-
cryption. The decryption process takes a total of N(N + 4)
clock cycles.
5. Implementation Results
In this paper, our designs were implemented with Verilog
language and synthesized by Synopsys Design Compiler
with a clock frequency of 500 kHz. The targeted ASIC
technology library we used is the HJTC 0.18 μm standard
cell library. We have also implemented AC Atici’s work
[5] for com pa rison.
Figure 5. Cont rol sequence in enc ryption process .
idle
load
multiplication
result
load
multiplication
add
load
multiplication
add
result result
idle
Repeat
N times
Repeat
N times
Repeat
N times
Step1Step2Step3

X. ZHAN ET AL.
491
We have first synthesized two encryption-only NTRUs
with the same parameters set
(, )(107,64)Nq=
and
rd
= 5, one is the implementatio n of AC Atici’s scheme and
another is our light-weight NTRU core.
Table 1 reveals that the proposed implementation of
the low-weight NTRU has a significant decrease in both
encryption delay and area. The encryption delay is found
to be 1498 μs, which is only 6.4% of AC Atici’s design.
This was expected since we took full advantage of sparse
polynomial r in our design. We can also see that the area
is much smaller than the contrast, only with 1175 equiv-
alent gates.
As shown in Table 2, the decrease in area is mainly
due to the needless of the r buffer, which is used to store
and rotate polynomial r with a consumption of 1243
gates, while the addition module —NCSG consumes on ly
466 gates. We also got a total power consumption of 1.51
μW from the result of Synopsys Design Compiler.
We have also synthesized our high -speed NTRU core,
which can perform both encryption and decryption func-
tion. We chose
(, )(251,128)Nq=
and
Fg dd= =
rd
=
72 as the parameters. For comparison, the delay and area
results of AC Atici’s encryption-decryption NTRU are
also listed.
Table 3 shows that the high-speed NTRU can finish
the process of encryption and decryption in 16,064 μs
and 128,010 μs, respectively, which gains much in speed
performance, especially in encryption process. However,
the area is 25,758 gates and the total power consumption
is 59.2 μW. The high-speed NTRU could be used in base
stations and servers of wireless network.
Table 1. Delay and area results of encryption-only NTRUs.
Work Enc. delay (μs) Area (eqv.gates)
AC Atici’s design 23,336 1949
Our Low-weight NTRU 1498 1175
Table 2. Area consumption of encryption-only NTRUs.
Block Area (eqv.gates)
AC Atici’s design Low-weight NTRU
control logic 382 429
lut 236 236
multiplication module 88 44
r buffer 1243 -
NCSG - 466
total 1949 1175
Table 3. Delay and area results of encryption-decryption
NTRUs.
Work Enc. delay (μs) Dec. delay (μs) Area (eqv.gates)
AC Atici’s design 127,508 263,550 14,441
Our High-speed
NTRU
16,064 128,010 25,758
By the way, as power consumption is not the target we
optimized for in this paper, low power methods such as
clock gating and operand isolation are not used in our
designs. If these methods are adopted, the power con-
sumption will be greatly reduced.
6. Conclusions
In this paper we presented two hardware architectures of
NTRU. The first one capable of encryption only is opti-
mized for small area and fast speed, has a gate-count of
1,175 gates and a total power consumption of 1.51 μW.
This NTRU core can finish the encryption process in
1498 μs at 500 kHz. It is very suitable for use in ul-
tra-low cost environment such as wireless portable de-
vices. Another one is designed for high speed with delays
of 16,064 μs and 128,010 μs in encryption and decryp-
tion respectively, obtaining significant gains when com-
pared with the original NTRU that provides the same
level of security. This circuit consists of 25,758 equiva-
lent gates and has a total power consumption of 59.2 μW.
So the high-speed encryption-decryption NTRU core is
recommended to be used in wireless base stations and
servers.
Besides, the designs can be sped up by using parallel
polynomial multiplier units.
7. Acknowledgements
This work was supported in part by National Natural
Science Foundation of China (Grant No. 60973034, No.
61006020 and No. 61176026).
REFERENCES
[1] G. Gaubatz, J. P. Kaps and B. Sunar, “Public Key Cryp-
tography in Sensor Networks—Revisited,” 1st European
Workshop on Security in Ad-Hoc and Sensor Networks,
2005, pp. 2-18
[2] J. Hoffstein, J. Pipher and J. H. Silverman, “NTRU: A
Ring-Base Public Key Cryptosystem,” In: J. P. Buhler,
Ed., Algorithmic Number Theory (ANTS III), Lecture
Notes in Computer Science, Springer-Verlag, Berlin,
1998, pp. 267-288,.
[3] C. M. O’Rourke, “Efficient NTRU Implementations,”
Master Thesis, Worcester Polytechnic Institute, Worce-
ster, 2002.
[4] J. Kaps, “Cryptography for Ultra-Low Power Devices,”
Ph.D. Thesis, Worcester Polytechnic Institute, Worcester,
2006.
[5] A. C. Atici, L. Batina, J. Fan, I. Verbauwhede and S. B. O.
Yalcin, “Low-Cost Implementations of NTRU for Perva-
sive Security,” International Conference on Applica-
tion-Specific Systems, Architectures and Processors, 2008.
pp. 79-84.
[6] J. Hoffstein and J. Silverman, “Optimizations for NTRU,”
Public-Key Cryptography and Computational Number

X. ZHAN ET AL.
492
Theory: Proceedings of the International Conference or-
ganized by the Stefan Banach International Mathematical
Center Warsaw, Poland, September 11-15, 2000, p. 77.
[7] J. Hoffstein and J. H. Silverman, “Random Small Ham-
ming Weight Products with Applications to Cryptogra-
phy,” Discrete A ppli e d Mathematics, Vol. 130, No. 1,
2003, pp. 37-49.
[8] J. H. Silverman and W. Whyte, “Estimating Decryption
Failure Probabilities for NTRUencrypt,” Technical Re-
port, NTRU Cryptosystems, 2005, Technical Report No.
18, Version 1.