Communicatio
n
http://dx.doi.or
g
Copyright © 2
0
Sp
a
ABSTRA
C
This paper pr
o
in the case o
f
b
asis and the
p
ervised offli
n
an increment
a
need the num
b
location esti
m
Keywords:
D
P
r
1. Introdu
c
Wireless loc
a
fields like co
m
radio astrono
m
p
ast decade.
T
zation proble
m
signal param
e
time of arriva
l
dinates of un
k
p
loiting the
p
though most l
centrate on t
h
eral as expla
i
novel DPD
m
indeed intere
s
have been p
r
nique that is
s
step methods
criterion gath
e
single emitte
r
p
roach to tre
a
measurement-
DPD method
n
s and Networ
k
g
/10.4236/cn.2
0
0
13 SciRes.
a
rsity-
B
1
The
N
a
2
The Jiangs
u
3
Key
L
C
T
o
poses an ada
p
f
time-varying
sparse soluti
o
n
e DL by usi
n
a
l fashion to a
d
b
er of emitter
s
m
ation accurac
y
D
ictionary Lea
r
r
ogramming
c
tion
a
lization as a
m
munications,
m
y has draw
n
T
he traditiona
l
m
consists of
t
e
ters such as
l
(TOA) are e
s
k
nown-locatio
n
p
arameters es
t
ocalization al
g
h
e two-step m
e
i
ned in refere
n
m
ethods that d
i
s
t to the en
d
-
u
r
oposed, as a
s
hown to out
p
[2]. Weiss e
t
e
ring all sign
a
r
[3] and the
n
a
t the multipl
e
to-association
can provide s
u
k
, 2013, 5, 421-
4
0
13.53B2077 P
u
B
ased
D
Two-s
t
Tin
g
Jiangsu Engin
e
a
njing Universi
t
u
Key Laborato
ry
N
L
aboratory of D
i
ap
tive sparsity
-
channels. Th
e
o
n based on a
n
g the quadrat
i
d
apt to the ti
m
s
a prior. Si
m
y
.
r
ning; Compr
e
fundamental
radar, sonar,
n
increasing
a
l
approach to
s
t
wo-step proc
e
angle of arri
v
s
timated, and
s
n
targets are c
a
t
imated in th
e
g
orithms prese
n
e
thod, it is su
b
n
ces [1]. Rec
e
i
rectly estima
t
u
ser, i.e., posit
i
promising
po
p
erform the co
n
t
al
p
roposed
a
ls of all stati
o
n
proposed a
e
emitters cas
e
step is avoide
d
u
perior locali
z
4
25
u
blished Online
D
irect L
t
ep Di
c
g
ting Wang
1,
2
e
ering Center o
f
t
y of Informatio
y
on Optoelectr
N
anjing Norm
U
i
saster Reducti
o
Ministry of Ci
v
w
Rece
i
-
based direct
p
e
novel featur
e
two-step dicti
i
c programmi
n
m
e-varying ch
a
m
ulation result
s
e
ssive Sensing
;
task in vario
u
seismology a
n
a
ttention in t
h
s
olve the loca
l
e
dure. First, t
h
v
al (AOA) a
n
s
econd the co
o
a
lculated b
y
e
x
e
first step.
A
n
ted so fa
r
co
n
b
optimal in ge
n
e
ntly, a kind
o
t
e the results
o
i
on coordinat
e
o
sitioning tec
h
n
ventional tw
o
a unique DP
o
ns firstly for
decoupled a
p
e
[4]. Since t
h
d
, the decou p l
e
z
ation capabili
t
September 201
3
ocatio
n
c
tionar
y
2
,3
, Wei Ke
2,
3
f
Meteorologica
l
n Scie nce and
T
onic Technolog
U
niversity, Nanj
o
n and Emergen
v
il Affairs, Beiji
n
w
kykw @sina.c
o
i
ve
d
May 2013
p
osition deter
m
e
of this meth
o
onary learnin
g
n
g approach,
a
a
nnel during t
h
s
demonstrate
;
Direct Locat
i
u
s
n
d
h
e
l
i-
h
e
n
d
o
r-
x
-
A
l-
n
-
n
-
o
f
o
f
e
s,
h
-
o
-
D
a
p
-
h
e
e
d
t
y
in mul
t
initial
p
to
b
e k
n
metho
d
[5,6].
B
of sup
p
functio
n
higher
exploit
Co
m
of atte
n
in the
t
mensi
o
are fe
w
rate D
P
Picard
a
sity re
p
fitting
m
mise t
h
tionary
In pra
c
channe
misma
t
mation
3
(http://www.s
c
n
Estim
a
y
Lear
n
3
, Gang Liu
2
l
Sensor Netwo
r
T
echnology, Na
n
y, School of Ph
y
ing, China
cy Response E
n
n
g, China
om
m
ination (DP
D
o
d is to dyna
m
g
(DL) frame
w
a
nd then the
d
h
e online stag
e
the perfor ma
n
i
on; Time -Var
y
t
i-emitter cont
e
p
osition estim
a
n
own a priori.
d
to handle th
B
asically, the
a
p
ort points in
w
n
is evaluated.
complexity th
a
the explicit g
e
m
pressed sensi
n
n
tion in recent
t
wo-step loca
l
o
ns of measur
e
w
works discu
s
P
D estimation.
a
nd Weiss tre
a
p
resentation
b
m
ethod in [9].
h
at the predef
i
) is ideal and
i
c
tice, due to
t
ls and rando
m
t
ch the actual
s
performance
c
irp.org/journal
/
a
tion
B
n
ing
r
k Technology,
n
jing, China
y
sics and Tech
n
n
gineering of th
e
D
) appoach to
m
ically adjust
b
w
ork. The me
t
d
ictionary is c
o
e
. Furthermor
e
n
ce of the pro
p
y
ing Channel;
e
xt. But this
m
a
tes, and the n
u
Other studies
h
e global navi
g
a
bove DPD al
g
w
hich the ma
x
Therefore, th
e
a
n the two-ste
p
e
ometric relati
n
g (CS), whic
h
years, has be
e
l
ization meth
o
e
ment vectors
s
sing the CS
p
To the best
o
a
t the DPD pr
o
b
y exploiting
However, thi
i
ned overcom
p
i
nvariable in t
h
t
he dynamica
l
m
noise, the
s
ignals stocha
s
is degraded.
I
/
cn)
B
ased o
n
n
ology,
e
locate multipl
b
oth the over
c
t
hod first perf
o
o
ntinuously u
p
e
, the method
p
osed algorith
m
Quadratic
m
ethod depen
d
u
mber of sour
c
h
ave extend ed
g
ation satellit
e
g
orithms gene
r
x
imum likelih
e
se DPD meth
o
p
approach,
w
onship.
h
receives a g
r
e
n successfull
y
o
d by reducin
g
[7,8]. Howe
v
p
attern for m
o
o
f our knowle
d
o
ble
m
as a spa
t
the covarian
c
s work makes
p
lete basis (a.
h
e localizatio
n
l
change of
m
predefined b
a
s
tically so that
I
n this paper,
CN
n
e targets
c
omplete
o
rms su-
p
dated in
does not
m
on the
d
s on the
c
es ne eds
the DPD
e
system
r
ate a set
ood cost
o
ds have
w
hich can
r
eat deal
y
applie
d
g
the di-
v
er, there
o
re accu-
d
ge, only
t
ial sp ar -
c
e-matrix
the pre-
k.a. dic-
n
process.
m
ultipath
a
sis may
the esti-
we p
r
o-

T. T. WANG ET AL.
422
pose an adaptive sparsity-based DPD (ASDPD) algori thm
to dynamically adjust both the overcomplete basis and th e
sparse solution so that the solution can better match the
actual scenario. The method first performs supervised of-
fline dictionary training by using the quadratic program-
ming approach. Dur ing the online stage, the dictionary is
continuously updated in an incremental fashion to adapt
to time-varying factors.
The notation used in this paper is according to the
convention. Symbols for matrices (upper case) and vec-
tors (lower case) are in boldface. ()
H
⋅, 0 θ, 1 θ, 2 θ,
N
I, ⊗ and CN denote conjugate transpose (Hermitian),
0
l norm, 1 l norm, 2 l norm, identity matrix with the
dimension N, the Kronecker product and complex Gaus-
sian distribution, respectively. For any matrix Y, vec( )Y
is denoted as the vertical concatenation of the columns of
Y. Finally, ˆ
x denotes the estimate of the parameter of
interest x.
The remainder of the paper is organized as follows.
Section 2 briefly describes the system model assumed
throughout th is p aper and formulates as a sparse recovery
problem. In Section 3, we introduce a scheme calibrating
the overcomplete basis dynamically and estimating the
sparse solution adaptively. Simulation results are given
in Section 4. Finally, Section 5 concludes the paper.
2. System Model and Problem Formulation
Consider N base stations (BS) intercepting the narrow-
band signals transmitted by L possible sources. Each BS
which knows its coordinates is equipped with an antenna
array consisting of M elements. Denote the lth unknown
target position by the vector of coordinates l P. We use
the far-field point-target model, which is commo nly used
for source localization du e to its simplicity [3,4,9]. Based
on this model, the received signal observed by the nth BS
is given by
1
()() (())(),0
L
nnllnln
l
tst ttT τ
=
=−+≤≤

rappv (1)
where ()
l
s
t is the signal waveform considered known.
()
nl
ap is the array response at the nth BS from a signal
transmitted position, and the propagation delay from the
lth transmitter to the nth BS is given by ()
nl
τ p. The
vector ,{1,,}
nn n
nN∈=+rHθv represents noise
terms, which is assumed as the independent and identi-
cally distributed (i.i.d.) complex Gaussian process, un-
correlated with the signals.
We divide the area of interest into K grids. In general,
KML>. Then, we formulate the location problem
as a following CS problem
,{1,,}
nn n
nN∈=+rHθv (2)
where () ()
1
[,,]
nn
nK
=Hh h is an overcomplete basis ma-
trix at the nth BS, and ()n
i
h corresponds to the noiseless
signal vector between the ith grid and the nth BS.
1
[, ,]
K
θθ =θis a sparse vector that having in total L
nonzero entries, where the indices of nonzero entries in
θ which represents the actual locations. It should be
emphasized that the above matrix n H is constructed by
ideal signals, where the parameters such as AOA and
TOA can be calculated according to the geometric rela-
tionship directly. Denote H the matrix obtained by
concatenation of all the matricesn
H, i.e.,
1
[,, ]
TTT
N
=HH H. Similarly, by denoting
1
[,,]
TTT
N
=Rr r and 1 [,, ]
TTT
N
=Vv v, we can obtain
=+RHθV (3)
Note that H is known under the id eal channel condi-
tion, which means that we can estimate the actual coor-
dinates of targets as long as we find the positions of
nonzero values in θ. That is, the problem of localization
is converted into one of sparse signal recovery from (3).
Moreover, the number of these dominant nonzero values
gives L.
However, the non-ideal factors are inevitable in a prac-
tical localization system. These factors include the chan-
nel attenuation, phase error, time-varying fluctuations of
the radio channel and so forth. When these happen, the
predefined dictionary cannot effectively express the ac-
tual signal, which will cause performance degradation in
sparse recovery process.
For avoiding the difficulty of estimate all kinds of the
time-varying factors, we assume the error dictionar y ma-
trix Γ which describe the difference between the prede-
fined dictionary and the practical received signals. Note
that the error matrix Γ is time-varying and cannot be
known in advance. In this scenario, the sparse position-
ing model is correspondingly modified as:
=+ +RΓHθVDθV (4)
where =DΓH denotes the actual overcomplete basis
with the time-varying interference. To prevent D from
having arbitrarily large values (which would lead to arbi-
trarily small values of θ), it is common to constrain its
columns 1,,
K
dd to have a 2 l norm less than or
equal to one. Obviously, the mismatch exists between the
columns of D and the corresponding columns of the pre-
defined basis H, and thus the performance degradation
is inevitable in the sparse recovery process. Focused on
this problem, an adaptive sparse recovery algorithm is
proposed in this paper, which dynamically calibrate the
overcomplete basis so that the sparse solution can better
fit the actual scenario.
3. Sparse Representation Based on the
Two-stage Dictionary Learning
The key feature of adaptive sparse recovery is the adap-

T. T. WANG ET AL.
423
tive adjustment of the overcomplete basis. This process
generally learns the uncertainty of the dictionary, which
is not available from the prior knowledge, but rather has
to be estimated using a given set of training samples.
Several different DL algorithms have been presented re-
cently [10]. However, these methods generally cannot
effectively handle very large training sets or dynamic
training data changing over time. To overcome these
shortcomings, we propose a two-stage DL approach that
can adapt to the varied upcoming samples.
So far, the most DL methods are generally based on
alternating minimization. In one step, a sparse recovery
algorithm finds sparse representations of the training sam-
ples with a fixed dictionary. In the other step, the dictio-
nary is updated to decrease the average approximation
error while the sparse coefficients remain fixed. The pro-
posed method in this paper also uses this formulation of
alternating minimization.
3.1. Sparse Recovery Phase
The above problem of noisy sparse signal recovery can
then be converted into a following optimization problem
2
21
min/ 2 λ −+RDθθ (5)
where
λ is the regularization parameter. However, it
should be emphasized that larger coefficients in θ are
penalized more heavily in the 1 l norm than smaller coef-
ficients, unlike the more democratic penalization of the
0
l norm [11]. In practice, large coefficients are usually
the entries corresponding to the actual positions of tar-
gets, while small coefficients commonly represent the
noise entries. The imbalance of the 1 l norm penalty will
seriously influence the recovery accuracy, which may
result in many false targets. Therefore, in this paper we
choose the reweighted 1 l norm minimization algorithm
in [11] as our sparse recovery method, which can over-
come the mismatch between 0 l norm minimization and
1
l norm minimization while keeping the problem solva-
ble with convex estimation tools.
3.2. Dictionary Learning Phase
In this paper, we propose a two-stage DL framework in
which the offline DL method allows to train the dictio-
nary in a supervised manner to integrate the large train-
ing sets, and the incremental DL method based on the
results in the offline stage handles the unseen online var-
iation to enhance its adaptability.
1) Offline dictionary learning
In this stage, the ideal overcomplete basis H is op-
timized to better represent the data of the training sets.
Since the sparse coefficients θ are fixed in the DL
stage, the resulting optimization problem becomes:
2
2
min/ 2,. .1,1,,
H
ii
s
tiK−≤=RDθdd  (6)
in which 2
2
−RDθcan be written as
2
2tr[( )( )]
tr() 2tr()tr()
vec() ()vec()
2vec() vec()tr()
H
HHHH H
HHH H
HH HH
−=− −
=−+
=⊗
−+
RDθRDθRDθ
Dθθ DRθDRR
DIθθD
θRDRR
(7)
Let’s introduce several new expressions for clarity of
notation
vec( )
vec( )
H
H
H
⊗
αD
GIθθ
γθR



Omitting the terms that do not depend on D, the objec-
tive function in (6) can be equivalent to
1
min,..1,1,,
2
HH H
ii
s
tiK−≤=αGαγα dd  (8)
Note that (8) is a standard form of constrained qua-
dratic programming problem which can be solved by any
standard optimization method, such as the gradient pro-
jection algorithm in [12]. Moreover, the matrix G is ob-
viously a positively definite matrix, and thus (8) is con-
vex function and can be guaranteed to find a global op-
timum [13] in this DL phase.
2) Online dictionary learning
Although the of fline DL stage has adjust the overcom-
plete basis according the training data, it is impossible to
be fit for all kinds of time-varying interference patterns.
Moreover, its computation load is quite large for real-
time localization. On the contrary, the online incremental
learning is especially applicable when one seeks to find
the variation in the sense that the time-varying channels
pattern might not be specifically learned offline but can
be distinguished from the past online observations. Based
on the incremental learning pattern, the online learning
algorithm in [14] can use the result of the offline DL
stage as a warm restart for computing the next dictionary
where the new samples will be fed into the online dictio-
nary learning procedure, and thus a single iteration has
empirically been found to be enough [14].
For completeness, a full description of the algorithm is
given in Algorithm 1.
Algorithm 1 Two-stage DL algorithm
Initialization: set the training sample set; generate the ideal dictionary
H
Offline DL stage:
Input: the training sample set; (0)
off
ˆ=DH; the number of itera-
tions T;
for j=1 to T
1) use the reweighted 1-norm algorithm to compute the vecto
r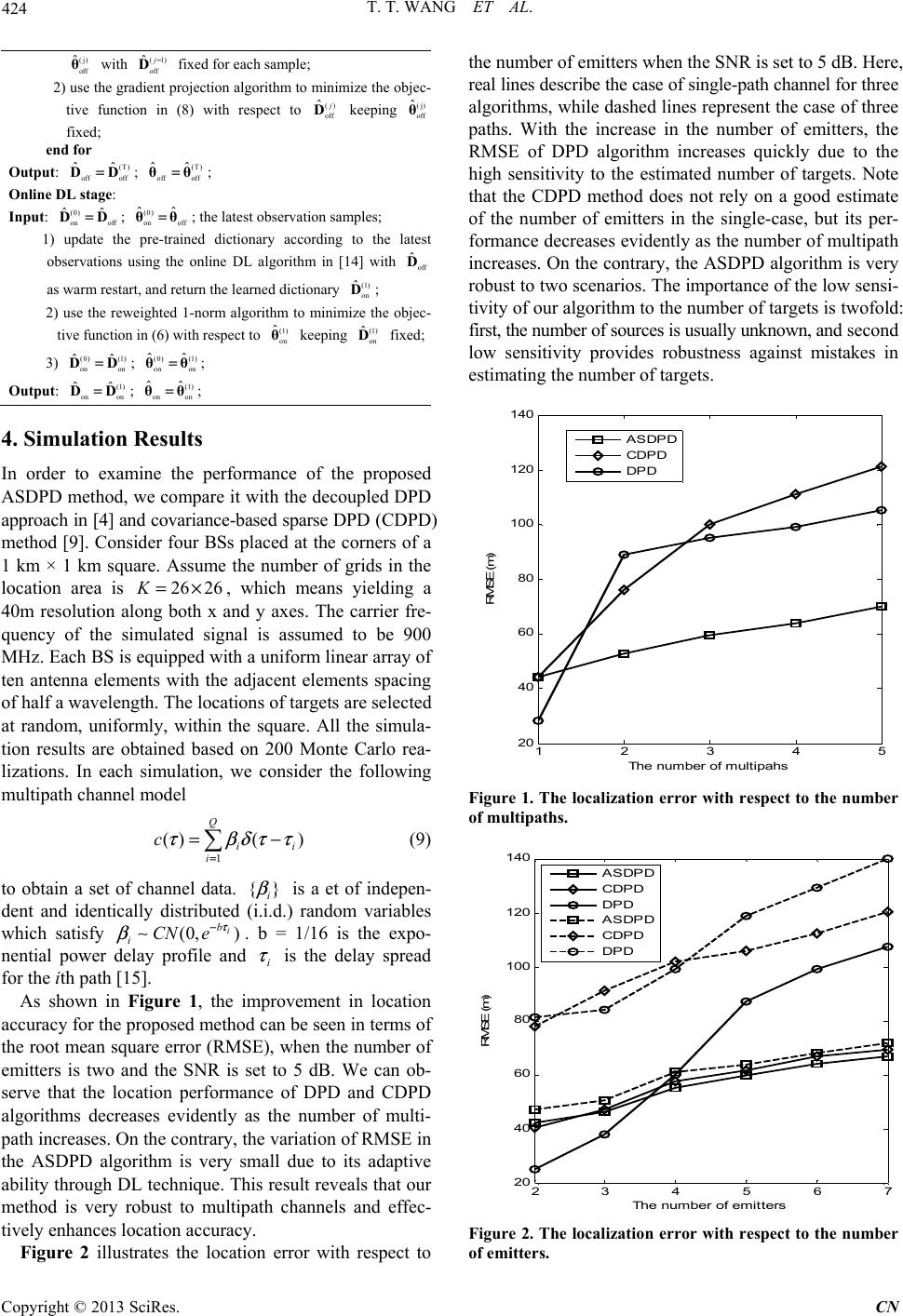

T. T. WANG ET AL.
424
(j)
off
ˆ
θ with (1)
off
ˆj−
D fixed for each sample;
2) use the gradient projection algorithm to minimize the objec-
tive function in (8) with respect to ()
off
ˆj
D keeping (j)
off
ˆ
θ
fixed;
end for
Output: (T)
off off
ˆˆ
=DD; (T)
off off
ˆˆ
=θθ;
Online DL stage:
Input: (0)
on off
ˆˆ
=DD; (0)
on off
ˆˆ
=θθ; the latest observation samples;
1) update the pre-trained dictionary according to the lates
t
observations using the online DL algorithm in [14] with off
ˆ
D
as warm restart, and return the learned dictionary (1)
on
ˆ
D;
2) use the reweighted 1-norm algorithm to minimize the objec-
tive function in (6) with re sp ec t to (1 )
on
ˆ
θ keeping (1)
on
ˆ
D fixed;
3) (0)(1)
on on
ˆˆ
=DD; (0) (1)
on on
ˆˆ
=θθ;
Output: (1)
on on
ˆˆ
=DD; (1)
on on
ˆˆ
=θθ;
4. Simulation Results
In order to examine the performance of the proposed
ASDPD method, we compare it with the decoupled DPD
approach in [4] and covariance-based sparse DPD (CDP D)
method [9]. Consider four BSs placed at the corners of a
1 km × 1 km square. Assume the number of grids in the
location area is 26 26K=×, which means yielding a
40m resolution along both x and y axes. The carrier fre-
quency of the simulated signal is assumed to be 900
MHz. Each BS is equipped with a uniform linear array of
ten antenna elements with the adjacent elements spacing
of half a wavelength. The locations of targets are selected
at random, uniformly, within the square. All the simula-
tion results are obtained based on 200 Monte Carlo rea-
lizations. In each simulation, we consider the following
multipath channel model
1
()( )
Q
ii
i
c τ
β
δτ τ
=
=−
 (9)
to obtain a set of channel data. {}
i
β
is a et of indepen-
dent and identically distributed (i.i.d.) random variables
which satisfy (0, )
i
b
iCNe
τ
β
−
. b = 1/16 is the expo-
nential power delay profile and i τ is the delay spread
for the ith path [15].
As shown in Figure 1, the improvement in location
accuracy for the proposed method can be seen in terms of
the root mean square error (RMSE), when the number of
emitters is two and the SNR is set to 5 dB. We can ob-
serve that the location performance of DPD and CDPD
algorithms decreases evidently as the number of multi-
path increases. On the contrary, the variation of RMSE in
the ASDPD algorithm is very small due to its adaptive
ability through DL technique. This result reveals that our
method is very robust to multipath channels and effec-
tively enhances location accuracy.
Figure 2 illustrates the location error with respect to
the number of emitters when the SNR is set to 5 dB. Here,
real lines describe the case of single-path channel for three
algorithms, while dashed lines represent the case of three
paths. With the increase in the number of emitters, the
RMSE of DPD algorithm increases quickly due to the
high sensitivity to the estimated number of targets. Note
that the CDPD method does not rely on a good estimate
of the number of emitters in the single-case, but its per-
formance decreases evidently as the number of multipath
increases. On the contrary, the ASDPD algorithm is very
robust to two scenarios. The importance of the low sensi-
tivity of our algorithm to the number of targets is twofold:
first, the number of sources is usually unknown, and second
low sensitivity provides robustness against mistakes in
estimating the number of targ ets.
Figure 1. The localization error with respect to the number
of multipaths.
Figure 2. The localization error with respect to the number
of emitters.
12345
20
40
60
80
100
120
140
The number of mult i pahs
RMSE (m)
ASDPD
CDPD
DPD
23 4 5 6 7
20
40
60
80
100
120
140
The number of emi t t ers
R M SE (m )
ASDPD
CDPD
DPD
ASDPD
CDPD
DPD

T. T. WANG ET AL.
425
5. Conclusion
In this paper, we exploit the inherent spatial sparsity to
present a novel direct location method by combining the
offline training and online learning into a unified DL
framework, thereby better matching time-varying scena-
rios. The effectiveness of the proposed scheme has been
demonstrated by simulation results where substantial im-
provement for localization performance is achieved. Fur-
ther research will emphasize on the off-grid error analy-
sis and the theoretic bound on the location estimation
precision.
6. Acknowledgements
This work is supported in part by the priority academic
program development of Jiangsu higher education insti-
tutions, and in part by the Open Research Fund of Key
Laboratory of Disaster Reduction and Emergency Response
Engineering of the Ministry of Civil Affairs under grant
No. LDRERE20120303.
REFERENCES
[1] J. Bosse, A. Ferréol, C. Germond and P. Larzabal, “Pas-
sive Geolocalization of Radio Transmitters: Algorithm
and Performance in Narrowband Context,” Signal Pro-
cessing, Vol. 92, No. 4, 2012, pp. 841-852.
http://dx.doi.org/10.1016/j.sigpro.2011.09.008
[2] A. Amar and A. J. Weiss, “New Asymptotic Results on
Two Fundamental Approaches to Mobile Terminal Loca-
tion,” Proceedings of 2008 ISCCSP, pp. 1320-1323.
[3] A. J. Weiss, “Direct Position Determination of Narrow-
band Radio Frequency Transmitters,” IEEE Signal Pro-
cessing Letters, Vol. 11, No. 5, 2004, pp. 513-516.
http://dx.doi.org/10.1109/LSP.2004.826501
[4] A. Amar and A. J. Weiss, “A Decoupled Algorithm for
Geolocation of Multiple Emitters,” Signal Processing,
Vol. 87, No. 10, 2007, pp. 2348-2359.
http://dx.doi.org/10.1016/j.sigpro.2007.03.008
[5] P. Closas, C. Fernandez-Prades and J. Fernandez-Rubio,
“Maximum Likelihood Estimation of Position in GNSS,”
IEEE Signal Processing Letters, Vol. 14, No. 5, 2007, pp.
359-362. http://dx.doi.org/10.1109/LSP.2006.888360
[6] P. Closas, C. Fernandez-Prades and J. Fernandez-Rubio,
“Cramér-Rao Bound Analysis of Position Approaches in
GNSS Receivers,” IEEE Transactions on Signal Pro-
cessing, Vol. 57, No. 10, 2009, pp. 3775-3786.
http://dx.doi.org/10.1109/TSP.2009.2025083
[7] C. Feng, S. Valaee and Z. Tan, “Multiple Target Locali-
zation Using Compressive Sensing,” Proceedings of 2009
GLOBECOM, pp. 1-6.
[8] B. Zhang, X. Cheng, N. Zhang, Y. Cui, Y. Li and Q.
Liang, “Sparse Target Counting and Localization in Sen-
sor Networks Based on Compressive Sensing ,” Pro-
ceedings of 2011 IEEE INFOCOM, pp. 2255-2263.
[9] J. S. Picard and A.J. Weiss, “Localization of Multiple
Emitters by Spatial Sparsity Methods in the Presence of
Fading Channels,” Proceedings of 2010 WPNC, pp.
62-67.
[10] R. Rubinstein, A. M. Bruckstein and M. Elad, “Dictiona-
ries for Sparse Representation Modeling,” Proceedings of
IEEE, Vol. 98, No. 6, Jun. 2010, pp. 1045-1057.
http://dx.doi.org/10.1109/JPROC.2010.2040551
[11] E. J. Candes, M. B. Wakin and S. P. Boyd, “Enhancing
Sparsity by Reweighted l1 Minimization,” Journal of
Fourier Analysis and Applications, Vol. 14, No. 5-6,
2008, pp. 877-905.
http://dx.doi.org/10.1007/s00041-008-9045-x
[12] J. Nocedal and S. J. Wright, “Numerical Optimization,”
Springer Verlag, New York, 2006.
[13] J. Dattorro, “Convex Optimization and Euclidean Dis-
tance Geometry,” Meboo Publishing, Palo Alto, 2005.
[14] J. Mairal, F. Bach, J. Ponce and G. Sapiro, “Online
Learning for Matrix Factorization and Sparse Coding,”
Journal of Machine Learning Research, Vol. 11, No. 3,
2010, pp. 19-60.
[15] M. R. Raghavendra and K. Giridhar, “Improving Channel
Estimation in OFDM Systems for Sparse Multipath
Channels,” IEEE Signal Processing Letters, Vol. 12, No.
1, 2005, pp. 52-55.
http://dx.doi.org/10.1109/LSP.2004.839702