Paper Menu >>
Journal Menu >>
 Journal of Applied Mathematics and Physics, 2013, 1, 12-17 Published Online November 2013 (http://www.scirp.org/journal/jamp) http://dx.doi.org/10.4236/jamp.2013.15003 Open Access JAMP Research on Credit Risk Measurement Based on Uncertain KMV Model Ni Zhan, Liang Lin, Ting Lou College of Science, Guilin University of Technology, Guilin, China Email: zhanni105@163.com Received May 25, 2013; revised June 25, 2013; accepted July 15, 2013 Copyright © 2013 Ni Zhan et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT Regarding KMV model identification credit risk profile of small and medium-sized listed companies, at present, do- mestic scholars has made some achievements in the process of the KMV model combined with China’s national condi- tions. In this paper, we will amend the model by using uncertain in terest rate instead of fixed rate on the basis of exist- ing research. Comparing the uncertain KMV model to traditional KMV model with ST-listed companies and non- ST-listed companies in Shanghai and Shenzh en stock exchange, we find that it performs slightly be tter as a predictor in uncertain KMV model and in out of sample forecasts. Keywords: Credit Risks; KMV Model; Uncertain Interest Rate 1. Introduction With the improvement of the activeness in economic activities and enhancement of national economic rela- tionships between countries, people found that it’s im- portant and necessary to be on guard and control the various risks in economic activities. Barings Bank event as well as a series of major financial institutions crisis since the mid-1990 s of the 20th century, makes the Banks increasingly concerned about the risk prevention, meas- urement and management. Nowadays commercial banks face two kinds of risk, one is non-systemic risk, such as credit risk, settlement risk, and th e other is systemic risk, such as market risk, interest rate risk, currency risk and so on, and credit risk is the main risk in that commercial banks face in the course of business. And how to guard against and reduce credit risk is an urgent requirement to the commercial banks. W. Zhang [1] carried out a theoretical study of the credit risk of listed companies measurement and ana- lyzed the samples of China’s listed companies. Research shows that at this stage, KMV model based on options pricing breach theory could well apply to China’s credit risk measurement of listed companies. Z. J. Zhang & X. H. Chen [2] set two credit warning lines to monitor the credit crisis of small and medium-sized listed companies by KMV model. X. Y. Liang [3] made the empirical analysis of KMV model widely used in foreign countries combined with the actual situation in China, and they amended parameters accordingly in order to enhance the applicability of the model in the Chinese market. S. C. Yang [4] used qualitative and demonstration method to carry on the theoretical analysis and empirical research on credit risk measure model, furthermore, he made analysis on KMV model used in Chinese enterprise with newest data o f corporat ion in sto ck market . Most of the existing credit risk measurement methods are “static” models by using risk-free rate to estimate the uncertain risk. As we all know, interest rate in real life is uncertain. In order to reflect and solve practical problems better, we will introduce the uncertain variable into the research of credit risk. 2. KMV Model Theory 2.1. The Basic Assumptions of the Model KMV model basic idea is that viewed the company eq- uity as a European call options, viewed market value of assets as the subject, the nominal value of company’s debt as exercise price. Compan y will choose to repay the debt when market value of assets is greater than the value of the debt, default while market value of assets is less than the value of debt . 1) Satisfy the basic assumptions of the Merton model: the company’s stock price is a random process, transac-  N. ZHAN ET AL. 13 tion is no friction, etc., and the change of enterprise’s value obeys Ito Process. 2) Company will default to its creditors and share- holders when the company’s asset value falls below a certain level. 3) The capital structure of the borrower only includes owner’s equity, short-term debt, long-term debt and con- vertible prefe rr ed st ock . 2.2. The KMV Calculated Steps 1) The Asset Value and Volatility If E V represents market value of equity, A repre- sents firm’s asset value, then the relationship between the companies’ equity and asset value can be expressed as V 1 erT EA VVNd DNd 2 (1) where represents book value of debt which is due at time , is the risk free interest rate, D Tr ·N is the cumulative standard normal distribution function, and are given by 1 d 2 d 2 1 1 ln 2 AA A Vr D dT (2) 21A dd T (3) Equity volatility and asset volatility relationship: 1A E A E VNd V (4) where E A is equity volatility, The asset value and volatility implied by the equity value, equity volatility and liabilities are calculated by solving the call price and volatili ty equ ation s, (1) and (4), simultaneously. is asset volatility. 2) Default to Distance The default point (DPT) is generally determined by the short-term liabilities and long-term liabilities: 1 DPT STDLTD 2 (5) Distance to default (DD) is the relative distance be- tween the future value of the assets and default point. Once this numerical solution is obtained, the distance to default can be calculated as DPT DD A AA V V (6) 3) EDF (Expected Default Frequency) The theoretical value of expected default frequency is based on the assumption that market value of the assets follows a normal distribution, EDF DDN (7) It still lacks large amounts of data resources to estab- lish an effective database in China, so the empirical sec- tion, we select the distance to default to measure credit risk. The greater the distance to default, the smaller the likelihood of default, the comp any’s credit status is better; on the contrary, the smaller the distance to default, the higher the risk of de faul t . The vast majority of scholars simply assumed r is a free-rate and did not give a reasonable explanation, but we all know interest rate in real life is uncertain, we will introduce the uncertain variable into the research of credit risk. 3. Uncertainty KMV Model Uncertainty theory was founded by Liu [5] in 2007 and refined by Liu [6] in 2010, which is a branch of mathe- matics based on normality, monotonicity, self-duality, countable subadditivity, and product measure axioms. 3.1. Uncertain Measure and Uncertain Variable Let be a nonempty set, and a -algebra over . Each element is called an event. Uncertain measure was introduced as a set function satisfying the following five axioms [5]: Axiom 1. (Normality Axiom) 1for the uni- versal set . Axiom 2. (Monotonicity Axiom) 12 whenever 12 . Axiom 3. (Self-Duality Axiom) 1 c for any event . Axiom 4. (Countable Subadditivity Axiom) For every countable sequence of events i , we have 1 1ii i i . Axiom 5. (Product Measure Axiom) Let k be non- empty sets on which k are uncertain measures 1, 2,,kn , respectively. Then the product uncertain measure is an uncertain measure on the product -algebra 12 n satisfying 1 1 min n kk kn k k . where ,1,2,, kk kn . Definition 3.1.1 (Liu [5]) Let be a nonempty set, and be a -algebra over , and an uncertain measure. Then the triplet ,, is called an uncer- tainty space. Definition 3.1.2 (Liu [5]) An uncertain variable is a measurable functio n from an uncertainty space ,, to the set of real numbers. Open Access JAMP  N. ZHAN ET AL. 14 3.2. Uncertain Distribution and Inverse Uncertain Distribution Definition 3.2.1 [6] The uncertainty distribution of an uncertain variable is defined by x Mx Definition 3.2.2 [6]: An uncertain variable is called linear if it has a linear uncertainty distribution 0, (, 1, x a x xabaaxb x b (7) denoted by where a and b are real numbers with . Distribution shown in Figure 1. ,ab ab Definition 3.2.3 [6]: An uncertain variabe is called normal if it has a normal uncertainty distribution 1 1exp 3 ex x (8) denoted by ,e where e and are real num- bers with 0 . Distribution shown in Figure 2. Definition 3.2.4 (Liu [6]) An uncertainty distribution is call lognormal if ln is a normal uncertain vari- able ,e . In other words, a lognormal uncertain variable has an uncertainty distribution Figure 1. A linear uncertainty distribution. 1 lnex 1e xp 3, 0xx denoted by ,e , where and e are real numbers wit h 0 . Distribution shown in Fure 3. Definition 3Liu [6])An uncertainty distributio ig .2.5 (n is said to be regular if its inverse function 1 sts and is unique for each exi 0,1 . As we all know, the firm’slue is a asset vad fu ecreasing nction of interest r which is adjusted irregularly [7]. Let r be an uncertain variable with regular lognormal unceainty distributionrt .Then the inverse function 1 is called the inversuncertainty distribution ofr. sy to verify that the inverse uncertainty distributi of lognormal uncertain variable is: e It’s eaon 3 1exp 1 er (10) 4. Numerical Examples nd *ST-listed companies, t In this paper, we choose 6 ST a which are added ST and *ST in 2011, and 6 non-ST- listed companies in Shanghai and Shenzhen stock ex- change as empirical research samples, in which ST and *ST companies are considered as default samples while non-ST companies are considered as normal samples. Data is from http://finance.sina.com.cn/. After finishing the row data, we ge E Vand E delsh 4.1. Traditional KMV Model % at the end of 2011, own in Table 1. Compare the traditional V mo which uses a fixed interest rate and uncertain KMV model by using the above data. KM We select deposit interest rate-3.5 put E Vand E into formulas (1)-(4), and obtain each listempanmarket value of asset and asset volatil- ity by the iterate program of MATLAB as shown in Ta- d coy’s Figure 3. A lognormal uncertainty distribution. Figure 2. A normal uncertainty distribution. Open Access JAMP  N. ZHAN ET AL. Open Access JAMP 15 ble 2t to art of the *ST and ST co 4.2. Uncertain KMV Model h normal uncertainty imum interest rate? ac o you think is the maximum interest rate? ac o you think is a likely interest rate? , 0.75) is the belief degree that the real interest rate is pert’s experimental data (0.04, 0.8) is ac is the belief degree that the real interest rate . Put the data in Table 2 into (6) obtain defaulis less than 0.045? distance, as shown in Table 3. From Table 3, we find that pA5: 0.9. (an expert’s experimental data (0.045, 0.9) is acquired)). mpanies’ DD are bigger than non-ST companies which may lead to an evaluation error. Where (0.02, 0.3), (0.035, 0.75), (0.04, 0.8), (0.04 5, 0.9), (0.05, 1) represents 0.30.02 0.02 , 0.050 1.05 , 0.035 030.0 .75 , 0.04 0.80.04 , 0.045 00.045 .9 , respectively. Let r be an uncertain variable wit distribution and can be obtain by Delphi method. The consultation process is as follows: Q1: What do you think is the minSo we obtain the inverse uncertainty distribution of lognormal uncertain variable by using expert’s experi- mental data: A1: 0.02. (an expert’s experimental data (0.02, 0.3) is quired). Q2: What d 0.747 1exp3.89 1r A2: 0.05. (an expert’s experimental data (0.05, 1) is quired). Q3: What dWe get DD by using uncertainty interest rate shown in Table 4: A3: 0.03. (an expert’s experimental data (0.035 acquired)). Q4: What isCompare DD1 and DD2 in the same drawing. From Figure 4, we can find that, for *ST and ST com- panies, calculations of uncertain KMV model are smaller than traditional KMV model’s; for non-ST-companies, calculations of uncertain KMV model are bigger than traditional KMV model’s. By this example, it is verified less than 0.04? A4: 0.8. (an ex quired)). Q5: What Table 1. Equity value and equity volatility. Equity Value E V (Ten thousand) Equity volatility E Debt D (Ten thousand) *ST Yuancheng 94.10000 6 0.40924 47636.68 *ST Zhongda 302186.68 0.45036 2441 4812 ST Lig 4 S 20.24 *ST Tianrun 123571.38 0.52767 27944.7 ST Guofa 178142.36 0.44814 8.76 Luodun 229618.29 0.58704 56683.21 ST Tianyi 103130.9 0.41686 41352.81 Jinma 240603 0.42448 63062.24 anchuan60546.020.51624 75134.07 Kaile 364071.6 0.38353 181406.34 Batian 194009.26 0.53973 12566.91 Jiahua 1358366 0.3553 60442.38 henghua194814 0.47719 47517.91 ST Company (Ten thousand) Table 2. Market value of asset and asset volatility. A VA Non-ST Company (Ten thousand) A VA *ST Yuancheng 148305.98 0.27410.333831 Jinma 304425.81 59 *ST Zhongda 549348.01 0.245261 Lianchuang Batian ST 1419 0. Shenghua 536586.69 0.441627 *ST Tianrun 151854.66 0.427553 Kaile 547666.55 0.252987 ST Guofa 226851.81 0.350167 206727.72 0.5058 Luodun 287007.76 0.467563 Jiahua 537. 27 339649 ST Tianyi 144982.83 0.294551 242905.55 0.380962 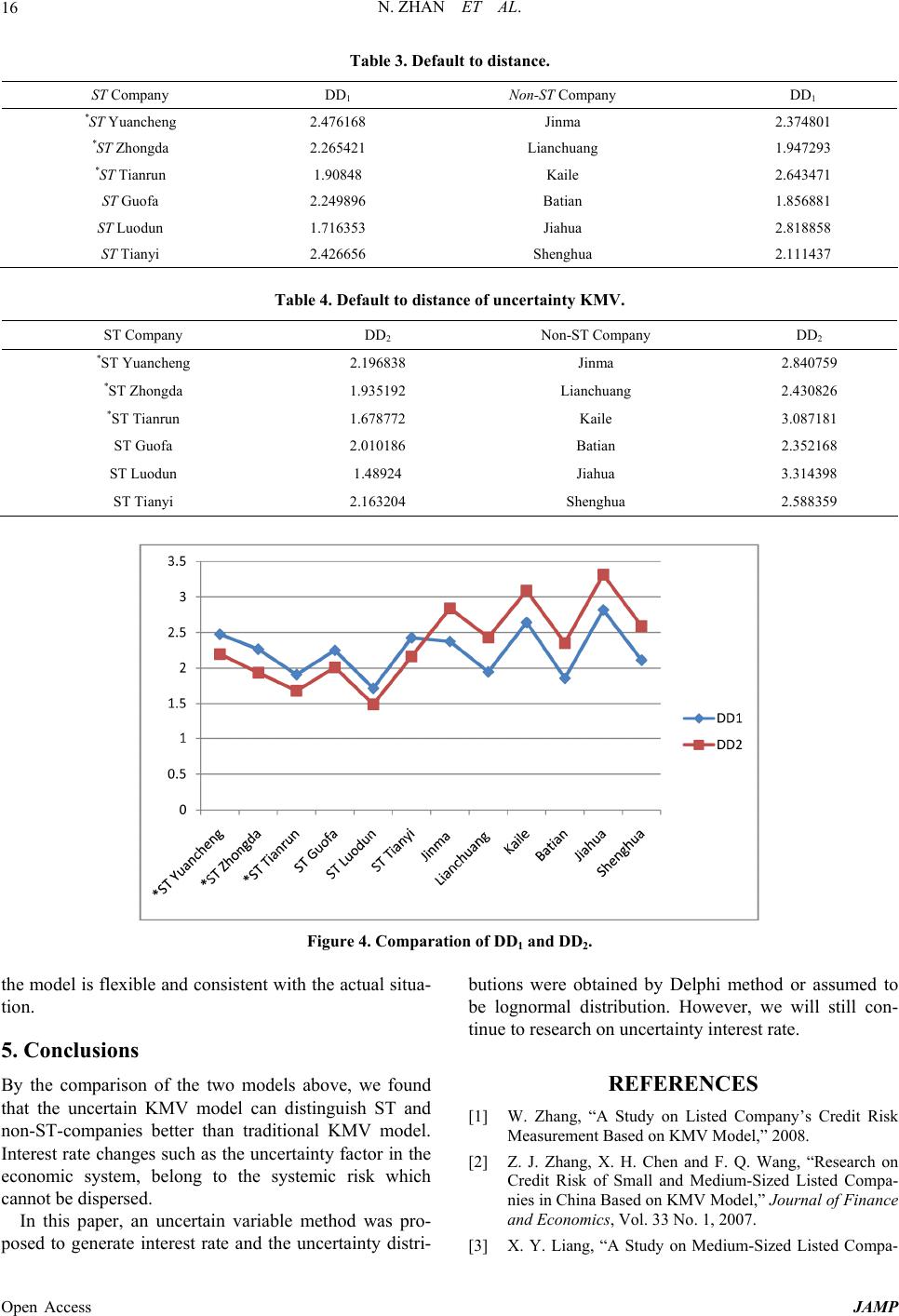 N. ZHAN ET AL. 16 Taault to di ST Company DDmpany DD1 ble 3. Defstance. 1 Non-ST Co *2.8 2.1 ST Yuancheng 47616Jinma 37480 *ST Zhongda 2.265421 Lig Shenghua anchuan1.947293 *ST Tianrun 1.90848 Kaile 2.643471 ST Guofa 2.249896 Batian 1.856881 ST Luodun 1.716353 Jiahua 2.818858 ST Tianyi 2.426656 2.111437 Tabllt to distance of uncertainV. ST Company DD2 e 4. Defauty KM DD2 Non-ST Company *2.8 2.9 ST Yuancheng 19683Jinma 84075 *ST Zhongda 1.935192 Li Shenghua anchuang 2.430826 *ST Tianrun 1.678772 Kaile 3.087181 ST Guofa 2.010186 Bati an 2.352168 ST Luodun 1.48924 Jiahua 3.314398 ST Tianyi 2.163204 2.588359 Figure 4. Comparation of DD1 and DD2. e model is flexib le and consistent with nclusions f the two models above, we found ained by Delphi method or assumed to [1] W. Zhang, “A Study on Listed Company’s Credit Risk Measurement 2008. th the actual situa-butions were obt tion. 5. Co By the comparison o that the uncertain KMV model can distinguish ST and non-ST-companies better than traditional KMV model. Interest rate changes such as the uncertainty factor in the economic system, belong to the systemic risk which cannot be dispersed. In this paper, an uncertain variable method was pro- posed to generate interest rate and the uncertainty distri- be lognormal distribution. However, we will still con- tinue to research on uncertainty interest rate. REFERENCES Based on KMV Model,” [2] Z. J. Zhang, X. H. Chen and F. Q. Wang, “Research on Credit Risk of Small and Medium-Sized Listed Compa- nies in China Based on KMV Model,” Journal of Finance and Economics, Vol. 33 No. 1, 2007. [3] X. Y. Liang, “A Study on Medium-Sized Listed Compa- Open Access JAMP  N. ZHAN ET AL. 17 nies’ Credit Risk Measurement Based on KMV M ethods and KMV Model,” 2010. J. Zhou, “Structure of Default Risk, Interest odel,” for Modeling Human Uncertainty,” Springer-Verlag, Ber- lin, 2010. [7] S. Zeng and 2012. [4] S. C. Yang, “Empirical Study on Credit Risk Measure- ment M [5] B. Liu, “Uncertainty Theory,” 2nd Edition, Springer-Ver- lag, Berlin, 2007. [6] B. Liu, “Uncertainty Theory: A Branch of Mathematics Rate Fluctuations and Debt maturity—Interest Rate’s Feedback Effects of Corporate Debt Financing,” Journal of Jiangxi University of Finance and Ecomomics, No. 3, 2008. Open Access JAMP |

