Journal of Applied Mathematics and Physics, 2013, 1, 1-7
Published Online November 2013 (http://www.scirp.org/journal/jamp)
http://dx.doi.org/10.4236/jamp.2013.15001
Open Access JAMP
Simulation of Thermal Explosion of Catalytic Granule
in Fluctuating Temperature Field
Igor Derevich, Daria Galdina
Department of Applied Mathematics, Faculty of Fundamental Sciences,
Moscow State Technical University by N.E. Bauman (BMSTU), Moscow, Russian Federation
Received July 29, 2013; revised August 29, 2013; accepted September 15, 2013
Copyright © 2013 Igor Derevich, Daria Galdina. This is an open access article distributed under the Creative Commons Attribution
License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
Method for numerical simulation of the temperature of granule with internal heat release in a medium with random
temperature fluctuations is proposed. The method utilized the solution of a system of ordinary stochastic differential
equations describing temperature fluctuations of the surrounding and granule. Autocorrelation function of temperature
fluctuations has a finite decay time. The suggested method is verified by the comparison with exact analytical results.
Random temperature b ehavior of granule with internal heat release qualitatively differs fro m the results obtained in the
deterministic approach. Mean first passage time of granules temperature intersecting critical temperature is estimated at
different regime parameters.
Keywords: Stochastic Ordinary Differential Equation; Autocorrelation Function; Heat Explosion; Semenov’s Diagram;
Temperature Fluctuations
1. Introduction
The catalytic synthesis processes are generally accompa-
nied by heat release. Synthesis of heavy hydrocarbons in
the Fischer-Tropsch process (GTL technology) is associ-
ated with essential heat generation [1]. GTL techno logy can
solve a number of environmental and economic problem s.
In the Technological Institute for Superhard and Nov el
Carbon Materials (Troitsk, Russian Federation), industrial
reactor is developed with a capacity of 5000 Nm3/h of syn-
thesis gas with a production of 500 kg/h stabilized liquid hy-
drocarbons. The reactor used fixed bed of catalyst granules.
Exothermic heat of reaction is transferred from the
volume of catalytic granules to the boundary of the gran-
ules. At the boundary heat is removed to the liquid prod-
ucts of the synthesis. Exceeding heat generation over
heat transfer leads to uncontrolled growth temperature
(thermal explosion). Loss of thermal stability of catalyst
granules is responsible of thermal explosion of the reac-
tor. Therefore, investigation of critical conditions of
thermal explosion is an important practical problem.
Reasons leading to thermal explosion in deterministic
situation have been well studied [2-6]. There is a critical
temperature, the excess of which causes a significant
increase in temperature of granules. The situation drasti-
cally changes when the temperature of the environment
is a random process. In this case there is always a
non-zero probability for a temperature fluctuation, the
magnitude of which exceeds a critical value, which may
lead to the loss of thermal stability. Stud y of the effect of
random noise is dedicated to the behavior of systems
with explosive features, for example, [7-11]. The results
of this study can also be applicable in modeling of igni-
tion conditions of dispersed fuel in aircraft and rocket
engines, and power stations. Main trends obtained in the
paper are helpful for the estimation of the probability of
thermal explosion in storages and transportation lines of
dispersed combustible materials.
Investigation on effect of noise is devoted to the be-
havior of systems with explosive behavior [7-11]. Study
of random temperature fluctuations was carried out in the
framework of probability density fun ction approach [12].
This approach requires the use of modern methods of
stochastic processes and functional analysis and yields
results which have practical importance. However, the
method of the probability density function does not take
into account some important details of the complicated
chemical kinetics. In this situ ation, it is appropriate to us e
the methods of modeling of temperature dynamics which
is based on direct numerical solutions of stochastic ordi-

I. DEREVICH, D. GALDINA 2
nary differential equations [13-17].
In this paper we propose a method for direct numerical
modeling of a random temperature of granule with inter-
nal heat generation with accounted temperature fluctua-
tions in the surrounding. We construct temperature fluc-
tuations with internal temporal structure. The autocorre-
lation function of temperature fluctuations of the sur-
rounding has a finite decay time. This approach can be
used in future for modeling stochastic behavior in not
only temperature, but also reactant concentration inside
the granule with detailed complex kinetics. Verification
of the proposed algo rithm is based on a comparison with
exact analytical solutions. We illustrate va rious scenarios
of the loss of thermal stability of catalytic granule. Cal-
culations on results of the average waiting time of ther-
mal explos ion are pre sented.
2. Equation for Temperature of Granule
with Internal Heat Release. Semenov’s
Diagram
In this section we write down the equation for the tem-
perature of the granule with internal heat source and per-
form the analysis of Semenov’s diagram.
2.1. Equation for Temperature of the Catalytic
Granule
We investigate spherical granule with diameter
p
d,
which is placed in liquid products with temperature
f

.
Thermal effect of exothermal reaction inside the granule
is Q. Rate of chemical reactions is modeled as Arrhenius
law with activation energy E. Heat transfer coefficient is
α. Equation for the volume-averaged temperature of the
granule
p
has the following fo rm

de
d
p
E
R p
ppp fpp
mc SVQA
t



 .
Here
p
m is mass of the granule; 2
p
p
Sd area of
the granule surface; 36
pp
Vd is volume of the gran-
ule; A is the frequency factor; is the universal gas
constant. R
The equation for the granule temperature can be re-
written in the relaxation form
de
d
p
E
R pfp
pp
QA
tc





, (1)
where
p
pp
dc


 is thermal relaxation time of the
granule.
Temperature of the surrounding liquid is given as
 
fff
tt   ,
where
f
 is averaged temperature of the fluid;
is temperature fluctuations;

ft


0
ft
 .
Angular brackets denote the results of averaging over
an ensemble of random realization of fluid temperature.
Equation (1) in dimensionless variables has the form


1
de
d
p
E
fp
pQ








. (2)
Here
p
pf

 is dimensionless temperature of
the granule;
E
tT


is dimensionless time; TE is inte-
gral time scale of fluid temperature autocorrelation func-
tion;
f
pf


 is a dimensionless temperature
fluctuation of fluid surrounding;
f
EER
  is
dimensionless activation energy;

pp f
QQA c 

is dimensionless heat of exothermal reaction;
E
T



 is parameter of thermal inertia of the
granule.
2.2. Semenov’s Diagram
Based on the analysis of Semenov’s diagram we show
the existence of critical temperature. Infinitely small ex-
cess above the critical temperature leads to uncontrolled
increase of temperature of the granule (thermal explo-
sion).
Analysis of Semenov’s diagra m is provided for steady-
state temperature of the liquid medium. Looking for a
stationary temperature of the granule from the following
equation
d1
0, e
d
p
E
pp
Q







. (3)
We introduce dimensionless power of heat transfer to
the liquid phase


*1
p
W



  and dimensionless
power of heat release

exp
Qp
WQ E
 

.
Figure 1 represent Semenov’s diagram. It is evident
that there is a region with three stationary temperatures
of the granule. This region with three roots of Equation
(3) is bounded by the tangential lines, whose position is
determined by the values of thermal relaxation parameter
of the granule.
Figure 1. Semenov’s diagram.
Open Access JAMP

I. DEREVICH, D. GALDINA 3
At the tangential lines b and c in Figure 1 the tem-
perature of the granule returns to a steady state with low
or high temperatures, respectively. To study the types of
stationary temperature we performed numerical integra-
tion of the nonlinear Equation (2) without taking into
account fluctuations in the temperature of the medium.
Figure 2 illustrates the dynamics of change of tem-
perature of the granule, if the initial temperature is close
to the second root on the Semenov’s diagram. It can be
seeing, that infinitely small disturbance above
I
I

give
a loss of thermal stability of the granule.
If initial temperature of the granule is infinitively less
than the value
I
I, the temperature of the granule pro-
ceeds to low value close to ambient temperature. The
second root at the Semenov’s diagram may be regarded
as critical value .

cr II

3. Autocorrelation Function of Temperature
Fluctuations. Exact Results
In this section, we obtain some exact results for com-
parison with data of numerical simulation. Exact solu-
tions exist for linear equations. We consider the equation
for the fluctuations of temperature of the granule (1)
without the chemical heat source
  
d
d
pfp
tt
t




t
. (4)
Temperature fluctuations of fluid is statistic-
cally stationary random process with correlation

ft

 
2
ff ff
tt tt  
 



. (5)
We use the relationship between the autocorrelation
function and its spectrum
  
1e
2
it
f
t

d
f





, (6)
 
e
is
ff
d
s
s





. (7)
Figure 2. Temperature of the granule with initial value near
second root on Semenov’s diagram.
Solution of Equation (4) has the form
 
0
1ed
ts
t
pf
ts







s.
Correlation function of temperature fluctuations of the
granule is written as




 
2
00
11
de de
pp pp
tst s
tt
ff
tt tt
s
ss

 



   



 

s

 
 .
With the help of spectrum of the fluid temperature
autocorrelation function (5) and (6) we write down ex-
pression for granule autocorrelation
 

2
2
2
ed
21
ff
it
pp
t





 


. (8)
Square of dispersion of the granule temperature fluc-
tuations is follows from expression (8) at t = 0


2
2
2d
21
ff
p





 

.
Let us consider two special cases of the autocorrela-
tion function of the temperature fluctuations of the fluid.
3.1. Delta-Correlated in Time Random Process
Temperature fluctuations is delta-correlated in
time random process. The autocorrelation function

ft

(5)
has the form


2
ftt tt



   
. (9)
Here

 is integral time scale
 
00
dd
fss ss




 


.
Spectrum of autocorrelation function (9) is found from
expression (7)
 
2e d2
is
fss

 



 
.
Substitution expression for the spectrum into formula
(8) leads to autocorrelation function of the granule tem-
perature fluctuations

22
e
t
pp f
t







 
.
Intensity of temperature fluctuations and autocorrela-
tion function of granule are

222
,e
t
pffp
p
t








. (10)
Open Access JAMP

I. DEREVICH, D. GALDINA 4
Delta-correlation approach is correct for granule with
high thermal inertia. Autocorrelation functio
perature fluctuations of the granule has exponential form
w
orrelation Function
ation of fluid
n of tem-
ith integral temporary scale equal to the granule relaxa-
tion time.
3.2. Exponential Approximation of
Autoc
Second approach is exponential approxim
temperature

ft
 autocorrelation function

e
E
t
T
ft

 (11)
Spectrum of the autocorrelation function (11) follows
from formula (7)
 
2
2
ed
E
t
itTE
f
T
t




.
1E T

 
Correlation of the granule temperature fluctuation is
obtained from formula (11)

 
2
22e d
21
it
fE
pp
T
t


22
1
E
T








 



 
Calculation of the above integral under theory of fu-
tions with complex variables leads to the result
.
nc



22 2
ee
E
t t
T
E
pp f
T
t





 


 .
1E T

(12)
Square of dispersion of the granule tempera
tuations is follows from Equation (12) at t = 0 ture fluc-

2
2
1
f
p
E
T



. (13)
Autocorrelation function of the gra
fluctuation als o obtai ned from Equatinule temperature on (12)



ee
1
E
t t
T
E
p
T
tT




 


 .
E
(14)
Integral time scale of the granule temp
tion is erature fluctua-

d
pE
TttT
0




.
One can conclude about existence o two granules
types. Granule with small thermal inertia with thermal
relaxation time much smaller than integral time scale of
flu
f
id temperature autocorrelation function
E
T

. In
that case dispersion of temperature fluctuations of the
granule and fluid is close 22
p
f

 , and integral time
scale of granule temperature fluctuations is
E
TT


. For
granule with high thermal inertia
E
T

 dispersion of
granule temperature flucess then fluid tuations is l


22
p
Ef
T



. Integral time scale of tem-
perature fluctuations is close to ure relaxation
time T
granule
temperat




, and granule autocorrelation function de-
cays as




p
ptext



gorithm
emperature of surrou
rrelation
ly on
theic ordinary equations.
 (see, also Equation (10)).
Obtained exact results will be used for testing numeri-
cal al of simulation of temperature of granule in a
random tndings.
4. System of Stochastic Differential
Equations
Analytical results show that modeling autoco
function with finite relaxation time is possible on
base of stochast
Write down system of differential equations for tem-
perature fluctuations of fluid and the granule with heat
release

 
d
d
f
f




 , (15)
 




1
d
d
E
f
ptt
t







Here
ep
pt
Q



. (16)




lta-correlatedis seeded Gaussian random process with de function




2
2tt tt  

 


.
Integration of the system of Equations (15) and (16) is
carried out by explicit Euler method


11nn nn
ff f
 

 ,

 




*
1
1*e
1n
p
E
fp
nn
pp Q





nn





 






.
Here n is the number of temporary steps; randon-
crement of seeded process is modeled as m i
 
2
2
nn

 


,
where
 n

is random realization of the normalized
Gausess (white noise) with zero mean and unit
dispersion.
re 3
nclude that increasing the thermal inertia re-
du
sian proc
Figu illustrates the effect of thermal inertia of the
granules on temperature fluctuations without heat source.
It can be co
ces the amplitude of temperature fluctuations of the
granule.
Figure 4 shows influence of thermal inertia of the
granule on dispersion of temperature fluctuations. The
Open Access JAMP

I. DEREVICH, D. GALDINA 5
increasing thermal inertia decreases the intensity of tem-
pe
s of numerical simulations satisfactory agree
w
g time of Explosion
scenar-
al heat
rature fluctuations of the granule. From the Figure 4 is
also evident a satisfactory agreement between the results
of calculations by the exact formula (13) and numerical
data obtained by averaging random realizations of tem-
perature.
Autocorrelation function of the granule temperature
fluctuations are shown in Figure 5. It can be seen that
the result
ith obtained ex act results. The growth of thermal inertia
increases the damping region of the autocorrelation func-
tion of the g ranules.
5. Simulation of Thermal Explosion.
Average Waitin
This section presents results showing the various
ios of behavior of granule temperature with intern
Figure 3. Random temperatures of surroundings and gran-
ule.
generation with account temperature fluctuatuation of the
fluid. Figure 6 shows the behavior of the actual tem-
perature of the granules with heat generation. On the
figure


1
ff
t   is actual temperature of sur-
rounding fluid. It can be seen that fluctuations of magni-
tude of chemical reactions make a significant contribu-
tion to the value of random temperature of the granule.
On all illustrations following next the initial tempera-
ture of the granule is less than the critical value corre-
sponding to the second root
I
I
gram).
Random process with nonzero probability may exceed
any level. After some random ti the actual temperature
of
 (see Semenov’s dia-
me
the granule will be over the critical value cr II


and there will be a loss of thermal stability. This scenario
is illustrated by Figure 7.
The waiting time of a thermal explosion we define as
the average time of first crossing by random temperature
of the granule the critical level cr
. Waiting time of
Figure 5. Autocorrelation functions of temperature fluctua-
tions fluid and granule. Points are numerical simulations
lines are the formulas (11) and (14). Dashed line is exponen, -
tial approximation (10).
Figure 4. The ratio between dispersions of temperature
fluctuations of granule and the fluid: points are simulation
results; curve is the formula (13). Figure 6. Example of granule temperature without heat
explosion.
Open Access JAMP

I. DEREVICH, D. GALDINA 6
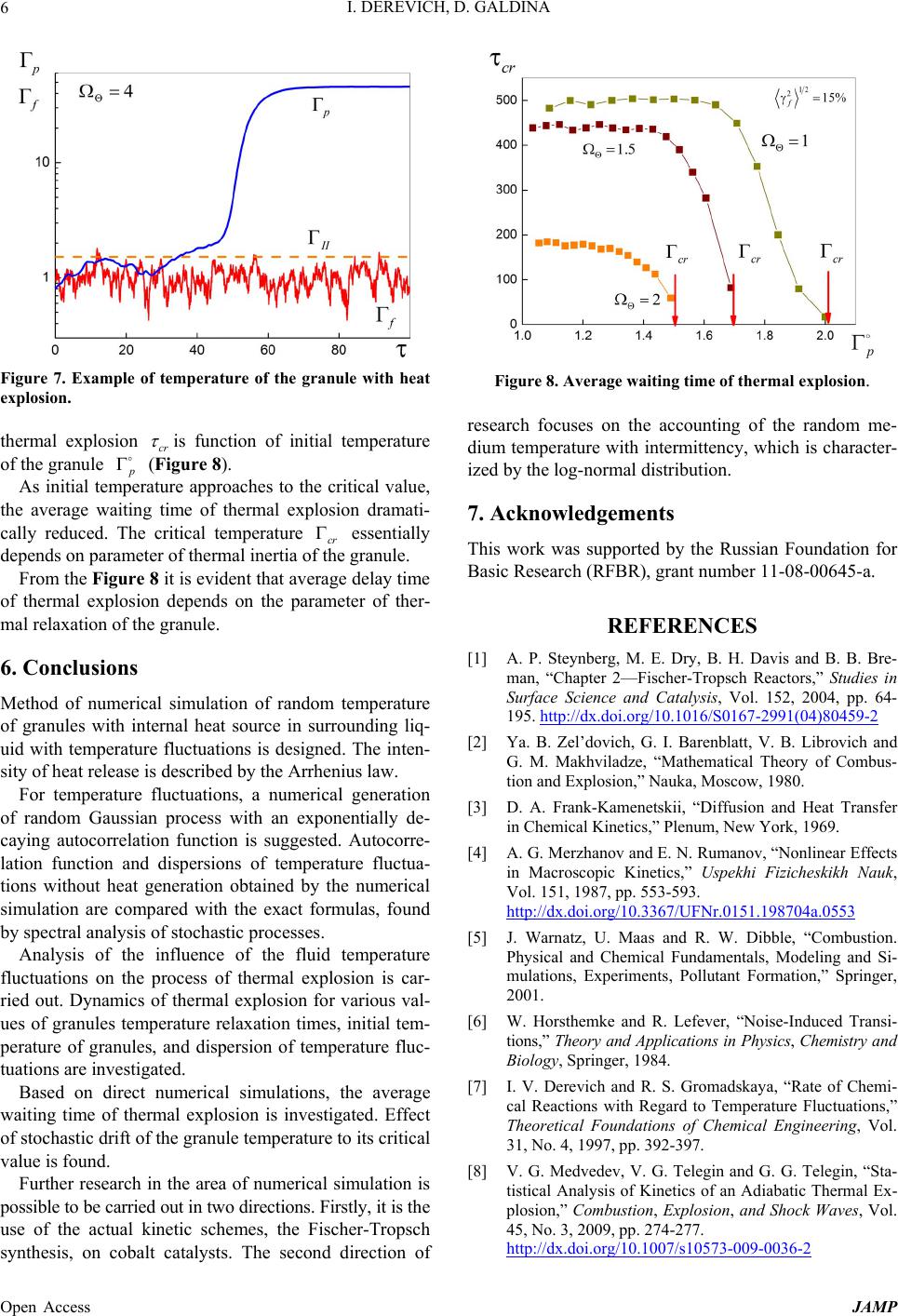
Figure 7. Example of temperature of the granule with heat
explosion.
thermal explosion cr

is function of initial temperature
of the granule
p

mp (Fi eratur
gure 8).
As initial tee approaches to the critical value,
the average waiting time of thermal explosion dramati-
cally reduced. The critical temperature essentially
depends on parameter of thermal inertiagranule.
From the Figure 8 it is ev ident that averag e delay time
of thermal explosion depends on the parameter of ther-
mal relaxation of the granule.
6. Conclusions
Method of numerical simulation of random temperatue
of granules with internal heat source in surrounding l-
release is described by the Arrhenius law.
flu
ss
explosion for various val-
erature relaxation times, initial te
and dispersion of temperature fluc-
al
va
cr

of the
r
iq
uid with temperature fluctuations is designed. The inten-
ity of heatsFor temperature ctuations, a numerical generation
of random Gauian process with an exponentially de-
caying autocorrelation function is suggested. Autocorre-
lation function and dispersions of temperature fluctua-
tions without heat generation obtained by the numerical
simulation are compared with the exact formulas, found
by spectral analysis of stochastic processes.
Analysis of the influence of the fluid temperature
fluctuations on the process of thermal explosion is car-
ried out. Dynamics of thermal
ues of granules temp
perature of granules, m-
tuations are investigated.
Based on direct numerical simulations, the average
waiting time of thermal explosion is investigated. Effect
of stochastic drift of the granule temperature to its critic
lue is found.
Further research in the area of numerical simulation is
possible to be carried out in two directions. Firstly, it is the
use of the actual kinetic schemes, the Fischer-Tropsch
synthesis, on cobalt catalysts. The second direction of
Figure 8. Average waiting time of thermal explosion.
research focuses on the accounting of the random me-
dium temperature with intermittenc y, which is character-
ized by the log-normal distribution.
7. Acknowledgements
This work was supported by the Russian Foundation for
Basic Research (RFBR), grant number 11-08-00645-a.
REFERENCES
[1] A. P. Steynberg, M. E. Dry, B. H. Davis and B. B. Bre-
man, “Chapter 2—Fischer-Tropsch Reactors,” Studies in
Surface Science and Catalysis, Vol. 152, 2004, pp. 64-
195. http://dx.doi.org/10.1016/S0167-2991(04)80459-2
[2] nd
[4] A. G. Merzhanov and E. N. Rumanov, “Nonlinear Effects
Uspekhi Fizicheskikh Nauk,
3.
Ya. B. Zel’dovich, G. I. Barenblatt, V. B. Librovich a
G. M. Makhviladze, “Mathematical Theory of Combus-
tion and Explosion,” Nauka, Moscow, 1980.
[3] D. A. Frank-Kamenetskii, “Diffusion and Heat Transfer
in Chemical Kinetics,” Plenum, New York, 1969.
in Macroscopic Kinetics,”
Vol. 151, 1987, pp. 553-59
http://dx.doi.org/10.3367/UFNr.0151.198704a.0553
[5] J. Warnatz, U. Maas and R. W. Dibble, “Combustion.
Physical and Chemical Fundamentals, Modeling and Si-
mulations, Exmation,” Springer,
2001.
i-
al Ex-
periments, Pollutant For
[6] W. Horsthemke and R. Lefever, “Noise-Induced Transi-
tions,” Theory and Applications in Physics, Chemistry and
Biology, Springer, 1984.
[7] I. V. Derevich and R. S. Gromadskaya, “Rate of Chem
cal Reactions with Regard to Temperature Fluctuations,”
Theoretical Foundations of Chemical Engineering, Vol.
31, No. 4, 1997, pp. 392-397.
[8] V. G. Medvedev, V. G. Telegin and G. G. Telegin, “Sta-
tistical Analysis of Kinetics of an Adiabatic Therm
plosion,” Combustion, Explosion, and Shock Waves, Vol.
45, No. 3, 2009, pp. 274-277.
http://dx.doi.org/10.1007/s10573-009-0036-2
Open Access JAMP

I. DEREVICH, D. GALDINA 7
[9] I. V. Derevich, “Temperature O
Particle of Fischer-Tropsch Synthesi s,” International J
scillation in a Catal
our-
ytic
nal of Heat and Mass Transfer, Vol. 53, No. 1-3, 2010,
pp. 135-153.
http://dx.doi.org/10.1016/j.ijheat masst ransfer.200 9.09.045
[10] I. V. Derevich, “Effect of Temperature Fluctuations of
.ijheatmasstran sfer.2010.07.03 1
Fluid on Thermal Stability of Particles with Exothermic
Chemical Reaction,” International Journal of Heat and
Mass Transfer, Vol. 53, No. 25-26, 2010, pp. 5920-5932.
http://dx.doi.org/10.1016/j
34/S0010508211050078
[11] I. V. Derevich, “Influence of Temperature Fluctuations on
the Thermal Explosion of a Single Particle,” Combustion,
Explosion, and Shock Waves, Vol. 47, No. 5, 2011, pp.
538-547. http://dx.doi.org/10.11
[12] V. I. Klyatskin, “Stochastic Equations Eyes of the Physi-
cist: Substantive Provisions, Exact Results and Asymp-
totic Approaches,” FIZMATHLIT, Moscow, 2001.
[13] G. Y. Liang, L. Cao and D. J. Wu, “Approximate Fok-
ker-Planck Equation of System Driven by Multiplicative
Colored Noises with Colored Cross-Correlation,” Physica
A, Vol. 335, No. 3-4, 2004, pp. 371-384.
http://dx.doi.org/10.1016/j.physa.2003.12.023
[14] D. T. Gillespie, “Exact Numerical Simulation of the Orn-
stein-Uhlenbeck Process and Its Integral,” Physical Re-
view E, Vol. 54, No. 2, 1996, pp. 2084-2091.
http://dx.doi.org/10.1103/PhysRevE.54.2084
[15] S. Ilie and A. Teslya, “An Adaptive Stepsize Method for
the Chemical Langevin Equation,” Journal of Chemical
Physics, Vol. 136, No. 18, 2012, Article ID
[16] C. W. Gardiner, “Handbook of Stochastic M
: 184101.
ethods for
Physics, Chemistry and the Natural Sciences,” Springer,
1983. http://dx.doi.org/10.1007/978-3-662-02377-8
[17] P. Lévy, “Processus Stochastiques et Mouvem
nien,” Gauthier-Villars, Paris, 1965. ent Brow-
Open Access JAMP