Surgical Science, 2011, 2, 25-30
doi:10.4236/ss.2011.21007 Published Online January 2011 (http://www.SciRP.org/journal/ss)
Evaluation of Stress Strain Patterns in a Stentless Aortic
Valve and Its Leaflets
Gideon Praveen Kumar, Lazar Mathew
School of Biosciences an d Technology, VIT University, Vellore, India.
Received August 17, 2010; revised August 27, 2010; accepted September 10, 2010
Abstract
Objective: To design a new trileaflet aortic valve and investigate its mechanical behavior using finite ele-
ment methods. Background: Quantification of aortic valve deformation during cardiac cycle is essential in
understanding normal and pathological valvular function and eventually in the design of valves. We have
designed and analyzed a new tissue valve model to investigate the mechanics of the valve and its compo-
nents. Methods: Steps involves in 3D CAD based geometric modeling of a trileaflet aortic valve and the ef-
fects of different component dimensions on the mechanical behavior of valve is presented in this paper.
Conceptual designing of individual components was used to build the total geometric model. Different
physiological pressures were applied on the valve model and its deformation patterns were studied. Results:
A new geometric model of a trileaflet aortic valve was designed. Its mechanical behavior was studied. Ge o-
metric analysis and simulation of these models enhanced the designer to optimize the geometry suitable for
performance during and after implantation. Conclusion: The geometry-based model presented here allows
determining quickly if the new set of valve component dimensions results in a functional valve. This is of
great interest to designers of new prosthetic heart valve models, as well as to surgeons involved in valve-
sparing surgery.
Keywords: Blood Flow, Aortic Valve Mechanics, Conceptual Design, Finite Element Analysis
1. Introduction
Valvular heart disease is a life-threatening disease that
afflicts millions of people globally and leads to approxi-
mately 250,000 valve repair and/or replacement surgeries
every year [1]. Malfunction of a native valve impairs its
efficient mechanical and hemodynamic performance.
Although the functional mechanisms of the aortic valve
has been studies extensively through experimental analy-
sis, subtle influences of sinus geometry, leaflet and aortic
root mechanics and hemodynamic loading on the valve
function are not fully understood. A functional under-
standing of the aortic valve mechanics is essential for
assessment for assessment and management of valvular
pathologies [2].
Assessment of heart valve mechanics is critical part of
computer aided engineering of these valves. This is very
much imperative in the case of bioprosthetic aortic valve
[BAVs], which are generally preferred over mechanical
valves due to their superior hemodynamics, low throm-
bogenicity and minimally invasive deployment method-
ologies [3]. The design of BAVs has provides cardiac
surgeons with devices that can be used to replace the
diseased valve in patients with little or no anti-coagula-
tion therapy. BAVs, in comparison to mechanical valves,
however, have a shorter durability. The mechanisms of
structural deterioration in BAVs are not clearly under-
stood, but it is generally hypothesized that tissue degra-
dation is stress related. Understand ing the stresses which
occur in a BAV should lead to better understanding of
the degenerative processes. This eventually helps de-
signers come up with robust valve models. Finite ele-
ment analysis based simulations of complex BAVs have
become increasingly popular these days. The aim of this
paper is to bring out a 3D CAD based conceptual design
of a BAV and subject it to finite element analysis to
study the deformation patterns involved which may help
in investigating their deterioration processes. The ulti-
mate objective of this work is to accurately simulate the
behavior of the valve under normal operating conditions.
The insight gained from a numerical parametric investi-
gation of the valve mechanics may be h elpful in improv-

G. P. KUMAR ET AL. 26
ing the performance and durability of BAVs.
2. Methods
2.1. Geometry and Assumptions
Geometric modeling of a complex structure such as the
aortic valve necessitates assumptions to make the ap-
proach tractable. First, it is assumed that the three leaflets
are identical in size and properties, and lie at 120 degree
from each other in the circumferential direction of the
valve [15]. Figure 1 shows the base profile of the new
aortic valve modeled by our team. Shown are the pri-
mary parameters that can be used to define the valve
dimensions: Do, the outer diameter at the base; Di, the
inner diameter at the base, and H, the valve height. The
valve dimensions are tabulated in Table 1. Most impor-
tantly, it is further considered that the dimensions of the
valve components do not change significantly enough
during the cardiac cycle that their variation should be
accounted for in a first-order analysis.
The total configuration of our valv e model is shown in
Figure 2. The overall shape of the bioprosthesis is de-
termined by the woven Dacron fabric [5]. This fabric
provides a structure to which the tissue can be sewn
thereby helping in preventing leakage of the valve after
implantation and contributing to the aesthetics of the
valve. Three leaflets have been designed which are at-
tached to the prosthetic apparatus. These leaflets are
pushed out of the way during forward flow of blood
through the valve.
Figure 1. Base profile of the model used for the study.
Table 1. Dimensions (mm) measured in commissure based
aortic valve.
Dimension Measurement [mm]
Outer Diameter [Do] 18
Inner Diameter [Di] 16
Valve Height [H] 9
Figure 2. 3D geometry of the valve model used for the study.
During backflow, however, the leaflets are forced to-
gether to the center of the aorta and press against each
other under the influence of pressure so that they form a
tight seal, thus preventing backflow [11-13].As the back
pressure peaks, the leaflets transmit stresses due to pres-
sure acting on them onto the fabric where they are at-
tached. In order to reduce the complexity of the model
and to gain better understanding of leaflet contribution to
stresses, the aorta is excluded from our model.
2.2. Material Model
Trileaflet symmetry is adopted and the compliant aortic
root is assumed to be isotropic. The leaflets are rein-
forced with collagen giving the structure physiological
material characteristics [6-10]. The material properties of
the valve model that were considered for the study are
tabulated in Table 2 below
3. Finite Element Model
3.1. Loading and Boundary Conditions
Finite element analysis was performed using COSMOS-
Works 2009, an FEA package. The valve was constrained
Table 2. Properties of materials used for the analysis.
Anatomy Young’s
Modulus
[MPa]
Poisson’s
Ratio Density [kg/mm3 ]
Yield
strength
[MPa]
Aortic leaflets
with root 1 0.45 1.1* 10-4 1.74
Dacron graft 7.84 0.3 0.6* 10-4 9.15
Aorta 2 0.45 2*10-4 1.74

G. P. KUMAR ET AL. 27
strained at the aortic root and the origin of the valve leaf-
lets as shown in Figure 3. Stresses ranging between
10,665.8 N / m2 and 26,664 N / m2 were loaded on to the
valve in the direction of valve opening, as shown in Fig-
ure 4. These pressures were selected as they are equiva-
lent to the normal human blood pressure which ranges
from 80 mm Hg to 200 mm Hg [13,14].
3.2. Stress Distribution and Deformation in the
Valve
The aortic valve was subjected to finite element analysis
with the aforemen tioned material properties, loading an d
boundary conditions. Examples of simulation of the
valve are shown in Figure 5.
The opening behavior of the valve during different
phases of the cardiac cycle is shown in Figure 6.
Figure 3. Part of the valve constrained.
Figure 4. Application of load on the valve.
(a)
(b)
(c)
(d)

G. P. KUMAR ET AL. 28
(e)
(f)
Figure 5. (a) Stress distribution in the closed valve, (b)
Stress distribution when the valve opens. (c) Displacement
in the closed valve. (d) Displacement of leaflets when the
valve opens. (e) Strain on the closed valve. (f) Strain en-
countered when the valve opens.
3.3. Leaflet Analysis
Characteristics one would typically require from an aor-
tic valve are smooth opening and closing. To understand
the folding mechanism of the valve leaflets, study of the
mechanical behavior of the leaflets is imperative [7]. The
leaflet stresses and its deformation are given in Figure 7.
The valve leaflets and the material properties used are
the same as described in the previous section.
4. Results
A stentless aortic valve model was subjected to finite
element analysis and studied. To understand its deforma-
tion mechanism, individual leaflet analysis was done to
understand attachment forces and displacement. The re-
sults of the finite element analysis are tabulated in Ta-
bles 3, 4 and 5. It is apparently clear that there was con-
siderable amount of displacement of the leaflets in order
to allow passing of blood from the lest ventricle to the
aorta during systole. The same was shown in Figure 4.
Maximum strain in the valve is seen at the attach ment of
the leaflets to the aorta. This is again reinforced during
analysis of individual leaflets. Hence it is clear that de-
formation occurs mostly at the leaflet attachment spots.
These areas are also prone for mechanical degeneration
over a period of time. Thus the stress distribution and the
resultant displacement in an aortic valve were studied to
understand its mechanical behaviour patterns. The results
of the studies are tabulated in tables Th e highest stress in
the leaflet was found at the attachment points at
7.76583e + 007 N / m^2.
(a)
(b)
(c)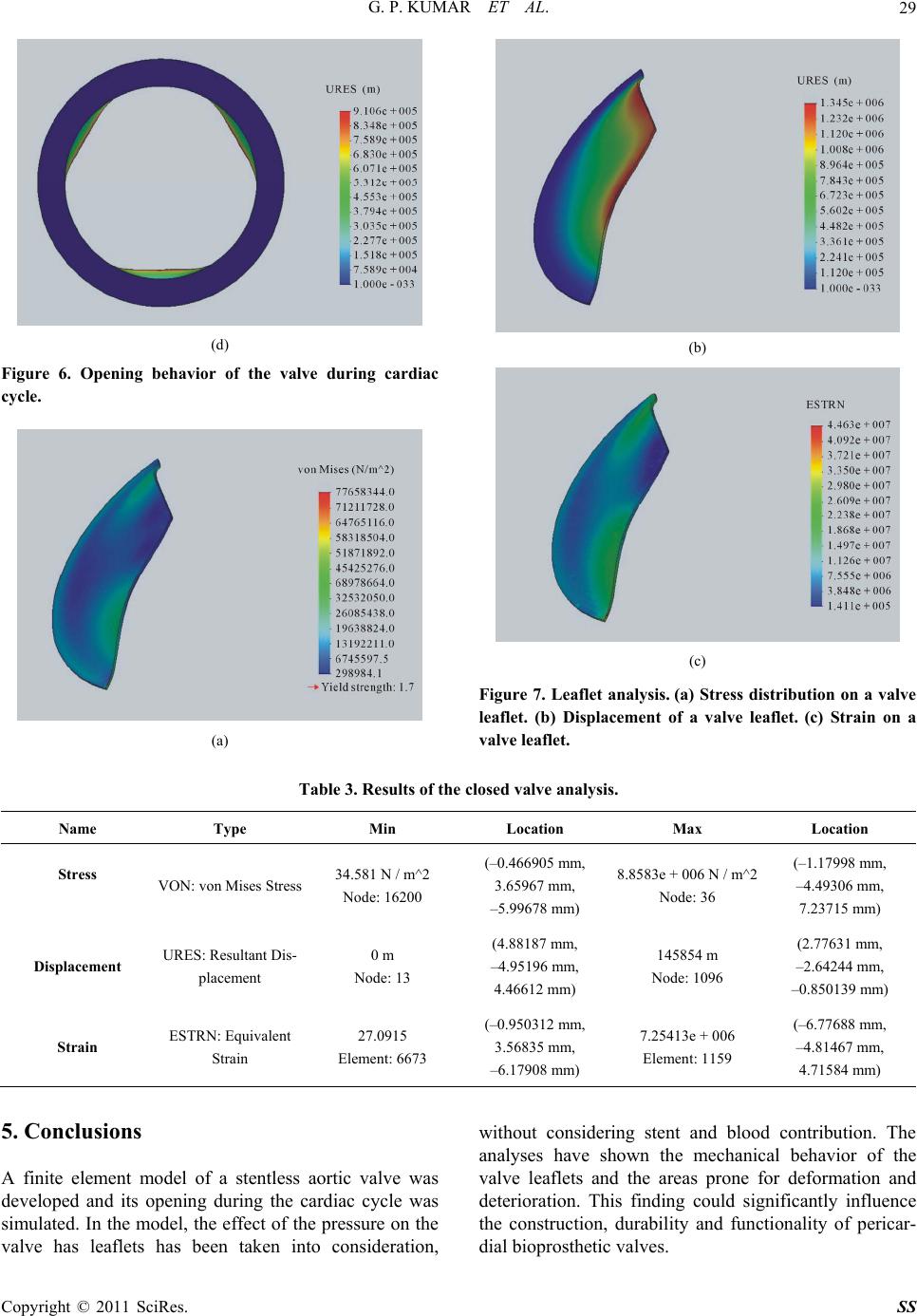

G. P. KUMAR ET AL. 29
(d)
Figure 6. Opening behavior of the valve during cardiac
cycle.
(a)
(b)
(c)
Figure 7. Leaflet analysis. (a) Stress distribution on a valve
leaflet. (b) Displacement of a valve leaflet. (c) Strain on a
valve leaflet.
Table 3. Results of the closed valve analysis.
Name Type Min Location Max Location
Stress
VON: von Mises Stress 34.581 N / m^2 Node: 16200
(–0.466905 mm,
3.65967 mm,
–5.99678 mm)
8.8583e + 006 N / m^2
Node: 36
(–1.17998 mm,
–4.49306 mm,
7.23715 mm)
Displacement URES: Resultant Dis-
placement
0 m
Node: 13
(4.88187 mm,
–4.95196 mm,
4.46612 mm)
145854 m
Node: 1096
(2.77631 mm,
–2.64244 mm,
–0.850139 mm)
Strain ESTRN: Equivalent
Strain
27.0915
Element: 6673
(–0.950312 mm,
3.56835 mm,
–6.17908 mm)
7.25413e + 006
Element: 1159
(–6.77688 mm,
–4.81467 mm,
4.71584 mm)
5. Conclusions
A finite element model of a stentless aortic valve was
developed and its opening during the cardiac cycle was
simulated. In the model, the effect of the pressure on the
valve has leaflets has been taken into consideration,
without considering stent and blood contribution. The
analyses have shown the mechanical behavior of the
valve leaflets and the areas prone for deformation and
deterioration. This finding could significantly influence
the construction, durability and functionality of pericar-
dial bioprosthetic valves.

G. P. KUMAR ET AL. 30
Table 4. Results of the open valve analysis.
Name Type Min Location Max Location
Stress VON: von Mises
Stress
0 N / m^2
Node: 4231
(–1.18031 mm,
–5.05196 mm,
5.5504e + 007 N /
m^2
(–8.74397 mm,
–1.90671 mm,
Displacement URES: Resultant
Displacement
0 m
Node: 2
(0.335239 mm,
–1.92087 mm,
910639 m
Node: 3015
(–1.16512 mm,
2.33546 mm,
Strain ESTRN: Equivalent
Strain
0
Element: 1925
(–7.9765 mm,
–3.33865 mm,
3.04957e + 007
Element: 1279
(–8.65226 mm,
–1.83037 mm,
Table 5. Results of the leaflet analysis.
Name Type Min Location Max Location
Stress VON: von Mises
Stress
298984 N / m^2
Node: 14973
(–0.185681 mm,
2.311 mm,
7.76583e + 007 N /
m^2
(5.8779 mm,
0.0444383 mm,
Displacement URES: Resultant
Displacement
0 m
Node: 1
(6.06218 mm,
0 mm,
1.34454e + 006 m
Node: 1409
(–2.47146 mm,
2.05275 mm,
Strain ESTRN: Equivalent
Strain
141127
Element: 6831
(–0.0432563 mm,
2.35132 mm,
4.46251e + 007
Element: 6794
(–5.79161 mm,
0.0884588 mm,
6. References
[1] D. Berdajs, P. Lajos and M. Turina, “The Anatomy of the
Aortic Root,” Cardiovascular Surgery, Vol. 10, No. 4,
2002, pp. 320-327.
doi:10.1016/S0967-2109(02)00018-2
[2] S. J. Choo, G. McRae, J. P. Olomon, G. St George, W.
Davis, C. L. Burleson-Bowles, D. Pang, H. H. Luo, D.
Vavra, D. T. Cheung, J. H. Oury and C. M. Duran “Aor-
tic Root Geometry: Pattern of Differences between Leaf-
lets and Sinuses of Valsalva,” The Journal of Heart Valve
Disease, Vol. 8, No. 4, 1999, pp. 407-415.
[3] P. Dagum, R. Green, F. J. Nistal, et al., “Deformational
Dynamics of the Aortic Root—Modes and physiology
determinants,” Circulation 100 (Suppl II), II-54-II-62.
1999.
[4] T. E. David, “Aortic Valve-Sparing Operations,” The
Annals of Thoracic Surgery, Vol. 73, No. 4, 2002, pp.
1029-1030. doi:10.1016/S0003-4975(02)03487-2
[5] K. Furukawa, H. Ohteki, Z.-L. Cao, K. Doi, Y. Narita, N.
Minato and T. Itoh, “Does Dilatation of the Sinotubular
Junction Cause Aortic Regurgitation?” The Annals of
Thoracic Surgery, Vol. 68, No. 3, 1999, pp. 949-954.
doi:10.1016/S0003-4975(99)00698-0
[6] K. S. Kunzelman, K. J. Grande, T. E. David, et al., “Aor-
tic Root and Valve Relationships,” Journal of Thoracic
Cardiovascular Surgery, Vol. 107, No. 6, 1994, pp.
162-170.
[7] E. Lansac, H. S. Lim, Y. Shomura, et al., “A Four-Di-
mensional Study of the Aortic Root Dynamics,” Euro-
pean Journal of Cardiothoracic Surgery, Vol. 22, No. 4,
2002, pp. 497-503. doi:10.1016/S1010-7940(02)00405-0
[8] K. J. Lockie, M. Butterfield, J. Fisher, et al., “Geometry
of Homograft Valve Leaflets: Effects of Dilatation of the
Aorta and of the Aortic Root,” The Annals of Thoracic
Surgery, Vol. 60, 1993, pp. S384-S390.
[9] J. L. Mercer, M. Benedicty and H. T. Bahnson, “The
Geometry and Construction of the Aortic Leaflet,” Jour-
nal of Thoracic Cardiovascular Surgery, Vol. 65, No. 4,
1973, pp. 511-518.
[10] W. M. Swanson and R. E. Clark, “Dimensions and Geo-
metric Relationships of the Human Aortic Valve as a
Function of Pressure,” Circulation Research, Vol. 35, No.
6, 1974, pp. 871-882.
[11] M. J. Thubrikar, “The Aortic Valve,” CRC Press, Boca
Raton, 1990.
[12] M. J. Thubrikar, F. Robicsek, G. G. Gong and B. L.
Fowler, “A New Aortic Root Prosthesis with Compliant
Sinuses for Valvesparing Operations,” The Annals of
Thoracic Surgery, Vol. 71, 2001, pp. S318-S322.
doi:10.1016/S0003-4975(01)02541-3
[13] M. Trenkner, S. Raczynski and R. Gutkowski, “Optimal
Diameter of the Stent for Aortic Valvular Grafts.
I-Studies on Valve Function and Geometry,” Journal of
Thoracic Cardiovascular Surgery, Vol. 72, No. 4, 1976,
pp. 613-617.
[14] J. G. Webb, M. Chandavimol, C. R. Thompson, D. R.
Ricci, R. G. Carere, B. I. Munt, C. E. Buller, S. Pasupati
and S. Lichtenstein, “Percutaneous Aortic Valve Implan-
tation Retrograde from the Femoral Artery,” Circulation,
Vol. 113, No. 6, 2006, pp. 842-850.
doi:10.1161/CIRCULATIONAHA.105.582882
[15] G. P. Kumar and L. Mathew, “3D CAD Based Geometric
Modeling of a New Tri-Leaflet Aortic Valve,” Artificial
Organs 2009, in press.