 Journal of Applied Mathematics and Physics, 2013, 1, 60-66 http://dx.doi.org/10.4236/jamp.2013.13010 Published Online August 2013 (http://www.scirp.org/journal/jamp) Hilbert’s Fourth Problem: Searching for Harmonic Hyperbolic Worlds of Nature A. P. Stakhov1,2 1International Higher Education Academy of Sciences, Moscow, Russia 2Institute of the Golden Section, Academy of Trinitarism, Moscow, Russia Email: goldenmuseum@rogers.com Received June 14, 2013; revised July 15, 2013; accepted September 1, 2013 Copyright © 2013 A. P. Stakhov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT Recently the new unique classes of hyperbolic functions-hyperbolic Fibonacci functions based on the “golden ratio”, and hyperbolic Fibonacci -functions based on the “metallic proportions” ( is a given natural number), were intro- duced in mathematics. The principal distinction of the new classes of hyperbolic functions from the classic hyperbolic functions consists in the fact that they have recursive properties like the Fibonacci numbers (or Fibonacci -numbers), which are “discrete” analogs of these hyperbolic functions. In the classic hyperbolic functions, such relationship with integer numerical sequences does not exist. This unique property of the new hyperbolic functions has been confirmed recently by the new geometric theory of phyllotaxis, created by the Ukrainian researcher Oleg Bodnar (“Bodnar’s hy- perbolic geometry). These new hyperbolic functions underlie the original solution of Hilbert’s Fourth Problem (Alexey Stakhov and Samuil Aranson). These fundamental scientific results are overturning our views on hyperbolic geometry, extending fields of its applications (“Bodnar’s hyperbolic geometry”) and putting forward the challenge for theoretical natural sciences to search harmonic hyperbolic worlds of Nature. The goal of the present article is to show the unique- ness of these scientific results and their vital importance for theoretical natural sciences and extend the circle of readers. Another objective is to show a deep connection of the new results in hyperbolic geometry with the “harmonic ideas” of Pythagoras, Plato and Euclid. Keywords: hyperbolic Geometry of Lobachevski; Hyperbolic Fibonacci Functions; Bodnar’s Geometry of Phyllotaxis; Hilbert’s Fourth Problem; New Hyperbolic Worlds of Nature 1. Introduction Recently a number of the important scientific results have been obtained in modern science [1-9]. They relate to hyperbolic geometry and have a direct relation to the theoretical natural sciences in the whole. This direction includes the following scientific results: 1) Fibonacci hyperbolic trigonometry, based on the “golden ratio” [1-3]. 2) A new geometric theory of phyllotaxis (“Bodnar’s hyperbolic geometry”) [4,5]. 3) The general theory of hyperbolic functions, based on the “metallic proportions” [6,7]. 4) The original solution of Hilbert’s Fourth Problem [7,8]. 5) The “mathematics of harmony” [9] as a revival of the ancient “mathematics of harmony” (Pythagoras, Plato, Euclid) in modern science. The purpose of this article is to give a brief survey of these scientific results in order to emphasize their unique- ness and importance for the development of hyperbolic geometry and theoretical natural sciences. The other pur- pose is to show a deep connection of these results with “harmonic ideas” of Pythagoras, Plato and Euclid. Sear- ching for new hyperbolic worlds of Nature, based on the “golden” and “metallic” proportions, is a reflection of the ancient doctrine on the numerical harmony of Universe in modern mathematics and theoretical natural sciences. 2. The Uniqueness of the Hyperbolic Fibonacci Functions Definitions. Let us compare the classic hyperbolic func- tions ee ee sh; ch 22 xx xx x (1) with the symmetric hyperbolic Fibonacci functions, in- C opyright © 2013 SciRes. JAMP 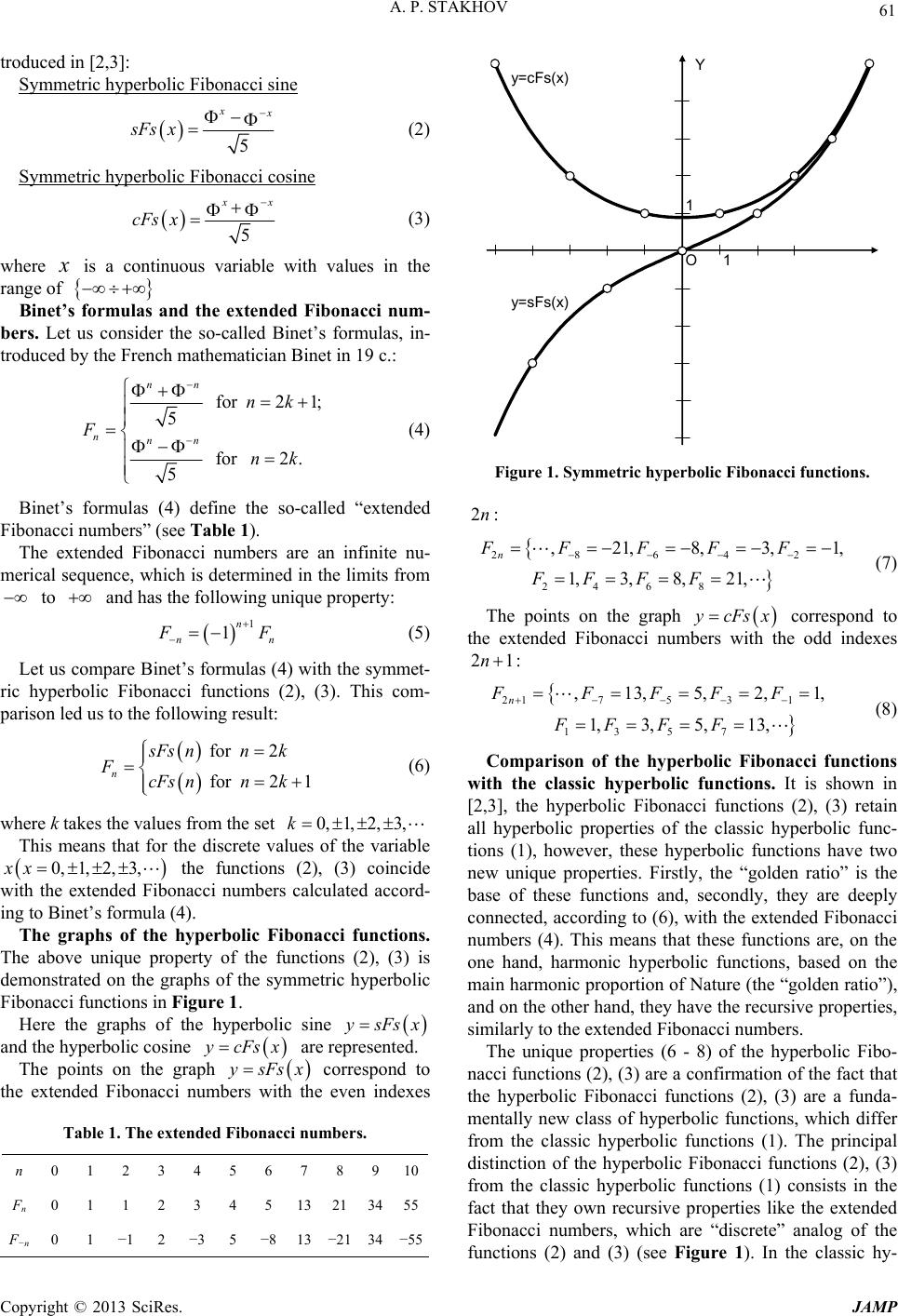 A. P. STAKHOV 61 troduced in [2,3]: Symmetric hyperbolic Fibonacci sine 5 x sFs x (2) Symmetric hyperbolic Fibonacci cosine 5 x cFs x (3) where is a continuous variable with values in the range of Binet’s formulas and the extended Fibonacci num- bers. Let us consider the so-called Binet’s formulas, in- troduced by the French mathematician Binet in 19 c.: for 21; 5 for 2. 5 nn nnn nk F nk (4) Binet’s formulas (4) define the so-called “extended Fibonacci numbers” (see Table 1). The extended Fibonacci numbers are an infinite nu- merical sequence, which is determined in the limits from to and has the following unique property: 1 1n nn F (5) Let us compare Binet’s formulas (4) with the symmet- ric hyperbolic Fibonacci functions (2), (3). This com- parison led us to the following result: for 2 for 21 n Fs nnk FcFs nnk (6) where k takes the values from the set 0, 1, 2, 3,k This means that for the discrete values of the variable the functions (2), (3) coincide with the extended Fibonacci numbers calculated accord- ing to Binet’s formula (4). 0, 1,2, 3,xx The graphs of the hyperbolic Fibonacci functions. The above unique property of the functions (2), (3) is demonstrated on the graphs of the symmetric hyperbolic Fibonacci functions in Figure 1. Here the graphs of the hyperbolic sine sFs x and the hyperbolic cosine cFs x are represented. The points on the graph sFsx correspond to the extended Fibonacci numbers with the even indexes Table 1. The extended Fibonacci numbe r s. n 0 1 2 3 4 5 6 7 8 910 Fn 0 1 1 2 3 4 5 13 21 3455 F−n 0 1 −1 2 −3 5 −8 13 −21 34 −55 Y O1 1 y= sFs (x ) y= cFs (x ) Figure 1. Symmetric hyperbolic Fibonacci functions. 2n: 28642 24 6 8 ,21,8,3, 1, 3, 8, 21, n FFFFF FF F F 1, (7) The points on the graph cFs x correspond to the extended Fibonacci numbers with the odd indexes 21n : 2175 3 1 13 57 ,13,5,2, 1,3,5, 13, n FFFFF FF FF 1, (8) Comparison of the hyperbolic Fibonacci functions with the classic hyperbolic functions. It is shown in [2,3], the hyperbolic Fibonacci functions (2), (3) retain all hyperbolic properties of the classic hyperbolic func- tions (1), however, these hyperbolic functions have two new unique properties. Firstly, the “golden ratio” is the base of these functions and, secondly, they are deeply connected, according to (6), with the extended Fibonacci numbers (4). This means that these functions are, on the one hand, harmonic hyperbolic functions, based on the main harmonic proportion of Nature (the “golden ratio”), and on the other hand, they have the recursive properties, similarly to the extended Fibonacci numbers. The unique properties (6 - 8) of the hyperbolic Fibo- nacci functions (2), (3) are a confirmation of the fact that the hyperbolic Fibonacci functions (2), (3) are a funda- mentally new class of hyperbolic functions, which differ from the classic hyperbolic functions (1). The principal distinction of the hyperbolic Fibonacci functions (2), (3) from the classic hyperbolic functions (1) consists in the fact that they own recursive properties like the extended Fibonacci numbers, which are “discrete” analog of the functions (2) and (3) (see Figure 1). In the classic hy- Copyright © 2013 SciRes. JAMP  A. P. STAKHOV Copyright © 2013 SciRes. JAMP 62 ometry “shows that the “phyllotaxis world “is a hyper- bolic world based on the Fibonacci hyperbolic functions (2), (3). These functions are not “fiction” of mathematic- cians, they are “natural functions” that are used in natural objects during millions, maybe billions of years long before humanity’s appearance. That is why, the hyper- bolic Fibonacci functions [2,3], together with “Bodnar’s geometry” [4,5] can be attributed to the category of fun- damental scientific discoveries, and as such, they are destined to remain in science. The vital importance of the hyperbolic Fibonacci functions (2), (3) for theoretical physics and theoretical natural sciences in the whole fol- lows from these reasoning’s. perbolic functions (1) such relationship with integer nu- merical sequences does not exist. This is the uniqueness of the hyperbolic Fibonacci functions (2), (3) in com- parison to the classic hyperbolic functions (1). This unique property of the new hyperbolic functions (2), (3) has been confirmed recently by the new geometric theory of phyllotaxis, created by the Ukrainian researcher Oleg Bodnar [4,5]. Taking into account the unique properties of the hy- perbolic Fibonacci functions (2), (3), we have every right to say that the hyperbolic geometry, based on the classic hyperbolic functions (1), would have developed differ- ently if the functions (2), (3) were known to Lobachevski. The authority of Nature (Bodnar’s geometry). How- ever, the new geometric theory of phyllotaxis, created by Ukrainian researcher Oleg Bodnar [4,5], is the most powerful confirmation of the uniqueness of the hyper- bolic Fibonacci functions. Bodnar has studied growth’s problem of the phyllotaxis objects (pine cone, pineapple, cactus, sunflower’s head, etc.) and came to the following results.The first key Bodnar’s idea is the following: the transformation of the phyllotaxis lattices in the process of its growth are carried out by means of the hyperbolic rotation, the main geometric transformation of hyperbolic geometry [10]. This transformation is accompanied by the modification of the so-called dynamic symmetry [5], which can be simulated by the sequential passage from the object with the smaller symmetry order to the object with the larger symmetry order. 3. The Uniqueness of the Hyperbolic Fibonacci -Functions Definition. In the works [6,7] the hyperbolic Fibonacci -functions have been introduced: Hyperbolic Fibonacci -sine 2 4 x sF x (9) Hyperbolic Fibonacci -cosine 2 4 x cF x (10) where 1, 2, 3, is a given natural number, is a positive root of the following algebraic equation: However, the use of the hyperbolic Fibonacci func- tions (2), (3) for modelling of the growth of phyllotaxis objects is the most important Bodnar’s idea. Based on these ideas, Oleg Bodnar came to the special class of hyperbolic geometry, this geometry differs substantially from the classic Lobachevski’s geometry or Minkovski’s four-dimensional world, based on the classic hyperbolic functions (1). This difference consists in the fact that the main correlations of this geometry are based on the hy- perbolic Fibonacci functions (2) and (3), which are con- nected with the extended Fibonacci numbers by the sim- ple correlation (6). 210xx (12) The root has the following form: 2 4 2 (13) Note that for the case 1 the formula (13) is re- duced to the classic “golden ratio” 1 15 2 . This means that the formula (13) gives an infinite number of new mathematical constants called “metallic means” or “metallic proportions” by the Argentinean mathematic- cian Vera de Spinadel [11]. The most important, that the unique mathematical property (6) is the main cause of the Fibonacci spirals on the surface of the phyllotaxis objects. If we take in (13) 1,2, 3, 4 , then we get the fol- lowing mathematical constants, having the following names (according to Vera de Spinadel [11]): The importance of the hyperbolic Fibonacci func- tions for theoretical natural sciences. “Bodnar’s ge- It is clear that the number of the “metallic proportions” 12 34 15 golden proportion,1 12silver proportion,2 2 313 bronze proportion,3 25cooper proportion,4. 2 (13) is theoretically infinite. The most significant is the fact that for the case 1 the formula (13) is reduced  A. P. STAKHOV 63 to the classic “golden ratio”. This means that the “metal- lic proportions” like the “golden ratio” may express some new kinds of “mathematical harmony,” which can actu- ally exist in Nature. Gazale’s formulas. The algebraic Equation (12) fol- lows from the recursive relation: 21;00,1FnFn FnFF 1. (14) The recursive relation (14) “generates” an infinite number of the new numerical sequences, because every number “generates” its own numerical sequence (14). The numerical sequences, generated by the recursive relation (14), are called Fibonacci -numbers. For the case 1 we get the classic Fibonacci numbers: 0,1,1,2,3,5,8,13, 21,… and for the case 2 we get Pell numbers: [12]. 0,1,2,5,12,29,70,... The Fibonacci -numbers have many remarkable properties, similar to the properties of the classic Fibo- nacci numbers. It is proved that the Fibonacci -num- bers, as well as the classical Fibonacci numbers, can be “extended” to the negative values of the discrete variable n. Table 2 shows the four “extended” Fibonacci -se- quences, corresponding to the values 1,2,3,4 . It is easy to prove [7] the following generalized Cassini formula for the Fibonacci -numbers: 1 2111 n F nFnFn (15) The formula (14) give the Fibonacci -numbers re- cursively. However, the Fibonacci -numbers can be represented in analytical form through the “metallic pro- portions” (13). Such formulas have been deduced by the French mathematician Midhat Gazale [13]: 2 2 for 21; 4 for 2 4 nn nn nk Fn nk (16) where . 0, 1, 2, 3,k Gazale’s formulas (16) are a generalization of Binet’s formulas (4). A distinctive feature of (16) is that they generate an infinite number of the formulas (16), because each natural number 1,2,3, corresponds to the different Gazale’s formulas (16). In particular, for the case =1 Gazale’s formulas (16) are reduced to Binet’s formulas (4). Connection of the hyperbolic Fibonacci -functions with Gazale’s formulas. It is proved [6,7] that the hy- perbolic Fibonacci -functions (9), (10) coincide with the extended Fibonacci -numbers, given by Gazale’s formulas (16) for the discrete values of the variable Table 2. The “extended” Fibonacci -numbers (λ = 1,2,3,4). n 012 3 4 5 6 7 8 F1(n)011 2 3 4 8 13 21 F1(−n)0 1 −12 3 5 8 13 −21 F1(n)012 5 12 29 70 169408 F2(−n)0 1 −25 −12 29 −70 169−408 F1(n)013 1033 109 360 11893927 F3(−n)0 1 −310−33 109 360 11893927 F1(n)014 1772 305 1292 547323184 F4(−n)0 1 −417−72 305 −1292 5473−23184 0, 1,2, 3,,xn that is, , 2 , 21 sF nnk Fn cF nnk (17) The formula (17) determines the uniqueness of the hyperbolic Fibonacci -functions. They retain all the above unique mathematical properties of the symmetric hyperbolic Fibonacci functions (2), (3). A peculiarity of the hyperbolic Fibonacci -functions (9), (10) consists in the fact that a number of the hyperbolic functions, given by (9), (10), is theoretically infinite because every natural number 1, 2, 3, “generates” its own variant of the hyperbolic functions of the kind (9), (10). 4. A New Approach to Hilbert’s Fourth Problem Hilbert’s Fourth Problem. In the articles [7,8] the ori- ginal solution of Hilbert’s Fourth Problem is described. Hilbert’s Fourth Problem [14,15], which relates to the non-Euclidean geometry, was formulated by David Hil- bert as follows [16]: “The more general question now arises: Whether from other suggestive standpoints geometries may not be de- vised which, with equal right, stand next to Euclidean geometry”. Hilbert’s citation contains the formulation of a very important scientific problem, which is of fundamental interest not only for mathematics, but also for all theo- retical natural sciences: are there non-Euclidean geome- tries, which are close to the Euclidean geometry and are interesting from the “other suggestive standpoints?” If we consider it in the context of theoretical natural sci- ences, then Hilbert’s Fourth Problem is about finding NEW HYPERBOLIC WORLDS OF NATURE, which are close to the Euclidean geometry and reflect some new properties of Nature’s structures and phenomena. Unfortunately, the attempts at solving Hilbert’s Fourth Copyright © 2013 SciRes. JAMP  A. P. STAKHOV 64 Problem, made by German mathematician Herbert Hamel (1901) and later by the Soviet mathematician Alexey Pogorelov [17] (1974), have not lead to signify- cant progress, as described in Wikipedia’s articles “Hil- bert problems” [14] and the “Fourth Hilbert problem” [15]. In these articles, the status of Hilbert’s Fourth Problem is formulated as “too vague to be stated resolved or not” and Pogorelov’s solution [17] even is not men- tioned in [14,15]. About the same point of view on Hil- bert’s Fourth Problem is presented in the remarkable book [18]. So from the standpoint of Wikipedia’s ma- thematical community, the reason why Hilbert’s Fourth Problem is not resolved until now, is own fault of Hilbert, who formulated this problem not clearly enough. From the “game of postulates” to the game of func- tions”. According to [19], the reason lies elsewhere. All the known attempts to solve this problem (Hamel, Po- gorelov) were in the traditional framework; let’s call this the “game of postulates”. This “game” started from the works by Gauss, Lobachevski and Bolyai, when Euclid’s 5th postulate was replaced by the opposite one. This was the most major step in the development of the non- Euclidean geometry, called “Lobachevski’s geometry”. The first non-Euclidean geometry (Lobachevski’s ge- ometry), which changed the traditional geometric ideas, is also known as “hyperbolic geometry”. This name highlights the fact that this geometry is based on the hy- perbolic functions (1). It is important to emphasize that the very name of “hyperbolic geometry” points on another way for the solution of Hilbert’s Fourth Problem: searching for the new classes of “hyperbolic functions,” which can be the basis for other hyperbolic geometries. Every new class of the hyperbolic functions generates its own new variant of the “hyperbolic geometry”. By analogy with the “game of postulates” this way to solve Hilbert’s Fourth Problem can be named the “game of functions” [19]. An original solution of Hilbert’s Fourth Problem. For the first time, this way (the “game of functions”) is used in the works [7,8]. The “game of functions” led in [7,8] to the original solution of Hilbert’s Fourth Problem. The essence of this solution consists in the following. Developing the idea of the metric form of Lobachevski’s plane, known in hyperbolic geometry, the following formula for the metric form of Lobachevski’s plane, based on the hyperbolic Fibonacci -functions (9), (10), has been derived in [7,8]: 22 22 24 dln dd 4 2 usFu v (18) where 2 4 2 is the “metallic proportion” (13) and Fu is the hyperbolic Fibonacci -sine (9). The forms (18) are called the metric -forms of Lobachevski’s plane [7,8]. This formula gives an infinite number of new “Lo- bachevski’s geometries” (“golden,” “silver,” “bronze,” “copper” and so on to infinity) according to the used class of the hyperbolic Fibonacci -functions (9), (10). The formula (18) sets an infinite number of the metric forms of Lobachevski’s plane. This means that there is infinite number of Lobachevski’s geometries, which are based on the “metallic proportions” (13). These new Lo- bachevski’s geometries “with equal right, stand next to Euclidean geometry” (David Hilbert). Thus, the formula (18) can be considered as the partial original solution to Hilbert’s Fourth Problem, based on the “game of func- tions”. There is an infinite number of Lobachevski’s geometries, described by the formula (18), which are close to Euclidean geometry. Every of these geometries manifest itself in Fibonacci -numbers (14), which can appear in physical world similarly to “Bodnar’s hyper- bolic geometry,” where the classic Fibonacci numbers appear at the surface of phyllotaxis objects. A new challenge to theoretical natural sciences. Thus, the main result of the research, described in [7-9], is a proof of the existence of an infinite number of the hyperbolic functions (9), (10), based on the “metallic proportions” (13). In addition, each class of the hyper- bolic functions, corresponding to (9), (10), “generates” for the given 1, 2, 3, its own “hyperbolic geome- try,” which leads to the appearance of the “physical world” with specific properties, which depend on the “metallic proportions” (13). The new geometric theory of phyllotaxis, created by Oleg Bodnar [4,5], is a striking example of this. Bodnar proved that “the world of phyl- lotaxis” is a specific “hyperbolic world,” in which a “hyperbolicity” manifests itself in the “Fibonacci spirals” on the surface of “phyllotaxis objects”. However, the hyperbolic Fibonacci functions (4), (5), which underlie the “hyperbolic world of phyllotaxis,” are a special case of the hyperbolic Fibonacci -functions (9), (10). In this regard, there are all reasons to suppose that other types of hyperbolic functions (9), (10), based on the “metallic proportions,” can be good models for the new “hyperbolic worlds” that can really exist in Nature. Mo- dern science cannot find these special “hyperbolic worlds,” because hyperbolic functions (9), (10) were unknown until now. Basing on the success of “Bodnar’s hyperbolic geometry” [4,5], one can put forward in front to theo- retical physics, chemistry, crystallography, botany, biol- ogy, and other branches of theoretical natural sciences the challenge to search the new “hyperbolic worlds of Nature,” based on other classes of hyperbolic functions (9), (10). In this case, perhaps, the next candidate for the new “hyperbolic world” of Nature (after “Bodnar’s hyper- bolic geometry”) may be, for example, silver hyperbolic Copyright © 2013 SciRes. JAMP  A. P. STAKHOV 65 functions: 22 2 112 12 822 xx x sF x 22 2 112 12 822 xx x cF x which are connected with Pell numbers [12] and are based on the “silver proportion” 212 , connected with the fundamental mathematical constant 2. 5. Back to Pythagoras, Plato and Euclid Platonic Solids and the golden ratio in the history of science. Differentiation of science and its division into separate spheres often do not allow to see a general pic- ture of science and the main trends of its development. However, in science there are research objects, which unite disparate scientific facts into a coherent whole. Platonic solids and the golden ratio belong to the cate- gory of such geometric objects. The ancient Greeks raised them up to the level of the main indicators of the Universe Harmony, and put the problem of harmony in the center of their science. Over the centuries, or even millennia, starting from Pythagoras, Plato, Euclid, these wonderful geometric objects have been the subject of admiration and worship of the brightest minds of mankind (Leonardo da Vinci, Luca Pacholi, Johannes Kepler in the Renaissance, Zeis- ing, Lucas, Binet, Klein in the 19th century, Harold Coxeter, Nikolai Vorobyov, Verner Hoggat in the 20th century). The development of this direction has led to the creation of the “Mathematics of Harmony” as a new in- terdisciplinary direction of modern science. [9]. A role of the Platonic Solids and the Golden Ratio in modern science. The newest discoveries of modern science, based on the Platonic solids, the golden ratio, and the Fibonacci numbers, (fullerenes [20], quasicrys- tals [21], a new geometric theory of phyllotaxis [4,5], the “golden “genomatrices [22], the general theory of hy- perbolic functions [7], the solution of Hilbert’s Fourth Problem [7,8], algorithmic measurement theory and Fi- bonacci codes [23-25], the number systems with irra- tional base [26], the codes of the golden p-proportion [27], the “golden” number theory [28], the ternary mir- ror-symmetrical arithmetic [29], the generalized Fibo- nacci matrices [30], a new coding theory based on the Fibonacci matrices [31], “Proclus hypothesis” and the new view on the history of mathematics, starting from Euclid [32], the “golden” matrices [33], the Fibonacci Lorenz transformations and the “golden” interpretation of the special theory of relativity [34], the “Mathematics of Harmony” [9,35] and so on) create a general picture of the movement of modern science to the “Golden” Sci- entific Revolution what is one of the enduring trends in the development of modern science. The most striking results of modern “mathematics of harmony” [9] are the following: the general theory of hyperbolic functions [7], which lead to the original solu- tion of Hilbert’s Fourth Problem [8] and new geometric theory of phyllotaxis (“Bodnar’s hyperbolic geometry”) [4,5]. “Bodnar’s hyperbolic geometry” is the most con- vincing evidence of the numerical harmony of Nature. The above results relate to Lobachevski’s hyperbolic geometry, which, according to academician Kolmogorov, is opening a new stage in mathematics development. Thanks to these scientific results, the hyperbolic geome- try becomes a “harmonic theory”. Its “hidden” harmony is expressed through the “golden ratio” and “metallic proportions”. 6. Conclusions 1) The hyperbolic Fibonacci functions (2), (3) with the unique mathematical property (6) and the hyperbolic Fibonacci -functions (9), (10) with the unique mathe- matical property (17) are opening a new stage in the de- velopment of the hyperbolic geometry. The peculiarity of this stage consists in the fact that the creation of new hyperbolic geometries is based on the new classes of the harmonic hyperbolic functions (the “game of functions” [19]). If the hyperbolic Fibonacci functions (2), (3) were well-known to Lobachevski, the development of the hy- perbolic geometry has gone in a new direction. 2) Bodnar’s hyperbolic geometry, which is based on the Fibonacci hyperbolic functions (2), (3) and underlies the botanical phenomenon of phyllotaxis, is a brilliant example of the new class of hyperbolic geometry. The authority of Nature is hard to dispute. Bodnar’s hyper- bolic geometry is the most convincing proof of the uniqueness of the hyperbolic Fibonacci functions (2), (3). If we assume that Nature follows to the scenario, sug- gested by Oleg Bodnar [4,5], then we must conclude that Nature is a unique mathematician, who uses the hyper- bolic Fibonacci functions (2), (3) for the creation of life forms. 3) The hyperbolic Fibonacci -functions (9), (10) gen- erate an infinite number of hyperbolic geometries, which are close to Euclidean geometry. This fact is the basis for the original solution of Hilbert’s Fourth Problem, which is described in [7,8]. The original solution of Hilbert’s Fourth Problem puts forward in front of theoretical natu- ral sciences a challenge to search the harmonic hyper- bolic worlds, which can exist in Nature. 4) New approach to hyperbolic geometry is closely re- lated to the Pythagorean doctrine of the numerical har- mony of the Universe and Plato’s cosmology, based on the Platonic Solids. Pythagoras and Plato’s “harmonic ideas” were embodied in Euclid’s Elements. The “har- monic ideas” by Pythagoras, Plato and Euclid are con- Copyright © 2013 SciRes. JAMP  A. P. STAKHOV Copyright © 2013 SciRes. JAMP 66 firmed brilliantly in modern science with the hyperbolic Fibonacci functions, “Bodnar’s hyperbolic geometry” and the original solution of Hilbert’s Fourth Problem. REFERENCES [1] A. P. Stakhov and I. S. Tkachenko, “Fibonacci Hyper- bolic Trigonometry (Russian),” Reports of the Academy of Sciences of Ukraine, Vol. 208, No. 7, 1993, pp. 9-14. [2] A. Stakhov and B. Rozin, “On a New Class of Hyperbolic Functions,” Chaos, Solitons & Fractals, Vol. 23, No. 2, 2004, pp. 379-389. http://dx.doi.org/10.1016/j.chaos.2004.04.022 [3] A. Stakhov and B. Rozin, “The Golden Section, Fibo- nacci series, and New Hyperbolic Models of Nature,” Visual Mathematics, Vol. 8, No. 3, 2006. http://www.mi.sanu.ac.rs/vismath/stakhov/index.html [4] O. Y. Bodnar, “The Golden Section and Non-Euclidean Geometry in Nature and Arts (in Russian),” Svit, Lvov, 1994. [5] O. Y. Bodnar, “Dynamic Symmetry in Nature and Archi- tecture,” Visual Mathematics, Vol. 12, No. 4, 2010. http://www.mi.sanu.ac.rs/vismath/BOD2010/index.html [6] A. P. Stakhov, “Gazale Formulas, a New Class of Hyper- bolic Fibonacci and Lucas Functions and the Improved Method of the ‘Golden’ Cryptography,” Academy of Tri- nitarism, Moscow. http://www.trinitas.ru/rus/doc/0232/004a/023210 63.htm [7] A. P. Stakhov, “On the General Theory of Hyperbolic Functions Based on the Hyperbolic Fibonacci and Lucas Functions and on Hilbert’s Fourth Problem,” Visual Ma- thematics, Vol. 15, No. 1, 2013. http://www.mi.sanu.ac.rs/vismath/2013stakhov/hyp.pdf [8] A. Stakhov and S. Aranson, “Hyperbolic Fibonacci and Lucas Functions, ‘Golden’ Fibonacci Goniometry, Bod- nar’s Geometry, and Hilbert’s Fourth Problem,” Applied Mathematics, Vol. 2, No. 3, 2011, pp. 283-293. [9] A. P. Stakhov, “The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science,” World Scientific, London, 2009. [10] V. G. Shervatov, “Hyperbolic Functions (in Russian),” Fizmatgiz, Moscow, 1958. [11] V. de Spinadel, “The family of Metallic Means,” Visual Mathematics, Vol. 1, No. 3, 1999. http://members.tripod.com/vismath/ [12] Pell Numbers. http://en.wikipedia.org/wiki/Pell_number [13] M. J. Gazale, “Gnomon. From Pharaohs to Fractals,” Princeton University Press, Princeton, 1999. [14] Hilbert’s Problems. http://en.wikipedia.org/wiki/Hilbert’s_problems [15] Hilbert’s Fourth Problem. http://en.wikipedia.org/wiki/Hilbert’s_fourth_problem [16] D. Hilbert, “Mathematical Problems”. http://aleph0.clarku.edu/~djoyce/hilbert/problems.html#pr ob4 [17] A. V. Pogorelov, “Hilbert’s Fourth Problem (in Rus- sian),” Nauka, Moscow, 1974. [18] B. H. Yandell, “The Honours Class—Hilbert’s Problems and Their Solvers,” A K Peters/CRC Press, Natick, 2003. [19] A. P. Stakhov, “Non-Euclidean Geometries. From the ‘Game of Postulates’ to the ‘Game of Function’ (in Rus- sian),” Academy of Trinitarizm, Мoscow. http://www.trinitas.ru/rus/doc/0016/001d/00162125.htm [20] Fullerene. http://en.wikipedia.org/wiki/Fullerene [21] Quasicrystal. http://en.wikipedia.org/wiki/Quasicrystal [22] S. Petoukhov, “Matrix Genetics, Algebra of the Genetic Code, Noise Immunity (in Russian),” Regular and Cha- otic Dynamics, Moscow, 2008. [23] A. P. Stakhov, “Introduction into Algorithmic Measure- ment Theory (in Russian),” Soviet Radio, Moscow, 1977. [24] A. P. Stakhov, “Algorithmic Measurement Theory (News in Life, Science and Technology, Series “Mathematics and Cybernetics) (in Russian),” Knowledge, Moscow, 1979. [25] A. P. Stakhov, “The Golden Section in the Measurement Theory,” Computers & Mathematics with Applications, 1989, Vol. 17, No. 4-6, pp. 613-638. http://dx.doi.org/10.1016/0898-1221(89)90252-6 [26] G. Bergman, “A Number System with an Irrational Base,” Mathematics Magazine, Vol. 31, No. 2, 1957, pp. 98-119. http://dx.doi.org/10.2307/3029218 [27] A. P. Stakhov, “Codes of Golden Proportion (in Rus- sian),” Radio and Communications, Moscow, 1984. [28] A. P. Stakhov, “Generalized Golden Sections and a New Approach to Geometric Definition of a Number,” Ukrain- ian Mathematical Journal, Vol. 56, No. 8, 2004, pp. 1143-1150. http://dx.doi.org/10.1007/s11253-005-0064-3 [29] A. P. Stakhov, “Brousentsov’s Ternary Principle, Berg- man’s Number System and Ternary Mirror-Symmetrical Arithmetic,” The Computer Journal, Vol. 45, No. 2, 2002, pp. 221-236. http://dx.doi.org/10.1093/comjnl/45.2.221 [30] A. P. Stakhov, “A Generalization of the Fibonacci Q-matrix,” Reports of the National Academy of Sciences of Ukraine, Vol. 9, 1999, pp. 46-49. [31] A. Stakhov “Fibonacci Matrices, a Generalization of the ‘Cassini formula,’ and a New Coding Theory,” Chaos, Solitons & Fractals, Vol. 30, No. 1, 2006, pp. 56-66. http://dx.doi.org/10.1016/j.chaos.2005.12.054 [32] A. P. Stakhov, “The Mathematics of Harmony: Clarifying the Origins and Development of Mathematics,” Con- gressus Numerantium, Vol. 193, 2008, pp. 5-48. [33] A. P. Stakhov, “The ‘Golden’ Matrices and a New Kind of Cryptography,” Chaos, Solitons & Fractals, Vol. 32, No. 3, 2007, pp. 1138-1146. http://dx.doi.org/10.1016/j.chaos.2006.03.069 [34] A. Stakhov and S. Aranson, “‘Golden’ Fibonacci Goni- ometry. Fibonacci-Lorentz Transformations, and Hilbert’s Fourth Problem,” Congressus Numerantium, Vol. 193, 2008, pp. 119-156. [35] A. P. Stakhov, “The Golden Section and Modern Har- mony Mathematics,” Applications of Fibonacci Numbers, Vol. 7, 1998, pp. 393-399..
|